Многочлены Чебышева
1. Многочлены
Чебышева
многочлен
чебышев алгебраический
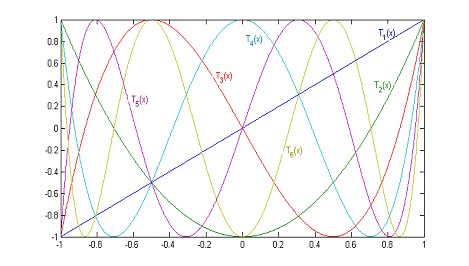
Многочлены Чебышева Тп (х) являются одним из
наиболее замечательных семейств многочленов. Они часто встречаются во многих
областях математики, от теории аппроксимации до теории чисел и топологии трехмерных
многообразий. Многочлены Чебышева - две последовательности ортогональных
многочленов Tn (x) и Un (x), n
= {0,1,2…}, названные в честь Пафнутия Львовича Чебышева. Многочлены Чебышева
играют важную роль в теории приближений, поскольку корни многочленов Чебышева
первого рода используются в качестве узлов в интерполяции алгебраическими
многочленами. Многочлен Чебышева первого рода - Tn (x) - характеризуется как
многочлен степени n со старшим коэффициентом 2n − 1, который меньше всего
отклоняется от нуля на интервале [− 1,1]. Впервые были рассмотрены самим
Чебышевым.
Рассмотрим множество функций
, 
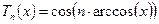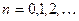, (1)
определенных на отрезке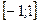 
и имеющих множества значений, принадлежащих отрезку 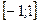. По формуле (1) непосредственно получим:
, 
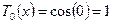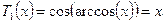. (2)
Покажем, что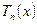 
совпадает с алгебраическим многочленом n-й степени при любом натуральном
значении n. Обозначим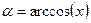 
. Тогда
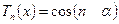. (3)
По известной тригонометрической
формуле
.
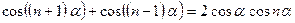Учитывая равенство (3), последнюю
формулу можно записать в виде
.
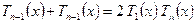Выразим из последней формулы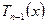 
и, учитывая равенства (2), получим рекуррентную формулу
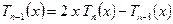. (4)
Вычисляя по этой рекуррентной
формуле функции последовательно при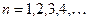 
получим
,
,
,
, …
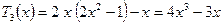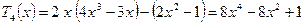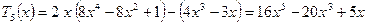Легко увидеть, что, продолжая эти
вычисления, мы на каждом шаге будем получать алгебраические многочлены, причем
степени их каждый раз будет увеличиваться на 1. Таким образом, функция 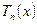совпадает в области определения с алгебраическим многочленом n-й степени при любом натуральном
значении n. Функции 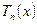получили
название многочленов Чебышева.
Найдем корни многочленов Чебышева.
Для этого решим уравнение
,
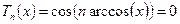при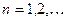 
. Из него непосредственно получим
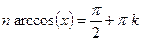. (5)
Здесь величина k может принимать любые целые
значения. Но уравнение (5) будет иметь решения относительно x только при тех значениях k, при которых значение величины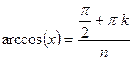 
будет заключено между 0 и 
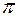. Поэтому уравнение (5) будет иметь решения относительно x только при тех значениях k, при которых
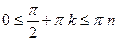. (6)
Условия (6) будут выполняться при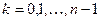 
().
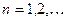Например, при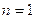 
величина
k может
принять только одно значение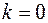 
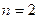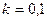. При 
- 
. При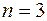 
- 
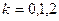и так
далее. Зафиксируем некоторое натуральное значение n. Для каждого из значений 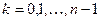уравнение (4.5.5) будет иметь единственное решение:
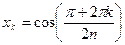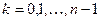, . (7)
Таким образом, функция 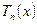(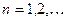) будет
иметь n корней на отрезке 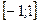и все
эти корни получаются по формулам (7).
Найдем коэффициенты при старшей
степени многочленов Чебышева. Рассматривая формулы для 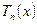при 
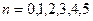легко
заметить, что при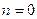 
единственный
коэффициент многочлена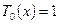 
равен
1, а при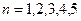 
коэффициенты при старшей степени многочленов 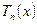равны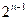 
.
Любую функцию f(x),
определённую на отрезке [-1,1] можно приблизить следующей формулой:
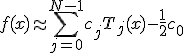
где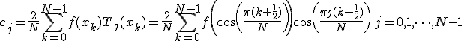 
которая в точности верна для всех x, являющихся корнями многочлена
TN(x).
Преимущество
разложения функции по полиномам Чебышева состоит в том, что при этом абсолютная
ошибка вычислений знакопеременна и распределена более или менее равномерно по
всему интервалу [-1,1]. Наилучшее приближение функции степенным рядом в том
смысле, что максимальная ошибка при этом приближении минимальна, называется
чебышевским приближением. Это приближение не совпадает с разложением по
Чебышевским многочленам, но обычно его поиски, которые требуют больших
вычислительных затрат, не оправдывают уменьшение ошибки. Т.е. приближение
Чебышевскими многочленами практически совпадает с чебышевским приближением и
гораздо более привлекательно в вычислительном плане.
. Программа численного расчета решения
задачи
Приблизить функцию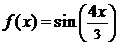 
многочленом
Чебышева.
Program
Project2;
var
n, i, j, c: integer;, b, l, m:
real;: array [0..100] of real;_X,f,f1,g: array [1..100] of real;shag (a,b:
real; c: integer): real;:=(b-a)/c;;
BEGIN
write ('Введите
левую границу: ');
readln (a);
write ('Введите
правую границу: ');
readln (b);
write ('Число
разбиений: ');
readln (c);:=a;i:=1 to c+1 do_X
[i]:= m;:=m + shag (a,b,c);;i:=1 to c+1 do(Arr_X [i]: 8: 2,' ');;
writeln
(Значение функции в точках: ');
for i:=1 to c+1 do
begin[i]:=sin((4*Arr_X[i])/3);;i:=1 to c+1 do(f[i]: 8: 2,' ');;('Введите
n: ');(n);n>1 theni:=1 to c+1 doj:=2 to n do[0]:=1;[1]:=Arr_X
[i];[j]:=2*Arr_X[i] *T[j-1] - T[j-2];;('x=',Arr_X [i]: 8: 2,'
');('T[',i,']=',T[j]:8:2,' ');
{writeln('T [',j,'] =',T [n]: 8: 2);
};;n=0 theni:=1 to c+1 do('x=',Arr_X [i]: 8: 2,' ');('T[',n,']=',1);;n=1
theni:=1 to c+1 do('x=',Arr_X [i]: 8: 2,' ');('T[',n,']=',Arr_X [i]: 8: 2);;
writeln('Коэффициенты
приближенной функции:');
g[1]:=-0.02;i:=1 to c+1 do begin
g[i]:=(2/n)*f[i]*T[i];
f1[i]:=g[i]*T[i]-g[1]/2;
write('f1[',i,']=',f1[i]: 6: 5,' ');
end;
end.
Протокол:
Введите левую границу: -1
Введите правую границу: 1
Число разбиений: 5
-1.00 -0.60 -0.20 0.20 0.60 1.00
Значение функции в точках:
-0.97 -0.72 -0.26 0.26 0.72 0.97
Введите n: 7
x= -1.00 T[1]= -1.00 = -0.60 T[2]=
-0.98 = -0.20 T[3]= 0.99 = 0.20 T[4]= -0.99 = 0.60 T[5]= 0.98
x= 1.00 T[6]= 1.00
Коэффициенты приближенной функции:[1]=-0.13885
f1[2]=-0.06611 f1[3]=0.06356 f1[4]=0.21414 f1[5]=0.34381 f1[6]=0.41654
. Тестовые примеры
Пример 1. Приблизить функцию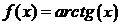 
Введите левую границу: -1
Введите правую границу: 1
Число разбиений: 7
.00 -0.71 -0.43 -0.14 0.14 0.43 0.71 1.00
Значение функции в точках:
.79 -0.62 -0.40 -0.14 0.14 0.40 0.62 0.79
Введите n: 7= -1.00 T[1]= -1.00 = -0.71 T[2]=
-0.65
x= -0.43 T[3]=
0.04
x= -0.14 T[4]=
0.84
x= 0.14 T[5]=
-0.84
x= 0.43 T[6]=
-0.04
x= 0.71 T[7]=
0.65 = 1.00 T[8]= 1.00
Коэффициенты приближенной функции:[1]=-0.11220
f1[2]=-0.06501 f1[3]=-0.00348 f1[4]=0.07166 f1[5]=0.15274 f1[6]=0.22788
f1[7]=0.28941 f1[8]=0.11220
Пример 2. Приблизить функцию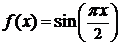 
Протокол:
Введите левую границу: -1
Введите правую границу: 1
Число разбиений: 7
-1.00 -0.71 -0.43 -0.14 0.14 0.43 0.71 1.00
Значение функции в точках:
.00 -0.90 -0.62 -0.22 0.22 0.62 0.90 1.00
Введите n: 9= -1.00 T[1]= -1.00 = -0.71 T[2]=
-0.77
x= -0.43 T[3]=
0.75
x= -0.14 T[4]=
-0.96
x= 0.14 T[5]=
0.96
x= 0.43 T[6]=
-0.75
x= 0.71 T[7]=
0.77 = 1.00 T[8]= 1.00
Коэффициенты приближенной функции:[1]=-0.11111
f1[2]=-0.08905 f1[3]=-0.02738 f1[4]=0.06169 f1[5]=0.16054 f1[6]=0.24961
f1[7]=0.31127 f1[8]=0.33333
Анализ результата
В вычислительной практике зачастую
гораздо важнее получить приближение с заданной точностью. А для этого
использовать наилучшие приближения не обязательно. Поэтому многочлены
наилучшего равномерного приближения до настоящего времени не применяются так
широко как интерполяция или метод наименьших квадратов.
Список литературы
многочлен чебышев алгебраический
1. П.Л. Чебышев
"Избранные труды". - том 2, - М.: издательство академии наук СССР,
1955. - 930 с.
2. Чебышев П.Л.,
Прудников В.Е. «Научное наследие П.Л. Чебышева. Математика». - М.: Выпуск
1,1945. - 174 с.
. С.Л. Табачников
«Многочлены» / С. Л. Табачников . - 2-е изд., пересмотр. - М. : ФАЗИС, 2000 . -
200 с.
. А.А. Самарский,
А.В. Гулин "Численные методы".- М.: "Наука", 1989, - 424 с.
. Вержбицкий В.М.
«Численные методы». - М.: "Высшая школа", 2001. - 192 с.
. Прасолов В.В.
«Многочлены». - М.: «Просвещение», 2000. - 336 с.