Многочлены Чебышева и их основные свойства
МИНистерство ОБРазования и НАУКИ РОССИи
Федеральное
государственное бюджетное образовательное учреждение
высшего
профессионального образования
«БРЯНСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ АКАДЕМИКА И.Г. ПЕТРОВСКОГО»
Физико-математический
факультет
Кафедра алгебры
и геометрии
Курсовая
работа
«Многочлены
Чебышева и их основные свойства»
Выполнила:
студентка
3 курса ОЗО ФМФ
направления
«Педагогическое
образование»
профиля
«Математика»
Ю.М.
Симонаева
Научный
руководитель:
Кандидат
физико-математических наук
М.М.
Сорокина
Брянск 2014
Содержание
Введение
Глава 1. Обозначения, определения и
известные результаты, используемые в работе
Глава 2. Основы теории многочленов
от одной переменной
Глава 3. Многочлены Чебышева и их
основные свойства
3.1 Определение и простейшие
свойства многочленов Чебышева
3.2 Основные теоремы о многочленах
Чебышева
Заключение
Список используемой литературы
Введение
Теория многочленов представляет один из
центральных разделов современной алгебры. Понятие многочлена от одной переменной
возникло в связи с задачей решения алгебраических уравнений от одной
переменной, которой занимались уже в глубокой древности. В XVI веке
итальянскими математиками были найдены формулы для решения уравнений третьей и
четвертой степени. Позднее Н.Абель и П.Руффини доказали, что, начиная с пятой
степени, общей формулы, использующей, кроме сложения и умножения, лишь
извлечение корней, не существует, а Э.Галуа открыл закономерности поведения
корней, приложимые к каждому конкретному уравнению.
Параллельно с этим К.Гаусс доказал основную
теорему алгебры, утверждающую, что всякий многочлен (коэффициенты многочлена
могут быть не только вещественными, но и комплексными числами) имеет хотя бы
один корень (возможно, являющийся не вещественным, а комплексным числом). В
дальнейшем многие ученые занимались изучением многочленов. Я.Бернулли, Э.Безу,
У.Горнер, Ж.Лагранж, П.Чебышев, С.Эйзенштейн, Д.Гильберт и многие другие
известные математики открыли немало нового и удивительного о многочленах,
ставшего впоследствии привычным и обыкновенным.
В XX веке роль многочленов стала меняться.
Буквы, входящие в многочлен, стали играть роль символов, не связанную с их
конкретными значениями. Современная математика изучает и использует в общем
случае многочлены от одной переменной, у которых коэффициенты а0, а1,
…, аn являются объектами произвольной природы, а не только числами.
Самые разные области математики и ее приложений стали использовать символьное
исчисление многочленов, не зависящее от теории функций (математическая логика,
топология, теория информации, дискретная и компьютерная математика и т.д.).
С изучением многочленов связан целый
ряд преобразований в математике: введение в рассмотрение нуля
<#"882806.files/image001.gif"> называется
правило или закон, по которому любым двум элементам из 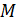 ,
необязательно различным, взятым в указанном порядке, ставится в соответствие
единственный элемент из
,
необязательно различным, взятым в указанном порядке, ставится в соответствие
единственный элемент из 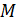 .
.
Определение бинарной алгебраической операции
можно сформулировать также следующим образом.
Определение 1′. Бинарной алгебраической
операцией на множестве 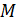 называется
отображение
называется
отображение 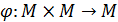 . Вместо
. Вместо 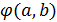 пишут
пишут
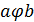 .
Бинарные алгебраические операции в общем виде обозначают символами
.
Бинарные алгебраические операции в общем виде обозначают символами  и
другими.
и
другими.
Определение 2. Непустое множество  с
определённой на нём бинарной алгебраической операцией
с
определённой на нём бинарной алгебраической операцией 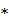 называется
группой, если выполняются следующие аксиомы (аксиомы группы):
называется
группой, если выполняются следующие аксиомы (аксиомы группы):
) операция 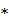 ассоциативна на
ассоциативна на 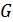 ,
т.е.
,
т.е.
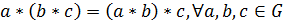 ;
;
) в 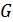 существует
нейтральный элемент относительно операции
существует
нейтральный элемент относительно операции 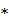 , т.е.
, т.е.
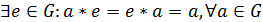 ;
;
) для каждого элемента из 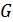 в
в
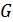 существует
симметричный ему элемент относительно операции
существует
симметричный ему элемент относительно операции 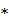 ,
т. е.
,
т. е. 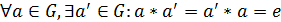 .
.
Определение 3. Группа 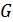 относительно
операции
относительно
операции 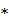 называется
абелевой, если операция
называется
абелевой, если операция 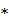 коммутативна на
коммутативна на 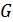 ,
т. е.
,
т. е. 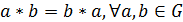 .
.
Определение 4. Группа относительно операции
сложения называется аддитивной.
Определение 5. Группа относительно операции
умножения называется мультипликативной.
Определение 6. Непустое множество  с
определенными на нем бинарными алгебраическими операциями сложения и умножения
называется кольцом, если выполняются следующие аксиомы (аксиомы кольца):
с
определенными на нем бинарными алгебраическими операциями сложения и умножения
называется кольцом, если выполняются следующие аксиомы (аксиомы кольца):
.  -
аддитивная абелева группа, т.е.
-
аддитивная абелева группа, т.е.
а) ассоциативность сложения на 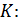
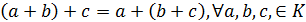 ;
;
б) 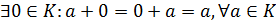 ;
;
в) 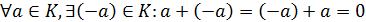 ;
;
г) коммутативность сложения на
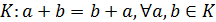 .
.
. В  выполняются
дистрибутивные законы, т.е.
выполняются
дистрибутивные законы, т.е. 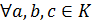
а) 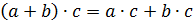 -
правый дистрибутивный закон,
-
правый дистрибутивный закон,
б) 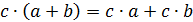 -
левый дистрибутивный закон.
-
левый дистрибутивный закон.
Определение 7. Кольцо  называется
ассоциативным, если операция умножения ассоциативна на
называется
ассоциативным, если операция умножения ассоциативна на  ,
т.е.
,
т.е. 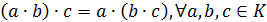 .
.
Определение 8. Кольцо  называется
коммутативным, если операция умножения коммутативна на
называется
коммутативным, если операция умножения коммутативна на  ,
т.е.
,
т.е. 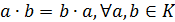 .
.
Определение 9. Кольцо  называется
ассоциативно-коммутатитвным, если
называется
ассоциативно-коммутатитвным, если  -
ассоциативное кольцо и коммутативное кольцо.
-
ассоциативное кольцо и коммутативное кольцо.
Определение 10. Кольцо  называется
кольцом с единицей, если в
называется
кольцом с единицей, если в  существует
единичный элемент, т.е.
существует
единичный элемент, т.е. 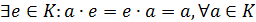 .
.
Определение 11. Элементы 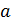 и
и
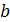 кольца
кольца
 называются
делителями нуля, если
называются
делителями нуля, если 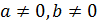 , но
, но 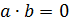 .
.
Определение 12. Ассоциативно-коммутативное
кольцо с единицей без делителей нуля называется областью целостности.
Определение 13. Пусть  -
ассоциативно-коммутативное кольцо с единицей. Элементы
-
ассоциативно-коммутативное кольцо с единицей. Элементы 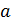 и
и
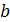 кольца
кольца
 называются
ассоциированными в
называются
ассоциированными в  и обозначаются
и обозначаются 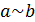 ,
если
,
если 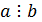 и
и
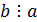 .
.
Определение 14. Пусть  -
ассоциативно-коммутативное кольцо с единицей. Элемент
-
ассоциативно-коммутативное кольцо с единицей. Элемент 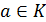 называется
обратимым в кольце
называется
обратимым в кольце  , если в кольце
, если в кольце  найдется
обратный к нему элемент, т.е. такой элемент
найдется
обратный к нему элемент, т.е. такой элемент 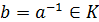 ,
что
,
что 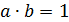 .
Иначе, элемент
.
Иначе, элемент 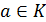 называется
необратимым элементом
называется
необратимым элементом  .
.
Определение 15. Полем называется
ассоциативно-коммутативное кольцо с единицей, в котором любой ненулевой элемент
обратим.
Определение 15'. Непустое множество 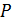 с
определёнными на нём бинарными алгебраическими операциями
с
определёнными на нём бинарными алгебраическими операциями  и
и
 называется
полем, если выполняются следующие аксиомы (аксиомы поля):
называется
полем, если выполняются следующие аксиомы (аксиомы поля):
. 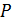 -
аддитивная абелева группа, т.е.
-
аддитивная абелева группа, т.е.
а) ассоциативность операции 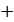 ,
т.е.
,
т.е.
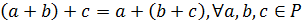 ;
;
б) 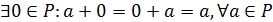 ;
;
в) 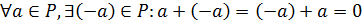 ;
;
г) коммутативность операции 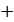 ,
т.е.
,
т.е. 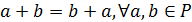 .
.
а) 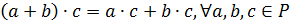 -
правый дистрибутивный закон;
-
правый дистрибутивный закон;
б) 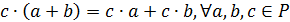 -
левый дистрибутивный закон.
-
левый дистрибутивный закон.
. 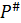 -
мультипликативная абелева группа, т.е.
-
мультипликативная абелева группа, т.е.
а) ассоциативность операции 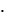 ,
т.е.
,
т.е.
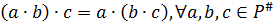 ;
;
б) 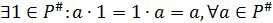 ;
;
в) 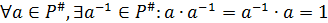 ;
;
г) коммутативность операции 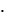 ,
т.е.
,
т.е. 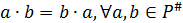 .
.
Определение 16. Множество 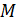 называется
числовым, если
называется
числовым, если  .
.
Определение 17. Поле  называется
числовым, если оно является числовым множеством, т.е.
называется
числовым, если оно является числовым множеством, т.е. 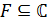 .
.
Глава 2. Основы теории многочленов от одной переменной
Определение 1. Пусть  и
и
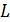 -
ассоциативно-коммутативные кольца с единицами. Кольцо
-
ассоциативно-коммутативные кольца с единицами. Кольцо 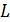 называется
простым расширением кольца
называется
простым расширением кольца  с помощью элемента
с помощью элемента
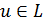 ,
если выполняются следующие условия:
,
если выполняются следующие условия:
)  -
подкольцо кольца
-
подкольцо кольца 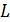 ;
;
) 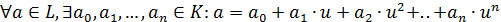 ,
и записывают
,
и записывают 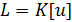 .
.
Определение 2. Простое расширение 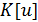 называется
простым трансцендентным расширением кольца
называется
простым трансцендентным расширением кольца  ,
если выполняется следующее условие:
,
если выполняется следующее условие: 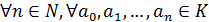 из
равенства
из
равенства 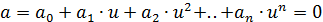 следует, что
следует, что 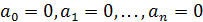 .
Элемент
.
Элемент 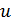 в
этом случае называется трансцендентным элементом над
в
этом случае называется трансцендентным элементом над  (относительно
(относительно
 ).
).
Лемма 1. Пусть 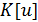 -
простое трансцендентное расширение ассоциативно-коммутативного кольца
-
простое трансцендентное расширение ассоциативно-коммутативного кольца  с
единицей,
с
единицей,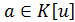 .
Если
.
Если
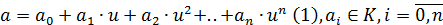 и
и
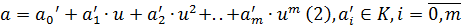 ,
,
то 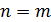 и
и
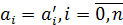 .
.
Лемма 2. Пусть 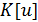 и
и
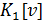 -
простые трансцендентные расширения ассоциативно-коммутативных колец
-
простые трансцендентные расширения ассоциативно-коммутативных колец  и
и
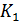 с
единицами. Если
с
единицами. Если 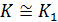 и
и  -
изоморфизм
-
изоморфизм  на
на 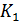 ,
то
,
то 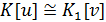 ,
причем существует единственный изоморфизм
,
причем существует единственный изоморфизм 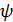 кольца
кольца
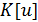 на
на
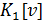 ,
который переводит элемент
,
который переводит элемент 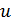 в элемент
в элемент 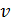 (т.е.
(т.е.
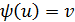 )
и продолжает изоморфизм
)
и продолжает изоморфизм  .
.
Следствие 2.1. Пусть 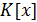 и
и
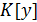 -
простое трансцендентное расширение ассоциативно-коммутативного кольца
-
простое трансцендентное расширение ассоциативно-коммутативного кольца  с
единицей. Тогда
с
единицей. Тогда 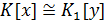 .
.
Лемма 3. Пусть  -
ассоциативно-коммутативное кольцо с единицей,
-
ассоциативно-коммутативное кольцо с единицей, 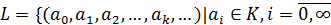 и
лишь конечное число
и
лишь конечное число 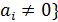 . Тогда множество
. Тогда множество 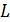 является
ассоциативно-коммутативным кольцом с единицей
является
ассоциативно-коммутативным кольцом с единицей 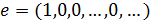 относительно
операций, заданных по правилу:
относительно
операций, заданных по правилу:
1) 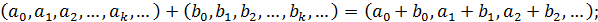
2) 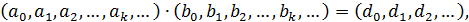 где
где
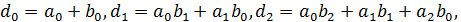 и т.д.,
и т.д.,
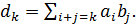
Теорема 1. Пусть  -
ассоциативно-коммутативное кольцо с единицей. Тогда для
-
ассоциативно-коммутативное кольцо с единицей. Тогда для  существуют
простые трансцендентные расширения, причём любые 2 из них изоморфны.
существуют
простые трансцендентные расширения, причём любые 2 из них изоморфны.
Замечание. Кольцо 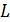 ,
построенное в лемме 3, и являющееся простым трансцендентным расширением кольца
,
построенное в лемме 3, и являющееся простым трансцендентным расширением кольца  согласно
теореме 1, называется кольцом многочленов (полиномов) от одной переменной
(неизвестной)
согласно
теореме 1, называется кольцом многочленов (полиномов) от одной переменной
(неизвестной) 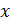 над кольцом
над кольцом  и
обозначается
и
обозначается 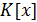 . Элементы кольца
. Элементы кольца 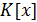 называются
многочленами (полиномами) над кольцом
называются
многочленами (полиномами) над кольцом  от
переменной
от
переменной 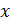 .
.
Пусть, например, 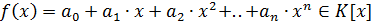 ,
причём
,
причём 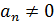 (ввиду
теоремы 1). Тогда
(ввиду
теоремы 1). Тогда 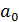 - свободный или
постоянный член многочлена
- свободный или
постоянный член многочлена  ,
, 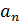 -
старший коэффициент многочлена
-
старший коэффициент многочлена  .
.
Определение 3. Пусть  -
ассоциативно-коммутативное кольцо с единицей,
-
ассоциативно-коммутативное кольцо с единицей,  Число
Число
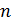 называется
степенью многочлена
называется
степенью многочлена 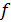 и обозначается
и обозначается 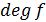 ,
т.е.
,
т.е. 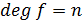 (степень
многочлена - это степень переменной при старшем коэффициенте).
(степень
многочлена - это степень переменной при старшем коэффициенте).
Определение 4. Нулевым многочленом называется
многочлен, все коэффициенты которого равны 0, и обозначается 0. По определению
полагают, что степень нулевого многочлена равна 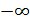 ,
т.е.
,
т.е. 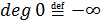 .
Таким образом, если
.
Таким образом, если  , то
, то 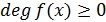 (
(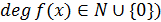 .
.
Теорема 2. Пусть  -
ненулевое ассоциативно-коммутативное кольцо с единицей,
-
ненулевое ассоциативно-коммутативное кольцо с единицей, 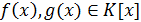 .
Тогда:
.
Тогда:
) 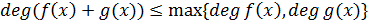 ;
;
) 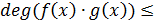
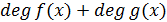 .
.
Следствие 2.1. Пусть  -
область целостности. Тогда
-
область целостности. Тогда 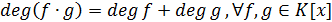 .
.
Теорема 3. Если  -
область целостности, то
-
область целостности, то 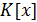 - область
целостности.
- область
целостности.
Теорема 4. Пусть  -
область целостности. Тогда для
-
область целостности. Тогда для 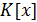 существует поле
частных.
существует поле
частных.
Определение 5. Пусть  -
ассоциативно-коммутативное кольцо с единицей. Говорят, что многочлен
-
ассоциативно-коммутативное кольцо с единицей. Говорят, что многочлен 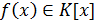 делится
на многочлен
делится
на многочлен 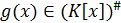 , если
, если 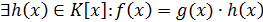 и
обозначается
и
обозначается 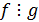 или
или 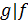 .
.
Простейшие свойства отношения делимости в 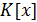 :
:
1) рефлексивность 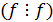 ;
; 
) транзитивность 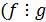 и
и 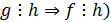 ;
;
)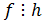 и
и 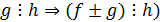 ;
;
) 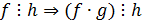 ;
;
)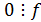 .
.
Определение 6. Пусть  -
ассоциативно-коммутативное кольцо с единицей,
-
ассоциативно-коммутативное кольцо с единицей, 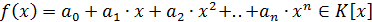 (т.е.
(т.е. 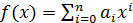 ),
), 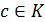 . Элемент
. Элемент 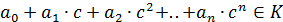 называется
значением многочлена
называется
значением многочлена  в точке
в точке 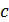 (на
элементе
(на
элементе 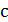 ) и обозначается
) и обозначается
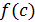 , то есть
, то есть 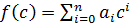 .
.
Теорема 5 (теорема Безу). Пусть  -
ассоциативно-коммутативное кольцо с единицей,
-
ассоциативно-коммутативное кольцо с единицей, 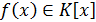 ,
, 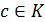 . Тогда существует
. Тогда существует 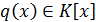 такой, что
такой, что 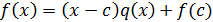 .
.
Доказательство. Пусть 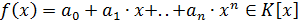 . Тогда
. Тогда 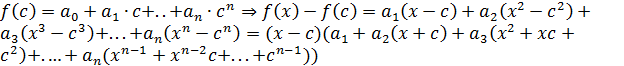 .
.
Таким образом, 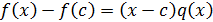 , где
, где 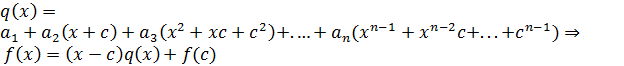 . Теорема
доказана.
. Теорема
доказана.
Определение 7. Пусть  -
ассоциативно-коммутативное кольцо с единицей,
-
ассоциативно-коммутативное кольцо с единицей, 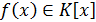 . Элемент
. Элемент 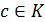 называется
корнем многочлена
называется
корнем многочлена  , если
, если 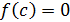 .
.
Следствие 5.1. Пусть  -
ассоциативно-коммутативное кольцо с единицей,
-
ассоциативно-коммутативное кольцо с единицей, 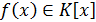 ,
, 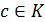 . Тогда
. Тогда 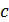 - корень
- корень 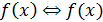 делится на
делится на 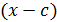 .
.
Следствие 5.2. При делении
многочлена  на
на 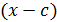 получается
остаток
получается
остаток 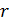 , равный
, равный 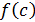 .
.
Теорема 6. Пусть  - область
целостности,
- область
целостности, 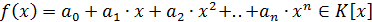 ,
, 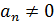 . Тогда
многочлен
. Тогда
многочлен  имеет не
более
имеет не
более 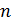 попарно
различных корней. Другими словами, любой ненулевой многочлен -й степени над
областью целостности имеет не более
попарно
различных корней. Другими словами, любой ненулевой многочлен -й степени над
областью целостности имеет не более 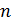 попарно различных корней.
попарно различных корней.
Доказательство. Доказательство
проведём методом математической индукции по параметру 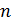 .
.
) Пусть 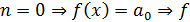 не имеет
корней, т.е.
не имеет
корней, т.е. 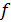 имеет нуль
корней и значит
имеет нуль
корней и значит 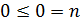 - верно.
- верно.
) Пусть 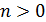 .
Предположим, что утверждение верно при
.
Предположим, что утверждение верно при 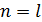 .
.
) Докажем, что утверждение верно при
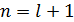 :
: 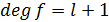 . Если
. Если 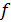 не имеет
корней, то число корней равно
не имеет
корней, то число корней равно 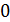 и
и 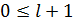 - верно. Пусть
- верно. Пусть 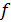 имеет хотя
бы один корень и
имеет хотя
бы один корень и 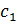 - корень
- корень  такой, что
такой, что 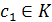 . Тогда по
теореме Безу
. Тогда по
теореме Безу 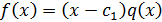 , где
, где 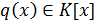 , причём
, причём 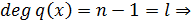 по пункту
2)
по пункту
2) 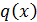 имеет не
более
имеет не
более 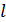 попарно
различных корней.
попарно
различных корней.
Покажем, что все корни многочлена  , отличные
от
, отличные
от 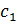 , являются
также корнями многочлена
, являются
также корнями многочлена 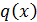 . Пусть
. Пусть 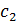 - корень
- корень  ,
, 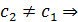
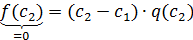 , т.е.
, т.е. 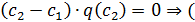 так как
так как  - область
целостности)
- область
целостности) 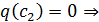
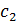 - корень
- корень 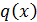 . Таким
образом, многочлен
. Таким
образом, многочлен  имеет
корень
имеет
корень 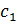 , а все
остальные корни многочлена
, а все
остальные корни многочлена 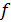 являются также корнями многочлена
являются также корнями многочлена 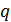 . Так как
. Так как 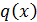 имеет не
более
имеет не
более 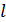 попарно
различных корней, то многочлен
попарно
различных корней, то многочлен 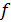 имеет не более, чем
имеет не более, чем 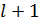 попарно
различных корней.
попарно
различных корней.
Из 1)-3) по методу математической
индукции следует, что утверждение верно для любого 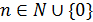 . Теорема
доказана.
. Теорема
доказана.
Следствие 6.1. Пусть  - область
целостности,
- область
целостности, 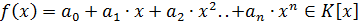 . Если
многочлен
. Если
многочлен  имеет более
имеет более
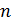 попарно
различных корней, то
попарно
различных корней, то  является
нулевым многочленом.
является
нулевым многочленом.
Определение 8. Пусть 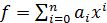 ,
, 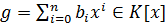 , где
, где  -
ассоциативно-коммутативное кольцо с единицей. Многочлены
-
ассоциативно-коммутативное кольцо с единицей. Многочлены 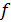 и
и 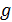 называются
алгебраически равными, если
называются
алгебраически равными, если 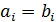 ,
, 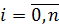 .
.
Определение 9. Многочлены 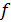 и
и 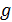 из
из 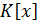 называются
функционально равными, если
называются
функционально равными, если 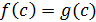 ,
, 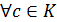 , т.е. значения многочленов
, т.е. значения многочленов 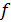 и
и 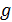 в любой
точке кольца
в любой
точке кольца  совпадают.
совпадают.
Теорема 7. Пусть  -
бесконечная область целостности,
-
бесконечная область целостности,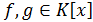 . Многочлены
. Многочлены 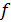 и
и 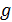 алгебраически
равны
алгебраически
равны 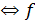 и
и 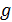 равны
функционально.
равны
функционально.
Теорема 8. Пусть  - поле,
- поле, 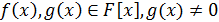 . Тогда
существуют единственные многочлены
. Тогда
существуют единственные многочлены 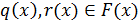 такие, что
такие, что 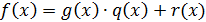 , причем
, причем 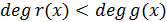 .
.
Определение 10. Пусть  - поле,
- поле, 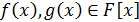 . Многочлен
. Многочлен 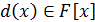 называется
наибольшим общим делителем многочленов
называется
наибольшим общим делителем многочленов  и
и 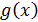 (или коротко, НОД
(или коротко, НОД  и
и 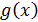 ) и
обозначается
) и
обозначается 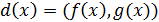 , если
выполняются два условия:
, если
выполняются два условия:
) 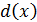 - общий делитель многочленов
- общий делитель многочленов  и
и 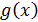 , т.е.
, т.е. 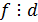 и
и 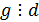 ;
;
) 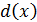 делится на любой общий делитель
многочленов
делится на любой общий делитель
многочленов  и
и 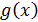 , т.е. если
, т.е. если 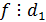 и
и 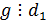 , то
, то 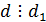 .
.
Лемма 4. Пусть  - поле,
- поле, 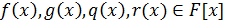 ,
, 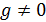 и
и 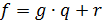 . Тогда НОД
многочленов
. Тогда НОД
многочленов 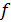 и
и 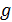 и НОД
многочленов
и НОД
многочленов 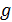 и
и 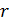 ассоциированы,
т.е.
ассоциированы,
т.е. 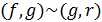 .
.
Лемма 5. НОД двух многочленов
определяется однозначно с точностью до ассоциированности.
Определение 11. Пусть  - поле,
- поле, 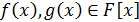 . Многочлен
. Многочлен 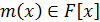 называется
наименьшим общим кратным многочленов
называется
наименьшим общим кратным многочленов  и
и 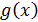 (или коротко, НОК
(или коротко, НОК  и
и 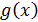 ) и
обозначается
) и
обозначается 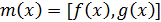 , если
выполняются два условия:
, если
выполняются два условия:
) 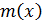 - общее кратное многочленов
- общее кратное многочленов  и
и 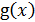 , т.е.
, т.е. 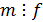 и
и 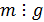 ;
;
Лемма 6. НОК двух многочленов
определяется однозначно с точностью до ассоциированности.
Пусть  - поле,
- поле, 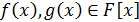 . Для
нахождения НОК многочленов
. Для
нахождения НОК многочленов  и
и 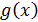 применяется следующая формула:
применяется следующая формула: 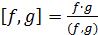 .
.
Теорема 9 (теорема о линейном
представлении НОД). Пусть  - поле,
- поле, 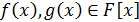 ,
, 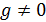 ,
, 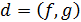 . Тогда
. Тогда 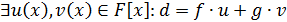 .
.
Определение 12. Пусть  - поле,
- поле, 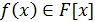 ,
, 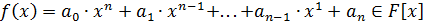 . Многочлен
вида
. Многочлен
вида 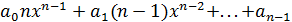 называется
формальной производной многочлена
называется
формальной производной многочлена  и обозначается
и обозначается 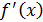 .
.
Нетрудно проверить, что формальная
производная многочлена удовлетворяет следующим свойствам:
) 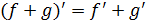 ;
;
) 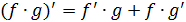 ;
;
) 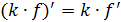 ;
;
) 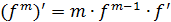 .
.
Определение 13. Многочлен  положительной
степени над полем
положительной
степени над полем  называется
неприводимым над
называется
неприводимым над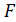 , если он не
допускает представления в виде произведения двух многочленов над полем
, если он не
допускает представления в виде произведения двух многочленов над полем  меньшей
степени.
меньшей
степени.
Определение 14. Многочлен  положительной
степени над полем
положительной
степени над полем  называется
приводимым над
называется
приводимым над  , если он
допускает представление в виде произведения двух многочленов над полем
, если он
допускает представление в виде произведения двух многочленов над полем  меньшей
степени.
меньшей
степени.
Лемма 7. Многочлен первой степени
неприводим над любым полем.
Лемма 8. Пусть  - поле,
- поле, 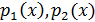 -
неприводимые над
-
неприводимые над  многочлены.
Если
многочлены.
Если 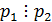 , то
, то 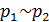 .
.
Замечание 1. Пусть  - поле.
Тогда
- поле.
Тогда  - область
целостности
- область
целостности 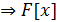 - область
целостности
- область
целостности 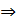 все
элементы области целостности
все
элементы области целостности 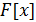 подразделяются на 4 вида:
подразделяются на 4 вида:
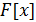 =
= 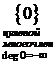
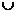
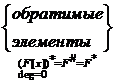
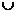

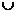

Замечание 2. Поскольку НОД и НОК
многочленов определяются однозначно с точностью до ассоциированности, то
многочлены 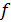 и
и 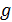 являются
взаимно простыми
являются
взаимно простыми 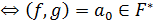 .
.
Замечание 3. Пусть 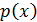 -
неприводимый над
-
неприводимый над  многочлен.
Если
многочлен.
Если 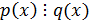 , то либо
, то либо 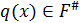 , либо
, либо 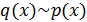 .
.
Лемма 9. Пусть  - поле,
- поле, 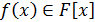 ,
, 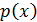 -
неприводимый над
-
неприводимый над  многочлен. f
многочлен. f 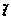 p
p 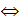
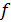 и
и 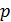 взаимно
просты.
взаимно
просты.
Лемма 10. Пусть  - поле,
- поле, 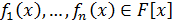 ,
, 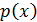 -
неприводимый над
-
неприводимый над  многочлен.
Если
многочлен.
Если 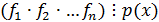 , то хотя бы
, то хотя бы
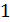 из
множителей
из
множителей 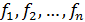 делится на
делится на 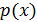 , то есть
, то есть 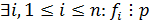 .
.
Теорема 10. (Основная теорема о
многочленах). Любой многочлен положительной степени над полем  допускает
представление в виде произведения неприводимых над
допускает
представление в виде произведения неприводимых над  многочленов,
причем такое представление единственно с точностью до порядка следования
множителей и ассоциированности.
многочленов,
причем такое представление единственно с точностью до порядка следования
множителей и ассоциированности.
Доказательство. 1) Существование. Пусть
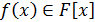 и
и 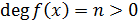 .
Доказательство проведем методом математической индукции по параметру
.
Доказательство проведем методом математической индукции по параметру 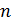 .
.
. Пусть 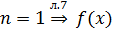 неприводим
над
неприводим
над 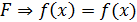 - искомое
представление.
- искомое
представление.
. Допустим, что утверждение верно
для любого многочлена положительной степени 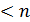 над полем
над полем  .
.
. Докажем утверждение для многочлена
 . Если
. Если  неприводим
над
неприводим
над  , то
, то 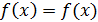 - искомое
представление. Пусть
- искомое
представление. Пусть  приводим
над
приводим
над 
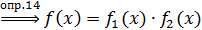 , где
, где 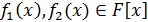 и
и 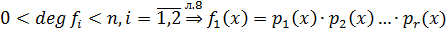 и
и 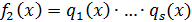 - представление
- представление 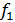 и
и 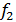 в виде
произведения неприводимых над
в виде
произведения неприводимых над  многочленов
многочленов 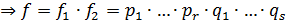 - искомое
представление.
- искомое
представление.
Из 1-3 по методу математической
индукции 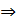 утверждение
верно для любого
утверждение
верно для любого 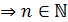 .
.
) Единственность. Пусть 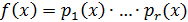 и
и 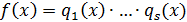 - требуемые
представления
- требуемые
представления 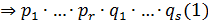 . Так как
. Так как 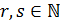 , то либо
, то либо 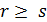 , либо
, либо 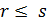 . Пусть,
например,
. Пусть,
например, 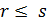 . Так как
левая часть
. Так как
левая часть 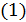 делится на
делится на 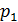 , то
, то 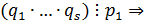 по лемме 4
хотя бы один из множителей делится на
по лемме 4
хотя бы один из множителей делится на 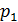 . Так как множители можем менять
местами, то будем считать, что
. Так как множители можем менять
местами, то будем считать, что 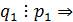 по лемме 8
по лемме 8 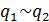 и по
замечанию 3
и по
замечанию 3 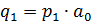 , где
, где 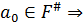
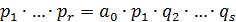 ,
, 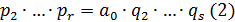 . Так как
левая часть
. Так как
левая часть 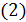 делится на
делится на 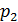 , то, как и
выше, получим
, то, как и
выше, получим 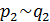 и
и 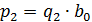 , где
, где 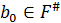 , причем
, причем 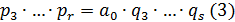 и т.д.,
через конечное число шагов получим
и т.д.,
через конечное число шагов получим 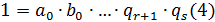 . Допустим, что
. Допустим, что 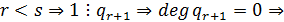 противоречие
противоречие
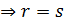 . Таким
образом, представление многочлена
. Таким
образом, представление многочлена  в виде требуемого произведения
определяется однозначно с точностью до порядка следования множителей и
ассоциированности. Теорема доказана.
в виде требуемого произведения
определяется однозначно с точностью до порядка следования множителей и
ассоциированности. Теорема доказана.
Определение 15. Пусть  - поле.
Многочлен
- поле.
Многочлен 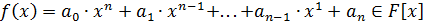 называется
нормированным или приведенным, если
называется
нормированным или приведенным, если 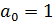 .
.
Следствие 10.1. Любой многочлен 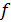 положительной
степени над полем
положительной
степени над полем  допускает
представление в виде:
допускает
представление в виде: 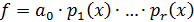 , где
, где 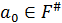 ,
, 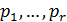 -
неприводимые над
-
неприводимые над  нормированные
многочлены.
нормированные
многочлены.
Определение 16. Пусть 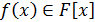 ,
,  - поле,
- поле, 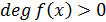 .
Представление многочлена
.
Представление многочлена  в виде
в виде 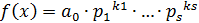 , где
, где 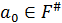 ,
,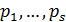 - попарно
различные неприводимые над полем
- попарно
различные неприводимые над полем  нормированные многочлены,
нормированные многочлены, 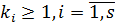 , называется
каноническим представлением многочлена
, называется
каноническим представлением многочлена 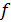 , число
, число 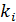 называется
кратностью множителя
называется
кратностью множителя 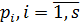 . Если
. Если 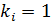 , то
, то 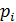 называется
простым неприводимым множителем многочлена
называется
простым неприводимым множителем многочлена 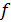 .
.
Определение 17. Пусть 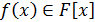 ,
,  -
ассоциативно-коммутативное кольцо с единицей,
-
ассоциативно-коммутативное кольцо с единицей, 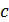 - корень
- корень  . Число
. Число 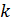 называется
кратностью корня
называется
кратностью корня 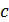 многочлена
многочлена  , если
, если 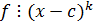 , но
, но 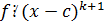 .
.
В этом случае пишут 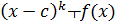 - данная
запись означает, что
- данная
запись означает, что 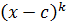 - это
наибольшая степень
- это
наибольшая степень 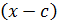 , которая
делит
, которая
делит 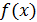 .
.
Теорема 11. Пусть 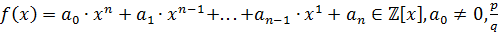 -
несократимая рациональная дробь. Если
-
несократимая рациональная дробь. Если  - корень
- корень  , то
, то 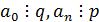 .
.
Доказательство. Так как  - корень
- корень  , то
, то 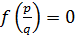 , то есть:
, то есть:
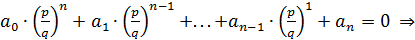
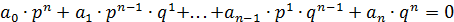 . Так как
. Так как 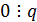 , то
, то 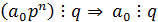 . Так как
. Так как 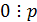 , то
, то 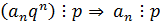 .
.
Теорема доказана.
Следствие 11.1. Рациональные корни
нормированного многочлена с целыми коэффициентами являются его целыми корнями.
Следствие 11.2. Целые корни
многочлена с целыми коэффициентами являются делителями свободного числа.
Теорема 12. Пусть 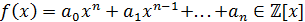 ,
, 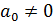 ,
,  -
несократимая рациональная дробь. Если
-
несократимая рациональная дробь. Если  - корень
- корень  , то
, то 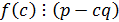 ,
, 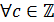 .
.
Следствие 12.1. Пусть 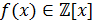 ,
,  -
несократимая рациональная дробь. Если
-
несократимая рациональная дробь. Если  - корень
- корень 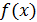 , то
, то 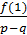 ,
, 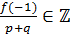 .
.
Глава 3. Многочлены
Чебышева и их основные свойства
3.1 Определение
и простейшие свойства многочленов Чебышева
многочлен чебышев корень переменная
Определение 1. Многочлены 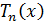 ,
где
,
где 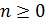 ,
определенные рекуррентным соотношением
,
определенные рекуррентным соотношением 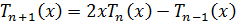 и
начальными условиями
и
начальными условиями 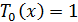 и
и 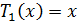 называют
многочленами Чебышева.
называют
многочленами Чебышева.
Определение многочленов Чебышева основано на
том, что 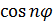 полиномиально
выражается через
полиномиально
выражается через 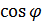 , т.е. существует
такой многочлен
, т.е. существует
такой многочлен 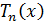 , что
, что 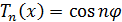 при
при
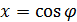 .
.
Формула 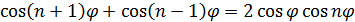 показывает,
что многочлены
показывает,
что многочлены 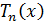 , определенные
рекуррентным соотношением
, определенные
рекуррентным соотношением 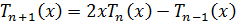 и начальными
условиями
и начальными
условиями 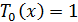 и
и 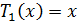 ,
обладают нужным свойством.
,
обладают нужным свойством.
Непосредственно из того, что 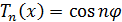 при
при
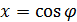 ,
следует, что
,
следует, что 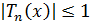 при
при 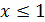 .
А из рекуррентного соотношения следует, что
.
А из рекуррентного соотношения следует, что 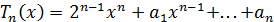 ,
где
,
где 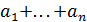 -
целые числа.
-
целые числа.
Теорема 1. Пусть 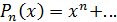 -
многочлен степени
-
многочлен степени 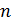 со старшим
коэффициентом 1, причем
со старшим
коэффициентом 1, причем 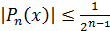 при
при 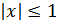 .
.
Тогда 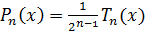 .
Другими словами, многочлен
.
Другими словами, многочлен 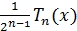 - наименее
уклоняющийся от нуля на интервале
- наименее
уклоняющийся от нуля на интервале 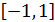 многочлен
степени
многочлен
степени 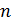 со
старшим коэффициентом 1.
со
старшим коэффициентом 1.
Доказательство. Воспользуемся свойством
многочлена 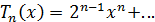 , а именно тем, что
, а именно тем, что
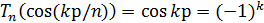 при
при
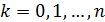 .
Рассмотрим многочлен
.
Рассмотрим многочлен 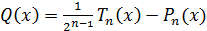 . Его степень не
превосходит
. Его степень не
превосходит 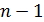 , поскольку старшие
члены многочленов
, поскольку старшие
члены многочленов 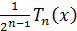 и
и 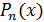 равны.
Из того, что
равны.
Из того, что 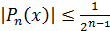 при
при 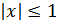 ,
следует, что в точке
,
следует, что в точке
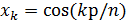 знак числа
знак числа 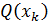 cовпадает
со знаком числа
cовпадает
со знаком числа 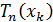 . Таким образом, в
концах каждого отрезка
. Таким образом, в
концах каждого отрезка 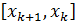 многочлен
многочлен 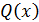 принимает
значения разного знака. Поэтому у многочлена
принимает
значения разного знака. Поэтому у многочлена 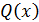 на
этом отрезке есть корень. В случае, когда
на
этом отрезке есть корень. В случае, когда 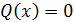 ,
либо
,
либо 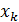 -
двукратный корень, либо внутри одного из отрезков
-
двукратный корень, либо внутри одного из отрезков 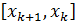 и
и
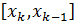 есть
еще один корень. Это следует из того, что в точках
есть
еще один корень. Это следует из того, что в точках 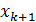 и
и
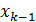 мнгочлен
мнгочлен
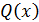 принимает
значения одного знака (рис.1).
принимает
значения одного знака (рис.1).
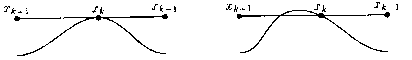
Рис.1
Количество отрезков 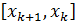 равно
равно
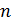 ,
поэтому многочлен
,
поэтому многочлен 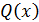 имеет по крайней
мере
имеет по крайней
мере 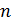 корней.
Для многочлена степени не более
корней.
Для многочлена степени не более 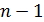 это означает, что
он тождественно равен нулю, т.е.
это означает, что
он тождественно равен нулю, т.е. 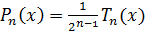 .
Теорема доказана.
.
Теорема доказана.
Теорема 2. Пусть 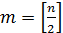 .
Тогда
.
Тогда
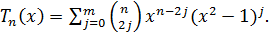
Доказательство. Поскольку  ,
то
,
то 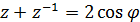 и
и
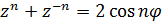 .
Следовательно,
.
Следовательно, 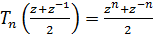 .
.
Пусть 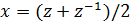 и
и
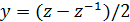 .
Тогда
.
Тогда 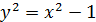 и
и
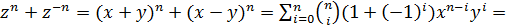
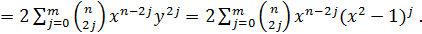
Теорема доказана.
Следствие 1. Пусть 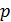 -
нечетное простое число. Тогда
-
нечетное простое число. Тогда
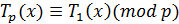 .
.
Доказательство. Запишем 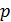 в
виде
в
виде 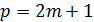 .
Тогда
.
Тогда
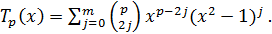
Если 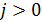 ,
то
,
то 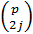 делится
на
делится
на 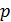 .
Поэтому
.
Поэтому
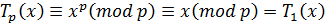 . Следствие
доказано.
. Следствие
доказано.
Определение 2. Композиция многочленов 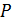 и
и
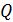 определяется
равенством
определяется
равенством 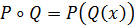 .
.
Определение 3. Многочлены 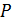 и
и
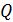 называются
коммутирующими, если
называются
коммутирующими, если 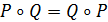 , т.е.
, т.е. 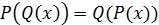 .
.
Доказательство. Пусть 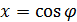 .
Тогда
.
Тогда 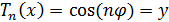 и
и
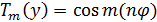 .
Поэтому
.
Поэтому 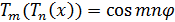 .
Аналогично
.
Аналогично 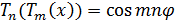 . Таким образом,
равенство
. Таким образом,
равенство 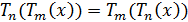 выполняется при
выполняется при 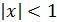 ,
а значит, это равенство выполняется при всех
,
а значит, это равенство выполняется при всех 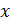 .
Теорема доказана.
.
Теорема доказана.
Определение 4. Пусть 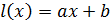 ,
где
,
где 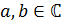 и
и
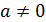 .
Говорят, что пара многочленов
.
Говорят, что пара многочленов 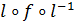 и
и 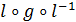 эквивалентна
паре многочленов
эквивалентна
паре многочленов 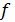 и
и 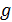 .
.
Теорема 4 (Ритт). Пусть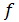 и
и
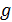 -
коммутирующие многочлены. Тогда пара многочленов
-
коммутирующие многочлены. Тогда пара многочленов 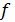 и
и
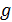 эквивалентна
одной из следующих пар:
эквивалентна
одной из следующих пар:
(1) 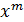 и
и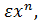 где
где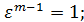
(2) 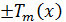 и
и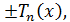 где
где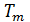 и
и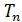 - многочлены Чебышева;
- многочлены Чебышева;
(3) 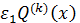 и
и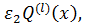 где
где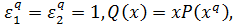
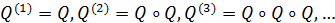
Теорема 4 была доказана в 1922 году американским
математиком Риттом; все известные ее доказательства весьма сложные. Современное
изложение доказательства теоремы Ритта приведено в книге Прасолова В.В.,
Шварцмана О.В. [13].
В некоторых случаях вместо многочлена 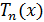 рассматривают
многочлен
рассматривают
многочлен 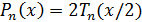 со старшим
коэффициентом 1. Многочлены
со старшим
коэффициентом 1. Многочлены 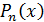 удовлетворяют
рекуррентному соотношению
удовлетворяют
рекуррентному соотношению 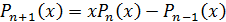 . Поэтому
. Поэтому 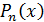 -
многочлен с целыми коэффициентами.
-
многочлен с целыми коэффициентами.
Если 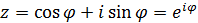 ,
то
,
то 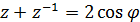 и
и
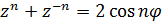 .
Следовательно,
.
Следовательно, 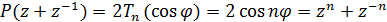 , т.е. многочлен
, т.е. многочлен 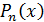 соответствует
полиномиальному выражению величины
соответствует
полиномиальному выражению величины 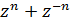 через
через
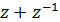 .
.
С помощью многочленов 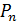 можно
доказать следующее утверждение.
можно
доказать следующее утверждение.
Теорема 5. Если оба числа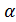 и
и 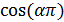 рациональны,
то число
рациональны,
то число 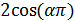 целое,
т.е.
целое,
т.е.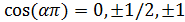 .
.
Доказательство. Пусть 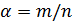 -
несократимая дробь и
-
несократимая дробь и 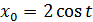 , где
, где 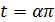 .
Тогда
.
Тогда 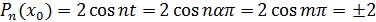 .
Поэтому
.
Поэтому 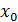 -
корень многочлена
-
корень многочлена 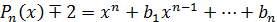 с целыми
коэффициентами. Пусть
с целыми
коэффициентами. Пусть 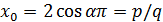 - несократимая
дробь. Тогда
- несократимая
дробь. Тогда 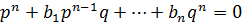 , и значит,
, и значит, 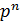 делится
на
делится
на 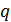 .
Однако числа
.
Однако числа 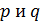 взаимно простые.
Поэтому
взаимно простые.
Поэтому 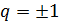 ,
т.е.
,
т.е. 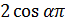 -
целое число. Теорема доказана.
-
целое число. Теорема доказана.
3.2 Основные
теоремы о многочленах Чебышева
Определение 5. Многочлены 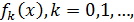 называют
ортогональными многочленами на отрезке
называют
ортогональными многочленами на отрезке 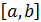 с
весовой функцией
с
весовой функцией 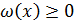 , если
, если 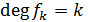 и
и
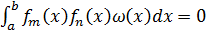 при
при
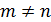 .
.
В пространстве 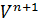 многочленов
степени не более
многочленов
степени не более 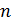 задают скалярное
произведение формулой
задают скалярное
произведение формулой 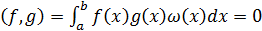 .
.
Ортогональные многочлены 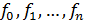 образуют
ортогональный базис в пространстве
образуют
ортогональный базис в пространстве 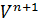 с
таким скалярным произведением.
с
таким скалярным произведением.
Если задан отрезок и весовая функция, то
ортогональные многочлены определены однозначно с точность до
пропорциональности. В самом деле, они получаются в результате ортогонализации
базиса 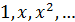
Наиболее известны следующие ортогональные
многочлены:
|
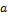
|
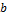
|
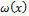
|
Название
|
|
-1
|
1
|
1
|
многочлены
Лежандра
|
|
-1
|
1
|
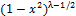
|
многочлены
Гегенбауэра
|
|
-1
|
1
|
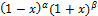
|
многочлены
Якоби
|
|
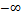
|
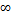
|
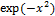
|
многочлены
Эрмита
|
|
0
|
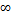
|
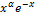
|
многочлены
Лагерра
|
Теорема 6.
Многочлены Чебышева образуют ортогональную систему многочленов на отрезке 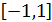 с
весовой функцией
с
весовой функцией 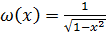 .
.
Доказательство. Сделаем замену 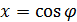 .
Получим
.
Получим
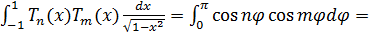

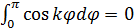
при 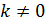 .
Теорема доказана.
.
Теорема доказана.
Следствие 2. Если 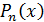 -
многочлен степени
-
многочлен степени 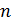 и
и
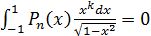
при 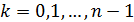 ,
то
,
то 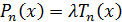 ,
где
,
где 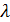 -
некоторое число.
-
некоторое число.
Доказательство. В пространстве 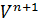 со
скалярным произведением
со
скалярным произведением
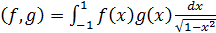
ортогональное дополнение к подпространству,
порожденному многочленами 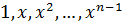 , порождено
многочленом Чебышева
, порождено
многочленом Чебышева 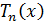 . Следствие
доказано.
. Следствие
доказано.
Теорема 7. Многочлены Чебышева можно вычислять
по формуле
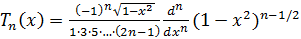 .
.
Доказательство. Индукцией по 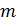 доказывается,
что при
доказывается,
что при 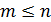
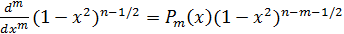 ,
где
,
где 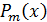 -
многочлен степени
-
многочлен степени 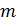 , причем
, причем 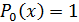 ,
,
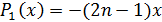 и
и
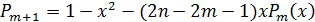 при
при 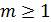 .
.
Следовательно, 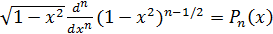 -
многочлен степени
-
многочлен степени 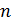 .
.
Проверим, что 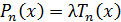 ,
т.е.
,
т.е.
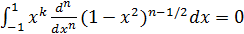
при 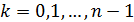 .
Интегрируя по частям получаем
.
Интегрируя по частям получаем
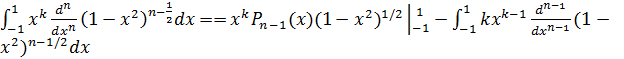
Первое слагаемое равно нулю, так как 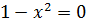 при
при
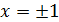 .
Затем интегрируем по частям второе слагаемое и т.д. Чтобы в конце концов
получить нуль, необходимо проинтегрировать по частям
.
Затем интегрируем по частям второе слагаемое и т.д. Чтобы в конце концов
получить нуль, необходимо проинтегрировать по частям 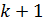 раз.
При этом на последнем шаге возникнет дифференциал
раз.
При этом на последнем шаге возникнет дифференциал 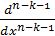 .
Это означает, что число
.
Это означает, что число 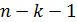 должно быть
неотрицательно, т.е.
должно быть
неотрицательно, т.е. 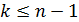 .
.
Остается проверить, что 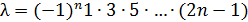 .
Для этого вычисляют
.
Для этого вычисляют 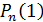 . Действительно,
что при
. Действительно,
что при 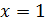 рекуррентное
соотношение
рекуррентное
соотношение 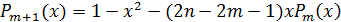
принимает вид 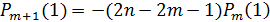 .
Таким образом,
.
Таким образом,
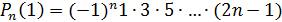 . Кроме того,
. Кроме того, 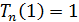 .
Теорема доказана.
.
Теорема доказана.
Теорема 8. Пусть многочлен 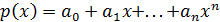 ,
где
,
где 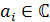 ,
таков, что
,
таков, что 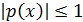 при
при 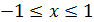 .
Тогда
.
Тогда 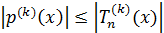 при
при
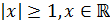 .
.
Доказательство. Воспользуемся тем, что 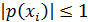 при
при
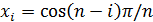 ,
,
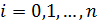 .
Многочлен
.
Многочлен 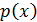 полностью
определяется значениями
полностью
определяется значениями 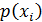 .
.
Где
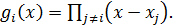
Дифференцируя 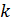 раз
соотношение (1), получим
раз
соотношение (1), получим
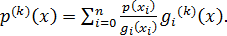
Так как 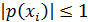 ,
то
,
то
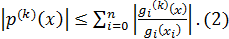
Многочлен 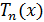 в
точке
в
точке 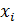 принимает
значение
принимает
значение 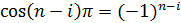 .
Поэтому
.
Поэтому
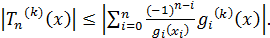
Кроме того, 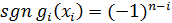 .
Далее, при
.
Далее, при 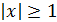 знак числа
знак числа 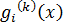 не
зависит от
не
зависит от 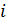 . Действительно,
все корни многочлена
. Действительно,
все корни многочлена 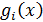 принадлежат
отрезку
принадлежат
отрезку 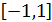 .
Поэтому все корни многочлена
.
Поэтому все корни многочлена 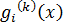 также принадлежат
этому отрезку. Следовательно,
также принадлежат
этому отрезку. Следовательно, 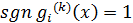 при
при 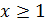 и
и
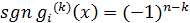 при
при
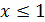 .
.
В итоге при 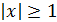 получаем
получаем
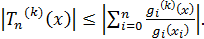
В этом случае из неравенства (2) следует, что 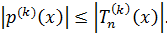 Теорема
доказана.
Теорема
доказана.
Теорема 9. Пусть многочлен 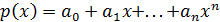 ,
где
,
где 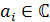 ,
таков, что
,
таков, что 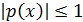 при
при 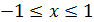 .
Тогда
.
Тогда 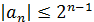 .
.
Доказательство. Так как 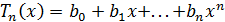 ,
где
,
где 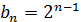 ,
то по теореме 8 при
,
то по теореме 8 при 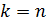 получим
получим 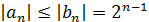 .
Теорема доказана.
.
Теорема доказана.
Теорема 10. При 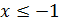 и
при
и
при 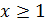 выполняется
неравенство
выполняется
неравенство 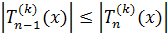 .
.
Доказательство. Для многочлена 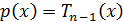 выполняется
условие теоремы 8. Поэтому
выполняется
условие теоремы 8. Поэтому 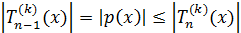 . Теорема доказана.
. Теорема доказана.
Теорема 11. При 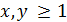 выполняется
неравенство
выполняется
неравенство
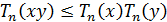 .
.
Доказательство. Пусть 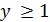 .
Рассмотрим многочлен
.
Рассмотрим многочлен 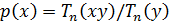 . Проверим, что
многочлен
. Проверим, что
многочлен 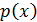 удовлетворяет
условию теоремы 8, т.е. что
удовлетворяет
условию теоремы 8, т.е. что 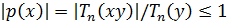 при
при 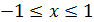 .
При вещественном
.
При вещественном 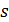 функция
функция 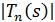 зависит
только от
зависит
только от 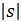 , причем если
, причем если 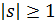 ,
то
,
то 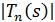 монотонно
возрастает с возрастанием
монотонно
возрастает с возрастанием 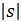 . Кроме того,
. Кроме того,
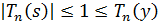 при
при 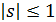 .
Следовательно, если
.
Следовательно, если 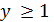 и
и 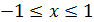 ,
то
,
то 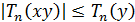 .
.
Согласно теореме 8 при 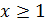 выполняется
неравенство
выполняется
неравенство 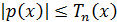 , т.е.
, т.е. 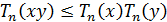 .
Теорема доказана.
.
Теорема доказана.
Определение 6. Для
последовательности функций 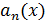 рассматривают ряд
рассматривают ряд 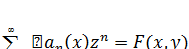 .
Если радиус сходимости данного ряда положителен, то функцию
.
Если радиус сходимости данного ряда положителен, то функцию 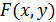 называют
производящей функцией последовательности
называют
производящей функцией последовательности 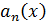 .
.
Теорема 12. При 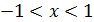 и
и
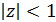 выполняются
следующие равенства:
выполняются
следующие равенства:
(а) 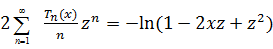
(б)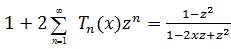 .
.
Доказательство.
а) Пусть 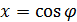 .
Тогда
.
Тогда 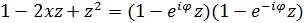 .
Поэтому
.
Поэтому 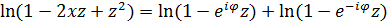 .
Кроме того,
.
Кроме того,
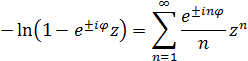
при 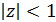 .
Следовательно,
.
Следовательно,
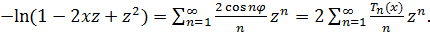
Теорема доказана.
б) Продифференцировав по 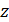 обе
части равенства (а), получим
обе
части равенства (а), получим
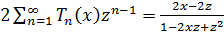
Следовательно,
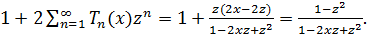
Теорема доказана.
Теорема 13. Пусть 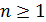 и
и
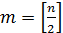 .
Тогда
.
Тогда
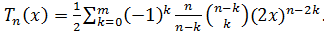
Доказательство. Согласно теореме 12 (а),
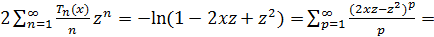

Поэтому
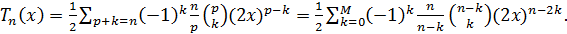
Суммирование ведется до тех пор, пока 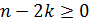 .
Поэтому
.
Поэтому 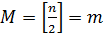 .
Теорема доказана.
.
Теорема доказана.
Для многочлена 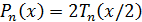 :
:
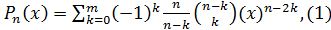
где 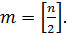
При 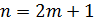 выполняется
равенство
выполняется
равенство
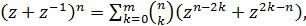
а при 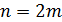 выполняется
равенство
выполняется
равенство
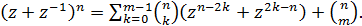
Таким образом, если 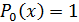 ,
а при
,
а при 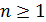 многочлены
многочлены
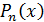 задаются
формулой (1), то выполняется соотношение
задаются
формулой (1), то выполняется соотношение
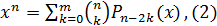
где 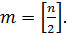
Соотношения (1) и (2) можно записать следующим
образом. Пусть 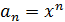 и
и 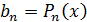 ,
где
,
где 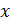 -
некоторое фиксированное число. Тогда
-
некоторое фиксированное число. Тогда
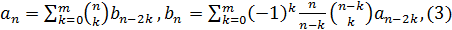
(при  второе
соотношение принимает вид
второе
соотношение принимает вид 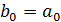 ). Покажем, что
соотношения (3) эквивалентны не только для указанных последовательностей, но и
для произвольных последовательностей. Заметим, что первое соотношение имеет вид
). Покажем, что
соотношения (3) эквивалентны не только для указанных последовательностей, но и
для произвольных последовательностей. Заметим, что первое соотношение имеет вид
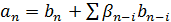 ,
а второе соотношение имеет вид
,
а второе соотношение имеет вид 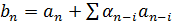 . Поэтому каждое
соотношение однозначно определяет как последовательность
. Поэтому каждое
соотношение однозначно определяет как последовательность 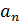 по
последовательности
по
последовательности 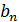 , так и
последовательность
, так и
последовательность 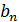 по
последовательности
по
последовательности 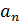 . Для
последовательностей
. Для
последовательностей 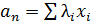 ,
, 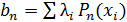 ,
где
,
где 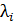 и
и
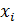 -
фиксированные наборы чисел, соотношения (3) эквивалентны, поскольку они
эквивалентны для последовательностей
-
фиксированные наборы чисел, соотношения (3) эквивалентны, поскольку они
эквивалентны для последовательностей 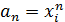 ,
,
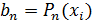 .
Проверим, что для любой последовательности
.
Проверим, что для любой последовательности 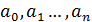 можно
подобрать такие числа
можно
подобрать такие числа 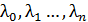 и
и 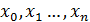 ,
что
,
что
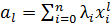
при 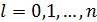 .
Выберем произвольные попарно различные числа
.
Выберем произвольные попарно различные числа 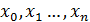 .
Тогда для чисел
.
Тогда для чисел 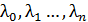 получим систему
линейных уравнений с определителем
получим систему
линейных уравнений с определителем
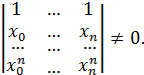
Эта система уравнений имеет решение при любых 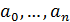 .
.
Соотношение (3) позволяют получать нетривиальные
тождества с биномиальными коэффициентами. Пусть, например, 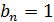 при
всех
при
всех 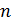 .
Тогда
.
Тогда
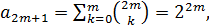
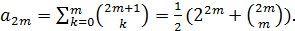
Данные тождества получаются из разложений 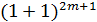 и
и
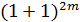 по
биному Ньютона. В таком случае соотношение
по
биному Ньютона. В таком случае соотношение 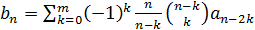
принимает вид
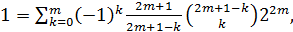
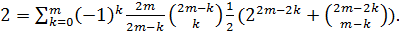
Заключение
В курсовой работе
¾ изучены основные понятия теории
многочленов от одной переменной (многочлен, степень многочлена, нулевой
многочлен, неприводимый (приводимый) над полем многочлен, наибольший общий
делитель и наименьшее общее кратное многочленов над полем, каноническое
представление многочлена, корень многочлена, кратность корня многочлена и др.),
приведены примеры многочленов (многочлены над числовыми полями), рассмотрены
основные свойства многочленов от одной переменной (свойства кольца многочленов
над областью целостности, свойства степени многочлена, свойства неприводимых
многочленов над полем и др.);
Список используемой литературы
1. Прасолов
В.В. Многочлены. - М.: МЦНМО, 2001.
2. Винберг
Э.Б. Курс алгебры. - М.: МЦНМО, 2011.
. Куликов
Л.Я. Алгебра и теория чисел. - М.: Оникс, 2012.
. Кострикин
А.И. Введение в алгебру. В 3-х частях. Часть 1: Основы алгебры: учебник. - М.:
МЦНМО, 2009.
. Кострикин
А.И. Введение в алгебру. В 3-х частях. Часть 2: Линейная алгебра: учебник. -
М.: МЦНМО, 2012.
. Кострикин
А.И. Введение в алгебру. В 3-х частях. Часть 3: Основные структуры алгебры:
учебник. - М.: МЦНМО, 2009.
. Курош
А.Г. Основы высшей алгебры. - СПб.: Лань, 2011.
. Курош
А.Г. Лекции по общей алгебре. - СПб.: Лань, 2007.
. Родина
М.А., Солодовников А. С. Задачник-практикум по алгебре. - М.: Просвещение,
1986.
. Фаддеев
Д.К. Лекции по алгебре. - СПб.: Лань, 2007.
. Фаддеев
Д.К., Соминский И.С. Задачи по высшей алгебре. - СПб.: Лань, 2008.
. Окунев
Л.Я. Высшая алгебра. - СПб.: Лань, 2009.
. Прасолов
В.В., Шварцман О.В. Азбука римановых поверхностей. - М.: Фазис, 1999.