Теория вероятностей и математическая статистика
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФГБОУ ВПО
«Уральский государственный экономический университет»
Центр
дистанционного образования
Контрольная
работа
"Теория
вероятностей и математическая статистика"
Исполнитель:
Целищев Сергей Сергеевич
Екатеринбург
Задача 1
Студент знает 15 вопросов из 20. В билете 3
вопроса. Составить закон распределения случайной величины Х - числа известных
студенту вопросов в билете. Вычислить математическое ожидание, дисперсию и
среднеквадратическое отклонение случайной величины.
Решение
Введем дискретную случайную величину
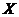 =
(Количество известных студенту вопросов в билете). Она может принимать значения
0, 1, 2 или 3. Найдем соответствующие вероятности.
=
(Количество известных студенту вопросов в билете). Она может принимать значения
0, 1, 2 или 3. Найдем соответствующие вероятности.
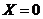 , если все три вопроса
студенту неизвестны. Вероятность
этого события по классическому определению вероятности равна:
, если все три вопроса
студенту неизвестны. Вероятность
этого события по классическому определению вероятности равна:
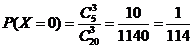 .
.
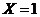 , если один вопрос
известен и два вопроса студенту неизвестны. Вероятность этого события по
классическому определению вероятности равна:
, если один вопрос
известен и два вопроса студенту неизвестны. Вероятность этого события по
классическому определению вероятности равна:
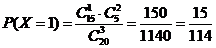 .
.
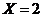 , если один вопрос
неизвестен и два вопроса студенту известны. Вероятность этого события по
классическому определению вероятности равна:
, если один вопрос
неизвестен и два вопроса студенту известны. Вероятность этого события по
классическому определению вероятности равна:
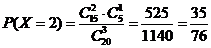 .
.
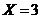 , если все три вопроса
студенту известны. Вероятность
этого события по классическому определению вероятности равна:
, если все три вопроса
студенту известны. Вероятность
этого события по классическому определению вероятности равна:
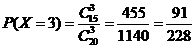 .
.
Закон распределения случайной
величины 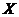 имеет вид:
имеет вид:
|
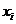 0123 0123
|
|
|
|
|
|
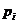 1/11415/11435/7691/228 1/11415/11435/7691/228
|
|
|
|
|
Сумма вероятностей равна 1, поэтому расчеты
проведены верно.
Найдем математическое ожидание, дисперсию и
функцию распределения.
Математическое ожидание
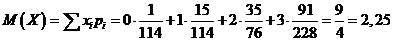 .
.
Дисперсия
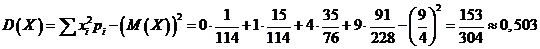 .
.
Среднеквадратическое отклонение
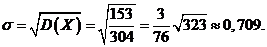
Задача 2
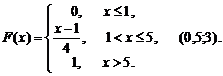
Решение
Найдем плотность распределения
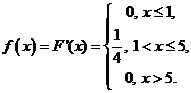
Это плотность распределения
равномерного на отрезке  распределения.
распределения.
Найдем математическое ожидание:
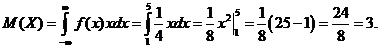
Найдем дисперсию:
Найдем вероятность попадания
случайной величины в интервал (α,β) = (0,5; 3). Получим:
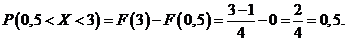
Построим схематично графики 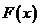 и
и  .
.
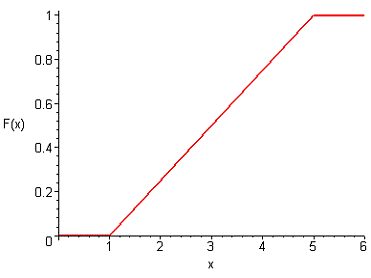
Рисунок 1
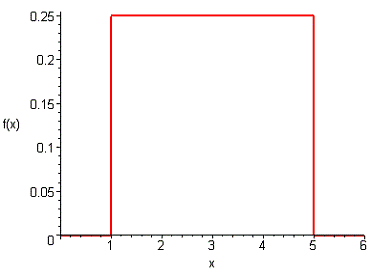
Рисунок 2