Расчет статических и динамических характеристик асинхронного электропривода
Содержание
Введение
. Содержание курсовой работы
. Задание на курсовой проект
. Расчет параметров Г-образной схемы
замещения
. Расчет мощности, потребляемой из сети
. Расчет характерных точек механической
характеристики
. Построение механической и энергомеханической
характеристик при номинальных напряжении и частоте
. Выбор закона регулирования 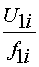 в зависимости от заданной
характеристики момента нагрузки
в зависимости от заданной
характеристики момента нагрузки
. Построение механических характеристик
при выбранном законе регулирования 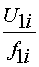
. Скалярное управление скоростью
асинхронного двигателя
Литература
Приложение
Введение
Курсовая работа является итоговой при изучении курса "Электропривод
переменного тока". Курсовая работа выполняются на ПЭВМ с использованием
пакета MathCad и пакета моделирования динамических
систем Simulink, являющегося составной частью среды Matlab. Моделирование асинхронного
двигателя при частотном управлении предполагает использование
специализированных библиотек пакета Simulink - SimPowerSystem Toolbox.
Перед выполнением работы необходимо ознакомиться с теоретическими
сведениями, уяснить суть работы. На основании варианта исходных данных
рассчитать параметры схемы замещения асинхронного двигателя, мощность,
потребляемую из сети, характерные точки механической характеристики. Построить
механическую и энергомеханическую характеристики при номинальных напряжении и
частоте. Выбрать закон регулирования 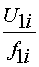 в зависимости от заданной
характеристики момента нагрузки. Построить механические характеристики при
выбранном законе регулирования
в зависимости от заданной
характеристики момента нагрузки. Построить механические характеристики при
выбранном законе регулирования 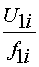 . Исследовать переходные процессы в системе преобразователь
частоты - асинхронный двигатель, при скалярном управлении.
. Исследовать переходные процессы в системе преобразователь
частоты - асинхронный двигатель, при скалярном управлении.
При защите курсовой работы необходимо знать ее содержание и
соответствующие разделы курса "Электропривод переменного тока".
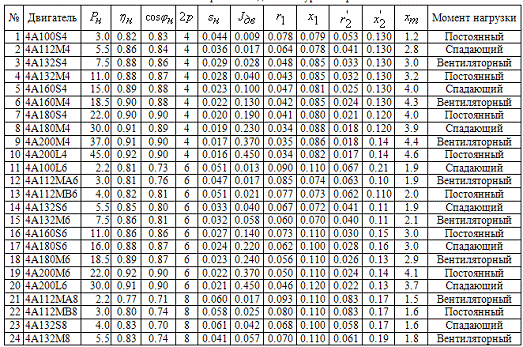
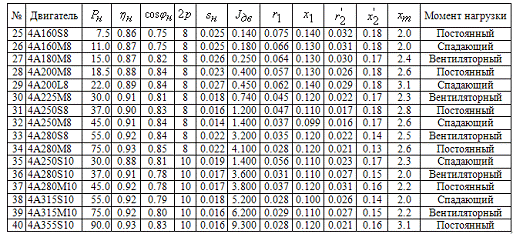
Варианты заданий для выполнения курсовой работы приведены в приложении 1.
Методические указания к выполнению курсовой работы "Расчет
статических и динамических характеристик асинхронного электропривода"
Целью курсовой работы является углубление знаний, полученных на лекциях,
лабораторных и практических занятиях, а также подготовка к дипломному
проектированию.
В качестве темы курсовой работы выбран электропривод переменного тока с
асинхронным электродвигателем.
Методические указания содержат практические рекомендации по выполнению
задания на курсовую работу, необходимые справочные материалы, а также
требования к содержанию и оформлению проекта.
1. Содержание курсовой работы
Курсовая работа состоит из пояснительной записки на 20-25 страницах.
Содержание пояснительной записки:
·
титульный лист,
·
аннотация,
·
оглавление,
·
расчет параметров
схемы замещения асинхронного двигателя,
·
расчет мощности,
потребляемой из сети,
·
расчет
характерных точек механической характеристики,
·
построение
механической и энергомеханической характеристик при номинальных напряжении и
частоте,
·
выбор закона
регулирования 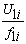 в зависимости от заданной характеристики момента нагрузки,
в зависимости от заданной характеристики момента нагрузки,
·
построение
механических характеристик при выбранном законе регулирования 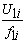 ,
,
·
скалярное
управление скоростью:
§ структурная схема системы преобразователь частоты - асинхронный
двигатель,
§ расчёт положительной обратной связи по току,
§ расчёт П-регулятора скорости,
§ расчёт ПИ-регулятора скорости,
§ графики переходных процессов при пуске асинхронного двигателя и набросе
момента нагрузки в установившемся режиме работы,
§ определение статической ошибки регулирования скорости при набросе момента
нагрузки в установившемся режиме работы.
·
литература.
2. Задание на курсовой проект
асинхронный двигатель напряжение частота
Рассчитать статические и динамические характеристики асинхронного
электропривода. Варианты исходных данных приведены в приложении 1.
3. Расчет параметров Г-образной схемы замещения
Все двигатели, приведенные в приложении 1, рассчитаны на напряжение
питающей сети: фазное напряжение 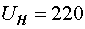 В, линейное напряжение
В, линейное напряжение 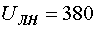 В. Номинальная частота тока
В. Номинальная частота тока 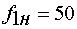 Гц. Число фаз
Гц. Число фаз 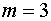 .
.
В приложении 1 даны следующие параметры асинхронных двигателей.
§ 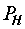 - номинальная мощность на валу, кВт;
- номинальная мощность на валу, кВт;
§ 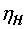 - номинальный КПД,
- номинальный КПД,
§ 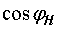 - сдвиг по фазе в номинальном
режиме,
- сдвиг по фазе в номинальном
режиме,
§ 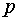 - число полюсов,
- число полюсов,
§ 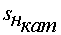 - номинальное скольжение,
- номинальное скольжение,
§ 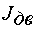 - момент инерции двигателя, кГм2,
- момент инерции двигателя, кГм2,
Параметры Г-образной упрощенной схемы замещения приводятся в
относительных единицах:
§ 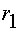 - активное сопротивление статора,
- активное сопротивление статора,
§ 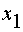 - индуктивное сопротивление
рассеивания статора,
- индуктивное сопротивление
рассеивания статора,
§ 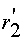 - активное сопротивление ротора,
- активное сопротивление ротора,
§ 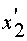 - индуктивное сопротивление
рассеивания ротора,
- индуктивное сопротивление
рассеивания ротора,
§ 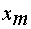 - индуктивное сопротивление
намагничивающего контура.
- индуктивное сопротивление
намагничивающего контура.
Параметры Г-образной схемы замещения даны в относительных единицах. Для
их перевода в абсолютные единицы необходимо определить номинальный ток и
базовое сопротивление:
|
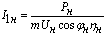 , А , А
|
(1)
|
|
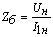 , Ом. , Ом.
|
(2)
|
С учетом формулы (2.2) параметры Г-образной упрощенной схемы замещения в
абсолютных единицах определятся:
|
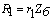 , Ом; , Ом;
|
(3)
|
|
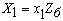 , Ом; , Ом;
|
(4)
|
|
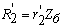 , Ом; , Ом;
|
(5)
|
(6)
|
|
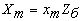 , Ом. , Ом.
|
(7)
|
Г-образная упрощенная схема замещения в абсолютных единицах изображена на
рис. 1.
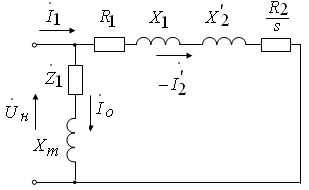
Рисунок 1 - Г-образная упрощенная схема замещения в абсолютных единицах
На рис. 1 в цепи намагничивания показан комплекс полного сопротивления
статора  .
.
По номинальным данным определяются число полюсов 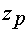 и синхронная частота вращения
и синхронная частота вращения 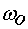 :
:
Расчеты по формулам (1) - (9) выполнить в среде MathCad.
4. Расчет мощности, потребляемой из сети
Активная, реактивная и полная мощности, потребляемые из сети в
номинальном режиме работы, определяются по формулам:
|
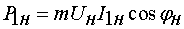 Вт; Вт;
|
(10)
|
|
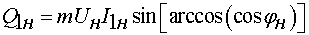 , Вар; , Вар;
|
(11)
|
|
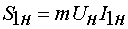 , ВА. , ВА.
|
(12)
|
Расчеты по формулам (10) - (12) выполнить в среде MathCad.
5. Расчет характерных точек механической характеристики
Механическая характеристика асинхронного двигателя (рис. 2) имеет
характерные точки:
точка идеального холостого хода 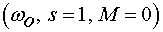 ,
,
точка номинального режима 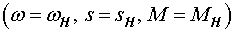 ,
,
точка критического момента 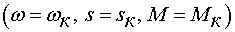 ,
,
точка минимального момента 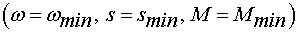 ,
,
точка короткого замыкания 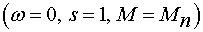 .
.
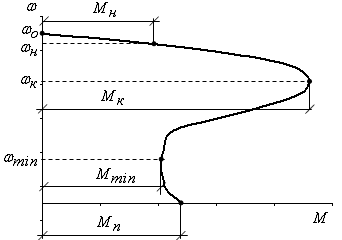
Рисунок 2 - Механическая характеристика асинхронного двигателя
Точка идеального холостого хода, 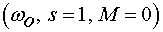
Частота вращения при идеальном холостом ходе рассчитывается по формуле
(9):
|
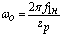 , , 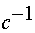 . .
|
(13)
|
Точка номинального режима 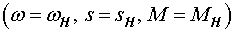
Номинальный момент:
|
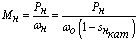 , Нм. , Нм.
|
(14)
|
Номинальное скольжение, рассчитанное по параметрам схемы замещения, можно
найти из выражения:
|
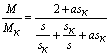 , ,
|
(15)
|
где 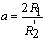 .
.
Положив в выражении (15) 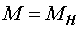 , получим:
, получим:
|
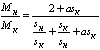 , ,
|
(16)
|
Разрешим уравнение (16) относительно  :
:
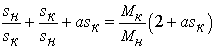
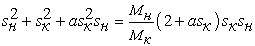
Приведем уравнение (17) к каноническому виду квадратного уравнения:
|
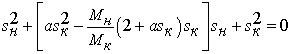 . .
|
(18)
|
Решение квадратного уравнения (18) имеет вид:
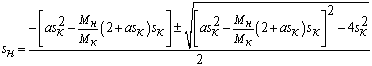 .
.
Знак 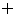 относится к генераторному режиму, знак
относится к генераторному режиму, знак 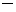 к двигательному режиму работы.
к двигательному режиму работы.
Номинальная расчетная частота вращения:
|
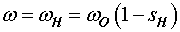 , , 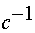 . .
|
(20)
|
Точка критического момента 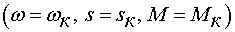 :
:
Точка минимального момента 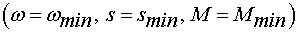 по данным схемы замещения не
рассчитывается. Минимальный момент обусловлен влиянием высших гармоник и
вытеснением тока в обмотке ротора. Данные факторы не учитываются Г-образной
схемой замещения.
по данным схемы замещения не
рассчитывается. Минимальный момент обусловлен влиянием высших гармоник и
вытеснением тока в обмотке ротора. Данные факторы не учитываются Г-образной
схемой замещения.
Точка короткого замыкания 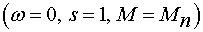
Момент при коротком замыкании  определяется по формуле (15), если в
ней положить
определяется по формуле (15), если в
ней положить 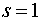 :
:
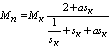
Расчеты по формулам (13), (14), (19) - (24) выполнить в среде MathCad.
Уравнение механической характеристики представляет собой зависимость
скольжения  (частоты вращения
(частоты вращения 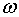 ) от момента
) от момента 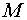 :
:
|
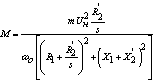 , Нм. , Нм.
|
(25)
|
Энергомеханические характеристики представляю собой зависимость токов 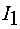 статора и ротора
статора и ротора 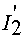 от скольжения
от скольжения  .
.
Ток 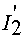 вычисляется по формуле:
вычисляется по формуле:
|
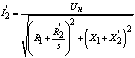 , А. , А.
|
(26)
|
Ток 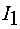 является векторной суммой токов ротора
является векторной суммой токов ротора 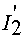 и тока намагничивания
и тока намагничивания 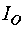 . Модуль тока статора в этом случае
будет равен:
. Модуль тока статора в этом случае
будет равен:
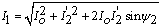 , А. (27)
, А. (27)
где 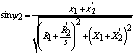 - сдвиг по фазе тока ротора.
- сдвиг по фазе тока ротора.
Механическую и энергомеханические характеристики в соответствии с
уравнениями (25) - (27) для двигательного режима работы построить на одном
графике в среде MathCad.
7. Выбор закона регулирования 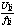 в зависимости от заданной
характеристики момента нагрузки
в зависимости от заданной
характеристики момента нагрузки
В задании на курсовую работу (приложение 1) указана характеристика
момента нагрузки:
· постоянный момент нагрузки,
· нелинейно спадающий момент нагрузки,
· вентиляторный характер момента нагрузки.
В соответствии с вариантом задания момент нагрузки рассчитывается по
одной из следующих формул.
Постоянный момент нагрузки. В этом случае принимается, что момент
нагрузки равен номинальному моменту двигателя:
|
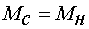 . .
|
(28)
|
Нелинейно спадающий момент нагрузки:
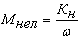
где 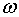 - частота вращения ротора,
- частота вращения ротора, 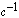 ;
; 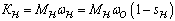 - коэффициент, определяющий крутизну
изменения момента нагрузки,
- коэффициент, определяющий крутизну
изменения момента нагрузки, 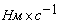 .
.
Момент вентиляторной нагрузки:
|
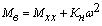 , ,
|
(30)
|
где 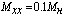 - момент холостого хода, Нм;
- момент холостого хода, Нм; 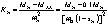 - коэффициент, определяющий крутизну
изменения момента нагрузки,
- коэффициент, определяющий крутизну
изменения момента нагрузки, 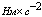 .
.
. Построение механических характеристик при выбранном законе
регулирования 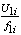
При изменении частоты напряжения на статоре будут изменяться синхронная
частота вращения 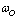 , скольжение
, скольжение  и индуктивные сопротивления рассеивания статора и ротора
и индуктивные сопротивления рассеивания статора и ротора 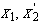 :
:
С учетом выражений (31), (33) уравнение (25) механической характеристики
запишется в виде:
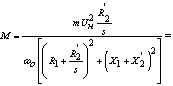
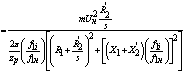
Закон управления при постоянной нагрузке
При постоянном нагрузочном моменте 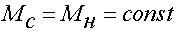 соотношение между напряжением и
частотой определяется законом
соотношение между напряжением и
частотой определяется законом
|
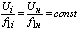 . .
|
(35)
|
С учетом уравнения (35) формула (34) запишется в виде:
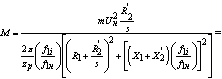
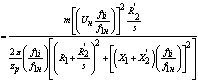
Механические характеристики асинхронного двигателя для двигательного
режима работы строятся по уравнениям (36), (32) в среде MathCad. Характеристики строятся на одном
графике для следующих значений частоты напряжения статора:
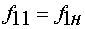 ,
,
1. 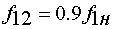 ,
,
2. 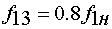 ,
,
3. 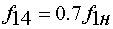 ,
,
4. 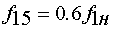 .
.
На том же графике строится уравнение момента нагрузки для следующего
случая:
5. момент нагрузки равен номинальному моменту двигателя 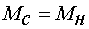 .
.
Закон управления при нелинейно спадающем моменте нагрузки
При нелинейно спадающем моменте нагрузки уравнение момента нагрузки имеет
вид (29):
|
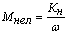 . .
|
(37)
|
В этом случае соотношение между напряжением и частотой определяется
законом
|
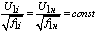 . .
|
(38)
|
С учетом уравнения (38) формула (34) запишется в виде:
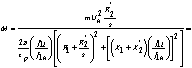
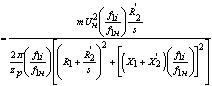 .
.
Механические характеристики асинхронного двигателя строятся по уравнениям
(39), (32) для двигательного режима работы в среде MathCad. Характеристики строятся на одном графике для
следующих значений частоты напряжения статора:
1. 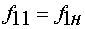 ,
,
2. 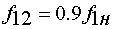 ,
,
3. 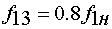 ,
,
4. 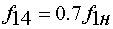 ,
,
5. 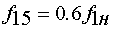 ,
,
На том же графике строится уравнение момента нагрузки для следующего
случая:
Закон управления при вентиляторном характере момента нагрузки
При вентиляторном характере момента нагрузки уравнение момента нагрузки
имеет вид (30):
|
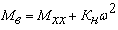 . .
|
(40)
|
В этом случае соотношение между напряжением и частотой определяется
законом
|
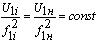 . .
|
(41)
|
С учетом уравнения (41) формула (34) запишется в виде:
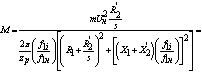
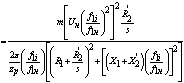
Механические характеристики асинхронного двигателя строятся по уравнениям
(42), (32) для двигательного режима работы в среде MathCad. Характеристики строятся на одном графике для следующих
значений частоты напряжения статора:
1. 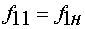 ,
,
2. 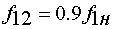 ,
,
3. 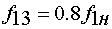 ,
,
4. 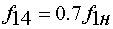 ,
,
5. 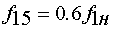 ,
,
На том же графике строится уравнение момента нагрузки для следующего
случая:
6. момент вентиляторной нагрузки 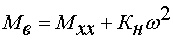 .
.
. Скалярное управление скоростью асинхронного двигателя
Система управления ПЧ-АД со скалярной  -компенсацией
-компенсацией
Структурная схема системы управления со скалярной  -компенсацией приведена на рис. 3.
-компенсацией приведена на рис. 3.
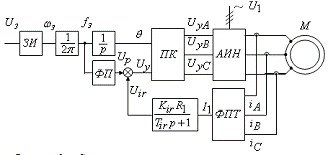
Рисунок 3 - Структурная схема частотного управления со скалярной  -компенсацией
-компенсацией
Задатчик интенсивности 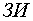 формирует кривую разгона двигателя. Сигналу задания
формирует кривую разгона двигателя. Сигналу задания 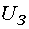 соответствует задание на частоту
соответствует задание на частоту 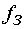 . Функциональный преобразователь
. Функциональный преобразователь 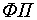 формирует требуемую зависимость
между частотой и напряжением преобразователя, устанавливая один из законов
управления
формирует требуемую зависимость
между частотой и напряжением преобразователя, устанавливая один из законов
управления 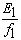 .
.
При скалярной 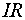 -компенсации сигнал управления
-компенсации сигнал управления 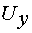 является суммой сигнала
регулирования
является суммой сигнала
регулирования 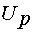 и сигнала положительной обратной связи по току
и сигнала положительной обратной связи по току 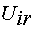 :
:
|
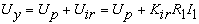 . .
|
(43)
|
где 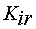 - коэффициент положительной обратной связи по току;
- коэффициент положительной обратной связи по току; 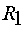 - активное сопротивление обмоток
статора;
- активное сопротивление обмоток
статора; 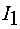 - сигнал, пропорциональный
действующим значениям токов
- сигнал, пропорциональный
действующим значениям токов 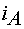 ,
, 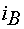 ,
, 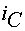 обмоток статора двигателя.
обмоток статора двигателя.
Сигнал управления 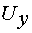 является входным сигналом для прямого координатного
преобразователя
является входным сигналом для прямого координатного
преобразователя 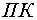 , на выходе которого формируются три синусоидальных
напряжения управления
, на выходе которого формируются три синусоидальных
напряжения управления 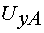 ,
, 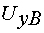 ,
, 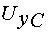 , сдвинутые друг относительно друга на угол
, сдвинутые друг относительно друга на угол 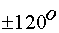 , с амплитудами, пропорциональными
напряжению управления. Сигналы
, с амплитудами, пропорциональными
напряжению управления. Сигналы 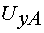 ,
, 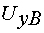 ,
, 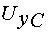 формируют фазные напряжения на выходе автономного инвертора
напряжения
формируют фазные напряжения на выходе автономного инвертора
напряжения 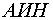 .
.
Интенсивность 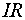 -компенсации зависит от параметров апериодического звена,
установленного в цепи положительной обратной связи по току:
-компенсации зависит от параметров апериодического звена,
установленного в цепи положительной обратной связи по току:
|
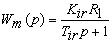 . .
|
(44)
|
где 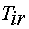 - постоянная времени задержки контура тока, с.
- постоянная времени задержки контура тока, с.
На рис. 4 показана структурная схема модели скалярного управления
скоростью асинхронного двигателя с положительной обратной связью по току. Схема
реализована на блоках библиотек SimPowerSystem. Структурная схема модели содержит:
§ 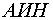 - автономный инвертор напряжения
(показан пунктиром);
- автономный инвертор напряжения
(показан пунктиром);
§ 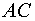 - асинхронный короткозамкнутый
двигатель;
- асинхронный короткозамкнутый
двигатель;
§ 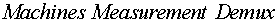 - блок, в котором создается вектор
выходных характеристик асинхронного двигателя;
- блок, в котором создается вектор
выходных характеристик асинхронного двигателя;
§ 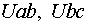 - блоки, конвертирующие сигналы Simulink в эквивалентные сигнал источника
напряжения;
- блоки, конвертирующие сигналы Simulink в эквивалентные сигнал источника
напряжения;
§ 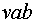 - блок для измерения напряжения;
- блок для измерения напряжения;
§ 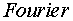 - блок выделения из входного сигнала
амплитуды и фазы гармонических колебаний;
- блок выделения из входного сигнала
амплитуды и фазы гармонических колебаний;
§ 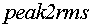 - блок, определяющий действующее
значение сигнала по амплитудному значению.
- блок, определяющий действующее
значение сигнала по амплитудному значению.
Задатчик интенсивности 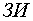 выполнен на блоках
выполнен на блоках  и
и  . Эти блоки формируют линейно
нарастающий сигнал изменении скорости:
. Эти блоки формируют линейно
нарастающий сигнал изменении скорости:
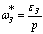 .
.
где 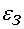 - угловое ускорение, с-2;
- угловое ускорение, с-2; 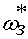 задание на частоту вращения в
относительных единицах.
задание на частоту вращения в
относительных единицах.
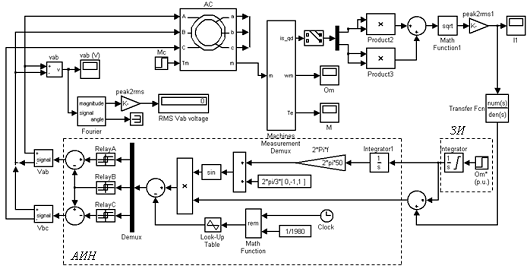
Рисунок 4 - Структурная схема модели асинхронного двигателя с учетом
механических и электромагнитных переходных процессов
Значение 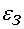 задается в блоке
задается в блоке . Скорость окончания разгона задается
в блоке
. Скорость окончания разгона задается
в блоке  . Верхний и нижний пределы
интегрирования должны соответствовать конечной скорости разгона
. Верхний и нижний пределы
интегрирования должны соответствовать конечной скорости разгона 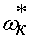 .
.
Формирование тока статора осуществляется по его проекциям на
ортогональные оси 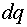 . Проекция тока статора на ось
. Проекция тока статора на ось 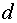 -
- 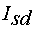 , на ось
, на ось 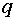 -
- 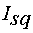 . Поскольку оси
. Поскольку оси 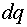 ортогональны, то амплитудное
значение тока статора:
ортогональны, то амплитудное
значение тока статора:
|
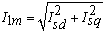 . .
|
(46)
|
Действующее значение тока статора:
|
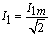 . .
|
(47)
|
Структурная схема модели, реализующая уравнения (46), (47) изображена на
рис. 5.
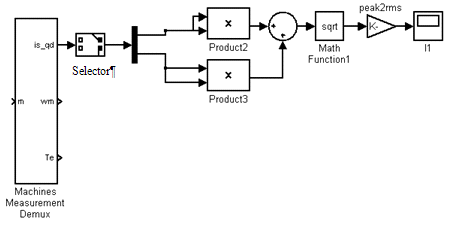
Рисунок 5 - Структурная схема модели, определяющей действующее значение
тока статора по его проекции на оси 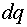
Селектор 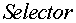 формирует проекции тока статора на ортогональные оси
формирует проекции тока статора на ортогональные оси 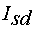 ,
,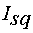 . На выходе умножителей
. На выходе умножителей 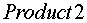 ,
, 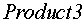 вычисляется сумма квадратов проекций
тока статора. После извлечения квадратного корня (блок
вычисляется сумма квадратов проекций
тока статора. После извлечения квадратного корня (блок 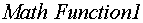 ) и деления на
) и деления на 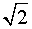 (блок
(блок 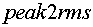 ) получаем действующее значение тока
статора
) получаем действующее значение тока
статора 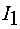 .
.
Передаточная функция апериодического звена 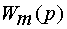 , установленного в цепи положительной
обратной связи по току, задается с помощью блока
, установленного в цепи положительной
обратной связи по току, задается с помощью блока 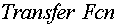 .
.
Для работы с моделью необходимо задать:
§ параметры асинхронного двигателя (блок 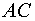 ),
),
§ параметры апериодического звена 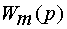 (блок
(блок 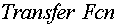 ),
),
§ задание на частоту вращения 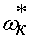 (блок
(блок  ).
).
§ задание на темп изменения скорости 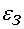 (блок
(блок 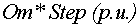 ).
).
§ момент статической нагрузки (блок 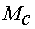 ),
),
В блок 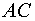 ввести следующие параметры асинхронного двигателя:
ввести следующие параметры асинхронного двигателя:
§ 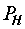 - номинальная мощность на валу, Вт;
- номинальная мощность на валу, Вт;
§ 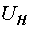 - номинальное фазное напряжение, В;
- номинальное фазное напряжение, В;
§ 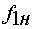 - номинальная частота питающего
напряжения, Гц;
- номинальная частота питающего
напряжения, Гц;
§  - активное сопротивление статора,
Ом;
- активное сопротивление статора,
Ом;
§  - индуктивность рассеивания статора,
Гн;
- индуктивность рассеивания статора,
Гн;
§ 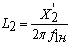 - индуктивность рассеивания ротора,
Гн;
- индуктивность рассеивания ротора,
Гн;
§ 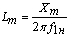 - индуктивность намагничивающего
контура, Гн;
- индуктивность намагничивающего
контура, Гн;
§ 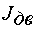 - момент инерции двигателя, кГм2;
- момент инерции двигателя, кГм2;
§ 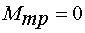 - момент трения, Нм;
- момент трения, Нм;
§ 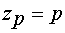 - число полюсов.
- число полюсов.
При введении данных в цепи управления необходимо помнить, что управление 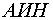 сформировано в относительных
единицах.
сформировано в относительных
единицах.
В блок 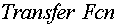 вводятся параметры апериодического звена
вводятся параметры апериодического звена 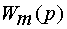 , формула (44):
, формула (44):
§  ;
;
§  - приведение сигнала
- приведение сигнала 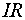 -компенсации, к системе относительных
единиц;
-компенсации, к системе относительных
единиц;
§ 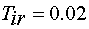 с.
с.
В блоке  вводится верхнее ограничение
вводится верхнее ограничение 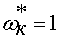 и нижнее ограничение
и нижнее ограничение 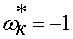 , что соответствует разгону двигателя
до частоты вращения ротора
, что соответствует разгону двигателя
до частоты вращения ротора 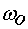 .
.
Темп изменения скорости определяется величиной 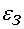 . Ее значение
. Ее значение 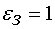 задается в блоке
задается в блоке 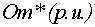 .
.
В блоке 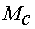 вводятся:
вводятся:
· время появления момента нагрузки 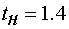 с,
с,
· начальное значение момента нагрузки 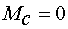 (пуск двигателя производится без
нагрузки),
(пуск двигателя производится без
нагрузки),
· конечное значение момента нагрузки 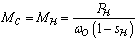 .
.
Время моделирования, в первом приближении, принять равным 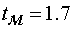 с.
с.
Выполнить моделирование, вывести графики изменения частоты вращения 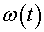 и электромагнитного момента
и электромагнитного момента 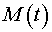 .
.
Определить статическую ошибку регулирования скорости.
|
 . .
|
(48)
|
Проанализировать графики 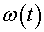 и
и 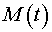 , сделать выводы.
, сделать выводы.
Система управления ПЧ-АД при скалярном управлении с отрицательной
обратной связью по скорости
Функциональная схема системы АИН-АД с отрицательной обратной связью по
скорости приведена на рис. 6.
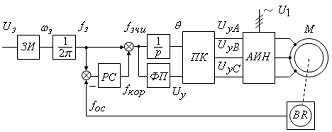
Рисунок 6 - Система АИН-АД с отрицательной обратной связью по скорости
В системе регулирования (рис. 6) питание асинхронного двигателя
осуществляется от инвертора напряжения 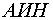 . Управляющим воздействием является
частота
. Управляющим воздействием является
частота 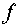 . Задание на напряжение формируется
функциональным преобразователем
. Задание на напряжение формируется
функциональным преобразователем 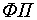 . Его передаточная функция зависит от выбранного закона
регулирования напряжения в функции частоты.
. Его передаточная функция зависит от выбранного закона
регулирования напряжения в функции частоты.
Характер изменения скорости определяется параметрами задатчика
интенсивности 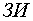 .
.
Система регулирования (рис. 6) относится к классу систем с полузамкнутым
управлением. Сигнал задания частоты складывается из двух сигналов: собственно
сигнала задания частоты 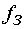 и корректирующего сигнала
и корректирующего сигнала 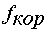 , являющегося выходом регулятора
скорости.
, являющегося выходом регулятора
скорости.
В быстро протекающих процессах действует сигнал управления заданной
частоты 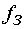 , что соответствует разомкнутому
управлению. В медленных процессах действует обратная связь по угловой скорости,
что соответствует замкнутому управлению.
, что соответствует разомкнутому
управлению. В медленных процессах действует обратная связь по угловой скорости,
что соответствует замкнутому управлению.
Сигнал корректирующей частоты определяется по выражению:
|
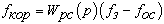 . .
|
(49)
|
На рис. 7 показана структурная схема модели скалярного управления
скоростью асинхронного двигателя с отрицательной обратной связью по скорости.
Схема реализована на блоках библиотек SimPowerSystem.

Рисунок 7 - Структурная схема модели скалярного управления скоростью
асинхронного двигателя с отрицательной обратной связью по скорости
Схема модели аналогична схеме, описанной в разделе 1. Отличительные
особенности схемы модели рис. 7:
§ отсутствуют блоки, формирующие положительную обратную связь по току,
§ отрицательная обратная связь по скорости с узлами суммирования и
регулятором скорости (блок 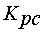 ).
).
Для работы с моделью необходимо задать:
§ параметры асинхронного двигателя (блок 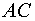 ),
),
§ задание на частоту вращения 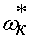 (блок
(блок  ),
),
§ задание на темп изменения скорости 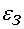 (блок
(блок 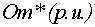 ),
),
§ момент статической нагрузки (блок 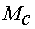 ),
),
§ передаточную функцию регулятора скорости 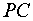 .
.
Задание параметров асинхронного двигателя (блок 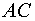 ), частоты вращения
), частоты вращения 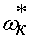 (блок
(блок  ), темпа изменения скорости
), темпа изменения скорости 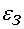 (блок
(блок 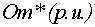 ), момента статической нагрузки (блок
), момента статической нагрузки (блок
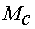 ) производится аналогично разделу
9.1.
) производится аналогично разделу
9.1.
П-регулятор скорости
Коэффициент усиления регулятора скорости:
|
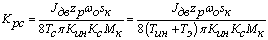 , ,
|
(50)
|
где 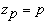 - число полюсов;
- число полюсов; 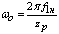 - синхронная частота вращения
ротора, с-1;
- синхронная частота вращения
ротора, с-1; 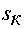 - критическое скольжение;
- критическое скольжение; 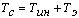 - суммарная малая постоянная времени
контура скорости, с;
- суммарная малая постоянная времени
контура скорости, с; 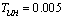 с - постоянная времени запаздывания инвертора напряжения;
с - постоянная времени запаздывания инвертора напряжения;  - электромагнитная постоянная
времени обмоток статора и ротора, с;
- электромагнитная постоянная
времени обмоток статора и ротора, с; 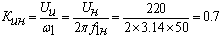 Вс - коэффициент передачи инвертора;
Вс - коэффициент передачи инвертора;
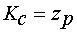 - коэффициент передачи цепи обратной
связи по скорости;
- коэффициент передачи цепи обратной
связи по скорости; 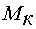 - критический момент, Нм.
- критический момент, Нм.
Время моделирования, в первом приближении, принять равным 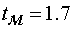 с.
с.
Выполнить моделирование, вывести графики изменения частоты вращения 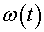 и электромагнитного момента
и электромагнитного момента 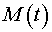 .
.
Определить статическую ошибку регулирования скорости 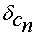 .
.
Проанализировать графики 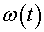 и
и 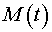 , сделать выводы.
, сделать выводы.
ПИ-регулятор скорости
В структурной схеме модели (рис. 6.5) П-регулятор скорости (блок 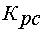 ) заменить ПИ-регулятором скорости с
передаточной функцией:
) заменить ПИ-регулятором скорости с
передаточной функцией:
|
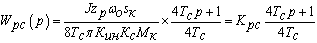 , ,
|
(51)
|
где 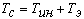 - суммарная малая постоянная времени контура скорости, с.
- суммарная малая постоянная времени контура скорости, с.
Время моделирования, в первом приближении, принять равным 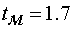 с.
с.
Выполнить моделирование, вывести графики изменения частоты вращения 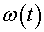 и электромагнитного момента
и электромагнитного момента 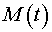 .
.
Определить статическую ошибку регулирования скорости 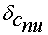 .
.
Проанализировать графики 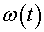 и
и 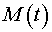 , сделать выводы.
, сделать выводы.
Литература
. Башарин А.В. Управление электроприводами: учеб. пособие для
студ. вузов /А.В. Башарин, В.А. Новиков, Г.Г. Соколовский, Л.: Энергоатомиздат,
Ленингр. отд-ние, 1982.-392 с.
. Браславский И.Я. Энергосберегающий асинхронный
электропривод: учеб. пособие для студ. вузов /И.Я. Браславский, 3.Ш. Ишматов,
В, Н. Поляков; под ред. И.Я. Браславского. М,: Издательский центр
"Академия", 2004.-256 с.
. Вешеневский С.Н. Характеристики двигателей в электроприводе
/С.Н. Вешеневский, М.: Энергия, 1966.-400 с.
. Зворыкин В.Б. Системы управления электроприводами. Модуль
2: Системы подчиненного управления. Учеб. пособие. - Днепропетровск: НМетАУ,
2008.-68 с.
. Зворыкин В.Б. Электропривод переменного тока. Учеб.
пособие.- Днепропетровск: НМетАУ, 2014.- 138 с.
. Поздеев А.Д Электромагнитные и электромеханические процессы
в частотно-регулируемых асинхронных электроприводах /А.Д. Поздеев. Чебоксары:
Изд-во Чуваш. ун-та, 1998.-172 с.
. Сабинин Ю.А. Частотно-регулируемые асинхронные
электроприводы /Ю.А Сабинин, В.Л. Грузов. Л.: Энергоатомиздат, Ленинг. отд-ние,
1985.-128 с.
. Системы подчиненного регулирования электроприводов
переменного тока с вентильными преобразователями /О.В. Слежановский, Л.Х.
Дацковский, И.С. Кузнецов, Е.Д. Лебедев и др. М,: Энергоатомиздат, 1983.-256 с.
. Соколовский Г.Г. Электроприводы переменного тока с
частотным управлением. /Г.Г. Соколовский. - М,: Издательский центр
"Академия", 2006.-264 с.
. Чернышев А.Ю. Электропривод переменного тока: учебное
пособие /А.Ю. Чернышев, Ю.Н. Дементьев, И.А. Чернышев. - Томск: Изд-во Томского
политехнического университета, 2011.-213 с.
. Цифровые электроприводы с транзисторными преобразователями
/С.Г. Герман-Галкин, В.Д. Лебедев, Б.А. Марков, Н.Г.Чичерин. Л.:
Энергоатомиздат, Ленингр. отд-ние, 1986.-248 с.
. Шрейнер Р. Т. Математическое моделирование электроприводов
переменного тока с полупроводниковыми преобразователями частоты /Р.Т. Шрейнер.
Екатеринбург: УРО РАН, 2000.-654 с.
. Шубенко В.А. Тиристорный асинхронный электропривод с
фазовым управлением / В.А. Шубенко, И.Я. Браславский. М,: Энергия, 1972.-200 с.
Приложение
Варианты заданий к курсовой работе