Теория вероятностей и математическая статистика
Министерство
образования и науки Российской федерации
Филиал
ГОУ ВПО БГУЭП «Байкальский государственный университет экономики и права» в
г.Усть-Илимске
Контрольная
работа по курсу
«Теория
вероятностей и математическая статистика»
Вариант
7
Выполнил
студент гр._______
Семенова
Е.С.
Усть-Илимск
Задача 1
Крупная торговая компания занимается оптовой
продажей материалов для строительства и ремонта жилья и, имея список
покупателей в 3 регионах, рассылает им по почте каталог товаров. Менеджер
компании полагает, что вероятность того, что компания не получит откликов на
разосланные предложения ни из одного региона, равна 0,25. Чему в этом случае
равна вероятность того, что компания получит ответ хотя бы из одного региона?
Решение. Введем следующие событие А={компания не
получит откликов на разосланные предложения ни из одного региона}, тогда
событие, что компания получит ответ хотя бы из одного региона ему
противоположное. Вероятность противоположного события равна и составляет 0,75.
Ответ: 0,75
Задача 2
В лотерее разыгрывается автомобиль стоимостью
5000 д.е., 4 телевизора стоимостью 250 д.е., 5 видеомагнитофонов стоимостью 200
д.е. Всего продается 1000 билетов по 7 д.е. Составить закон распределения
чистого выигрыша, полученного участником лотереи, купившим один билет. Найти
дисперсию этой случайной величины.
Решение. Пусть дискретная случайная величина Х
соответствует чистому выигрышу лотереи. Значения, которые может принимать
данная величина:
|
Чистый
выигрыш
|
Событие
лотереи
|
|
-7
|
Билет
не выиграл (проигрыш)
|
|
5000-7=4993
|
Билет
выиграл автомобиль
|
|
250-7
= 243
|
Билет
выиграл телевизор
|
|
200-7
= 193
|
Билет
выиграл видеомагнитофон
|
Количество выигрышных билетов составляет 1 + 4 +
5 = 10 шт. Тогда проигрышных билетов 1000 - 10 = 990 шт.
Определим вероятности событий лотереи:
Р(Х = -7) = 990/1000 = 0,99
Р(Х = 4993) = 1/1000 = 0,001
Р(Х = 243) = 4/1000 = 0,004
Р(Х = 193) = 5/1000 = 0,005
Составим ряд распределения:
|
хi
|
-7
|
193
|
243
|
4993
|
|
pi
|
0.99
|
0.005
|
0.004
|
0.001
|
Математическое ожидание случайной
величины Х найдем по формуле 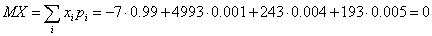 , то есть вся полученная выручка от
продажи билетов идет на приобретение призов.
, то есть вся полученная выручка от
продажи билетов идет на приобретение призов.
Для определения дисперсии
воспользуемся формулой 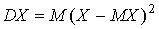 . Для
дискретной случайной величины имеем
. Для
дискретной случайной величины имеем 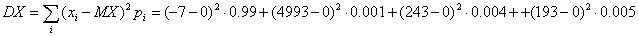
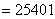
Ответ: 25401
Задача 3
Случайная величина Х распределена по
закону с плотностью 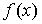 , зависящей
от постоянного параметра С:
, зависящей
от постоянного параметра С:
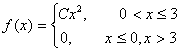 .
.
Найти: 1) значение постоянной С; 2)
функцию распределения 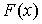 ; 3)
математическое ожидание и дисперсию случайной величины Х; 4) вероятность того,
что случайная величина Х примет значение из интервала (0, 2); 5) построить
графики функций
; 3)
математическое ожидание и дисперсию случайной величины Х; 4) вероятность того,
что случайная величина Х примет значение из интервала (0, 2); 5) построить
графики функций 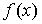 ,
, 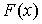 .
.
Решение. 1) Для определения
постоянной С воспользуемся основным свойством функции плотности
вероятности 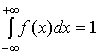 (пределы
интегрирования соответствуют спектру случайной величины или ее возможным значениям).
В нашем случае имеем
(пределы
интегрирования соответствуют спектру случайной величины или ее возможным значениям).
В нашем случае имеем 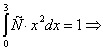
 =
=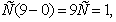 откуда
откуда 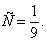
) Используя формулу 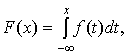 найдем
функцию распределения
найдем
функцию распределения
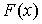 Если
Если  то
то 
Для 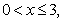
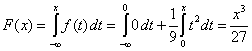
Если 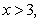 то
то 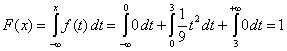
Таким образом, 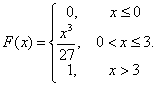
) Математическое ожидание и
дисперсию величины Х найдем по формулам 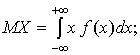
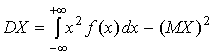 (пределы интегрирования также
соответствуют спектру случайной величины Х). В нашем случае
(пределы интегрирования также
соответствуют спектру случайной величины Х). В нашем случае 
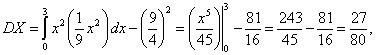
) Вероятность реализации значений
случайной величины Х в интервале 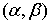 можно определить по формуле
можно определить по формуле 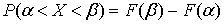 . С
использованием функции распределения
. С
использованием функции распределения 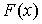 имеем
имеем 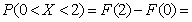
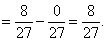
) Графики функций 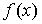 и
и 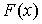 изображены
на рис.1 и рис.2.
изображены
на рис.1 и рис.2.
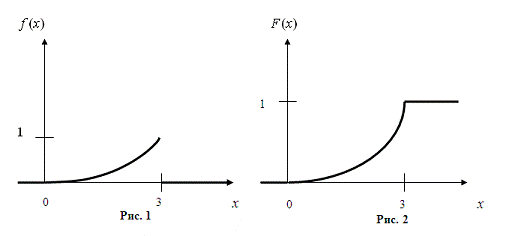
Задача 4
Цена некой ценной бумаги нормально распределена.
В течение последнего года на протяжении 20% рабочих дней цена была ниже 20. В
75% случаев цена была выше 25. Найти математическое ожидание и среднее
квадратическое отклонение цены.
Решение. Случайная величина Х - цена
некой ценной бумаги распределена по нормальному закону. Для решения задачи
используем формулу
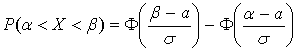 ,
,
где 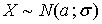 ,
, 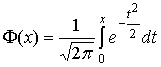 - функция Лапласа.
- функция Лапласа.
По условию задачи:
Р(Х<20) = 0.2
Р(Х>25) = 0.75
Вероятность 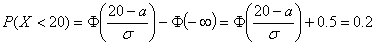
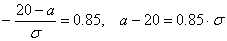
Вероятность 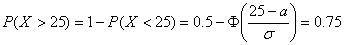
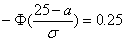 ,
,
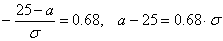
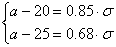
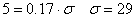
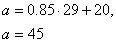
Ответ: МХ=45, 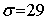
Задача 5
Имеются следующие данные о стоимости основных
фондов у 50 предприятий (млн. руб.): 9,4; 8; 6,3; 10; 15; 8,2; 7,3; 9,2; 5,8;
8,7; 5,2; 13,2; 8,1; 7,5; 11,8; 14,6; 8,5; 7,8; 10,5; 6; 5,1; 6,8; 8,3; 7,7;
7,9; 9; 10,1; 8; 12; 14; 8,2; 9,8; 13,5; 12,4; 5,5; 7,9; 9,2; 10,8; 12,1; 12,4;
12,9; 12,6; 6,7; 9,7; 8,3; 10,8; 15; 7; 13; 9,5.
Задание:
1. По данным выборки построить
точечный вариационный ряд, распределив значения 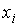 по частотам
по частотам 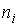 (ряд 1).
(ряд 1).
2. От ряда 1 перейти к интервальному ряду (ряд
2).
. От ряда 2 перейти к точечному ряду,
распределив значения по частотам (ряд 3) и относительным частотам в виде доли и
в виде процента (ряд 4).
. Построить: а) гистограмму относительных частот
для ряда 2; б) полигон частот для ряда 3; в) кумулятивную кривую для ряда 3.
. Найти эмпирическую функцию распределения
случайной величины Х, используя ряд 3, и построить ее график.
6.Определить выборочное среднее 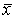 , выборочную
дисперсию DВ, выборочное
среднее квадратическое отклонение
, выборочную
дисперсию DВ, выборочное
среднее квадратическое отклонение  , коэффициент вариации V, моду
, коэффициент вариации V, моду 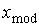 и медиану
и медиану 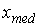 по точечному
ряду 1 и интервальному ряду 2.
по точечному
ряду 1 и интервальному ряду 2.
. Указать несмещенные оценки
неизвестного математического ожидания и неизвестной дисперсии случайной
величины Х - производительности труда.
. В предположении, что выборка
извлечена из нормальной генеральной совокупности, построить доверительные
интервалы для неизвестных математического ожидания и дисперсии (принять 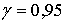 ).
).
Решение.
. Для того чтобы построить точечный
вариационный ряд, расположим наблюдаемые значения 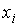 в порядке
их возрастания и относительно каждого
в порядке
их возрастания и относительно каждого 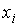 укажем частоту
укажем частоту 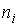 , т.е.
количество повторений
, т.е.
количество повторений 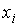 в выборке;
при этом сумма всех частот равна объему выборки n.
в выборке;
при этом сумма всех частот равна объему выборки n.
Ряд 1:
|
xi
|
5,1
|
5,2
|
5,5
|
5,8
|
6
|
6,3
|
6,7
|
6,8
|
7
|
7,3
|
7,5
|
7,7
|
7,8
|
7,9
|
|
ni
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
2
|
|
xi
|
8
|
8,1
|
8,2
|
8,3
|
8,5
|
8,7
|
9
|
9,2
|
9,4
|
9,5
|
9,7
|
9,8
|
10
|
10,1
|
|
ni
|
2
|
1
|
2
|
1
|
1
|
1
|
2
|
1
|
1
|
1
|
1
|
1
|
1
|
|
xi
|
10,5
|
10,8
|
11,8
|
12
|
12,1
|
12,4
|
12,6
|
12,9
|
13
|
13,2
|
13,5
|
14
|
14,6
|
15
|
|
ni
|
1
|
2
|
1
|
1
|
1
|
2
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
2
|
Объем выборки 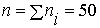 , а число
различных значений r =42.
, а число
различных значений r =42.
. Так как объем выборки велик и
число различных значений исследуемого случайного признака также велико, то
перейдем от точечного ряда 1 к интервальному. Наименьшее значение в выборке 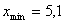 и
наибольшее
и
наибольшее 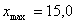 Обследуемый
диапазон [5,1;15,0] разбиваем на число интервалов k, где
Обследуемый
диапазон [5,1;15,0] разбиваем на число интервалов k, где 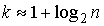 ≈7.Определяем
величину шага группирования h:
≈7.Определяем
величину шага группирования h:
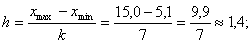
Ряд 2:
|
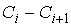 5,1.. 6,56,5.. 7,97,9.. 9,39,3..10,7 5,1.. 6,56,5.. 7,97,9.. 9,39,3..10,7
|
|
|
|
|
|
 69127 69127
|
|
|
|
|
|
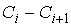 10,7
- 12,112,1
- 13,513,5
- 15,0 10,7
- 12,112,1
- 13,513,5
- 15,0
|
|
|
|
|
|
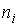 574 574
|
|
|
|
|
3. Перейдем от интервального ряда 2
к точечному. Для этого вычислим середины интервалов 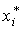 и
сопоставим им частоты
и
сопоставим им частоты 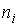 или
относительные частоты
или
относительные частоты 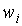 .
Распределение по частотам запишем в виде ряда 3, а распределение по
относительным частотам в виде ряда 4:
.
Распределение по частотам запишем в виде ряда 3, а распределение по
относительным частотам в виде ряда 4:
Ряд 3:
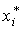 5,87,28,610,011,412,814,2
5,87,28,610,011,412,814,2
|
|
|
|
|
|
|
|
|
|
|
|
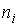 69127574 69127574
|
|
|
|
|
|
|
|
|
|
Ряд 4:
|
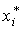 5,8 5,8
|
7,2
|
8,6
|
10,0
|
11,4
|
12,8
|
14,2
|
|
|
|
|
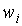 0,120,180,240,140,10,140,08 0,120,180,240,140,10,140,08 , ,
|
|
|
|
|
|
|
|
|
|
|
 12 12
|
18
|
24
|
14
|
10
|
14
|
8
|
|
4. Гистограмма относительных частот изображена
на рисунке 3.
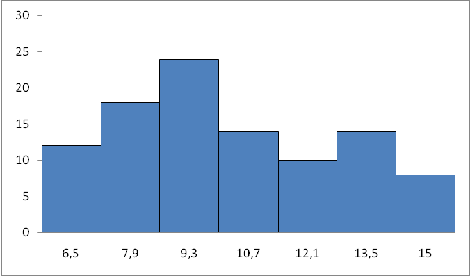
Рисунок 3 - Гистограмма относительных частот
Полигон частот показан на рисунке 4.
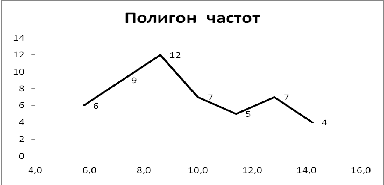
Рисунок 4 - Полигон частот
Для построения кумуляты представим
ряд 3 по накопленным частотам 
|
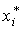 5,8 5,8
|
7,2
|
8,6
|
10,0
|
11,4
|
12,8
|
14,2
|
|
|
|
 6152734394650 6152734394650
|
|
|
|
|
|
|
|
|
Тогда кумулятой будет плавная кривая,
изображенная на рисунке 5.
Рисунок 5 - Кумулятивная кривая
. Эмпирическая функция распределения для ряда 3
запишется в виде:
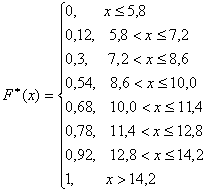
График 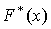 изображен
на рисунке 6.
изображен
на рисунке 6.
Рисунок 6 - Функция распределения
. Для упрощения вычислений расчет характеристик
выборки произведем по ряду 3.
Найдем выборочное среднее
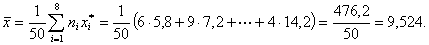
Выборочную дисперсию 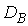 определим
по формуле:
определим
по формуле:
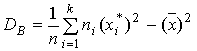 .
.
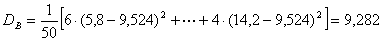
Выборочное среднее квадратическое
отклонение 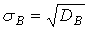 =3,05;
=3,05;
Коэффициент вариации 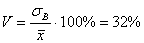 .
.
Определим моду и медиану. Мода 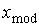 исследуемой
случайной величины Х есть такое ее возможное значение, которое наиболее
часто встречается в ряду наблюдений. В случае интервального ряда 2 вначале
определим интервал, содержащий моду, как наибольшей по частоте или
относительной частоте. Вычислим моду по формуле:
исследуемой
случайной величины Х есть такое ее возможное значение, которое наиболее
часто встречается в ряду наблюдений. В случае интервального ряда 2 вначале
определим интервал, содержащий моду, как наибольшей по частоте или
относительной частоте. Вычислим моду по формуле:
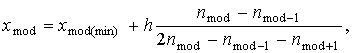
Для данной выборки интервал,
содержащий моду - [7,9-9,3] (ему соответствует наибольшая частота 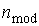 , равная
12).
, равная
12).
Здесь 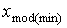 = 7,9; h = 1,4;
= 7,9; h = 1,4; 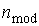 = 12,
= 12, 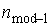 = 9,
= 9,  = 7,
= 7,
тогда 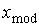
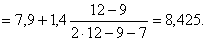
Медиана 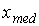 определяется
как средний (серединный) член в упорядоченной последовательности значений
случайной величины.
определяется
как средний (серединный) член в упорядоченной последовательности значений
случайной величины.
п = 50, поэтому в качестве
медианы возьмем любое значение между 25-м и 26-м членами ряда 1: 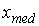 = 9,0.
= 9,0.
В случае интервального ряда вначале
определим интервал, содержащий медиану, по накопленным частотам: медианному
интервалу соответствует первая из накопленных частот, превышающая половину
объема выборки. Затем медиану определим по формуле
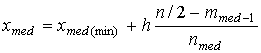 .
.
Медианному интервалу заданного
эмпирического распределения в виде ряда 2 соответствует накопленная частота 71,
отсюда 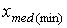 =7,9; h=1,4;
=7,9; h=1,4; 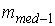 = 15;
= 15; 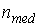 =12.
Используя формулу, получим
=12.
Используя формулу, получим
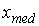 =
=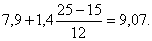
Таким образом, средняя стоимость
основных фондов изученных предприятий составила 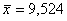 (тыс. руб.), абсолютный разброс
значений показателя Х равен
(тыс. руб.), абсолютный разброс
значений показателя Х равен 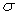 =3,05 (тыс. руб.), относительный
разброс
=3,05 (тыс. руб.), относительный
разброс 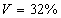 . Наибольшее
число предприятий имеют стоимость основных фондов, равную 8,425 (тыс. руб.), а
половина - более 9,07 (тыс. руб.)
. Наибольшее
число предприятий имеют стоимость основных фондов, равную 8,425 (тыс. руб.), а
половина - более 9,07 (тыс. руб.)
Построенные вариационные ряды 1-3,
их графические изображения (рис. 3-6) представляют данные в компактном виде.
Кроме этого имеется возможность получить сведения о законе распределения
вероятностей исследуемой случайной величины. Здесь внешний контур гистограммы
(рис. 3), графики кумулятивной кривой (рис. 5) и эмпирической функции
распределения (рис. 6) свидетельствуют о близости эмпирического распределения к
нормальному закону. К этому же выводу можно прийти, сравнивая значения
выборочного среднего, моды, медианы. Так как 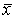 ,
, 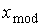 и
и 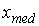 незначительно отличаются друг от
друга (
незначительно отличаются друг от
друга (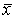 »
»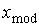 »
»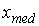 »9,00), есть основание
предполагать, что теоретическое распределение симметрично относительно своего
среднего значения, что является еще одним доводом в пользу выбора модели
нормального закона.
»9,00), есть основание
предполагать, что теоретическое распределение симметрично относительно своего
среднего значения, что является еще одним доводом в пользу выбора модели
нормального закона.
. Если считать, что случайная
величина Х - стоимость основных фондов - нормально распределена с
математическим ожиданием 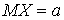 и
дисперсией
и
дисперсией 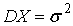 , то
несмещенными оценками этих параметров, найденными по выборке объема
, то
несмещенными оценками этих параметров, найденными по выборке объема 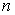 , будут
, будут 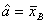 и
и 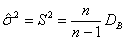 . В нашем
случае
. В нашем
случае 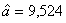 (тыс.
руб.),
(тыс.
руб.), 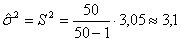 ,
, 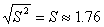 (тыс.
руб.).
(тыс.
руб.).
. Интервальные оценки для
неизвестных параметров или доверительные интервалы, покрывающие истинные
(неизвестные) значения параметров с заданной доверительной вероятностью
(надежностью) 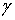 , найдем по
формулам
, найдем по
формулам
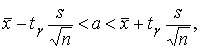
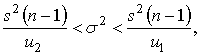
где 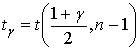 находится из таблицы квантилей
распределения Стьюдента при числе степеней свободы, равном
находится из таблицы квантилей
распределения Стьюдента при числе степеней свободы, равном 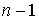 , и уровне
, и уровне 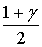 ;
; 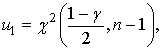
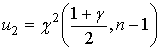 - квантили
распределения
- квантили
распределения 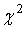 .
.
Для 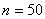 и
и 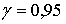 имеем
имеем 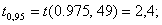
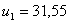 и
и 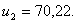 Следовательно,
Следовательно,
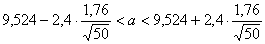 ,
,
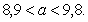
То есть мы на 95% уверены в том, что
средняя стоимость основных фондов для предприятий данной отрасли будет от 8,9
до 9,8 (т.руб.).
Для неизвестной дисперсии можно
записать
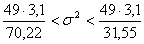 ,
,
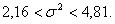
Задача 6
Страховая компания изучает
вероятность ДТП для подростков, имеющих мотоциклы. За прошедший год проведена
случайная выборка 2000 страховых полисов подростков-мотоциклистов и выявлено,
что 15 из них попадали в ДТП и предъявили компании требование о компенсации за
ущерб. Может ли аналитик компании отклонить гипотезу о том, что менее 1% всех
подростков-мотоциклистов, имеющих страховые полисы, попали в ДТП в прошлом году
(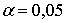 )?
)?
Решение. Предположим, что случайная величина Х
- количество подростков-мотоциклистов, имеющих страховые полисы, которые попали
в ДТП в прошлом году - биноминально распределена с параметрами
N=2000,
p=15/2000
= 0.0075
X~B(N,p).
Следуя общей схеме проверки гипотез, имеем:
этап - формулировка гипотезы:
H0
: p
< 0.01, H1
: p
≥
0.01
Необходимо проверить основную
гипотезу Н0 - вероятность, того что подростки-мотоциклисты,
имеющие страховые полисы, попавшие в ДТП в прошлом году, не превосходит 0,01
(1%). Конкурирующая гипотеза 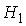 определяется как обратное условие.
определяется как обратное условие.
этап - выбор уровня значимости 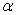 , который
равен вероятности отвергнуть Н0, при условии, что она верна
(ошибка первого рода).
, который
равен вероятности отвергнуть Н0, при условии, что она верна
(ошибка первого рода).
α=0,05.
этап - выбор критерия. Статистика
критерия
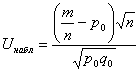
является случайной величиной,
распределенной по стандартному биноминальному закону.
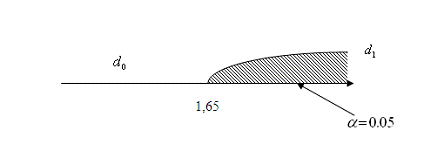
этап - выбор критической точки. Так
как критическая область 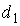 или область
отклонения гипотезы Н0 определяется неравенством U > uкр, то есть
является правосторонней. Тогда uкр можно найти
по таблице значений функции Лапласа из условия:
или область
отклонения гипотезы Н0 определяется неравенством U > uкр, то есть
является правосторонней. Тогда uкр можно найти
по таблице значений функции Лапласа из условия:
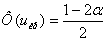
Ф(uкр) = 0,45 uкр = 1,65
этап - расчет наблюдаемого или
экспериментального значения критерия. В статистику критерия подставляем данные
выборки

Так как  , то
гипотеза
, то
гипотеза  принимается,
т.е. следует считать, что количество подростков-мотоциклистов, попавших в ДТП
меньше 1% из всех имеющих страховые полисы.
принимается,
т.е. следует считать, что количество подростков-мотоциклистов, попавших в ДТП
меньше 1% из всех имеющих страховые полисы.
Задача 7
При уровне 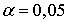 установить
значимость влияния фактора
установить
значимость влияния фактора 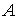 по следующим данным
по следующим данным
|
Номер
испытания
|
Уровни
фактора 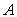 а1 а2 а3
а4 а1 а2 а3
а4
|
|
1
2 3 4
|
51
52 56 55 59 58 56 50 53 66 58 56 59 69 58 57
|
Дать экономическую интерпретацию
фактору 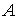 , его
уровнем
, его
уровнем 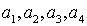 , а также
результату
, а также
результату 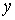 .
.
Решение.
|
Номер
испытания
|
Уровни
фактора  а1 а2 а3
а4 а1 а2 а3
а4
|
|
1
2 3 4
|
51
52 56 55 59 58 56 50 53 66 58 56 59 69 58 57
|
|
среднее
|
55,5
61,25 57 54,5
|
SSобщ 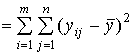 ,
,
SSА =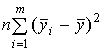
SSR 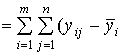 )2 =
SSобщ - SSА.
)2 =
SSобщ - SSА.
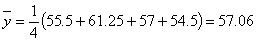 ;
;
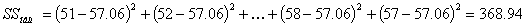 ;
;
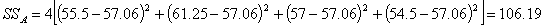 ;
;
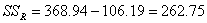 .
.
статистическая
математическая задача дисперсия
Проверка значимости влияния фактора
А соответствует проверке основной гипотезы 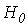 :
: 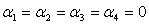 , где αi - средний
эффект
, где αi - средний
эффект 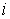 -го уровня
фактора А,
-го уровня
фактора А, 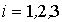 ,4 т. е.
гипотеза
,4 т. е.
гипотеза 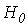 состоит в
том, что все уровни фактора, исследуемые в эксперименте, не оказывают
существенного влияния. Проверку этой гипотезы осуществляем на 5% уровне
значимости. Расчеты сведем в таблицу дисперсионного анализа:
состоит в
том, что все уровни фактора, исследуемые в эксперименте, не оказывают
существенного влияния. Проверку этой гипотезы осуществляем на 5% уровне
значимости. Расчеты сведем в таблицу дисперсионного анализа:
Однофакторный дисперсионный анализ
Источник
изменчивости Число степеней свободы Сумма квадратов Средний
квадрат Критерий Фишера 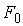 Критическая точка
Критическая точка
|
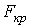 Гипотеза Гипотеза 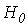
|
|
|
|
|
Фактор
А
|
3
|
106.19
|
35.4
|
3
|
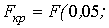 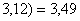 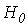 : : 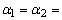 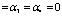
|
|
|
Ошибка
|
12
|
262.75
|
21.9
|
-
|
|
|
|
Итог
|
15
|
368.94
|
-
|
-
|
|
|
Так как 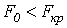 (3<3,49),
гипотезу
(3<3,49),
гипотезу 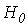 на уровне
значимости 0,05 следует принять, т. е. отклонить значимость фактор А.
на уровне
значимости 0,05 следует принять, т. е. отклонить значимость фактор А.