Линии с распределенными параметрами

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

"Московский Государственный Институт

Радиотехники, электроники и автоматики (технический университет)"

Контрольная работа

по электротехнике

Линии с распределенными параметрами.

Выполнил: Соловьев А.А.

Проверил: Любарская Т.А.

Москва, 2012 г.

Задача

Линии с распределенными параметрами.

По данным в Таблицы №1 параметрам линии (R₀, L₀, G₀, C₀), частоте f и длиннее линии l, комплексным значениям 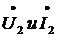 в конце линии, сопротивлению нагрузки 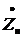требуется:

. Рассчитать 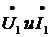 в начале линии, активную P и полную S мощности в начале и конце линии, а так же КПД линии.

. Пологая, что линия стала линии без потерь (R₀ = G₀ = 0), а нагрузка на конце линии, а нагрузка на конце линии стала активной и равной модулю комплексной нагрузки, определить напряжение и ток 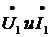в начале линии, а также длину волны электромагнитной линии .

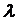. Для линии без потерь из пункта 2 построить график распределения действующего значения напряжения вдоль линии в функции координаты у.

Таблица №1

Схема линий с распределенными параметрами

Найдем 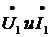. Затем рассчитаем активную P и полную S мощности в начале и конце линии, а так же КПД линии.

Напишем телеграфные уравнения для синусоидального сигнала

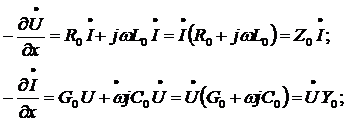
где

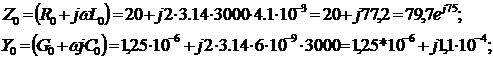
Теперь найдем 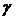 - это постоянная распространения и  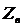- это волновое сопротивление:

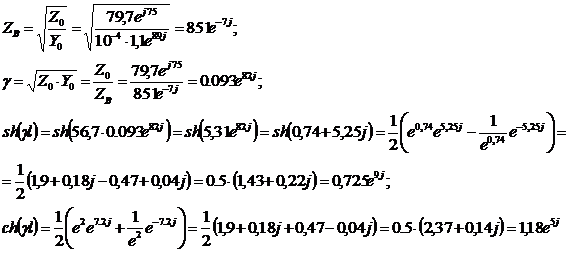
Используя следующие выражения для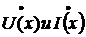  

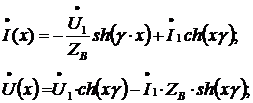
При х = l, мы получим что U (x) = U₂, а I (x) = I₂. Выражаем 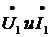из этих двух уравнений, так как остальные части этих уравнений нам известны или были вычислены выше, то получим систему из 2х уравнений и 2х неизвестных: .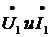

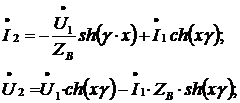
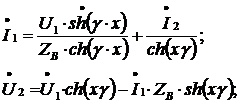
Подставим первое уравнение во второе и получим:

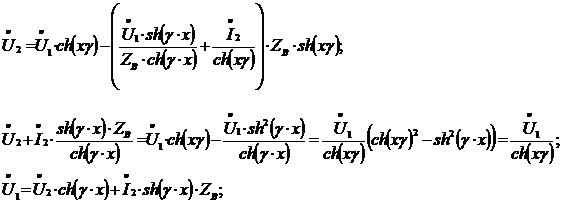
Подставляя уравнение 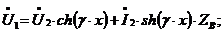 (2) в уравнение в уравнение 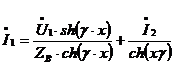, получим уравнение для тока I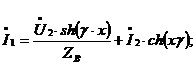₁:

 (1)

Теперь подставим в уравнения (1) и (2) числа и получаем результат. При этом учесть что U₂ = I₂ * Z_н = > I₂ = U_2/Z_н = 42,3/423 = 0,1А.

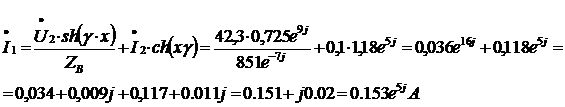
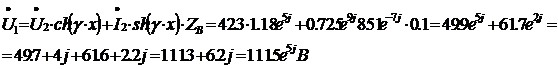
Теперь рассчитаем мощности и КПД:

,

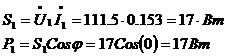КПД линии:

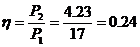
линия распределенный параметр электрическая

Для линии без потерь, рассчитаем напряжение U₁ и ток I₁ в начале линии и длину электрической волны.

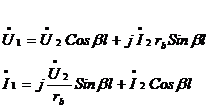  (1)

где:

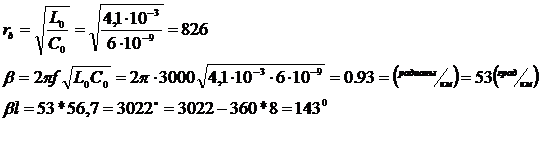
Тогда рассчитаем систему уравнений (1) и получим:

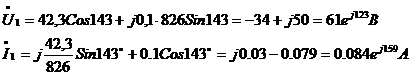
Длина электрической волны:

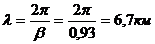
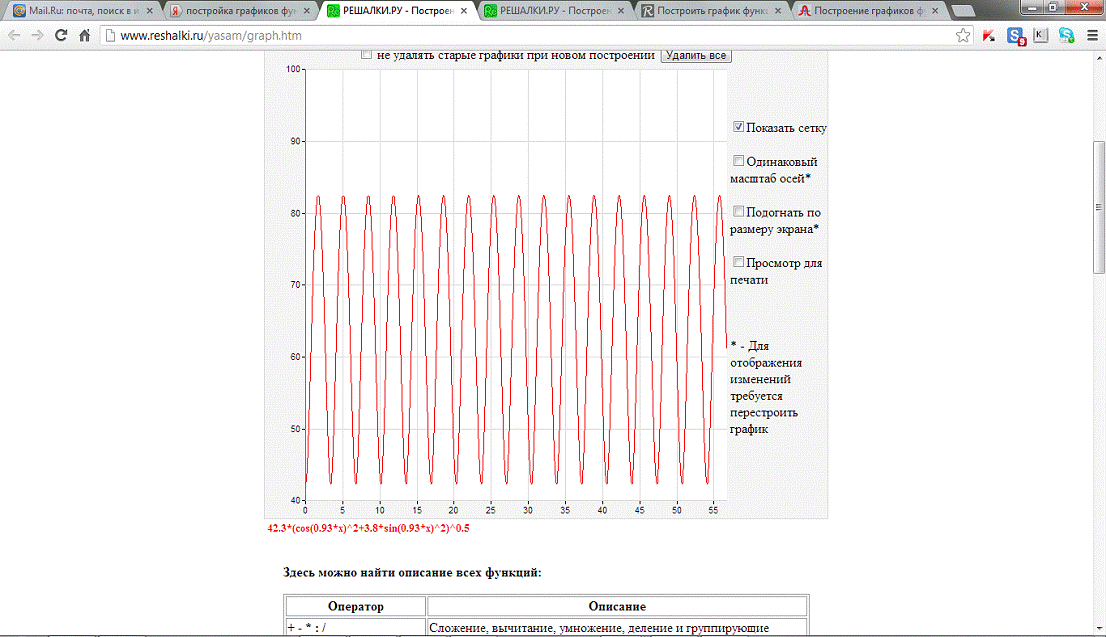
Построим график распределения действующего значения напряжения вдоль линии в функции координаты у

С помощью уравнения 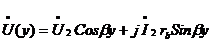составим функцию, которая выражала бы значение напряжения U от длинны у. Сделаем это с помощь соотношения .

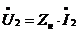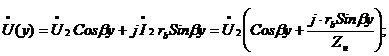
Теперь возьмем модуль этой функции, так как числ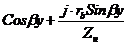о  - комплексное, а напряжение действительное, то:

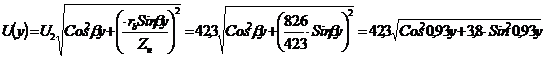
График зависимости напряжения U от расстояния у.