Цепи с распределенным параметрами
Введение
Интерес к распределенным электромагнитным
системам возник еще в середине XIX в. под влиянием ряда актуальных для того
времени технических задач, связанных с передачей вначале телеграфных, а затем и
телефонных сообщений на значительные расстояния. Первым объектом изучения среди
распределенных электромагнитных систем стала линия передачи, образованная,
например, двумя параллельными проводниками при условии, что протяженность
системы вдоль оси сравнима с длиной волны передаваемых колебаний. Подобные
линии передачи в то время назвали «длинными линиями». Но данная проблема
актуальна и в наше время, так как линии используются для передачи
электроэнергии и сигналов различного рода. Так же широко используются
направленные линии передачи принципиально иной структуры - так называемые полые
волноводы, представляющие собой металлические трубы, обычно прямоугольного или
круглого сечения. Эти линии передачи, широко применяемые в радиотехнике для
передачи колебаний с частотами в гигагерцевом диапазоне.
Для оценки, к какому типу отнести
цепь: с сосредоточенными или распределенными параметрами - следует сравнить ее
длину 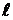 с длиной
электромагнитной волны
с длиной
электромагнитной волны 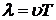 . Если
. Если 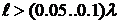 , т.е. при T=0.02 c, и
, т.е. при T=0.02 c, и 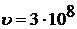 м/с,
получаем
м/с,
получаем 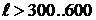 км. Для
км. Для 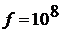 Гц и
Гц и 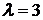 м, т.е. уже
при
м, т.е. уже
при 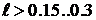 м к линии
следует подходить как к цепи с распределенными параметрами.
м к линии
следует подходить как к цепи с распределенными параметрами.
Ранее, при изучении цепей с сосредоточенными
параметрами уже рассматривались линии электропередачи, при частоте 50 Гц и
напряжениях до 35 кВ небольшой длины, в которых можно пренебречь токами,
обусловленными емкостью между проводами (токами смещения) и проводимостью
изоляции (токами утечки через гирлянды изоляторов и токами, обусловленными
коронным электрическим разрядом вблизи поверхности проводов). При больших
напряжениях, встречающихся в электроэнергетике, и при больших частотах, с
которыми имеет дело электросвязь, а также при значительной длине линии
пренебрегать токами смещения и утечки недопустимо. Следовательно, ток в
проводах не одинаков в разных сечениях линии.
Ток в проводах линии вызывает падение напряжения
в активном сопротивлении проводов и создает переменное магнитное поле, которое
в свою очередь наводит вдоль всей линии э.д.с. самоиндукции. Поэтому напряжение
между проводами также не остается постоянным вдоль линии.
Чтобы учесть изменение тока и напряжения вдоль
линии, нужно считать, что сколь угодно малый элемент линии обладает
сопротивлением и индуктивностью, а между проводами - проводимостью и емкостью,
то есть рассматривать линию как цепь с распределенными параметрами. Такую линию
называют длинной.
Для идеализации считается, что сопротивление,
индуктивность, проводимость и емкость равномерно распределены вдоль линии.
Такую линию принято называть однородной.
Об идеализации следует говорить, так как в
реальной линии утечку тока через гирлянды изоляторов нужно рассматривать как
совокупность ряда сосредоточенных процессов. Кроме того, провес проводов на
длине пролета линии изменяет равномерность распределения их емкости и индуктивности.
В цепях с распределенными параметрами, например
в длинных линиях, обмотках электрических машин и трансформаторов и т.п.,
включение и отключение какого-либо участка сопровождается переходными
процессами (так же как и в цепях с сосредоточенными параметрами). При большой
протяженности линий изменение внешних электрических и магнитных полей, например
при грозовых разрядах, также вызывает переходные процессы. Переходные процессы
в линиях возникают и при передаче телеграфных и телефонных сигналов, телемеханических
импульсов или специальных импульсов для проверки линий и выявления места их
повреждения.
Во всех случаях при анализе переходных процессов
в цепях с распределенными параметрами необходимо исходить из общих
закономерностей и дифференциальных уравнений, рассмотренных для случая
однородной длинной линии.
Постановка задачи
1. Рассчитать исходные данные работы
согласно варианту задания и записать их.
2. Найти распределение действующих значений
напряжения и тока вдоль линии, замкнутой на заданную нагрузку в установившемся
режиме. Построить графики U(y), I(y).
. Произвести расчёт установившегося
режима в линии, заменив нагрузку волновым сопротивлением. Построить графики U(y),
I(y).
. Произвести расчёт установившегося
значения в линии при отключённой нагрузке (режим холостого хода). Построить
графики U(y), I(y).
. Построить графики uп(x),
iп(x)
распределения падающих волн напряжения и тока в переходном режиме для момента,
когда фронт падающих волн достигнет конца линии.
. Определить законы изменения тока и
напряжения нагрузки в переходном режиме. Построить графики uн(t),
iн(t).
. Определить законы изменения отражённых
волн напряжения и тока в сечении нагрузки. Построить графики uо(t),
iо(t).
8. Построить графики uо(x), iо(x)
распределения напряжения и тока отражённой волны вдоль линии при переходном
режиме для момента времени, когда фронт отражённой волны достигнет точки на
расстоянии “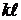 ” от конца
линии.
” от конца
линии.
. Построить графики u(x), i(x) распределения
напряжения и тока вдоль линии при переходном режиме для момента времени, когда
фронт отражённой волны достигнет точки на расстоянии “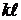 ” от конца
линии.
” от конца
линии.
. Построить графики u(t), i(t) при
переходном режиме для точки, находящейся на расстоянии “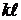 ” от конца
линии.
” от конца
линии.
Расчёт
. Номер варианта определяется числом 16166.
Тогда, согласно исходным данным получим:
1m
= 20(1 + N/2) = 20(1 + 16/2)
= 180 В;
f = 100(50 - N)
= 100(50 - 16) = 3400 Гц;
l = 5(N
+ 3) = 5(16 + 3) = 95 км;
k = 0.4; p
= 0.8 .
Параметры нагрузки: r1
= 200 Ом; L = 0.1 Гн.
Схема нагрузки приведена ниже
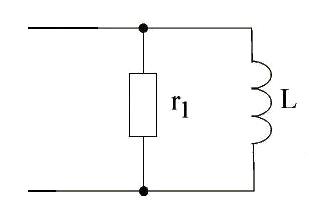
.Найдем распределение действующих значений
напряжения и тока вдоль линии, замкнутой на заданную нагрузку в установившемся
режиме. Построим графики U(y),
I(y)
Напряжение и ток в произвольном сечении линии
без потерь, находящемся на расстоянии “y”
от конца линии, описываются выражениями:
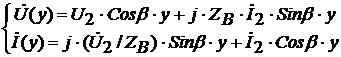 (1)
(1)
где 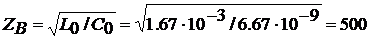 Ом;
Ом;
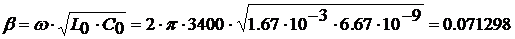 рад/км.
рад/км.
Преобразуем систему уравнений (1) к
следующему виду:
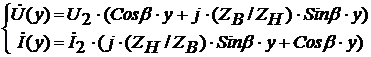 (2)
(2)
где 
Согласно варианту задания,
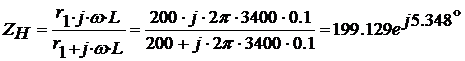 Ом.
Ом.
Полагая y = l, из первого
уравнения системы (2) выразим напряжение
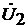
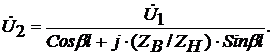
После подстановки конкретных
значений получим
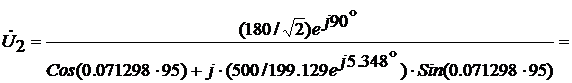
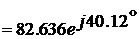
Тогда ток в конце линии определяется
как
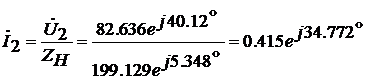
Комплексы действующих значений
напряжения и тока в произвольном сечении линии, находящемся на расстоянии “y” от её
конца, получим из системы уравнений (2) с учетом определенных значений  и
и  :
:
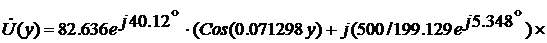
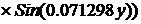
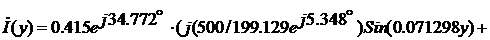
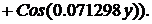
В комплексных выражениях 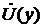 и
и 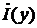 выделим
действительные и мнимые части:
выделим
действительные и мнимые части:
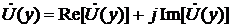 ;
; 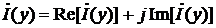 .
.
Модули действующих значений U(y) и I(y) напряжения
и тока:
 ;
; 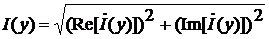 .
.
По полученным выражениям U(y) и I(y) с учетом
численных значений построим графики, представленные на рис. 1 и 2.
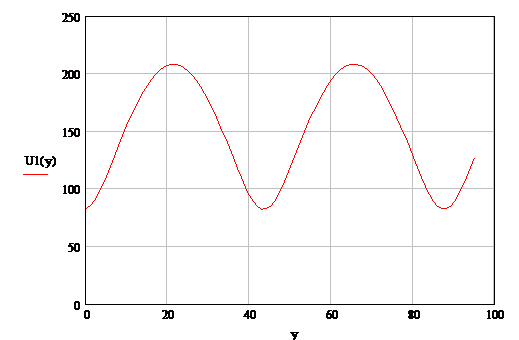
Рисунок 1 Распределение действующих
значений напряжения вдоль линии.
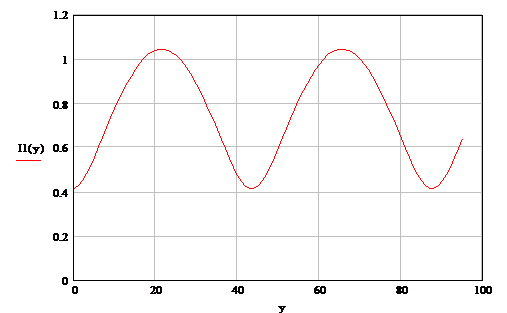
Рисунок 2 Распределение действующих
значений тока вдоль линии.
3. Расчет установившегося режима в
линии (замена нагрузки волновым сопротивлением). Построим графики U(y) и I(y)
Полагая ZH=ZB, из системы
уравнений (2) получим:
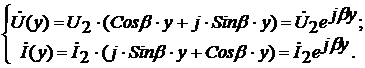
Модули действующих значений
напряжения и тока в произвольном сечении линии не зависят от расстояния, т.е. U(y)=U2; I(y)=I2.
В линии имеет место режим бегущих
волн. Напряжение и ток в произвольном сечении линии равны входным значениям
напряжения и тока:
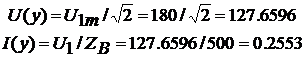
Графики U(y) и I(y)
представлены на рис. 3, 4.
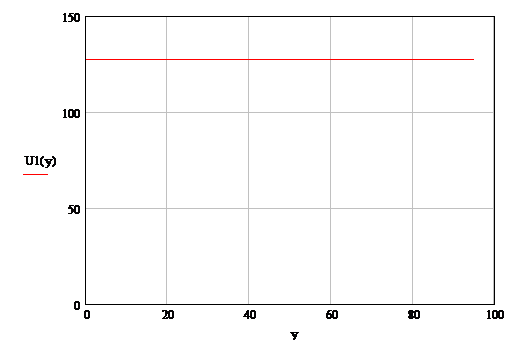
Рисунок 4 Распределение действующих
значений тока вдоль линии в установившемся режиме.
. Расчёт установившегося режима в
линии при отключённой нагрузке (режим холостого хода). Построим графики U(y) и I(y)
В режиме холостого хода ток I2=0, тогда
система уравнений (1) примет следующий вид:
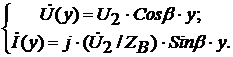
Полагая в первом уравнении y = l, определим
напряжение 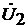 :
:
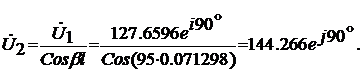
Комплексы действующих значений
напряжения и тока в произвольном сечении линии на расстоянии “y” от её
конца получим из вышеуказанной системы уравнений с учетом найденного значения 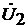 :
:
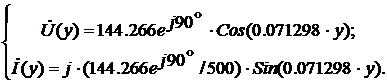
Из этих уравнений получим модули
действующих значений напряжения и тока в произвольном сечении линии на
расстоянии “y” от её
конца:
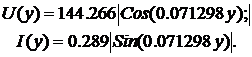
Графики U(y) и I(y)
представлены на рис. 5, 6.
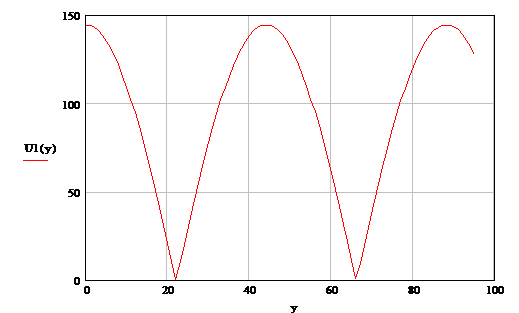
Рисунок 5 Распределение действующих
значений напряжения вдоль линии в режиме холостого хода.
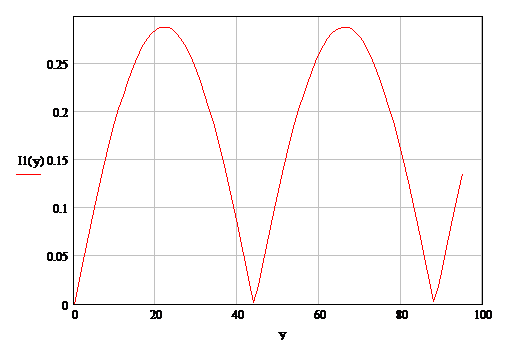
Рисунок 6 Распределение действующих
значений тока вдоль линии в режиме холостого хода.
. Построим графики uп(x), iп(x)
распределения падающих волн напряжения и тока в переходном режиме, когда фронт
падающих волн достигнет конца линии
К линии подключается источник
постоянного напряжения U1=U1m=180 B.
При этом возникают падающие волны
напряжения и тока uп и iп,
распространяющиеся вдоль линии с фазовой скоростью
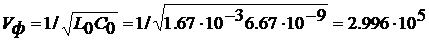 км/с.
км/с.
Величины напряжения и тока падающих
волн равны uп=180 В; iп= =uп/ZB=180/500=0,36
А. Графики распределения падающих волн uп(x), iп(x)
представлены на рис. 7,8.

Рисунок 7 Распределения падающих волн
напряжения в переходном режиме.

Рисунок 8 Распределения падающих
волн тока в переходном режиме.
6. Определим законы изменения тока и
напряжения нагрузки в переходном режиме. Построим графики uН(t), iН(t)
Эквивалентная схема цепи имеет вид:
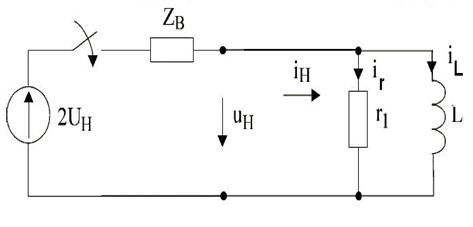
Произведем расчет uН(t)
классическим методом. Решение найдем в виде суммы принужденной и свободной
составляющих:
Н(t)= uНПР(t)+
uНСВ(t).
Определим принужденную составляющую
переходного напряжения на нагрузке
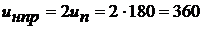 В.
В.
Запишем и найдем корни
характеристического уравнения данной цепи
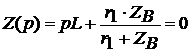
определяем p=-1428.5714,
следовательно uНСВ(t)=Ае-1428,5714t .
Для определения постоянной
интегрирования решение
uН(t)= 360 +
Ае-1428,5714t
рассмотрим при t = 0+ : uН(0+)=360 + A.
Зависимые начальные условия uН(0+)
определим с учетом независимых начальных условия iL(0-)=iL(0+)=0:
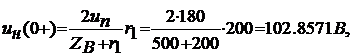
тогда А = uН(0+) - 360
= -257.1429 В.
Окончательно получим uН(t)= 360 -
257,1429е-1428,5714t.
Для определения тока в нагрузке
составим систему уравнений в соответствии с первым и вторым законами Кирхгофа
для рассматриваемой цепи:
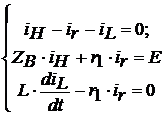
Так как 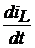 равно UН(t), из
вышеуказанной системы уравнений получим:
равно UН(t), из
вышеуказанной системы уравнений получим:
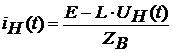
Подставляя численные значения,
получим
Н(t)=
0.648+0.0514е-1428,5714t .
Графики uН(t), iН(t)
представлены на рис. 9, 10.
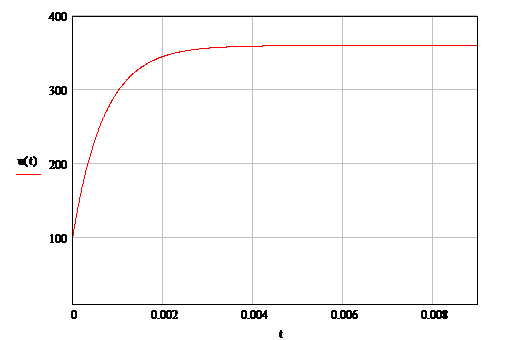
Рисунок 9 Закон изменения напряжения
нагрузки в переходном режиме.
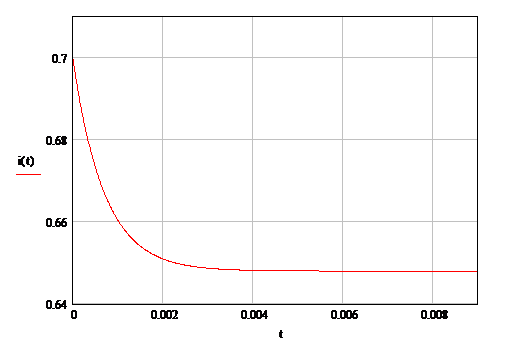
Рисунок 10 Закон изменения тока
нагрузки в переходном режиме.
7. Определим законы изменения
отражённых волн напряжения и тока в сечении нагрузки. Построим графики uо(t), iо(t)
Если сопротивление нагрузки линии не
равно волновому, то возникают отражённые волны. Напряжение и ток в любом
сечении линии складываются из напряжения и тока падающей и отраженной волны:
= uп
+ uо;
i = iп
- iо
.
Для сечения нагрузки имеем uн(t) = uп + uо(t); iн(t) = iп - iо(t).
С учётом результатов пунктов 5, 6
получим
о(t) = uн(t)
- uп
= 360 - 257,1429е-1428,5714t
- 180 = 180 - 257,1429е-1428,5714t;о(t) = iп - iн(t) = 0,36 -
1,2857е-1428,5714t.
Графики uо(t), iо(t)
представлены на рис. 11, 12.
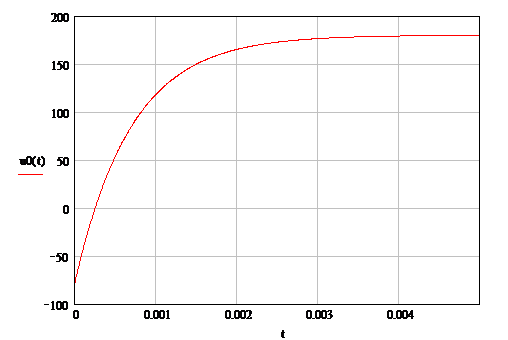
Рисунок 11 Закон изменения
отражённых волн напряжения в сечении нагрузки.
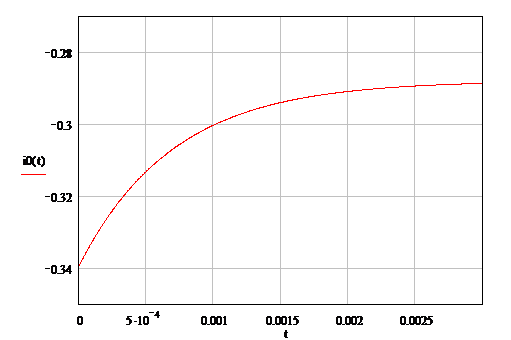
Рисунок 12 Закон изменения
отражённых волн тока в сечении нагрузки.
. Определим распределение напряжения
и тока отражённой волны вдоль линии при переходном режиме для момента времени,
когда фронт отраженной волны достигнет точки на расстоянии “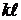 ” от конца
линии
” от конца
линии
Возникнув в сечении нагрузки,
отражённые волны тока и напряжения распространяются к началу линии с фазовой
скоростью Vф. За время t = 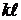 /Vф =
/Vф = 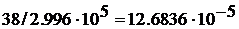 c фронт
отражённой волны достигнет точки, отстоящей от конца линии на
c фронт
отражённой волны достигнет точки, отстоящей от конца линии на 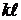 = 0.4*95 =
38 км. Напряжение и ток отражённой волны в произвольном сечении линии из
интервала [
= 0.4*95 =
38 км. Напряжение и ток отражённой волны в произвольном сечении линии из
интервала [ ] = [57, 95]
км определяем по выражениям uо(t) и iо(t) из пункта
7, при t = x/Vф. При этом x принимает
значения из диапазона [
] = [57, 95]
км определяем по выражениям uо(t) и iо(t) из пункта
7, при t = x/Vф. При этом x принимает
значения из диапазона [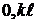 ] = [0, 38].
] = [0, 38].
Графики uо(x), iо(x)
представлены на рис. 13, 14.
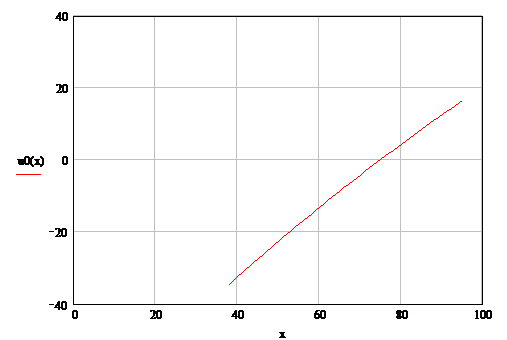
Рисунок 13 Закон распределения
напряжения отражённой волны вдоль линии при переходном режиме для момента
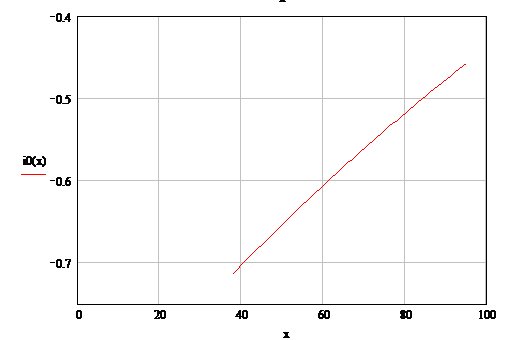
времени, когда фронт отраженной волны достигнет точки на расстоянии “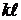 ” от конца
линии.
” от конца
линии.
9. Определим распределение
напряжения и тока вдоль линии при переходном режиме для момента времени, когда
фронт отраженной волны достигнет точки на расстоянии “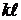 ” от конца
линии
” от конца
линии
Так как в произвольном сечении линии
напряжение и ток складываются из падающих и отражённых волн, то соответствующие
распределения представленные на рисунках 15, 16, получаются из графиков на рис.
7, 13 и из графиков на рис 8, 14 с учетом следующих соотношений:
u(x) = uп
+ u0(t)(x) = iп
- i0(t)
Рисунок 15 Закон распределения
напряжения вдоль линии при переходном режиме для момента времени, когда фронт
отраженной волны достигнет точки на расстоянии “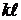 ” от конца линии.
” от конца линии.
Рисунок 16 Закон распределения тока
вдоль линии при переходном режиме для момента времени, когда фронт отраженной
волны достигнет точки на расстоянии “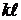 ” от конца линии.
” от конца линии.
. Определим распределение тока и
напряжения при переходном режиме для точки, находящейся на расстоянии “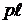 ” от конца
линии
” от конца
линии
За время 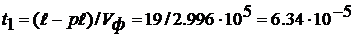 с. падающие
волны напряжения и тока, возникающие в линии при подключении источника
напряжения, достигнут точки на расстоянии
с. падающие
волны напряжения и тока, возникающие в линии при подключении источника
напряжения, достигнут точки на расстоянии  км от конца линии (или на
расстоянии
км от конца линии (или на
расстоянии 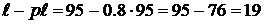 км от начала
линии).
км от начала
линии).
Далее падающие волны
распространяются к нагрузке. Возникшие в сечении нагрузки отражённые волны
достигают точки “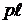 ” спустя
время
” спустя
время
 c.
c.
После этого в точке “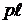 ” появляются
отражённые волны, которые складываются с падающими. Закон изменения отражённых
волн получен в п.7. Построенные с учетом вышеуказанного графики u(t) и i(t)
представлены на рис. 17, 18.
” появляются
отражённые волны, которые складываются с падающими. Закон изменения отражённых
волн получен в п.7. Построенные с учетом вышеуказанного графики u(t) и i(t)
представлены на рис. 17, 18.
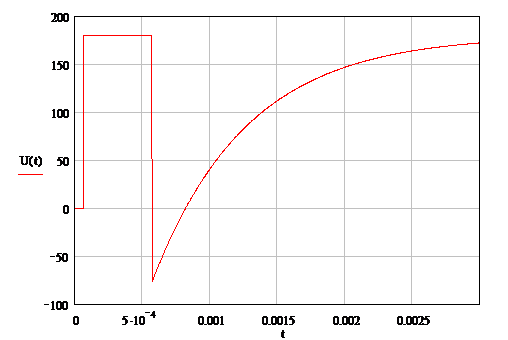
Рисунок 17 Закон распределения
напряжения при переходном режиме для точки, находящейся на расстоянии “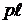 ” от конца
линии.
” от конца
линии.
линия ток напряжение
нагрузка
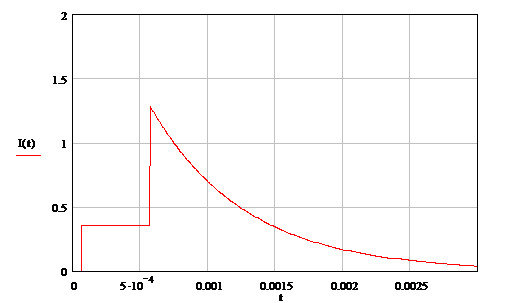
Рисунок 18 Закон распределения тока
при переходном режиме для точки, находящейся на расстоянии “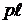 ” от конца
линии.
” от конца
линии.
Заключение
В ходе данной работы проводилось
исследование однородной длинной линии без потерь в установившемся и переходном
режимах. В целом же, понятие однородной линии без потерь является идеализацией,
так как невозможно полностью пренебречь затуханием сигнала в линии, к тому же
для линии без потерь волновое сопротивление чисто активное и не зависит от
частоты, точно так же как фазовая скорость в линиях с данным допущением. Такая
идеализация допускается при приближённой качественной и количественной оценки
исследуемых явлений. Например для коротких высокочастотных линий, применяемых в
радиотехнике, часто с достаточно большой степенью точности можно пренебречь
сопротивлением r0 и g0 по
сравнению с 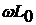 и
и 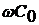 . Поэтому в
радиотехнике очень часто рассматривают двухпроводные воздушные линии и
коаксиальные кабели как линии без потерь.
. Поэтому в
радиотехнике очень часто рассматривают двухпроводные воздушные линии и
коаксиальные кабели как линии без потерь.
В результате работы были определены
распределения напряжений и токов, а также некоторые параметры линии в различных
режимах работы. В частности, в режимах холостого хода, в установившемся режиме,
а также в переходном режиме. Также была получена система уравнений для описания
длинной линии:
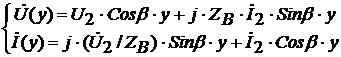
которая получается из
гиперболических уравнений линии, ввиду того, что гиперболические функции с
мнимым аргументом преобразуются в тригонометрические функции.
Энергия, передаваемая по линии,
складывается из энергии электрического и магнитного полей.
В случае установившегося режима
(нагрузка заменена волновым сопротивлением), на любом отрезке линии соблюдается
условие равенства электрической и магнитной энергий, то есть как для линии без
искажений. При этом вся энергия, доставляемая падающей волной, полностью
поглощается нагрузкой. Если сопротивление нагрузки отлично от волнового, то в
месте присоединения нагрузки энергия перераспределяется между полями, в
результате чего возникают отражённые волны.
В случае же, когда линия на конце
разомкнута (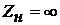 ), энергия
магнитного поля переходит в энергию электрического поля и возникает отражённая
волна того же знака, что и падающая. В случае, когда линия замкнута накоротко (
), энергия
магнитного поля переходит в энергию электрического поля и возникает отражённая
волна того же знака, что и падающая. В случае, когда линия замкнута накоротко (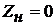 ),энергия
электрического поля переходит в энергию магнитного поля и возникает отражённая
волна противоположная по знаку падающей.
),энергия
электрического поля переходит в энергию магнитного поля и возникает отражённая
волна противоположная по знаку падающей.
Итак, при отсутствии потерь в
однородной линии без потерь, как напряжение, так и ток могут быть представлены
в виде суммы или разности двух волн, движущихся с одинаковой скоростью, но в
различных направлениях. К тому же, в реальной линии, при наличии
неоднородностей возможно появление преломлённой волны, которую также необходимо
учитывать.
Литература
1. Г.В.
Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов. Основы теории цепей. Учебник
для вузов. Изд. 4-е, переработанное. - М.:
“Энергия”,
1975.
2. С.И.
Баскаков. Радиотехнические цепи с распределенными параметрами. - М., 1980.
. Батура,
М.П. Теория электрических цепей / М.П. Батура, А.П. Кузнецов, А.П. Курулев. -
Минск : Выш. шк., 2004.