Анализ установившихся и переходных процессов в линейных электрических цепях

Анализ установившихся и переходных процессов в линейных электрических цепях

Техническое задание

. Расчет источника гармонических колебаний (ИГК)

Представить исходную схему ИГК относительно первичной обмотки трансформатора эквивалентным источником напряжения. Определить его параметры и значение тока в первичной обмотке трансформатора. В качестве первичной обмотки трансформатора выбрать индуктивность в любой ветви, кроме ветви с идеальным источником тока.

Записать мгновенные значения тока и напряжения в первичной обмотке трансформатора и построить их волновые диаграммы.

Определить значения Mnq, Mnp, Lq, Lp из условия, что индуктивность первичной обмотки Ln известна, U1=5В, U2=10В. Коэффициент магнитной связи обмоток k следует выбрать самостоятельно в диапазоне: 0,5<k<0,95.

. Расчет установившихся значений напряжений и токов четырехполюснике при синусоидальном входном воздействии

Рассчитать значение параметра реактивного элемента из условия, что постоянная времени цепи равна периоду входного воздействия.

Рассчитать токи и напряжения в схеме четырехполюсника методом входного сопротивления (или входной проводимости) при u1=u3=uвх.

Записать мгновенные значения uвх, iвх и uвых, определить сдвиг по фазе между выходным и входным напряжениями, а также отношение их действующих значений.

Определить передаточные функции W(s)=Uвых(s)/Uвх(s), W(jw)=Uвых/Uвх.

Определить и построить амплитудно- и фазочастотные характеристики. АЧХ и ФЧХ построить в диапазоне частот от 0 до 5000 1/с. Используя частотные характеристики, определить uвых при заданном uвх. Сравнить этот результат с полученным в п. 2.3.

Построить годограф - линию семейства точек комплексной передаточной функции при разных частотах в диапазоне частот от 0 до ¥ на комплексной плоскости.

. Расчет резонансных режимов в электрической цепи

Включить в схему четырехполюсника реактивное сопротивление (индуктивность или емкость) таким образом, чтобы uвх и iвх совпадали по фазе (режим резонанса напряжений). Определить значение параметра реактивного элемента, а также входное сопротивление, входной ток, добротность и ширину полосы пропускания резонансного контура.

Определить и построить амплитудно- и фазочастотную характеристики I(ω), z(ω), φ(ω). Частотные характеристики тока и сопротивления построить по оси ординат в относительных единицах.

Пользуясь этими характеристиками, определить добротность и ширину полосы пропускания цепи. Сравнить этот результат с результатом, полученным в п. 3.1.

. Расчет переходных процессов классическим методом

Определить и построить переходную и импульсную характеристики четырехполюсника для входного тока и выходного напряжения. Показать связь переходной и импульсной характеристик с передаточной функцией.

Переключатель Кл перевести в положение 2 (см. рис.2) в момент времени, когда входное напряжение u3(t)=0, du3/dt> 0, т.е. в момент начала положительного импульса напряжения u4(t). Это условие будет выполнено при равенстве аргумента входного напряжения (wt + yu3) = 2 kp, где k = 0, 1, 2, 3. Рассчитать и построить графики изменения тока iвх и напряжения uвых четырехполюсника при подключении его к клеммам с напряжением u4(t) в момент времени t=(2kp - yu3)/w с учетом запаса энергии в элементах цепи от предыдущего режима:

а) на интервале t [0+, T], где T - период изменения напряжения u4;

б) с использованием ЭВМ на интервале t [0+, nT], где n - количество периодов, при котором наступает квазиустановившийся режим.

. Расчет установившихся значений напряжений и токов в четырехполюснике при несинусоидальном входном воздействии

Рассчитать законы изменения тока iвх(t) и напряжения uвых(t) частотным методом, представив напряжение uвх(t) = u4(t) в виде ряда Фурье до 5-й гармоники:uвх(t) = S (4 Um / kp) sinkwt, где k - целое нечетное число.

Построить графики uвх(t) = u4(t), uвх(t), iвх(t), uвых(t) в одном масштабе времени один под другим, где uвх(t), iвх(t),и uвых(t) - суммарные мгновенные значения.

Определить действующие значения uвх(t), iвх(t),и uвых(t), а также активную мощность, потребляемую четырехполюсником, коэффициенты искажения iвх(t), uвых(t). Сделать выводы.

Заменить несинусоидальные кривые uвх(t), iвх(t) эквивалентными синусоидами и построить их графики.

Вариант задания

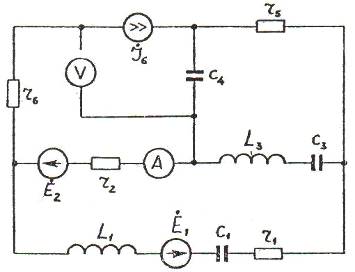
Рис. 1. Схема источника гармонических колебаний.

Исходные данные:

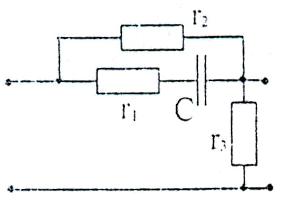
Ðèñ. 2. Ñõåìà ÷åòûð¸õïîëþñíèêà.

Èñõîäíûå äàííûå:

1. Ðàñ÷åò èñòî÷íèêà ãàðìîíè÷åñêèõ êîëåáàíèé (ÈÃÊ)

Ïðåäñòàâèòü èñõîäíóþ ñõåìó ÈÃÊ îòíîñèòåëüíî ïåðâè÷íîé îáìîòêè òðàíñôîðìàòîðà ýêâèâàëåíòíûì èñòî÷íèêîì íàïðÿæåíèÿ. Îïðåäåëèòü åãî ïàðàìåòðû è çíà÷åíèå òîêà â ïåðâè÷íîé îáìîòêå òðàíñôîðìàòîðà.  êà÷åñòâå ïåðâè÷íîé îáìîòêè òðàíñôîðìàòîðà âûáðàòü èíäóêòèâíîñòü â ëþáîé âåòâè, êðîìå âåòâè ñ èäåàëüíûì èñòî÷íèêîì òîêà.

Ïåðåõîä â êîìïëåêñíóþ ôîðìó:

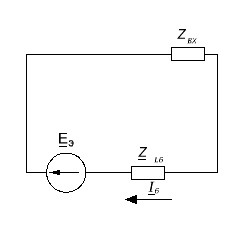
Ðèñ. 3. Ñõåìà ÈÃÊ äëÿ ìåòîäà ýêâèâàëåíòíîãî ãåíåðàòîðà.

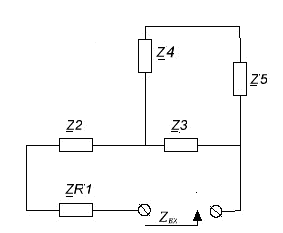
Ðèñ. 4. Ñõåìà íàõîæäåíèÿ Zâõ äëÿ ìåòîäà ýêâèâàëåíòíîãî ãåíåðàòîðà.

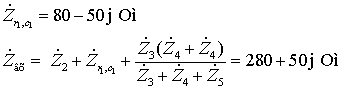
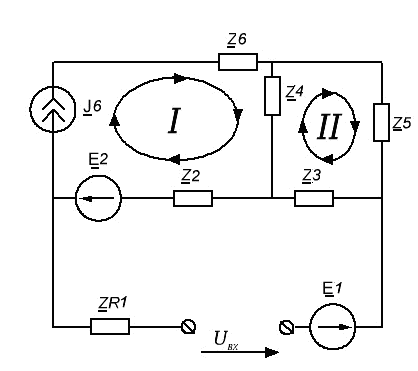
Íàõîäèì Uâx. , èñïîëüçóÿ ìåòîä êîíòóðíûõ òîêîâ:

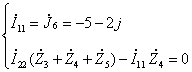
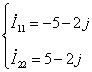
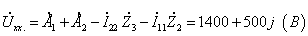
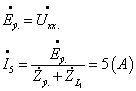
Ðèñ. 5. Ïðåäñòàâëåíèå ñõåìû ÈÃÊ îòíîñèòåëüíî ïåðâè÷íîé îáìîòêè òðàíñôîðìàòîðà ýêâèâàëåíòíûì èñòî÷íèêîì íàïðÿæåíèÿ.

.1 Çàïèñàòü ìãíîâåííûå çíà÷åíèÿ òîêà è íàïðÿæåíèÿ ïåðâè÷íîé îáìîòêè òðàíñôîðìàòîðà è ïîñòðîèòü èõ âîëíîâûå äèàãðàììû

Ðàññ÷èòàåì ìãíîâåííûå çíà÷åíèÿ òîêà è íàïðÿæåíèÿ íà èíäóêòèâíîñòè :

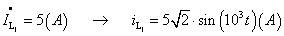
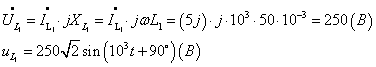
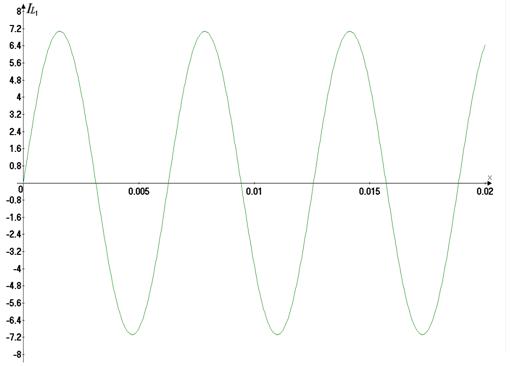
Ðèñ. 6. Ãðàôèê

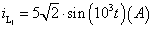
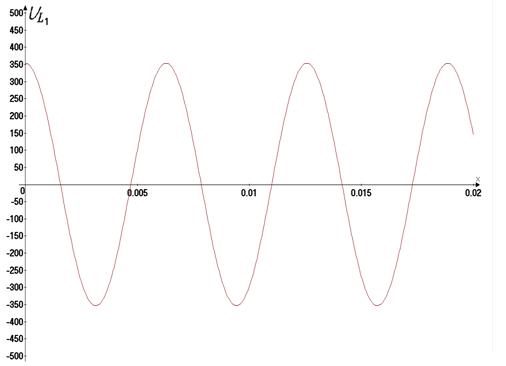
Ðèñ. 7. Ãðàôèê

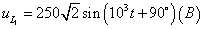
1.2 Îïðåäåëèòü çíà÷åíèÿ Ì58 , Ì59 , L8 , L9 òðàíñôîðìàòîðà èç óñëîâèÿ, ÷òî èíäóêòèâíîñòü ïåðâè÷íîé îáìîòêè L5 èçâåñòíà, U1=5 B, U2=10 B, à êîýôôèöèåíò ìàãíèòíîé ñâÿçè îáìîòîê k ñëåäóåò âûáðàòü èç óêàçàííîãî äèàïàçîíà: 0.5 <k< 0.95

Âûáèðàåì k = 0.7.

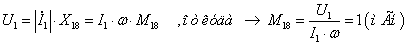
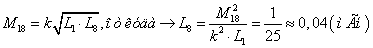
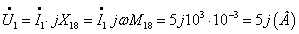
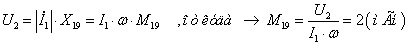
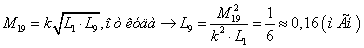
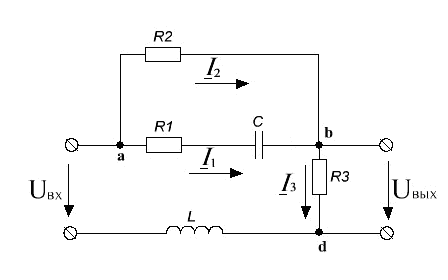
2. Ðàñ÷¸ò ÷åòûð¸õïîëþñíèêà

.1. Ðàññ÷èòàòü òîêè è íàïðÿæåíèÿ ìåòîäîì âõîäíîãî ñîïðîòèâëåíèÿ (èëè âõîäíîé ïðîâîäèìîñòè), ïîñòðîèòü âåêòîðíóþ äèàãðàììó òîêîâ è íàïðÿæåíèé

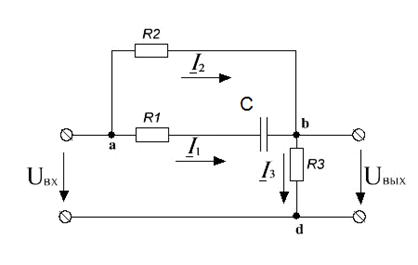
ðèñ.8. Ñõåìà ÷åòûðåõïîëþñíèêà

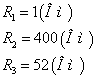
2.2     Ðàññ÷èòàåì çíà÷åíèå ïàðàìåòðà ðåàêòèâíîãî ýëåìåíòà èç óñëîâèÿ, ÷òî ïîñòîÿííàÿ âðåìåíè öåïè ðàâíà ïåðèîäó âõîäíîãî âîçäåéñòâèÿ.

Èç óñëîâèÿ, ÷òî ïîñòîÿííàÿ âðåìåíè öåïè ðàâíà ïåðèîäó âõîäíîãî âîçäåéñòâèÿ:

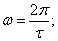
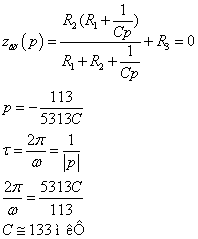
.3 Ðàññ÷èòàòü òîêè è íàïðÿæåíèÿ â ñõåìå ÷åòûðåõïîëþñíèêà ìåòîäîì âõîäíîãî ñîïðîòèâëåíèÿ (èëè âõîäíîé ïðîâîäèìîñòè) ïðè u1=u3=uâõ

Îïðåäåëèì âõîäíîå ñîïðîòèâëåíèå ÷åòûðåõïîëþñíèêà:

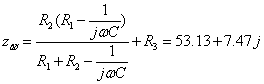
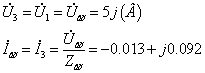
Íàéäåì òîêè è íàïðÿæåíèÿ:

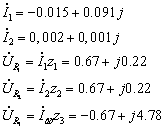
2.4 Çàïèñàòü ìãíîâåííûå çíà÷åíèÿ uâõ ,iâõ è uâûõ ;îïðåäåëèòü ñäâèã ïî ôàçå ìåæäó âûõîäíûì è âõîäíûì íàïðÿæåíèÿìè, à òàêæå îòíîøåíèå èõ äåéñòâóþùèõ çíà÷åíèé.

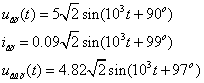
Ôàçîâûé ñäâèã è îòíîøåíèå äåéñòâóþùèõ çíà÷åíèé âõîäíîãî è âûõîäíîãî íàïðÿæåíèÿ:

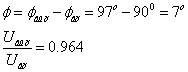
2.5 Îïðåäåëèòü ïåðåäàòî÷íûå ôóíêöèè: W(s)= Uâûõ(s)/ Uâõ(s), W(jw) = Uâûõ/Uâõ .

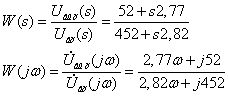
.6 Îïðåäåëèòü è ïîñòðîèòü àìïëèòóäíî- è ôàçî÷àñòîòíûå õàðàêòåðèñòèêè. À×Õ è Ô×Õ ïîñòðîèòü â äèàïàçîíå ÷àñòîò îò 0 äî 5000 1/ñ. Èñïîëüçóÿ ÷àñòîòíûå õàðàêòåðèñòèêè, îïðåäåëèòü uâûõ ïðè çàäàííîì uâõ.

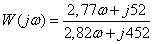
À×Õ: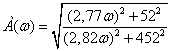

Ô×Õ: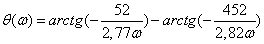

Ñòðîèì ãðàôèêè À×Õ è Ô×Õ :

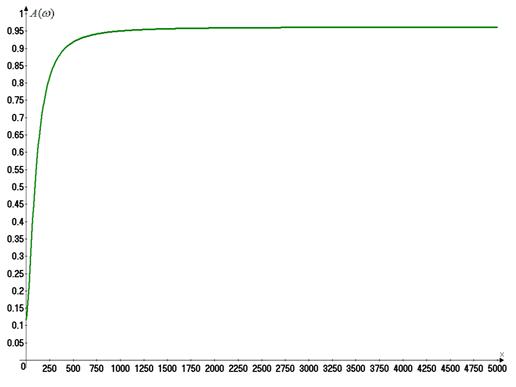
ðèñ.9 Àìïëèòóäíî-÷àñòîòíàÿ õàðàêòåðèñòèêà.

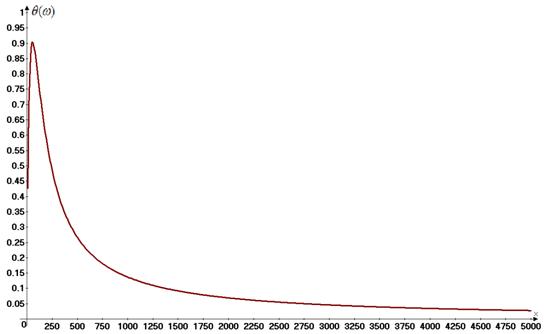
ðèñ.10 Ôàçî-÷àñòîòíàÿ õàðàêòåðèñòèêà.

Îïðåäåëèì Uâûõ:

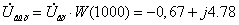
Ïîëó÷åííîå çíà÷åíèå âûõîäíîãî íàïðÿæåíèÿ ñîâïàäàåò ñ íàéäåííûì â ï. 2.2.

.6 Ïîñòðîèòü ãîäîãðàô - ëèíèþ ñåìåéñòâà òî÷åê êîìïëåêñíîé ïåðåäàòî÷íîé ôóíêöèè â äèàïàçîíå ÷àñòîò îò 0 äî ¥ íà êîìïëåêñíîé ïëîñêîñòè. Óêàçàòü íà ãîäîãðàôå òî÷êè, ñîîòâåòñòâóþùèå ÷àñòîòàì 0, 1000 1/ñ.

ãàðìîíè÷åñêèé êîëåáàíèå íàïðÿæåíèå òîê

À×Õ: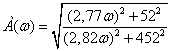

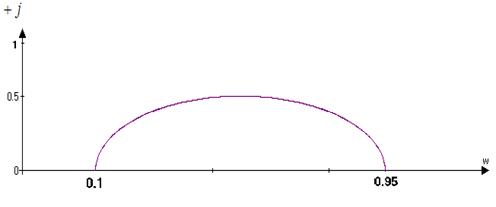
ðèñ.11Ãîäîãðàô.

3. Ðàñ÷åò ðåçîíàíñíûõ ðåæèìîâ

.1 Âêëþ÷èòü â ñõåìó ÷åòûðåõïîëþñíèêà ðåàêòèâíîå ñîïðîòèâëåíèå (èíäóêòèâíîñòü èëè åìêîñòü) òàêèì îáðàçîì, ÷òîáû uâõ è iâõ ñîâïàäàëè ïî ôàçå (ðåæèì ðåçîíàíñà íàïðÿæåíèé)

Îïðåäåëèòü çíà÷åíèå ïàðàìåòðà ðåàêòèâíîãî ýëåìåíòà, à òàêæå âõîäíîå ñîïðîòèâëåíèå, âõîäíîé òîê, äîáðîòíîñòü è øèðèíó ïîëîñû ïðîïóñêàíèÿ ðåçîíàíñíîãî êîíòóðà.

ðèñ.12

Âõîäíîå ñîïðîòèâëåíèå â ýòîì ñëó÷àå áóäåò èìåòü âèä:

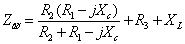
Óñëîâèåì ðåçîíàíñà ÿâëÿåòñÿ ðàâåíñòâî íóëþ ìíèìîé ÷àñòè âõîäíîãî ñîïðîòèâëåíèÿ:

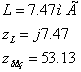
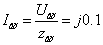
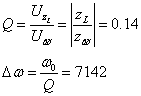
.2 Îïðåäåëèòü è ïîñòðîèòü àìïëèòóäíî- è ôàçî÷àñòîòíóþ õàðàêòåðèñòèêè: I(ω), z(ω), φ(ω).

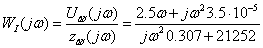
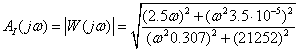
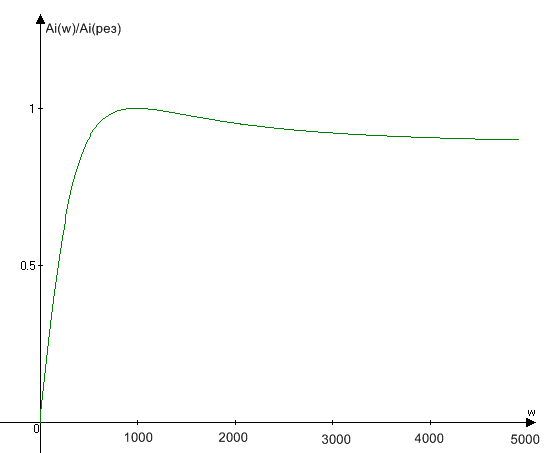
Ðèñ. 13. À×Õ òîêà â îòíîñèòåëüíûõ åäèíèöàõ.

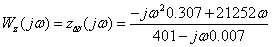
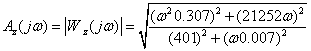
Ðèñ. 14. À×Õ ñîïðîòèâëåíèÿ â îòíîñèòåëüíûõ åäèíèöàõ.

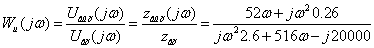
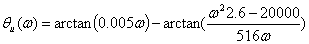
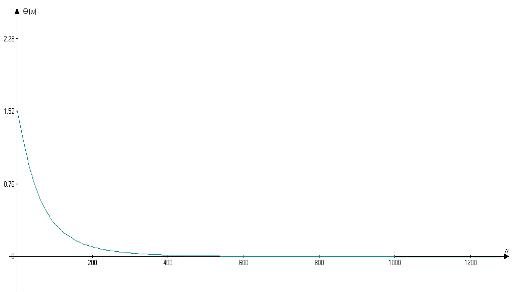
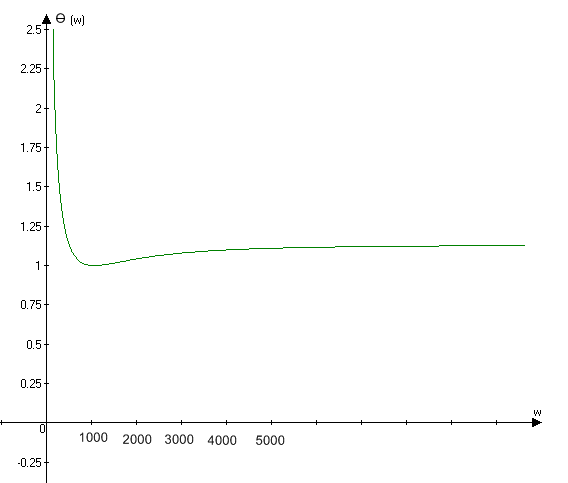
Ðèñ. 15. Ô×Õ.

.3 Ïîëüçóÿñü ýòèìè õàðàêòåðèñòèêàìè, îïðåäåëèòü äîáðîòíîñòü è øèðèíó ïîëîñû ïðîïóñêàíèÿ öåïè. Ñðàâíèòü ýòîò ðåçóëüòàò ñ ðåçóëüòàòîì, ïîëó÷åííûì â ï. 3.1

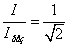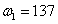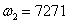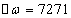Íà ãðàíèöàõ ïîëîñû ïðîïóñêàíèÿ: . Ýòî çíà÷åíèÿ ÷àñòîò è , è èç ýòîãî ñëåäóåò , à 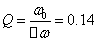. Ýòîò ðåçóëüòàò ñîâïàäàåò ñ ðåçóëüòàòîì, ïîëó÷åííûì â ï.3.1

4.Ðàñ÷¸ò ïåðåõîäíûõ ïðîöåññîâ êëàññè÷åñêèì ìåòîäîì

.1 Îïðåäåëèòü è ïîñòðîèòü ïåðåõîäíóþ è èìïóëüñíóþ õàðàêòåðèñòèêè ÷åòûðåõïîëþñíèêà äëÿ âõîäíîãî òîêà è âûõîäíîãî íàïðÿæåíèÿ.

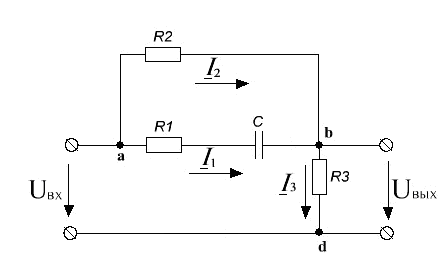
Ðèñ 16. Ñõåìà ÷åòûðåõïîëþñíèêà.

Ïðèìåíèì êëàññè÷åñêèé ìåòîä ðàñ÷¸òà ïåðåõîäíûõ ïðîöåññîâ. Õàðàêòåðèñòè÷åñêîå óðàâíåíèå ïðè çàäàííûõ ïàðàìåòðàõ ýëåìåíòîâ ñõåìû:

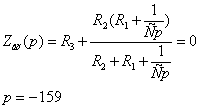
Ðåøåíèå áóäåò èìåòü âèä:

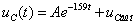
Íàéäåì íà÷àëüíûå è âûíóæäåíèÿ çíà÷åíèÿ íàïðÿæåíèÿ íà êîíäåíñàòîðå:

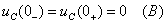
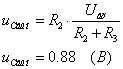
Îïðåäåëèì ïîñòîÿííóþ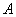 èç íà÷àëüíûõ óñëîâèé:

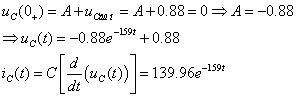
Òîãäà ñîãëàñíî çàêîíàì Êèðõãîôà:

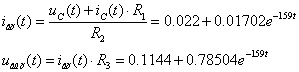
Îïðåäåëèì ïåðåõîäíûå è èìïóëüñíûå õàðàêòåðèñòèêè ñõåìû:

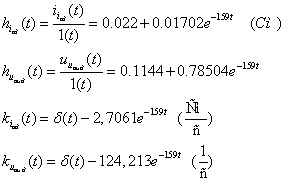
Íèæå ïðèâåäåíû ãðàôèêè íàéäåííûõ ôóíêöèé

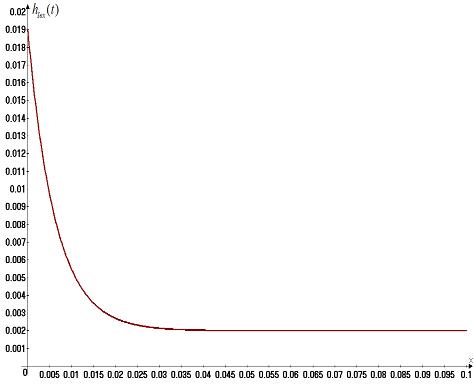
Ðèñ. 17. Ïåðåõîäíàÿ õàðàêòåðèñòèêè äëÿ òîêà.

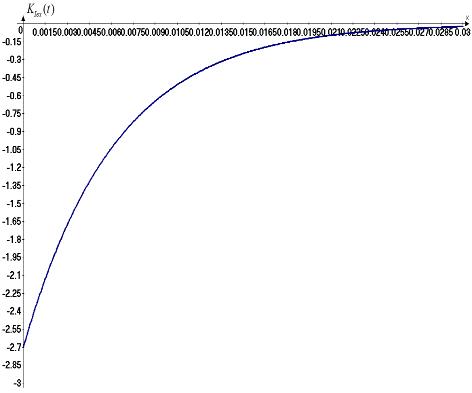
Ðèñ. 20. Èìïóëüñíàÿ õàðàêòåðèñòèêè äëÿ òîêà.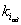

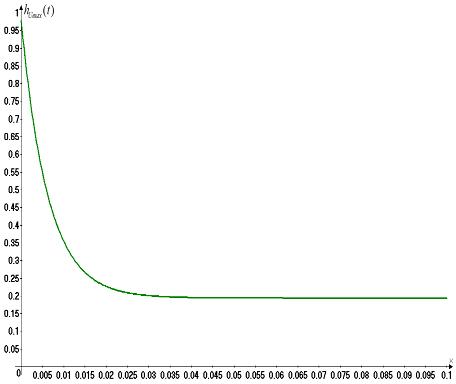
Ðèñ. 21. Ïåðåõîäíàÿ õàðàêòåðèñòèêè äëÿ íàïðÿæåíèÿ.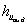

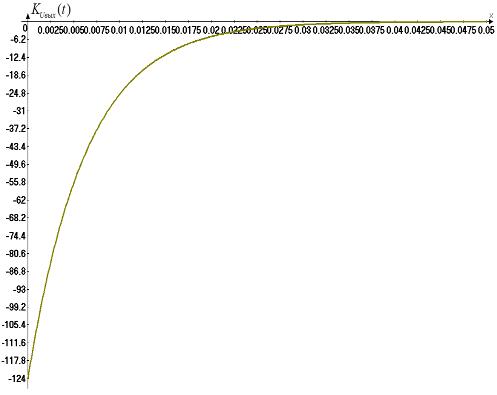
Ðè.ñ 22. Èìïóëüñíàÿ õàðàêòåðèñòèêè äëÿ íàïðÿæåíèÿ.

Ïîêàæåì ñâÿçü ìåæäó ïåðåõîäíîé è ïåðåäàòî÷íîé ôóíêöèÿìè:

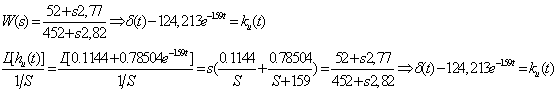
Ïîëó÷åííûå çíà÷åíèÿ ñîâïàäàþò.

.2 Ðàñ÷åò è ïîñòðîåíèå ãðàôèêîâ èçìåíåíèÿ òîêà iâõ è íàïðÿæåíèÿ uâûõ ÷åòûð¸õïîëþñíèêà ïðè ïîäêëþ÷åíèè åãî ê êëåììàì ñ íàïðÿæåíèåì u4(t) â ìîìåíò âðåìåíè t0 = (2k- u3)/ñ ó÷åòîì çàïàñà ýíåðãèè â ýëåìåíòàõ ñõåìû îò ïðåäûäóùåãî ðåæèìà ðàáîòû

.2 Ïåðåêëþ÷àòåëü Êë ïåðåâåñòè â ïîëîæåíèå 2 (ñì. ðèñ.2) â ìîìåíò âðåìåíè, êîãäà âõîäíîå íàïðÿæåíèå u3(t)=0, du3/dt> 0, ò.å. â ìîìåíò íà÷àëà ïîëîæèòåëüíîãî èìïóëüñà íàïðÿæåíèÿ u4(t)

Ýòî óñëîâèå áóäåò âûïîëíåíî ïðè ðàâåíñòâå àðãóìåíòà âõîäíîãî íàïðÿæåíèÿ (wt + yu3) = 2 kp, ãäå k = 0, 1, 2, 3. Ðàññ÷èòàòü è ïîñòðîèòü ãðàôèêè èçìåíåíèÿ òîêà iâõ è íàïðÿæåíèÿ uâûõ ÷åòûðåõïîëþñíèêà ïðè ïîäêëþ÷åíèè åãî ê êëåììàì ñ íàïðÿæåíèåì u4(t) â ìîìåíò âðåìåíè t=(2kp - yu3)/w ñ ó÷åòîì çàïàñà ýíåðãèè â ýëåìåíòàõ öåïè îò ïðåäûäóùåãî ðåæèìà:

à) íà èíòåðâàëå t [0+, T], ãäå T - ïåðèîä èçìåíåíèÿ íàïðÿæåíèÿ u4;

Ïîñëå êîììóòàöèè íà ñõåìó ïîäàþòñÿ ïðÿìîóãîëüíûå èìïóëüñû ñ àìïëèòóäîé 10Â.

Äëÿ èíòåðâàëà

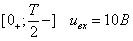
Èç ï. 2.1. íàéä¸ì ìãíîâåííîå çíà÷åíèå íàïðÿæåíèÿ íà êîíäåíñàòîðå:

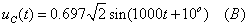
Îïðåäåëèì çíà÷åíèå íàïðÿæåíèÿ íà êîíäåíñàòîðå â ìîìåíò êîììóòàöèè:

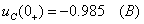
Èùåì ðåøåíèå â âèäå: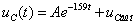

Èç ïðåäûäóùåãî ðàñ÷åòà íàì èçâåñòíî:

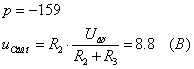
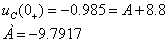
Òîãäà:

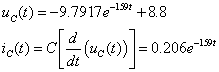
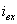Äëÿ îïðåäåëåíèÿ  è  âîñïîëüçóåìñÿ çàêîíàìè Êèðõãîôà:

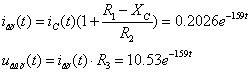
Àíàëîãè÷íî äëÿ èíòåðâàëà 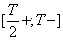, ó÷èòûâàÿ, ÷òî çíàê âõîäíîãî íàïðÿæåíèÿ ìåíÿåòñÿ è, ñëåäîâàòåëüíî, ìåíÿåòñÿ çíàê âûíóæäåííîãî òîêà. Ïî çàêîíó êîììóòàöèè:

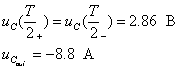
Îïðåäåëèì ïîñòîÿííóþ 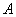 èç íà÷àëüíûõ óñëîâèé:

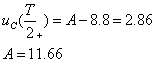
Òîãäà:

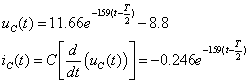
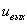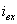Äëÿ îïðåäåëåíèÿ  è  âîñïîëüçóåìñÿ çàêîíàìè Êèðõãîôà:

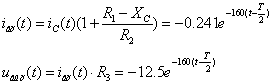
Ðèñ. 23. Ãðàôèê âûõîäíîãî íàïðÿæåíèÿ äëÿ ïåðâîãî ïåðèîäà.

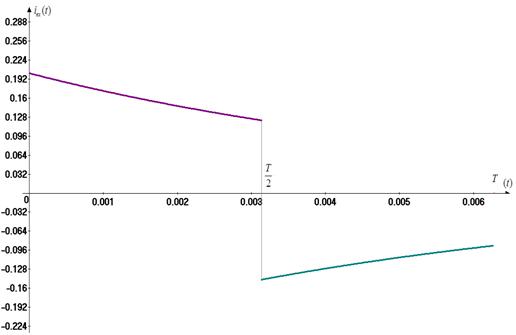
Ðèñ. 24. Ãðàôèê âõîäíîãî òîêà äëÿ ïåðâîãî ïåðèîäà.

á) Ðàñ÷åò è ïîñòðîåíèå ãðàôèêîâ èçìåíåíèÿ òîêà iâõ è íàïðÿæåíèÿ uâûõ ÷åòûð¸õïîëþñíèêà íà èíòåðâàëå, ïðè êîòîðîì íàñòóïàåò êâàçèóñòàíîâèâøèéñÿ ðåæèì.

Ðàññ÷èòàåì ïðîìåæóòîê âðåìåíè

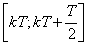
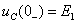
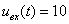 Â íà èíòåðâàëå

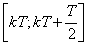
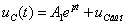
Èç ïðåäûäóùåãî ðàñ÷åòà íàì èçâåñòíî:

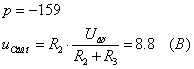
Ïî çàêîíó êîììóòàöèè:

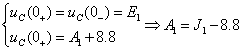
Òîãäà:

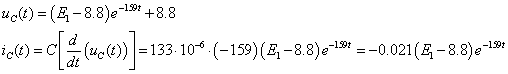
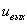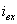Äëÿ îïðåäåëåíèÿ  è  âîñïîëüçóåìñÿ çàêîíàìè Êèðõãîôà:

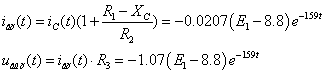
Àíàëîãè÷íî äëÿ èíòåðâàëà 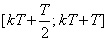, ó÷èòûâàÿ, ÷òî çíàê âõîäíîãî íàïðÿæåíèÿ ìåíÿåòñÿ è, ñëåäîâàòåëüíî, ìåíÿåòñÿ çíàê âûíóæäåííîãî òîêà. Ïî çàêîíó êîììóòàöèè:

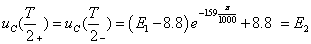
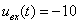 Â íà èíòåðâàëå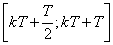

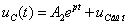
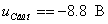
Îïðåäåëèì ïîñòîÿííóþ 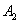 èç íà÷àëüíûõ óñëîâèé:

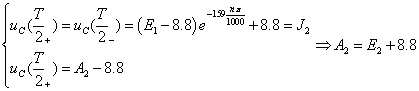
Òîãäà:

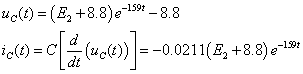
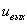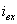Äëÿ îïðåäåëåíèÿ  è  âîñïîëüçóåìñÿ çàêîíàìè Êèðõãîôà:

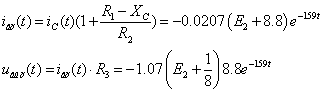
Ïðèìåíèì ñôîðìóëèðîâàííûé îáùèé àëãîðèòì äëÿ ÷åòûð¸õ ïåðèîäîâ:

Ïåðâûé ïåðèîä:

ïåðâûé ïîëóïåðèîä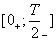

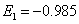
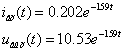
âòîðîé ïîëóïåðèîä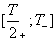

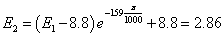
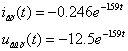
Âòîðîé ïåðèîä:

ïåðâûé ïîëóïåðèîä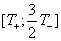

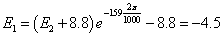
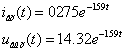
âòîðîé ïîëóïåðèîä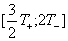

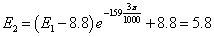
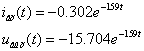
Òðåòèé ïåðèîä:

ïåðâûé ïîëóïåðèîä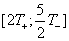

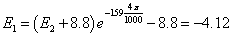
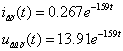
âòîðîé ïîëóïåðèîä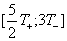

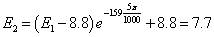
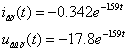
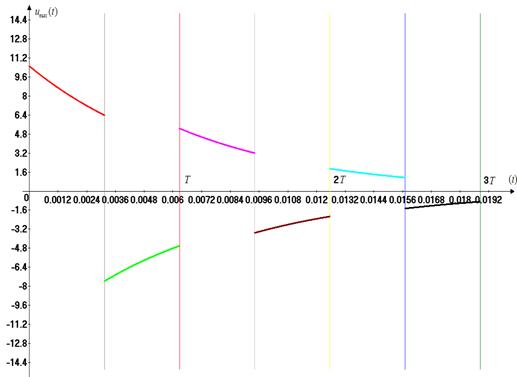
Ðèñ. 25. Ãðàôèê âûõîäíîãî íàïðÿæåíèÿ äëÿ òð¸õ ïåðèîäîâ.

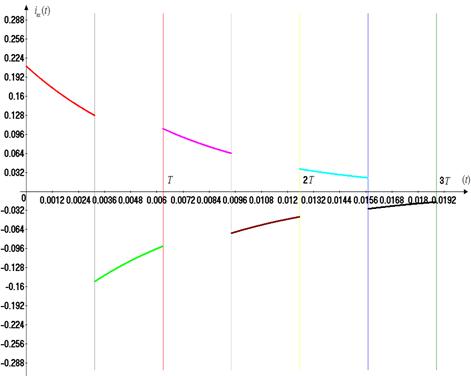
Ðèñ. 26. Ãðàôèê âõîäíîãî òîêà äëÿòð¸õ ïåðèîäîâ.

5. Ðàñ÷¸ò óñòàíîâèâøèõñÿ çíà÷åíèé òîêîâ è íàïðÿæåíèé â ÷åòûðåõïîëþñíèêå ïðè íåñèíóñîèäàëüíîì âõîäíîì âîçäåéñòâèè

.1 Ðàññ÷èòàòü çàêîíû èçìåíåíèÿ òîêà iâõ(t) è íàïðÿæåíèÿ uâûõ(t) ÷àñòîòíûì ìåòîäîì, ïðåäñòàâèâ íàïðÿæåíèå uâõ(t) = u4(t) â âèäå ðÿäà Ôóðüå äî 5-é ãàðìîíèêè

Âõîäíîå íàïðÿæåíèå çàäàíî ôîðìóëîé (ðÿä Ôóðüå):

Âõîäíîå âîçäåéñòâèå ìîæíî çàïèñàòü â âèäå:

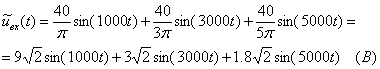
Ðàññ÷èòàåì 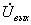äëÿ êàæäîé ãàðìîíèêè:

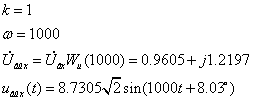
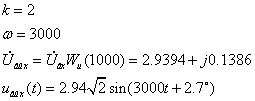
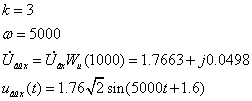
Òîãäà âûõîäíîå íàïðÿæåíèå èìååò âèä:

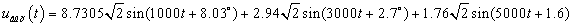
Âõîäíîé òîê èìååò âèä :

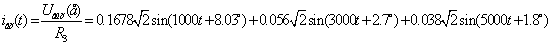
Èòàê:

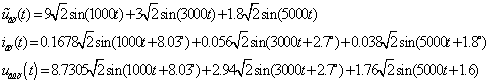
.2 Ïîñòðîèòü ãðàôèêè uâõ(t) = u4(t), uâõ(t), iâõ(t), uâûõ(t) â îäíîì ìàñøòàáå âðåìåíè îäèí ïîä äðóãèì, ãäå uâõ(t), iâõ(t),è uâûõ(t) - ñóììàðíûå ìãíîâåííûå çíà÷åíèÿ

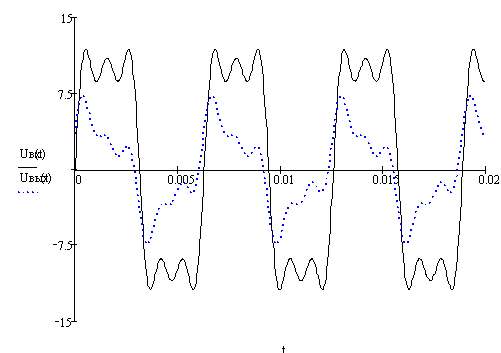
Ðèñ 27. Ãðàôèêè âõîäíîãî è âûõîäíîãî íàïðÿæåíèé.

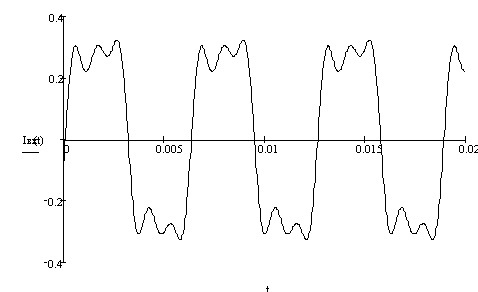
Ðèñ 15. Ãðàôèê âõîäíîãî òîêà.

.3 Îïðåäåëèòü äåéñòâóþùèå çíà÷åíèÿ uâõ(t), iâõ(t), uâûõ(t), à òàêæå àêòèâíóþ ìîùíîñòü, ïîòðåáëÿåìóþ ÷åòûðåõïîëþñíèêîì, è êîýôôèöèåíòû èñêàæåíèÿ iâõ(t), uâûõ(t)

Äåéñòâóþùèå çíà÷åíèÿ ñèãíàëîâ:

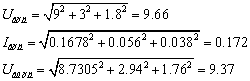
Àêòèâíàÿ ìîùíîñòü:

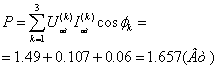
Ïîëíàÿ ìîùíîñòü:

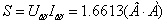
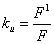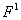Êîýôôèöèåíò èñêàæåíèÿ , ãäå F - äåéñòâóþùåå çíà÷åíèå ôóíêöèè, -äåéñòâóþùåå çíà÷åíèå ôóíêöèè ïðè ïåðâîé ãàðìîíèêå.

Äëÿ íàïðÿæåíèÿ :

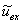Äëÿ íàïðÿæåíèÿ :

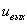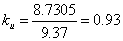
Äëÿ òîêà :

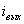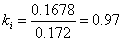
.4. Çàìåíèòü íåñèíóñîèäàëüíûå êðèâûå uâõ(t), iâõ(t) ýêâèâàëåíòíûìè ñèíóñîèäàìè è ïîñòðîèòü èõ ãðàôèêè

Îïðåäåëèì êîýôôèöèåíò ìîùíîñòè:

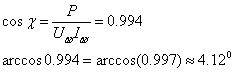
Òîãäà ñîîòâåòñòâóþùèå ýêâèâàëåíòíûå ñèíóñîèäû áóäóò èìåòü âèä:

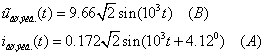
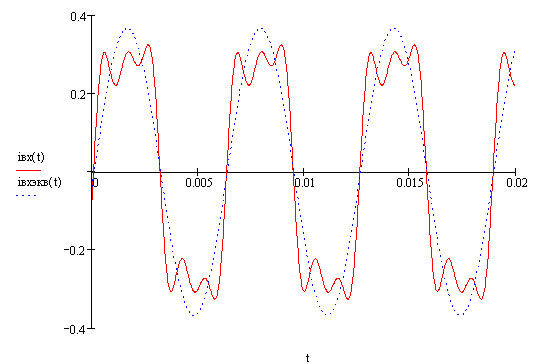
Ðèñ 28. Ãðàôèêè íåñèíóñîèäàëüíîãî âõîäíîãî òîêà è åãî ýêâèâàëåíòíîé ñèíóñîèäû.

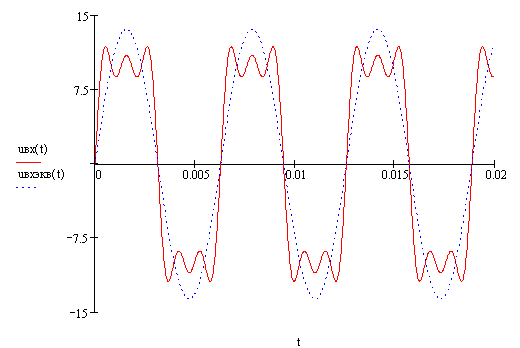
Ðèñ 29. Ãðàôèêè íåñèíóñîèäàëüíîãî âõîäíîãî íàïðÿæåíèÿ è åãî ýêâèâàëåíòíîé ñèíóñîèäû.

Âûâîäû

Èññëåäîâàíèå èñòî÷íèêà ãàðìîíè÷åñêèõ êîëåáàíèé ïîêàçàëî, ÷òî ðàñ÷åò íàïðÿæåíèé è òîêîâ íà åãî ýëåìåíòàõ ìîæíî ïðîâîäèòü ðàçíûìè ìåòîäàìè. Íàïðèìåð, ìåòîäîì êîíòóðíûõ òîêîâ èëè ìåòîäîì ýêâèâàëåíòíîãî ãåíåðàòîðà ÝÄÑ. Êàê è ïðåäïîëàãàëîñü, âñå ìåòîäû äàþò îäèí è òîò æå ðåçóëüòàò. Íî èñïîëüçîâàíèå ìåòîäà êîíòóðíûõ òîêîâ ïîçâîëÿåò óìåíüøèòü êîëè÷åñòâî âû÷èñëåíèé ïî ñðàâíåíèþ ñ ìåòîäîì ýêâèâàëåíòíîãî èñòî÷íèêà.

Ðàñ÷åò áàëàíñà ìîùíîñòåé äëÿ ñõåìû ïîçâîëÿåò ïðîâåðèòü ïðàâèëüíîñòü ïîâåäåííûõ ðàñ÷åòîâ ïî îïðåäåëåíèþ íàïðÿæåíèé è òîêîâ íà ýëåìåíòàõ ñõåìû.

Ðàñ÷åòû ïåðåõîäíûõ ïðîöåññîâ â ÷åòûðåõïîëþñíèêå äëÿ îïðåäåëåíèÿ âõîäíîãî òîêà è âûõîäíîãî íàïðÿæåíèÿ è ðàñ÷åòû ïðîöåññîâ â ÷åòûðåõïîëþñíèêå ñ èñïîëüçîâàíèåì ðàçëîæåíèÿ íåñèíóñîèäàëüíîãî âõîäíîãî âîçäåéñòâèÿ â ðÿä Ôóðüå äàþò áëèçêèå ðåçóëüòàòû. Èõ íåáîëüøîå îòëè÷èå îáúÿñíÿåòñÿ òåì, ÷òî ðàçëîæåíèå ñèãíàëà â ðÿä Ôóðüå èìååò íåêîòîðóþ ïîãðåøíîñòü ïî ñðàâíåíèþ åãî èñòèííûì çíà÷åíèåì. Íàèáîëüøóþ òî÷íîñòü ðàñ÷åòà â äàííîì ñëó÷àå äàåò êëàññè÷åñêèé ìåòîä ðàñ÷åòà ïåðåõîäíûõ ïðîöåññîâ. Äîïîëíèòåëüíîå îòëè÷èå ðåçóëüòàòîâ ïîëó÷åííûõ ýòèì ìåòîäîì ïî ñðàâíåíèþ ñ ìåòîäîì, èñïîëüçóþùèì ðàçëîæåíèå â ðÿä Ôóðüå, äàåò òî, ÷òî ïðè ðàñ÷åòå ïåðåõîäíîãî ïðîöåññà ó÷èòûâàåòñÿ çàïàñû ýíåðãèè îò ïðåäûäóùåãî ðåæèìà ðàáîòû, ÷òî íå ó÷èòûâàëîñü â ïåðâîì ñëó÷àå.

Àíàëèç ÷åòûðåõïîëþñíèêà ïîêàçàë, ÷òî ïðîõîäÿùèé ÷åðåç íåãî ñèãíàë ïðåòåðïåâàåò çíà÷èòåëüíûå èçìåíåíèÿ è îñëàáåâàåò. Ýòî îáúÿñíÿåòñÿ òåì, ÷òî â ÷åòûðåõïîëþñíèêå ïðîèñõîäèò íåêîòîðàÿ ïîòåðÿ ýíåðãèè íà åãî ýëåìåíòàõ.

 õîäå ðàáîòû ñòàëà ÿñíà î÷åâèäíîñòü èñïîëüçîâàíèÿ âû÷èñëèòåëüíîé òåõíèêè ïðè ðàçëè÷íûõ ðàñ÷åòàõ, â îñîáåííîñòè ïðè ðàñ÷åòàõ ïåðåõîäíûõ ïðîöåññîâ, òàê êàê ýòîò ðàñ÷åò òðåáóåò áîëüøèõ âû÷èñëåíèé. Ñ öåëüþ óïðîùåíèÿ âû÷èñëåíèé è ïîñòðîåíèÿ ãðàôèêîâ èñïîëüçîâàëèñü ìàòåìàòè÷åñêèå ïðîãðàììûMathCAD14 è AdvancedGrapher 2.11

Ñïèñîê ëèòåðàòóðû

1. Ïîïîâ Â.Ï. Îñíîâû òåîðèè öåïåé: Ó÷åáíèê äëÿ âóçîâ ñïåö. ðàäèîòåõíèêà - Ì.: Âûñøàÿ øêîëà, 1985.

. Àòàáåêîâ Ã.È. Îñíîâû òåîðèè öåïåé: Ó÷åáíèê äëÿ âóçîâ. -Ì.: Ýíåðãèÿ, 1969.

. Áåññîíîâ Ë.À. Òåîðåòè÷åñêèå îñíîâû ýëåêòðîòåõíèêè. Ýëåêòðè÷åñêèå öåïè: Ó÷åáíèê äëÿ ýëåêòðî-òåõí., ýíåðã., ïðèáîðîñòðîèò.ñïåö âóçîâ. - Ì.: Âûñøàÿ øêîëà, 1996.

. Ìàëàíüèí Â.À., Øåðñòíÿêîâ Þ.Ã. Àíàëèç óñòàíîâèâøèõñÿ è ïåðåõîäíûõ ïðîöåññîâ â ëèíåéíûõ ýëåêòðè÷åñêèõ öåïÿõ. - Ì.: Èçä-âî ÌÃÒÓ, 1991.

Ðàçìåùåíî íà Allbest.ru