Эмпирические распределения. Гистограммы
Задача.Контролируется
время (в часах) работы компьютерного класса в день. Данные сведены в таблицу.
Провести статистическую обработку данных по указанной выше методике.
52 28 36 95 49 12 54 25 26
46 22 5 30 18 72 30 63 37 55
Решение. Объем
выборки 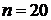 . Расположим
выборочные данные в порядке неубывания, получим вариационный ряд:
. Расположим
выборочные данные в порядке неубывания, получим вариационный ряд:
512 18 22 25 26 28 30 30 36
39 46 49 52 54 55 63 72 95 .
Находим 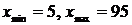 . Значит,
размах выборки
. Значит,
размах выборки 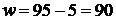 .
.
Промежуток варьирования выборочных
данных 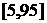 разбиваем
на 5 равных частей точками:
разбиваем
на 5 равных частей точками: 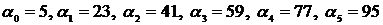 , получим 5 промежутков:
, получим 5 промежутков: 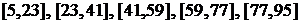 . Считаем
количество попаданий выборочных данных в каждый промежуток; при этом если
какая-то варианта попадает на общую границу промежутков, мы добавляем по 0,5 к
частотам обоих промежутков. В итоге получим интервальный статистический ряд.
. Считаем
количество попаданий выборочных данных в каждый промежуток; при этом если
какая-то варианта попадает на общую границу промежутков, мы добавляем по 0,5 к
частотам обоих промежутков. В итоге получим интервальный статистический ряд.
|
Интервалы
|
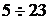 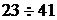 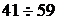 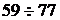 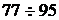
|
|
|
|
|
|
Частоты
|
4
|
8
|
5
|
2
|
1
|
По интервальному статистическому ряду строим
гистограмму (см. рис. 1).
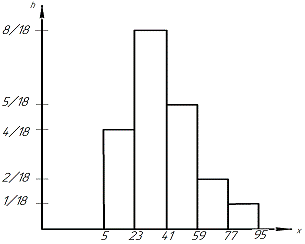
Рис.1. Гистограмма абсолютных частот.
Чтобы перейти от интервального статистического
ряда к группированному, нужно найти середины интервалов
Записываем группированный
статистический ряд.
|
 1432506886 1432506886
|
|
|
|
|
|
|
Частоты
|
4
|
8
|
5
|
2
|
1
|
Строим полигон абсолютных частот (см. рис. 2).
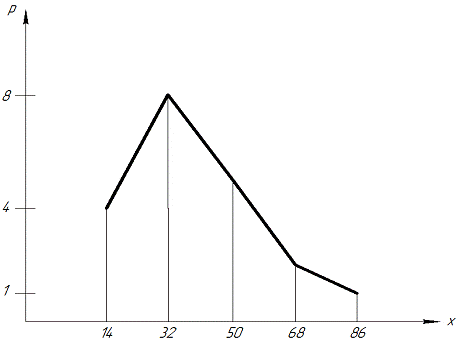
Рис.2. Полигон абсолютных частот.
Для построения графика эмпирической
функции распределения 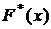 найдем ее
значения. Если
найдем ее
значения. Если 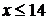 , то
, то 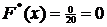 . Если
. Если 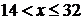 , то
, то 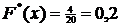 . Если
. Если 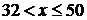 , то
, то 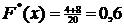 . Если
. Если 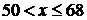 , то
, то 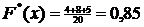 . Если
. Если 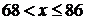 , то
, то 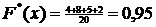 . Если
. Если 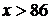 , то
, то 
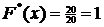 .Эмпирическая функция распределения
построена на рис. 3.
.Эмпирическая функция распределения
построена на рис. 3.
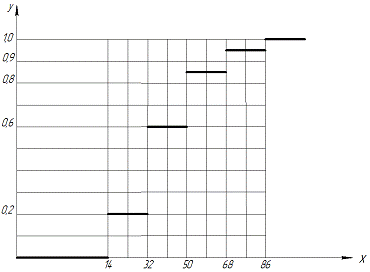
Рис.3. График функции 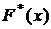 .
.
Используя группированный
статистический ряд, находим выборочную среднюю, исправленную выборочную
дисперсию и среднее квадратическое отклонение соответственно по формулам (2),
(4) с учетом (3) и (5). Получим
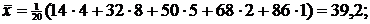
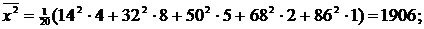
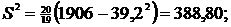
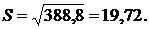
Для выбора теоретического закона
построим огибающую к границе гистограммы (см. рис. 4). Вид огибающей похож на
график плотности нормального распределения, поэттому выдвигаем гипотезу, что
генеральная совокупность распределена по номальному закону. Известно, что
нормальный закон имеет два параметра 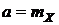 и
и 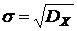 . Учитывая найденные статистические
оценки математического ожидания и дисперсии, положим
. Учитывая найденные статистические
оценки математического ожидания и дисперсии, положим
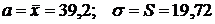 . Значит, теоретическое
распределение будет иметь вид
. Значит, теоретическое
распределение будет иметь вид
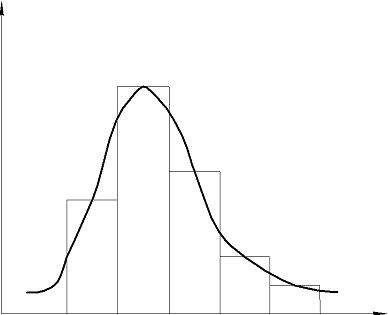
Рис.4. Огибающая гистограммы.
Строим график теоретического
распределения (см рис. 5).
функция график распределение
гистограмма
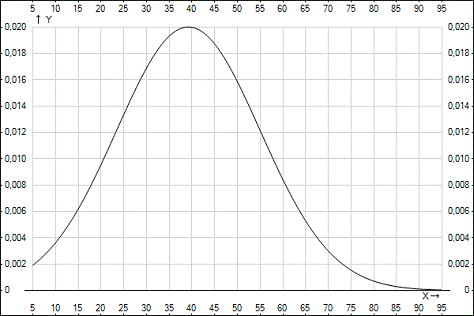
Рис.5.Теоретическое распределение генеральной
совокупности.