Исследование эмпирических функций распределения и расчет основных статических характеристик реки Керженец в створе с. Хахалы
РОССИЙСКИЙ
ГОСУДАРСТВЕННЫЙ ГИДРОМЕТЕОРОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
Факультет
заочного обучения
,
г. Санкт-Петербург, Малоохтинский пр. д.98, тел.444-41-32 ФЗО
КОНТРОЛЬНАЯ
РАБОТА №1
Исследование
эмпирических функций распределения и расчет основных статических характеристик
р. Керженец в створе с. Хахалы
По
дисциплине
«Методы
статистической обработки гидрометеорологической информации»
Год
издания методических указаний 2003
Студента 4 курса,
специальности «Гидрология»
Сечков Антон Владимирович
Таблица 1
Исходные данные. Среднегодовые расходы воды реки
Керженец - с. Хахалы
|
№п/п
|
Год
|
Qср.год, м3/с
|
|
1
|
1930
|
17,5
|
|
2
|
1931
|
20,9
|
|
3
|
1932
|
21,6
|
|
4
|
1933
|
15,5
|
|
5
|
1934
|
15,3
|
|
6
|
1935
|
17,3
|
|
7
|
1936
|
19,3
|
|
8
|
1937
|
9,88
|
|
9
|
1938
|
18,2
|
|
10
|
1939
|
16,2
|
|
11
|
1940
|
18,6
|
|
12
|
1941
|
18,5
|
|
13
|
1942
|
23,1
|
|
14
|
1943
|
18,2
|
|
15
|
1944
|
20,1
|
|
16
|
1945
|
21,3
|
|
17
|
1946
|
19,0
|
|
18
|
1947
|
34,6
|
|
19
|
1948
|
21,0
|
|
20
|
1949
|
12,0
|
|
21
|
1950
|
13,4
|
|
22
|
1951
|
12,4
|
|
23
|
1952
|
20,6
|
|
24
|
1953
|
26,6
|
|
25
|
1954
|
16,7
|
|
26
|
1955
|
23,9
|
|
27
|
1956
|
19,1
|
|
28
|
1957
|
21,2
|
|
29
|
1958
|
27,9
|
|
30
|
1959
|
22,8
|
|
31
|
1960
|
17,1
|
|
32
|
1961
|
15,5
|
|
33
|
1962
|
21,6
|
|
34
|
1963
|
18,4
|
|
35
|
1964
|
9,65
|
|
36
|
1965
|
17,9
|
|
37
|
1966
|
26,4
|
|
38
|
1967
|
10,1
|
|
39
|
1968
|
17,2
|
|
40
|
1969
|
19,3
|
|
41
|
1970
|
22,4
|
|
42
|
1971
|
16,6
|
|
43
|
1972
|
15,6
|
|
44
|
1973
|
11,9
|
|
45
|
1974
|
10,9
|
|
46
|
1975
|
12,7
|
Основные сведения по расчетному створу
представлены в таблице 2.
Таблица 2. Основные характеристики реки Керженец
- с. Хахалы
|
Региональная
принадлежность
|
Длина
ряда
|
Площадь
водосбора, F, км2
|
Длина
реки, км
|
Уклон
реки, ‰
|
Озерность,
%
|
|
Верхняя
Волга
|
46
|
5760
|
290
|
0,42
|
1
|
Построение гистограммы эмпирических
частот и эмпирических функций распределения
. Определить размах R:
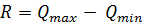
R
= 34.6 - 9.65 = 24.95
. Определить длину расчетного интервала L.
Для
построении гистограммы эмпирических частот размах статического ряда разбивается
на m равных
интервалов. Количество интервалов зависит о длины ряда n
и приближенно определяется по эмпирической формуле:
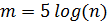 = 5
= 5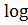 (46)
= 8.31 ≈ 8
(46)
= 8.31 ≈ 8
Длина расчетного интервала определяется по
формуле
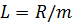 = 24.95/8 = 3.12 ≈
3.5
= 24.95/8 = 3.12 ≈
3.5
. Построить гистограмму эмпирических частот.
Таблица 3
Расчет эмпирических частот для ряда
среднегодовых расходов воды р. Керженец - с. Хахалы
|
Интервал
значений расходов воды, м3/с
|
Число
значений в интервале
|
Частота,
р
|
|
|
в
долях единицы
|
в
процентах
|
|
9.0-12.5
|
7
|
0.152
|
15.2
|
|
12.5-16.0
|
6
|
0.130
|
13.0
|
|
16.0-19.5
|
17
|
0.370
|
37.0
|
|
19.5-23.0
|
10
|
0.217
|
21.7
|
|
23.0-26.5
|
3
|
0.065
|
6.50
|
|
26.5-30.0
|
2
|
0.044
|
4.40
|
|
30.0-33.5
|
0
|
0.000
|
0.00
|
|
33.5-37.0
|
1
|
0.022
|
2.20
|
|
сумма
|
46
|
1.00
|
100
|
Гистограмма эмпирических частот приведена на
рисунке 1. Сглаживая гистограмму частот, получаем эмпирическую функцию
плотности вероятности f(Q).
. Построить интегральную функцию распределения и
функцию обеспеченностей.
Таблица 4
Расчет координат интегральной функции
распределения и функции обеспеченностей, р. Керженец - с. Хахалы
|
Значение
расхода воды, м3/с
|
Число
случаев непревышения
|
Число
случаев превышения
|
Относительное
число случаев непревышения, F(Q)
|
Относительное
число случаев превышения, P(Q)
|
|
9.0
|
0
|
46
|
0
|
1.00
|
|
12.5
|
7
|
39
|
0.15
|
0.85
|
|
16.0
|
13
|
33
|
0.28
|
0.72
|
|
19.5
|
30
|
16
|
0.65
|
0.35
|
|
23.0
|
40
|
6
|
0.87
|
0.13
|
|
26.5
|
43
|
3
|
0.93
|
0.07
|
|
30.0
|
45
|
1
|
0.98
|
0.02
|
|
33.5
|
45
|
1
|
0.98
|
0.02
|
|
37.0
|
46
|
0
|
1.00
|
0.00
|
График интегральной функции распределения и
функции обеспеченностей приведены на рисунке 1.
Расчет
числовых характеристик и их погрешностей
1. Рассчитать оценки характеристик положения
(моды, медианы, математического ожидания).
Модой непрерывной случайной величины называется
такое ее значение, которому соответствует максимум плотности вероятностей. Для
определения моды воспользуемся графиком плотности вероятностей (рисунок 1).
Мо = 17.4
м3/с.
Медианой непрерывной случайной величины
называется такое ее значение, для которого вероятность превышения равна
вероятности непревышения и равна 0.5.
Ме = 18.1
м3/с.
Оценкой математического ожидания является
среднее арифметическое значение:
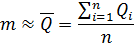
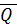 = 18.4
= 18.4
Полученные значения моды, медианы,
математического ожидания нанесены на рисунок 1.
Рисунок 1 Гистограмма эмперических частот и
графики эмперических функций распределения среднегодовых расходов
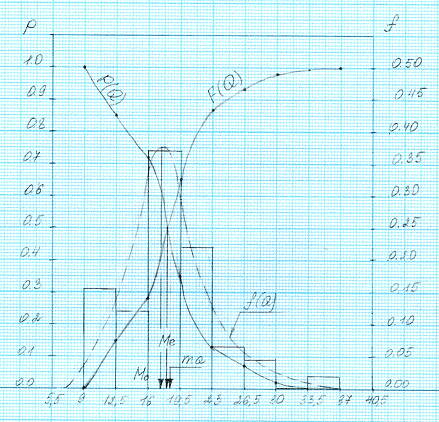
А(Q)
- интегральная функция распеделения;
P(Q)
- функция обеспеченностей;
f(Q)
- функция плотности вероятности.
. Рассчитать оценки характеристик рассеивания.
Расчет производится методом моментов.
Таблица 5
Вспомогательная таблица для расчета основных
статистических характеристик ряда среднегодовых расходов воды, р. Керженец - с.
Хахалы
|
№
п/п
|
Q, м3 /с
|
k
|
(k-1)
|
(k-1)2
|
(k-1)3
|
|
1
|
17,50
|
0,9516
|
-0,0484
|
0,0023
|
-0,0001
|
|
2
|
20,90
|
1,1365
|
0,1365
|
0,0186
|
0,0025
|
|
3
|
21,60
|
1,1746
|
0,1746
|
0,0305
|
0,0053
|
|
4
|
15,50
|
0,8429
|
-0,1571
|
0,0247
|
-0,0039
|
|
5
|
15,30
|
0,8320
|
-0,1680
|
0,0282
|
-0,0047
|
|
6
|
17,30
|
0,9407
|
-0,0593
|
0,0035
|
-0,0002
|
|
7
|
19,30
|
1,0495
|
0,0495
|
0,0024
|
0,0001
|
|
8
|
9,88
|
0,5373
|
-0,4627
|
0,2141
|
|
9
|
18,20
|
0,9897
|
-0,0103
|
0,0001
|
0,0000
|
|
10
|
16,20
|
0,8809
|
-0,1191
|
0,0142
|
-0,0017
|
|
11
|
18,60
|
1,0114
|
0,0114
|
0,0001
|
0,0000
|
|
12
|
18,50
|
1,0060
|
0,0060
|
0,0000
|
0,0000
|
|
13
|
23,10
|
1,2561
|
0,2561
|
0,0656
|
0,0168
|
|
14
|
18,20
|
0,9897
|
-0,0103
|
0,0001
|
0,0000
|
|
15
|
20,10
|
1,0930
|
0,0930
|
0,0086
|
0,0008
|
|
16
|
21,30
|
1,1583
|
0,1583
|
0,0250
|
0,0040
|
|
17
|
19,00
|
1,0332
|
0,0332
|
0,0011
|
0,0000
|
|
18
|
34,60
|
1,8815
|
0,8815
|
0,7770
|
0,6849
|
|
19
|
21,00
|
1,1419
|
0,1419
|
0,0201
|
0,0029
|
|
20
|
12,00
|
0,6525
|
-0,3475
|
0,1207
|
-0,0419
|
|
21
|
13,40
|
0,7287
|
-0,2713
|
0,0736
|
-0,0200
|
|
22
|
12,40
|
0,6743
|
-0,3257
|
0,1061
|
-0,0346
|
|
23
|
20,60
|
1,1202
|
0,1202
|
0,0144
|
0,0017
|
|
24
|
26,60
|
1,4465
|
0,4465
|
0,1993
|
0,0890
|
|
25
|
16,70
|
0,9081
|
-0,0919
|
0,0084
|
-0,0008
|
|
26
|
23,90
|
1,2996
|
0,2996
|
0,0898
|
0,0269
|
|
27
|
19,10
|
1,0386
|
0,0386
|
0,0015
|
0,0001
|
|
28
|
21,20
|
1,1528
|
0,1528
|
0,0234
|
0,0036
|
|
29
|
27,90
|
1,5171
|
0,5171
|
0,2674
|
0,1383
|
|
30
|
22,80
|
1,2398
|
0,2398
|
0,0575
|
0,0138
|
|
31
|
17,10
|
0,9299
|
-0,0701
|
0,0049
|
-0,0003
|
|
32
|
15,50
|
0,8429
|
-0,1571
|
0,0247
|
-0,0039
|
|
33
|
21,60
|
1,1746
|
0,1746
|
0,0305
|
0,0053
|
|
34
|
18,40
|
1,0006
|
0,0006
|
0,0000
|
0,0000
|
|
35
|
9,65
|
0,5247
|
-0,4753
|
0,2259
|
-0,1073
|
|
36
|
17,90
|
0,9734
|
-0,0266
|
0,0007
|
0,0000
|
|
37
|
26,40
|
1,4356
|
0,4356
|
0,1897
|
0,0826
|
|
38
|
10,10
|
0,5492
|
-0,4508
|
0,2032
|
-0,0916
|
|
39
|
17,20
|
0,9353
|
-0,0647
|
0,0042
|
-0,0003
|
|
40
|
19,30
|
1,0495
|
0,0495
|
0,0024
|
0,0001
|
|
41
|
22,40
|
1,2181
|
0,2181
|
0,0476
|
0,0104
|
|
42
|
16,60
|
0,9027
|
-0,0973
|
0,0095
|
-0,0009
|
|
43
|
15,60
|
0,8483
|
-0,1517
|
0,0230
|
-0,0035
|
|
44
|
11,90
|
0,6471
|
-0,3529
|
0,1245
|
-0,0440
|
|
45
|
10,90
|
0,5927
|
-0,4073
|
0,1659
|
-0,0676
|
|
46
|
12,70
|
0,6906
|
-0,3094
|
0,0957
|
-0,0296
|
|
Сумма
|
845,93
|
46,0
|
0,00
|
3,351
|
0,533
|
|
Среднее
|
18,39
|
1,00
|
0,00
|
-
|
-
|
Рассчитываем требуемые статистические
характеристики:
коэффициент вариации:
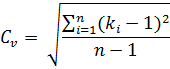
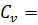 0.273
0.273
- коэффициент асимметрии:
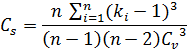
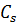 = 0.609
= 0.609
- среднеквадратичное отклонение:
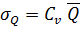
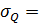 5.02
5.02
- дисперсия:
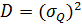
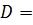 25.2
25.2
. Составить сводную таблицу основных
статистических характеристик гидрологического ряда.
Таблица 6
Основные статистические характеристики ряда
среднегодовых расходов воды, р. Керженец - с. Хахалы
|
Mo
|
Me
|
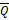
|
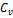
|
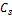
|
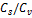
|
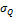
|
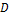
|
|
17.4
|
18.1
|
18.4
|
0.27
|
0.61
|
2.23
|
5.02
|
25.2
|
. Рассчитать абсолютные и относительные
погрешности среднего значения, коэффициента вариации и коэффициента асимметрии.
Абсолютные погрешности:
для среднего значения:
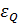 =
=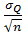
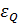 = 0.74
= 0.74
для коэффициента вариации:
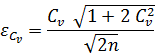
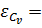 0.030
0.030
для коэффициента
асимметрии:
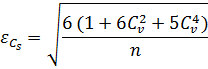
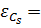 0.437
0.437
Относительные ошибки:
для среднего значения:
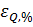 =
=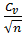 100%
100%
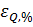 = 4.0%
= 4.0%
для коэффициента вариации:
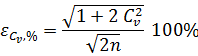
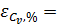 12%
12%
для коэффициента асимметрии:
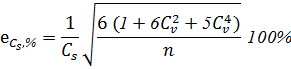
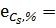 72%
72%
Результаты расчета представлены в таблице 7.
Таблица 7
Оценка точности расчета числовых характеристик
ряда среднегодовых расходов воды, р. Керженец - с. Хахалы
|
Числовая
характеристика
|
Значение
|
Абсолютная
погрешность
|
Относительная
погрешность, %
|
|
Среднее
значение, 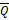
|
18.4
|
0.74
|
4.0
|
|
Коэффициент
вариации, 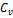
|
0.27
|
0.030
|
12
|
|
Коэффициент
асимметрии, 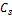
|
0.61
|
0.437
|
72
|
Проверка
ряда на однородность
Для проверки ряда на однородность используем два
критерия: критерий Стьюдента и критерий Фишера. Критерий Стьюдента позволит
провести проверку ряда на однородность по среднему значению, критерий Фишера -
по дисперсии.
Таблица 8
Основные статистические характеристики
среднегодовых расходов воды по первой и второй частям ряда, р. Керженец - с.
Хахалы
|
Выборка
|
Длина
выборки
|
Среднее
значение
|
СКО
|
Дисперсия
|
|
I часть ряда
|
23
|
18.5
|
4.89
|
23.9
|
|
II часть ряда
|
23
|
18.3
|
5.26
|
27.7
|
|
весь
ряд
|
46
|
18.4
|
5.02
|
25.2
|
. Проверка ряда на однородность по дисперсии
(критерий Фишера).
Эмпирическое значение критерия Фишера:
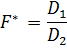
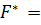 1.16
1.16
Эмпирическое значение статистики Фишера
сравнивается с теоретическим FТ
при уровне значимости 2α
= 5%.
Теоретическое значение статистики Фишера
определяется в зависимости от принятого уровня значимости и числа степеней
свободы v1 и
v2:
v1 =
n1
- 1, v1 =
22
v2 =
n2
- 1, v2 =
22
FТ
= 2.36
Поскольку эмпирическое значение статистики
Фишера меньше теоретического:
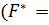 1.16) < (FТ
= 2.36),
1.16) < (FТ
= 2.36),
то можно считать различие в дисперсиях по
отдельным частям ряда незначительным. В этом случае говорят, что гипотеза об
однородности ряда по критерию Фишера при уровне значимости 2α
= 5% не
опровергается.
. Проверка ряда на однородность по среднему
значению (критерий Стьюдента).
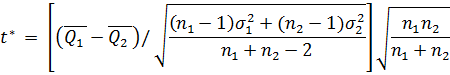
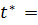 0.134
0.134
Эмпирическое значение статистики Стьюдента
сравнивается с теоретическим tТ
при уровне значимости 2α
= 5%.
Теоретическое значение статистики Стьюдента
определяется в зависимости от принятого уровня значимости и числа степеней
свободы v:
v
=
n - 1, v
=
45
tТ
= 2.015
Поскольку эмпирическое значение статистики
Стьюдента меньше теоретического:
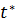 = 0.134 < (tТ
= 2.015),
= 0.134 < (tТ
= 2.015),
то можно считать различие в средних значениях по
отдельным частям ряда незначительным. В этом случае говорят, что гипотеза об
однородности ряда по критерию Стьюдента при уровне значимости 2α
= 5% не
опровергается.
В работе исследовался ряд среднегодовых расходов
по р. Керженец - с. Хахалы. длина ряда 46 лет. Эмпирическая функция плотности
вероятностей одномодальная. Распределение имеет положительную асимметрию, на
что указывает знак при коэффициенте асимметрии и то, что на рисунке 1
математическое ожидание расположено правее медианы.
Расчет статистических характеристик можно
считать надежным, так как погрешность среднего значения ряда не превышает
5-10%, а погрешность коэффициента вариации не превышает 10-15%.
Погрешность расчета коэффициента асимметрии
большая, 72%, поэтому для практических расчетов следует воспользоваться
районным соотношением 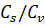 .
.
Проверка ряда на однородность показала, что
гипотеза об однородности ряда не опровергается как по критерию Фишера, так и по
критерию Стьюдента.
гистограмма
расход вода погрешность
РОССИЙСКИЙ
ГОСУДАРСТВЕННЫЙ ГИДРОМЕТЕОРОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
Факультет
заочного обучения
,
г. Санкт-Петербург, Малоохтинский пр. д.98, тел.444-41-32 ФЗО
КОНТРОЛЬНАЯ
РАБОТА №2
Построение
эмпирических и аналитических кривых обеспеченностей и расчет расходов воды
различной вероятности ежегодного превышения р. Керженец в створе с. Хахалы
По
дисциплине
«Методы
статистической обработки гидрометеорологической информации»
Год издания методических указаний 2003
Студента 4 курса, специальности «Гидрология»
Сечков Антон Владимирович
Таблица 1
Исходные данные. Среднегодовые расходы воды реки
Керженец - с. Хахалы
|
№п/п
|
Год
|
Qср.год, м3/с
|
|
1
|
1930
|
17,5
|
|
2
|
1931
|
20,9
|
|
3
|
1932
|
21,6
|
|
4
|
1933
|
15,5
|
|
5
|
1934
|
15,3
|
|
6
|
1935
|
17,3
|
|
7
|
1936
|
19,3
|
|
8
|
1937
|
9,88
|
|
9
|
1938
|
18,2
|
|
10
|
1939
|
16,2
|
|
11
|
1940
|
18,6
|
|
12
|
1941
|
18,5
|
|
13
|
1942
|
23,1
|
|
14
|
1943
|
18,2
|
|
15
|
1944
|
20,1
|
|
16
|
1945
|
21,3
|
|
17
|
1946
|
19,0
|
|
18
|
1947
|
34,6
|
|
19
|
1948
|
21,0
|
|
20
|
1949
|
12,0
|
|
21
|
1950
|
13,4
|
|
22
|
1951
|
12,4
|
|
23
|
1952
|
20,6
|
|
24
|
1953
|
26,6
|
|
25
|
1954
|
16,7
|
|
26
|
1955
|
23,9
|
|
27
|
1956
|
19,1
|
|
28
|
1957
|
21,2
|
|
29
|
1958
|
27,9
|
|
30
|
1959
|
22,8
|
|
31
|
1960
|
17,1
|
|
32
|
1961
|
15,5
|
|
33
|
1962
|
21,6
|
|
34
|
1963
|
18,4
|
|
35
|
1964
|
9,65
|
|
36
|
1965
|
17,9
|
|
37
|
1966
|
26,4
|
|
38
|
1967
|
10,1
|
|
39
|
1968
|
17,2
|
|
40
|
1969
|
19,3
|
|
41
|
1970
|
22,4
|
|
42
|
1971
|
16,6
|
|
43
|
1972
|
15,6
|
|
44
|
1973
|
11,9
|
|
45
|
1974
|
10,9
|
|
46
|
1975
|
12,7
|
Основные сведения по расчетному створу
представлены в таблице 2.
Таблица 2
Основные характеристики реки Керженец - с.
Хахалы
|
Региональная
принадлежность
|
Длина
ряда
|
Площадь
водосбора, F, км2
|
Длина
реки, км
|
Уклон
реки, ‰
|
Озерность,
%
|
|
Верхняя
Волга
|
46
|
5760
|
290
|
0,42
|
1
|
Построение
эмпирической кривой обеспеченностей
Таблица 3
Расчет ординат эмпирической кривой обеспеченностей
среднегодовых расходов, р. Керженец - с. Хахалы
|
№
п/п
|
Расходы
воды, Q м3/с
|
Ранжированные
расходы воды, QR
м3/с
|
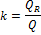
|
P, %
|
|
1
|
17,5
|
34,6
|
1,88
|
2,13
|
|
2
|
20,9
|
27,9
|
1,52
|
4,26
|
|
3
|
21,6
|
26,6
|
1,45
|
6,38
|
|
4
|
15,5
|
26,4
|
1,43
|
8,51
|
|
5
|
15,3
|
23,9
|
1,30
|
10,6
|
|
6
|
17,3
|
23,1
|
1,26
|
12,8
|
|
7
|
19,3
|
22,8
|
1,24
|
14,9
|
|
8
|
9,88
|
22,4
|
1,22
|
17,0
|
|
9
|
18,2
|
21,6
|
1,17
|
19,1
|
|
10
|
16,2
|
21,6
|
1,17
|
21,3
|
|
11
|
18,6
|
21,3
|
1,16
|
23,4
|
|
12
|
18,5
|
21,2
|
1,15
|
25,5
|
|
13
|
23,1
|
21,0
|
1,14
|
27,7
|
|
14
|
18,2
|
20,9
|
1,14
|
29,8
|
|
15
|
20,1
|
20,6
|
1,12
|
31,9
|
|
16
|
21,3
|
20,1
|
1,09
|
34,0
|
|
17
|
19,0
|
19,3
|
1,05
|
36,2
|
|
18
|
34,6
|
19,3
|
1,05
|
38,3
|
|
19
|
21,0
|
19,1
|
1,04
|
40,4
|
|
20
|
12,0
|
19,0
|
1,03
|
42,6
|
|
21
|
13,4
|
18,6
|
1,01
|
44,7
|
|
22
|
12,4
|
18,5
|
1,01
|
46,8
|
|
23
|
20,6
|
18,4
|
1,00
|
48,9
|
|
24
|
26,6
|
18,2
|
0,99
|
51,1
|
|
25
|
16,7
|
18,2
|
0,99
|
53,2
|
|
26
|
23,9
|
17,9
|
0,97
|
55,3
|
|
27
|
19,1
|
17,5
|
0,95
|
57,4
|
|
28
|
21,2
|
17,3
|
0,94
|
59,6
|
|
29
|
27,9
|
17,2
|
0,93
|
61,7
|
|
30
|
22,8
|
17,1
|
0,93
|
63,8
|
|
31
|
17,1
|
16,7
|
0,91
|
66,0
|
15,5
|
16,6
|
0,90
|
68,1
|
|
33
|
21,6
|
16,2
|
0,88
|
70,2
|
|
34
|
18,4
|
15,6
|
0,85
|
72,3
|
|
35
|
9,65
|
15,5
|
0,84
|
74,5
|
|
36
|
17,9
|
15,5
|
0,84
|
76,6
|
|
37
|
26,4
|
15,3
|
0,83
|
78,7
|
|
38
|
10,1
|
13,4
|
0,73
|
80,9
|
|
39
|
17,2
|
12,7
|
0,69
|
83,0
|
|
40
|
19,3
|
12,4
|
0,67
|
85,1
|
|
41
|
22,4
|
12,0
|
0,65
|
87,2
|
|
42
|
16,6
|
11,9
|
0,65
|
89,4
|
|
43
|
15,6
|
10,9
|
0,59
|
91,5
|
|
44
|
11,9
|
10,1
|
0,55
|
93,6
|
|
45
|
10,9
|
9,88
|
0,54
|
95,7
|
|
46
|
12,7
|
9,65
|
0,52
|
97,9
|
Эмпирическая и аналитические кривые
обеспеченностей среднегодовых расходов воды р. Керженец - с. Хахалы приведена
на рис. 1.
Построение
аналитической кривой обеспеченностей нормального закона распределения
Таблица 4. Расчет координат аналитической кривой
обеспеченностей нормального закона распределения для среднегодовых расходов
воды, р. Керженец - с. Хахалы 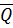 = 18.4,
= 18.4, 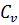 =
0.27
=
0.27
|
P, %
|
tp
|
kp
|
QR
|
|
0,01
|
3,72
|
2,00
|
36,9
|
|
0,1
|
3,09
|
1,83
|
33,8
|
|
1
|
2,33
|
1,63
|
30,0
|
|
5
|
1,64
|
1,44
|
26,6
|
|
10
|
1,28
|
1,35
|
24,8
|
|
20
|
0,84
|
1,23
|
22,6
|
|
30
|
0,52
|
1,14
|
21,0
|
|
50
|
0,00
|
1,00
|
18,4
|
|
70
|
-0,52
|
0,86
|
15,8
|
|
80
|
-0,84
|
0,77
|
14,2
|
|
90
|
-1,28
|
0,65
|
12,0
|
|
95
|
-1,64
|
0,56
|
10,3
|
|
99
|
-2,33
|
0,37
|
6,83
|
|
99,9
|
-3,09
|
0,17
|
3,50
|
Аналитическая кривая обеспеченностей нормального
закона распределения приведена на рисунке 1.
Построение
аналитической кривой обеспеченностей логарифмически нормального закона
распределения
Таблица 5. Вспомогательная таблица для расчета
статистических характеристик ряда zi,
р. Керженец - с. Хахалы
|
№
п/п
|
Расход
воды, Q м3/с
|
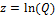
|
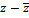
|
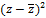
|
|
1
|
17,5
|
2,862
|
-0,013
|
0,0002
|
|
2
|
20,9
|
3,040
|
0,165
|
0,0272
|
|
3
|
21,6
|
3,073
|
0,198
|
0,0392
|
|
4
|
15,5
|
2,741
|
-0,134
|
0,0179
|
|
5
|
15,3
|
2,728
|
-0,147
|
0,0216
|
|
6
|
17,3
|
2,851
|
-0,024
|
0,0006
|
|
7
|
19,3
|
2,960
|
0,085
|
0,0073
|
|
8
|
9,88
|
2,291
|
-0,584
|
0,3413
|
|
9
|
18,2
|
2,901
|
0,027
|
0,0007
|
|
10
|
16,2
|
2,785
|
-0,090
|
0,0081
|
|
11
|
18,6
|
2,923
|
0,048
|
0,0023
|
|
12
|
18,5
|
2,918
|
0,043
|
0,0019
|
|
13
|
23,1
|
3,140
|
0,265
|
0,0703
|
|
14
|
18,2
|
2,901
|
0,027
|
0,0007
|
|
15
|
20,1
|
3,001
|
0,126
|
0,0159
|
|
16
|
21,3
|
3,059
|
0,184
|
0,0338
|
|
17
|
19,0
|
2,944
|
0,070
|
0,0049
|
|
18
|
34,6
|
3,544
|
0,669
|
0,4477
|
|
19
|
21,0
|
3,045
|
0,170
|
0,0288
|
|
20
|
12,0
|
2,485
|
-0,390
|
0,1520
|
|
21
|
13,4
|
2,595
|
-0,279
|
0,0781
|
|
22
|
12,4
|
2,518
|
-0,357
|
0,1275
|
|
23
|
20,6
|
3,025
|
0,151
|
0,0227
|
|
24
|
26,6
|
3,281
|
0,406
|
0,1650
|
|
25
|
16,7
|
2,815
|
-0,059
|
0,0035
|
|
26
|
23,9
|
3,174
|
0,299
|
0,0895
|
|
27
|
19,1
|
2,950
|
0,075
|
0,0056
|
|
28
|
21,2
|
3,054
|
0,179
|
0,0321
|
|
29
|
27,9
|
3,329
|
0,454
|
0,2060
|
|
30
|
22,8
|
3,127
|
0,252
|
0,0635
|
|
31
|
17,1
|
2,839
|
-0,036
|
0,0013
|
|
32
|
15,5
|
2,741
|
-0,134
|
0,0179
|
|
33
|
21,6
|
3,073
|
0,198
|
0,0392
|
|
34
|
18,4
|
2,912
|
0,038
|
0,0014
|
|
35
|
9,65
|
2,267
|
-0,608
|
0,3694
|
|
36
|
17,9
|
2,885
|
0,010
|
0,0001
|
|
37
|
26,4
|
3,273
|
0,399
|
0,1589
|
|
38
|
10,1
|
2,313
|
-0,562
|
0,3161
|
|
39
|
17,2
|
2,845
|
-0,030
|
0,0009
|
|
40
|
19,3
|
2,960
|
0,085
|
0,0073
|
|
41
|
22,4
|
3,109
|
0,234
|
0,0549
|
16,6
|
2,809
|
-0,065
|
0,0043
|
|
43
|
15,6
|
2,747
|
-0,127
|
0,0162
|
|
44
|
11,9
|
2,477
|
-0,398
|
0,1586
|
|
45
|
10,9
|
2,389
|
-0,486
|
0,2362
|
|
46
|
12,7
|
2,542
|
-0,333
|
0,1110
|
|
Cумма
|
845,9
|
132,2
|
0,000
|
3,5094
|
|
Cреднее
|
18,4
|
2,875
|
0,000
|
-
|
Рассчитываем статистические характеристики для
ряда р. Керженец - с. Хахалы:
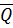 = 18.4,
= 18.4, 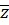 =
2.88
=
2.88
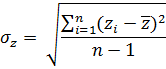
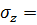 0.279
0.279
Дальнейший расчет сводится в таблицу 6.
Таблица 6
Расчет координат аналитической кривой
обеспеченностей логнормального закона распределения для среднегодовых расходов
воды, р. Керженец - с. Хахалы 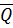 = 18.4,
= 18.4, 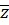 =
2.88,
=
2.88, 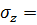 0.279
0.279
|
Р%
|
tp
|
zp
|
Qp
|
kp
|
|
0,01
|
3,72
|
3,91
|
50,0
|
2,72
|
|
0,1
|
3,09
|
3,74
|
42,0
|
2,28
|
|
1
|
2,33
|
3,53
|
34,0
|
1,85
|
|
5
|
1,64
|
3,33
|
28,0
|
1,52
|
|
10
|
1,28
|
3,23
|
25,3
|
1,38
|
|
20
|
0,84
|
3,11
|
22,4
|
1,22
|
|
30
|
0,52
|
3,02
|
20,5
|
1,11
|
|
50
|
0,00
|
2,88
|
17,7
|
0,96
|
|
70
|
-0,52
|
2,73
|
15,3
|
0,83
|
|
80
|
-0,84
|
2,64
|
14,0
|
0,76
|
|
90
|
-1,28
|
2,52
|
12,4
|
0,67
|
|
95
|
-1,64
|
2,42
|
11,2
|
0,61
|
|
99
|
-2,33
|
2,22
|
9,25
|
0,50
|
|
99,9
|
-3,09
|
2,01
|
7,48
|
0,41
|
По данным таблицы 6 строится аналитическая
кривая обеспеченностей логнормального закона распределения, рисунок 1.
Построение
аналитической кривой обеспеченностей Гумбеля
Для р. Керженец - с. Хахалы 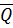 =
18.4,
=
18.4, 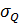 =
5.02. Расчет сводится в таблицу 7.
=
5.02. Расчет сводится в таблицу 7.
Во второй столбец таблицы 7 записываем
нормированные ординаты кривой обеспеченностей Гумбеля yр.
Переход от yр
к расходам воды осуществляется по формуле:
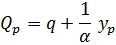
Значения 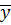 и
и
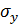 определяются
в зависимости от длины исходного ряда.
определяются
в зависимости от длины исходного ряда.
Для р. Керженец - с. Хахалы n=46,
следовательно:
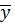 = 0.547,
= 0.547, 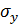 =
1.154
=
1.154
Расчет параметров производится по формулам:
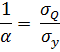
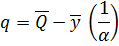
Для р. Керженец - с. Хахалы получаем:
1/α = 4.35; q=
16.02
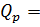 16.02 + 4.35
16.02 + 4.35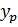
Таблица 7
Расчет координат аналитической кривой
обеспеченностей Гумбеля для среднегодовых расходов воды, р. Керженец - с.
Хахалы 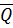 =
18.4,
=
18.4, 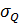 =
5.02
=
5.02
|
Р%
|
yp
|
Qp
|
kp
|
|
0,01
|
9,09
|
55,6
|
3,02
|
|
0,1
|
6,89
|
46,0
|
2,50
|
|
1
|
4,60
|
36,0
|
1,96
|
|
5
|
2,97
|
28,9
|
1,57
|
|
10
|
2,25
|
25,8
|
1,40
|
|
20
|
1,50
|
22,6
|
1,23
|
|
30
|
1,03
|
20,5
|
1,11
|
|
50
|
0,37
|
17,6
|
0,96
|
|
70
|
-0,19
|
15,2
|
0,83
|
|
80
|
-0,48
|
13,9
|
0,76
|
|
90
|
-0,83
|
12,4
|
0,67
|
|
95
|
-1,10
|
11,2
|
0,61
|
|
99
|
-1,53
|
9,36
|
0,51
|
|
99,9
|
-1,93
|
7,62
|
0,41
|
По данным таблицы 7 строится аналитическая
кривая обеспеченностей Гумбеля, рисунок 1.
Построение
аналитической кривой обеспеченностей Пирсона III
типа
Для р. Керженец - с. Хахалы 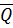 =
18.4,
=
18.4, 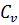 =
0.27,
=
0.27, 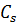 =
0.61.
=
0.61.
Для р. Керженец - с. Хахалы эмпирическое
значение 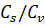 =
2.23, следовательно, принимаем для расчетов
=
2.23, следовательно, принимаем для расчетов 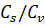 =
2. Тогда:
=
2. Тогда:
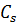 = (
= (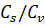 )
)
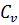 ;
;
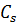 =
0.54.
=
0.54.
Расчет сводится в таблицу 8.
Таблица 8
Расчет координат аналитической кривой
обеспеченностей Пирсона III
типа для среднегодовых расходов воды, р. Керженец - с. Хахалы 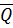 =
18.4,
=
18.4, 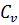 =
0.27,
=
0.27, 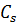 =
0.54
=
0.54
|
Р%
|
tp
|
kp
|
Qp
|
|
0,01
|
4,92
|
2,33
|
42,8
|
|
0,1
|
3,87
|
2,04
|
37,6
|
|
1
|
2,71
|
1,73
|
31,9
|
|
5
|
1,79
|
1,48
|
27,3
|
|
10
|
1,33
|
1,36
|
25,0
|
|
20
|
0,81
|
1,22
|
22,4
|
|
30
|
0,45
|
1,12
|
20,6
|
|
50
|
-0,09
|
0,98
|
18,0
|
|
70
|
-0,58
|
0,84
|
15,5
|
|
80
|
-0,85
|
0,77
|
14,2
|
|
90
|
-1,21
|
0,67
|
12,4
|
|
95
|
-1,47
|
0,60
|
11,1
|
|
99
|
-1,93
|
0,48
|
8,81
|
|
99,9
|
-2,35
|
0,37
|
6,73
|
По данным таблицы 8 строится аналитическая
кривая обеспеченностей Пирсона III
типа, рисунок 1.
Построение
аналитической кривой обеспеченностей Крицкого-Менкеля
Для р. Керженец - с. Хахалы 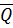 =
18.4,
=
18.4, 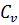 =
0.27,
=
0.27, 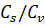 =
2,23
=
2,23
Для расчетов принимаем 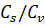 =
2. Расчет сводится в таблицу 9.
=
2. Расчет сводится в таблицу 9.
Таблица 9
Расчет координат аналитической кривой
обеспеченностей Крицкого-Менкеля для среднегодовых расходов воды, р. Керженец -
с. Хахалы 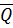 = 18.4,
= 18.4, 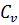 =
0.27,
=
0.27, 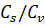 =
2
=
2
|
Р%
|
0,01
|
0,1
|
1
|
5
|
10
|
20
|
30
|
50
|
70
|
80
|
90
|
95
|
99
|
99,9
|
|
kp
|
2,34
|
2,05
|
1,73
|
1,48
|
1,36
|
1,22
|
1,12
|
0,97
|
0,84
|
0,77
|
0,67
|
0,60
|
0,48
|
0,37
|
|
Qp
|
43,1
|
37,7
|
31,8
|
27,2
|
25,0
|
22,4
|
20,6
|
17,8
|
15,5
|
14,2
|
12,3
|
11,0
|
8,83
|
6,81
|
По данным таблицы 9 строится аналитическая
кривая обеспеченностей Крицкого-Менкеля, рисунок 1.
В работе исследовался ряд среднегодовых расходов
по р. Керженец - с. Хахалы. Длина ряда 46 лет. При рассмотрении построенных
аналитических кривых обеспеченностей, можно сказать, что наиболее соответствует
эмпирическим точкам кривая обеспеченностей Гумбеля (1), которая описывает весь
спектр эмпирических точек, а также охватывает выделяющиеся эмпирические точки.
Кривая обеспеченностей нормального закона распределения (3) и кривые
обеспеченностей Крицкого-Менкеля и Пирсона III
типа (2) описывает не весь спектр эмпирических точек.
Таким образом, для дальнейших расчетов следует
использовать кривую обеспеченностей Гумбеля.