Статистический анализ данных
Министерство
образования и науки Российской Федерации
Федеральное
агентство по образованию
Южный
федеральный университет
Факультет
электроники и приборостроения (ФЭП)
Кафедра
информационных измерительных технологий и систем (ИИТиС)
Пояснительная
записка к курсовой работе
Статистический
анализ данных
Выполнил:
Косторниченко В.Г.
Таганрог
2013 г.
Задание
|
Вариант
- №12
|
|
Объем
выборки Х1 = 112
|
|
Объем
выборки Х2 = 102
|
|
Дисперсия
= 3
|
|
Математическое
ожидание = 12
|
В ходе курсовой работы необходимо выполнить
статистические задачи:
. Построить гистограммы распределения и
эмпирической функции распределения
. Найти доверительный интервал для оценки
математического ожидания:
С известной дисперсией.
С неизвестной дисперсией.
. Проверить статистические гипотезы:
Гипотеза о численной величине среднего значения.
Гипотеза о числовом значение дисперсии.
Гипотеза о равенстве средних значений.
Гипотеза о равенстве дисперсий.
Гипотеза о виде распределения выборки.
Оглавление
гистограмма распределение интервал
дисперсия
1.
Цель работы
.
Построение гистограммы и эмпирической функции распределения
.
Нахождение доверительного интервала
.1
Нахождение доверительного интервала для оценки математического нормального
распределения при известной дисперсии 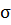
3.2
Нахождение доверительного интервала при неизвестной дисперсии 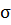
4.
Проверка статистической гипотезы
.1
Проверка гипотезы о равенстве средних значений
.2
Проверка гипотезы о равенстве дисперсий
4.3
Гипотеза о численной величине среднего значения
.4
Гипотеза о численном значении дисперсии
.5
Проверка гипотезы о виде закона распределения
1. Цель работы
В данной курсовой работе проводится анализ
данных двух выборок, состоящих из 112 и 102 случайных величин. Данные выборок
получены в программе "Statistica" с помощью формулы
(k/4)+k,
где k - мой порядковый номер в списке журнала,
отсюда получаем формулу = RndNormal(3)+12.
|
Var1
|
|
1
|
13,90844
|
|
2
|
16,26087
|
|
3
|
14,5209
|
|
4
|
12,03951
|
|
5
|
8,733121
|
|
..
|
………….
|
|
112
|
8,851047
|
|
Var1
|
|
1
|
9,76348529
|
|
2
|
9,81413258
|
|
3
|
10,6819403
|
|
4
|
9,42766778
|
|
5
|
9,75843679
|
|
..
|
................
|
|
102
|
9,42001527
|
2. Построение гистограммы и эмпирической функции
распределения
Гистограмма- это способ представления
статистических данных в графическом виде - в виде столбчатой диаграммы. Она
отображает распределение отдельных измерений параметров изделия или процесса.
Иногда ее называют частотным распределением, так как гистограмма показывает
частоту появления измеренных значений параметров объекта.
Выборка 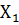 .
.
1. Сгенерируем выборку 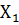 ,состоящую
из 112 случайных величин.
,состоящую
из 112 случайных величин.
. Найдем наименьший и набольший элемент в
выборке: Xmin=5,188972; Xmax=20,77344.
. Для упрощения процедуры обработки и с целью
уменьшения ошибок при вычислениях вычтем из каждого элемента ряда постоянное
число (например, округленное Xmin) и используем в расчетах не сами размеры, а
их отклонениями.
Наименьший элемент ряда Xmin=5,188972, округлим
его до 6 и вскоре вычислим из каждого элемента выборки.
. Для группировки данных необходимо: 1) Разбить
весь диапазон R = Xmax -Xmin = 20,77344- 5,188972= 15.584468 (округлим до 16)
на r интервалов. Число интервалов r устанавливают в зависимости от числа
наблюдений n: для 112 наблюдений удобно взять r=12. 2) Назначить длину
интервалов по формуле Dx = R/r=16/12 =1.3. 3) Подсчитать
количество попаданий размера 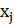 в интервал
в интервал  <
<
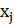 £
£
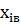
Таблица 1.
|
Номера
интервалов
|
Границы
интервалов, <размерность>
|
Частота, mi
|
Частость 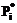
|
Эмпирическая
плотность вероятности pi
|
Середина
интервала xi
|
|
xн
|
xв
|
|
|
|
|
|
1
|
0
|
0.2
|
2
|
0,018
|
0,018
|
0,1
|
|
2
|
0.2
|
0.4
|
5
|
0,045
|
0,046
|
0.3
|
|
3
|
0.4
|
0.6
|
12
|
0,109
|
0,109
|
0.5
|
|
4
|
0.6
|
0.8
|
19
|
0,173
|
0,174
|
0.7
|
|
5
|
0.8
|
1
|
24
|
0,218
|
0,218
|
0.9
|
|
6
|
1
|
1.2
|
17
|
0,155
|
0,155
|
1.1
|
|
7
|
1.2
|
1.4
|
18
|
0,164
|
0,164
|
1.3
|
|
8
|
1.4
|
1.6
|
2
|
0,018
|
0,018
|
1.5
|
|
9
|
1.6
|
1.8
|
6
|
0,055
|
0,055
|
1.7
|
|
10
|
1.8
|
2
|
5
|
0,045
|
0,046
|
1.9
|
|
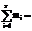 112 112
|
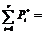 1 1
|
|
Сумма всех частот равна количеству случайных
величин в выборке и сумма всех частостей равна единице, следовательно, мы не
допустили ошибку.
В таблице:
Частота - количество элементов выборки,
попадающих в интервал.
Частость - отношение частоты 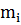 к
общему числу наблюдений n:
к
общему числу наблюдений n:
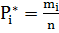 - представляет
собой эмпирическую оценку вероятности попадания результатов наблюдений Хj в i
интервал. Сумма всех частостей равна единицы.
- представляет
собой эмпирическую оценку вероятности попадания результатов наблюдений Хj в i
интервал. Сумма всех частостей равна единицы.
Эмпирическая плотность вероятностей равна:
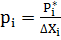 .
.
Середины интервалов необходимы для дальнейших
геометрических построений.
Построение гистограммы распределения
Для построения гистограммы по оси абсцисс
указывают значения границ интервалов и на их основании строят прямоугольники,
высота которых пропорциональна частотам.
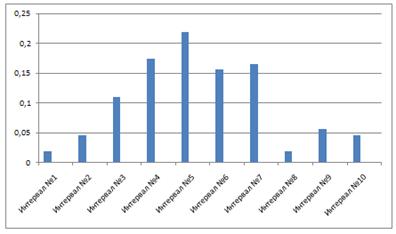
Рисунок 1.
Построение эмпирической функции распределения.
Для эмпирической функции распределения на оси
абсцисс указывают значения границ интервалов, а на оси ординат вероятности
попадания случайных величин левее интервала. (Рисунок 2).
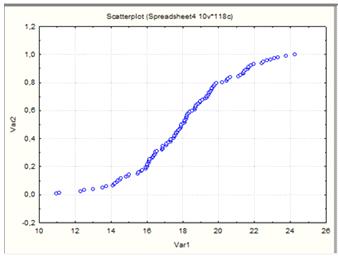
Рисунок 2.
Выборка 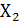 .
.
. Сгенерируем выборку 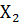 ,
состоящую из 102 случайных величин.
,
состоящую из 102 случайных величин.
. Найдем наименьший и набольший элемент в
выборке Xmin=8,97239964; Xmax=19,30817.
.Наименьший элемент ряда Xmin=3,580073,
округляем до 4 и вычислим из каждого элемента выборки.
. Для группировки данных необходимо: 1).Разбить
весь диапазон R = Xmax -Xmin =19,30817-3,580073=15,728097 (округляем до 16) на
r интервалов. Число интервалов r устанавливают в зависимости от числа
наблюдений n: для 102 наблюдений, возьмем r=12.2). Назначить длину интервалов
R/r=16/12=1.3 3).Подсчитать количество попаданий размера 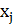 в
интервал
в
интервал 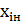 <
<
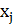 £
£
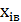 .Далее
заполним таблицу.
.Далее
заполним таблицу.
Таблица 2.
|
Номера
интервалов
|
Границы
интервалов, <размерность>
|
Частота,
mi
|
Частость,
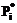
|
Эмпирическая
плотность вероятности pi
|
Середина
интервала xi
|
|
xн
|
xв
|
|
|
|
|
|
1
|
0
|
0.2
|
3
|
0.03
|
0.04
|
0,1
|
|
2
|
0.2
|
0.4
|
1
|
0.01
|
0.02
|
0.3
|
|
3
|
0.4
|
0.6
|
13
|
0.13
|
0.13
|
0.5
|
|
4
|
0.6
|
0.8
|
13
|
0.13
|
0.13
|
0.7
|
|
5
|
0.8
|
1
|
22
|
0.22
|
0.22
|
0.9
|
|
6
|
1
|
1.2
|
15
|
0.15
|
0.15
|
1.1
|
|
7
|
1.2
|
1.4
|
12
|
0.12
|
0.12
|
1.3
|
|
8
|
1.4
|
1.6
|
13
|
0.13
|
0.13
|
1.5
|
|
9
|
1.6
|
1.8
|
7
|
0.07
|
0.07
|
1.7
|
|
10
|
1.8
|
2
|
1
|
0.01
|
0.02
|
1.9
|
|
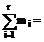 110 110
|
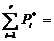 1 1
|
|
Сумма всех частот равна количеству случайных
величин в выборке и сумма всех частотностей равна единице, следовательно, мы не
совершили ошибку.
Построение гистограммы распределения.
Для построения гистограммы по оси абсцисс
указывают значения границ интервалов и на их основании строят прямоугольники,
высота которых пропорциональна частотам. (Рисунок 3).
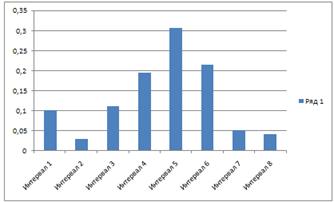
Рисунок 3.
Построение эмпирической функции распределения.
Для эмпирической функции распределения на оси
абсцисс указывают значения границ интервалов, а на оси ординат вероятности
попадания случайных величин левее интервала. (Рисунок 4).
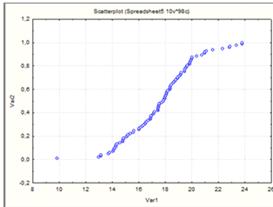
Рисунок 4.
3. Нахождение доверительного интервала
Доверительным называется интервал, который с
заданной надежностью  покрывает
оцениваемый параметр.
покрывает
оцениваемый параметр.
Квантиль в математической статистике - значение,
которое заданная случайная величина не превышает с фиксированной вероятностью.
.1 Нахождение доверительного интервала для
оценки математического нормального распределения при известной дисперсии 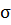
Пример 1. Пусть среднее квадратическое
отклонение нормально распределенного признака X генеральной совокупности равно
0.4, а-математическое ожидание неизвестно; объём выборки n равен 112 и
выборочное среднее (mean) 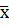 =12
=12
Задача: Найдем доверительный интервал, который
покроет математическое ожидание а с доверительной вероятностью P=0,9
Решение: Сгенерируем выборку, состоящую из 112
элементов и найдем среднее квадратичное отклонение выборки S=0,4 .
Для оценки математического ожидания служит
интервал:
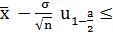 a
a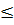
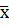 +
+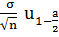 ,
,
где 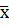 -выборочное
среднее, n - объём выборки,
-выборочное
среднее, n - объём выборки, 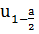 квантиль
нормального распределения N(1;0) и уровнем надежности a=0,05,
квантиль
нормального распределения N(1;0) и уровнем надежности a=0,05, 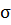 -дисперсия
выборки.
-дисперсия
выборки.
Все величины, квантиля - 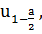 известны.
Найдем
известны.
Найдем 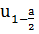 с
помощью нормального распределения N (0;1) в статистическом калькуляторе.
(Рисунок 5).
с
помощью нормального распределения N (0;1) в статистическом калькуляторе.
(Рисунок 5).
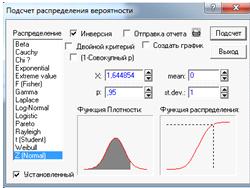
Рисунок 5.
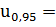 1,644854
1,644854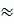 1,64
-квантиль нормального распределения.
1,64
-квантиль нормального распределения.
Подставим все известные значения в формулу и
подсчитаем:
 *
*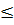 a
a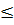
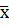 +
+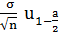 .
.
11,53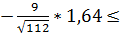 a
a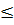
 или
-1,04
или
-1,04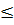 a
a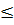 0,83
0,83
Таким образом, делаем вывод , что доверительный
интервал (-1,04; 0,83) с вероятностью P=0,9 покрывает математическое ожидание
данной выборки.
Пример 2. Пусть среднее квадратическое
отклонение нормально распределенного признака X генеральной совокупности равно
0,4, а-математическое ожидание неизвестно, объём выборки n равен 102 и
выборочное среднее (mean) 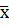 =9.9,
=9.9,
Задачa: Найти доверительный интервал, который
покроет математическое ожидание выборки с доверительной вероятностью α=0,95.
Решение: Сгенерируем выборку, состоящую из 102
элементов и найдем среднее квадратическое отклонение S=0,4.
Для оценки математического ожидания служит
интервал:
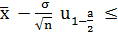 a
a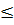
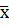 +
+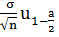 ,
,
где 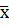 -выборочное
среднее,
-выборочное
среднее,
n - объём выборки,
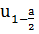 - квантиль
нормального распределения с уровнем надежности a,
- квантиль
нормального распределения с уровнем надежности a, 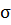 -дисперсия
выборки
-дисперсия
выборки
Известны все величины, кроме квантиля - 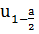 .
Найдем
.
Найдем 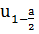 с
помощью нормального распределения N (0;1) в вероятностном калькуляторе
(Рисунок. 6).
с
помощью нормального распределения N (0;1) в вероятностном калькуляторе
(Рисунок. 6).
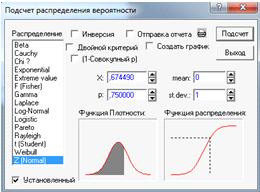
Рисунок 6.
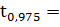 1,674490
1,674490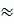 1,68
-квантиль нормального распределения.
1,68
-квантиль нормального распределения.
Подставим все известные значения в формулу и подсчитаем:
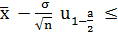 a
a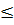
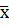 +
+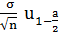 ;
;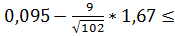 a
a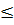 0,095+
0,095+ ;
;
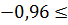 a
a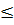 1,14;
1,14;
Таким образом, можно сделать вывод о том,
доверительный интервал (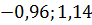 ) с доверительной
вероятностью a=0,95, покроет математическое ожидание выборки.
) с доверительной
вероятностью a=0,95, покроет математическое ожидание выборки.
3.2 Нахождение доверительного интервала при
неизвестной дисперсии 
Пример 1. Пусть количественный признак X
генеральной совокупности распределен нормально, причем среднее квадратическое
отклонение неизвестно. Требуется оценить математическое ожидание при помощи
доверительного интервала. Объём выборки n равен 112, среднее значение
(mean) 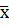 =
-0,106; среднеквадратичное отклонение (St. Dev.) = 2,44.
=
-0,106; среднеквадратичное отклонение (St. Dev.) = 2,44.
Задача: Найти доверительный интервал, который
покроет математическое ожидание выборки при доверительной вероятностьи а=0,9 .
Решение: Для нахождения доверительного интервала
мы воспользуемся распределением Стьюдента и формулой:
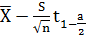 (n-1)
(n-1)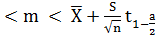 (n-1),
(n-1),
где 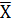 - среднее выборочное
значение;
- среднее выборочное
значение;
S - среднеквадратичное отклонение;
A - коэффициент надежности (а=1-0,9=0,1),
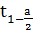 (n-1)
(n-1)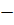 квантиль
распределения Стьюдента с n-1 - степенями свободы.
квантиль
распределения Стьюдента с n-1 - степенями свободы.
Квантиль распределения Стьюдента 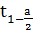 (n-1)
(n-1) -
найдем при помощи статистического калькулятора.
-
найдем при помощи статистического калькулятора.
Df = 112-1=111- степени свободы; P=1- =1-
=1-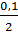 =0,95-
доверительная вероятность, а=0,1 -коэффициент надежности. Подсчитаем в
статистическом калькуляторе. (Рисунок 7).
=0,95-
доверительная вероятность, а=0,1 -коэффициент надежности. Подсчитаем в
статистическом калькуляторе. (Рисунок 7).
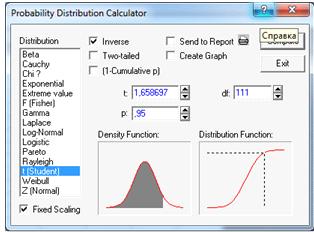
Рисунок 7.
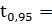 1,65-квантиль
распределения Стьюдента.
1,65-квантиль
распределения Стьюдента.
Подставим все полученные значения в формулу и
получим:
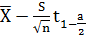 (N-1)
(N-1)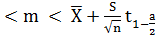 (N-1);
(N-1);
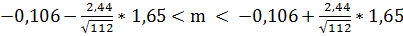 или -0,366 < m
< 0,184.
или -0,366 < m
< 0,184.
Вывод: Доверительный интервал (-0,366; 0,184)
покроет математическое ожидание выборки с доверительной вероятностью а=0,9.
Пример 2. Пусть количественный признак X
генеральной совокупности распределен нормально, причем среднее квадратическое
отклонение неизвестно. Требуется оценить математическое ожидание при помощи
доверительного интервала. Объём выборки n равен 102, среднее значение
(mean) 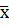 =
-0,04; среднеквадратичное отклонение (St. Dev.) = 2,17.
=
-0,04; среднеквадратичное отклонение (St. Dev.) = 2,17.
Задача: Найти доверительный интервал, который
покроет математическое ожидание с доверительной вероятностью а=0,95.
Решение: Для нахождения доверительного интервала
мы воспользуемся распределением Стьюдента и формулой:
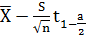 (n-1)
(n-1)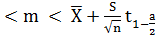 (n-1),
(n-1),
где 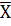 -среднее
выборочное значение; S-среднеквадратичное отклонение; a- коэффициент надежности
(а=1-0,9=0,1),
-среднее
выборочное значение; S-среднеквадратичное отклонение; a- коэффициент надежности
(а=1-0,9=0,1), 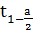 (n-1)
(n-1)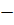 квантиль
распределения Стьюдента с n-1 - степенями свободы.
квантиль
распределения Стьюдента с n-1 - степенями свободы.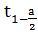 (n-1)
(n-1) -
найдем при помощи распределения Стьюдента.= 102-1=101-степени свободы, P=1-
-
найдем при помощи распределения Стьюдента.= 102-1=101-степени свободы, P=1-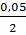 =0,975-доверительная
вероятность, а=0,05-коэффициент надежности. Подсчитаем в статистическом
калькуляторе (Рисунок 8).
=0,975-доверительная
вероятность, а=0,05-коэффициент надежности. Подсчитаем в статистическом
калькуляторе (Рисунок 8).
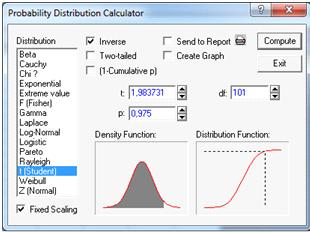
Рисунок 8.
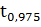 =1,99-квантиль
распределения Стьюдента.
=1,99-квантиль
распределения Стьюдента.
Подставим все полученные значения в формулу и
получим:
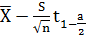 (n-1)
(n-1)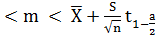 (n-1);
(n-1);
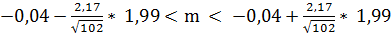 или -0,47 < m
< 0,04.
или -0,47 < m
< 0,04.
Таким образом, можно сделать вывод о том, что
доверительный интервал
(-0,47; 0,04) покроет математическое ожидание
выборки с доверительной вероятностью а=0,95.
4. Проверка статистической гипотезы
Статистическая гипотеза - это любое
предположение о виде неизвестного закона распределения или о параметрах
известных распределений.
Проверить статистическую гипотезу - значит
проверить, согласуются ли выборочные данные с выдвинутой гипотезой.
Для проверки гипотезы, нужно подсчитать
статистический критерий (случайнаую величину, которая используется с целью
проверки нулевой гипотезы), который обозначается буквой  и
посмотреть попадает ли он в область допустимых значений, т.е. область множества
возможных значений статистического критерия, в которой гипотеза принимается.
и
посмотреть попадает ли он в область допустимых значений, т.е. область множества
возможных значений статистического критерия, в которой гипотеза принимается.
Критические точки [квантили] - это точки,
которые разграничивают критическую область и область принятия гипотезы.
Уровень значимости - это вероятность совершить
ошибку.
.1 Проверка гипотезы о равенстве средних
значений
). Дано: Пусть 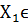 N
(12; 3),
N
(12; 3), 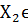 N
(12; 3) и дисперсии
N
(12; 3) и дисперсии 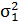 и
и 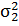 известны.
известны.
Имеются выборки x=(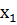
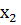 …
…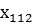 )
и y= (
)
и y= (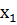
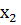 …
…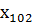 )из
генеральных совокупностей
)из
генеральных совокупностей 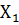 и
и 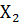 .
.
Сгенерируем выборки X и Y, состоящие из 112 и из
102 случайных величин. Найдем среднее значение выборки X 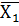 =
=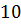 и среднее значение выборки Y
и среднее значение выборки Y 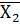 =
=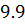 .
.
Задача: Проверить гипотезу о том, что
действительно ли средние распределение двух выборок равны, т.е. равны ли
математические ожидания двух выборок.
Если гипотеза 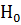 выполняется,
то статистика
выполняется,
то статистика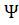 =
=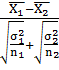 будет иметь стандартное нормальное распределение N (1;0) и доверительную
вероятность, близкую к 1. Гипотеза
будет иметь стандартное нормальное распределение N (1;0) и доверительную
вероятность, близкую к 1. Гипотеза 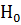 применяется,
если
применяется,
если 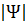 <
<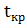 ,
т.е. если значение статистики окажется меньше значения критической точки
[квантиля].
,
т.е. если значение статистики окажется меньше значения критической точки
[квантиля].
Проверим гипотезу: Подставим все известные
значения в формулу и подсчитаем статистику.
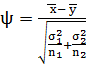 =
=  =
=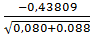 =
=
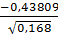 =
=
=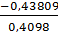 = -1.069.
= -1.069.
Критическую точку 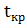 найдем
при помощи нормального распределения N (0;1) при доверительной вероятности P=1-
найдем
при помощи нормального распределения N (0;1) при доверительной вероятности P=1-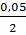 =0,975,где
0,05 -уровень значимости. Подсчитаем при помощи статистического калькулятора.
(Рисунок 9).
=0,975,где
0,05 -уровень значимости. Подсчитаем при помощи статистического калькулятора.
(Рисунок 9).
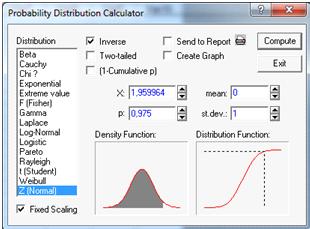
Рисунок 9.
Критическая точка равна 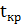 =1,96.
=1,96.
Проведя расчёты, мы видим, что 1.812 <1,96, ⃒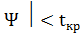 - значение случайной величины меньше значения критической точки.
- значение случайной величины меньше значения критической точки.
Вывод: Так как значение статистики  получилось
меньше значения критической точки
получилось
меньше значения критической точки 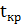 ,
то у нас есть все основания полагать, что выдвинутая нами гипотеза окажется
верной.
,
то у нас есть все основания полагать, что выдвинутая нами гипотеза окажется
верной.
2). Дисперсии 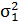 и
и
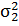 неизвестны,
но равны.
неизвестны,
но равны.
Задача: Проверить гипотезу о равенстве дисперсии
у выборок.
Решение: Выдвинем гипотезу 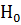 :
:
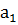 =
=
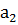 ,
, ,
при этом
,
при этом 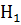 :
:
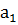 ≠
≠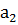 ,
где
,
где 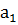 -математическое
ожидание выборки X,
-математическое
ожидание выборки X, 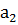 -математическое
ожидание выборки Y.
-математическое
ожидание выборки Y.
Доказано, что в случае справедливости гипотезы,
о том что математические ожидания двух выборок будут равны, статистика -
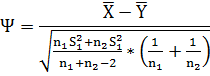
Будет иметь распределение Стьюдента с k=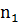 +
+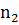 -2
степенями свободы,
-2
степенями свободы,
где 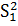 и
и
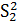 выборочные
дисперсии,
выборочные
дисперсии,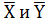 - средние значения
выборок.
- средние значения
выборок.
В этом случае гипотеза применяется , если 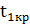 <
<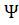 <
<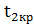 ,
т.е. если статистика окажется в области допустимых значений, находящимся между
критическими точками.
,
т.е. если статистика окажется в области допустимых значений, находящимся между
критическими точками.
Проверим гипотезу: найдем выборочные дисперсии
для выборок - 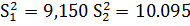
Подставим в формулу все известные значения и
вычислим статистику
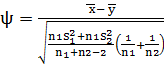 =
=  =
=
=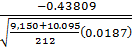 =
= 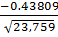 =
=
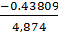 =-0.0140
=-0.0140
При помощи распределения Стьюдента с k=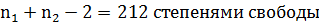 по заданной доверительной вероятности P=0,95 найдем критические точки,
воспользовавшись статистическим калькулятором.
по заданной доверительной вероятности P=0,95 найдем критические точки,
воспользовавшись статистическим калькулятором.
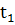 =1-
=1-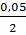 =0,975-квантиль
распределения Стьюдента, где 0,05 - уровень надежности. df=112+102 -2 =212
-степени свободы. (Рисунок10).
=0,975-квантиль
распределения Стьюдента, где 0,05 - уровень надежности. df=112+102 -2 =212
-степени свободы. (Рисунок10).
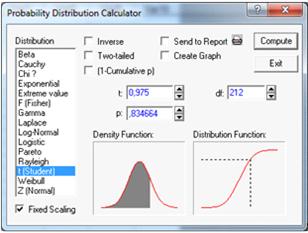
Рисунок 10.
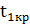 - правая
критическая точка равна 0,83.
- правая
критическая точка равна 0,83.
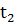 =
=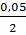 =0,025-квантиль
распределения Стьюдента. df=212-степени свободы (см. Рисунок 11).
=0,025-квантиль
распределения Стьюдента. df=212-степени свободы (см. Рисунок 11).
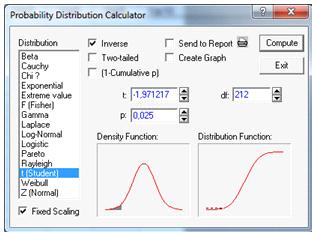
Рисунок 11.
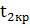 - левая критическая
точка равна -1,97.
- левая критическая
точка равна -1,97.
Случайная величина  (статистика)
попадает в область допустимых значений, т.е. в промежуток между критическими
точками
(статистика)
попадает в область допустимых значений, т.е. в промежуток между критическими
точками 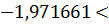 0,0140
<0,834643.
0,0140
<0,834643.
Вывод: так как случайная величина попадает в
область допустимых значений, то у нас есть все основания принять выдвинутую
нами гипотезу.
4.2 Проверка гипотезы о равенстве дисперсий
Гипотезы о дисперсиях возникают довольно часто,
поскольку дисперсия характеризует такие важные показатели, как точность
приборов, технологических процессов, риск, связанный с отклонением доходности
от заданного уровня, и т.д.
Дано: пусть имеются две выборки x=(
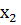 …
…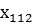 )
и y= (
)
и y= (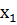
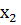 …
…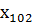 )
из генеральных совокупностей
)
из генеральных совокупностей 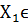 N (12; 3) и
N (12; 3) и 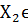 N
(12; 3).
N
(12; 3).
Сгенерируем выборку Х, состоящую из 112
случайных величин и найдем среднее выборочной квадратичное отклонение  .
.
Сгенерируем выборку Y, состоящую из 102
случайных величин и найдем среднее выборочное квадратичное отклонение 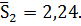
Задача: Проверить гипотезу о равенстве дисперсия
у выборок.
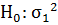 =
= 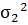 против
альтернативной -
против
альтернативной -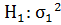 ≠
≠ 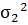 .
.
Решение: для проверки гипотезы о равенстве
дисперсий у выборок, используют статистический критерий -
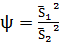 ;
;
которая имеет распределение Фишера со степенями
свободы (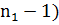 и (
и (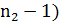 .
.
Подставим в формулу все известные значения и
подсчитаем
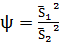 =
=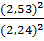 =
=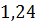 .
.
Для проверки гипотезы , нужно найти критические
точки (U и V).
Гипотезы применяется при условии U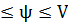 ,
т.е. если статистика попадёт в область допустимых значений.
,
т.е. если статистика попадёт в область допустимых значений.
Критические точки [квантили] найдем при помощи
распределения Фишера со степенями свободы 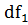 =112-1=111,
=112-1=111,
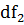 =102-1=101
и доверительной вероятностью P=0,95.
=102-1=101
и доверительной вероятностью P=0,95.
Подсчитаем с помощью статистического
калькулятора.
Для нахождения правой критической точки V,
вероятность P=1-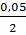 =0,975-квантиль
распределения Фишера.
=0,975-квантиль
распределения Фишера.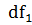 =112-1=111,
=112-1=111, 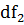 =102-1=101
(см. Рисунок.12).
=102-1=101
(см. Рисунок.12).
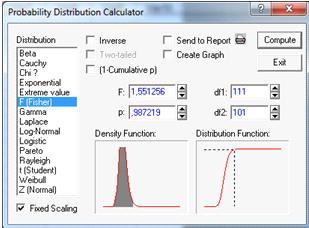
Рисунок 12.
Критическая точка V=1,4.
Для нахождения левой критической точки U. P=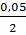 =0,25-квантиль
распределения Фишера,
=0,25-квантиль
распределения Фишера, 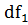 =112-1=111,
=112-1=111, 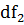 =102-1=101.
(см. Рисунок 13).
=102-1=101.
(см. Рисунок 13).
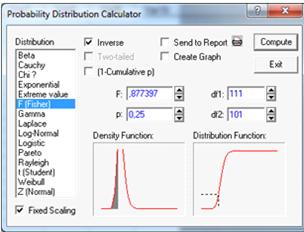
Критическая точка U=0,87.
Статистический критерий, статистика 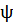 -
попадает в область допустимых значений, то есть в отрезок, находящийся между
критическими точками условии U
-
попадает в область допустимых значений, то есть в отрезок, находящийся между
критическими точками условии U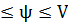 ; 0,87
; 0,87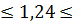 1,4.
1,4.
Вывод: Так как статистика 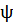 попадает
в область допустимых значений, то у нас есть все основания принять выдвинутую
нами гипотезу.
попадает
в область допустимых значений, то у нас есть все основания принять выдвинутую
нами гипотезу.
4.3 Гипотеза о численной величине среднего
значения
Дано: случайная величина 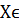 N
(12; 3) и n-выборка её значений x=(
N
(12; 3) и n-выборка её значений x=(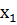
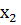 …
…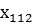 ).
).
Сгенерируем выборку состоящую из 112 случайных
величин и найдем значения, которые понадобятся для дальнейших вычислений 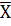 =18,05
-среднее выборочное значение,
=18,05
-среднее выборочное значение, 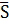 =2,6 - средне
квадратичное отклонение.
=2,6 - средне
квадратичное отклонение.
Задача: Рассмотреть гипотезу о численной
величине среднего значения.
. Дисперсия известна 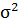
Решение: Выдвинем гипотезу 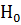 :
: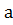 =
=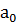 ,
где a=среднему значению построенной нами выборки 17,7, и её альтернативу
,
где a=среднему значению построенной нами выборки 17,7, и её альтернативу 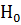 :
: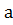 ≠
≠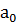 .
Проверим гипотезу
.
Проверим гипотезу 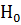 на доверительном
уровне
на доверительном
уровне 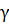 =0,05.
=0,05.
Статистический критерий (статистика) -
Ψ=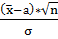 будет иметь стандартное нормальное распределение, если
будет иметь стандартное нормальное распределение, если 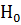 верна
(т.е.
верна
(т.е. 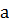 =
=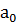 ).
При заданном уровне доверия
).
При заданном уровне доверия 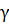 =0,05.
=0,05.
Гипотеза применяется, если |
Ψ |< 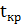 . Тогда
критическими значениями будут
. Тогда
критическими значениями будут 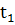 =-
=-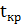 ,
,
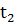 =
=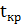 .
.
Подсчитаем статистику, Ψ=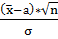 =
=
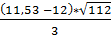 =-1,65.
=-1,65.
Найдем критическую точку 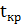 с
помощью нормального распределения где P=1-
с
помощью нормального распределения где P=1- 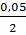 =0,975-квантиль
нормального распределения в статистическом калькуляторе (см. Рисунок 14).
=0,975-квантиль
нормального распределения в статистическом калькуляторе (см. Рисунок 14).
Рисунок 14.
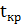 =1,96 - критическая
точка.
=1,96 - критическая
точка.
Видно, что | Ψ |< 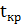 ,
-1,65<1,96 - статистика меньше критической точки.
,
-1,65<1,96 - статистика меньше критической точки.
Вывод: так как критическая точка оказалась
меньше , чем статистика Ψ, то у нас
есть все основания принять выдвинутую нами гипотезу.
2) Дисперсия 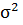 неизвестна.
неизвестна.
Дано: случайная величина 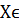 N
(12; x) и n-выборка её значений
N
(12; x) и n-выборка её значений
x=(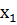
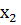 …
…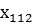 ).
).
Решение: Выдвинем гипотезу 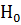 :
: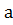 =
=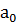 ,
где a=среднему значению построенной нами выборки 17,7, и её альтернативу
,
где a=среднему значению построенной нами выборки 17,7, и её альтернативу 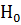 :
: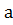 ≠
≠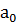 .
Проверим гипотезу
.
Проверим гипотезу 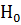 на доверительном
уровне
на доверительном
уровне 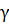 =0,05.
=0,05.
В этом случае в качестве статистики берут - Ψ=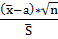 ,
,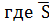 - средне
квадратичное отклонение. Установлено, что статистика
Ψ
будет иметь распределение Стьюдента с n-1 степенями свободы. Для заданного
уровня доверия
- средне
квадратичное отклонение. Установлено, что статистика
Ψ
будет иметь распределение Стьюдента с n-1 степенями свободы. Для заданного
уровня доверия 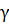 =0,05, гипотеза
=0,05, гипотеза 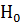 принимается,
если |Ψ|<
принимается,
если |Ψ|<
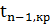 .
.
Подсчитаем статистику Ψ=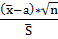 =
=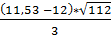 =0,2
и критические точки с помощью распределение Стьюдента с n-1 степенями
свободы.=1-
=0,2
и критические точки с помощью распределение Стьюдента с n-1 степенями
свободы.=1-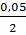 =0,975-квантиль
распределения Стьюдента, df=112-1=111-степени свободы в статистическом
калькуляторе (см. Рисунке 15).
=0,975-квантиль
распределения Стьюдента, df=112-1=111-степени свободы в статистическом
калькуляторе (см. Рисунке 15).
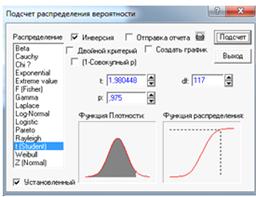
Рисунок 15.
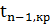 =1,98 - критическая
точка.
=1,98 - критическая
точка.
Видно, что |Ψ|<
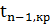 ,
0,2<1,98 - статистика меньше, чем критическая точка.
,
0,2<1,98 - статистика меньше, чем критическая точка.
Вывод: так как оказалось, что статистический
критерий меньше критической точки, то у нас есть все основания для того чтобы
принять выдвинутую нами гипотезу.
.4 Гипотеза о численном значении дисперсии
Дано: случайная величина 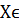 N
(12; 3) и n-выборка её значений
N
(12; 3) и n-выборка её значений
x=(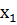
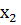 …
…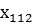 ).
).
Сгенерируем выборку и найдем значения, которые
понадобятся для дальнейших вычислений среднее выборочное значение 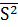 =
=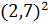 =7,29
и дисперсия
=7,29
и дисперсия 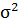 =
=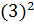 =9
=9
Задача: Проверить гипотезу о численном значении
дисперсии.
Решение: Выдвинем гипотезу 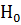 :
: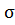 =
=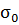 ,
где
,
где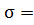 построенной нами выборки 9 и её альтернативу
построенной нами выборки 9 и её альтернативу 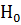 :
: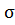 ≠
≠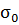 .
Проверим гипотезу
.
Проверим гипотезу 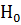 на доверительном
уровне
на доверительном
уровне 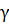 =0,05.
=0,05.
В качестве статистики выбираем величину равную -
Ψ=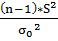 ,
,
Где 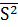 -
выборочное среднее значение выборки,
-
выборочное среднее значение выборки, 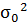 -дисперсия
выборки.
-дисперсия
выборки.
Подставим все известные значения в формулу и
подсчитаем
Ψ=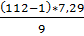 =89,91
=89,91
Статистический критерий будет иметь хи-квадрат
распределение с n-1 степенями свободы. Для заданного уровня значимости а=0,95
найдем критические точки U и V.
Гипотезу принимаем при условии, если 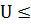 Ψ
Ψ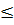 V.
V.
Найдем критические точки с помощью распределения
хи-квадрат распределение с 111 степенями свободы в статистическом калькуляторе.
При квантиле t=1-0,025=0,975 и степенью свободы
df=111 (см. рисунок 16).
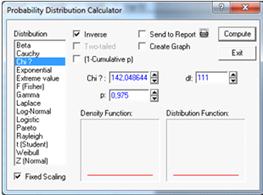
Рисунок 16.
Правая критическая точка V=142,048.
При квантиле t=0,025 и степенью свободы df=111
(см. Рисунок 17).
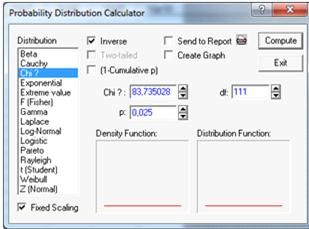
Рисунок 17.
Левая критическая точка U=83,73
Видно, что статистический критерий Ψ,
попал
в отрезок , находящийся между критический точками U и V,т.е. в область
допустимых значений. 83,73<89,91<142,048.
Вывод: Так как значение статистического критерия
Ψ
лежит в области допустимых значений, то у нас есть все основания, для того
чтобы принять выдвинутую нами гипотезу.
.5 Проверка гипотезы о виде закона распределения
Законом распределения случайной величины
называется всякое соотношение, устанавливающее связь между возможными
значениями случайной величины и соответствующими им вероятностями.
Дано: случайная величина 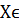 N
(12; 3) и n-выборка её значений
N
(12; 3) и n-выборка её значений
x=(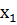
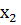 …
…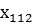 ).
).
Задача: Проверить гипотезу о том, что закон
распределения случайной величины нормальный.
Гипотеза применяется, если значения 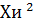 попадёт
в область допустимых значений, т.е. окажется в промежутке между критическими
точками V<
попадёт
в область допустимых значений, т.е. окажется в промежутке между критическими
точками V<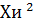 <U.
<U.
Решение: Сгенерируем выборку, состоящую из 112
случайных величин и найдем минимальное и максимально значение ряда: 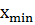 =5,188
и
=5,188
и 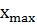 =20,77.
=20,77.
Использую выборку, построим гистограмму
распределения (см. Рисунок 18).
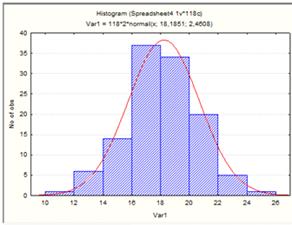
Рисунок 18.
На рисунке видно, что математическое ожидание
выборки а=18,1, среднее квадратическое отклонение S=2,4.
Далее, нужно по гистограмме, нужно подсчитать
сколько элементов выборки попало в каждый интервал.
В интервал от 10 до 12: 1 элемент, от 12 до 14:
6 элементов, от 14 до 16: 14 элементов, от 16 до 18: 37 эл, от 18 до 20: 34 эл,
от 20 до 22: 20 эл, от 22 до 24: 5 эл, от 24 до 26: 1 эл.
С помощью нормального распределения N(12; 3)
найдем вероятности попадания, элементов выборки во все интервалы,
воспользовавшись вероятностным калькулятором.
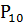 =0,004-
вероятность, попадания элементов выборки левее интервала 10 (см. Рисунок 19).
=0,004-
вероятность, попадания элементов выборки левее интервала 10 (см. Рисунок 19).
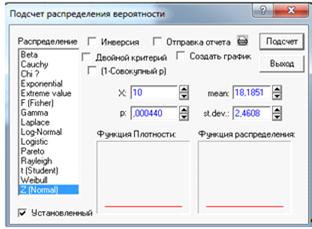
Рисунок 19.
Подсчитаем так для всех интервалов:
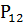 =0,005978;
=0,005978;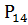 =0,044499;
=0,044499;
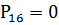 ,187280;
,187280;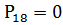 ,470020;
,470020;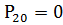 ,769598;
,769598;
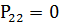 ,939461;
,939461;
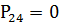 ,990936.
,990936.
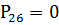 ,999253.
,999253.
Далее найдем 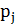 -
вероятность попадания элементом в каждую выборку.
-
вероятность попадания элементом в каждую выборку.
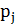 =
=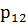 -
-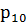 ;
;
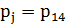 -
-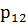 и так далее для каждой выборки.
и так далее для каждой выборки.
Таблица 3
|
j
|
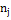 частота частота
|
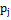
|
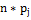
|
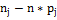
|
|
1
|
1
|
0,0197
|
2,3
|
-1,9
|
|
2
|
6
|
0,038521
|
4,5
|
1,5
|
|
3
|
14
|
0,144781
|
17
|
-3
|
|
4
|
37
|
0,28274
|
33,3
|
11,04
|
|
5
|
34
|
0,299578
|
35,3
|
-1,3
|
|
6
|
20
|
0,169863
|
20,04
|
-0,04
|
|
7
|
5
|
0,051475
|
6,07
|
1,07
|
|
8
|
1
|
0,008317
|
0,98
|
0,08
|
В таблице: 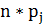 -
количество элементов, попадающих в каждый интервал.
-
количество элементов, попадающих в каждый интервал.
Для того чтобы найти значение 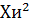 ,
необходимо использовать формулу:
,
необходимо использовать формулу:
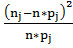
и подсчитать для каждого интервала, а потом все
полученные значения сложить.
Подсчитаем и получим значение 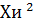 =
5,9167.
=
5,9167.
Для того чтобы проверить гипотезу найдем
критические точки (квантили) с помощью 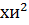 распределения
в статистическом калькуляторе.
распределения
в статистическом калькуляторе.
Степени свободы df=n-3, где n- количество
столбцов в гистограмме распределения, df=12-3=9. Доверительная вероятность
близка к еденице P=0,975.
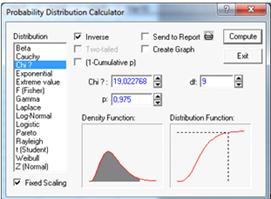
Рисунок 20.
Правая критическая точка U=19
Таким же способом найдем вторую левую
критическую точку. (см. Рисунок 21).
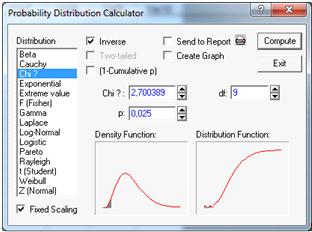
Рисунок 21
Левая критическая точка V=2,7.
Мы видим, что значение 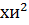 =5,9167
находится в области допустимых значений, т.е. между значениями U и V,
2,7<5,9167<19.
=5,9167
находится в области допустимых значений, т.е. между значениями U и V,
2,7<5,9167<19.
Вывод: у нас имеются все основания принять
выдвинутую нами гипотезу.