|
№ интервала
|
ai
|
bi
|
Частота ni
|
|
1
|
17
|
24
|
18
|
|
2
|
24
|
31
|
21
|
|
3
|
31
|
38
|
20
|
|
4
|
38
|
45
|
11
|
|
5
|
45
|
15
|
|
6
|
52
|
59
|
8
|
|
7
|
59
|
66
|
6
|
|
|
Еще
|
1
|
Построенный вариационный ряд показывает, что возраст работников одного
предприятия по состоянию на 1 января текущего года от 24 до 66 лет.
Построить для полученного вариационного ряда гистограмму и
эмпирическую функцию распределения:
Установим в диалоговом окне программы Гистограмма дополнительно флажки
"Интегральный процент" для построения эмпирической функции
распределения и "Вывод графика" для построения гистограммы частот.
Получим:
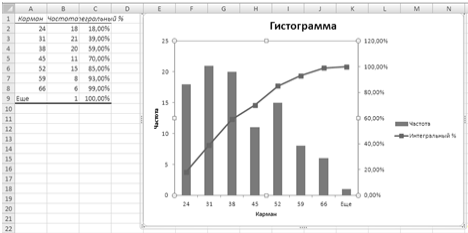
Гистограмма частот наглядно отражает особенности интервального
вариационного ряда, в частности позволяет предположить, что величина Х
(возраст сотрудников) распределена по нормальному закону.
Эмпирическая функция распределения (интегральный процент) показывает,
какова доля сотрудников, возраст которых оказался меньше указанной величины
("карман"). Так, например, возраст 30% сотрудников менее 60 лет;
возраст 85% сотрудников - менее 24 лет.
Определить выборочные оценки числовых характеристик случайной
величины: выборочную среднюю, медиану, моду, дисперсию, выборочное среднее
квадратическое отклонение, коэффициент вариации, коэффициент асимметрии и
коэффициент эксцесса.
Для определения числовых характеристик случайной величины Х
воспользуемся сервисом Данные / Анализ данных / Описательная статистика
(использование программы требует размещения исходных данных в одном столбце).
Для получения результатов следует установить флажок "Итоговая
статистика".
В результате получим:
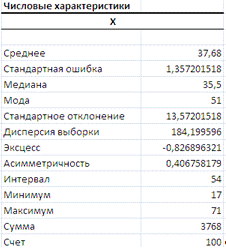
Коэффициент вариации определим по формуле 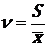 = 0,36. Средние величины (среднее,
медиана, мода) характеризуют значение признака, вокруг которого концентрируются
наблюдения - центральную тенденцию распределения:
= 0,36. Средние величины (среднее,
медиана, мода) характеризуют значение признака, вокруг которого концентрируются
наблюдения - центральную тенденцию распределения:
- Средний возраст работников по организации составил 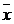 = 37,68 лет.;
= 37,68 лет.;
- медиана, равная 35,5 лет показывает возраст сотрудников:
возраст 50% сотрудников не больше, чем 35,5 лет, а для 50% - не меньше, чем
35,5 лет;
- мода равна 51
Наиболее важными показателями вариации (рассеяния) наблюдений вокруг
средней величины являются дисперсия выборки S2 = 184,1996; выборочное среднее квадратическое
(стандартное) отклонение S
= 13,5; коэффициент вариации n = 3,6%. Невысокая величина коэффициента вариации 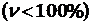 свидетельствует об однородности
значений признака Х (возраст сотрудников).
свидетельствует об однородности
значений признака Х (возраст сотрудников).
Коэффициент асимметрии составил 0,4. с
Коэффициент эксцесса равен -0,8. Близкое к нулю значение говорит о том,
что рассматриваемое распределение по крутости приближается к нормальной кривой.
Оценить точность выборки.
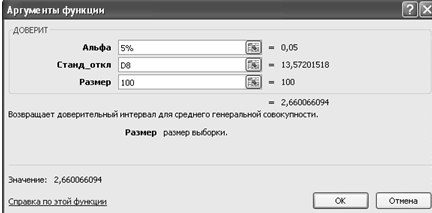
Примем уровень значимости 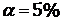 . С помощью функции ДОВЕРИТ определим ошибку выборки - размах
доверительного интервала для математического ожидания генеральной совокупности:
e = 2,6.
. С помощью функции ДОВЕРИТ определим ошибку выборки - размах
доверительного интервала для математического ожидания генеральной совокупности:
e = 2,6.
Нижняя и верхняя границы доверительного интервала для математического
ожидания генеральной совокупности равны соответственно 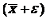 =37,68-2,6=35,01 и
=37,68-2,6=35,01 и 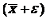 =37,68+2,6=40,34. Таким образом, с
надежностью 7,06% средний возраст сотрудников по организации заключен в
границах от 35,01 до 40,34 лет.
=37,68+2,6=40,34. Таким образом, с
надежностью 7,06% средний возраст сотрудников по организации заключен в
границах от 35,01 до 40,34 лет.
Для оценки точности выборки рассчитаем относительную ошибку 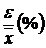 = 2,6/37,68=7,06% и сделаем вывод в
соответствии со схемой:
= 2,6/37,68=7,06% и сделаем вывод в
соответствии со схемой:
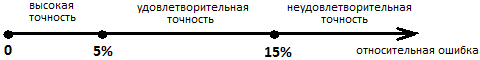
На уровне значимости 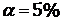 точность выборки следует признать удовлетворительной.
точность выборки следует признать удовлетворительной.
Провести выравнивание статистического ряда с помощью
нормального закона распределения, в качестве параметров использовать выборочные
оценки математического ожидания и среднего квадратического отклонения. Показать
на одной диаграмме гистограмму эмпирических частот и теоретическую нормальную
кривую.
Для проведения вычислений подготовим таблицу. Занесем в нее границы ai и bi интервалов группировки, середины xi этих интервалов, соответствующие
частоты ni.
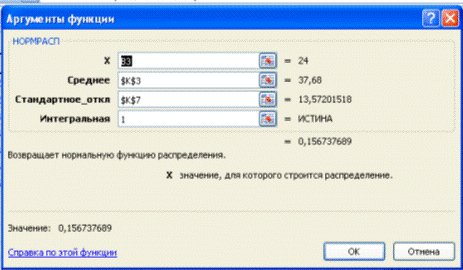
Построим интегральную функцию нормального распределения с параметрами 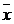 и
и 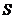 . Используем функцию НОРМРАСП; для
каждого интервала в качестве значения, для которого строится распределение,
укажем верхнюю границу bi.
Для последнего интервала занесем в таблицу значение
. Используем функцию НОРМРАСП; для
каждого интервала в качестве значения, для которого строится распределение,
укажем верхнюю границу bi.
Для последнего интервала занесем в таблицу значение 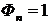 .
.
Определим теоретические вероятности 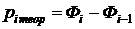 попадания нормально распределенной
величины в i-ый интервал группировки (для первого интервала укажем
попадания нормально распределенной
величины в i-ый интервал группировки (для первого интервала укажем 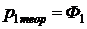 ).
).
Рассчитаем теоретические частоты 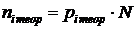 , соответствующие интервалам
группировки. Проверим выполнение условия
, соответствующие интервалам
группировки. Проверим выполнение условия  .
.
|
ai
|
bi
|
xi
|
ni
|
функция норм. распр. Ф(х)
|
pi теор
|
ni теор
|
|
17
|
24
|
20,5
|
18
|
0,156737689
|
0,156737689
|
15,67376891
|
|
24
|
31
|
27,5
|
21
|
0,311292781
|
0,154555092
|
15,45550918
|
|
31
|
38
|
34,5
|
20
|
0,509405361
|
0,19811258
|
|
38
|
45
|
41,5
|
11
|
0,705175626
|
0,195770265
|
19,57702645
|
|
45
|
52
|
48,5
|
15
|
0,854313014
|
0,149137388
|
14,91373883
|
|
52
|
59
|
55,5
|
8
|
0,941894676
|
0,087581662
|
8,7581662
|
|
59
|
66
|
62,5
|
7
|
1
|
0,058105324
|
5,810532414
|
|
|
|
100
|
|
|
100
|
Покажем на одной диаграмме гистограмму частот и нормальную кривую:
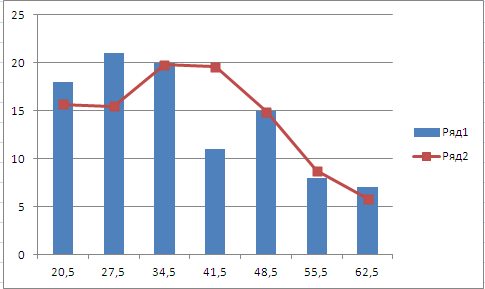
Диаграмма показывает соответствие гистограммы частот и нормальной кривой
с параметрами 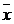 и
и 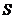 .
.
Проверить согласованность теоретического и статистического
распределений, используя критерий 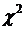 Пирсона.
Пирсона.
Критерий Пирсона основан на сравнении эмпирических и теоретических
частот. Для его использования необходимо, чтобы в каждом интервале группировки
было достаточное количество данных. В случае малочисленных эмпирических частот
(niэмп< 5) следует объединить соседние
интервалы, в этом случае и соответствующие им теоретические частоты также
складываются. При этом необходимо следить за правильностью расчета значений
функции нормального распределения, теоретических частот и выполнением условия  . Объединим первый и второй
интервалы, частота для объединенного интервала будет 6+14=20. Объединим восьмой
и девятый интервалы, частота для объединенного последнего интервала 2+2=4.
Общее количество интервалов группировки после объединения m=7. Дополним
скорректированную таблицу столбцом "мера расхождения", выполнив расчеты
по формуле Пирсона
. Объединим первый и второй
интервалы, частота для объединенного интервала будет 6+14=20. Объединим восьмой
и девятый интервалы, частота для объединенного последнего интервала 2+2=4.
Общее количество интервалов группировки после объединения m=7. Дополним
скорректированную таблицу столбцом "мера расхождения", выполнив расчеты
по формуле Пирсона 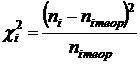 .
.
Таблица
|
ai
|
bi
|
xi
|
ni
|
функция норм. распр. Ф(х)
|
pi теор
|
ni теор
|
хи2 i
|
|
17
|
24
|
20,5
|
18
|
0,156737689
|
0,156737689
|
15,67376891
|
0,345249
|
|
24
|
31
|
27,5
|
21
|
0,311292781
|
0,154555092
|
15,45550918
|
1,989024
|
|
31
|
38
|
34,5
|
20
|
0,509405361
|
0,19811258
|
19,81125802
|
0,001798
|
|
38
|
41,5
|
11
|
0,705175626
|
0,195770265
|
19,57702645
|
3,75774
|
|
45
|
52
|
48,5
|
15
|
0,854313014
|
0,149137388
|
14,91373883
|
0,000499
|
|
52
|
59
|
55,5
|
8
|
0,941894676
|
0,087581662
|
8,7581662
|
0,065632
|
|
59
|
66
|
62,5
|
7
|
1
|
0,058105324
|
5,810532414
|
0,243495
|
|
|
|
|
|
|
|
6,403437
|
|
|
|
100
|
|
|
100
|
|
Фактически наблюдаемое значение статистики Пирсона составляет
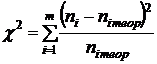 =6,403.
=6,403.
Критическое значение статистики 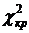 = 9,49 найдено для уровня значимости
5% и числа степеней свободы k=m-3=4 с помощью функции ХИ2ОБР. Сравним фактическое значение статистики
= 9,49 найдено для уровня значимости
5% и числа степеней свободы k=m-3=4 с помощью функции ХИ2ОБР. Сравним фактическое значение статистики 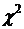 с критической величиной
с критической величиной 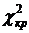 и сделаем вывод в соответствии со
схемой:
и сделаем вывод в соответствии со
схемой:

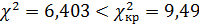 Þ теоретическое и статистическое распределения согласованы, на уровне
значимости
Þ теоретическое и статистическое распределения согласованы, на уровне
значимости 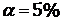 следует принять гипотезу о нормальном законе распределения
случайной величины Х возраста сотрудников.
следует принять гипотезу о нормальном законе распределения
случайной величины Х возраста сотрудников.
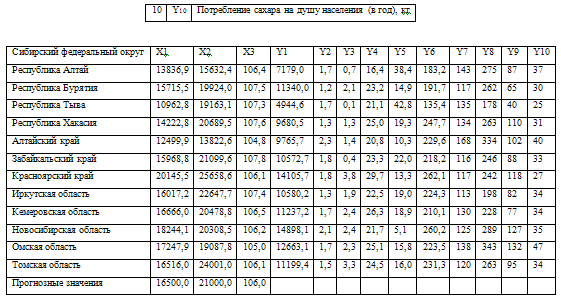
Задача 2.
Статистический анализ связей
Исходными данными для моделирования являются социально-экономические
показатели субъектов Сибирского федерального округа (Приложение 1). Требуется
исследовать зависимость результирующего признака Y, соответствующего
варианту задания, от факторных переменных Х1, Х2 и
Х3:
1. Рассчитать матрицу парных
коэффициентов корреляции; проанализировать тесноту и направление связи
результирующего признака Y
с каждым из факторов Х; оценить статистическую значимость коэффициентов
корреляции r(Y, Xi); выбрать наиболее информативный фактор. вариационный
статистический корреляция регрессия
2. Построить модель парной регрессии с
наиболее информативным фактором; дать экономическую интерпретацию коэффициента
регрессии.
3. Проверить значимость коэффициентов
модели с помощью t-критерия Стьюдента (принять уровень значимости α=0,05).
4. Оценить качество модели с помощью
средней относительной ошибки аппроксимации, коэффициента детерминации и F - критерия Фишера (принять уровень
значимости α=0,05).
5. С доверительной вероятностью γ=80% осуществить прогнозирование
среднего значения показателя Y (прогнозные
значения факторов приведены в Приложении 1). Представить графически фактические
и модельные значения Y,
результаты прогнозирования.
Решение:
Рассчитать матрицу парных коэффициентов корреляции;
проанализировать тесноту и направление связи результирующего признака Y с каждым из факторов Х;
оценить статистическую значимость коэффициентов корреляции r(Y, Xi); выбрать наиболее информативный
фактор.
Используем Excel (Данные /
Анализ данных / КОРРЕЛЯЦИЯ):
Получим матрицу коэффициентов парной корреляции между всеми имеющимися
переменными:
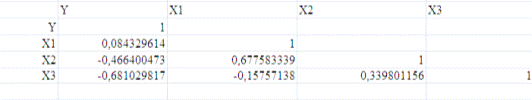
Проанализируем коэффициенты корреляции между результирующим признаком Y и каждым из факторов Xj:
r (Y,X1)= 0,084>0, следовательно, между переменными Y и Х1 наблюдается
прямая корреляционная зависимость: чем выше среднедушевые
денежные доходы (в месяц), тем больше потребление сахара на душу населения (в
год).
r (Y,X2)=-0,466<0, значит, между переменными Y и Х2 наблюдается
обратная корреляционная зависимость: чем среднемесячная
номинальная начисленная заработная плата работников организаций, тем ниже потребление сахара на душу населения (в год).
r (Y,X3)=-0,68<0, значит, между переменными Y и Х3 наблюдается
обратная корреляционная зависимость: чем индекс
потребительских цен (декабрь к декабрю предыдущего года) больше, тем меньше
потребление сахара на душу населения (в год).
Для проверки значимости найденных коэффициентов корреляции используем
критерий Стьюдента.
Для каждого коэффициента корреляции 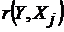 вычислим t-статистику по формуле
вычислим t-статистику по формуле 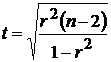 и занесем результаты расчетов в
дополнительный столбец корреляционной таблицы:
и занесем результаты расчетов в
дополнительный столбец корреляционной таблицы:
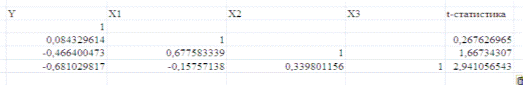
По таблице критических точек распределения Стъюдента при уровне
значимости 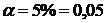 и числе степеней свободы k=n-2=12-2=10, определим критическое значение tкр.=2,23 (функция СТЬЮДРАСПОБР).
и числе степеней свободы k=n-2=12-2=10, определим критическое значение tкр.=2,23 (функция СТЬЮДРАСПОБР).
Сопоставим фактические значения t с критическим tkp, и сделаем выводы в соответствии со
схемой:
t (r(Y,X1))=0,28<tкр.=2,22 , следовательно, коэффициент 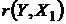 не является значимым.
не является значимым.
t (r(Y,X2))=1,68<tкр.=2,22, следовательно, коэффициент 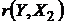 не является значимым.
не является значимым.
t (r(Y,X3))=2,94<tкр.=2,22, следовательно, коэффициент 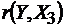 является значимым.
является значимым.
Построить модель парной регрессии с наиболее информативным
фактором; дать экономическую интерпретацию коэффициента регрессии.
Для построения парной линейной модели 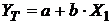 используем программу РЕГРЕССИЯ
(Данные / Анализ данных). В качестве "входного интервала Х"
покажем значения фактора Х1.
используем программу РЕГРЕССИЯ
(Данные / Анализ данных). В качестве "входного интервала Х"
покажем значения фактора Х1.
Результаты вычислений представлены в таблицах:
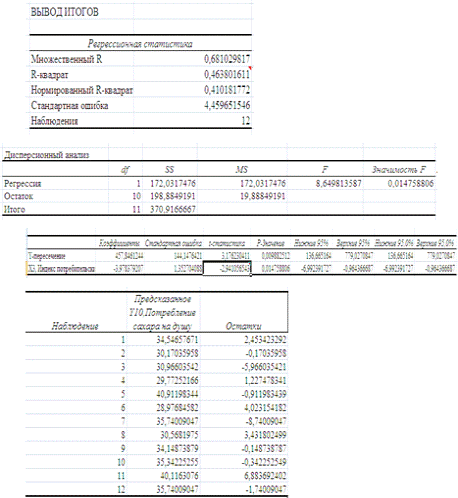
Коэффициенты модели содержатся в третьей таблице итогов РЕГРЕССИИ
(столбец Коэффициенты).
Таким образом, модель парной регрессии построена, ее уравнение имеет вид
Проверить значимость коэффициентов модели с помощью t-критерия
Стьюдента (принять уровень значимости α=0,05).
Значимость коэффициентов модели проверим с помощью t - критерия Стьюдента.
t -
статистики для коэффициентов уравнения регрессии приведены в столбце
"t-статистика" третьей таблицы итогов РЕГРЕССИИ:
- для свободного коэффициента a= 457,85 определена статистика
t(a)= 3,18.
- для коэффициента регрессии b= -3,98 определена статистика
t(b)= -2,94.
Критическое значение tкр=2,23 найдено для уровня значимости a=5% и числа степеней свободы 10 (функция СТЬЮДРАСПОБР).
Схема проверки:
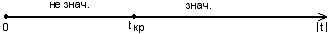
t (a)=3,18>tкр. Þ свободный коэффициент а является значимым.
t(b)=2,94>tкр. Þ коэффициент регрессии b
является значимым.
Выводы о значимости коэффициентов модели сделаны на уровне значимости a=5%. Рассматривая столбец "Р-значение",
отметим, что свободный коэффициент а можно считать значимым на уровне
0,00988; коэффициент регрессии b - на уровне 0,015.
Оценить качество модели с помощью средней относительной
ошибки аппроксимации, коэффициента детерминации и F - критерия Фишера (принять уровень
значимости α=0,05).
Для вычисления средней относительной ошибки аппроксимации
рассмотрим остатки модели 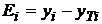 , содержащиеся в столбце Остатки итогов программы
РЕГРЕССИЯ (таблица "Вывод остатка"). Дополним таблицу столбцом
относительных погрешностей, которые вычислим по формуле
, содержащиеся в столбце Остатки итогов программы
РЕГРЕССИЯ (таблица "Вывод остатка"). Дополним таблицу столбцом
относительных погрешностей, которые вычислим по формуле 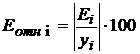 с помощью функции ABS.
с помощью функции ABS.
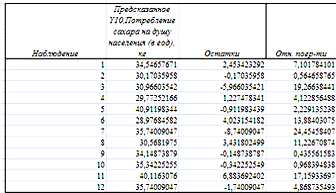
По столбцу относительных погрешностей найдем среднее значение Eотн=8,86
(функция СРЗНАЧ).
Оценим точность построенной модели в соответствии со схемой:
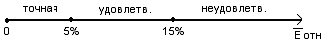
Eотн=8,86 - модель имеет удовлетворительную точность.
Коэффициент детерминации R-квадрат определен программой РЕГРЕССИЯ
(таблица "Регрессионная статистика") и составляет R2=0,463. Таким образом, вариация (изменение)
потребления сахара Y
на 46,3% объясняется по уравнению модели вариацией индекса потребительских цен.
Проверим значимость полученного уравнения с помощью F - критерия Фишера.
F - статистика определена программой РЕГРЕССИЯ (таблица "Дисперсионный
анализ") и составляет F =
8,65.
Критическое значение Fкр= 4,964
найдено для уровня значимости a=5% и чисел степеней свободы k1=1, k2=10 (функция FРАСПОБР).
Схема проверки:
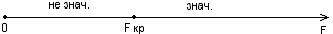
Сравнение показывает: F =
8,65 > Fкр = 4,964; следовательно, уравнение
модели является значимым, его использование целесообразно, зависимая переменная
Y (потребление сахара) достаточно
хорошо описывается включенной в модель факторной переменной Х1
(индекс потребительских цен).
С доверительной вероятностью γ=80% осуществить прогнозирование
среднего значения показателя Y (прогнозные значения факторов
приведены в Приложении 1). Представить графически фактические и модельные
значения Y,
результаты прогнозирования.
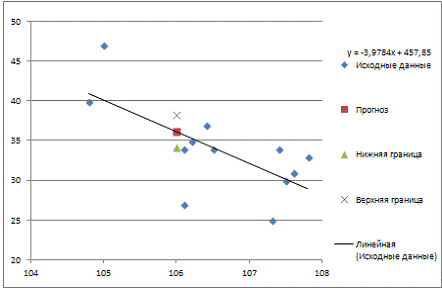
Согласно условию задачи прогнозное значение факторной переменной Х3
составляет 106,0. Рассчитаем по уравнению модели прогнозное значение показателя
Y:
Y = 457,85 - 3,9783 * 106 = 36,15
Таким образом, если индекс потребительских цен составит 106, то
потребление сахара будет около 36,15 кг.
Зададим доверительную вероятность 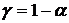 и построим доверительный прогнозный
интервал для среднего значения Y.
и построим доверительный прогнозный
интервал для среднего значения Y.
Для этого нужно рассчитать стандартную ошибку прогнозирования для
среднего значения результирующего признака
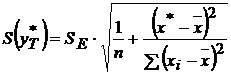 .
.
Предварительно подготовим:
- стандартную ошибку модели SE= 4,46 (таблица "Регрессионная статистика"
итогов РЕГРЕССИИ);
по столбцу исходных данных Х1 найдем среднее значение
равное 106,56 (функция СРЗНАЧ) и определим ∑(xi-x)2= 10,86916667 (функция
КВАДРОТКЛ);
- 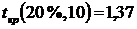 (функция СТЬЮДРАСПОБР).
(функция СТЬЮДРАСПОБР).

Для построения чертежа используем Мастер диаграмм (точечная)
- покажем исходные данные (поле корреляции).
Список использованной литературы
1. Кремер Н.Ш. Теория
вероятностей и математическая статистика: Учебник / Н.Ш. Кремер. - 3-е изд.,
перераб. и доп. - М: ЮНИТИ-ДАНА. - 2012. - 551 с., ЭБС Book.ru
2. Козлов А. Ю.
Статистический анализ данных в MS Excel: Учебное пособие / А.Ю. Козлов, В.С.
Мхитарян, В.Ф. Шишов. - М.: ИНФРА-М, 2012. - 320 с., ЭБС Znanium
3. М.Л. Поддубная. Анализ данных.
Методические указания по решению задач и выполнению контрольной работы (для
студентов, обучающихся по направлению 080500.62 "Бизнес-информатика",
квалификация (степень) бакалавр). - Барнаул: Изд-во АлтГТУ, 2014. - 34 с.