Математический анализ
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФГБОУ ВПО
«Уральский государственный экономический университет»
Центр
дистанционного образования
Контрольная
работа
Математический
анализ
Выполнил:
Власова А.В.
Задание 1. Пределы функции
Вычислить пределы:
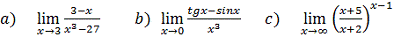
Решение:
a)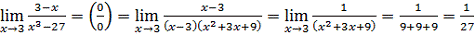 
b)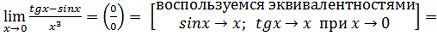 
)
=
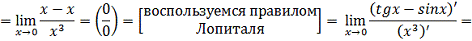
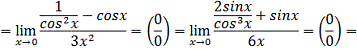
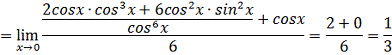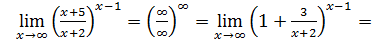
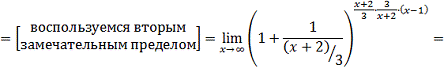
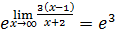
Задание 2. Исследование функции
Используя дифференциальное исчисление, провести
полное исследование функции и построить ее график: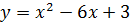 
Решение:
) Область определения функции D(y):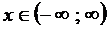 
) Множество значений функции E(y):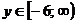 
) Проверим, является ли функция четной или
нечетной: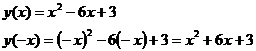 
Так как 
,
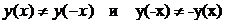то функция не является ни четной ни нечетной.
) Найдем координаты точек пересечения графика
функции с осями координат:
а) с осью ОУ: х=0;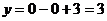 
График
пересекает ось ординат в точке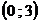 
б) с осью ОХ: у=0;
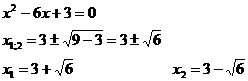
График функции пересекает ось абсцисс в точках: 
5) Найдем промежутки возрастания и убывания
функции, а так же точки экстремума:
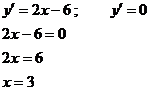
Так как на промежутке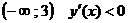
,
то на этом промежутке функция убывает. Так как на промежутке
,
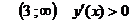то на этом промежутке функция возрастает. Так как при переходе через точку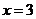 
производная
меняет свой знак с - на + то в этой точке функция имеет минимум: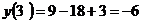 
6)
Найдем промежутки выпуклости и точки перегиба функции: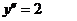 
Так
как 
,
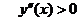на всей области определения, то график функции направлен выпуклостью вниз. Так
как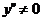 
то
график функции не имеет точек перегиба
) Так как точек разрыва функция не имеет, то она
не имеет вертикальных асимптот. Проверим, имеет ли данная функция наклонные
асимптоты:
б) Наклонные асимптоты вида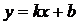 
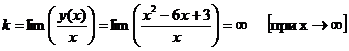следовательно
наклонных асимптот функция не имеет
) Построим график данной функции:
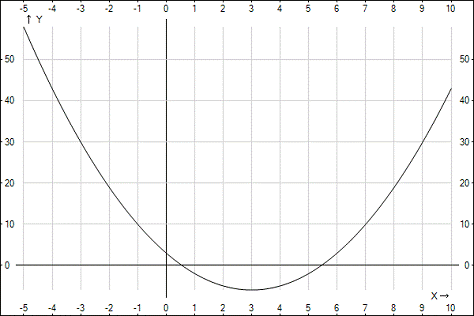
Рисунок 1
Задание 3. Неопределенный интеграл
Вычислить неопределенные интегралы, используя
методы интегрирования:
а) - непосредственное интегрирование;
б) - замены переменной;
в) - интегрирования по частям.
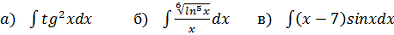
Решение:
а)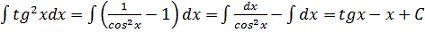 
б)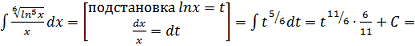 
) 
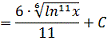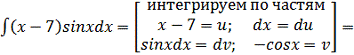
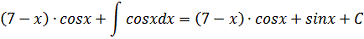
Задание 4. Определенный интеграл
.1 Вычислить определенный интеграл:
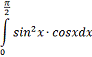
Решение:
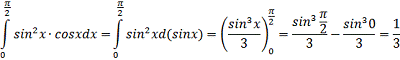
4.2 Вычислить площадь плоской фигуры,
ограниченной заданными кривыми. Сделать чертеж.
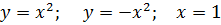
Решение:
Выполним чертеж:
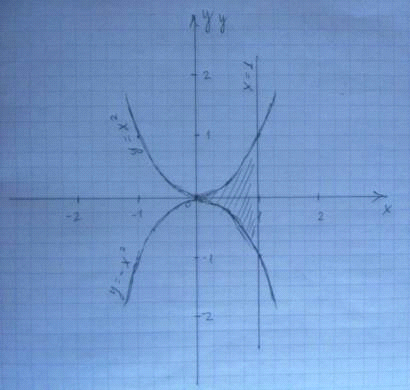
Рисунок 2
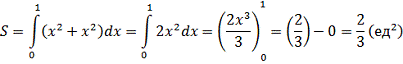
Задание 5. Несобственный интеграл
Вычислить интеграл или установить его
расходимость:
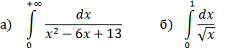
Решение:
а)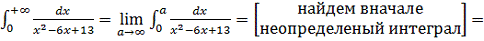 
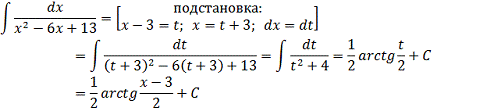
Тогда получаем: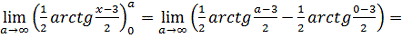 
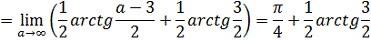
б)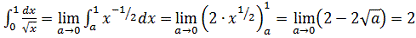 
интеграл функция дифференциальный
уравнение
6.1 Числовые ряды. Исследовать ряд на
сходимость:
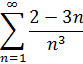
Решение
Воспользуемся интегральным признаком сходимости
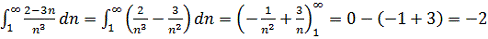
Следовательно, ряд сходится
.2 Степенные ряды. Определить область сходимости
степенного ряда:
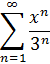
Решение: Воспользуемся
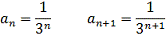
Радиус сходимости ряда равен: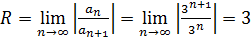 
Область сходимости ряда есть промежуток (-3; 3),
внутри промежутка ряд сходится, проверим сходимость ряда на концах этого
промежутка:
а) при х=3 получаем ряд:
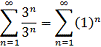
Ряд расходится
б)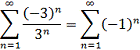 
получили знакопеременный ряд, который не
удовлетворяет признакам сходимости знакопеременного ряда, следовательно он
расходится
Итак, область сходимости (-3; 3)
Задание 7. Функции нескольких переменных
Исследовать функцию двух переменных на
экстремум:
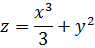
Решение:
Найдем стационарные точки, решив систему: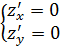 
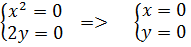Получили одну
стационарную точку М(0; 0), проверим выполняется ли для этой точки достаточное
условие экстремума.
Найдем частные производные второго порядка:
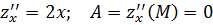
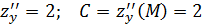
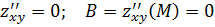
Тогда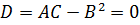 
Вопрос
о наличии экстремума остается открытым. Проведем дополнительные исследования:
а) при х=0, получаем функцию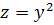 
,
которая в точке у=0 имеет минимум
б) при у=0, получаем функцию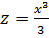 
,
которая в точке x=0 не имеет
экстремума
Следовательно, функция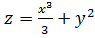 
в
точке М(0; 0) не имеет экстремума
Задание 8. Решение дифференциальных уравнений
.1 Найти общее и частное решения дифференциального
уравнения:
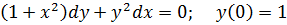
Решение:
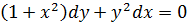
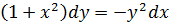
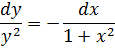
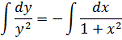
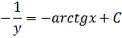
Найдем частное решение, удовлетворяющее
начальным условиям:
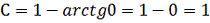
Итак, частное решение имеет вид: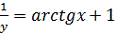 
.2. Найти частное решение дифференциального
уравнения, удовлетворяющее заданным начальным условиям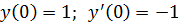 
:
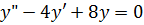
Решение: Найдем корни характеристического уравнения:
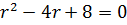
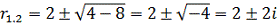
Так как корни характеристического уравнения
мнимые числа, то общее уравнение имеет вид:
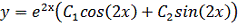
Найдем частное решение удовлетворяющее начальным
условиям, для этого решим систему:
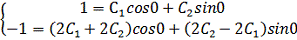
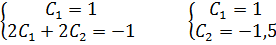
Тогда частное решение имеет вид:
