Вклад Л.Эйлера в совершенствование математического анализа

Вклад Л.Эйлера в совершенствование математического анализа

План

Введение

1 Понятие математического анализа. Исторический очерк

2 Вклад Л.Эйлера в развитие математического анализа

3 Дальнейшее развитие математического анализа

Заключение

Список литературы

Введение

Л. Эйлер - самый продуктивный математик в истории, автор более чем 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближённым вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и др. Многие его работы оказали значительное влияние на развитие науки.

Почти полжизни Эйлер провёл в России, где энергично помогал создавать российскую науку. В 1726 году он был приглашён работать в Санкт-Петербург. В 1731-1741 и начиная с 1766 года был академиком Петербургской Академии Наук (в 1741-1766 годах работал в Берлине, оставаясь почётным членом Петербургской Академии). Хорошо знал русский язык, часть своих сочинений (особенно учебники) публиковал на русском. Первые русские академики по математике (С. К. Котельников), и по астрономии (С. Я. Румовский) были учениками Эйлера. Некоторые из его потомков до сих пор живут в России.

Л.Эйлер внес очень большой вклад в развитие математического анализа.

Цель реферата - изучить историю развития математического анализа в XVIII веке.

1 Понятие математического анализа. Исторический очерк

Математический анализ - совокупность разделов математики <#"457099.files/image001.gif">,

достигающее экстремальных значений в точках перегиба <#"457099.files/image002.gif">. В выражениях это число используется наряду с натуральными числами. Напр., считается допустимым такое выражение для экспоненты

,

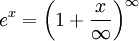в котором лишь поздние авторы видели предельный переход. С аналитическими выражениями производились разнообразные преобразования, позволившие Эйлеру найти представления для элементарных функций в виде рядов, бесконечных произведений и т. д. Эйлер преобразует выражения для счёта так, как это делают в алгебре, не обращая внимания на возможность вычислить значение функции в точке по каждой из написанных формул.

В отличие от Лопиталя Эйлер подробно рассматривает трансцендентные функции и в особенности два наиболее изученные их классы - показательные и тригонометрические. Он обнаруживает, что все элементарные функции могут быть выражены при помощи арифметических действий и двух операций - взятия логарифма и экспоненты.

Сам ход доказательства прекрасно демонстрирует технику использования бесконечно большого. Определив синус и косинус при помощи тригонометрического круга, Эйлер выводит из формул сложения следующее:

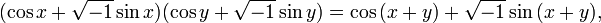
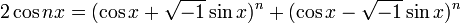
Полагая и z = nx, он получает

,

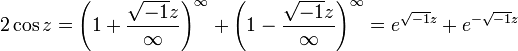отбрасывая бесконечно малые величины большего порядка. Используя это и аналогичное выражение, Эйлер получает и свою знаменитую формулу

.

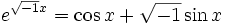Указав различные выражения для функций, которые теперь называют элементарными, Эйлер переходит к рассмотрению кривых на плоскости, начертанным свободным движением руки. По его мнению, не для всякой такой кривой можно отыскать единое аналитическое выражение. В XIX веке с подачи Казорати это утверждение считалось ошибочным: по теореме Вейерштрасса всякая непрерывная в современном смысле кривая может быть приближенно описана полиномами. На самом деле Эйлера это едва ли убедило, ведь нужно ещё переписать предельный переход при помощи символа .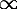

Изложение дифференциального исчисления Эйлер начинает с теории конечных разностей, за ним в третьей главе следует философское разъяснение о том, что «бесконечно малое количество есть точно нуль», более всего не устроившее современников Эйлера. Затем из конечных разностей при бесконечно малом приращении образуются дифференциалы, а из интерполяционной формулу Ньютона <#"457099.files/image009.gif">, которое, однако, рассматривается как отношение двух бесконечно малых. Последние главы посвящены приближенному вычислению при помощи рядов.

В трёхтомном интегральном исчислении Эйлер трактует понятие интеграла так:

«Та функция, дифференциал которой = Xdx, называется его интегралом и обозначается знаком S, поставленным спереди».

В целом же эта часть трактата Эйлера посвящена более общей с современной точки зрения задаче об интегрировании дифференциальных уравнений. При этом Эйлер находит ряд интегралов и дифференциальных уравнений, которые приводят к новым функциям, напр., Γ-функции, эллиптические функции и т. д. Строгое доказательство их неэлементарности было дано в 1830-х годах Якоби <#"457099.files/image010.gif">,

коэффициенты которого будут новыми функциями x. Остаётся назвать p производной (дифференциальным коэффициентом) и обозначить его как f'(x). Таким образом, понятие производной вводится на второй странице трактата и без помощи бесконечно малых. Остаётся заметить, что

,

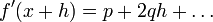поэтому коэффициент q является удвоенной производной производной f(x), то есть

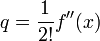и т. д.[24] <#"457099.files/image013.gif">

доопределённую нулём в нуле. Эта функция всюду гладкая на вещественной оси и в нуле имеет нулевой ряд Маклорена, который, следовательно, не сходится к значению f(x). Против этого примера Пуассон <#"457099.files/image014.gif">. Лишь в конце XIX века Прингсхейм <#"457099.files/image015.gif">.

В XVIII веке <http://ru.wikipedia.org/wiki/XVIII_%D0%B2%D0%B5%D0%BA> были разработаны и практически применены такие разделы анализа, как вариационное исчисление <http://ru.wikipedia.org/wiki/%D0%92%D0%B0%D1%80%D0%B8%D0%B0%D1%86%D0%B8%D0%BE%D0%BD%D0%BD%D0%BE%D0%B5_%D0%B8%D1%81%D1%87%D0%B8%D1%81%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5>, обыкновенные дифференциальные уравнения <http://ru.wikipedia.org/wiki/%D0%9E%D0%B1%D1%8B%D0%BA%D0%BD%D0%BE%D0%B2%D0%B5%D0%BD%D0%BD%D1%8B%D0%B5_%D0%B4%D0%B8%D1%84%D1%84%D0%B5%D1%80%D0%B5%D0%BD%D1%86%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D0%B5_%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D1%8F> и дифференциальные уравнения в частных производных <http://ru.wikipedia.org/wiki/%D0%94%D0%B8%D1%84%D1%84%D0%B5%D1%80%D0%B5%D0%BD%D1%86%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5_%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5_%D0%B2_%D1%87%D0%B0%D1%81%D1%82%D0%BD%D1%8B%D1%85_%D0%BF%D1%80%D0%BE%D0%B8%D0%B7%D0%B2%D0%BE%D0%B4%D0%BD%D1%8B%D1%85>, преобразования Фурье <http://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B5%D0%BE%D0%B1%D1%80%D0%B0%D0%B7%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5_%D0%A4%D1%83%D1%80%D1%8C%D0%B5> и производящие функции <http://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%BE%D0%B8%D0%B7%D0%B2%D0%BE%D0%B4%D1%8F%D1%89%D0%B0%D1%8F_%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F_%D0%BF%D0%BE%D1%81%D0%BB%D0%B5%D0%B4%D0%BE%D0%B2%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D0%BE%D1%81%D1%82%D0%B8>. На фундаменте анализа возникла математическая физика <http://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D1%84%D0%B8%D0%B7%D0%B8%D0%BA%D0%B0>, аналитические методы глубоко проникли в геометрию и даже в теорию чисел <http://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B8%D1%8F_%D1%87%D0%B8%D1%81%D0%B5%D0%BB>.

В XIX веке <http://ru.wikipedia.org/wiki/XIX_%D0%B2%D0%B5%D0%BA> Коши <http://ru.wikipedia.org/wiki/%D0%9A%D0%BE%D1%88%D0%B8,_%D0%9E%D0%B3%D1%8E%D1%81%D1%82%D0%B5%D0%BD_%D0%9B%D1%83%D0%B8> первым дал анализу твёрдое логическое обоснование, введя понятие предела последовательности <http://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B5%D0%B4%D0%B5%D0%BB_%D0%BF%D0%BE%D1%81%D0%BB%D0%B5%D0%B4%D0%BE%D0%B2%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D0%BE%D1%81%D1%82%D0%B8>, он же открыл новую страницу комплексного анализа <http://ru.wikipedia.org/wiki/%D0%9A%D0%BE%D0%BC%D0%BF%D0%BB%D0%B5%D0%BA%D1%81%D0%BD%D1%8B%D0%B9_%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7>. Пуассон <http://ru.wikipedia.org/wiki/%D0%9F%D1%83%D0%B0%D1%81%D1%81%D0%BE%D0%BD>, Лиувилль <http://ru.wikipedia.org/wiki/%D0%9B%D0%B8%D1%83%D0%B2%D0%B8%D0%BB%D0%BB%D1%8C,_%D0%96%D0%BE%D0%B7%D0%B5%D1%84>, Фурье <http://ru.wikipedia.org/wiki/%D0%A4%D1%83%D1%80%D1%8C%D0%B5,_%D0%96%D0%B0%D0%BD_%D0%91%D0%B0%D1%82%D0%B8%D1%81%D1%82_%D0%96%D0%BE%D0%B7%D0%B5%D1%84> и другие изучали дифференциальные уравнения в частных производных и гармонический анализ <http://ru.wikipedia.org/wiki/%D0%93%D0%B0%D1%80%D0%BC%D0%BE%D0%BD%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7>.

В последней трети XIX века <http://ru.wikipedia.org/wiki/XIX_%D0%B2%D0%B5%D0%BA> Вейерштрасс <http://ru.wikipedia.org/wiki/%D0%92%D0%B5%D0%B9%D0%B5%D1%80%D1%88%D1%82%D1%80%D0%B0%D1%81%D1%81,_%D0%9A%D0%B0%D1%80%D0%BB> произвёл арифметизацию анализа, полагая геометрическое обоснование недостаточным, и предложил классическое определение предела <http://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B5%D0%B4%D0%B5%D0%BB_%D0%BF%D0%BE%D1%81%D0%BB%D0%B5%D0%B4%D0%BE%D0%B2%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D0%BE%D1%81%D1%82%D0%B8> через ε-δ-язык. Он же создал первую строгую теорию множества <http://ru.wikipedia.org/wiki/%D0%9C%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2%D0%BE> вещественных чисел <http://ru.wikipedia.org/wiki/%D0%92%D0%B5%D1%89%D0%B5%D1%81%D1%82%D0%B2%D0%B5%D0%BD%D0%BD%D0%BE%D0%B5_%D1%87%D0%B8%D1%81%D0%BB%D0%BE>. В это же время попытки усовершенствования теоремы <http://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0> об интегрируемости по Риману <http://ru.wikipedia.org/wiki/%D0%98%D0%BD%D1%82%D0%B5%D0%B3%D1%80%D0%B0%D0%BB> привели к созданию классификации разрывности <http://ru.wikipedia.org/wiki/%D0%A0%D0%B0%D0%B7%D1%80%D1%8B%D0%B2%D0%BD%D0%B0%D1%8F_%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F> вещественных функций. Также были открыты «патологические» примеры (нигде не дифференцируемые непрерывные функции <http://ru.wikipedia.org/wiki/%D0%9D%D0%B5%D0%BF%D1%80%D0%B5%D1%80%D1%8B%D0%B2%D0%BD%D0%BE%D0%B5_%D0%BE%D1%82%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5>, заполняющие пространство кривые <http://ru.wikipedia.org/wiki/%D0%9A%D1%80%D0%B8%D0%B2%D0%B0%D1%8F>). В связи с этим Жордан <http://ru.wikipedia.org/wiki/%D0%96%D0%BE%D1%80%D0%B4%D0%B0%D0%BD> разработал теорию меры <http://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%80%D0%B0>, а Кантор <http://ru.wikipedia.org/wiki/%D0%9A%D0%B0%D0%BD%D1%82%D0%BE%D1%80,_%D0%93%D0%B5%D0%BE%D1%80%D0%B3> - теорию множеств <http://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B8%D1%8F_%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2>, и в начале XX века <http://ru.wikipedia.org/wiki/XX_%D0%B2%D0%B5%D0%BA> математический анализ был формализован с их помощью. Другим важным событием XX века стала разработка нестандартного анализа <http://ru.wikipedia.org/wiki/%D0%9D%D0%B5%D1%81%D1%82%D0%B0%D0%BD%D0%B4%D0%B0%D1%80%D1%82%D0%BD%D1%8B%D0%B9_%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7> как альтернативного подхода к обоснованию анализа.

Заключение

Завершая работу над рефератом можно прийти к выводу, что математический анализ - это совокупность разделов математики <http://articles.gourt.com/ru/математика>, посвященных исследованию функций <http://articles.gourt.com/ru/функция%20(математика)> и их обобщений методами дифференциального <http://articles.gourt.com/ru/дифференциальное%20исчисление> и интегрального <http://articles.gourt.com/ru/интегральное%20исчисление> исчислений. В него также входят теории функций действительного и комплексного переменного, теория дифференциальных уравнений <http://articles.gourt.com/ru/теория%20дифференциальных%20уравнений>, вариационное исчисление <http://articles.gourt.com/ru/вариационное%20исчисление> ряд других математических дисциплин.

Список литературы

1.       Артемьева Т. В. Леонард Эйлер как философ <http://www.ideashistory.org.ru/pdfs/07euler.pdf> // Философия в Петербургской Академии наук XVIII века <http://dic.academic.ru/dic.nsf/ruwiki/456>. - СПб.: 1999. - 182 с.

2.      Гиндикин С. Г. Рассказы о физиках и математиках <http://www.mccme.ru/free-books/gindikin/index.html>. - 3-е изд., расш. - М.: МЦНМО <http://dic.academic.ru/dic.nsf/ruwiki/1016236>, 2001. - 465 с.

3.      Делоне Б. Н. <http://dic.academic.ru/dic.nsf/ruwiki/12126> Леонард Эйлер <http://kvant.mccme.ru/1974/05/leonard_ejler.htm> // Квант <http://dic.academic.ru/dic.nsf/ruwiki/8106>. - 1974. - № 5.

4.      К 250-летию со дня рождения Л. Эйлера: Сборник. - Изд-во АН СССР, 1958.

5.      Летопись Российской Академии наук. Том 1. 1724-1802. - М.: Наука, 2000.

6.      Математика XVIII столетия <http://ilib.mccme.ru/djvu/istoria/istmat3.htm> / Под редакцией А. П. Юшкевича <http://dic.academic.ru/dic.nsf/ruwiki/236450>. - М.: Наука, 1972. - Т. 3. - (История математики в 3-х томах).

7.      Полякова Т. С. Леонард Эйлер и математическое образование в России. - КомКнига, 2007. - 184 с.

8.      Прудников В. Е. Русские педагоги-математики XVIII-XIX веков. - 1956.

9.      Юшкевич А. П. <http://dic.academic.ru/dic.nsf/ruwiki/236450> История математики в России. - М.: Наука, 1968.