Математический анализ
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное
государственное бюджетное образовательное учреждение высшего профессионального
образования
«Южно-Уральский
государственный университет»
ИОДО
Контрольная
работа
Математический
анализ
Выполнила
Козлова Вероника Валерияновна
Проверила
Шунайлова С.А
Задание 1. Найдите производные функций
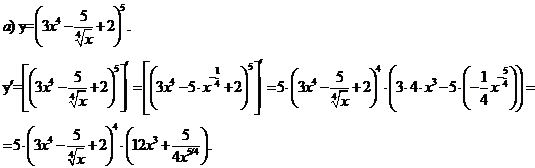
б)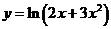 .
.
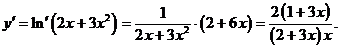
Задание 2. Найдите производные
функций.
а) 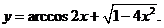
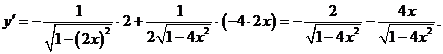
б) 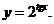
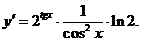
Задание 3. Найдите наибольшее и
наименьшее значения функции у = f(x) на отрезке
[а;b].
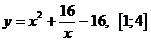
Решение. Находим производную
функции: 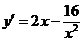 , приравниваем
её к нулю и находим критические точки, принадлежащие этому отрезку:
, приравниваем
её к нулю и находим критические точки, принадлежащие этому отрезку: 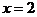 .
.
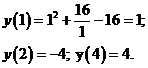
Тогда наибольшее значение: 4 и
наименьшее значение (-4).
Задание 4. Исследуйте функцию  с помощью
производной и постройте ее график:
с помощью
производной и постройте ее график: 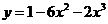 .
.
Решение.
1. Область определения данной
функции D(y): 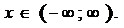
. График функции пересекает ось OY в точке 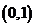 .
.
. Функция непрерывна при 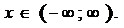
Следовательно, вертикальных асимптот
нет.
4. При исследовании на четность, нечетность
найдем y(-x).
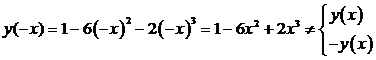
Следовательно, функция не является
четной, не является нечетной.
Функция не является периодической.
. Находим интервалы возрастания,
убывания и экстремум функции, для этого:
а) найдем производную функции
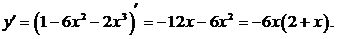
б) Производная обращается в нуль при
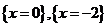
|
x
|
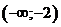 -2 -2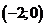 0 0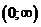
|
|
|
|
|
|
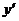 -0+0- -0+0-
|
|
|
|
|
|
|
y
|
Min -7
|
возрастает
|
Max 1
|
убывает
|
. Находим интервалы выпуклости, вогнутости и
точки перегиба.
а) найдем производную второго порядка.
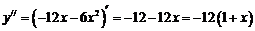
б) вторая производная обращается в
нуль при х=-1
Строим график функции

Задание 5. Дана функция 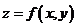 и точка M0(x0,у0).
Найдите градиент функции в точке М0 и производную функции: в точке М0 по
направлению вектора
и точка M0(x0,у0).
Найдите градиент функции в точке М0 и производную функции: в точке М0 по
направлению вектора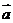 .
.
функция экстремум перегиб возрастание
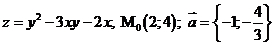 .
.
Решение. Градиент функции двух
переменных 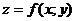 равен
равен
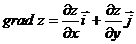 .
.
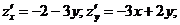 .
.
Найдём значения частных производных
в точке 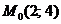 :
:
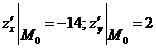 .
.
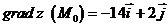
Производная функции 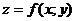 по
направлению вектора
по
направлению вектора 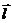 равна:
равна:
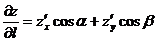
где 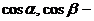 направляющие косинусы вектора
направляющие косинусы вектора 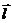 .
.
Находим направляющие косинусы
вектора 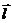 :
:
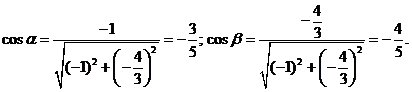
Окончательно получим:
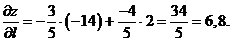
Задание 6. Исследуйте функцию на
экстремум: 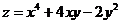 .
.
Решение. Находим стационарные точки.
Для этого находим частные производные первого порядка и приравниваем их к нулю:
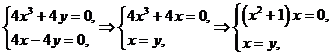
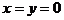 .
.
Находим частные производные второго
порядка:
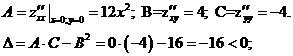
в точке О (0;0) нет экстремума.