Функции Бесселя
Федеральное государственное
образовательное бюджетное
учреждение высшего профессионального
образования
«Финансовый университет при
Правительстве Российской Федерации»
Кафедра «Прикладная математика»
Дисциплина «Дифференциальные
уравнения»
Домашнее творческое задание
На тему «Функции Бесселя»
Выполнила:
Студенка гр. ПМ2-1
Голубева В.И.
Проверил:
Свирщевский Сергей Ростиславович
Москва - 2014
Оглавление
Введение
. Уравнение Лапласа в цилиндрических
координатах
. Бесселевы функции первого рода
. Общее решение уравнения Бесселя
. Функции Бесселя полуцелого порядка
. Некоторые дифференциальные
уравнения, приводимые к уравнению Бесселя
. Применения
Заключение
Список использованной литературы
Введение
Немецкий астроном и математик Фридрих Вильгельм
Бессель (1784-1846) родился в небольшом городе Минден на северо-западе Германии
в семье мелкого чиновника. Свой жизненный путь Бессель начал торговым
служащим. В юности был астрономом-любителем. Серьезно занимался
самообразованием. В 1804 самостоятельно вычислил орбиту кометы Галлея, чем
заслужил похвалу Г.В. Ольберса. В 1806 стал ассистентом частной обсерватории
И.И. Шрётера в Лилиентале. В 1810 был приглашен в Кёнигсберг для организации
новой обсерватории, директором которой проработал до последних лет своей жизни.
Бессель является одним из основоположников астрометрии Разработал теорию
ошибок инструмента и последовательно проводил в жизнь идею о необходимости
вносить соответствующие поправки в результаты наблюдений. При обработке
результатов наблюдений широко применял различные математические методы, в
частности использовал результаты теории вероятностей и метод наименьших
квадратов. В честь немецкого математика и астронома было названо
дифференциальное уравнение, Бессель подробно исследовал его и показал (в 1824
году), что решения уравнения выражаются через специальный класс функций,
получивших название цилиндрических функций или функций Бесселя.
Функции Бесселя в математике - семейство функций,
являющихся каноническими решениями дифференциального уравнения Бесселя:
х2 у'' + ху' + (х2 - ν2)у = 0
где ν - произвольное вещественное число,
называемое порядком.
Наиболее часто используемые функции Бесселя - функции
целых порядков.
Хотя ν и (-ν) порождают одинаковые уравнения,
обычно договариваются о том, чтобы им соответствовали разные функции (это
делается, например, для того, чтобы функция Бесселя была гладкой по ν).
Функции Бесселя впервые
были определены швейцарским математиком Даниилом Бернулли, а названы в честь
Фридриха Бесселя.
1.
1. Уравнение Лапласа в цилиндрических координатах
Чтобы объяснить происхождение бесселевых функций, рассмотрим уравнение
Лапласа в пространстве:
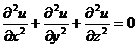 . (1)
. (1)
Если перейти к цилиндрическим координатам по формулам:
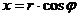 ,
, 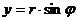 ,
, 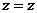 ,
,
то
уравнение (1) примет следующий вид:
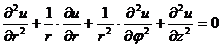 . (2)
. (2)
Поставим задачу: найти все такие решения уравнения, которые могут быть представлены
в виде произведения трех функций, каждая из которых зависит только от одного
аргумента, то есть найти все решения вида:
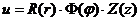 ,
,
где
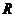 ,
, 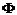 ,
, 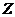 предполагаются дважды непрерывно дифференцируемыми.
предполагаются дважды непрерывно дифференцируемыми.
Пусть
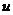 есть решение упомянутого вида. Подставляя его в (2),
получим:
есть решение упомянутого вида. Подставляя его в (2),
получим:
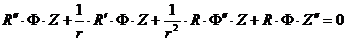 ,
,
откуда
(после деления на 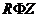 )
)
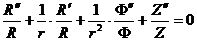 .
.
Записав
это в виде:
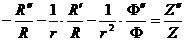 ,
,
найдем,
что левая часть не зависит от 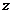 , правая
не зависит от
, правая
не зависит от  ,
, 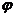 ;
следовательно, общая величина этих выражений есть некоторая постоянная
;
следовательно, общая величина этих выражений есть некоторая постоянная  . Отсюда:
. Отсюда:
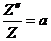 ;
; 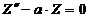 ;
;
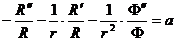 ;
; 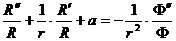 ;
;
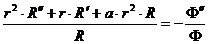 .
.
В
последнем равенстве левая часть не зависит от 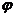 , правая
не зависит от
, правая
не зависит от 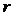 ; следовательно, общая величина этих выражений есть
некоторая постоянная
; следовательно, общая величина этих выражений есть
некоторая постоянная 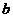 . Отсюда:
. Отсюда:
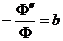 ,
, 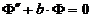 ;
;
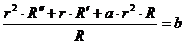 ,
, 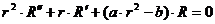 .
.
Таким
образом, 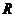 ,
, 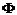 ,
, 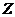 должны удовлетворять линейным дифференциальным
уравнениям второго порядка:
должны удовлетворять линейным дифференциальным
уравнениям второго порядка:
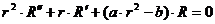 , (3)
, (3)
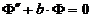 ,
, 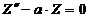 ,
,
из
которых второе и третье есть простейшие линейные уравнения с постоянными
коэффициентами, а первое является линейным уравнением с переменными коэффициентами
нового вида.
Обратно,
если 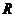 ,
, 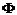 ,
, 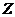 удовлетворяют уравнениям (3), то
удовлетворяют уравнениям (3), то 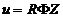 есть решение уравнения (2). В самом деле, подставляя
есть решение уравнения (2). В самом деле, подставляя 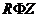 в левую часть (2) и деля затем на
в левую часть (2) и деля затем на 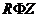 , получим:
, получим:
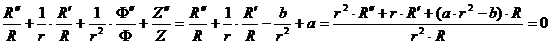 .
.
Таким
образом, общий вид всех трех решений уравнения (2), которые являются
произведением трех функций, каждая из которых зависит от одного аргумента, есть
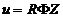 , где
, где 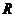 ,
, 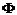 ,
, 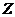 - любые
решения уравнений (3) при любом выборе чисел
- любые
решения уравнений (3) при любом выборе чисел  ,
, 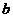 .
.
Первое
из уравнений (3) в случае 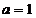 ,
,  называется
уравнением Бесселя. Полагая в этом случае
называется
уравнением Бесселя. Полагая в этом случае 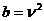 ,
обозначая независимую переменную буквой
,
обозначая независимую переменную буквой  (вместо
(вместо 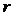 ), а неизвестную функцию - буквой
), а неизвестную функцию - буквой 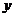 (вместо
(вместо 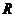 ),
найдем, что уравнение Бесселя имеет вид:
),
найдем, что уравнение Бесселя имеет вид:
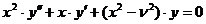 . (4)
. (4)
Это
линейное дифференциальное уравнение второго порядка с переменными
коэффициентами играет большую роль в приложениях математики. Функции, ему
удовлетворяющие, называются бесселевыми, или цилиндрическими, функциями.
2. Бесселевы
функции первого рода
Будем искать решение уравнения Бесселя (4) в виде ряда ( по теореме о
разложении в обобщённый степенной ряд):
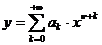 .
.
Тогда
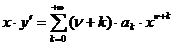 ,
,
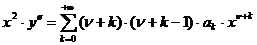 ,
,
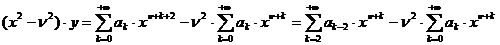 ,
,
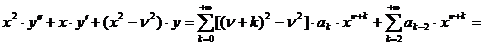
Следовательно,
приходим к требованию
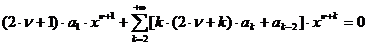
или
к бесконечной системе уравнений
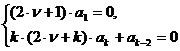
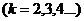 ,
,
которая
распадается на две системы:
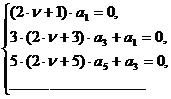
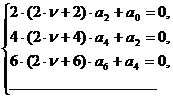
Первая
из них удовлетворится, если взять 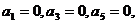 … Во
второй системе
… Во
второй системе 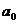 можно взять произвольно; тогда
можно взять произвольно; тогда 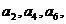 … однозначно определяются (если
… однозначно определяются (если 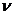 не является целым отрицательным числом). Взяв
не является целым отрицательным числом). Взяв 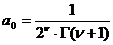 , ( Г-гамма-функция Эйлера) найдем последовательно:
, ( Г-гамма-функция Эйлера) найдем последовательно:
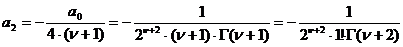 ,
,
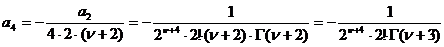 ,
,
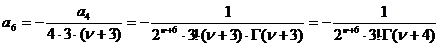 ,
,
и
в качестве решения уравнения (4) получим ряд:
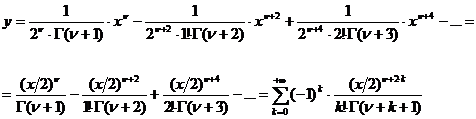
Этот
ряд, формально удовлетворяющий уравнению (4), сходится для всех положительных
значений  и, следовательно, является решением уравнения (4) в
области
и, следовательно, является решением уравнения (4) в
области 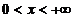 (в случае целого
(в случае целого 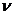 в
области
в
области 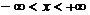 ).
).
Функция
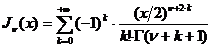 (5)
(5)
называется
бесселевой функцией первого рода с индексом 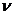 . Она
является одним из решений уравнения Бесселя (4). В случае целого неотрицательного
индекса
. Она
является одним из решений уравнения Бесселя (4). В случае целого неотрицательного
индекса 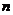 получим:
получим:
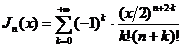 , (5`)
, (5`)
*Г-функция является гомоморфным продолжением последовательности
факториалов для любого натурального n: Г(n)=(n-1)! и, в частности,
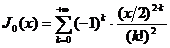 . (5``)
. (5``)
3. Общее
решение уравнения Бесселя
В
случае нецелого индекса 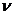 функции
функции 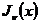 и
и 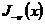 являются решениями уравнения (4). Эти решения линейно
независимы, так как начальные члены рядов, изображающих эти функции, имеют
коэффициенты, отличные от нуля, и содержат разные степени
являются решениями уравнения (4). Эти решения линейно
независимы, так как начальные члены рядов, изображающих эти функции, имеют
коэффициенты, отличные от нуля, и содержат разные степени  . Таким образом, в случае нецелого индекса общее
решение уравнения Бесселя есть:
. Таким образом, в случае нецелого индекса общее
решение уравнения Бесселя есть:
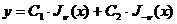 . (6)
. (6)
Если
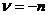 (целое отрицательное число), то функция, определяемая
формулой (5) (учитывая, что
(целое отрицательное число), то функция, определяемая
формулой (5) (учитывая, что 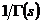 равно
нулю для
равно
нулю для 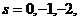 …), принимает вид:
…), принимает вид:
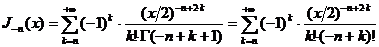 (5```)
(5```)
или,
после замены индекса суммирования 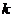 на
на 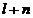 ,
,
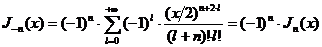 , (7)
, (7)
откуда
видно, что 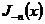 удовлетворяет вместе с
удовлетворяет вместе с 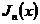 уравнению
Бесселя
уравнению
Бесселя
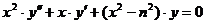 .
.
Но
формула (6) в случае целого 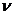 уже не
дает общего решения уравнения (4).
уже не
дает общего решения уравнения (4).
Полагая
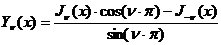 (
(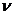 - не целое) (8)
- не целое) (8)
и
дополняя это определение для 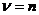 (целое
число) формулой:
(целое
число) формулой:
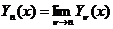 , (8`)
, (8`)
получим
функцию 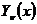 , удовлетворяющую уравнению Бесселя (4) и во всех
случаях линейно независимую от
, удовлетворяющую уравнению Бесселя (4) и во всех
случаях линейно независимую от 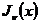 (в
случае
(в
случае 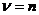 , где
, где 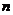 -
целое). Функция
-
целое). Функция 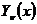 называется бесселевой функцией второго рода с
индексом
называется бесселевой функцией второго рода с
индексом 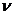 . Общее решение уравнения Бесселя (4) можно записать
во всех случаях в виде:
. Общее решение уравнения Бесселя (4) можно записать
во всех случаях в виде:
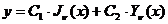 . (9)
. (9)
4. Функции
Бесселя полуцелого порядка
Хотя в общем случае функции Бесселя не выражаются
через элементарные функции, в частном случае полуцелого порядка это возможно:
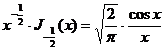 , (10)
, (10)
Остальные порядки могут быть получены с помощью рекуррентного
соотношения:
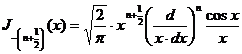 . (11)
. (11)
5. Некоторые
дифференциальные уравнения, приводимые к уравнению Бесселя
.
Еще одним хорошо известным уравнением данного класса является модифицированное
уравнение Бесселя, которое получается из регулярного уравнения Бесселя
заменой x на −ix. Это уравнение имеет вид:
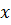 2
2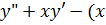 2+v2)
2+v2)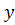 =0 (12)
=0 (12)
Решение данного уравнения выражается через так называемые модифицированые
функции Бесселя первого и второго рода:
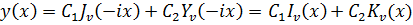 (13)
(13)
где Iv(x) и Kv(x) обозначают модифицированные
функции Бесселя, соответственно, первого и второго рода.
2.
Дифференциальное уравнение Эйри, известное в астрономии и физике,
записывается в виде:
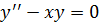 (14)
(14)
Его также можно свести к уравнению Бесселя. Решение уравнения Эйри
выражается через функции Бесселя дробного порядка 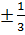 :
:
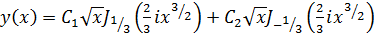 (15)
(15)
.
Дифференциальное уравнение вида
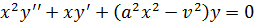 (16)
(16)
отличается от уравнения Бесселя лишь множителем a2 перед x2
и имеет общее решение в следующем виде:
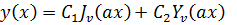 (17)
(17)
.
Похожее дифференциальное уравнение
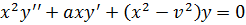 (18)
(18)
также сводится к уравнению Бесселя
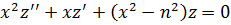 (19)
(19)
с помощью подстановки
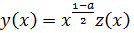 (20)
(20)
Здесь параметр n2 обозначает
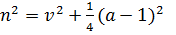 (21)
(21)
В результате, общее решение данного дифференциального уравнения определяется
формулой
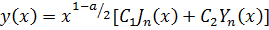 (22)
(22)
6. Применения
дифференциальный уравнение лаплас бессель
Уравнение Бесселя возникает во время нахождения решений уравнения Лапласа
и уравнения Гельмгольца в цилиндрических и сферических координатах. Поэтому
функции Бесселя применяются при решении многих задач о распространении волн,
статических потенциалах и т. п., например:
· электромагнитные
волны
<http://ru.wikipedia.org/wiki/%D0%AD%D0%BB%D0%B5%D0%BA%D1%82%D1%80%D0%BE%D0%BC%D0%B0%D0%B3%D0%BD%D0%B8%D1%82%D0%BD%D1%8B%D0%B5_%D0%B2%D0%BE%D0%BB%D0%BD%D1%8B>
в цилиндрическом волноводе
<http://ru.wikipedia.org/wiki/%D0%92%D0%BE%D0%BB%D0%BD%D0%BE%D0%B2%D0%BE%D0%B4>;
· теплопроводность
<http://ru.wikipedia.org/w/index.php?title=%D0%97%D0%B0%D0%BA%D0%BE%D0%BD_%D1%82%D0%B5%D0%BF%D0%BB%D0%BE%D0%BF%D1%80%D0%BE%D0%B2%D0%BE%D0%B4%D0%BD%D0%BE%D1%81%D1%82%D0%B8&action=edit&redlink=1>
в цилиндрических объектах;
· формы
колебания тонкой круглой мембраны
· распределение
интенсивности света, дифрагированного на круглом отверстии.
· скорость
частиц в цилиндре, заполненном жидкостью и вращающемся вокруг своей оси.
· волновые
функции в сферически симметричном потенциальном ящике.
Функции Бесселя применяются и в решении других задач,
например, при обработке сигналов.
Заключение
Сегодня в качестве математического аппарата во многих отраслях
современной прикладной математики, математической физики и технических
приложениях широко используются функции Бесселя и цилиндрические функции.
Области приложения этих функций крайне разнообразны. Они обеспечивают очень
быструю и корректную сходимость решений целого ряда прикладных задач, которые
могут быть так или иначе сведены к уравнению Бесселя. Интерес математиков и
инженеров к специальным функциям матфизики не угасает.
Список
использованной литературы:
1. Эльсгольц Л.Э. Дифференциальные уравнения и
вариационное исчисление, Москва 2002
. Балакин А.Б. Лекции по теории функции Бесселя,
Казань 2009.
. http://www.math24.ru/bessel-equation.html
. http://ru.wikipedia.org/wiki/Функции_Бесселя
5. Курант Р. Гильберт Д.
Методы математической физики т.1
<http://page-book.ru/search/?sb=4&q=%D0%9A%D1%83%D1%80%D0%B0%D0%BD%D1%82%20%D0%A0.%20%D0%93%D0%B8%D0%BB%D1%8C%D0%B1%D0%B5%D1%80%D1%82%20%D0%94.%20%D0%9C%D0%B5%D1%82%D0%BE%D0%B4%D1%8B%20%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B9%20%D1%84%D0%B8%D0%B7%D0%B8%D0%BA%D0%B8%20%D1%82.1>
<http://page-book.ru/i46486>
. И.Г. Араманович,
В.И. Левин. Уравнения математической физики. 1969.