Моделювання нестаціонарних процесів теплопровідності методом гібридного диференціального оператора Лежандра–Бесселя-Фур’є в припущенні, що межа середовища м’яка по відношенню до відбиття хвиль
Зміст
теплопровідність
диференціальний рівняння лежандр
Вступ
.
Моделювання процесу теплопровідності в неоднорідному середовищі з м’якими
межами методом гібридного диференціального оператора Лежандра - Бесселя - Фур’є
на полярній осі
.
Моделювання процесів теплопровідності в неоднорідних середовищах з м’якими
межами методом гібридного диференціального оператора Лежандра - Фур’є - Бесселя
на полярній осі 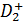
.
Моделювання процесів теплопровiдностi в неоднорідних середовищах з м'якими
межами методом гібридного диференціального оператора Лежандра - Фур'є - Бесселя
на полярнiй осi 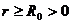
.
Моделювання процесiв теплопровiдностi в неоднорiдних середовищах з м'якими
межами методом гiбридного диференцiального оператора Лежандра - Бесселя - Фур'є
на полярнiй осi 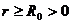
.
Охорона праці
Список
використаних джерел
Вступ
Процеси теплопровідності, які
постійно відбуваються в навколишньому середовищі, привертали до себе увагу вчених
на протязі всієї історії розвитку людства. Найпростішою математичною моделлю
такого процесу є диференціальне рівняння теплопровідності параболічного типу
[1]
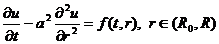 (1)
(1)
з відповідною початковою умовою та
крайовими умовами.
Потреби практики приводили до
різного узагальнення рівняння (1): перехід до квазілінійності та нелінійності,
перехід до кусково-однорідних коефіцієнтів, перехід до нових ортогональних
криволінійних систем координат (у випадку розмірності простору 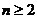 );
перехід до диференціальних рівнянь параболічного типу вищих порядків та ін. В
усіх випадках процеси теплопровідності вивчалися в припущенні, що межа
середовища жорстка по відношенню до відбиття хвиль. Різко змінюється картина
розповсюдження тепла, якщо межа середовища є м’якою по відношенню до відбиття
хвиль. Математично це означає наявність в крайових операторах та
диференціальних операторах спряження похідної стосовно часової змінної.
);
перехід до диференціальних рівнянь параболічного типу вищих порядків та ін. В
усіх випадках процеси теплопровідності вивчалися в припущенні, що межа
середовища жорстка по відношенню до відбиття хвиль. Різко змінюється картина
розповсюдження тепла, якщо межа середовища є м’якою по відношенню до відбиття
хвиль. Математично це означає наявність в крайових операторах та
диференціальних операторах спряження похідної стосовно часової змінної.
Особливу увагу заслуговує дуже
поширений в другій половині ХХ-го століття для вивчення фізико-технічних
характеристик композитних об’єктів метод кусково-сталих коефіцієнтів. Це
привело навіть у випадку жорсткості області середовища до диференціальних
рівнянь із сингулярними коефіцієнтами типу дельта-функції та її похідних. Та
одержати інтегральне зображення точного аналітичного розв’язку таких задач
навіть у найпростішому випадку неможливо. Ці труднощі можна обійти, якщо
здійснити моделювання процесів поширення тепла методом гібридних диференціальних
операторів.
Дана робота присвячена моделюванню
нестаціонарних процесів теплопровідності методом гібридного диференціального
оператора Лежандра - (Бесселя, Фур’є) в припущенні, що межа середовища м’яка по
відношенню до відбиття хвиль.
Такий підхід здійснено вперше в
математичній літературі. Це дало можливість одержати інтегральне зображення
точного аналітичного розв’язку в алгоритмічній формі достатньо широкого класу
задач теплопровідності неоднорідного середовища. Така форма розв’язку зручна і
для теоретичного дослідження і для інженерних розрахунків.
1. Моделювання процесу
теплопровідності в неоднорідному середовищі з м’якими межами методом гібридного
диференціального оператора Лежандра - Бесселя - Фур’є на полярній осі
Побудуємо обмежений в області 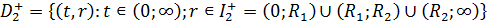 розв’язок
сепаратної системи диференціальних рівнянь теплопровідності параболічного типу
[1]
розв’язок
сепаратної системи диференціальних рівнянь теплопровідності параболічного типу
[1]
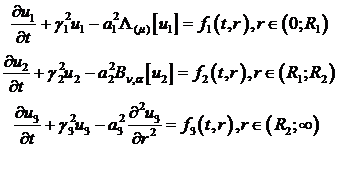 (1.1)
(1.1)
за початковими умовами
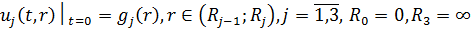 (1.2)
(1.2)
та умовами спряження
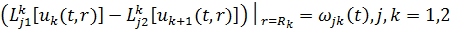 (1.3)
(1.3)
У рівностях (1.1) беруть участь
диференціальні оператори Лежандра [2]
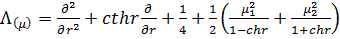 ,
,
Бесселя
[3] 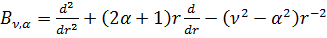
та Фур’є [4]
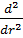
(диференціальний оператор Лапласа у
випадку одновимірного простору [1]);
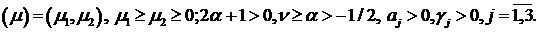
У рівностях (1.3) беруть участь
узагальнені диференціальні оператори спряження
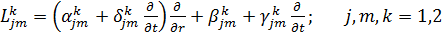 .
.
Припустимо, що виконані умови на
коефіцієнти:
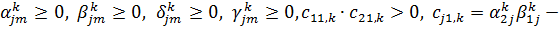
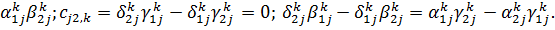
Розв’язок задачі (1.1)-(1.3)
одержимо методом інтегрального перетворення Лапласа стосовно t [5] в
припущенні, що шукані та задані функції є зображення за Лапласом стосовно
змінної t [5]:
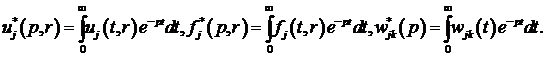
У зображенні за Лапласом отримуємо
крайову задачу: побудувати обмежений на множині 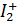 розв’язок
сепаратної системи звичайних диференціальних рівнянь Лежандра, Бесселя та Фур’є
для модифікованих функцій
розв’язок
сепаратної системи звичайних диференціальних рівнянь Лежандра, Бесселя та Фур’є
для модифікованих функцій
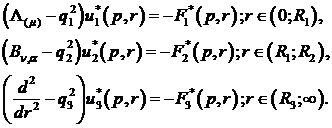 (1.4)
(1.4)
за
умовами спряження
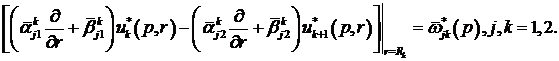 (1.5)
(1.5)
У рівностях (1.4), (1.5) беруть
участь функції:
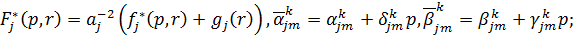
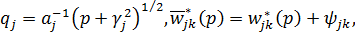
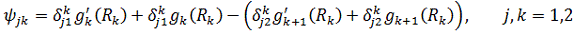
Зауважимо, що можна вважати
початкові умови 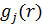 нульовими. Тоді
нульовими. Тоді 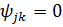 для
для
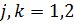 .
Якщо
.
Якщо 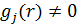 ,
то перейдемо до нових початкових умов
,
то перейдемо до нових початкових умов 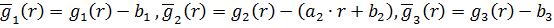 і
визначимо числа
і
визначимо числа 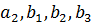 із неоднорідної
алгебраїчної системи чотирьох рівнянь відносно чотирьох невідомих:
із неоднорідної
алгебраїчної системи чотирьох рівнянь відносно чотирьох невідомих:
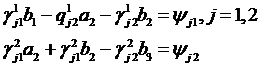 (1.6)
(1.6)
Тут прийняті позначення:
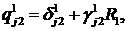
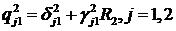 .
.
Введемо до розгляду числа:
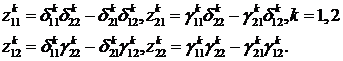
Оскільки визначник алгебраїчної
системи (1.6)
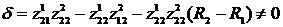 (1.7)
(1.7)
то алгебраїчна система (1.6) має
єдиний розв’язок [6]:
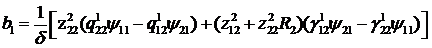 (1.8)
(1.8)
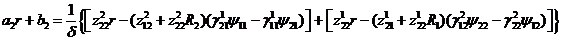
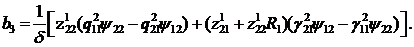
Фундаментальну систему розв’язків
для диференціального рівняння Лежандра 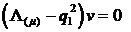 складають
узагальнені приєднані функції Лежандра першого роду
складають
узагальнені приєднані функції Лежандра першого роду 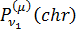 та
другого роду
та
другого роду 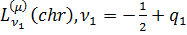 [2];
фундаментальну систему розв’язків для диференціального рівняння Бесселя
[2];
фундаментальну систему розв’язків для диференціального рівняння Бесселя 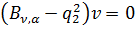 складають
функції Бесселя уявного аргументу першого роду
складають
функції Бесселя уявного аргументу першого роду 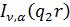 та
другого роду
та
другого роду 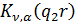 [3];
фундаментальну систему розв’язків для диференціального рівняння Фур’є
[3];
фундаментальну систему розв’язків для диференціального рівняння Фур’є 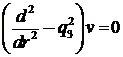 складають
функції
складають
функції 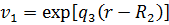 та
та
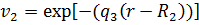 [4].
[4].
Наявність фундаментальної системи
розв’язків дозволяє побудувати розв’язок крайової задачі (1.4), (1.5) методом
функцій Коші [4,7]:
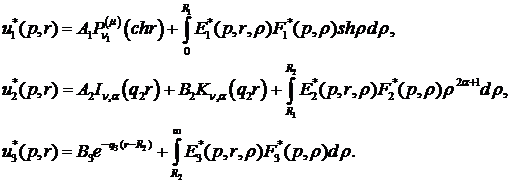 (1.9)
(1.9)
У рівностях (1.9) 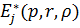 - функції Коші
[4,7]:
- функції Коші
[4,7]:
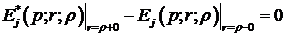 , (1.10)
, (1.10)
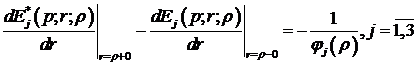
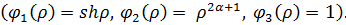
Припустимо, що функція Коші
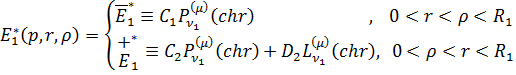
Властивості (1.10) функції Коші
дають алгебраїчну систему з двох рівнянь:
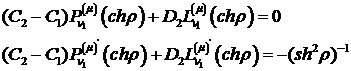
Звідси знаходимо співвідношення:
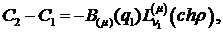
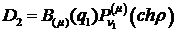 (1.11)
(1.11)
Доповнимо рівності (1.11)
алгебраїчним рівнянням:
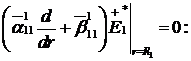
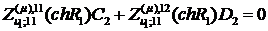 (1.12)
(1.12)
Із алгебраїчної системи (1.11) та
(1.12) знаходимо, що
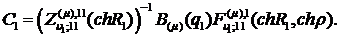
Цим функція Коші 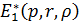 визначена
й внаслідок симетрії відносно діагоналі
визначена
й внаслідок симетрії відносно діагоналі 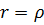 має
структуру:
має
структуру:
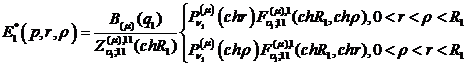 (1.13)
(1.13)
У рівностях (1.11)-(1.13) беруть
участь функції:
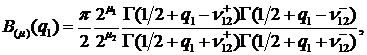
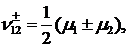
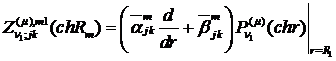
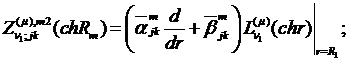
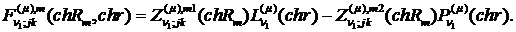
Нехай функція Коші
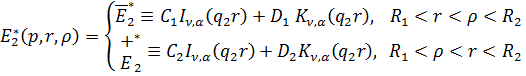
Властивості (1.10) функції Коші
дають алгебраїчну систему з двох рівнянь:
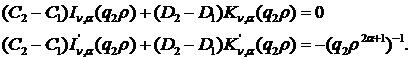
Звідси отримуємо співвідношення:
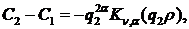
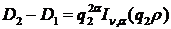 (1.14)
(1.14)
Доповнимо рівності (1.14)
алгебраїчними рівняннями:
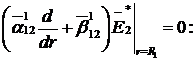
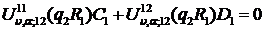 (1.15)
(1.15)
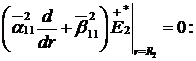
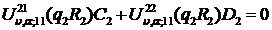
Внаслідок співвідношень (1.14)
алгебраїчна система (1.15) набуває вигляду:
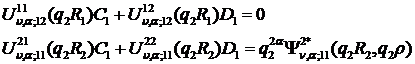 (1.16)
(1.16)
Розв’язуємо
алгебраїчну систему (1.16) за правилом Крамера:
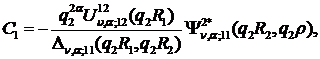
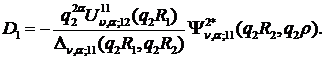
Цим функція Коші 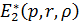 визначена
й внаслідок симетрії відносно діагоналі
визначена
й внаслідок симетрії відносно діагоналі 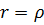 має
структуру:
має
структуру:
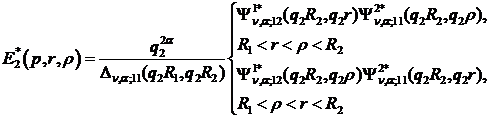 (1.17)
(1.17)
У рівностях (1.15)-(1.17) беруть
участь функції:
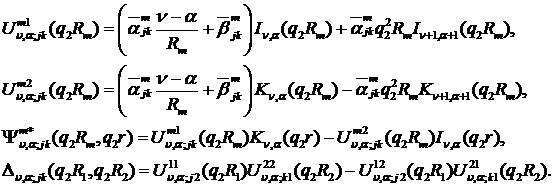
Нехай функція Коші
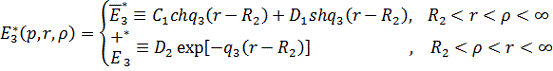
Властивості (1.10) функції Коші
дають алгебраїчну систему з двох рівнянь:
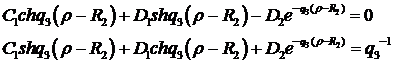
Звідси отримуємо співвідношення:
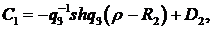
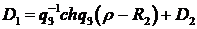 (1.18)
(1.18)
Доповнимо рівності (1.18)
алгебраїчним рівнянням:
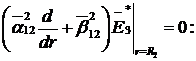
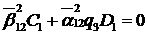 (1.19)
(1.19)
Із алгебраїчної системи (1.18),
(1.19) одержуємо,що
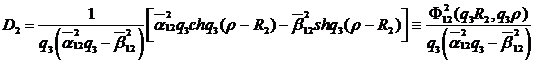
Цим функція Коші 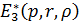 визначена
й внаслідок симетрії відносно діагоналі
визначена
й внаслідок симетрії відносно діагоналі 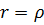 має
структуру:
має
структуру:
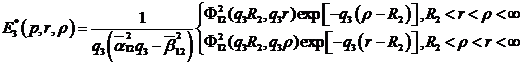 (1.20)
(1.20)
Повернемося до формул (1.9). Умови
спряження (1.5) для визначення чотирьох невідомих величин A1,A2,B2,B3 дають
неоднорідну алгебраїчну систему із чотирьох рівнянь:
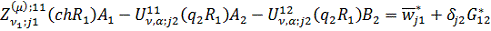 (1.21)
(1.21)
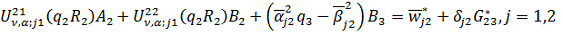
У рівностях (1.21) беруть участь
функції
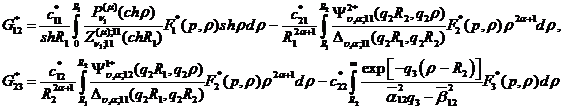
та символ Кронекера
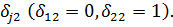
Введемо до розгляду функції:
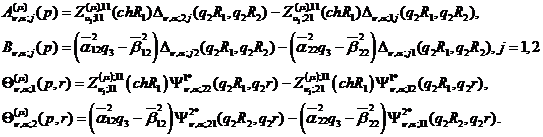
Припустимо, що виконана умова
однозначної розв’язності крайової задачі (1.4), (1.5): для
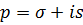 з
з 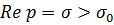 ,
,
де 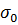 -
абсциса збіжності інтеграла Лапласа, та
-
абсциса збіжності інтеграла Лапласа, та
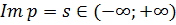
визначник алгебраїчної системи
(1.21) відмінний від нуля:
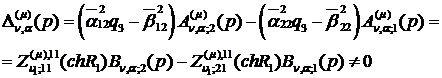 (1.22)
(1.22)
Визначаємо головні розв’язки
крайової задачі (1.4), (1.5):
) породжені неоднорідністю умов
спряження функції Гріна
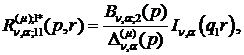
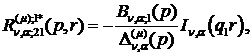
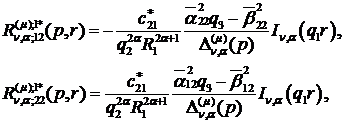
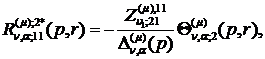
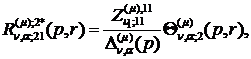
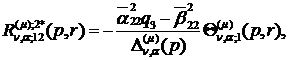
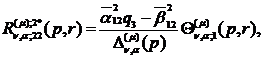
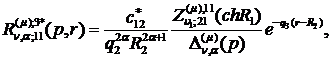 (1.23)
(1.23)
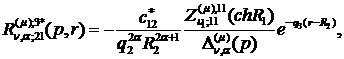
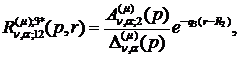
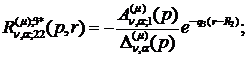
) породжені неоднорідністю системи
(1.4) функції впливу:
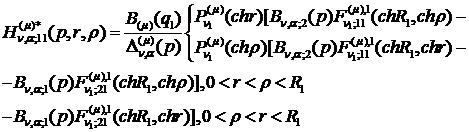
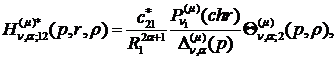
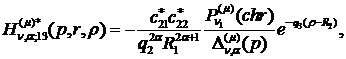
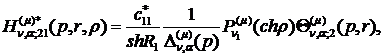
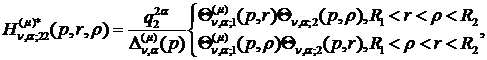
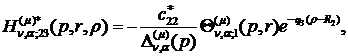 (1.24)
(1.24)
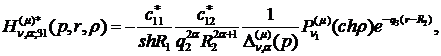
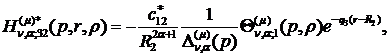
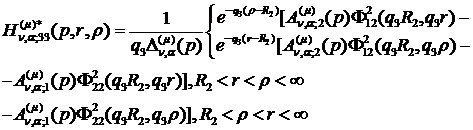
У результаті однозначної
розв’язності алгебраїчної системи (1.21) й підстановки визначених величин 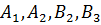 у
рівності (1.9) маємо єдиний розв’язок крайової задачі (1.4), (1.5):
у
рівності (1.9) маємо єдиний розв’язок крайової задачі (1.4), (1.5):
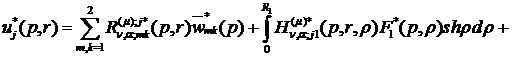
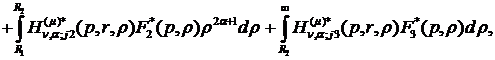
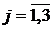 (1.25)
(1.25)
Перехід у формулах (1.25) до
оригіналу дає єдиний розв’язок параболічної задачі (1.1)-(1.3):
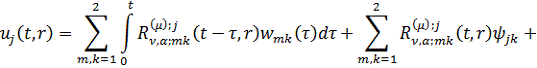
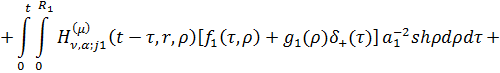
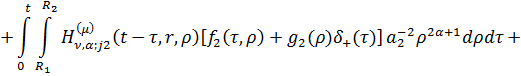
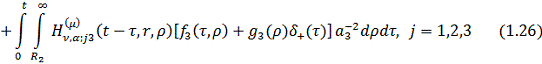
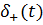 - дельта-функція,
зосереджена в точці
- дельта-функція,
зосереджена в точці 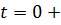 [7].
[7].
У формулах (1.26) за означенням [5]
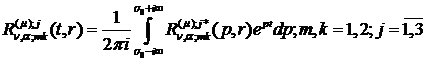 (1.27)
(1.27)
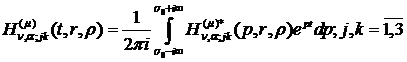 (1.28)
(1.28)
Теорема: Якщо 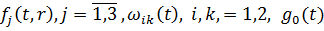 є оригіналом за
Лапласом,
є оригіналом за
Лапласом, 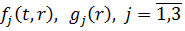 - двічі неперервно
диференційовні за змінною r та задовольняють однорідні умови спряження, то
задача (1.1)-(1.3) має розв’язок
- двічі неперервно
диференційовні за змінною r та задовольняють однорідні умови спряження, то
задача (1.1)-(1.3) має розв’язок 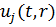 ,
що визначається формулою (1.26), а при виконанні умови однозначної розв’язності
алгебраїчної системи (1.22) він єдиний.
,
що визначається формулою (1.26), а при виконанні умови однозначної розв’язності
алгебраїчної системи (1.22) він єдиний.
Особливими точками функції Гріна 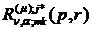 та
функції впливу
та
функції впливу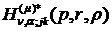 є точки галуження
є точки галуження 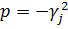 та
та
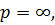
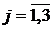 .
Покладемо
.
Покладемо 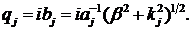 Одержимо:
Одержимо: 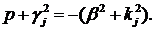 Якщо
Якщо
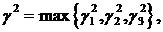 то
при
то
при 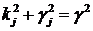 маємо:
маємо:
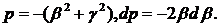 Вирази
(1.27), (1.28) з використанням методу контурного інтегралу в поєднанні з лемою
Жордана й теоремою Коші приводимо до розрахункових формул:
Вирази
(1.27), (1.28) з використанням методу контурного інтегралу в поєднанні з лемою
Жордана й теоремою Коші приводимо до розрахункових формул:
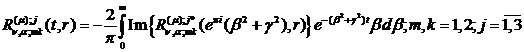
(1.29)
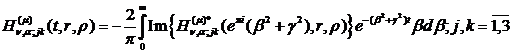 (1.30)
(1.30)
При 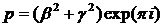 маємо:
маємо:
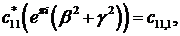
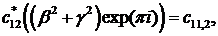
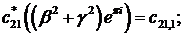
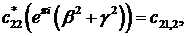
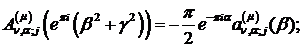
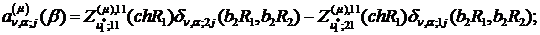
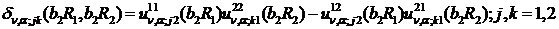
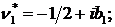
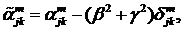
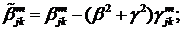
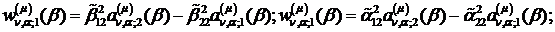
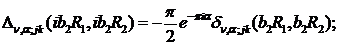
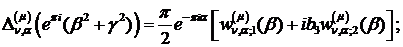
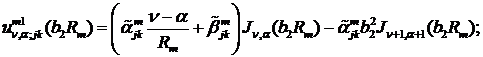
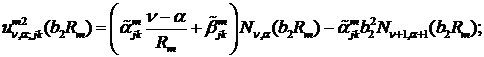
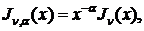
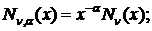
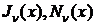 - функції Бесселя
першого та другого роду відповідно.
- функції Бесселя
першого та другого роду відповідно.
Визначимо величини та функції:
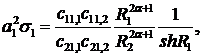
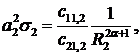
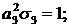
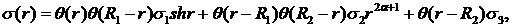
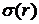 - вагова функція,
- вагова функція, 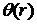 -
одинична функція Гевісайда [7].
-
одинична функція Гевісайда [7].
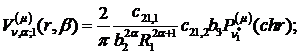
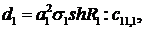
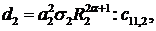
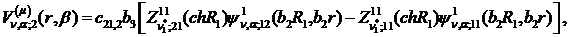
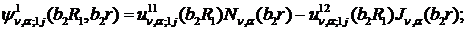
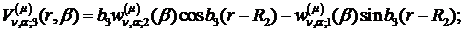
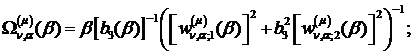
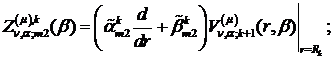
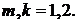
Якщо виконати зазначені у рівностях
(1.29), (1.30) операції, то будемо мати функції:
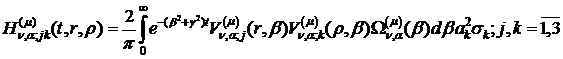 (1.31)
(1.31)
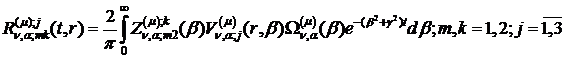 (1.32)
(1.32)
Інтегральне зображення (1.26)
розв’язку параболічної задачі (1.1)-(1.3) можна зобразити в такому вигляді:
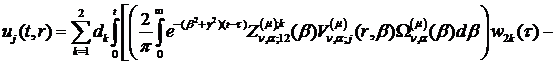
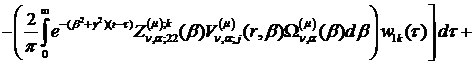
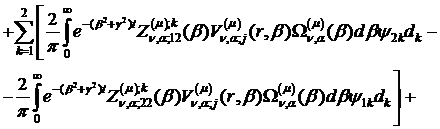
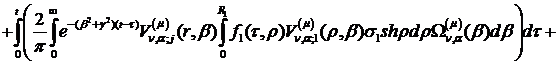
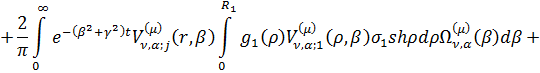
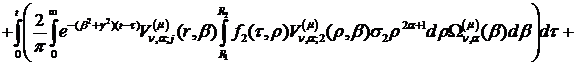
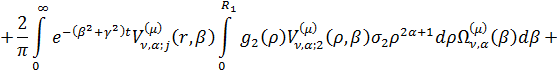
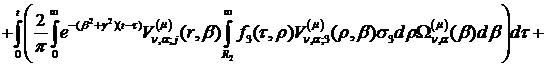
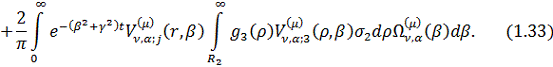
Наслідок 1. Нехай умови спряження
однорідні (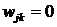 ,
, 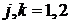 ),
густини теплових джерел
),
густини теплових джерел 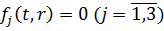 , а початкові умови
такі, що
, а початкові умови
такі, що
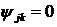 (
(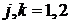 ).
Формули (1.33) у цьому випадку дають при
).
Формули (1.33) у цьому випадку дають при 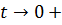 інтегральні
зображення:
інтегральні
зображення:
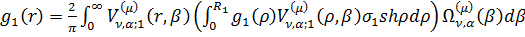 , (1.34)
, (1.34)
 , (1.35)
, (1.35)
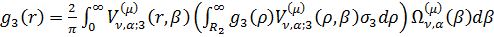 . (1.36)
. (1.36)
Введемо до розгляду вектор-функцію
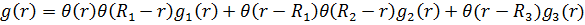
та спектральну функцію
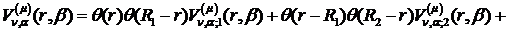
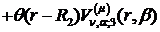 (1.37)
(1.37)
Інтегральне зображення (1.34)-(1.36)
дають інтегральне зображення вектор-функції 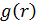 :
:
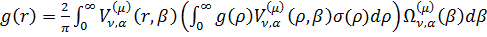 , (1.38)
, (1.38)
Рівність (1.38) є суперпозицією двох
інтегральних операторів
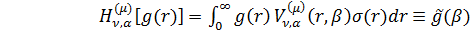 , (1.39)
, (1.39)
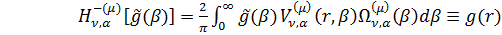 , (1.40)
, (1.40)
Висновок: Інтегральне зображення
(1.38) вектор-функції 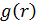 визначає пряме
визначає пряме 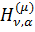 і
обернене
і
обернене 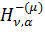 інтегральне
перетворення. Отже, параболічну задачу (1.1)-(1.3) можна було розв’язати
методом інтегрального перетворення (1.39), (1.40).
інтегральне
перетворення. Отже, параболічну задачу (1.1)-(1.3) можна було розв’язати
методом інтегрального перетворення (1.39), (1.40).
Зауважимо, що: 1) вектор-функція 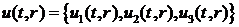 повністю
визначає однозначно тепловий процес, що відбувається в даному середовищі; 2)
інтегральне зображення (1.33) розв’язку задачі поліпараметричне й носить
алгоритмічний характер.
повністю
визначає однозначно тепловий процес, що відбувається в даному середовищі; 2)
інтегральне зображення (1.33) розв’язку задачі поліпараметричне й носить
алгоритмічний характер.
2. Моделювання процесів теплопровідності
в неоднорідних середовищах з м’якими межами методом гібридного диференціального
оператора Лежандра - Фур’є - Бесселя на полярній осі 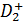
Побудуємо обмежений в області 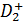 розв’язок
сепаратної системи диференціальних рівнянь теплопровідності параболічного типу
[1]
розв’язок
сепаратної системи диференціальних рівнянь теплопровідності параболічного типу
[1]
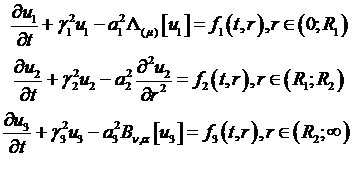 (2.1)
(2.1)
за початковими умовами
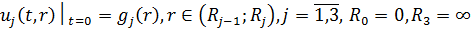 (2.2)
(2.2)
та умовами спряження
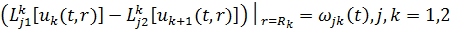 (2.3)
(2.3)
Розв’язок задачі (2.1)-(2.3)
побудуємо методом інтегрального перетворення Лапласа стосовно t [5] в
припущенні, що вектор-функція 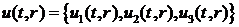 ,вектор-функція
,вектор-функція 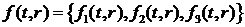 та
функція
та
функція 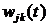 є
оригіналами за Лапласом.
є
оригіналами за Лапласом.
У зображенні за Лапласом маємо
крайову задачу: побудувати на множині 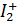 обмежений
розв’язок сепаратної системи звичайних диференціальних рівнянь Лежандра, Фур’є
та Бесселя для модифікованих функцій
обмежений
розв’язок сепаратної системи звичайних диференціальних рівнянь Лежандра, Фур’є
та Бесселя для модифікованих функцій
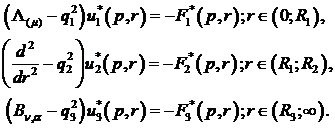 (2.4)
(2.4)
за
умовами спряження
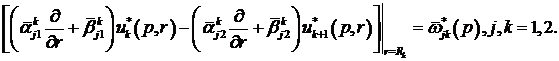 (2.5)
(2.5)
Наявність фундаментальну систему
розв’язків 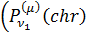 та
та 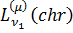 для
першого рівняння;
для
першого рівняння; 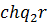 та
та 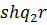 для
другого рівняння;
для
другого рівняння; 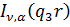 та
та 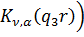 дозволяє
побудувати розв’язок крайової задачі (2.4), (2.5) методом функцій Коші [4,7]:
дозволяє
побудувати розв’язок крайової задачі (2.4), (2.5) методом функцій Коші [4,7]:
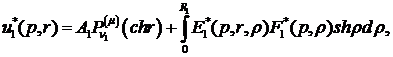
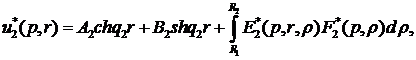 (2.6)
(2.6)
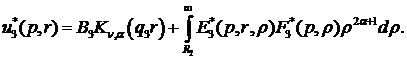
Тут 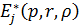 -
функції Коші [4,7].
-
функції Коші [4,7].
Згідно правила (1.13) функція Коші
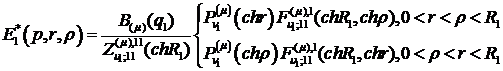 (2.7)
(2.7)
Припустимо, що функція Коші
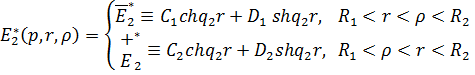
Властивості (1.10) функції Коші
дають алгебраїчну систему з двох рівнянь:
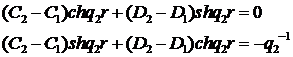
Звідси одержуємо співвідношення:
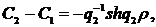
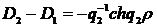 (2.8)
(2.8)
Доповнимо рівності (2.8)
алгебраїчними рівняннями:
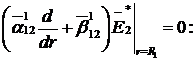
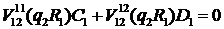 (2.9)
(2.9)
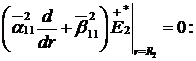
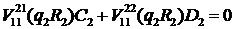
Внаслідок співвідношень (2.8)
алгебраїчна система (2.9) набуває вигляду:
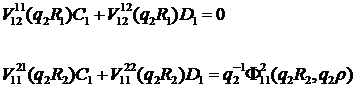 (2.10)
(2.10)
Розв’язок
алгебраїчної системи (2.10) знаходимо за правилом Крамера [6]
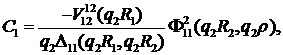
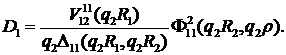
Цим функція Коші 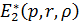 визначена
й внаслідок симетрії відносно діагоналі
визначена
й внаслідок симетрії відносно діагоналі 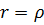 має
структуру:
має
структуру:
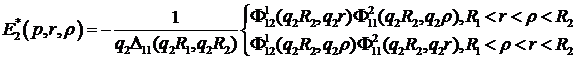 (2.11)
(2.11)
У рівностях (1.15)-(1.17) беруть
участь функції:
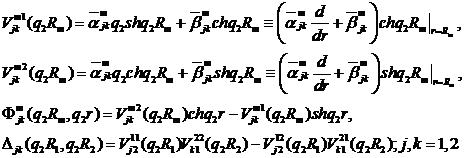
Нехай функція Коші
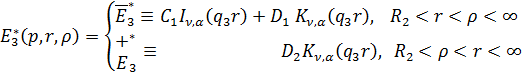
Властивості (1.10) функції Коші
дають алгебраїчну систему з двох рівнянь:
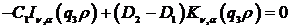
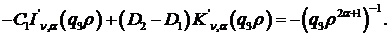
Звідси отримуємо співвідношення:
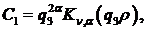
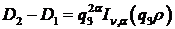 (2.12)
(2.12)
Доповнимо рівності (2.12)
алгебраїчним рівнянням:
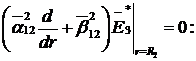
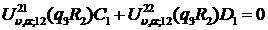 (2.13)
(2.13)
Із алгебраїчної системи (2.12),
(2.13) знаходимо, що
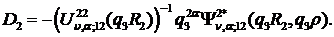
Цим функція Коші 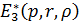 визначена
й внаслідок симетрії відносно діагоналі
визначена
й внаслідок симетрії відносно діагоналі 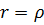 має
структуру:
має
структуру:
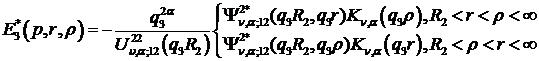 (2.14)
(2.14)
Повернемося до формул (2.6). Умови
спряження (2.5) для визначення величин A1,A2,B2,B3 дають неоднорідну
алгебраїчну систему з чотирьох рівнянь:
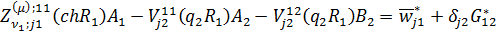 (2.15)
(2.15)
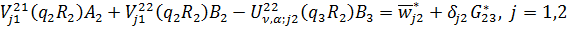
У системі (2.15) беруть участь
функції
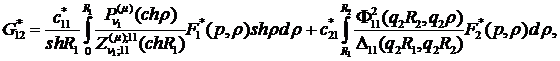
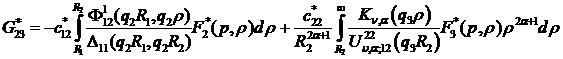
та символ Кронекера 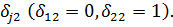
Введемо до розгляду функції:
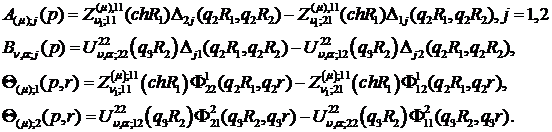
Припустимо, що виконана умова
однозначної розв’язності крайової задачі (2.4), (2.5): для 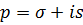 із
із
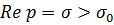 ,
де
,
де 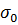 -
абсциса збіжності інтеграла Лапласа, та
-
абсциса збіжності інтеграла Лапласа, та 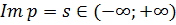 визначник
алгебраїчної системи (2.15) відмінний від нуля:
визначник
алгебраїчної системи (2.15) відмінний від нуля:
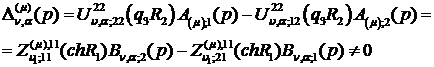 (2.16)
(2.16)
Визначаємо головні розв’язки
крайової задачі (2.4), (2.5):
) породжені неоднорідністю умов
спряження функції Гріна
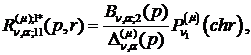
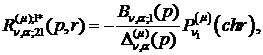
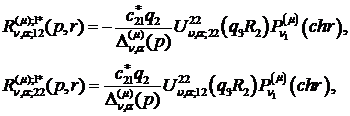
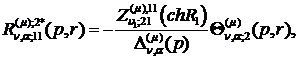
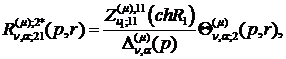
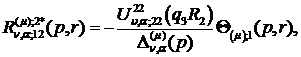
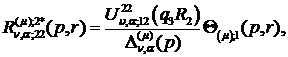
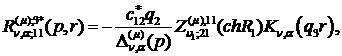 (2.17)
(2.17)
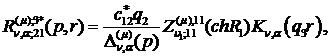
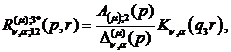
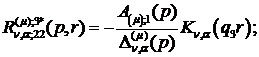
) породжені неоднорідністю системи
функції впливу:
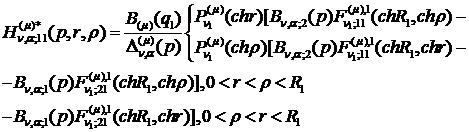
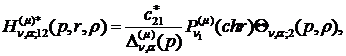
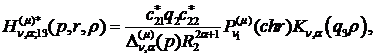
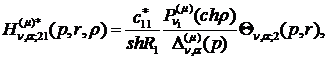
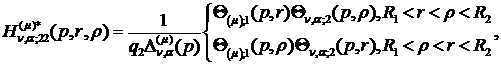
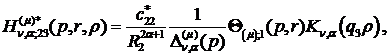 (2.18)
(2.18)
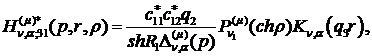
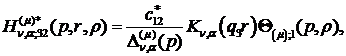
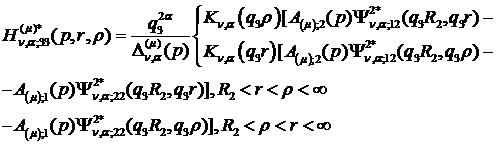
У результаті однозначної
розв’язності алгебраїчної системи (2.15) й підстановки одержаних значень 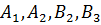 у
рівності (2.6) маємо єдиний розв’язок крайової задачі (2.4), (2.5):
у
рівності (2.6) маємо єдиний розв’язок крайової задачі (2.4), (2.5):
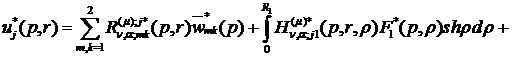
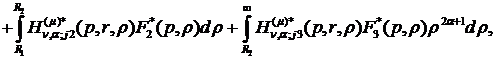
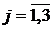 (2.19)
(2.19)
Повертаючись у рівностях (2.19) до
оригіналу, одержуємо єдиний розв’язок параболічної задачі (2.1)-(2.3):
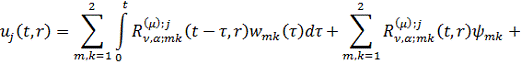
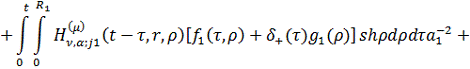
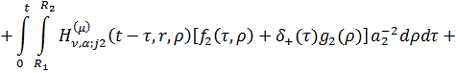
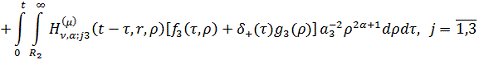
(2.20)
У формулах (2.20) за означенням [5]
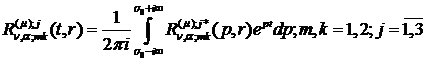 (2.21)
(2.21)
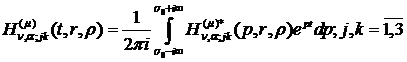 (2.22)
(2.22)
Теорема: Якщо 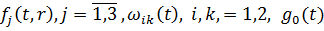 є оригіналом за Лапласом,
є оригіналом за Лапласом, 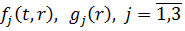 -
двічі неперервно диференційовні за змінною r та задовольняють однорідні умови
спряження, то задача (2.1)-(2.3) має розв’язок
-
двічі неперервно диференційовні за змінною r та задовольняють однорідні умови
спряження, то задача (2.1)-(2.3) має розв’язок 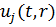 ,
що визначається формулою (2.20), а при виконанні умови однозначної розв’язності
алгебраїчної системи (2.16) він єдиний.
,
що визначається формулою (2.20), а при виконанні умови однозначної розв’язності
алгебраїчної системи (2.16) він єдиний.
Особливими точками функції Гріна 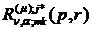 та
функції впливу
та
функції впливу 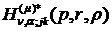 є точки галуження
є точки галуження 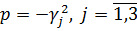 та
та
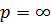 .
Якщо покласти
.
Якщо покласти 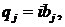 то будемо мати
то будемо мати
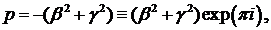
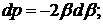
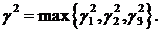
Метод контурного інтегралу з
використанням леми Жордана й теореми Коші [5] приводить формули (2.21), (2.22)
до розрахункових:
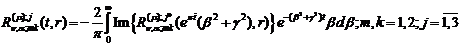 (2.23)
(2.23)
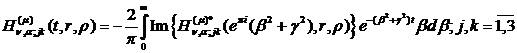 (2.24)
(2.24)
Визначимо величини та функції:
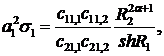
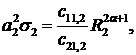
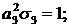
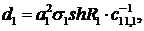
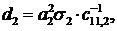
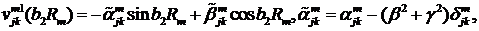
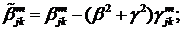
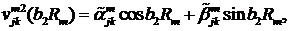
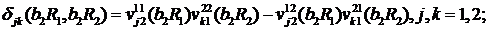
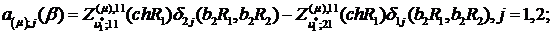
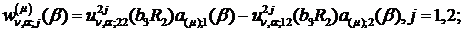
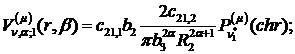
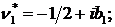
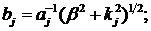
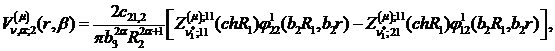
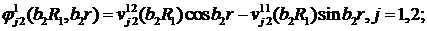
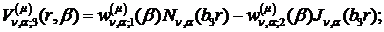
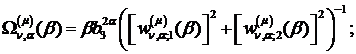
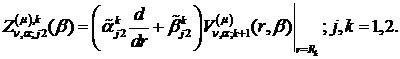
У результаті виконання в рівностях
(2.23), (2.24) зазначених операцій та низки елементарних перетворень отримаємо
функції:
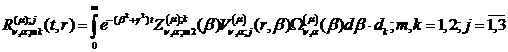 (2.25)
(2.25)
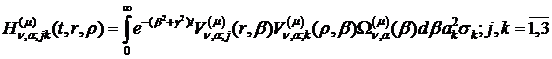 (2.26)
(2.26)
Інтегральне зображення (2.20)
розв’язку задачі (2.1)-(2.3) набуває вигляду:
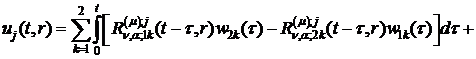
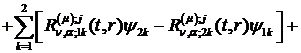
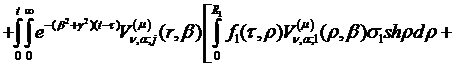
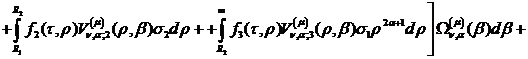
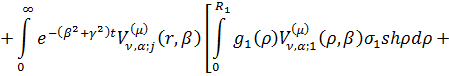
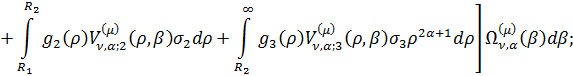
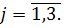 (2.27)
(2.27)
Якщо початкові умови нульові 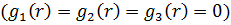 ,
то
,
то 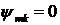 і
формули (2.27) мають вигляд:
і
формули (2.27) мають вигляд:
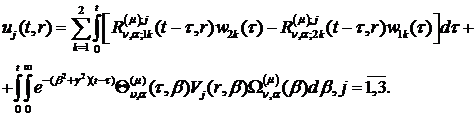 (2.28)
(2.28)
Тут бере участь функція
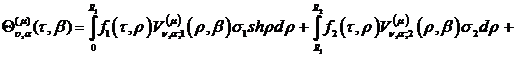
Якщо початкові умови 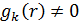 ,
але такі, що
,
але такі, що 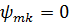 , то в рівностях
(2.27):
, то в рівностях
(2.27):
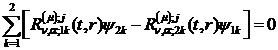
Якщо ж початкові умови 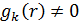 й
й
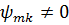 ,
то переходом до нових початкових умов
,
то переходом до нових початкових умов
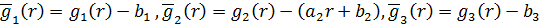
і знаходимо числа 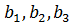 та
та
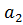 з
алгебраїчної системи рівнянь (1.6). Вони однозначно визначаються за формулами
(1.8).
з
алгебраїчної системи рівнянь (1.6). Вони однозначно визначаються за формулами
(1.8).
Висновок: Вектор-функція 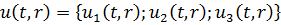 ,
де функції
,
де функції 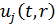 подані формулами
(2.27), визначає єдиний розв’язок параболічної задачі (2.1)-(2.3) та описує
повністю процес теплопровідності, що відбувається в даному середовищі.
подані формулами
(2.27), визначає єдиний розв’язок параболічної задачі (2.1)-(2.3) та описує
повністю процес теплопровідності, що відбувається в даному середовищі.
3. Моделювання процесів
теплопровiдностi в неоднорідних середовищах з м'якими межами методом гібридного
диференціального оператора Лежандра - Фур'є - Бесселя на полярнiй осi 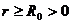
Побудуємо обмежений в області
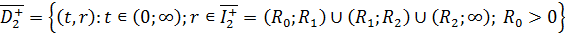
розв’язок сепаратної системи
диференціальних рівнянь теплопровідності параболічного типу [1]
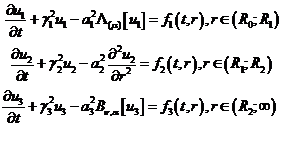 (3.1)
(3.1)
за початковими умовами
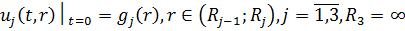 (3.2)
(3.2)
крайовими умовами
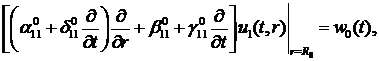
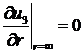 (3.3)
(3.3)
та умовами спряження
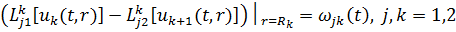 (3.4)
(3.4)
У рівностях (3.1)-(3.4) беруть
участь: 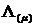 -
диференціальний оператор Лежандра,
-
диференціальний оператор Лежандра, 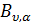 -
диференціальний оператор Бесселя,
-
диференціальний оператор Бесселя, 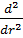 -
диференціальний оператор Фур’є (одновимірний диференціальний оператор Лапласа)
та диференціальні оператори
-
диференціальний оператор Фур’є (одновимірний диференціальний оператор Лапласа)
та диференціальні оператори 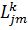 , визначені в
першому параграфі.
, визначені в
першому параграфі.
Припустимо, що виконані умови на
коефіцієнти:
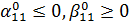
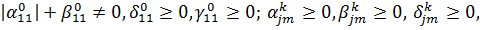
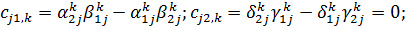
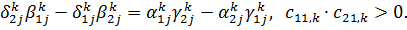
Нехай задані та шукані функції є
оригіналами Лапласа стосовно t [5].
У зображенні за Лапласом одержуємо
крайову задачу: побудувати обмежений на множині 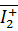 розв’язок
сепаратної системи звичайних диференціальних рівнянь Лежандра, Фур’є та Бесселя
для модифікованих функцій
розв’язок
сепаратної системи звичайних диференціальних рівнянь Лежандра, Фур’є та Бесселя
для модифікованих функцій
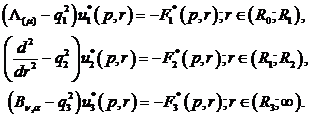 (3.5)
(3.5)
за крайовими умовами
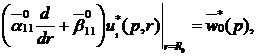
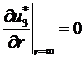 (3.6)
(3.6)
та
умовами спряження
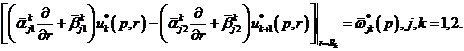 (3.7)
(3.7)
У рівностях (3.5)-(3.7) прийняті
позначення:
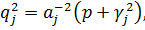
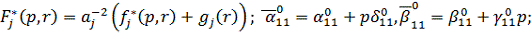
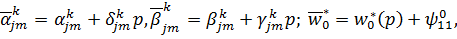
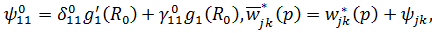
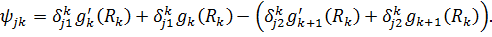
Можна вважати, що 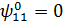 і
і
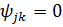 .
Якщо не так, то переходимо до нових початкових даних:
.
Якщо не так, то переходимо до нових початкових даних:
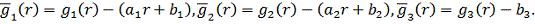
Невідомі величини 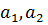 та
та
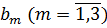 знаходимо
із неоднорідної алгебраїчної системи з п’яти рівнянь:
знаходимо
із неоднорідної алгебраїчної системи з п’яти рівнянь:
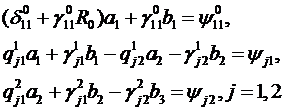 (3.8)
(3.8)
Тут прийняті позначення:
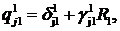
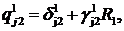
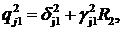
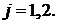
При виконанні умов на коефіцієнти
алгебраїчна система (3.8) сумісна й має єдиний розв’язок.
Наявність фундаментальної системи
розв’язків дозволяє побудувати розв’язок крайової задачі(3.5)-(3.7) методом
функцій Коші [4,7]:
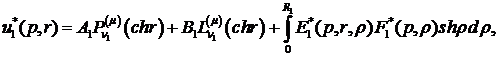
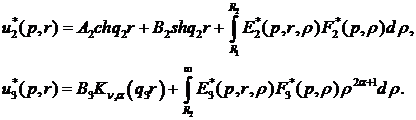 (3.9)
(3.9)
Тут 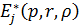 -
функції Коші [4,7];
-
функції Коші [4,7]; 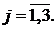
Припустимо, що функція Коші
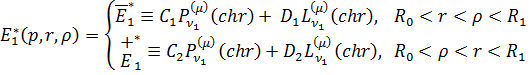
Властивості (1.10) функції Коші
дають алгебраїчну систему:
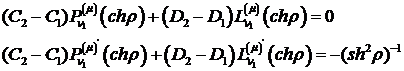
Звідси отримуємо співвідношення:
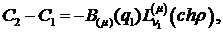
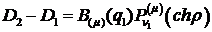 (3.10)
(3.10)
Доповнимо рівності (3.10)
алгебраїчними рівняннями:
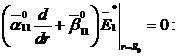
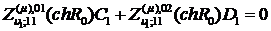
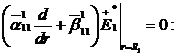
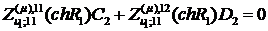 (3.11)
(3.11)
Внаслідок співвідношень (3.10)
алгебраїчна система (3.11) набуває вигляду:
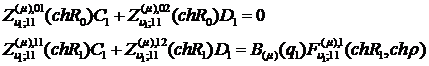 (3.12)
(3.12)
Розв’язуємо
алгебраїчну систему (3.12) за правилами Крамера [6]:
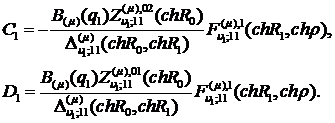
Цим функція Коші 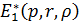 визначена
й внаслідок симетрії відносно діагоналі
визначена
й внаслідок симетрії відносно діагоналі 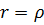 має
структуру:
має
структуру:
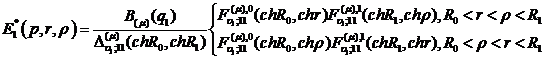 (3.13)
(3.13)
Тут прийнято позначення:
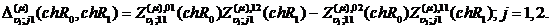
Згідно формули (2.11) функція Коші
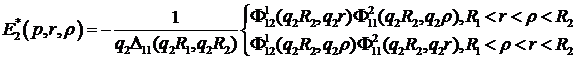 (3.14)
(3.14)
Згідно формули (2.14) функція Коші
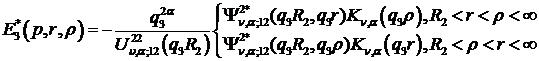 (3.15)
(3.15)
Крайова умова в точці 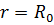 й умови спряження (3.7) для визначення величин
й умови спряження (3.7) для визначення величин 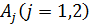 та
та
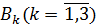 дають
неоднорідну алгебраїчну систему з п’яти рівнянь:
дають
неоднорідну алгебраїчну систему з п’яти рівнянь:
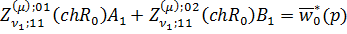
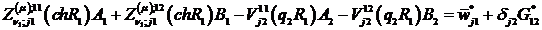
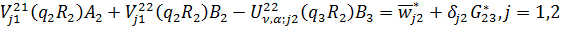 (3.16)
(3.16)
В алгебраїчній системі (3.16) беруть
участь функції
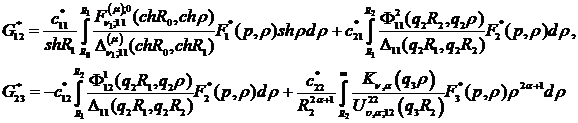
та символ Кронекера 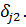
Введемо до розгляду функції:
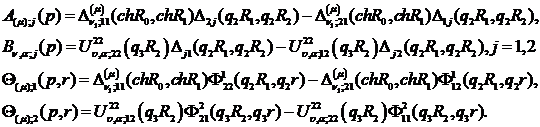
Припустимо, що виконана умова
однозначної розв’язності крайової задачі (3.5)-(3.7): для 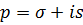 із
із
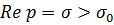 ,
де
,
де 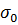 -
абсциса збіжності інтеграла Лапласа, та
-
абсциса збіжності інтеграла Лапласа, та 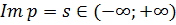 визначник
алгебраїчної системи (3.16) відмінний від нуля
визначник
алгебраїчної системи (3.16) відмінний від нуля
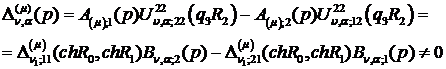 (3.17)
(3.17)
Визначаємо головні розв’язки
крайової задачі (3.5)- (3.7):
) породжені неоднорідністю крайової
умови в точці 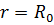 функції Гріна:
функції Гріна:
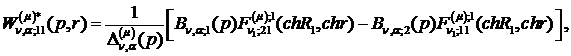 (3.18)
(3.18)
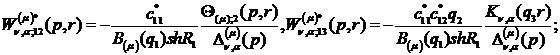
) породжені неоднорідністю умов
спряження функції Гріна:
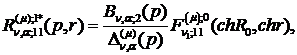
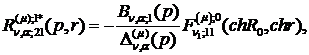
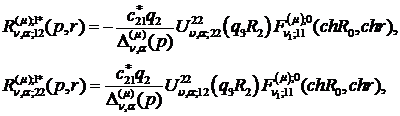
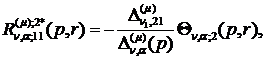
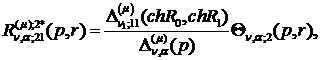
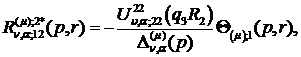
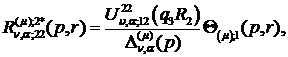
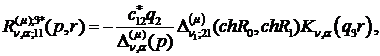 (3.19)
(3.19)
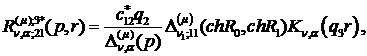
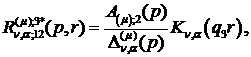
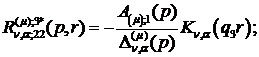
) породжені неоднорідністю системи
(3.5) функції впливу:
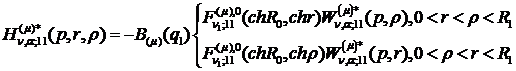
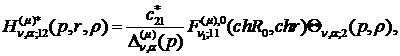
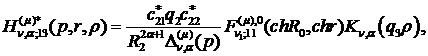
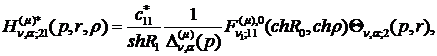
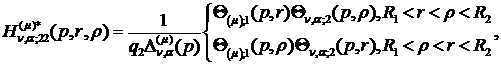
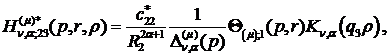 (3.20)
(3.20)
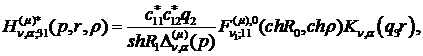
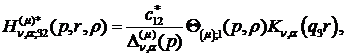
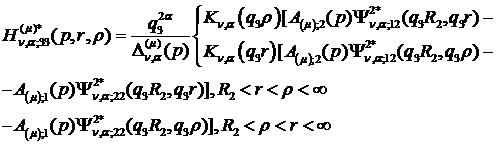
У результаті однозначної
розв’язності алгебраїчної системи (3.16) й підстановки одержаних значень 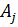 та
та
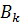 у
формули (3.9) маємо єдиний розв’язок крайової задачі (3.5)-(3.7):
у
формули (3.9) маємо єдиний розв’язок крайової задачі (3.5)-(3.7):
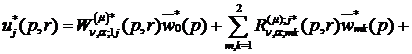
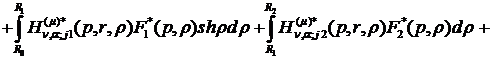
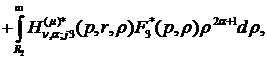
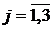 (3.21)
(3.21)
Повертаючись до оригіналу, маємо
єдиний розв’язок параболічної задачі (3.1)-(3.4):
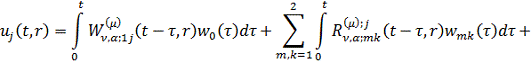
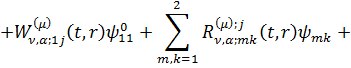
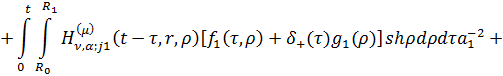
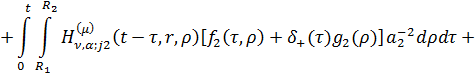
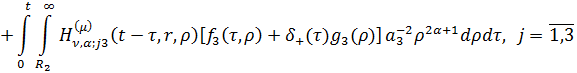
(3.22)
У рівностях (3.22) за означенням [5]
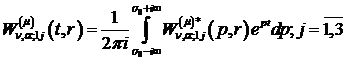 (3.23)
(3.23)
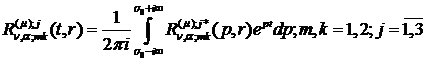 (3.24)
(3.24)
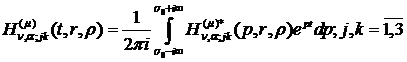 (3.25)
(3.25)
Теорема:
Якщо 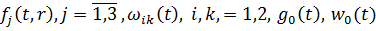 є
оригіналом за Лапласом,
є
оригіналом за Лапласом, 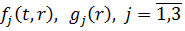 - двічі неперервно
диференційовні за змінною r та задовольняють однорідні умови спряження, то
задача (3.1)-(3.4) має розв’язок
- двічі неперервно
диференційовні за змінною r та задовольняють однорідні умови спряження, то
задача (3.1)-(3.4) має розв’язок 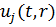 ,
що визначається формулою (3.22), а при виконанні умови однозначної розв’язності
алгебраїчної системи (3.16) він єдиний.
,
що визначається формулою (3.22), а при виконанні умови однозначної розв’язності
алгебраїчної системи (3.16) він єдиний.
Особливими точками функцій 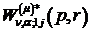 ,
,
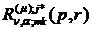 та
та
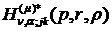 є
точки галуження
є
точки галуження 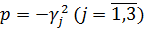 й точка
й точка 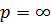 .
.
Якщо знову покласти 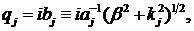 при
при
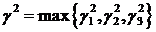 знаходимо,
що
знаходимо,
що 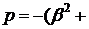
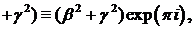
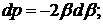
Використовуючи метод контурного
інтегралу, лему Жордана й теорему Коші, приходимо до розрахункових формул:
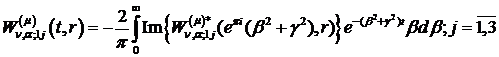 (3.26)
(3.26)
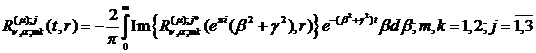
(3.27)
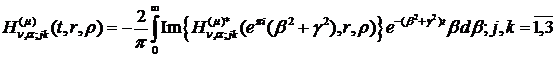 (3.28)
(3.28)
Тут 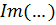 означає
уявну частину виразу
означає
уявну частину виразу 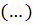 .
.
Визначимо величини та функції:
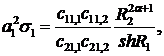
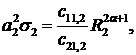
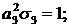
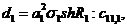
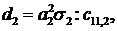
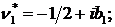
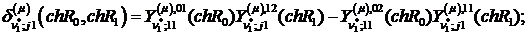
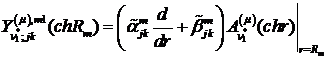 ,
,
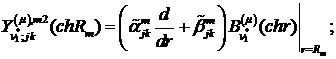
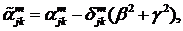
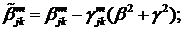
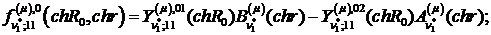
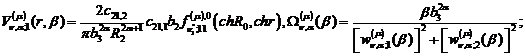
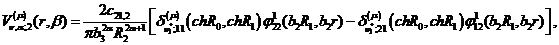
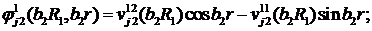
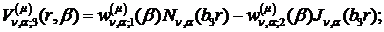
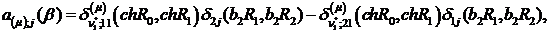
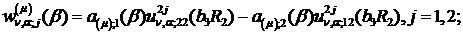
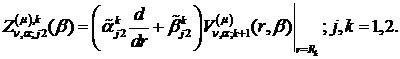
Всі інші функції відомі [2,8].
У результаті виконання зазначених в
рівностях (3.26)-(3.28) операцій одержуємо функції:
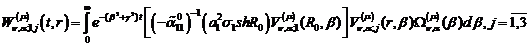
(3.29)
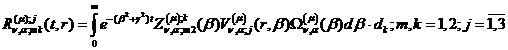 (3.30)
(3.30)
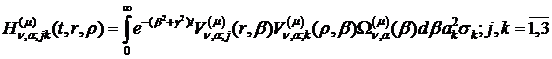 (3.31)
(3.31)
Якщо прийняти до уваги, що
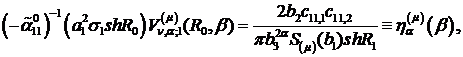
то формула (3.29) набуде вигляду:
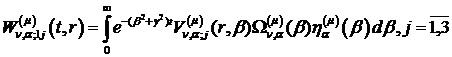 (3.32)
(3.32)
Введемо до розгляду функції:
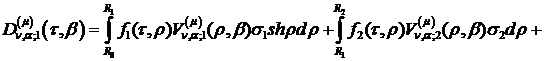
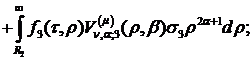
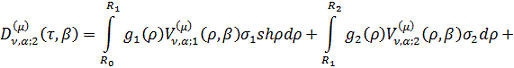
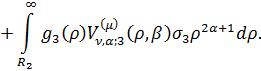
Інтегральне зображення (3.22)
аналітичного розв’язку параболічної задачі (3.1)-(3.4) буде мати структуру:
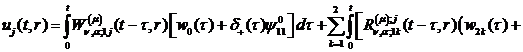
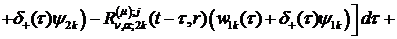
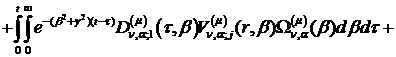
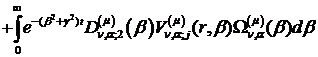 ,
, 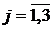 (3.33)
(3.33)
Тут 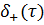 -
дельта-функція, зосереджена в точці
-
дельта-функція, зосереджена в точці 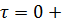 [7].
[7].
Якщо початкові умови нульові
(практично це завжди так), то розв’язком параболічної задачі (3.1)-(3.4) є
функції
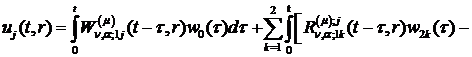
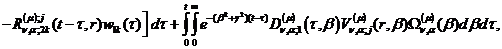
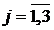 (3.34)
(3.34)
Якщо початкові умови підібрані так,
що 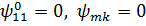 ,
то в функції
,
то в функції 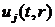 мають структуру
(3.33) при
мають структуру
(3.33) при 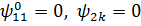 та
та 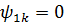 .
.
Набір функцій 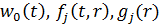 та
та
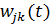 дозволяє
варіювати процесом теплопровідності в даному середовищі. Розв’язок даної задачі
дозволяє
варіювати процесом теплопровідності в даному середовищі. Розв’язок даної задачі
 поліпараметричний
та має замкнутий алгоритмічний характер. Це дає змогу використовувати його як в
числових розрахунках, так і в теоретичних дослідженнях.
поліпараметричний
та має замкнутий алгоритмічний характер. Це дає змогу використовувати його як в
числових розрахунках, так і в теоретичних дослідженнях.
. Моделювання процесiв
теплопровiдностi в неоднорiдних середовищах з м'якими межами методом гiбридного
диференцiального оператора Лежандра - Бесселя - Фур'є на полярнiй осi 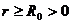
Побудуємо обмежений в області 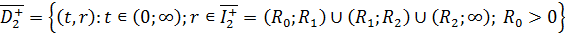 розв’язок
сепаратної системи диференціальних рівнянь теплопровідності параболічного типу
[1]
розв’язок
сепаратної системи диференціальних рівнянь теплопровідності параболічного типу
[1]
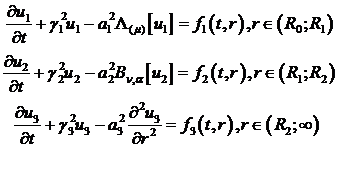 (4.1)
(4.1)
за початковими умовами
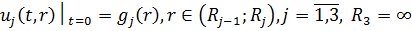 (4.2)
(4.2)
крайовими умовами
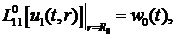
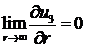 (4.3)
(4.3)
та умовами спряження
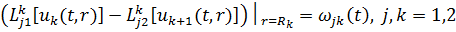 (4.4)
(4.4)
У рівностях (4.1)-(4.4) беруть
участь диференціальні оператори Лежандра 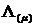 , Бесселя
, Бесселя 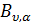 ,
Фур’є
,
Фур’є 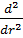 та
диференціальні оператори
та
диференціальні оператори
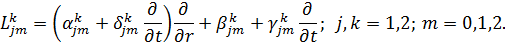
Умови на коефіцієнти наведені в
попередньому параграфі.
Нехай задані та шукані функції є
оригіналами Лапласа стосовно t [5]. У зображенні за Лапласом одержуємо крайову
задачу: побудувати обмежений на множині 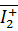 розв’язок
сепаратної системи звичайних диференціальних рівнянь Лежандра, Бесселя та Фур’є
для модифікованих функцій
розв’язок
сепаратної системи звичайних диференціальних рівнянь Лежандра, Бесселя та Фур’є
для модифікованих функцій
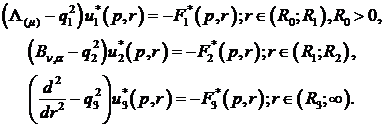 (4.5)
(4.5)
за крайовими умовами
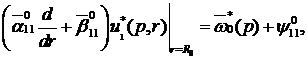
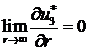 (4.6)
(4.6)
та
умовами спряження
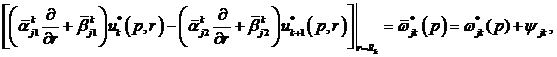
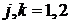 . (4.7)
. (4.7)
Будемо в подальшому вважати, що 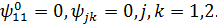
Наявність фундаментальної системи
розв’язків дозволяє побудувати розв’язок крайової задачі(4.5)-(4.7) методом
функцій Коші [4,7]:
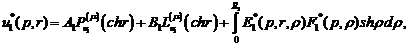
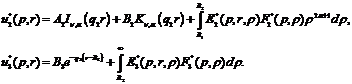 (4.8)
(4.8)
Тут 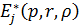 -
функції Коші [4,7];
-
функції Коші [4,7]; 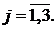
Згідно формули (3.13) функція Коші
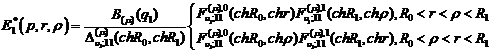 (4.9)
(4.9)
Згідно формули (1.17) функція Коші
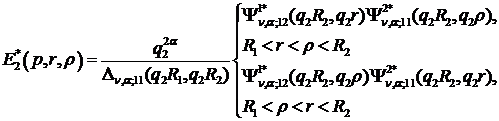 (4.10)
(4.10)
Згідно формули (1.20) функція Коші
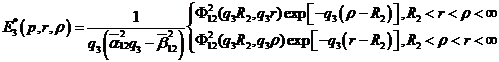 (4.11)
(4.11)
Крайова умова в точці 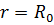 й
умови спряження (4.7) для визначення величин
й
умови спряження (4.7) для визначення величин 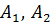 та
та
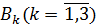 дають
неоднорідну алгебраїчну систему з п’яти рівнянь:
дають
неоднорідну алгебраїчну систему з п’яти рівнянь:
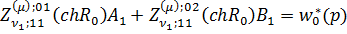
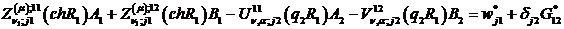
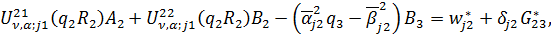
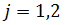 (4.12)
(4.12)
У системі (4.12) беруть участь
функції
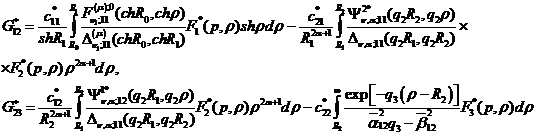
та символ Кронекера 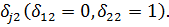
Введемо до розгляду функції:
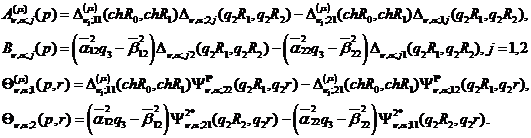
Припустимо, що виконана умова
однозначної розв’язності крайової задачі (4.5)-(4.7): для 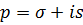 із
із
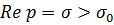 ,
де
,
де 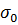 -
абсциса збіжності інтеграла Лапласа та
-
абсциса збіжності інтеграла Лапласа та 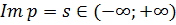 визначник
алгебраїчної системи (4.12) відмінний від нуля
визначник
алгебраїчної системи (4.12) відмінний від нуля
 (4.13)
(4.13)
Визначаємо головні розв’язки
крайової задачі (4.5)- (4.7):
) породжені неоднорідністю крайової
умови в точці 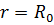 функції Гріна
функції Гріна
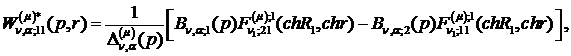
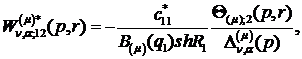 (4.14)
(4.14)
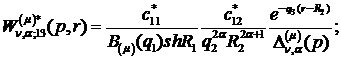
) породжені неоднорідністю умов
спряження функції Гріна:
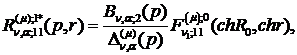
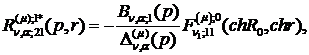
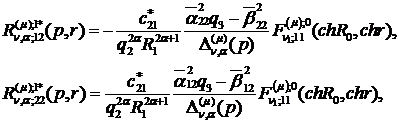
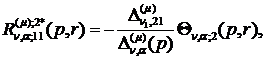
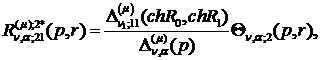
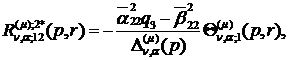
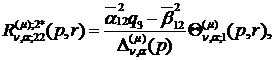
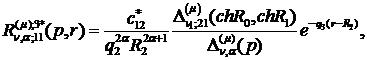 (4.15)
(4.15)
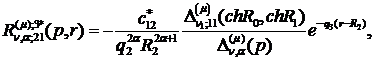
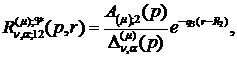
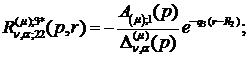
) породжені неоднорідністю системи
функції впливу:
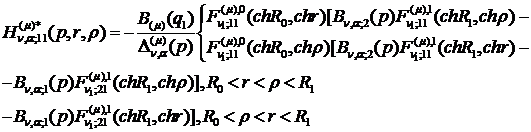
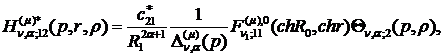
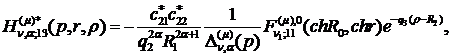
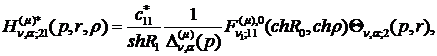
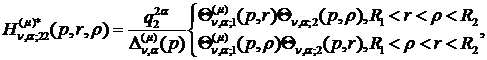
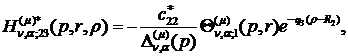 (4.16)
(4.16)
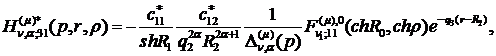
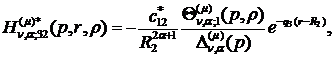
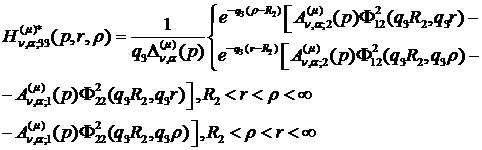
У результаті однозначної розв’язності
алгебраїчної системи (4.12) й підстановки одержаних значень величин 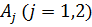 та
та
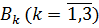 у
рівності (4.8) маємо єдиний розв’язок крайової задачі (4.5)-(4.7):
у
рівності (4.8) маємо єдиний розв’язок крайової задачі (4.5)-(4.7):
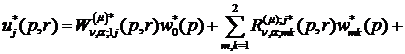
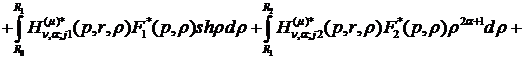
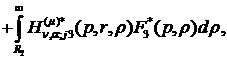
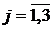 (4.17)
(4.17)
Перейшовши у формулах (4.17) до
оригіналу, маємо єдиний розв’язок параболічної задачі (4.1)-(4.4):
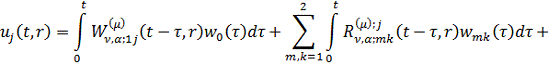
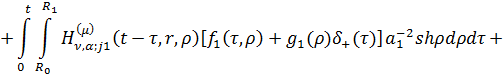
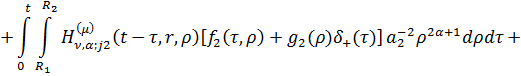
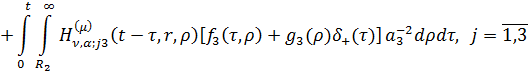
(4.18)
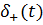 - дельта-функція,
зосереджена в точці
- дельта-функція,
зосереджена в точці 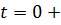 [7].
[7].
У формулах (4.18) за означенням [5]
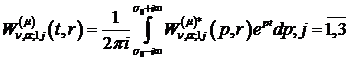 (4.19)
(4.19)
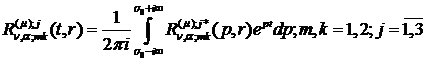 (4.20)
(4.20)
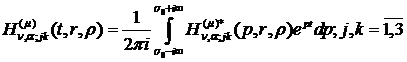 (4.21)
(4.21)
Теорема: Якщо 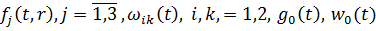 є
оригіналом за Лапласом,
є
оригіналом за Лапласом, 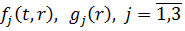 - двічі неперервно
диференційовні за змінною r та задовольняють однорідні умови спряження, то
задача (4.1)-(4.4) має розв’язок
- двічі неперервно
диференційовні за змінною r та задовольняють однорідні умови спряження, то
задача (4.1)-(4.4) має розв’язок 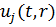 ,
що визначається формулою (4.18), а при виконанні умови однозначної розв’язності
алгебраїчної системи (4.12) він єдиний.
,
що визначається формулою (4.18), а при виконанні умови однозначної розв’язності
алгебраїчної системи (4.12) він єдиний.
Особливими точками функцій Гріна 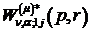 ,
,
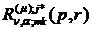 та
функцій впливу
та
функцій впливу 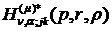 є точки галуження
є точки галуження 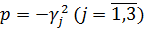 та
та
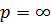 .
Якщо покласти
.
Якщо покласти 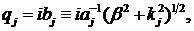 то одержимо, що
при
то одержимо, що
при 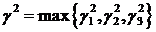
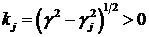 й
й
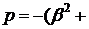
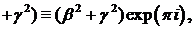
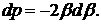
Вирази (4.19), (4.20) та (4.21)
методом контурного інтегралу в поєднанні з лемою Жордана й теореми Коші
перетворюємо до розрахункових формул:
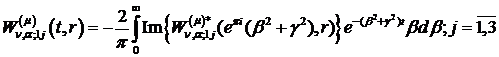 (4.22)
(4.22)
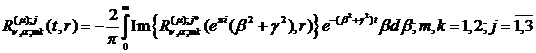
(4.23)
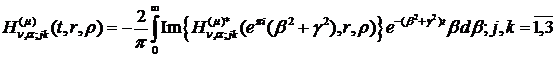 (4.24)
(4.24)
Тут 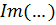 означає
уявну частину виразу
означає
уявну частину виразу 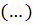 .
.
Визначимо величини та функції:
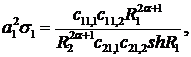
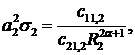
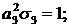
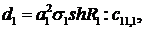
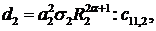
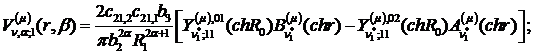
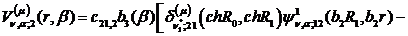
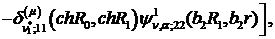
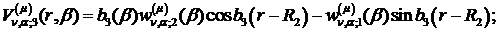
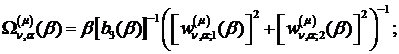
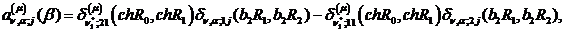
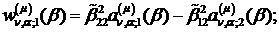
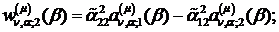
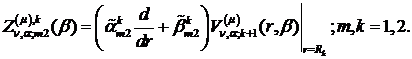
У результаті виконання в рівностях
(4.22)-(4.24) зазначених операцій одержуємо функції:
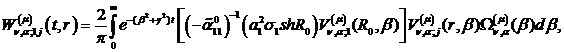
(4.25)
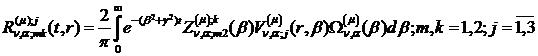 (4.26)
(4.26)
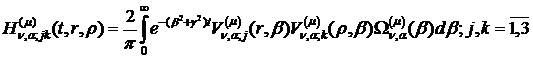 (4.27)
(4.27)
Розв’язком параболічної задачі
(4.1)-(4.4) є функції:
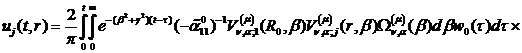
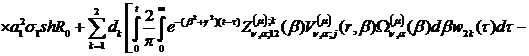
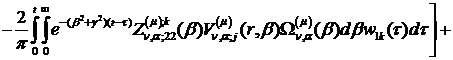
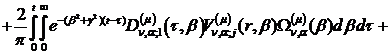
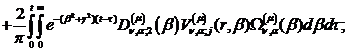
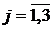 (4.28)
(4.28)
У рівностях (4.28) беруть участь
функції:
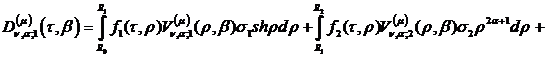
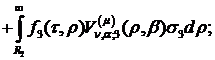
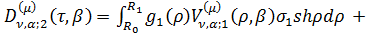
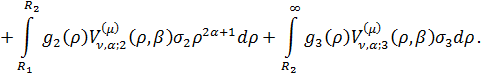
Зауваження 1. Якщо 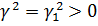 ,
то
,
то 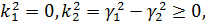
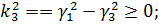 якщо
якщо
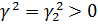 ,
то
,
то 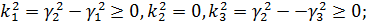 якщо
якщо
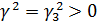 ,
то
,
то 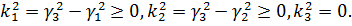
Зауваження 2. Якщо початкові умови
ненульові, то в рівності (4.28) присутні ще доданки
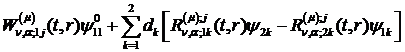
в припущенні, що не переходимо до
нових початкових умов.
Зауваження 3. Якщо початкові умови
нульові, то 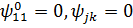 та
та 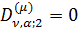 .
.
Зауваження 4. Набір функцій 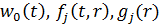 та
та
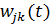 дають
можливість регулювати процес передачі тепла в даному середовищі.
дають
можливість регулювати процес передачі тепла в даному середовищі.
Зауваження 5. Вектор-функція 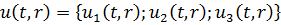 ,
де функції
,
де функції 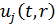 визначені формулою
(4.28), повністю описує процес теплопровідності. Одержаний розв’язок задачі
поліпараметричний та має алгоритмічний характер. Його можна використовувати як
в теоретичних дослідження, так і в числових розрахунках. Вибором параметрів
безпосередньо можна одержати структуру головних розв’язків (а, значить, і
розв’язку) для найбільш важливих практичних випадків ( в рамках даної моделі).
визначені формулою
(4.28), повністю описує процес теплопровідності. Одержаний розв’язок задачі
поліпараметричний та має алгоритмічний характер. Його можна використовувати як
в теоретичних дослідження, так і в числових розрахунках. Вибором параметрів
безпосередньо можна одержати структуру головних розв’язків (а, значить, і
розв’язку) для найбільш важливих практичних випадків ( в рамках даної моделі).
. Охорона праці
. Загальні питання охорони праці
Охорона праці - це система правових,
соціально-економічних, організаційно-технічних, санітарно-гігієнічних і лікувально-профілактичних
заходів та засобів, спрямованих на збереження життя, здоров'я і працездатності
людини у процесі трудової діяльності [10].
Вагомий вплив на працездатність і
здоров’я користувачів комп’ютерів робить виробниче середовище, яке у виробничих
приміщення (офісах), в основному, визначається мікрокліматом, освітленням,
наявністю шкідливих речовин у повітрі, рівнем шуму та випромінюванням.
Під виробничим приміщенням розуміють
замкнутий простір в спеціально призначених будівлях і спорудах, в яких постійно
(по змінах) або періодично (протягом робочого дня) здійснюється трудова
діяльність людей.
Виробничі приміщення для роботи з
візуально-дисплейними терміналами (ВДТ) повинні відповідати СНиП 2.09.02-85
"Производственные здания", СНиП 2.01.02-85 "Противопожарные
нормы" та низці інших нормативних документів [10], [11].
Враховуючи специфіку зорової роботи
з ВДТ найбільш придатними є приміщення з одностороннім розташуванням вікон,
причому бажано, щоб площа засклення не перевищувала 25-50%. Найкраще, коли
вікна зорієнтовані на північ чи північний схід. Вікна необхідно обладнати
регульованими пристроями (жалюзі, завіски, зовнішні козирки). Щоб виключити
попадання відбитих відблисків в очі користувачів, поверхні в приміщенні повинні
мати матову чи напівматову фактуру. Коефіцієнт відбиття має становити: для
стелі 0,7-0,8; стін - 0,5-0,6; підлоги - 0,3-0,5; інших поверхонь - 0,4-0,5.
Вимоги стосовно виробничих
приміщень, в яких встановлені ВДТ ПК відображені в ДНАОП 0.00-1.31-99 та
ДСанПіН 3.3.2-007-98 [10]. Відповідно до цих нормативних документів,
неприпустиме розташування приміщень призначених для роботи з ВДТ, у підвалах і
цокольних поверхах. Поверхня підлоги має бути рівною, неслизькою, зручною для
очищення та вологого прибирання, мати антистатичні властивості. У приміщеннях з
ВДТ найкращим вважається покриття підлоги антистатичним лінолеумом.
Внутрішнє оздоблення приміщень з ВДТ
здійснюється матеріалами, які не виділяють у повітря шкідливих, хімічних
речовин і дозволені органами та установами державної санітарно-епідеміологічної
служби.
Для забезпечення нормованих значень
мікроклімату, вмісту шкідливих речовин, іонного складу повітря приміщення для
роботи з ВДТ мають бути обладнані системами опалення, кондиціювання повітря або
припливно-витяжною вентиляцією.
Відповідно до ГОСТ 12.1.005-88 в
повітрі робочої зони вміст озону не повинен перевищувати 0,03 мг/м3; вміст
оксидів азоту - 5 мг/м3; вміст пилу 4 мг/м3.
Відповідно до ДНАОП 0.00-1.31-99
поверхневий електростатичний потенціал відеотерміналу не повинен перевищувати
500 В. Напруженість електростатичного поля на робочих місцях, в тому числі й з
ВДТ, не повинна перевищувати 20 кВ/м, відповідно до ГОСТ 12.1.045-84
"ССБТ. Электростатические поля. Допустимые уровни на рабочих местах й
требования к проведению контроля" [10].
Відповідно до ДНАОП 0.00-1.31-99
освітлення у приміщеннях з ВДТ має бути суміщеним, при якому недостатнє за
нормами природне освітлення доповнюється штучним. Природне освітлення повинно
бути боковим, бажано одностороннім. Для уникнення засліплюючої дії сонячних
променів найкраще, коли світлові отвори (вікна) зорієнтовані на північ чи
північних схід. Коефіцієнт природної освітленості (КПО) повинен бути не нижче
1,5%, у відповідності до вимог СНиП 11-4-79 "Естественное й искусственное
освещение. Нормы проектирования" [10].
ДНАОП 0.00-1.31-99 регламентує
вимоги до організації робочого місця користувача ВДТ. Найкраще розмістити
робочі місця з ВДТ рядами, причому відносно вікон, вони повинні розміщуватися
так, щоб природне світло падало збоку, переважно зліва. Це дасть змогу
виключити дзеркальне відбиття на екрані джерел природного світла (вікон) та
потрапляння останніх в поле зору користувачів.
Організація робочого місця
користувача ВДТ повинна забезпечувати відповідність усіх елементів робочого
місця та їх взаємного розташування ергономічним вимогам ГОСТ 12.2.032 - 78
"ССБТ. Рабочее место при выполнении работ сидя. Общие эргономические
требования" [10], характеру та особливостям трудової діяльності.
Площа, виділена для одного робочого
місця з ВДТ або ПК, повинна складати не менше 6 м2, а об’єм - не менше 20 м3.
При розміщенні робочих місць необхідно дотримуватись таких вимог:
– робочі місця з ВДТ розміщуються
на відстані не менше 1 м від стін зі світловими прорізами;
– відстань між бічними
поверхнями відеотерміналів має бути не меншою за 1,2 м;
– відстань між тильною
поверхнею одного відеотерміналу та екраном іншого не повинна бути меншою 2,5м;
– прохід між рядами робочих
місць має бути не меншим 1 м.
Робочий стіл для ВДТ, як правило,
має бути обладнаним підставкою для ніг шириною не менше 300 мм та глибиною не
менше 400 мм, з можливістю регулювання по висоті в межах 150 мм та кута нахилу
опорної поверхні - в межах 20°. Підставка повинна мати рифлену поверхню та
бортик на передньому краї заввишки 10 мм. Застосування підставки для ніг тими,
у кого ноги не дістають до підлоги, коли робоче сидіння знаходиться на висоті,
потрібній для забезпечення оптимальної робочої пози, є обов’язковим.
Конструкція робочого стільця має
забезпечувати підтримання раціональної робочої пози під час виконання основних
виробничих операцій, створювати умови для зміни пози. Тому стілець повинен бути
підйомно-поворотним і регулюватися по висоті та кутах нахилу сидіння і спинки,
а також відстані спинки від переднього краю сидіння, висоті підлокітників.
Згідно діючим класифікаторам
професій - ДК-003-95, зміни (№1 до ДК-003-95) режим роботи користувача за
розробленою програмою - це оператори електронно-обчислювальних машин виконують
роботу, що пов’язана з тестуванням програмних моделей електронних схем
супроводжується перервами різної тривалості, пов’язана з виконанням іншої
роботи і характеризується як робота з напруженням зору, невеликим фізичними
зусиллями, нервовим напруженням середнього ступеня та виконується у вільному
темпі.
Графік відпочинку та
психофізіологічного розвантаження, відповідно санітарним правилам,
встановлюється при роботі з ПК тривалістю 15 хвилин через кожні дві години
(8-годинний робочий день). Про це працівника повідомляють під час проведення
інструктажів на робочому місці з метою ознайомлення з діючими інструкціями по
охороні праці для даної професії. При дотриманні правил техніки безпеки
забезпечується збереження здоров’я працівника на великий термін, зменшується
ризик професійних захворювань, збільшується час продуктивної роботи працівника.
2. Промислова санітарія
Продуктивність праці багато в чому
залежить від умов на виробництві, таких як: освітлення, склад повітря, шуми,
шкідливі випромінювання. Ці параметри по окремості й у комплексі впливають на
організм людини, визначаючи його самопочуття. Категорію роботи враховуємо по
фізичному навантаженню.
Робота на ПЕОМ не вимагає фізичної
напруги. Енерговитрати не перевищують 172 Дж/с. Робота з розробки відноситься
до категорії Iа (легка), тобто витрата енергії при виконанні роботи до 120
ккал/година і не вимагає фізичної напруги.
Відповідно до ГОСТ 12.1.005 - 88
ССБТ "Общие санитарно-гигиенические требования к воздуху рабочей
зоны" [10] оптимальні параметри мікроклімату для виконання роботи повинні
знаходитися в межах, зазначених у табл. 5.1. Параметри є оптимальними, тому що
категорія роботи напружена (розумова).
Таблиця 5.1.
Допустимі (оптимальні) параметри
мікроклімату
|
Категорія роботи
|
Період року
|
Температура t, c
|
Відносна вологість, Ф,%
|
Швидкість руху повітря V, м/с
|
|
Легка робота Iа
|
холодний
|
22...24
|
40...60
|
0,1
|
|
Легка робота Iа
|
теплий
|
23...25
|
40...60
|
0,1-0.2
|
Для забезпечення вище вказаних
оптимальних кліматичних умов у приміщенні передбачена система опалення
(загальне парове), вентиляції (загальна, приточно-витяжна, штучна) і
кондиціонування згідно СНІП 2.04.05-86 "Отопление, вентиляция,
кондиционирование".
Режим роботи кондиціонера повинний
забезпечити максимально можливе надходження зовнішнього повітря, але не менш
60% від продуктивності кондиціонера.
При проектуванні дисплейних класів
вузів необхідно передбачати приточно-витяжну вентиляцію.
Подача повітря повинна вироблятися у
верхню зону малими швидкостями з розрахунку створення рухливості повітря на
робочому місці не менш 0,1 м/с, краще через підшивну гофровану стелю.
Витяжка - природна з верхньої зони
стіни, протилежної віконним прорізам.
Якісний склад повітря: зміст кисню в
дисплейному класі повинне бути в межах 21-22 про. %.
Працездатність оператора багато в
чому залежить від освітлення. Незадовільне освітлення кількісно або якісно
стомлює не тільки зір, але і викликає стомлення організму в цілому, впливає на
продуктивність праці оператора.
Для забезпечення нормального
освітлення застосовуються природне і штучне освітлення, а також змішане, котрі
нормуються санітарними нормами і правилами СНИП II-4-79 "Естественное и
искусственное освещение. Нормы проектирования" [10]. В світлий час доби
використовується - природне, суміщене типи; а в темний час дня - штучне.
ЕЛТ генерує декілька типів
випромінювання, у тому числі: гама тормозне, рентгенівське, радіочастотне,
мікроволнове, видиме, ультрафіолетове й інфрачервоне випромінювання.
Рівні цих випромінювань не
перевищують діючих норм. Конструктивне рішення екрана дисплея таке, що
рентгенівське випромінювання від екрана на відстані 10 см не перевищує 100
мк/ч. У приміщеннях з дисплеями необхідно контролювати аероіонізацію (див.
табл. 5.2).
Таблиця 5.2.
Рівні іонізації повітря приміщень
|
Рівні
|
Число іонів в 1 см куб. повітря
|
Організаційно-технічні засоби захисту
|
|
n+
|
n-
|
Коефіцієнт полярності повинен знаходитися від
-0,5 до 0, згідно з нормами "Санітарно-гігієнічні норми допустимих
рівнів іонізації повітря виробничих і суспільних помешкань". Варто
враховувати, що м'яке рентгенівське випромінювання, що виникає при напрузі на
аноді 20-22 кВ, а також напруга на струмоведучих ділянках схеми викликає
іонізацію повітря з утворенням позитивних іонів, що вважаються несприятливими
для людини.
|
|
Мінімально необхідні
|
400
|
600
|
|
|
Оптимальні
|
1500 - 3000
|
30000 - 50000
|
|
|
Максимально допустимі
|
50000
|
50000
|
|
Таблиця 5.3.
Допустимі параметри електромагнітних
неіонізуючих випромінювань і електричного поля
|
Види поля
|
Допустимі параметри поля
|
Допустима поверхнева щільність потоку енергії
Вт/м2
|
Організаційно-технічні заходи захисту
|
|
Електрична складова Е, В/м
|
Магнітна складова Н, А/м
|
|
|
|
Напруженість электро- -магнітного поля 60 кГц
- 3 мГц 3 кГц - 30 мГц 30 кГц - 50 мГц 30 кГц- 300 мГц 300 кГц -300гГц
|
50 20 10 5 -
|
5 - 0,3 - -
|
10 Вт/м2
|
для розробників програм із застосуванням ЕОМ,
призначати регламентовану перерву для відпочинку тривалістю 15 хвилин через
кожну годину роботи за ВДТ
|
|
Електромагнітне поле оптичного діапазону
ультрафіолетовою частини спектру: УФ-С(220-280 гг) УФ-В(280-320 гг)
УФ-А(320-400 гг) у видимій частині спектру: 400-760 мм у інфрачервоній
частині спектру: 0,76-10,0 мкм
|
-
|
-
|
0,001 0,01 10,0 10,0 35,0-70,0
|
коли виробничі обставини не дозволяють
застосувати регламентовані перерви тривалість безперервної роботи з ВДТ не
повинна перевищувати 4 години. зміна характеру праці, чергування з іншими
видами діяльності, не пов'язаними з ВДТ
|
3. Електробезпека
Експлуатований ПК не є джерелом
механічних і теплових небезпек, але приміщення, де перебувають ЕОМ, є
однофазним споживачем електроенергії від трифазної мережі змінного струму
напругою 220 В частотою 50 Гц. Відповідно ГОСТ 12.2.007.0-75 "Изделия
электротехнические. Общие требования безопасности" [10] приймаємо I клас
захисту від поразки електричним струмом обслуговуючого персоналу тому, що
комп'ютер має робочу ізоляцію й елементи заземлення.
Причини поразки електричним струмом:
порушення правил, норм електробезпечності законодавства про працю,
недосконалість заходів, передбачених згаданими правилами, нормами й законами.
Існують технічні (невідповідність і несправності електроустановок, засобів
захисту й пристосувань вимогам безпеки), організаційні (невиконання або
неправильне виконання організаційних заходів безпеки), організаційно-технічні
(недотримання технічних заходів безпеки) і організаційно-соціальні причини
поразки (порушення трудової дисципліни).
Безпека експлуатації забезпечується
наступними захисними засобами: застосуванням ізоляції, неприступністю
струмоведучих частин, блокуваннями безпеки, методами орієнтації, застосуванням
малих напруг, ізоляцією електричних частин від землі, компенсацією емностної
складової струму замикання на землю, вирівнюванням потенціалів і застосуванням
ізолюючих площадок. Передбачено наступні заходи забезпечення
електробезпечності:
- конструктивні
заходи електробезпечності;
- схемно-конструктивні
заходи електробезпечності;
- експлуатаційні
заходи електробезпечності.
4. Ергономічні вимоги до робочого
місця
Параметри робочого місця [10], [11]
Конструкцією робочого місця повинно
бути забезпечене оптимальне положення працюючого, котре досягається
регулюванням:
висоти робочої поверхні, сидіння й
простору для ніг;
висоти сидіння й підставки для ніг
при нерегульованій висоті робочої поверхні.
Оптимальна висота робочої поверхні -
це відстань по вертикалі від підлоги до горизонтальної площини, у якій
виконуються основні трудові рухи.
Оптимальна робоча поза для
оператора, росту нижче 1800 мм, досягається за рахунок збільшення висоти
робочого сидіння й підставки для ніг на величину, рівну різниці між висотою
робочої поверхні для оператора ростом 1800 мм і висотою робочої поверхні,
оптимальної для росту даного працюючого.
Якщо регулювання висоти робочої
поверхні й підставки для ніг здійснити неможливо, то проектують і організують
робоче місце з нерегульованими параметрами.
Параметри клавіатури [10]
Виконання клавіатури у вигляді
окремого пристрою з можливістю вільного переміщення;
- наявність опорного пристрою, який
дає змогу змінювати кут нахилу клавіатуру в межах від 50 до 150 і виготовлений
з матеріалу з великим коефіцієнтом тертя, що перешкоджає його переміщенню;
- висота на рівні переднього
ряду не більше 15 мм;
виділення кольором та
місцем розташування окремих груп клавіш; наявність заглиблень посередині
клавіш;
однаковий хід всіх клавіш з
мінімальним опором натисканню 0,25 Н та максимальним не більше 1,5 Н;
виділення кольором на
клавішах символів різних алфавітів (англійського, українського або
російського).
Список використаних джерел
1. Тихонов
А.Н., Самарский А.А. Уравнения математической физики. - М.: Наука, 1972. - 735
с.
. Конет
I.М., Ленюк М.П. Iнтегральнi перетворення типу Мелера-Фока. - Чернiвцi: Прут,
2002. - 248 с.
. Ленюк
М.П. Исследование основных краевых задач для диссипативного волнового уравнения
Бесселя. - Киев, 1983. - 62 с. - (Препринт / АН УССР. Ин-т математики; 83.3).
. Степанов
В.В. Курс дифференциальных уравнений. - М.: Физматгиз. 1959. - 468 с.
. Лаврентьев
М.А., Шабат Б.В. Методы теории функций комплексной переменной. - М.: Наука ,
1987. - 688 с.
. Курош
А.Г. Курс высшей алгебры. - М.: Наука, 1971. - 432 с.
. Шилов
Г.Е. Математический анализ. Второй специальный курс. - М.: Наука,1965. - 328 с.
. Ленюк
М.П. Обчислення полiпараметричних невласних iнтегралiв за власними елементами
гiбридних диференцiа льних операторiв другого порядку. - Том VI. - Чернiвцi:
Прут, 2010. - 404 с.
. Ленюк
М.П., Мороз В.В . Побудова скiнченного гiбридного iнтегрального перетворення
при наявностi спектрального параметру в крайових умовах та умовах спряження //
Науковий вiсник Чернiвецького унiверситету. Випуск 314-315. Математика. -
Чернiвцi: Рута, 2006. - С. 105-113.
. Гандзюк
М.П., Желібо Є.П., Халімовський М.О. Основи охорони праці. Підручник. - К.:
Каравела, 2008. - 384 с.
. Катренко
Л.А., Пістун І.П. Охорона праці в галузі освіти. - Суми: Університетська книга,
2005.- 304 с.