Временные и частотные характеристики линейных электрических цепей
1. ЗАДАНИЕ
Схема исследуемой цепи [рис. 1] №22, в
соответствии с вариантом задания 22 - 13 - 5 - 4. Параметры элементов цепи: L
= 2 мГн, R = 2кОм, C
= 0,5 нФ.
Внешнее воздействие задано
функцией: 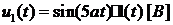 , где а
вычисляется по формуле (1) и равно
, где а
вычисляется по формуле (1) и равно 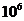 .
.
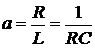 (1)
(1)
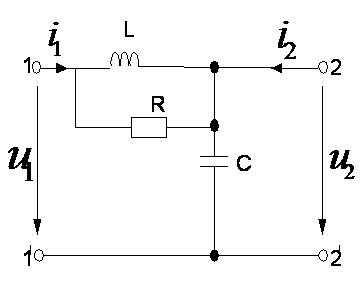
Рисунок 1. Электрическая схема
заданной цепи
Необходимо определить:
а) выражение для первичных параметров
заданного четырехполюсника в виде функции частоты;
б) комплексный коэффициент
передачи по напряжению 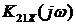 четырехполюсника
в режиме холостого хода на зажимах
четырехполюсника
в режиме холостого хода на зажимах 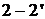 ;
;
в) амплитудно-частотную 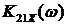 и
фазочастотную
и
фазочастотную 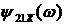 характеристики
коэффициента передачи по напряжению;
характеристики
коэффициента передачи по напряжению;
г) операторный коэффициент
передачи по напряжению 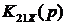 четырехполюсника
в режиме холостого хода на зажимах
четырехполюсника
в режиме холостого хода на зажимах 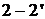 ;
;
д) переходную характеристику
цепи 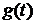 ;
;
е) импульсную характеристику
цепи 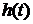 ;
;
ж) отклик цепи 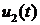 на заданное
входное воздействие
на заданное
входное воздействие 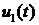 при
отключенной нагрузке.
при
отключенной нагрузке.
2. РАСЧЕТНАЯ ЧАСТЬ
.1 Определение
первичных параметров четырехполюсника
Для определения Z
- параметров четырехполюсника составим уравнения электрического равновесия цепи
по методу контурных токов используя комплексную схему замещения цепи [рис. 2]:
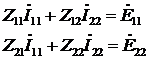
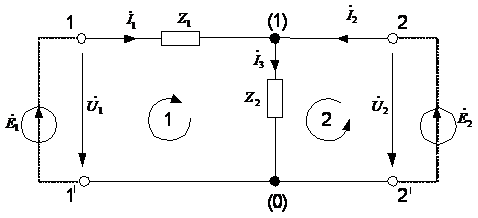
Рисунок 2. Комплексная схема
замещения заданной электрической цепи
Выбирая направление обхода контуров, как указано
на [рис. 2], и учитывая, что
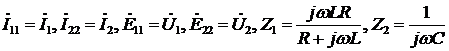 ,
,
запишем контурные уравнения цепи:
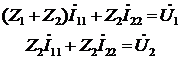
Подставим в полученные уравнения
значения 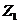 и
и 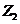 :
:
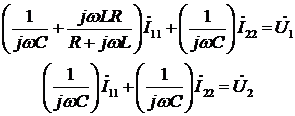 (2)
(2)
Полученные уравнения (2) содержат
только токи и напряжения на входных и выходных зажимах четырехполюсника и могут
быть преобразованы к стандартному виду записи основных уравнений
четырехполюсника в форме Z:
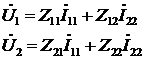 (3)
(3)
Преобразуя уравнения (2) к виду (3),
получим:

Сравнивая полученные уравнения с
уравнениями (3), получаем:
четырехполюсник напряжение холостой амплитудный
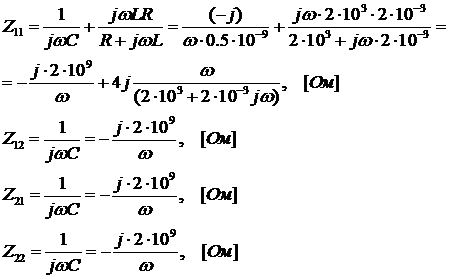
2.2 Определение коэффициента
передачи по напряжению 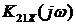 в режиме холостого хода на выходе
в режиме холостого хода на выходе
Комплексный коэффициент передачи по
напряжению от зажимов 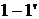 к зажимам
к зажимам 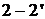 в режиме
холостого хода (
в режиме
холостого хода (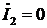 ) на выходе
найдем, используя полученные в пункте 2.1 выражения для первичных
параметров:
) на выходе
найдем, используя полученные в пункте 2.1 выражения для первичных
параметров:
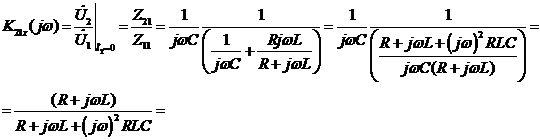
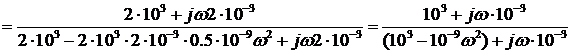
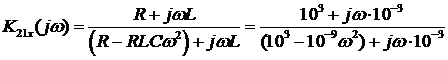 (4)
(4)
2.3 Определение амплитудно-частотной
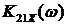 и
фазочастотной
и
фазочастотной 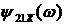 характеристик
коэффициента передачи по напряжению
характеристик
коэффициента передачи по напряжению
Рассмотрим полученное выражение для 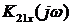 как
отношение двух комплексных чисел, находим выражение для АЧХ и ФЧХ.
как
отношение двух комплексных чисел, находим выражение для АЧХ и ФЧХ.
АЧХ будет иметь вид:
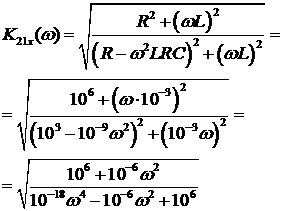
Из формулы (4) следует, что ФЧХ
будет иметь вид:
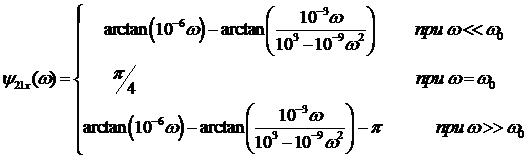
Где, 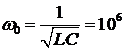 рад/с находится из уравнения
рад/с находится из уравнения 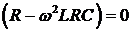
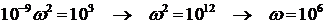
Графики АЧХ и ФЧХ приведены на
следующей странице. [рис.3, рис.4]
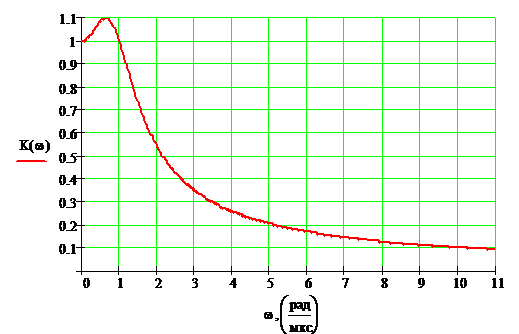
Рисунок 3.
Амплитудно-частотная характеристика 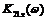
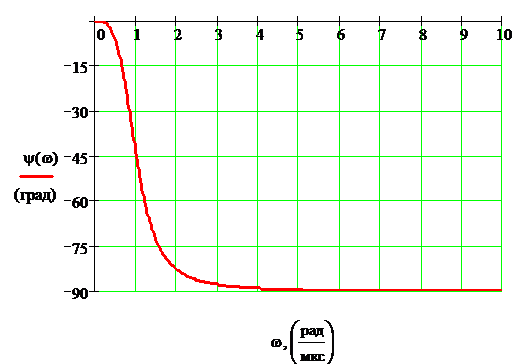
Рисунок 4. Фазочастотная
характеристика 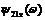
Предельные значения 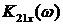 и
и 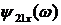 при
при 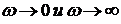 для
контроля вычислений полезно определить, не прибегая к расчетным формулам:
для
контроля вычислений полезно определить, не прибегая к расчетным формулам:
· учитывая, что сопротивление индуктивности при
постоянном токе равно нулю, а сопротивление емкости бесконечно велико, в схеме
[см. рис1] можно разорвать ветвь, содержащую емкость, и заменить индуктивность
перемычкой. В полученной схеме 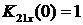 и
и 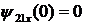 , т.к входное напряжение совпадает
по фазе с напряжением на зажимах
, т.к входное напряжение совпадает
по фазе с напряжением на зажимах 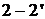 ;
;
· на бесконечно большой частоте ветвь, содержащую
индуктивность, можно разорвать, т.к. сопротивление индуктивности стремится к
бесконечности. Не смотря на то, что сопротивление емкости стремится к нулю, ее
нельзя заменить перемычкой, так как напряжение на емкости является откликом. В
полученной схеме [см. рис.5], при 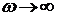 ,
, 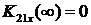 , входной ток опережает по фазе
входное напряжение на
, входной ток опережает по фазе
входное напряжение на 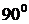 , а напряжение
выходе совпадает по фазе с напряжением на входе, поэтому
, а напряжение
выходе совпадает по фазе с напряжением на входе, поэтому 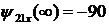 .
.

Рисунок 5. Электрическая схема
заданной цепи при 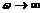 .
.
2.4 Определение операторный
коэффициент передачи по напряжению 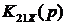 четырехполюсника в режиме холостого
хода на зажимах
четырехполюсника в режиме холостого
хода на зажимах 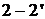
Операторная схема замещения цепи по
внешнему виду не отличается от комплексной схемы замещения [рис.2], так как
анализ электрической цепи проводится при нулевых начальных условиях. В этом
случае для получения операторного коэффициента передачи по напряжению
достаточно в выражении для комплексного коэффициента передачи заменить 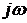 оператором
оператором 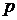 :
:
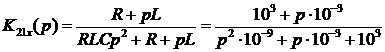
Преобразуем последнее выражение так,
чтобы коэффициенты при старших степенях 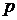 в числителе и знаменателе были
равны единице:
в числителе и знаменателе были
равны единице:
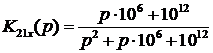
Функция 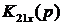 имеет два
комплексно-сопряженных полюса:
имеет два
комплексно-сопряженных полюса: 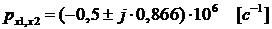 ; и один вещественный нуль:
; и один вещественный нуль: 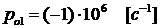 .
.
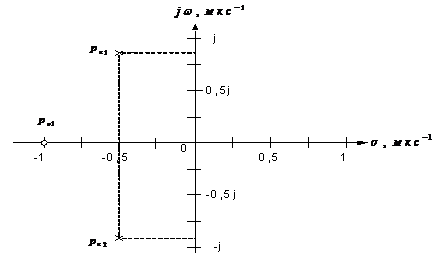
Рисунок 6. Полюсно-нулевая диаграмма
функции 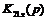
Полюсно-нулевая диаграмма функции 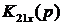 приведена
на рис.6. Переходные процессы в цепи имеют колебательный затухающий характер.
приведена
на рис.6. Переходные процессы в цепи имеют колебательный затухающий характер.
2.5 Определение переходной 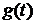 и
импульсной
и
импульсной 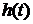 характеристик
цепи
характеристик
цепи
Операторное выражение 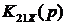 позволяет
получить изображения переходной и импульсной характеристик. Переходную
характеристику удобно определять, используя связь между изображением по Лапласу
переходной характеристики
позволяет
получить изображения переходной и импульсной характеристик. Переходную
характеристику удобно определять, используя связь между изображением по Лапласу
переходной характеристики 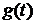 и
операторным коэффициентом передачи:
и
операторным коэффициентом передачи:
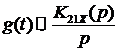 (5)
(5)
Импульсная характеристика цепи 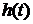 может быть
получена из соотношений:
может быть
получена из соотношений:
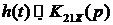 (6)
(6)
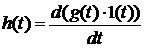 (7)
(7)
Используя формулы (5) и (6), запишем
выражения изображений импульсной и переходной характеристик:
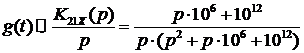
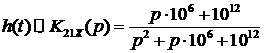
Преобразуем изображения переходной и
импульсной характеристик к виду, удобному для определения оригиналов временных
характеристик с помощью таблиц преобразований Лапласа:
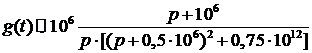 (8)
(8)
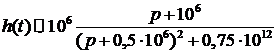 (9)
(9)
Таким образом, все изображения
сведены к следующим операторным функциям, оригиналы которых приведены в
таблицах преобразований Лапласа:
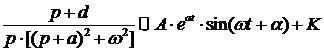 (11)
(11)
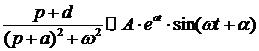 (12)
(12)
Учитывая, что для данного
рассматриваемого случая  ,
, 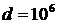 ,
, 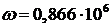 , найдем значения
постоянных
, найдем значения
постоянных 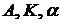 для
выражения (11) и значения постоянных
для
выражения (11) и значения постоянных 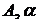 для выражения (12).
для выражения (12).
Для выражения (11):
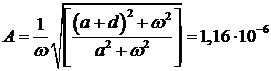

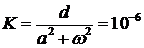
И для выражения (12):
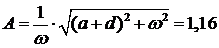
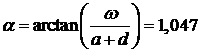
Подставляя полученные значения в
выражения (11) и (12), получим:
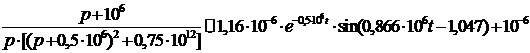
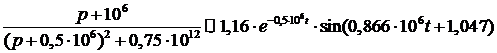
После преобразований получаем
окончательные выражения для временных характеристик:
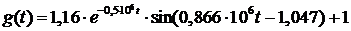 (13)
(13)
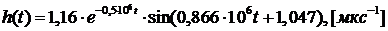 (14)
(14)
Переходной процесс в данной цепи заканчивается
после коммутации за время 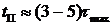 , где
, где 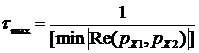 -
определяется как обратная величина к абсолютной минимальной величине
вещественной части полюса
-
определяется как обратная величина к абсолютной минимальной величине
вещественной части полюса 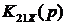 . Так как
. Так как 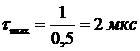 , то время
затухания равно (6 - 10) мкс. Соответственно, выбираем интервал расчета
численных значений временных характеристик
, то время
затухания равно (6 - 10) мкс. Соответственно, выбираем интервал расчета
численных значений временных характеристик 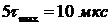 . Графики переходной и импульсной
характеристик приведены на рис.7 и 8.
. Графики переходной и импульсной
характеристик приведены на рис.7 и 8.
Для качественного объяснения вида
переходной и импульсной характеристик цепи к входным зажимам 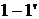 независимый
источник напряжения
независимый
источник напряжения 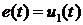 . Переходная
характеристика цепи численно совпадает с напряжением на выходных зажимах
. Переходная
характеристика цепи численно совпадает с напряжением на выходных зажимах 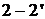 при
воздействии на цепь единичного скачка напряжения
при
воздействии на цепь единичного скачка напряжения 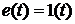 при нулевых начальных условиях. В
первоначальный момент времени после коммутации напряжение на емкости равно
нулю, так как по законам коммутации при конечном значении амплитуды скачка
напряжение на емкости скачком измениться не может. Следовательно,
при нулевых начальных условиях. В
первоначальный момент времени после коммутации напряжение на емкости равно
нулю, так как по законам коммутации при конечном значении амплитуды скачка
напряжение на емкости скачком измениться не может. Следовательно, 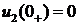 , то есть
, то есть 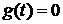 . При
. При 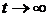 напряжение
на входе можно считать постоянным и равным 1В , то есть
напряжение
на входе можно считать постоянным и равным 1В , то есть 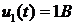 . В цепи,
соответственно, могут протекать только постоянные токи, поэтому емкость можно
заменить разрывом, а индуктивность перемычкой, следовательно в преобразованной
таким образом цепи
. В цепи,
соответственно, могут протекать только постоянные токи, поэтому емкость можно
заменить разрывом, а индуктивность перемычкой, следовательно в преобразованной
таким образом цепи 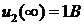 , то есть
, то есть 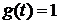 . Переход от
начального состояния к установившемуся происходит в колебательном режиме, что
объясняется процессом периодического обмена энергией между индуктивностью и
емкостью. Затухание колебаний происходит из-за потерь энергии на сопротивлении
R.
. Переход от
начального состояния к установившемуся происходит в колебательном режиме, что
объясняется процессом периодического обмена энергией между индуктивностью и
емкостью. Затухание колебаний происходит из-за потерь энергии на сопротивлении
R.
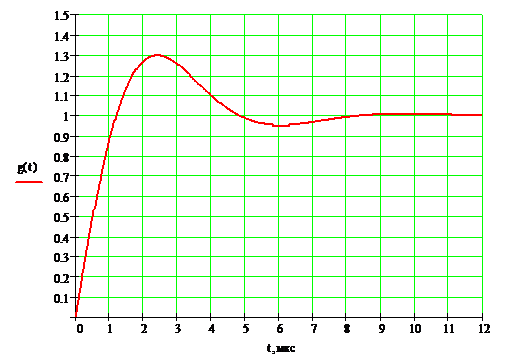
Рисунок 7. Переходная характеристика
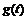 .
.
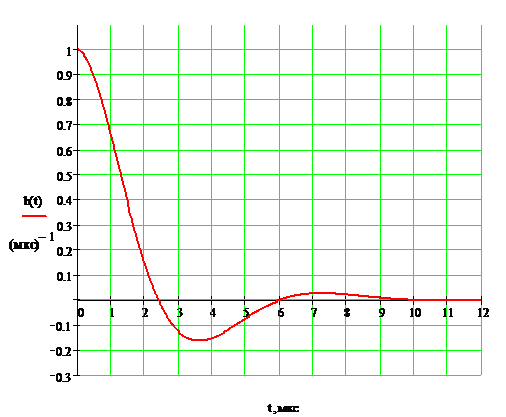
Рисунок 8. Импульсная характеристика
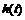 .
.
Импульсная характеристика цепи численно
совпадает с выходным напряжением при подаче на вход единичного импульса
напряжения 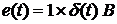 . В течении
действия единичного импульса емкость заряжается до своего максимального
значения, а напряжение на емкости становится равным
. В течении
действия единичного импульса емкость заряжается до своего максимального
значения, а напряжение на емкости становится равным
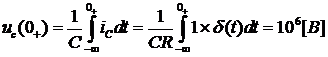 .
.
При 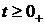 источник напряжения может быть
заменен короткозамкнутой перемычкой, а в цепи возникает затухающий
колебательный процесс обмена энергией между индуктивностью и емкостью. На
начальном этапе емкость разряжается, ток емкости плавно уменьшается до 0, а ток
индуктивности растет до своего максимального значения при
источник напряжения может быть
заменен короткозамкнутой перемычкой, а в цепи возникает затухающий
колебательный процесс обмена энергией между индуктивностью и емкостью. На
начальном этапе емкость разряжается, ток емкости плавно уменьшается до 0, а ток
индуктивности растет до своего максимального значения при 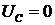 . Затем ток
индуктивности, плавно уменьшаясь, перезаряжает емкость в противоположном
направлении и т.д. При
. Затем ток
индуктивности, плавно уменьшаясь, перезаряжает емкость в противоположном
направлении и т.д. При 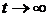 вследствие
рассеяния энергии в сопротивлении все токи и напряжения цепи стремятся к нулю.
Таким образом, затухающий с течением времени колебательный характер напряжения
на емкости и объясняет вид импульсной характеристики, причем
вследствие
рассеяния энергии в сопротивлении все токи и напряжения цепи стремятся к нулю.
Таким образом, затухающий с течением времени колебательный характер напряжения
на емкости и объясняет вид импульсной характеристики, причем 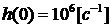 и
и 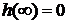 .
.
Корректность расчета импульсной
характеристики подтверждается качественно тем, что график 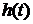 на рис.8
переходит через 0 в те моменты времени, когда график
на рис.8
переходит через 0 в те моменты времени, когда график 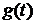 на рис.7
имеет локальные экстремумы, а максимумы
на рис.7
имеет локальные экстремумы, а максимумы 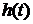 совпадают по времени с точками
перегиба графика
совпадают по времени с точками
перегиба графика 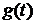 . А также
корректность расчетов подтверждается тем, что графики
. А также
корректность расчетов подтверждается тем, что графики 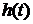 и
и 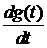 , в
соответствии с формулой (7), совпадают. Для проверки правильности нахождения
переходной характеристики цепи найдем эту характеристику при воздействии на
цепь единичного скачка напряжения
, в
соответствии с формулой (7), совпадают. Для проверки правильности нахождения
переходной характеристики цепи найдем эту характеристику при воздействии на
цепь единичного скачка напряжения 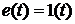 классическим методом:
классическим методом:
. Найдем независимые
начальные условия (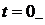 ):
):
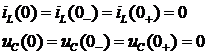
. Найдем зависимые начальные
условия (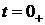 ):
):
Для этого обратимся к рис.9, на
котором изображена схема цепи в момент времени 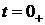 , тогда получим:
, тогда получим:
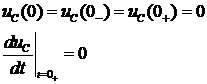
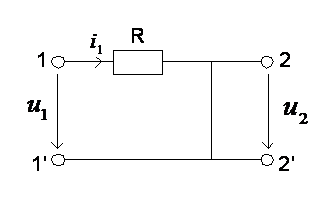
Рисунок 9. Схема цепи в момент
времени 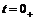
. Найдем принужденную составляющую
отклика:
Для этого обратимся к рис.10, на
котором изображена схема цепи при 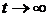 после коммутации. Тогда получаем,
что
после коммутации. Тогда получаем,
что 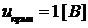

Рисунок 10. Схема цепи при 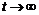 .
.
. Составим дифференциальное уравнение:
Для этого сначала запишем уравнение баланса
токов в узле по первому закону Кирхгофа и запишем некоторые уравнения на
основании второго законов Кирхгоффа:
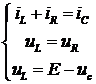
Используя компонентные уравнения
преобразуем первое уравнение:
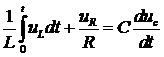
Выразим все неизвестные напряжения
через 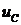 :
:
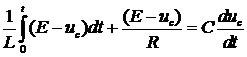
Теперь дифференцируя и преобразуя
получаем дифференциальное уравнение второго порядка:
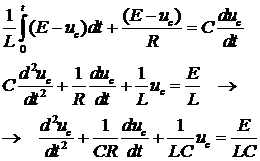
Подставим известные константы и
получим:
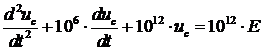
5. Запишем характеристическое уравнение и
найдем его корни:
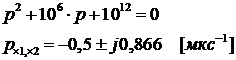
Отсюда мы найдем коэффициент
затухания и частоту свободных колебаний: 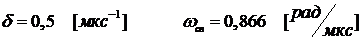
Таким образом, так как корни
характеристического уравнения комплексно - сопряженные, то свободную
составляющую отклика цепи можно найти в таком виде:
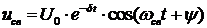
. Найдем постоянные 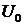 и
и 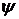 : Для этого
запишем систему уравнений, используя зависимые начальные условия и зная, что
отклик представляет собой сумму свободной и принужденной составляющей:
: Для этого
запишем систему уравнений, используя зависимые начальные условия и зная, что
отклик представляет собой сумму свободной и принужденной составляющей:
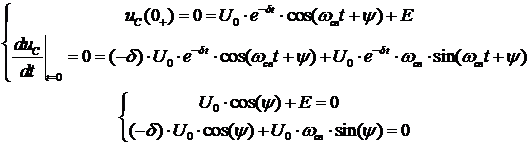
Представим 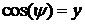 , тогда
, тогда
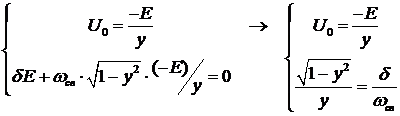
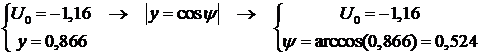
7. Теперь запишем уравнение отклика цепи и
построим его график (рис.11):

На рисунке 11 изображены два графика
переходных характеристик, найденных разными методами: операторным и классическим.
Так как они полностью совпадают можно сделать вывод, что переходная
характеристика найдена верно.
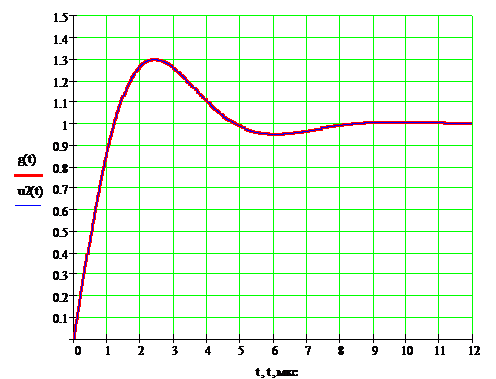
Рисунок 11. Графики переходной
характеристики g(t)
Рассмотрим расчет отклика в заданной
цепи при напряжении на входе
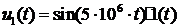 .
.
Отклик можно найти с помощью
классического или операторного методов анализа переходных процессов. Поскольку
начальные условия нулевые и известна операторная характеристика цепи,
воспользуемся операторным методом анализа переходных процессов.
Операторный отклик 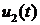 на
воздействие
на
воздействие 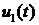 равен
произведению операторного коэффициента передачи цепи и изображения синусоиды по
Лапласу:
равен
произведению операторного коэффициента передачи цепи и изображения синусоиды по
Лапласу:
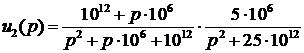 (15)
(15)
Преобразуем выражение (15) к виду,
удобному для применения обратного преобразования Лапласа:
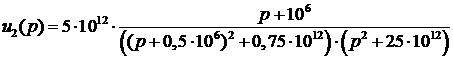 (16)
(16)
Выражение (16) соответствует в
таблице преобразований Лапласа следующему соотношению:
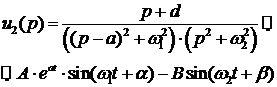 (17)
(17)
Учитывая, что:
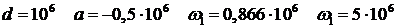
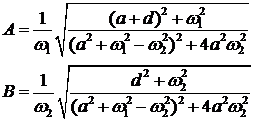
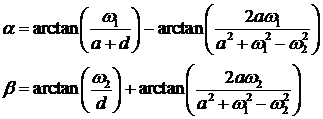
Получим оригинал отклика:
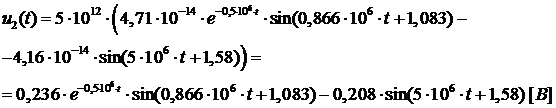
В итоге:
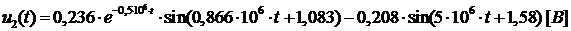
Графики воздействия на цепь и
отклика приведены на рис.12 и 13. Интервал расчета численных значений цепи на
заданное воздействие 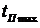 определяется
практическим окончанием переходных процессов после коммутации. В нашем случае
определяется
практическим окончанием переходных процессов после коммутации. В нашем случае 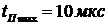 .
.
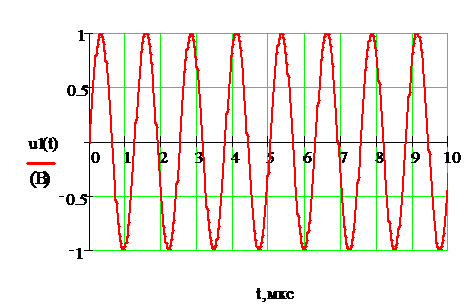
Рисунок 12. График воздействия 
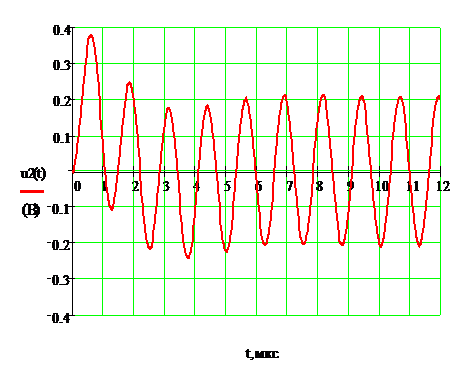
Рисунок 13. Отклик цепи на заданное
воздействие 
Выводы
Полученные результаты позволяют сделать
следующие выводы:
· Первичные параметры четырехполюсника
удовлетворяют условию взаимности: 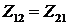 ; Не монотонность АЧХ
; Не монотонность АЧХ 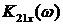 и не
монотонность крутизны ФЧХ
и не
монотонность крутизны ФЧХ 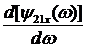 указывают
на возможность возникновения в цепи резонансных явлений. Частота резонанса
амплитуд по графику рис.3 составляет
указывают
на возможность возникновения в цепи резонансных явлений. Частота резонанса
амплитуд по графику рис.3 составляет 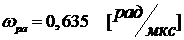 ;
;
· Комплексно - сопряженные полюсы операторного
коэффициента передачи указывают на колебательный характер переходных процессов
в цепи. Частота свободных колебаний 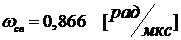 превышает частоту резонанса
амплитуд
превышает частоту резонанса
амплитуд 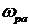 , постоянная
цепи;
, постоянная
цепи;
· Переходная характеристика 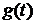 является
квазигармонической функцией, соотношения для изображения и оригинала выполнены:
является
квазигармонической функцией, соотношения для изображения и оригинала выполнены:
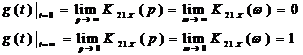
· Импульсная характеристика также является
квазигармонической функцией, стремящейся при 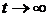 к нулю. Постоянная времени и
квазипериод колебания временных характеристик совпадают с результатами,
полученными из анализа операторного коэффициента передачи; АЧХ рассматриваемой
цепи близка к АЧХ идеального фильтра нижних частот с граничной частотой
к нулю. Постоянная времени и
квазипериод колебания временных характеристик совпадают с результатами,
полученными из анализа операторного коэффициента передачи; АЧХ рассматриваемой
цепи близка к АЧХ идеального фильтра нижних частот с граничной частотой 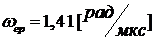 .
.
Список
использованной литературы
1. Попов
В.П. Основы теории цепей: Учебник для вузов - 4-ое изд., испр. - М.: Высш. шк.,
2003. - 575с.: ил.
. Корн
Г., Корн Т., Справочник по математике для инженеров и учащихся вузов. М.:
Наука, 1973, 832 с.