Временные и частотные характеристики линейных электрических цепей

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное

Учреждение высшего профессионального образования

«ЮЖНЫЙ ФЕДЕРАЛЬНЫЙУНИВЕРСИТЕТ»

ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ В г. ТАГАНРОГЕ

(ТТИ Южного Федерального Университета)

Курсовая Работа

Временные и частотные характеристики линейных электрических цепей

по курсу: Основы теории цепей

2012

Оглавление

1.      ЗАДАНИЕ К КУРСОВОЙ РАБОТЕ

.        ОПРЕДЕЛЕНИЕ Z-ПАРАМЕТРОВ ЧЕТЫРЁХПОЛЮСНИКА

.        ОПРЕДЕЛЕНИЕ КОМПЛЕКСНОГО КОЭФФИЦИЕНТА ПЕРЕДАЧИ ПО НАПРЯЖЕНИЮ К21Х(jw) В РЕЖИМЕ ХОЛОСТОГО ХОДА, АЧХ К21Х(w), ФЧХ φ21Х(w)

.        ОПРЕДЕЛЕНИЕ ОПЕРАТОРНОГО КОЭФФИЦИЕНТА ПЕРЕДАЧИ ПО НАПРЯЖЕНИЮ К21Х(р)

.        ОПРЕДЕЛЕНИЕ ПЕРЕХОДНОЙ g(t) И ИМПУЛЬСНОЙ h(t) ХАРАКТЕРИСТИК ЦЕПИ

.        ОПРЕДЕЛЕНИЕ ОТКЛИКА ЦЕПИ u2(t) НА ЗАДАННОЕ ВХОДНОЕ ВОЗДЕЙСТВИЕ u1(t)

Заключение

СПИСОК ЛИТЕРАТУРЫ

1.  ЗАДАНИЕ К КУРСОВОЙ РАБОТЕ

Вариант 20-10-6-4

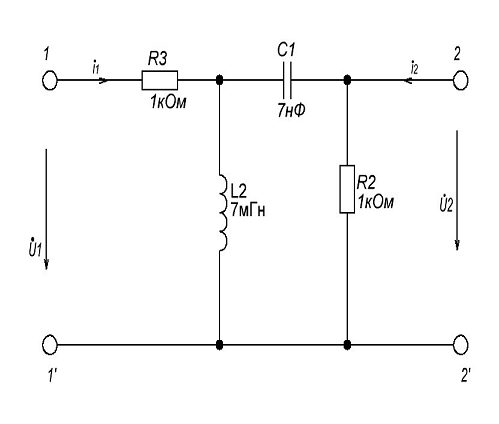
Рис 1.1 Схема заданного четырёхполюсника

Заданное внешнее воздействие:u₁( t )=cos(5αt)*(Φ(t))

В результате выполнения курсовой работы необходимо найти:

·        выражения для Z-параметров четырёхполюсника, схема которого представлена на Рис.1.1 в виде функций частоты;

·        комплексный коэффициент передачи по напряжению К_21Х( jw ) четырёхполюсника в режиме холостого хода на зажимах 2-2¢;

·        амплитудно-частотную К_21Х(w ) и фазо-частотную φ_21Х(w ) характеристики коэффициента передачи по напряжению;

·        операторный коэффициент передачи по напряжению К_21Х( р ) четырёхполюсника в режиме холостого хода на зажимах 2-2¢;

·        переходную характеристику цепи g(t);

·        импульсную характеристику цепи h(t);

·        отклик цепи u₂( t ) на заданное входное воздействие u₁( t );

2.  ОПРЕДЕЛЕНИЕ Z-ПАРАМЕТРОВ ЧЕТЫРЁХПОЛЮСНИКА

Так как четырехполюсник на рис.1.1 представляет собой каскадное соединение двух более простых четырехполюсников, по этому найдем A параметры четырехполюсников показанных на рис.2.1. Затем воспользуемся переходом из одной системы параметров в другую (A-Z).

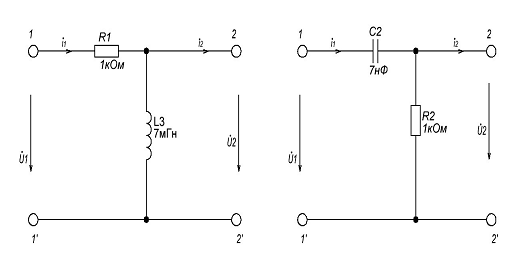
а                                                                б

Рис 2.1

Найдем параметры A₁₁ и A₂₁при холостом ходе (, рис.2.1).(где Z1=R1, Z2=jwL1). Рис.2.2

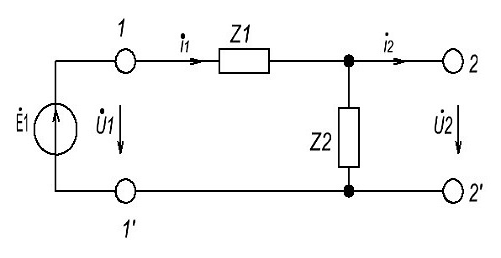
Рис 2.2. Комплексная схема замещения при холостом ходе на выходе

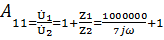
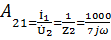
Найдем параметры A₁₂ и A₂₁при коротком замыкание на выходе (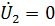, рис.2.3).

четырехполюсник цепь замыкание напряжение

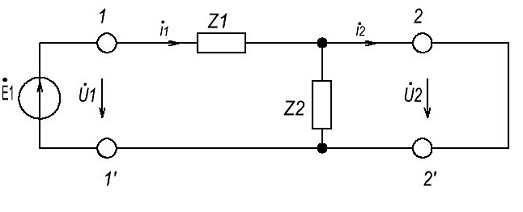
Рис 2.3. Комплексная схема замещения при коротком замыкании на выходе

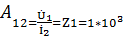
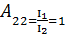
Точно такие же преобразования для схемы на рис.2.1 б).

Получаем две матрицы:

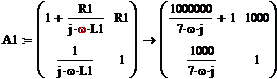
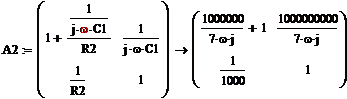
Таким образом, получаем матрицуA-параметров:

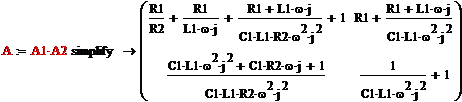
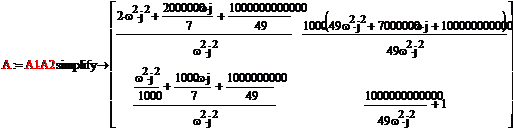
Теперь выразим Z-параметры через A-параметры, воспользуемся матрицей преобразования

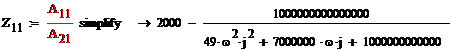
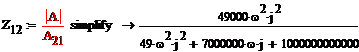
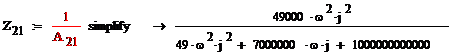
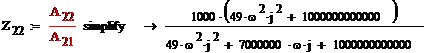
Получили искомую матрицу Z параметров:

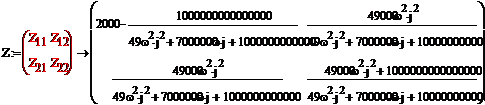
3.      ОПРЕДЕЛЕНИЕ КОМПЛЕКСНОГО КОЭФФИЦИЕНТА ПЕРЕДАЧИ ПО НАПРЯЖЕНИЮ К_21Х(jw) В РЕЖИМЕ ХОЛОСТОГО ХОДА, АЧХ К_21Х(w), ФЧХ φ_21Х(w)

Используя ранее найденный параметр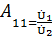найдем комплексный коэффициент передачи по напряжению 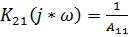 четырехполюсника в режиме холостого хода на зажимах 2-2’.

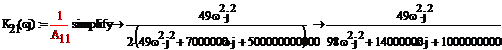
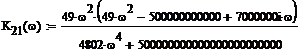
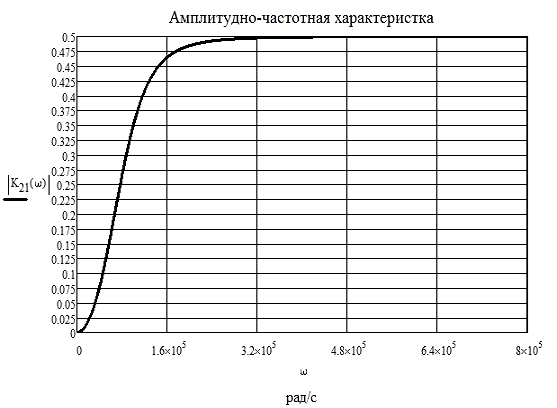
Рис 3.1

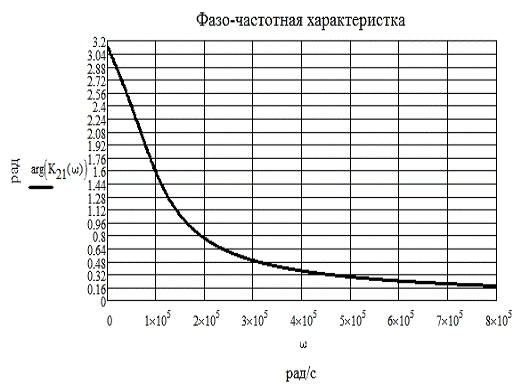
Рис 3.2

Для большей наглядности построим АЧХ и ФЧХ с помощью среды MultiSim(рис.3.3-3.4)

Рис 3.3

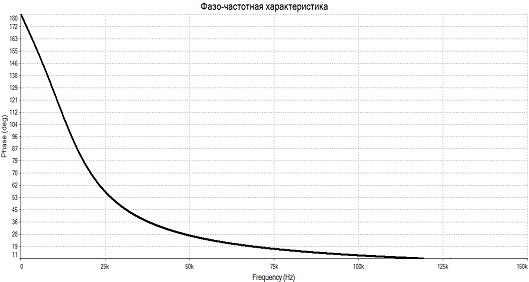
Рис 3.4

4.      ОПРЕДЕЛЕНИЕ ОПЕРАТОРНОГО КОЭФФИЦИЕНТА ПЕРЕДАЧИ ПО НАПРЯЖЕНИЮ К_21Х(s)

Чтобы получить операторный коэффициент передачи по напряжению, в выражении K_21x(jω)заменим jw оператором s:

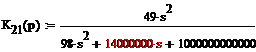
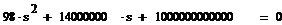
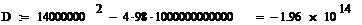
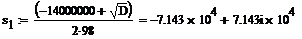
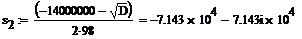
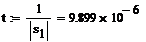
t.з=3-5 t=29-49мкс

Функция К₂₁(s) имеет два Комплексно-сопряженных полюса:, 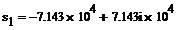, 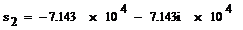и один нуль:,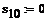

Комплексно-сопряженные полюсы операторного коэффициента передачи указывают на колебательный характер переходных процессов в цепи.

Полюсно-нулевая диаграмма функции К_21Х(s)

Рис 4.1

5. ОПРЕДЕЛЕНИЕ ПЕРЕХОДНОЙ g(t) И ИМПУЛЬСНОЙ h(t) ХАРАКТЕРИСТИК ЦЕПИ

Операторное выражение К₂₁(р) позволяет получить изображения переходной (рис 1.7) и импульсной(рис 1.8) характеристик:

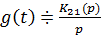
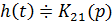
Для определения оригиналов временных характеристик используем таблицы преобразований Лапласа.

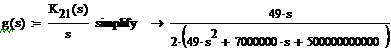
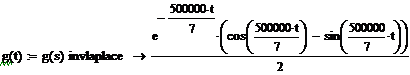
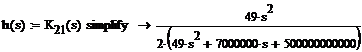
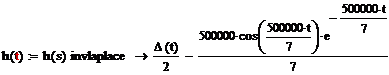
Переходной процесс в данной цепи практически заканчивается за время

t_п29 - 49 мкс (т. к. t_п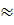(3 - 5)*τ_max , где τ_max = 1/|p_1x| = 9.9мкс).

За величину временного интервала выберем t = 49 мкс

Рис 5.1

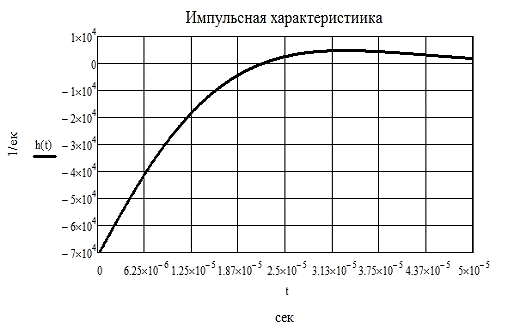
Рис 5.2

Для большей наглядности построим  и 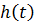 с помощью среды MultiSim(рис.5.3-5.4)

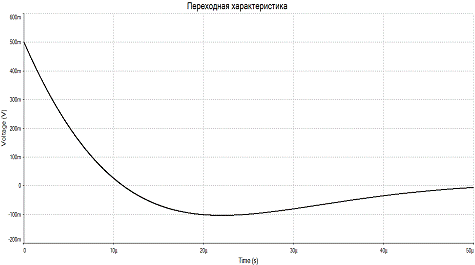
Рис 5.3

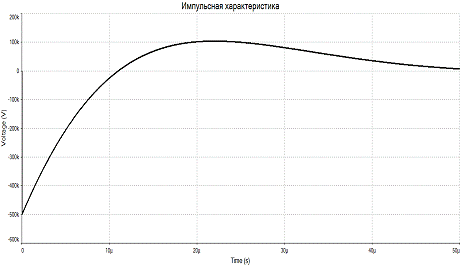
Рис 5.4

6       ОПРЕДЕЛЕНИЕ ОТКЛИКА ЦЕПИ u₂(t) НА ЗАДАННОЕ ВХОДНОЕ ВОЗДЕЙСТВИЕ u₁(t)

Проведём расчёт отклика при подаче на вход рассматриваемой цепи внешнего воздействия

u₁( t )=cos(5αt)*(Φ(t))

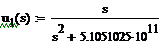
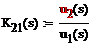
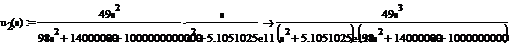
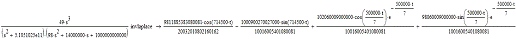
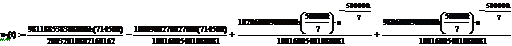
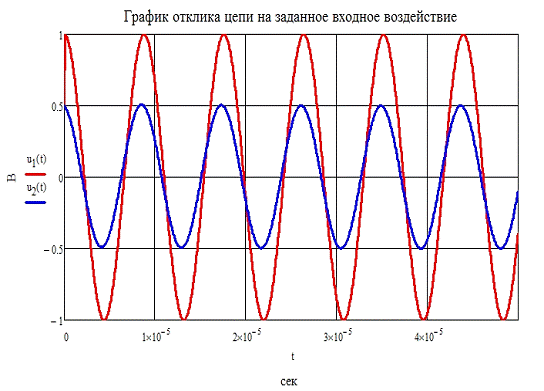
Рис 6.1

Графики полученные теоретически (рис 6.1) совпадают с графиками, полученными в среде Multisim(рис 6.2).

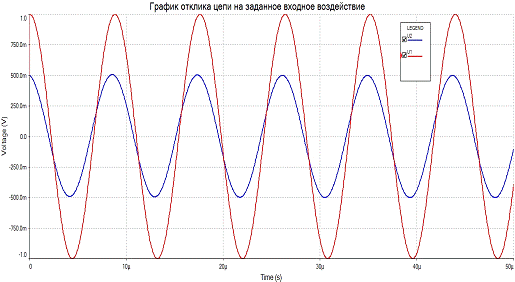
Рис 6.2

Заключение

В результате выполнения курсовой работы были получены результаты, не противоречащие теории изложенной в учебнике В.П. Попова «Основы теории цепей»: а именно:

Z₁₂ = Z₂₁

·    Комплексно-сопряженные полюсы операторного коэффициента передачи указывают на колебательный характер переходных процессов в цепи.

·        Графики, полученные в среде MathCAD полностью совпадают с графиками из Multisim.

СПИСОК ЛИТЕРАТУРЫ

1. Попов В.П. “Основы теории цепей” М.: “Высшая школа” 1998-575 с.

2. Корн Г., Корн Т. “Справочник по математике для научных работников и инженеров.” М. : “Наука”, 1978-831 с.