Вычисление интеграла
Курсовая работа
по дисциплине «Информатика»
Тема: «Вычисление интеграла»
Задание на выполнение курсовой работы
1. расчет, выполненный в математическом пакете Matlab (R2009b)
(файл-функция для описания подынтегральной функции, график функции, решение в
символьном и численном виде, вычисление с помощью циклов: четные и не четные
варианты).
2. Вычисление интеграла в электронных таблицах MS Excel (вид
подынтегральной функции, график функции, провести серию расчетов при n = 20,
30: методом левых и правых прямоугольников; методом трапеций и методом
Симпсона).
. Создание приложения для нахождения решения интегрального
уравнения в среде Delphi (вид подынтегральной функции, график на заданном
интервале, для каждого численного метода задать пользовательскую подпрограмму с
передачей параметров). Итоговые результаты отобразить на форме в виде таблицы и
в файле. Предусмотреть изменение точности значения (Е = 0,001).
. вид уравнения
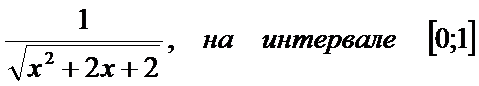
Введение
интеграл excel delphi
matlab
Численные
методы интегрирования универсальны: позволяют вычислить значение определенного
интеграла непосредственно по значениям подынтегральной функции f(x), независимо
от способа ее задания или вида аналитического выражения.
Геометрический
смысл определенного интеграла - площадь криволинейной трапеции, ограниченной
осью OX, кривой f(x), и прямыми x = a и x = b.
Численные
методы интегрирования основаны на различных способах оценки этой площади,
поэтому полученные формулы численного интегрирования называются квадратурными
(формулами вычисления площади).
1. Теория
вычисления интеграла. Описание используемых численных методов
Многие инженерные задачи, задачи физики, геометрии и многих других
технических областях, приводят к необходимости вычислять определенный интеграл
вида,
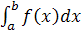
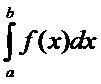
где
f(x) - подынтегральная функция, непрерывная на отрезке [a ; b].
Если
интеграл от данной функции не может быть вычислен по формуле Ньютона-Лейбница,
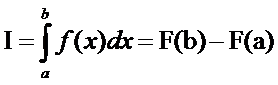
или
если функция f(x) задана графически или таблицей, то для вычисления
определенного интеграла применяют приближенные формулы. Для приближенного
вычисления интеграла существует много численных методов, таких как:
1) Метод прямоугольников (правых и левых);
) Трапеций;
) Симпсона и др.
Метод
прямоугольников (правых и левых)
Необходимость вычисления значений определенных интегралов при
моделировании возникает достаточно часто.
Формула Ньютона-Лейбница
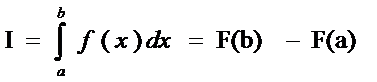(1)
имеет
ограниченное применение:
во-первых,
не позволяет вычислить интегралы от таблично заданной подынтегральной функции
f(x);
во-вторых,
не всякая подынтегральная функция имеет первообразную F(x).
Численные
методы интегрирования универсальны: позволяют вычислить значение определенного
интеграла непосредственно по значениям подынтегральной функции f(x), независимо
от способа ее задания или вида аналитического выражения.
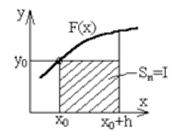
Геометрический
смысл определенного интеграла - площадь криволинейной трапеции, ограниченной
осью OX, кривой f(x), и прямыми x = a и x = b (Рис.1.).
Численные
методы интегрирования основаны на различных способах оценки этой площади,
поэтому полученные формулы численного интегрирования называются квадратурными
(формулами вычисления площади).
Рассмотрим
получение и применение простейших формул.
Отрезок
[a, b] делят на n необязательно равных частей - элементарных отрезков. Принято
такое деление отрезка называть сеткой, а точки xо, x1,…, xn - узлами сетки.
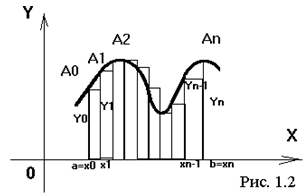
Рис.1.
Геометрический смысл определённого интеграла
Если
сетка равномерная, то
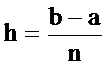(1)
шаг
сетки, при интегрировании - шаг интегрирования, а координата i-го узла
вычисляется по формуле:
, 
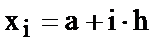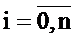(2)
Полная
площадь криволинейной трапеции состоит из n элементарных криволинейных трапеций
- элементарных площадей:
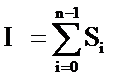(3)
Метод правых треугольников
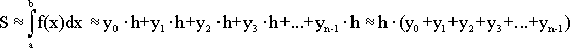
Метод левых прямоугольников
Метод
трапеций
Метод трапеций является одним из методов численного интегрирования. Он
позволяет вычислять определенные интегралы с заранее заданной степенью
точности.
Поставим
перед собой следующую задачу: пусть нам требуется приближенно вычислить
определенный интеграл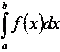 
, где подынтегральная функция y=f(x) непрерывна на
отрезке [a;b].
Разобьем
отрезок [a;b] на n равных интервалов длины h точками 
. В этом случае шаг разбиения находим как 
и узлы определяем из равенства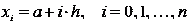 
.
Рассмотрим
подынтегральную функцию на элементарных отрезках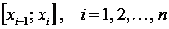 
.
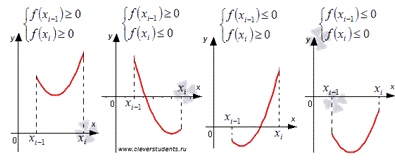
Возможны
четыре случая (на рисунке показаны простейшие из них, к которым все сводится
при бесконечном увеличении n):
На
каждом отрезке 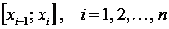заменим функцию y=f(x) отрезком прямой, проходящей
через точки с координатам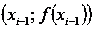и 
и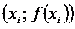 
. Изобразим их на рисунке синими линиями:
В
качестве приближенного значения интеграла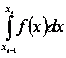 
возьмем
выражение 
, то есть, примем 
.
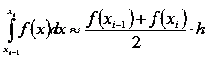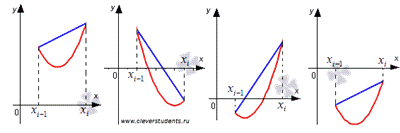
Давайте
выясним, что означает в геометрическом смысле записанное приближенное
равенство. Это позволит понять, почему рассматриваемый метод численного
интегрирования называется методом трапеций.
Мы
знаем, что площадь трапеции находится как произведение полу суммы оснований на
высоту. Следовательно, в первом случае площадь криволинейной трапеции
приближенно равна площади трапеции с основаниями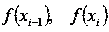 
и
высотой h, в последнем случае определенный интеграл 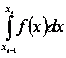приближенно равен площади трапеции с основаниями 
и высотой h, взятой со знаком минус. Во втором и
третьем случаях приближенное значение определенного интеграла 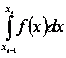равно разности площадей красной и синей областей,
изображенных на рисунке ниже.
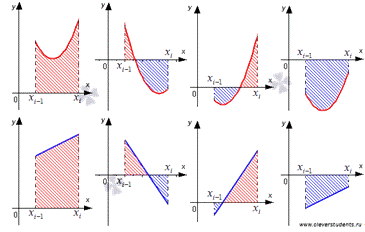
Таким
образом, мы подошли к сути метода трапеций, которая состоит в представлении
определенного 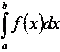интеграла в виде суммы интегралов вида 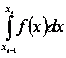на каждом элементарном отрезке и в последующей
приближенной замене .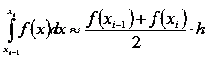
.
Формула метода трапеций
В
силу пятого свойства определенного интеграла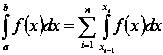 
.
Если
вместо интегралов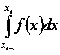 
подставить их приближенные значения, то получится
формула метода трапеций:
.
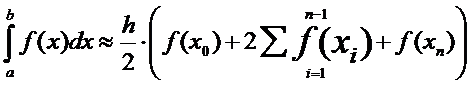
Оценка абсолютной погрешности метода трапеций
Абсолютная
погрешность метода трапеций оценивается как.
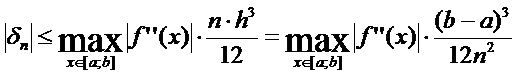
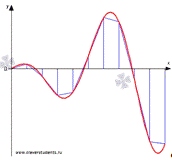
Графическая
иллюстрация метода трапеций.
4. Метод
Симпсона (парабол)
Это более совершенный способ - график подынтегральной функции
приближается не ломаной линией, а маленькими параболками. Сколько промежуточных
отрезков - столько и маленьких парабол. Если взять те же три отрезка, то метод
Симпсона даст ещё более точное приближение, чем метод прямоугольников или метод
трапеций.
Пусть
функция y = f(x) непрерывна на отрезке [a; b] и нам требуется вычислить
определенный интеграл .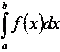
Разобьем
отрезок [a; b] на n элементарных отрезков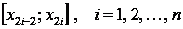 
длины 
точками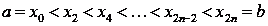 
. Пусть
точки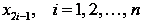 
являются серединами отрезков 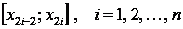соответственно. В этом случае все "узлы"
определяются из равенства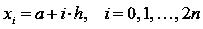 
.
Суть
метода парабол.
На
каждом интервале 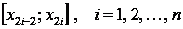подынтегральная функция приближается квадратичной
параболой 
, проходящей через точки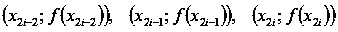 
. Отсюда и название метода - метод парабол.
Это
делается для того, чтобы в качестве приближенного значения определенного
интеграла 
взять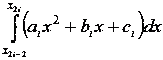 
, который
мы можем вычислить по формуле Ньютона-Лейбница. В этом и заключается суть
метода парабол.
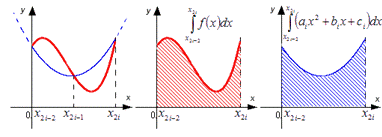
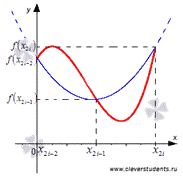
Красной
линией изображен график функции y=f(x), синей линией показано приближение
графика функции y=f(x) квадратичными параболами на каждом элементарном отрезке
разбиения.
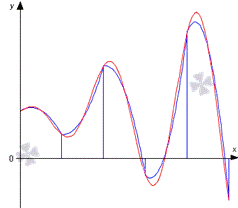
Графическая
иллюстрация метода парабол (Симпсона)
Вывод
формулы метода Симпсона (парабол)
В
силу пятого свойства определенного интеграла имеем
.
Для
получения формулы метода парабол (Симпсона) нам осталось вычислить
.
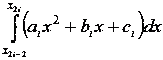Пусть
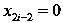(мы всегда можем к этому прийти, проведя
соответствующее геометрическое преобразования сдвига для любого i = 1, 2, ...,
n).
Сделаем
чертеж.
Покажем,
что через точки 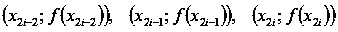проходит только одна квадратичная парабола . Другими словами, докажем, что коэффициенты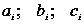 
определяются единственным образом.
Так
как 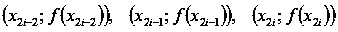- точки параболы, то справедливо каждое из уравнений
системы
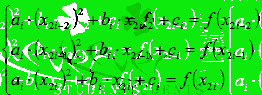
Записанная
система уравнений есть система линейных алгебраических уравнений относительно
неизвестных переменных 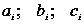. Определителем основной матрицы этой системы
уравнений является определитель Вандермонда 
, а он
отличен от нуля для несовпадающих точек 
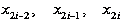. Это
указывает на то, что система уравнений имеет единственное решение (об этом
говорится в статье решение систем линейных алгебраических уравнений), то есть,
коэффициенты 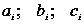определяются единственным образом, и через точки 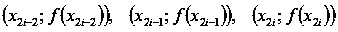проходит единственная квадратичная парабола.
Перейдем
к нахождению интеграла .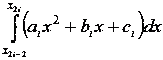
Очевидно:
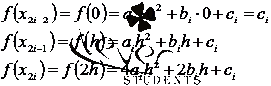
Используем
эти равенства, чтобы осуществить последний переход в следующей цепочке
равенств:
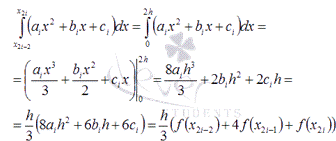
Таким
образом, можно получить формулу метода парабол:
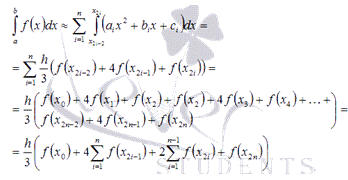
Формула
метода Симпсона (парабол) имеет вид
.
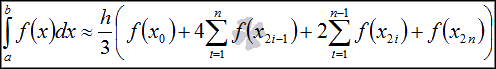Оценка
абсолютной погрешности метода Симпсона.
Абсолютная
погрешность метода Симпсона оценивается как
5. Расчеты в
математическом пакете Mat lab
В математическом пакете по условию задания был построен график функции и
найден корень уравнения с использованием символьного решения и в численном виде
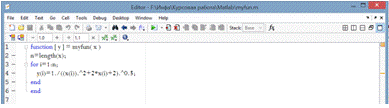
используя встроенные функции. Для описания функции создан m-файл функции.
На следующем рисунке представлен график функции:
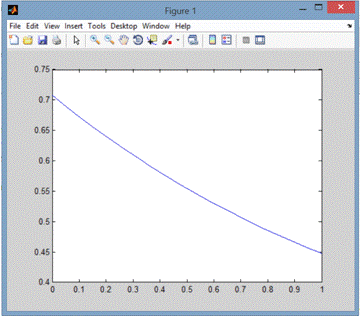
Для записи команд использован m-файл:
В командном окне были получены следующие результаты:
tochnoe
= 0.56226= 0.5555= 0.5691= 0.5623= 0.5623
6. Отчет о
результатах вычисления приближенного значения корня уравнения в MS Excel
В MS Excel был проведен расчет приближенного значения корня уравнения.
Интерфейс программы:
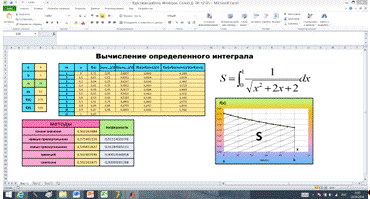
График уравнения:
Корни,
полученные в excel:
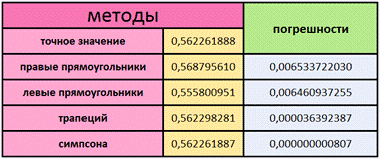
. Описание
приложения созданного в среде Delphi
При создании приложения в среде Delphi в интерфейсе был предусмотрен
вывод вида функции и графика. Нахождение корня уравнения интеграла было
реализовано с использование трех методов: метода правых и левых
прямоугольников, метода трапеций и метода Симпсона. В отличии от расчета в
Excel, где корни находились, в программе предусмотрен ввод точности вычисления
пользователем. Результаты расчета выводятся, как в окно приложения, так и в
текстовый файл.
8. Блок -
схемы, реализующие численные методы
Блок-схема для метода правых прямоугольников:
Блок-схема для метода левых прямоугольников
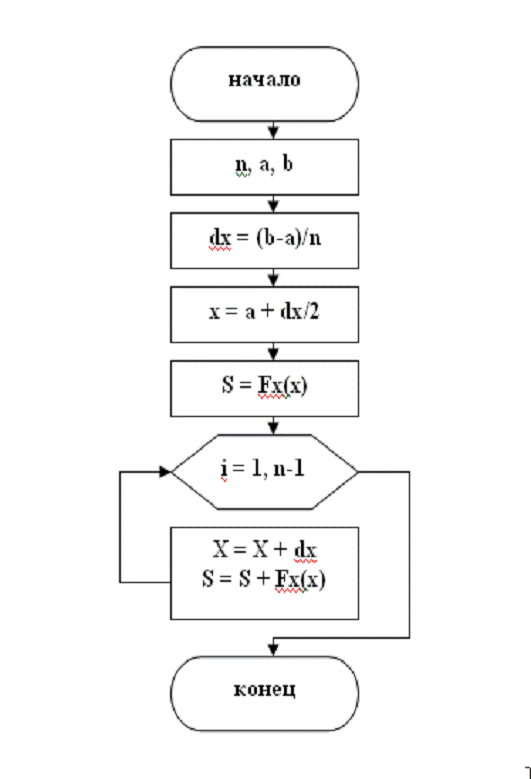
Блок-схема для метода трапеций
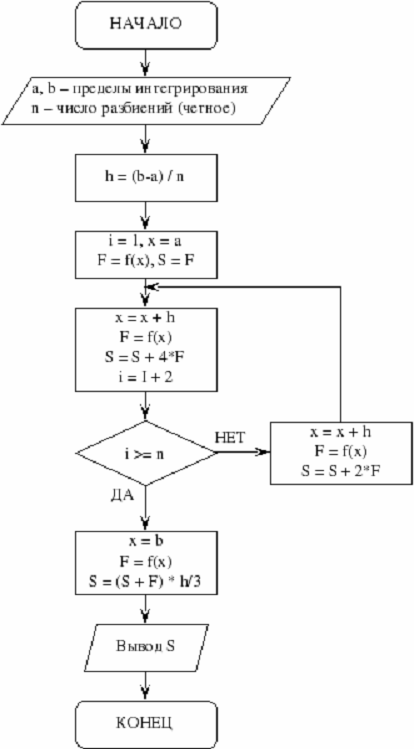
Блок-схема метода Симпсона:
9. Листинг
программы
unit
Unit1;, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,,
StdCtrls, Math, AxCtrls, OleCtrls, VCF1, ExtCtrls, TeeProcs,, Chart, Menus,
Series, OleCtnrs;= class(TForm): TButton;: TButton;: TEdit;: TButton;:
TEdit;Book1: TF1Book;: TEdit;: TButton;: TLabel;: TLabel;: TLabel;: TChart;:
TEdit;: TButton;: TLineSeries;: TMainMenu;: TMenuItem;: TMenuItem;: TLabel;:
TOleContainer;Button1Click(Sender: TObject);Button2Click(Sender:
TObject);Button3Click(Sender: TObject);Button5Click(Sender: TObject);Button4Click(Sender:
TObject);N1Click(Sender: TObject);N2Click(Sender: TObject);
{
Private declarations }
{
Public declarations };: TForm1;,b,h,s,x,e:real;,j,n:integer;:text;:string;
{$R
*.dfm}integral(x:real):real;:=1/sqrt(power(x,2)+2*x+2);;methlev;:=(b-a)/(n-1);:=0;:=0;abs(s)<e
doi:=2 to n do:=x+h;:=s+integral(x)*h;;;methpr;:=(b-a)/n;:=0;:=0;abs(s)<e
doi:=1 to n
do:=s+integral(x)*h;:=x+h;;;methtr;,sb:real;:=(b-a)/n;:=0;:=0;abs(s)<e
doi:=1 to n do:=integral(x);:=integral(x+h);:=s+h*(sa+sb)/2;:=x+h;;;meths;,sb,sh:real;:=(b-a)/n;:=0;:=0;abs(s)<e
doi:=1 to n
do:=integral(x);:=integral(x+h);:=s+(2*sa+sb)*h/3;:=x+h;;;TForm1.Button1Click(Sender:
TObject);:=StrToInt(Form1.Edit1.Text);:=StrToFloat(Form1.Edit2.Text);:=StrToFloat(Form1.Edit3.Text);:=StrToFloat(Edit4.Text);;Book1.textRC[1,1]:=
'Method';Book1.textRC[1,2]:='levix';Book1.textRC[2,1]:=
'S=';Book1.numberRC[2,2]:=s;;TForm1.Button2Click(Sender:
TObject);:=StrToInt(Edit1.Text);:=StrToFloat(Edit2.Text);:=StrToFloat(Edit3.Text);:=StrToFloat(Edit4.Text);;Book1.textRC[1,3]:='pravix';Book1.numberRC[2,3]:=s;;TForm1.Button3Click(Sender:
TObject);:=StrToInt(Edit1.Text);:=StrToFloat(Edit2.Text);:=StrToFloat(Edit3.Text);:=StrToFloat(Edit4.Text);;Book1.textRC[1,4]:='trapezii';Book1.numberRC[2,4]:=s;;TForm1.Button5Click(Sender:
TObject);:=StrToInt(Edit1.Text);:=StrToFloat(Edit2.Text);:=StrToFloat(Edit3.Text);:=StrToFloat(Edit4.Text);;Book1.textRC[1,5]:='sumpsona';Book1.numberRC[2,5]:=s;;TForm1.Button4Click(Sender:
TObject);y:real;.Chart1.Series[0].Clear;:=StrToInt(Edit1.Text);:=StrToFloat(Edit2.Text);:=StrToFloat(Edit3.Text);:=StrToFloat(Edit4.Text);:=
(b-a)/n;:=a;.Series[0].AddXY(x,y,'',clRed);i:=1 to n do
begin:=x+h;:=integral(x);.Series[0].AddXY(x,y,'',clRed);;;TForm1.N1Click(Sender:
TObject);;;TForm1.N2Click(Sender: TObject);(f,'Корни');(f);i:=1 to n do begin:='';j:=1 to n do
str:=str+F1Book1.TextRC[i,j]+' ';(f,str);;(f);
end;.
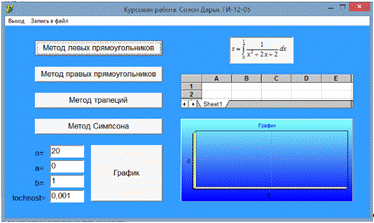
. Изображение
окна приложения
Первоначальный интерфейс имеет следующий вид:
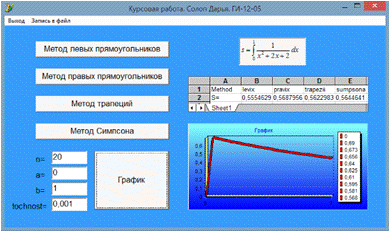
После выполнения расчетов при E<= 0,0001:
В качестве отчета был сформирован файл «Корни.txt»:
. Анализ полученных результатов
В соответствии с заданием на курсовую работу в математическом пакете мною
было найдено решение определенного интеграла и построен график.
В электронных таблицах был найден корень уравнения. Результаты
практически совпали с результатами в Matlab.
Для поиска корня в среде Delphi пользователь имеет возможность ввести
точность вычисления с клавиатуры.
Таким образом, расчеты показали, что можно найти решение определенного
интеграла в разных средах. Наиболее трудоемким расчет оказался в среде Delphi.
Литература
1. Фаронов
В.В. Delphi. Программирование на языке высокого уровня 2010
2. Уокенбах Д. Microsoft Office Excel 2011
3. Матющенко
М.А. Matlab. Первые шаги 2009