Математическое моделирование двигателя постоянного тока
Содержание
Вступление
.
Расчет статических и динамических параметров машины
.
Математическое моделирование ДПТ
.
Аппроксимация полученной переходной характеристики элементарными динамическими
звеньями
Вывод
Литература
Вступление
Для анализа и синтеза систем электроприводов
необходимо знать их математические модели. Выбор математической модели зависит
от целого ряда условий, важнейшими из которых являются: цель, которой модель
должна служить; необходима точность описания реального процесса; критерий адекватности
модели и объекта, степень изученности физических явлений процесса. В инженерной
практике часто ограничиваются представлением объекта в виде черного ящика, для
которого находят связь между входом и выходом. Такое нахождение связей по
экспериментальным данным называют идентификацией. По данным идентификации
определяют параметры и структуру черного ящика объекта.
Выделяют пять основных методов определения
модели объекта на основе:
) реакции объекта на детерминированный входной
сигнал (единичный скачок или импульс);
) частотных характеристик, полученных в
устойчивом состоянии при синусоидальном входном сигнале;
) моделирование на ЭВМ при дальнейшем уточнены
параметров модели;
) корреляция анализа входа и выхода;
) динамической модели, подстраивает (модели как
датчика характеристик объекта).
Целью идентификации будем считать получение
математического описания объекта в виде его передаточной функции на основании
экспериментальной переходной характеристики.
Основой идентификации является аппроксимация
переходной характеристики, соответствующей некоторой передаточной функции. В
настоящее время существует более 50 методов аппроксимации передаточных функций
по кривым разгона, которые отличаются по структуре передаточной функции и по
используемому математическому аппарату.
Переходные характеристики большинства
электроприводов, встречающихся на практике, промышленных объектов имеют не
колебательный вид, и обычно достаточно хорошо аппроксимируются элементарными
динамическими звеньями.
1. Расчет статических и динамических параметров
машины
В процессе математического моделирования, при
нахождении передаточных функций необходимо определить статические параметры
машины. Активное сопротивление якоря двигателя постоянного тока определяется
исходя из равенства переменных и постоянных расходов в двигателе, и может быть
определено как:
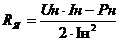 (Ом).
(Ом).
Коэффициент, который определяет магнитный поток
машины может быть определён с помощью следующего соотношения:
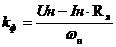 .
.
Рассчитаем электромеханические параметры
двигателя постоянного тока.
Активное сопротивление двигателя находится как:
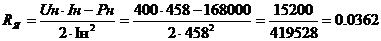 Ом.
Ом.
Находим количество пар полюсов:
Так как число пар полюсов в задании не задано,
то принимаю число пар полюсов равное двум.
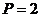 пары полюсов.
пары полюсов.
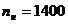 об/мин.
об/мин.
Индуктивность обмоток якоря находится по формуле
Уманского:
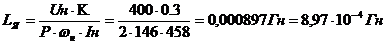 ;=(0,25..0,3),
K=0,3;
;=(0,25..0,3),
K=0,3;
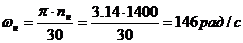 ;
;
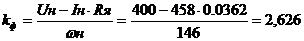 .
.
ЭДС которая возникает в обмотках якоря при
пересечении ими магнитного потока:
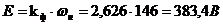 .
.
Момент номинальный:
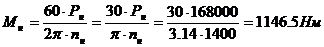
Ток якоря:
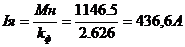 .
.
Напряжение якоря:
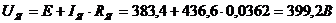 .
.
2. Математическое моделирование ДПТ
Для получения математической модели необходимо
получить систему дифференциальных уравнений (СДУ), которая описывает работу
системы электропривода. Описание объекта в виде СДУ является наиболее общим,
потому что из него, как частный случай, можно получить уравнение для
статических режимов, приравняв производные функций к нулю.
Математическая модель электрической машины (ЭМ)
любого типа состоит из уравнений электрического равновесия всех контуров ЭМ и
уравнения движения ротора.
Для ДПТ схема замещения будет иметь вид:
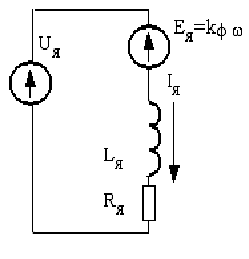
Рис. 1 Схема замещения ДПТ.
Будем считать, что все параметры схемы замещения
постоянные величины, и kф=const (для ДПТ независимого возбуждения).
Уравнение равновесия по второму закону Кирхгофа будет:
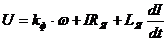 .
.
Уравнение движения:
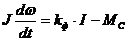 .
.
Или в канонической форме:
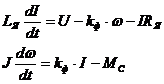 ;
;
где Мс - момент нагрузки.
Эта система уравнений линейная и допускает
аналитическое решение.
Записав полученные уравнения в операторной
форме, получим передаточные функции между напряжением, током, моментом и
скоростью, где
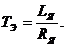
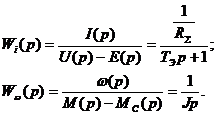
Эти передаточные функции положим в основу
структурной схемы модели:
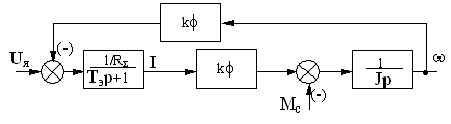
Рис. 2 Структурная схема модели.
При регулировании магнитного потока необходимо
учитывать динамические свойства обмотки возбуждения.
Дифференциальное уравнение обмотки возбуждения:
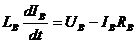
или в операторной форме
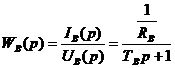
Кривая намагничивания может быть учтена
введением нелинейного уравнения 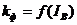 , а на структурной
схеме введением функционального блока.
, а на структурной
схеме введением функционального блока.
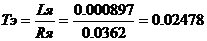 .
.
Передаточные функции электрической и
механической части двигателя:
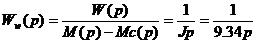 .
.
Передаточная функция разомкнутой системы:
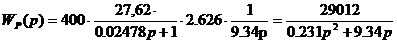 .
.
Передаточная функция замкнутой системы:
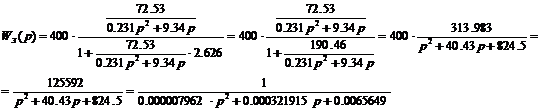
Моделирование двигателя постоянного тока
выполняем с помощью программного пакета Scilab 5.4.1
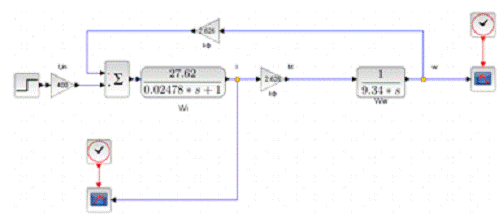
Рис. 3 Структурная схема реализованной
математической модели двигателя.
При реализации модели (рис. 3) не была учтена
нагрузка, т.к. конкретного значения нагрузки в задании не задано. В реальных
условиях нагрузка есть всегда, даже когда к двигателю не подключен приводимый
механизм. В этом случае нагрузкой выступают: сила трения якоря об воздух, сила
трения вала об подшипники, сила трения щеток об коллектор и т.д..
По графику кривой тока (рис. 4) можно видеть
огромный пусковой ток, более 7000 ампер, т.к. запуск двигателя в модели
осуществлён напрямую от источника питания. В реальных условиях используют
пускатели, которые ограничивают пусковой ток. Также по графику можно видеть
падение тока практически до нуля, это происходит из-за отсутствия нагрузки.
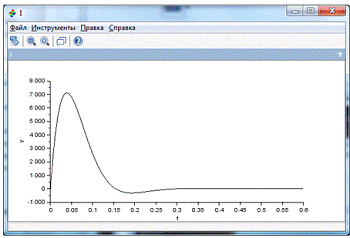
Рис. 4 График кривой тока.
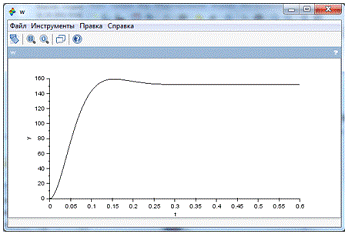
Рис. 5 График кривой угловой скорости.
3. Аппроксимация полученной переходной
характеристики элементарными динамическими звеньями
Из рисунка 5 видно, что характеристика
колебательная, колебания затухающие. Теперь необходимо представить переходную
характеристику в виде массива точек.
Таблица 2 Переходная характеристика в виде
точек.
|
x
|
0
|
0.006
|
0.009
|
0.012
|
0.022
|
0.055
|
0.08
|
0.099
|
0.1153
|
0.154
|
0.27
|
|
y
|
0
|
2
|
5
|
8
|
22
|
86
|
124
|
143
|
152.31
|
159.123
|
152.31
|
|
x
|
0.309
|
0.4113
|
0.6
|
|
|
y
|
152.02
|
152.31
|
152.31
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теперь строим график в программе Mathcad.
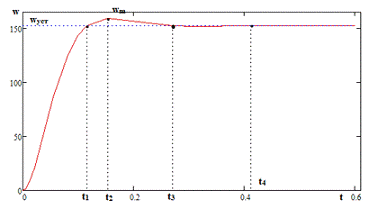
Рис. 6. График переходной характеристики
Способ 1.
Переходная характеристика описывается
колебательным звеном с передаточной функцией
 ,
,
где x - коэффициент
демпфирования, численное значение которого лежит в пределах 0 < x
< 1.
Дифференциальное уравнение колебательного звена,
соответствующее этой передаточной функции, имеет вид:
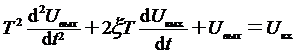 ,
,
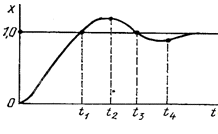
Рис. 7 Кривая разгона
Так как 0<x<1, то корни
характеристического уравнения будут комплексными:
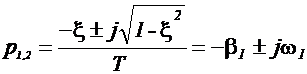 ,
,
где 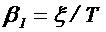 -
логарифмический декремент затухания;
-
логарифмический декремент затухания;
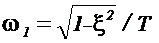 - частота
колебаний.
- частота
колебаний.
Решение дифференциального уравнения
колебательного звена имеет вид
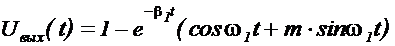 ,
,
где 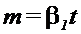 -
степень колебательности.
-
степень колебательности.
Искомые динамические параметры определяют из
переходной характеристики по формулам:
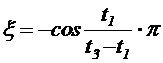 ,
, 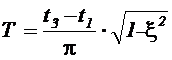 ;
k= ωуст=152.311=0.1153;
t3=0.27;
;
k= ωуст=152.311=0.1153;
t3=0.27; 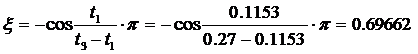 ;
;
Передаточная функция аппроксимированной первым
способом переходной характеристики.
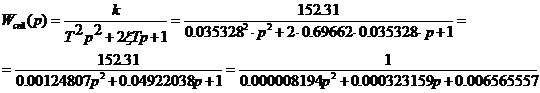

Рис. 8 Структурная схема модели
аппроксимированной первым способом передаточной функции.
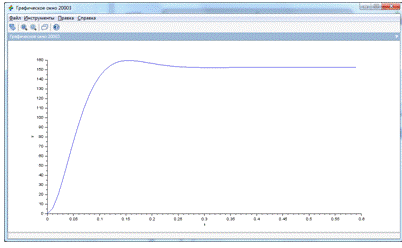
Рис. 9 График аппроксимированной первым способом
передаточной функции.
Способ 2
Переходная характеристика описывается
колебательным звеном с передаточной функцией
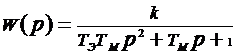 ,
,
Переходная характеристика описывается
дифференциальным уравнением вида
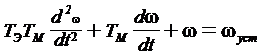 .
.
Введем в рассмотрение динамические параметры 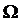 и
и
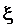 ,
которые однозначно связаны с
,
которые однозначно связаны с 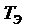 и
и 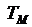 следующими
выражениями:
следующими
выражениями:
угловая частота недемпфированных колебаний,
определяющих масштаб времени процесса
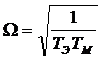 ;
;
относительный коэффициент затухания колебаний,
определяющий колебательность процесса
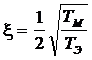 .
.
Из этих соотношений можно получить, что
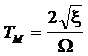 ,
, 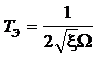 .
.
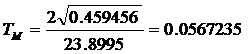 ,
,
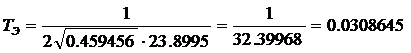
Вся область изменения 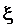 может
быть разбита на три интервала:
может
быть разбита на три интервала:
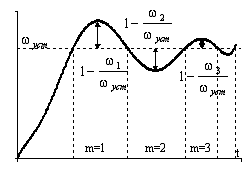
Рис. 10 кривая разгона.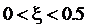 ;
;
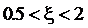 ;
;
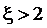 .
.
В первом интервале кривая разгона является резко
колебательной (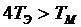 ) и по величине
перерегулирования может быть определена величина
) и по величине
перерегулирования может быть определена величина 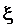
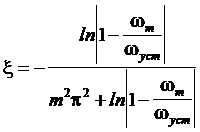 ,
,
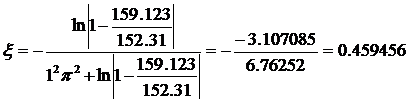
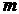 - порядковый номер
экстремума,
- порядковый номер
экстремума, 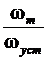 - ордината графика
в точке экстремума.
- ордината графика
в точке экстремума.
m=1; ωm=159.23;
ωуст=152.31;
k= ωуст=152.31.
Угловая частота колебаний 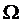 определяется
по выражению
определяется
по выражению
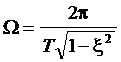 ,
,
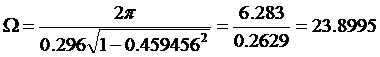
где 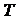 -
период колебаний.
-
период колебаний.
Т=0,4113-0,1153=0.296
Передаточная функция аппроксимированной способом
2 переходной характеристики
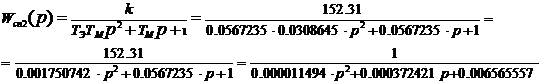
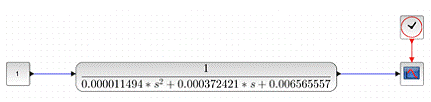
Рис. 11 Структурная схема модели
аппроксимированной вторым способом передаточной функции.
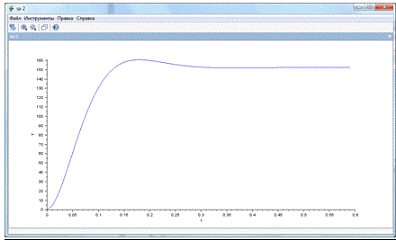
Рис. 12 График аппроксимированной вторым
способом передаточной функции.
Вывод
Для данной математической модели наиболее
оптимальным способом аппроксимации переходных характеристик элементарными
динамическими звеньями является первый способ аппроксимации колебательного
звена потому, что полученная в результате передаточная функция наиболее близкая
к исходной, полученной при математическом моделировании ДПТ в программе Scilab
5.4.1. Это хорошо видно на рисунке 13.
электропривод двигатель машина ток
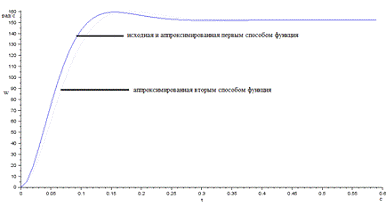
Рис. 13 Сравнение графиков исходной и
аппроксимированных функций
Теперь сравним коэффициенты исходной (Wз(p))
и аппроксимированных (Wсп1(p),Wсп2(p)) передаточных
функций:
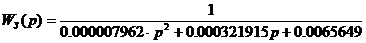
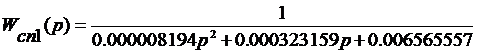
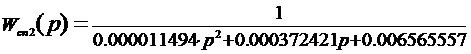
Сравнение коэффициентов заключается в нахождении
на сколько процентов коэффициенты аппроксимированных функций больше или меньше
исходных.
Способ 1
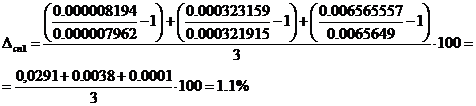
Коэффициенты аппроксимированной первым способом
передаточной функции больше чем у исходной в среднем на 1.1%
Способ 2
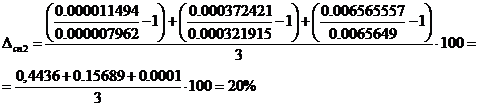
Коэффициенты аппроксимированной вторым способом
передаточной функции больше чем у исходной в среднем на 20%. Эта разница и
обуславливает увеличение запаздывания аппроксимированной вторым способом
передаточной функции.
Литература
1.
Бернас С., Цек С., Математические модели элементов электроэнергетических
систем, 1982 г.
.
Башарин А.В., Постников Ю.В., Примеры расчета автоматизированного
электропривода на ЭВМ, 1990 г.
.
Плахтина Е.Г., Математическое моделирование электро-машинно-вентильных систем,
1986 г.
.
Стульников В.И., Колчев Е.В., Моделирование полупроводниковых преобразователей,
1971 г.
.
Банде Б., Методы оптимизации. Вводный курс, 1988 г.
.
Алексеев Е.Р., Чеснокова О.В., Рудченко Е.А. Scilab. Решение инженерных и
математических задач. 2008 г.