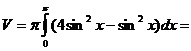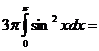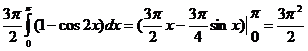Математический анализ
1.
Найти следующие пределы
точка функция дифференциальное исчисление
а)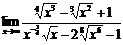 
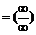
Решение:
Числитель и знаменатель разделим на наивысшую
степень -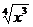 
=
= 
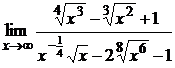
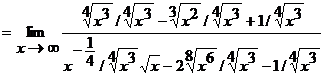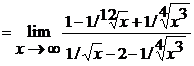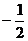
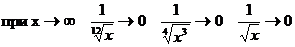
б)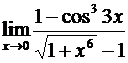 
~
.
~
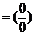
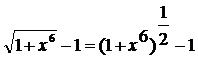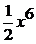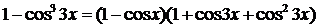
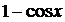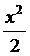
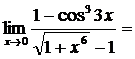
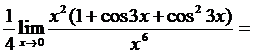
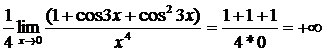
2.
Найти производные функций, заданных в явном и неявном виде
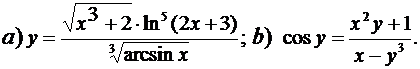
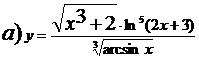
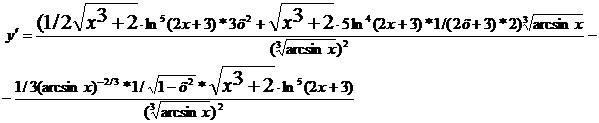
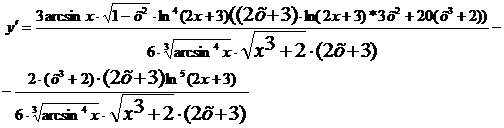
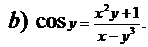
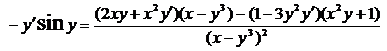
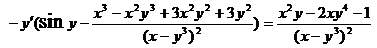
3.
Исследовать функцию методами дифференциального исчисления и построить ее график
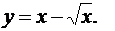
Решение:
1. 
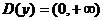
. y(x) непрерывна на D(y).
. Наклонные асимптоты:
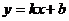
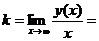
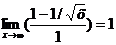
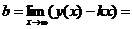
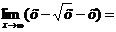
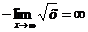
Асимптот
нет
4.
Точки экстремума
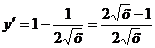
Приравняем
производную к нулю
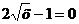
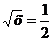
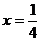
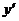не
существует в точке x = 0.
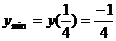
5.
Точки перегиба
Точек
перегиба нет
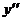не
существует в точке x=0
6.
Точки пересечения с осями
Ох: у=0,
=
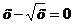
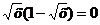0, x =1
(0,0) (1,0)
Оy: x = 0 ,
у=0 (0,0)
7.
График функции:
Найти градиент функции Z в точке М
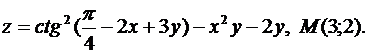
Рассматривая у как постоянную величину, дифференцируем
функцию по переменной х.
.
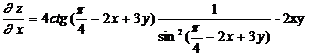Аналогично,
рассматривая х как постоянную величину, получаем:
.
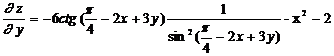Находим значения частных производных в точке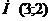 
:
,
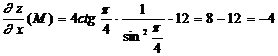Таким
образом,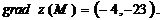 
Ответ: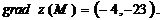
5. Вычислить неопределенные интегралы
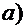
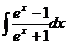
Замена: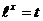 
=
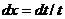
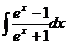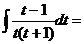
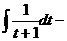
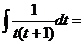
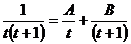
При t: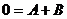 
При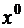 
:
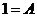=1,
B=-1
=
,
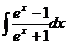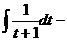
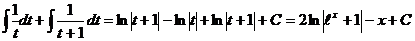
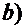
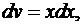
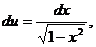
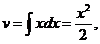
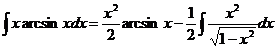
Зам а: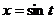 
.
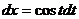
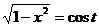
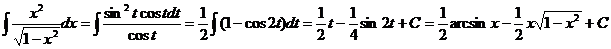
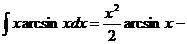
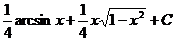
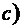
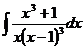Разложим правильную рациональную дробь на сумму
простейших дробей:
.
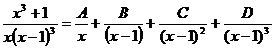Приводя дроби к общему знаменателю и приравнивая
числители, получим:
При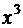 
:
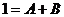
При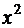 
:
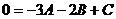
При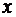 
:
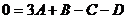
При :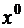
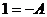=-1,
B=2, C=1, D=-2
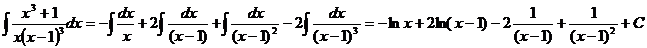6. Вычислить объем тела, образованного вращением фигуры, ограниченной графиками
функций, вокруг оси OX (2.11-2.15)
.
.
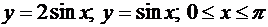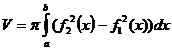