|
№
|
Наименование
|
Единицы
измерения
|
Числ.
Значения
|
Обозначения
|
|
1
|
Объем
аппарата
|
л
|
500
|
V
|
|
2
|
Теплоемкость
вещества в аппарате и входных потоках
|
кДж/кгК
|
4,19
|
Cр
|
|
3
|
Плотность
вещества в аппарате
|
кг/л
|
1,1
|

|
|
4
|
Поверхность
теплообмена
|
м2
|
2,3
|
Fт
|
|
5
|
Тепловой
эффект реакции
|
кДж/моль
|
100
|
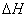
|
|
6
|
Предэкспоненциальный
множитель константы скорости
|
1/мин
|
20
1 10 2
|
k1
k2
k3 k4
|
|
7
|
Энергия
активации
|
кДж/моль
|
20000
25000 20000 20000
|
E1
E2
E3
E4.
|
|
8
|
Концентрация
компонента А на входе
|
моль/л
|
1
|
CА.вх
|
|
9
|
Расход
на входе в реактор V1
|
л/мин
|
1,5
|
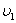
|
|
10
|
Расход
на входе в реактор V2
|
л/мин
|
0,5
|
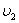
|
|
11
|
Расход
на выходе
|
л/мин
|
2
|
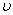
|
|
12
|
Температура
на входе в реактор t1
|
градС
|
25
|
t1
|
|
13
|
Температура
на входе в реактор t2
|
градС
|
35
|
t2
|
|
14
|
Диаметр
аппарата
|
м
|
0,86
|
Dp
|
|
15
|
Уровень
жидкости
|
м
|
0,86
|
Hp
|
2. Разработка математической модели
Исследование реактора, как объекта управления,
оптимизация режима работы на стадии проектирования предполагает наличие
математической модели. Математическая модель представляет собой уравнение
материальных балансов по массе и различным компонентам и тепловых балансов, которые
выражают закон сохранения вещества и энергии.
Формулировка упрощающих допущений:
) Структуры потоков в основной емкости
описываются моделью идеального перемешивания.
) Потерями тепла в окружающую среду
пренебрегаем.
) Теплоёмкостью стенок пренебрегаем.
) Расход теплоносителя на выходе и входе
одинаков.
) Теплофизические свойства реагирующей
смеси и теплоносители постоянны
Стехиометрический анализ и модель кинетики.
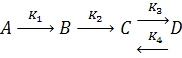
Разобьем реакцию на четыре стадии:
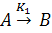
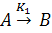
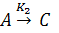
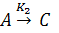
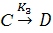
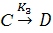
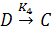
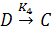
Для каждой стадии запишем свою скорость:
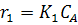
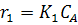 ,
, 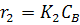
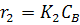 ,
, 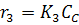
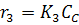 ,
, 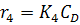
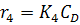 .
.
Где 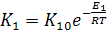
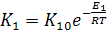 ,
, 
 ,
, 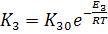
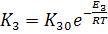 ,
, 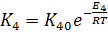
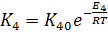 .
.
Выпишем матрицу стехиометрических коэффициентов:
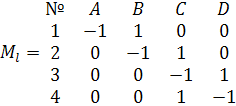
Скорости реакции по компонентам:
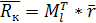
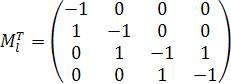
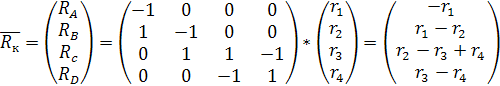
Скорость реакции по компонентам:
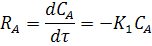
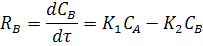
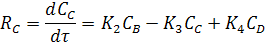
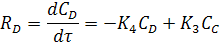
Уравнение общего материального баланса:
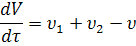
Уравнение материального баланса по компоненту А:
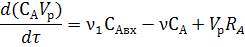
По компоненту B:
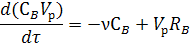
По компоненту C:
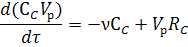
По компоненту D:
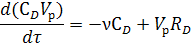
Уравнение теплового баланса для ёмкости:
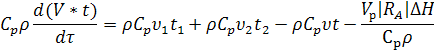
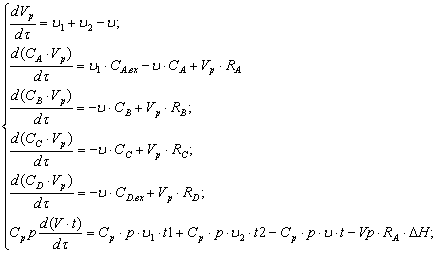 (1)
(1)
(1)Модель динамики объекта
представляет собой систему нелинейных дифференциальных уравнений
Начальные условия:
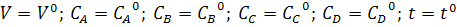
Модель статики:
= х1о + х2о
- хо
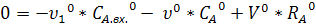
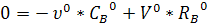
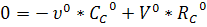
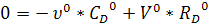
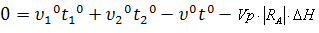
Полученная математическая модель
статики объекта представляет собой систему нелинейных алгебраических уравнений.
Для её решения можно воспользоваться численными методами.
3. Оптимизация объекта
Задача оптимизации: определить объём
аппарата и температуру, обеспечивающие максимальный выход целевого продукта при
заданных значениях входных переменных.
В качестве критерия оптимальности
объекта будем использовать выход целевого компонента B:
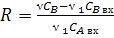
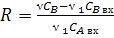 ,
,
где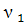
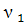 - расход входного потока;
- расход входного потока; 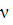
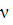 - расход реакционной массы в
выходном трубопроводе;
- расход реакционной массы в
выходном трубопроводе; 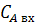
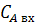 ,
, 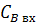
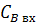 - концентрации соответствующих
компонентов в потоке
- концентрации соответствующих
компонентов в потоке 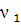
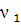 ;
; 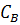
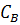 - концентрация целевого вещества в
выходном потоке.
- концентрация целевого вещества в
выходном потоке.
В соответствии с уравнением
математической модели можно сказать, что текущие значения величины 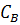
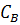 зависят от температуры и объема
аппарата, при заданных значениях входных переменных:
зависят от температуры и объема
аппарата, при заданных значениях входных переменных:
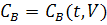
Таким образом задачей оптимизации
является:
Определение значения температуры и
объема, при которых R достигает максимальной величины.
t изменяется
в интервале от 70 °С до 90 °С, 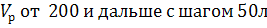
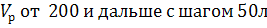
Порядок решения
1 Шаг.
Для решения задачи используем только
уравнения материального баланса по компонентам в статике.
Принимаем допущения, что объём
реакционной смеси есть величина постоянная Vр =const, тогда 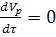
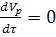 и
и 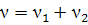
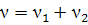
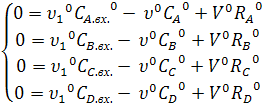
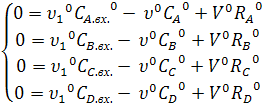 Рассчитываем величину R для
Рассчитываем величину R для 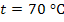
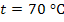 ,
, 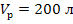
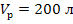 .
.


Аналогично рассчитываем R для 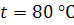
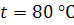 ,
, 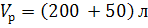
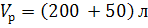 и для
и для 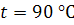
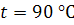 ,
, 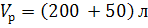
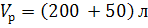 .
.
Зависимость R от V для 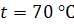
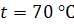 ,
, 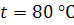
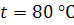 ,
, 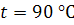
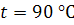 :
:
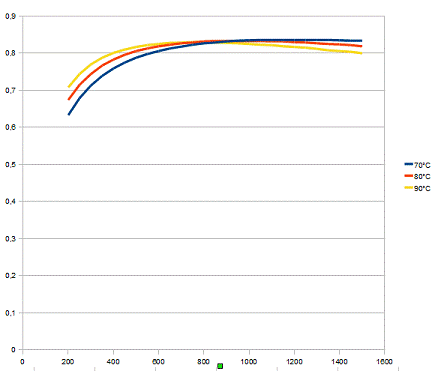
Рис.3.1. Зависимость выхода целевого
продукта от объема при температурах 70, 80 и 90 °С
Численные значения рассчитанных
величин
|
|
70°C
|
80°C
|
90°C
|
|
V
|
R
|
R
|
R
|
|
200
|
0,633
|
0,674
|
0,708
|
|
250
|
0,679
|
0,715
|
0,744
|
|
300
|
0,713
|
0,744
|
0,770
|
|
350
|
0,739
|
0,767
|
0,788
|
|
400
|
0,759
|
0,783
|
0,801
|
|
450
|
0,775
|
0,796
|
0,810
|
|
500
|
0,788
|
0,806
|
0,817
|
|
550
|
0,798
|
0,813
|
0,822
|
|
600
|
0,806
|
0,819
|
0,825
|
|
650
|
0,813
|
0,823
|
0,828
|
|
700
|
0,818
|
0,827
|
0,829
|
|
750
|
0,823
|
0,829
|
0,830
|
|
800
|
0,827
|
0,832
|
0,830
|
|
850
|
0,829
|
0,833
|
0,829
|
|
900
|
0,832
|
0,833
|
0,828
|
|
950
|
0,834
|
0,833
|
0,827
|
|
1000
|
0,835
|
0,833
|
0,825
|
|
1050
|
0,836
|
0,833
|
0,823
|
|
1100
|
0,836
|
0,832
|
0,822
|
|
1150
|
0,836
|
0,832
|
0,819
|
|
1200
|
0,836
|
0,830
|
0,817
|
|
1250
|
0,836
|
0,829
|
0,815
|
|
1300
|
0,836
|
0,827
|
0,812
|
|
1350
|
0,836
|
0,825
|
0,808
|
|
1400
|
0,835
|
0,824
|
0,806
|
|
1450
|
0,834
|
0,822
|
0,804
|
|
1500
|
0,834
|
0,819
|
0,800
|
Выход целевого продукта максимальный
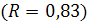
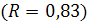 при
при 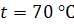
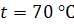 ,
, 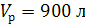
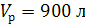 .
.
Концентрации компонентов CA, CB, CC, CD соответственно
при максимальном выходе целевого продукта 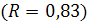
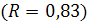 и расчет аппарата для V=900 л.
и расчет аппарата для V=900 л.

Выполним пересчет конструктивных параметров
реактора, учитывая оптимальные значения объема реактора и температуры
реакционной смеси в нем, при условии, что D=h.
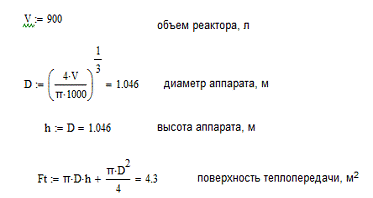
Шаг 2.
Определяем параметры теплового режима,
обеспечивающая оптимальные t, V,Ci
Для решения используем уравнение теплового
баланса:
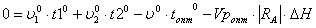
Листинг программы решения уравнения
теплового баланса.

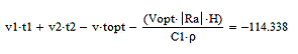
Результат решения уравнения
теплового баланса оказался отрицательным.
Это значит,что неправильно заданы
ориетировочные значения 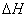 ,
,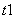 и
и 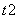 .
.
Зададимся 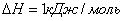 ,
,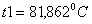 и
и 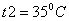 , тогда
, тогда
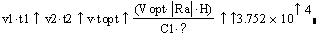
Проведём проверку правильности решения задачи.
Для этого решим нелинейную модель с начальными условиями, соответствующими
найденным значениям выходных переменных в оптимальном режиме. Если мы не будет
задавать входным переменным приращений, то графики изменения выходных
переменных во времени должны представлять собой прямые.
Листинг программы в среде MathCAD:
Исходные данные:
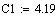
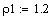
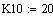
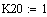

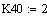
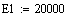
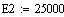
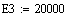
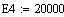
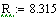
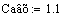
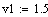
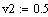
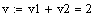
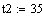
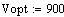
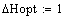

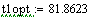
Постоянные коэффициенты:
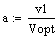
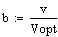
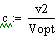
Константы скоростей:
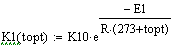

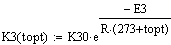
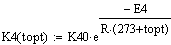
Вектор-функция правых частей дифференциальных
уравнений модели:
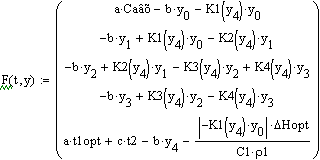
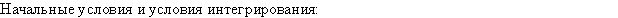
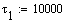
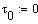
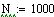
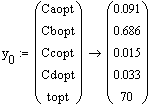
Результаты расчета:
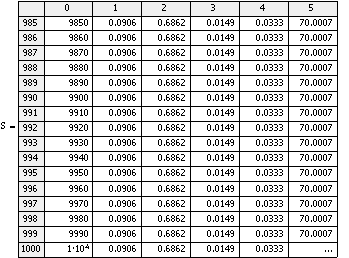
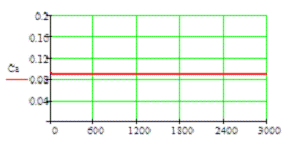
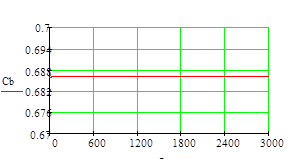
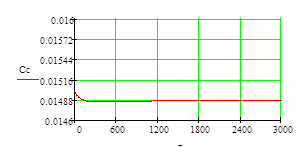
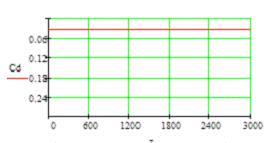
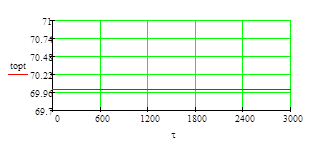
Полученные графики являются прямыми линиями,
можно сделать вывод о том, что найденные значения параметров являются верными и
программное средство написано правильно.
Таблица 3.Оптимальные значения основных
технологических параметров для моделирования объекта
|
|
Наименование
|
Единицы
измерения
|
Численное
значение
|
Обозначение
|
|
1.
|
Объем
аппарата
|
л
|
900
|
V
|
|
2.
|
Теплоемкость
вещества в аппарате и входных потоках
|
кДж/кг*К
|
4,19
|
Cp
|
|
3.
|
Плотность
вещества в аппарате и входных потоках
|
кг/л
|
1,2
|
ρ
|
|
4.
|
Тепловой
эффект реакции
|
кДж/моль
|
1
|
ΔH
|
|
5.
|
Предэкспоненциальный
множитель константы скорости
|
л/(мин*моль)
|
20
1 10 2
|
K10 K20 K30
K40
|
|
6.
|
Энергия
активации
|
Дж/моль
|
20000
25000 20000 20000
|
E1 E2 E3
E4
|
|
7.
|
Концентрация
компонента А на входе
|
моль/л
|
1.1
|
СAвх
|
|
8.
|
Расход
первого потока на входе в реактор
|
л/мин
|
1.5
|
υ1
|
|
9.
|
Расход
второго потока на входе в реактор
|
л/мин
|
0.5
|
υ2
|
|
10.
|
Температура
первого потока на входе в реактор
|
оС
|
81.862
|
t1
|
|
11.
|
Температура
второго потока на входе в реактор
|
оС
|
35
|
t2
|
|
12.
|
Диаметр
аппарата
|
м
|
1,046
|
D
|
|
13.
|
Уровень
жидкости
|
м
|
1,046
|
H
|
|
14.
|
Температура
в реакторе
|
оС
|
70
|
t
|
|
15.
|
Концентрация
компонента А на выходе В на выходе С на выходе D на выходе
|
моль/л
|
0,091 0,686 0,015 0,033
|
Ca Сb Cc Cd
|
4. Построение статических и динамических
характеристик объекта по различным каналам
.1 Построение статических характеристик
Статические характеристики получали методом
стационирования. Используются нелинейная модель объекта (2.2), и
предполагается, что уровень постоянен, т.е. V=const.
Программа расчета пускового режима аппарата написана в среде пакета Mathcad
с использованием встроенной функции для решения системы обыкновенных
дифференциальных уравнений Rkadapt.
Листинг программы рассмотрен на
примере канал 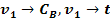
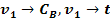
Постоянные коэффициенты
Исходные данные:
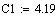
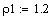
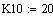
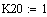

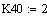
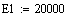
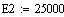
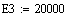
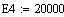
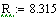
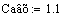
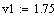
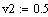
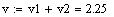
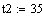
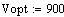
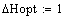

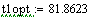
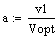
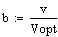
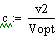
Константы скоростей:
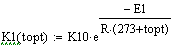

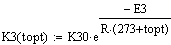
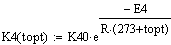
Вектор - функция правых частей дифференциальных
уравнений модели
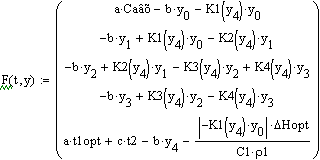
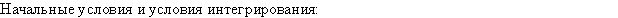
Решение дифференциальных уравнений
интегрирования:
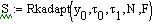
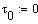
Результаты расчета:
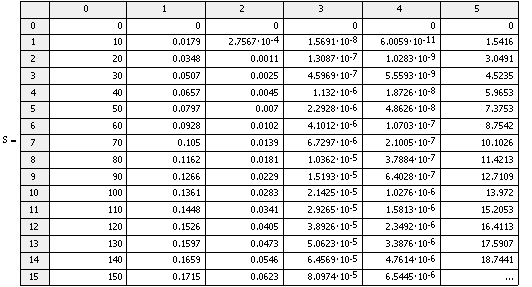
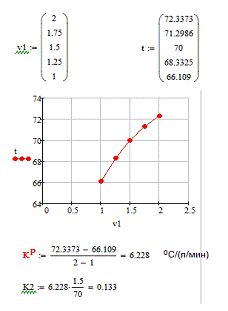
Статистические характеристики по каналам v1
--> Cb, v1 --> t:
Для определения размерного и безразмерного
коэффициента передачи по данному каналу проводим касательную в рабочей точке
статической характеристики (1.5; 0.686)
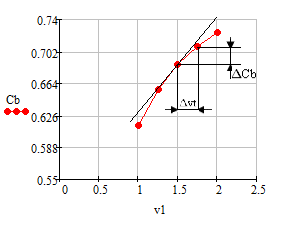
Размерный коэффициент передачи определяем по
следующей формуле:
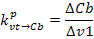
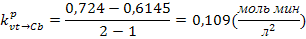
Безразмерный коэффициент передачи рассчитываем
по формуле:
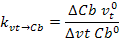
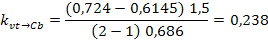
По аналогии строятся статические характеристики
и рассчитываются коэффициенты передачи по остальным каналам.
Статистические характеристики по каналам v2
--> Cb, v2 --> t:



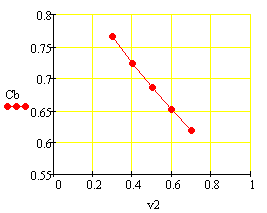
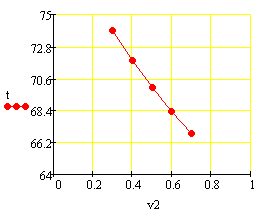
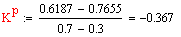
моль*мин/л2
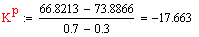
С/(л/мин)
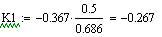
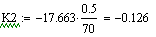
Статистические характеристики по каналам t1
--> t, t1 --> Cb:


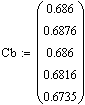
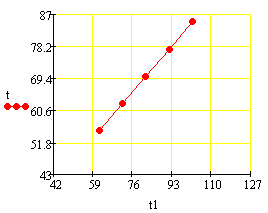
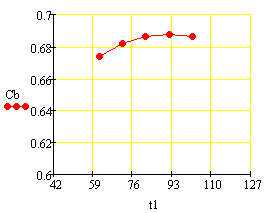
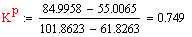
С/(л/мин)

моль*мин/л2
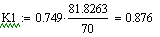
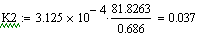
Статистические характеристики по каналам t2
--> t, t2 --> Cb:
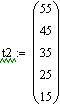
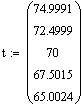
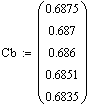

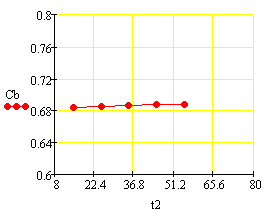
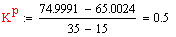
С/(л/мин)
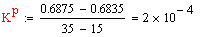
моль*мин/л2

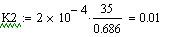
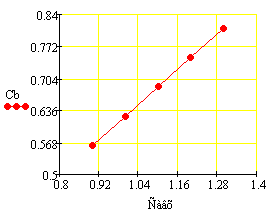
Статистические характеристики по каналам Савх
--> t, Савх --> Cb:


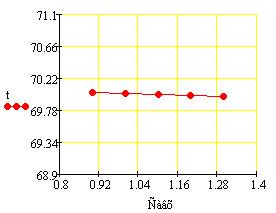
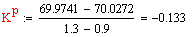
С/(л/мин)
моль*мин/л2
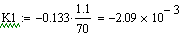
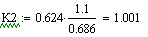
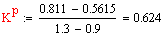
Вывод: таким образом, статические
характеристики имеют нелинейный характер по каналу 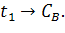
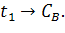 По остальным каналам они линейны
или близки к линейности.
По остальным каналам они линейны
или близки к линейности.
4.2 Построение динамических характеристик
Динамические свойства объекта исследовались путем
расчета реакции объекта на ступенчатое изменение входных переменных.
Ступенчатое изменение входной переменной задавалось путем соответствующего
изменения значения в уравнении (ступень не превышает 20 %). Начальные условия
интегрирования принимались равными значениям в статике.
Листинг программы рассмотрен на
примере каналов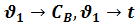
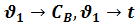 при положительных и отрицательных
относительно входных переменных изменениях входных переменных
при положительных и отрицательных
относительно входных переменных изменениях входных переменных

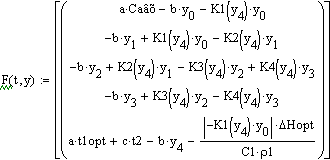
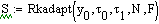
Результаты расчета:
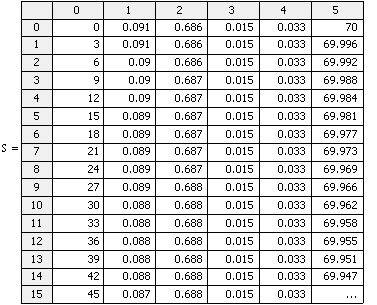
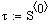
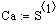
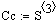

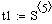
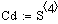
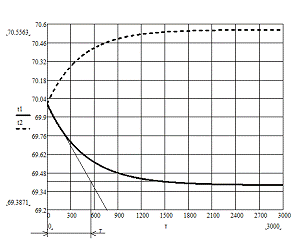
Время T
рассчитывается как среднее арифметическое постоянных времени, полученных при
отрицательном и положительном приращении :
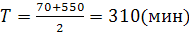
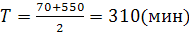
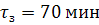
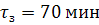
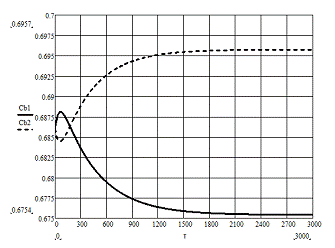

Динамические характеристики по
каналам 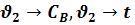
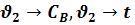
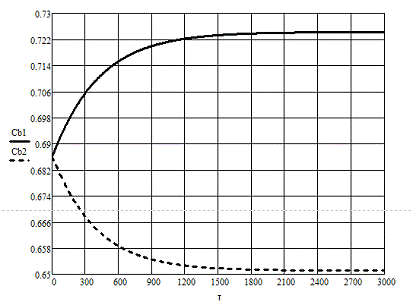
Т=500 мин
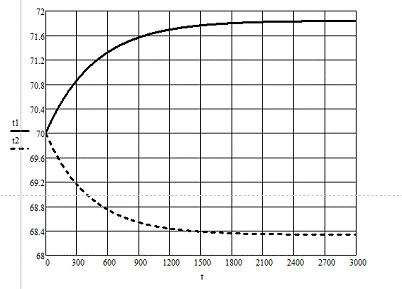
Т=485 мин
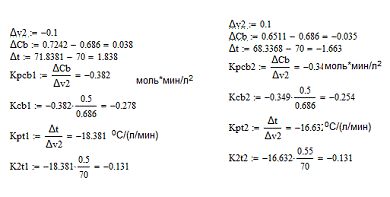
Расчет средних значений коэффицентов
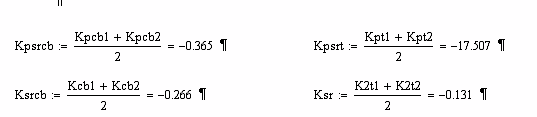
Динамические характеристики по
каналам 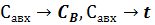
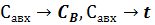
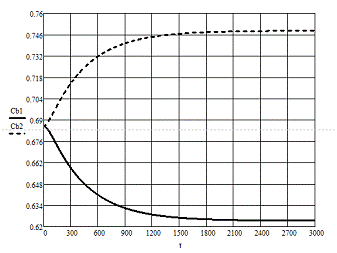
Т=620 мин
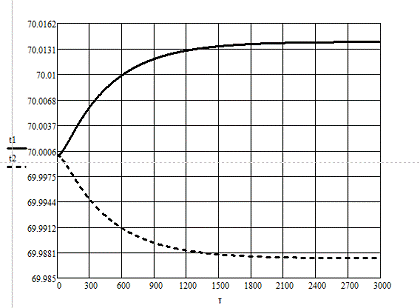
Т=662 мин

Расчет средних значений коэффицентов
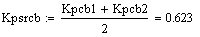
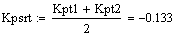
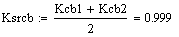
Динамические характеристики по каналам
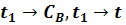
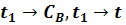
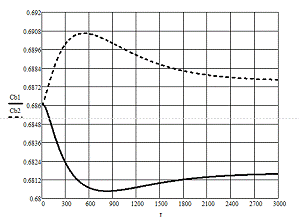
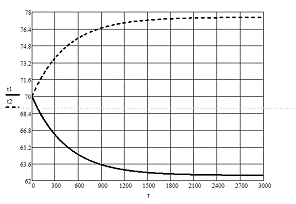
Т=481 мин
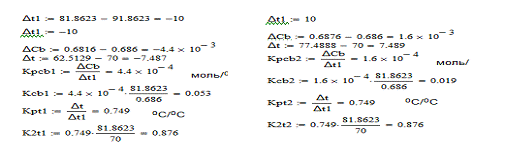
Расчет средних значений коэффицентов
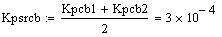
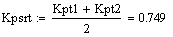

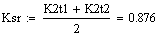
Динамические характеристики по
каналам 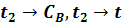
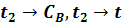
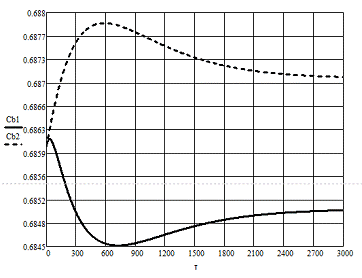
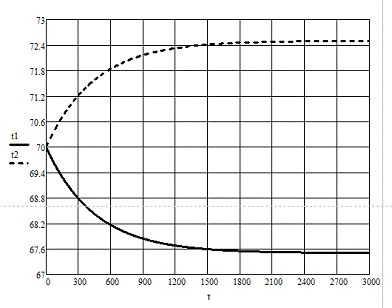
Т=448 мин
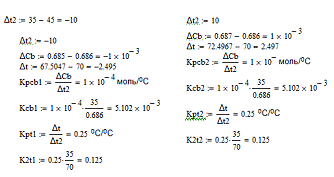
Расчет средних значений коэффицентов
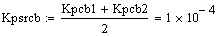
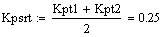

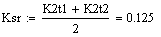
Вывод: Рассмотрев динамику по
различным каналам можно сделать вывод, что все каналы описываются как
последовательное соединение звена запаздывания и апериодического звена, кроме
канала 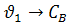
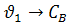
Таблица 4. Сводная таблица
параметров полученных по статическим и динамическим характеристикам:
|
Канал
|
Статика
|
Динамика
|
Ср.
знач.
|
|
Коб.р
|
Коб.бр
|
Коб.р
|
Коб.бр
|
Т
|
Коб.р
|
Коб.бр
|
|
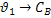
|
0,109(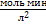 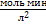 )0,2380,103( )0,2380,103(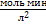 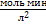 )0,226- 0,106
0.232 )0,226- 0,106
0.232
|
|
|
|
|
|
|
|
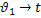
|
6,228(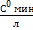 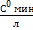 )0,1335,846( )0,1335,846(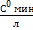 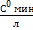 )0,1253106,037( )0,1253106,037(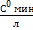 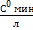 )0,129 )0,129
|
|
|
|
|
|
|
|
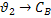
|
-0,367(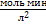 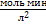 )-0,267-0,365( )-0,267-0,365(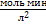 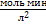 )-0,266500-0,366( )-0,266500-0,366(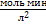 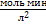 )-0,2665 )-0,2665
|
|
|
|
|
|
|
|
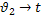
|
-17,663(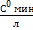 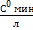 )-0,126-17,507( )-0,126-17,507(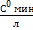 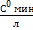 )-0,131485-17,585( )-0,131485-17,585(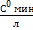 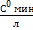 )-0,1285 )-0,1285
|
|
|
|
|
|
|
|
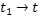
|
0,749(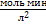 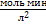 )0.8760,749( )0.8760,749(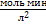 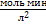 )0,8764810,749( )0,8764810,749(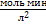 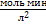 )0,876 )0,876
|
|
|
|
|
|
|
|
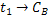
|
3,125*10-4(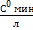 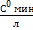 )0,0373*10-4( )0,0373*10-4(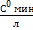 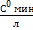 )0,036-3,0625( )0,036-3,0625(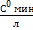 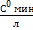 )0,0365 )0,0365
|
|
|
|
|
|
|
|
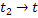
|
0,5(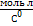 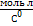 )0,250,25( )0,250,25(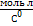 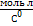 )0,1254480,375( )0,1254480,375(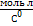 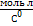 )0,1875 )0,1875
|
|
|
|
|
|
|
|
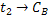
|
2*10-4
|
10,2*10-3
|
1*10-4
|
5,1*10-3
|
-
|
1,5*10-4
|
7,65*10-3
|
|
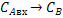
|
0,624
|
1,001
|
0,623
|
0,999
|
620
|
0,569
|
0,503225
|
|
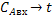
|
-0,133(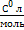 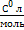 )-2,09*10-3-0,133( )-2,09*10-3-0,133(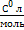 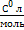 )-2,082*10-3662-0,133( )-2,082*10-3662-0,133(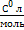 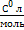 )2,086*10-3 )2,086*10-3
|
|
|
|
|
|
|
Выводы
При выполнении данной курсовой работы нами при
помощи методов математического моделирования был исследован химический реактор,
работающий в адиабатическом режиме. В ходе выполнения работы была проведена
оптимизация технологических параметров, результатом которой являются
оптимальные значения конструктивных и технологических параметров объекта. В
работе проводилось исследование статических и динамических свойств объекта. По
заданным каналам нами были построены статические и динамические характеристики.
Из полученных графиков нами были определены размерный и безразмерный
коэффициенты передачи для каждого исследуемого канала в статике и в динамике, а
также время запаздывания и постоянные времени Т.
Статические характеристики имеют нелинейный
характер по каналу 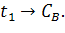
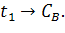 По остальным каналам они линейны
или близки к линейности.
По остальным каналам они линейны
или близки к линейности.
Анализируя характер кривых разгона
при положительном и отрицательном ступенчатом воздействии можно сделать вывод,
что реакция объекта симметрична, это означает, что объект близок к линейному в
динамике.
Значения коэффициента передачи
полученные в статике и в динамике оказались близки.
В качестве регулируемых переменных принимаем:
СB,
т.к. она определяет критерий эффективности.
t, т.к. на нее
наложены ограничения.
уровень V.
В качестве регулирующих воздействий принимаем:
Для поддержания концентрации CB,
можно выбрать Савх, т.к. по этому каналу безразмерный коэффициент
передачи больше, чем по другим каналам, реализовать это воздействие не сможем,
поэтому выбираем υ1.
Для поддержания температуры t
в качестве регулирующего воздействия используем расход на выходе из аппарата υ1.
- В качестве регулирующего воздействия на
уровень V, выбираем расход
на выходе из аппарата υ.
После анализа статических и динамических свойств
объекта, были выбраны регулирующие воздействия с целью решения задачи
стабилизации концентрации и температуры исходной смеси, с учетом возможностей
практической реализации.
Список используемых источников
1. Бесков В.С. Общая
химическая технология: учебник для вузов. - М.: ИКЦ "Академкнига",
2005. - 452 с.
2. Анализ технологических
процессов как объектов управления: метод.указания к выполнению курсовой работы
по дисциплине "Технологические процессы и производства" / Сост.: А.Н.
Лабутин, А.Е. Исаенков, ГВ. Волкова; Иван. гос. хим.-технол. ун-т. - Иваново,
2009. - 40с.
. Лабутин, А.Н., Волкова,
Г.В. Технологические процессы и производства как объекты управления: учебное
пособие / Иван. гос. хим. - технол. ун-т.; Иваново, 2010 - 96с.