Теория электрических и магнитных цепей
МІНІСТЕРСТВО
ОСВІТИ І НАУКИ УКРАЇНИ
КРИВОРІЗЬКИЙ
ІНСТИТУТ
ПВНЗ
«Кременчуцький університет економіки, інформаційних технологій та управління»
КУРС
ЛЕКЦІЙ
з
дисципліни
«Теорія
електричних та магнітних кіл»
для
студентів денної та заочної форм навчання
спеціальності
7.0901402
“Гнучкі
комп'ютеризовані системи та робототехніка”
Факультет
- інженерний
Кафедра
- технічної кібернетики
Кривий Ріг
2007
Розповсюдження і тиражування без
офіційного дозволу офіційного дозволу КІ ПВНЗ “КУЕІТУ” та укладача заборонено.
Курс лекцій з дисципліни «Теорія електричних та
магнітних кіл» складено згідно навчальної робочої програми цієї дисципліни і
містить основний теоретичний матеріал, знання якого обумовлено планом навчання.
Призначений для студентів денної та
заочної форм навчання інженерного факультету спеціальності 7.0901402 «Гнучкі
комп'ютеризовані системи та робототехніка».
Укладач: ст. викл. Супрунова Ю.А.
Методичні вказівки розглянуті та
рекомендовані до видання на засіданні кафедри технічної кібернетики
“30” серпня 2007 р., протокол № 1
Затверджено методичною радою
Криворізького інституту ПВНЗ КУЕІТУ
“13” вересня 2007 р., протокол № 1
Наклад згідно замовленню
Комп’ютерний набір: Супрунова Ю.А.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ 8
РАЗДЕЛ 1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ПОНЯТИЯ 10
1.1 Элементы электрической цепи 10
1.2 Источник ЭДС и источник тока 18
1.3 Схемы электрических цепей 21
1.4 Линейные электрические цепи 23
1.5 Основные законы электрических цепей 24
1.5.1 Закон Ома 25
1.5.2 Законы Кирхгофа 26
1.6 Энергия и мощность 28
1.7 Периодический и непериодический процессы в линейных
электрических цепях 31
1.8 Действующее и среднее значения периодической электрической
величины 33
РАЗДЕЛ 2. ЛИНЕЙНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА 35
2.1 Определение цепи постоянного тока 35
2.2 Напряжение на участке цепи 35
2.3 Закон Ома для участка цепи 36
2.3.1 Для участка, не содержащего э.д.с. 36
2.3.2 Для участка цепи, содержащего э.д.с. 37
2.4 Методы расчета цепей постоянного тока 37
2.4.1 Применение законов Кирхгофа к расчету цепей 37
2.4.2 Метод контурных токов 39
2.4.3 Метод наложения 43
2.4.4 Теорема взаимности 44
2.4.5 Теорема компенсации 45
2.4.6 Теорема об эквивалентном источнике 46
2.4.7 Теорема об эквивалентном источнике напряжения 46
2.4.8 Теорема об эквивалентном источнике тока 47
2.4.9 Замена параллельных ветвей, содержащих различные элементы,
одной 47
2.5 Преобразование электрических схем постоянного тока 52
2.5.1 Преобразование реального источника э.д.с. в реальный источник
тока 52
2.5.2. Преобразование звезды в треугольник и обратно 53
2.6. Активный и пассивный двухполюсник 56
2.6.1 Метод эквивалентного генератора 56
2.6.2 Передача энергии от активного двухполюсника нагрузке 58
РАЗДЕЛ 3. ТЕОРИЯ ЦЕПЕЙ ПЕРЕМЕННОГО СИНУСОИДАЛЬНОГО ТОКА 61
3.1 Основные соотношения в цепях синусоидального тока 61
3.1.1 Представление синусоидальных функции в виде проекций
вращающихся векторов 61
3.1.2 Действующее значение периодических токов, напряжений и э.д.с. 68
3.2 Элементы электрической цепи переменного синусоидального тока 70
3.2.1 Сопротивление 70
3.2.2 Емкость 70
3.2.3 Индуктивность 72
3.2.4 Последовательное соединение r, L, C 73
3.2.5 Параллельное соединение r, L, C 75
3.2.6 Мощность в цепи синусоидального тока 77
3.2.7 Цепь с активным сопротивлением (φ=0) 79
3.2.8 Реактивная цепь (=0,5) 80
3.2.9 Смешанная цепь 81
3.2.10 Баланс мощностей 84
3.2.11 Треугольник мощностей 84
3.2.12 Эквивалентные параметры и их экспериментальное определение 86
3.2.14 Применение комплексных чисел 89
3.2.15 Законы Ома и Кирхгофа в комплексной форме 99
3.2.16 Последовательное соединение r, L, С 99
3.2.17 Условие передачи источником максимума мощности приемнику 103
3.3 Резонанс в электрических цепях синусоидального переменного тока 105
РАЗДЕЛ 4. МНОГОФАЗНЫЕ ЦЕПИ
125
4.1 Понятие о многофазных электрических системах и цепях. 125
4.2 Симметричные многофазные системы с э.д.с 125
4.4 Связывание многофазных систем 128
4.5 Соединение звездой и треугольником в трехфазной системе 131
4.6 Расчет несимметричных трехфазных цепей при отсутствии
взаимоиндуктивности 132
ВВЕДЕНИЕ
электрическая магнитная
цепь ток
Электротехника - наука об
использовании электрических и магнитных явлений в практической деятельности
человека.
Начало развития электротехники
приходится на вторую половину XVII и первую половину XIX века, когда
были открыты основные закономерности в области электромагнитных и электрических
явлений.
Только 165 лет назад начались первые
попытки практического применение электричества, а уже в наше время тяжело
назвать какую-нибудь отрасль техники, где бы не использовалась электрическая
энергия. Современный технический прогресс зависит преимущественно от развития
электротехники. Невозможно даже представить себе жизнь современного общества
без широкого применения электричества.
Главное преимущество электрической
энергии перед другими видами энергии заключается в том, что, она универсальна и
имеет следующие ценные свойства: ее легко превратить в механическую, тепловую,
световую, химическую, звуковую и прочие виды энергий; ее удобно в больших
количествах при малых потерях передавать на большие расстояния; она дает
возможность осуществить механизацию и автоматизацию производства.
Только с применением электрической
энергии получены выдающиеся результаты в технике, связи, автоматике,
кибернетике, космонавтике, управлении производственными процессами и тому
подобное.
С применением электрической
аппаратуры и электронных приборов приобрели последующее развитие такие отрасли
науки, как медицина, биология, астрономия, геология, математика и др. Особенно
нужно отметить значение электронно-вычислительных машин для развития науки и
техники.
При изучении основ теоретической
электротехники перед студентами стоят две главные задачи.
Первая задача - всесторонне
ознакомиться и усвоить суть, электрических и магнитных явлений. Глубокое
понимание физической сути электрических и магнитных явлений дает возможность
целеустремленно использовать их при создании электротехнических устройств и
правильно эксплуатировать, избегая нежелательных и тем более вредных режимов.
Однако инженеру-системотехнику
недостаточно знаний одних физических явлений. Поэтому одновременно с изучением
физических явлений студенты должны приобретать навыки методов расчетов и
решении решения задач, которые будут возникать в практической деятельности
инженера-системотехника. Это вторая из упомянутых задач.
Понимание теории электрических
явлений и процессов базируется на знании студентов многих разделов математики и
физики. Из курса математики студенты должны знать алгебру комплексных чисел,
пользоваться соответствующим математическим аппаратом. Из курса физики студенты
должны знать основные электрические и магнитные величины (ток, напряжение,
потенциал, магнитная индукция, напряженность магнитного поля и законы, по
которыми их находят).
РАЗДЕЛ 1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ПОНЯТИЯ
.1 Элементы электрической цепи
Исследования и расчеты электрических цепей
основываются на различных допущениях и некоторой идеализации элементов цепи.
Под элементами в теории электрических цепей
подразумеваются обычно не физически существующие составные части какого-либо электрического
устройства, а идеализированные элементы цепи, теоретически обладающие особыми
электрическими или магнитными свойствами и в совокупности, приближенно
отображающие явления, происходящие в реальных устройствах.
Различают активные и пассивные элементы.
Активными элементами являются источники электрической
энергии. В них происходит процесс преобразования химической, механической или
другого вида энергии в электрическую энергию. Пассивными элементами
электрических цепей являются сопротивления, индуктивности, емкости.
Сопротивление R представляет элемент
цепи, в котором при прохождении тока происходит необратимый процесс
преобразования электрической энергии в тепловую.
Индуктивность L означает элемент цепи,
способный накапливать энергию магнитного поля,
Наконец, емкость C представляет собой
элемент цепи, способный накапливать энергию электрического поля.
Таким образом, каждому из этих элементов присущи свои
особые свойства.
Следует заметить, что каждый из этих терминов -
сопротивление, индуктивность, емкость и соответствующие им условные обозначения
R, L, C применяются в теории электрических цепей,
·во-первых, для обозначения самого элемента,
·во-вторых,-для обозначения его параметра, т. е. электрической или магнитной
величины, количественно характеризующей данный элемент.
В дальнейшем предполагается, что эти параметры не
зависят от напряжения или тока.
Так, термин сопротивление и соответствующее ему
буквенное обозначение R означают элемент цепи, в котором электрическая
энергия переходит в тепло и, вместе с тем, они выражают электрический параметр
данного элемента, равный отношению напряжения UR
на его зажимах к току i проходящему
через него, т.е.
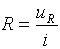 (1.1)
(1.1)
В системе СИ UR измеряется в
вольтах (В), i- в амперах (А), а R
в омах (ом).
В свою очередь, термин индуктивность и соответствующее
ему буквенное обозначение L означают элемент цепи, в котором
происходит, накопление энергии магнитного поля и, вместе с тем, они выражают
магнитную величину, равную отношению потокосцепления самоиндукции к току.
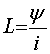 (1.2)
(1.2)
В системе СИ 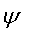 измеряется
в веберах (Вб),
измеряется
в веберах (Вб), 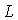 - в генри
(Гн).
- в генри
(Гн).
Электродвижущая сила (ЭДС) самоиндукции равна скорости
изменения потокосцепления (потокосцепление равно произведению магнитного потока
на число витков, пронизываемых этим потоком), т.е.
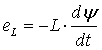 (1.3)
(1.3)
или с учетом (1.2),
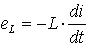 . (1.4)
. (1.4)
Знак “минус” в (1.4) обусловлен тем, что положительные
направления ЭДС самоиндукции и тока выбраны совпадающими.
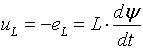 (1.5)
(1.5)
называется падением напряжения на индуктивности или,
что то же самое, напряжением на индуктивности.
Если часть магнитного потока, связанного с индуктивным
элементом, связана одновременно и с другим индуктивным элементом, то эти два
индуктивных элемента, кроме параметров L1 и L2,
обладают параметром M, именуемым взаимной индуктивностью.
Когда магнитные потоки и, соответственно,
потокосцепления являются линейными функциями тока, этот параметр определяется
отношением потокосцепления взаимной индукции к току
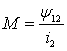 (1.6);
(1.6);
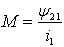 (1.7)
(1.7)
Здесь y12 - потокосцепление первого элемента, обусловленное
током второго элемента; а y12 -потокосцепление второго элемента, обусловленное
током первого элемента
В этом случае в первом и во втором элементах наводятся
ЭДС взаимной индукции, равные соответственно -
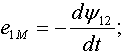 (1.8)
(1.8) 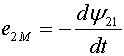 . (1.9).
. (1.9).
Из выражения (1.9) следует, что при скорости изменения
тока первого элемента, равной единице, во втором элементе наводится ЭДС, равная
M.
Если ЭДС, ток и время измеряются, соответственно, в
вольтах (В), амперах (А) и секундах (сек), то M
измеряется в генри (Гн).
В отличие от других параметров взаимная индуктивность
характеризует собой не самостоятельный элемент электрической цепи, а лишь
магнитную связь между индуктивными элементами.
Наконец, термин емкость и соответствующее ему
буквенное обозначение C означают элемент цепи, в котором
происходит накопление электрической энергии и, вместе с тем, они выражают
электрическую величину, равную отношению заряда к напряжению на этом элементе
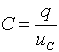 (1.10)
(1.10)
Если q и UC
измеряются в кулонах (к) и вольтах (В), то C измеряется
в фарадах (ф).
Допустим, что емкость C образована двумя
пластинами, разделенными диэлектриком. Под влиянием приложенного напряжения на
пластинах сосредоточены равные количества электричества противоположного знака:
пластина с более высоким потенциалом имеет положительный заряд (q>0),
а пластина с более низким потенциалом-отрицательный заряд (q<
0).
При изменении напряжения, приложенного к пластинам,
изменяется в соответствии с формулой (1.8) заряд q. На
пластину, потенциал которой возрастает, поступает положительный дополнительный
заряд, а на пластину, потенциал которой уменьшается, поступает такой же
отрицательный заряд.
Приток отрицательного заряда ко второй пластине
равносилен перемещению положительного заряда в обратную сторону - от второй
пластины во внешнюю цепь. Таким образом, с изменением напряжения на емкости в
цепи создается ток, величина которого определяется скоростью изменения
электрического заряда:
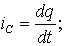 (1.11)
(1.11)
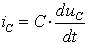 . (1.12)
. (1.12)
Этот ток рассматривается как ток проводимости в
проводниках, присоединенных к емкостному элементу (ток, обусловленный движением
электрических зарядов), и как ток смещения в диэлектрике емкостного элемента.
Последнее понятие, применяемое в теории поля, означает величину, прямо
пропорциональную скорости изменения напряженности электрического поля и имеющую
размерность тока. Благодаря введению этого понятия ток в цепи с емкостью
представляется замкнутым через диэлектрик.
Для сопротивления, индуктивности и емкости применяются
условные графические изображения, показанные на рис. 1.1.
R L C
Рис. 1.1 Условные изображения элементов электрических
схем
С помощью этих идеализированных элементов цепи
изображаются электрические схемы замещения различных физических устройств.
Следует заметить, что такие понятия, как индуктивная
катушка, конденсатор и реостат, означающие реальные электрические устройства, в
общем случае не совпадают с теоретическими понятиями индуктивность, емкость и
сопротивление, мыслящимися как раздельные, независимо друг от друга
существующие элементы цепи.
Представим себе простейшую индуктивную катушку в виде
кругового витка проводника, по которому проходит 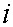 .
.
При постоянном токе 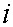 напряжение
на концах кругового витка определится величиной падения напряжения на его
сопротивлении в соответствии с (1.1) и ток во всех точках витка будет
одинаковым.
напряжение
на концах кругового витка определится величиной падения напряжения на его
сопротивлении в соответствии с (1.1) и ток во всех точках витка будет
одинаковым.
При переменном же токе изменяющееся магнитное поле
наведет в витке ЭДС самоиндукции; между концами, так же как и между другими
точками витка, электрическое поле станет переменным и в диэлектрике вокруг
витка возникнет ток смещения; в связи с этим в различных точках витка ток будет
неодинаковым.
Чем выше частота переменного тока, тем больше будут
ЭДС самоиндукции и ток смещения.
При низких частотах током смещения можно пренебречь.
При высоких же частотах ток смещения, обусловленный изменением напряженности
электрического поля, может быть соизмеримым с током в витке и даже превышать
его.
Таким образом, в зависимости от рабочего диапазона
частоты, электрическая схема замещения реального витка или катушки из 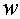 витков может состоять из различных теоретических
элементов.
витков может состоять из различных теоретических
элементов.
R
а) при постоянном токе;
R L
б)
при низкой частоте;
R L
C в) при высокой частоте.
Рис. 1.2 Электрические схемы замещения витка или
катушки
Представим себе теперь плоский конденсатор, состоящий
из двух параллельных пластин. При постоянном напряжении и идеальном диэлектрике
тока в цепи не будет. Если напряжение переменно, то в процессе изменения
электрического заряда возникнет переменный ток, создающий переменное магнитное
поле. Эффект, вызываемый магнитным полем, может быть учтен в электрической
схеме замещения с помощью некоторой индуктивности, включенной последовательно с
емкостью конденсатора. Обычно этой индуктивностью пренебрегают из-за её
малости.
Наконец, во всяком диэлектрике вследствие наличия
некоторой проводимости возникают тепловые токи, которые возрастают с ростом
частоты. Кроме того, происходит выделение тепла в пластинах конденсатора. Потери
на нагрев учитываются в схеме замещения конденсатора посредством сопротивления 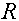 ,
включенного параллельно емкости
,
включенного параллельно емкости 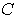 (рис.
1.3). R
(рис.
1.3). R
C
Рис 1.3 Электрическая схема замещения конденсатора.
Что касается реостатов и других устройств, именуемых
обычно сопротивлениями, то в них, наряду с зависимостью от температуры и
частоты, в той или иной степени проявляются и индуктивный и емкостный эффекты.
При низких частотах сопротивление мало отличается от
сопротивления при постоянном токе. С повышением же частот ток распределяется по
сечению проводника неравномерно, по мере приближения к центру проводника
плотность тока уменьшается, ток вытесняется к поверхности проводника, что
вызывает увеличение сопротивления.
Это явление, носящее название поверхностного эффекта,
учитывается обычно при высоких частотах и изучается в теории электромагнитного
поля.
Таким образом, в физических системах магнитные поля,
электрические поля и тепловые потери сопутствуют друг другу. Раздельное
рассмотрение индуктивностей, емкостей и сопротивлений используются лишь как
метод приближенного исследования явлений. Чем выше частота и чем больше
линейные размеры самих устройств, тем в большей мере проявляется взаимосвязь
электрических и магнитных параметров и неотделимость друг от друга
электрического и магнитного полей.
Такое положение, в частности, имеет место в линиях или
антеннах, протяженность которых соизмерима с длиной электромагнитной волны, и
больше нее.
Строго разграничить области частот, при которых
справедлива та или иная схема замещения, не представляется возможным, так как
это зависит от ряда факторов. Ориентировочно можно считать, что рассмотрение
устройств в виде отдельных элементов с сосредоточенными параметрами допустимо
при частотах, при которых длина электромагнитной волны не менее чем в 100 раз
превышает наибольший линейный размер устройств.
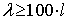 (1.13)
(1.13)
Длина электромагнитной волны равна отношению фазовой
скорости к частоте
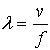 (1.14)
(1.14)
Если 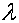 и l
измеряются в метрах, то, приравняв
и l
измеряются в метрах, то, приравняв 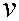 скорости
света (3×108 м/сек), получим на основании (1.13) и
(1.14)
скорости
света (3×108 м/сек), получим на основании (1.13) и
(1.14)
 . (1.15)
. (1.15)
Такое приближенное соотношение весьма условно, так как
диапазон частот, в котором процесс в цепи описывается простейшим уравнением
(1.5) или (1.12) зависит от конструкции.
.2 Источник ЭДС и источник тока
В качестве источников электрической энергии в теории
цепей используются условные устройства: источники ЭДС и источники тока.
Источник ЭДС представляет активный элемент с двумя
зажимами, напряжение u(t) на к`оторых не зависит от тока,
проходящего через источник. Предполагается, что внутри такого гипотетического
источника пассивные элементы отсутствуют, и поэтому прохождение через него тока
не вызывает в нем падения напряжения. Иначе говоря, напряжение на зажимах
такого источника равно его внутренней ЭДС. Условные обозначения источника ЭДС и
источника тока приведены на рис. 1.4, 1.5.
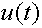
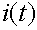
Рис 1.4 Источник ЭДС Рис 1.5 Источник тока.
Стрелкой указано положительное направление ЭДС, т.е.
направление возрастания потенциала в источнике для тех моментов времени, в
течение которых функция u(t) положительна.
Величина тока в электрической цепи, приключенной к
источнику ЭДС, зависит от параметров этой цепи и от u(t).
Если зажимы источника ЭДС замкнуть накоротко, то ток
теоретически должен быть бесконечно велик. Потому источник ЭДС является
источником бесконечной мощности (теоретическое понятие).
В действительности при замыкании зажимов физически
существующего источника электрической энергии (гальванического элемента,
аккумулятора или генератора), ток может иметь только конечное значение, так как
ЭДС источника компенсируется падением напряжения во внутреннем сопротивлении
или, соответственно, во внутренней индуктивности источника.
Схема замещения физического источника электрической
энергии представляется в виде источника ЭДС с последовательно включенным
пассивным элементом, характеризующим его внутреннее сопротивление и
индуктивность.
В дальнейшем такой источник, в отличие от источника
ЭДС, именуется источником напряжения. Обычно его внутренние параметры малы по
сравнению с параметрами внешней электрической цепи, они могут быть отнесены к
последней или в некоторых случаях могут вовсе не учитываться (в зависимости от
соотношения величин и требуемой точности расчета).
Источник тока представляет активный элемент, ток i(t)
которого не зависит от напряжения на зажимах.
Условное обозначение источника тока приведено на рис
1.6. Стрелки указывают положительное направление тока i(t), т. е.
направление движения положительных зарядов для тех моментов времени, в течение
которых функция i(t) положительна.
В случае источника постоянного тока направление
движения положительных зарядов совпадает с заданным положительным направлением
(ток положителен). В случае же синусоидальною тока i(t) в
одном из полу периодов положительные заряды перемещаются в направлении,
противоположном тому, которое принято за положительное. В этом полупериоде ток i(t)
отрицателен.
По мере неограниченного увеличения сопротивления
внешней цепи, присоединенной к источнику тока напряжение на его зажимах и,
соответственно, мощность, развиваемая им, неограниченно возрастают.
Поэтому источник тока, так же как и источник, ЭДС
является источником бесконечной мощности.
Пассивный элемент, характеризующий внутренние
параметры источника тока и присоединенный к его зажимам, ограничивает мощность
последнего.
Представляя собой теоретическое понятие, источник
тока, как будет показано ниже, применяется в ряде случаев для упрощения расчета
электрических цепей.
Некоторым подобием источника тока может служить
устройство, состоящее из аккумулятора, соединенного последовательно с большим
дополнительным сопротивлением. Другим примером источника тока является
полупроводниковый триод.
Эти устройства, имея сопротивления, несоизмеримо
большие, чем сопротивления внешней цепи, отдают ток, почти не зависящий от
изменения внешней нагрузки в широких пределах и именно в этом отношении они и
аналогичны источнику тока.
Зависимость напряжения на зажимах какого-либо
устройства от тока, проходящею через него, или зависимость тока от напряжения
называется вольтамперной характеристикой данного устройства.
Вольтамперные характеристики идеальных источников ЭДС
и тока представляют собой прямые, параллельные осям (рис. 1.6).
Вольтамперные характеристики реальных источников
электрической энергии могут приближаться к характеристикам источников ЭДС или
тока.
U
Источник ЭДС U Источник тока
I
I
Рис 1.6 Вольтамперные характеристики источника ЭДС и
источника тока
1.3 Схемы электрических цепей
Схема представляет графическое изображение
электрической цепи. Она показывает последовательность соединения элементов
электрической цепи.
“Электрическими” элементами схемы являются активные и
пассивные элементы, содержащиеся в данной цепи. Их условные обозначения были
приведены ранее.
“Геометрическими” элементами схемы являются узлы и
ветви.
Ветвь образуется одним или несколькими последовательно
включенными элементами, (рис. 1.7).
Узел - место соединения трех или большего числа ветвей
Линии, связывающие ветви в схеме, представляют
соединения без сопротивлений.
Узел Один узел
а) б)
Рис. 1.7 Узел электрической схемы.
Поэтому, например, схемы "а" и "б"
(рис. 1.7) в электрическом смысле одинаковы: они содержат один узел.
Ветви, присоединенные к одной паре узлов, называются
параллельными.
Узел
Ветвь Узел Рис 1.8
в виде примера
иллюстрирует схему
электрической цепи
содержащую 5 ветвей
и 3 узла
Узел
Ветвь
Любой замкнутый путь, проходящий по нескольким ветвям,
называется контуром. На рис 1.8 указан стрелкой один из контуров, образованных
в данной электрической схеме.
В зависимости от числа контуров, имеющихся в схеме,
различают одноконтурные и многоконтурные схемы.
Одноконтурная схема является простейшей. Пользуясь
правилами преобразования схем, в ряде случаев представляется возможным заменить
многоконтурную схему одноконтурной, что упрощает расчеты.
1.4 Линейные электрические цепи
Пассивные элементы электрической цепи называются
линейными, если напряжение и ток в элементе связаны между собой линейным
уравнением первого порядка - алгебраическим или дифференциальным.
Линейное сопротивление подчиняется закону Ома,
выражающему прямую пропорциональность между напряжением на зажимах
сопротивления и током, идущим через сопротивление.
Как видно из выражения (1.1), напряжение и ток в
сопротивлении прямо пропорциональны друг другу при условии, что величина r не
зависит от напряжения или тока,
В случае индуктивного или емкостного элементов
напряжение и ток связаны линейными дифференциальными уравнениями (1.5) или,
соответственно, (1.12) При этом предполагается, что величины L и C
не зависят от напряжения или тока.
Таким образом, сопротивление, а также индуктивный и
емкостный элементы линейны при условии, что значения R, Lи
C не зависят от электрических величин.
Что касается активных элементов электрической цепи, то
условием линейности источника ЭДС является независимость величины ЭДС от тока,
проходящего через источник. В свою очередь условием линейности источника тока
является независимость тока от напряжения на зажимах источника.
Электрическая цепь, состоящая из активных линейных и
пассивных элементов, называется линейной цепью.
Реальные электрические устройства, строго говоря, не
подчиняются линейному закону.
Так, например, при изменении тока в индуктивной
катушке с ферромагнитным сердечником соотношение между магнитным потоком (и,
соответственно, потокосцеплением) и током не сохраняется постоянным, т.е.
величина 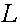 , входящая в
(1.2), в общем случае зависит от тока.
, входящая в
(1.2), в общем случае зависит от тока.
Кроме того, при прохождении тока через проводник
выделяется тепло, проводник нагревается и его сопротивление r изменяется.
В зависимости от типа диэлектрика в большей или
меньшей степени может также изменяться и емкость конденсатора в функции от
заряда (или от приложенного напряжения).
К нелинейным устройствам относятся, кроме того,
электронные, ионные и полупроводниковые приборы, параметры которых зависят от
электрических величин
Если в рабочем диапазоне, на который рассчитывается то
или иное устройство, т.е. при заданных ограниченных пределах изменения
электрических величин, закон линейности с достаточной для практики степенью
точности сохраняется, то такое устройство рассматривается как линейное.
Исследование и расчет линейных цепей сопряжены, как
правило, с меньшими трудностями, чем исследование и расчет нелинейных цепей. Поэтому
в тех случаях, когда линейный закон достаточно близко отражает физическую
действительность, цепь рассматривается как линейная.
Для облегчения решения задач часто пренебрегают
условиями, при которых реальные устройства теряют свойства линейности (например,
вследствие значительного перегрева), и электрическая цепь мыслится линейной
независимо от режима ее работы в неограниченном диапазоне.
1.5 Основные законы электрических цепей
Расчеты электрических цепей базируются на физических
законах, выражающих свойства электрических цепей. К числу основных законов
электрических цепей относятся законы Ома, Кирхгофа и Джоуля-Ленца.
1.5.1 Закон Ома
Закон Ома для линейных цепей выражает прямую
пропорциональность между напряжением на зажимах сопротивления и током, идущим
через данное сопротивление.
Если через линейное сопротивление R проходит
ток i, то потенциал зажима "1", в который ток входит, выше
потенциала зажима "2", из которого ток выходит.
Разность потенциалов между зажимами "1" и
"2", т.е. напряжение на сопротивлении r,
взятое по направлению тока, выражается формулой закона Ома
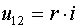 (1.16)
(1.16)
Напряжение, отсчитываемое в обратном направлении,
имеет противоположный знак
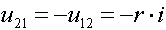 . (1.17)
. (1.17)
Порядок расположения индексов 1 и 2,
обозначающих зажимы, отвечает положительному направлению, выбранному для
напряжения. Поэтому для уяснения направления отсчета напряжения достаточно
руководствоваться индексами. При отсутствии индексов направление отсчета
указывается стрелкой.
Пользуясь величиной проводимости 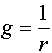 , можно, преобразовать формулу (1.16) в
, можно, преобразовать формулу (1.16) в
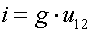 (1.18)
(1.18)
В соответствии с (I 16) или (1.18) сопротивление имеет
линейные вольтамперные характеристики, причем тангенс угла наклона
характеристики  к оси абсцисс пропорционален r:
к оси абсцисс пропорционален r:
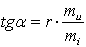 , (1.19)
, (1.19)
где mu и mi
--- масштабы, в которых отложены напряжения и токи.
В свою очередь, тангенс угла наклона характеристики 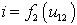 к оси абсцисс пропорционален
к оси абсцисс пропорционален 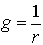
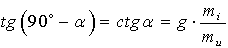 . (1.20)
. (1.20)
.5.2 Законы Кирхгофа
Первый закон Кирхгофа выражает тот факт, что в узле
электрический заряд не накапливается и не расходуется: сумма электрических
зарядов, приходящих к узлу, равна сумме зарядов, уходящих от узла, т.е.
алгебраическая сумма токов в узле равна нулю
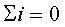 (1.21)
(1.21)
Суммирование распространяется на токи i в
ветвях, сходящихся в рассматриваемом узле. При этом знаки токов берутся с
учетом выбранных положительных направлений токов, указываемых обычно на схеме
стрелками; всем тикам, направленным к узлу, в уравнении (1.21) приписывается
одинаковый знак, например положительный, и, соответственно, все токи,
направленные от узла, входят в уравнение (1.21) с обратным знаком. Иначе
говоря, всякий ток, направленный от узла, может рассматриваться как ток,
направленный к узлу, но имеющий противоположный знак.
Первый закон Кирхгофа применим не только к узлу, но и
к любому замкнутому контуру.
Записав для всех узлов контура уравнения по первому
закону Кирхгофа и просуммировав их, получим, что сумма токов, подходящих к
данному контуру и отходящих от него, равна нулю.
При этом правило знаков, указанное выше, сохраняется.
Второй закон Кирхгофа формулируется следующим образом:
алгебраическая сумма напряжений на всех ветвях замкнутого контура равна нулю:
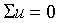 (1.22)
(1.22)
Обход контура совершается в произвольно выбираемом
направлении, например, по ходу часовой стрелки. При этом соблюдается следующее
правило знаков для ЭДС и падений напряжения, входящих в уравнение (1.22): ЭДС и
падения напряжения, совпадающие по направлению с направлением
обхода контура, берутся с разными знаками.
Таким образом, второй закон Кирхгофа устанавливает,
что алгебраическая сумма ЭДС в замкнутом контуре равна алгебраической сумме
падений напряжения в элементах этого контура.
E1 U2
Рис. 1.9
Направление
U1
обхода U3
E2 U4
Например, для схемы рис. 1.9 имеем:
E1 - U2 +U3 +U4 - E2 +U1= 0 или E1 - E2=U2 - U3 - U4.
Разность потенциалов или напряжение между двумя
точками электрической цепи равна работе, совершаемой при перемещении единичного
электрического заряда из одной точки в другую.
Следовательно, второй закон Кирхгофа устанавливает,
что работа, совершаемая при мысленном перемещении пробного заряда вдоль
замкнутого пути, равна нулю, поскольку заряд возвращается в исходное положение
(здесь учитывается различие знаков работы, совершаемой при перемещении
электрического заряда в сторону возрастания и убывания потенциала). Таким
образом, второй закон Кирхгофа соответствует закону сохранения энергии.
1.6 Энергия и мощность
Положим, что за элементарный промежуток времени dt через
электрическую цепь (приемник энергии) под воздействием приложенного напряжения и.
проходит электрический заряд dq.
Элементарная работа, совершаемая за этот промежуток
времени или, что то же, элементарная энергия, поступающая в приемник, равна
= u×dq = u×i×dt. (1.23)
В системе МКСА энергия измеряется в джоулях (дж).
Мгновенная мощность определяется как производная
энергии по времени
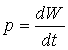 (1.24)
(1.24)
т.е. равна произведению мгновенных значений напряжения
и тока.
Рассмотрим в отдельности выражения мгновенных значений
энергии и мощности для разных элементов цепи.
Мощность р - величина алгебраическая; она
положительна при одинаковых знаках и и i.
Если положительные направления для напряжения и тока
приняты совпадающими, то при p>0 энергия поступает от источника к
приемнику, а при р<0 энергия возвращается из рассматриваемой цепи к
источнику.
В соответствии с (1.24) мощность, расходуемая в
сопротивлении r,
 (1.25)
(1.25)
Мощность на зажимах индуктивности
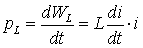 (1.26)
(1.26)
Мощность на зажимах емкости:
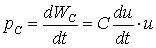 (1-27)
(1-27)
По закону Джоуля-Ленца энергия, необходимая для
поддержания тока i в сопротивлении r, равна
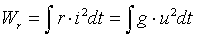 (1-28)
(1-28)
Пределы интеграла определяются рассматриваемым
промежутком времени, в течение которого электрическая энергия расходуется в
данном сопротивлении.
Энергия магнитного поля индуктивности L, через
которую проходит ток i, равна
 (1-29)
(1-29)
В свою очередь, энергия электрического поля емкости C,
напряжение на которой равно и, определяется по формуле:
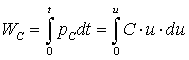 (1-30)
(1-30)
Из приведенных выше выражений видно, что энергия
представляет положительную величину.
1.7 Периодический и непериодический процессы в линейных
электрических цепях
Процессы в электрических цепях делятся на установившиеся
и переходные или, соответственно, на периодические и непериодические.
Установившийся процесс в электрический цепи
характеризуется тем, что электрические величины (напряжение, ток, заряд)
остаются в течение всего времени постоянными или изменяются периодически.
Функция f(t), аргумент которой физически
означает время, является периодической функцией, если для любого положительного
или отрицательного значения t соблюдается равенство
(t+T) =f(t). (1.27)
Здесь T - период, т. е. наименьший промежуток времени,
через который функция повторяется.
Геометрически это означает, что ординаты двух
произвольных точек графика f(t) с абсциссами, отличающимися на Т,
одинаковы
Величина, обратная периоду, т. е. число периодов в
единицу времени, называется частотой.
В системе СИ частота имеет размерность (сек)-1,
а единицей измерения частоты служит герц (частота равна 1 Гц,
если период равен 1 сек).
Если постоянную величину условиться рассматривать как
предел периодической функции с бесконечным периодом или, что то же, с частотой,
равной нулю, то установившийся режим в общем случае можно определить как
периодический.
Условие (1.31) выражает бесконечную периодическую
повторяемость явления; периодичность функции означает ее существование в любой
момент времени, предшествовавший рассматриваемому моменту.
Бесконечной периодической повторяемости явлений в
действительности нет. Поэтому периодическую функцию в строгом смысле следует
рассматривать как некоторую математическую абстракцию, применяемую при
практических расчетах.
С приближением, вполне достаточным для инженерной
практики, многие процессы в электрических цепях считаются периодическими и,
соответственно, режим работы цепи - установившимся.
Токи установившегося режима рассматриваются как
вынужденные колебания, обусловленные источниками электрической энергии,
например источниками ЭДС, действующими в цепи.
Частота этих колебаний совпадает с частотой
воздействующих ЭДС.
При рассмотрении остановившегося процесса в какой-либо
электрической цепи, содержащей элементы r, L и C, предполагается,
что с момента присоединения цепи к источнику электрической энергии до момента
наблюдения прошло столь большое (теоретически бесконечное) время, что
собственные колебания системы исчезли и в ней установился режим, задаваемый
источником.
Поэтому при исследовании установившегося процесса в
электрической цепи начало отсчета времени выбирается произвольно, в любой
конечный момент времени.
Выбор начала отсчета времени влияет только на величину
начальной фазы напряжения и тока при установившемся режиме.
Если условия, характеризующие заданный установившийся
режим работы цепи, в известный момент времени меняются, например, вследствие
изменения ЭДС или параметров самой цепи, то возникает переходный процесс, при
котором наряду с вынужденными колебаниями имеют место и собственные колебания
системы.
Переход к новому установившемуся режиму связан с
нарастанием или убыванием энергии электрического и магнитною полей и требует
времени, так как энергия этих полей не может изменяться скачкообразно.
В переходном режиме электрические величины,
обусловливаемые электрическими источниками, носят непериодический характер, не
подчиняясь формуле (1.31).
Переход от первоначального установившегося режима к
новому установившемуся режиму теоретически длится бесконечно долго, так как
собственные колебания исчезают только спустя бесконечно долгое время. Однако
уже через весьма малый промежуток времени собственные колебания достигают столь
ничтожно малых значений, что ими практически можно пренебречь, и процесс может
считаться установившимся.
1.8 Действующее и среднее значения периодической
электрической величины
О величине напряжения или тока обычно судят по
действующему (среднеквадратичному, эффективному)
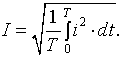 или
или 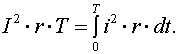 (1.28)
(1.28)
Эти равенства показывают, что
действующее значение периодического
тока равно по величине такому постоянному току, который, проходя через
неизменное сопротивление r, за период времени Т выделил бы то же количество тепла, что
и данный ток i.
Аналогично действующее значение периодического
напряжения
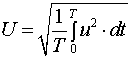 или
или 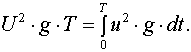 (1.29)
(1.29)
Эти равенства показывают, что
действующее значение периодического
напряжения u равно по величине постоянному напряжению, при подведении которого
к сопротивлению r за период времени Т выделяется то же количество тепла, что и
под воз действием данного напряжения и.
РАЗДЕЛ 2. ЛИНЕЙНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА
.1 Определение цепи постоянного тока
Если величина тока и напряжения на участках цепи не
зависит от времени, то такую цепь будем называть цепью постоянного тока.
Величины токов, ЭДС и напряжений в этом случае будем обозначать заглавными
латинскими буквами I,E,U.
2.2 Напряжение на участке цепи
Как уже отмечалось выше, под напряжением на участке
цепи мы понимаем разность потенциалов между крайними точками цепи. Ток течет от
точки с более высоким потенциалом к точке с меньшим потенциалом. Если ja,jb - потенциалы точек a,b ,
то согласно определению сопротивления для рисунка 2.1
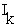
a b
R
Ток течет от точки a к точке b, и ja>jb на
величину 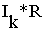 . ja=jb+IR, или
Uab=ja-jb=IR. Величину
Uab в электротехнике называют падением напряжения на сопротивлении.
. ja=jb+IR, или
Uab=ja-jb=IR. Величину
Uab в электротехнике называют падением напряжения на сопротивлении.
Положительное направление Uab
совпадает с направлением тока через сопротивление. Рассмотрим цепь,
показанную на рисунках 2.2а и 2.2б
По определению Uac=ja-jc.
Так как ток течет от более высокого потенциала к более низкому,
ja-jb=IR. (2.1.)
а) б)
Рисунок 2.2
При перемещении от точки b к точке с на
рисунке 2.2а потенциал jb<jc, так как направление э.д.с. совпадает с направлением
обхода, на величину Е. Следовательно, jb=jc-E. Подставив
значение jb в
уравнение (2.1.), получаем ja-jc+E=IR, или
Для рисунка 2.2б: jb>jc, так как э.д.с. направлена навстречу обхода: jb=jc+E. Подставив jb в уравнение (2-1), получим: ja-jc-E=IR, или:
ac=ja-jc=E+IR (2.2б.).
Положительное направление Uac
указывают стрелкой, очевидно, оно совпадает с направлением тока.
Согласно определению напряжения Ucа=jc-ja=-Uac.
2.3 Закон Ома для участка цепи
2.3.1 Для участка, не содержащего
э.д.с.
Закон Ома формулируется следующим
образом
Uab=I*R, или
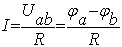 (2.3.)
(2.3.)
2.3.2 Для участка цепи, содержащего
э.д.с.
из уравнений (2-2а) и (2-2б) получаем:
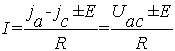 (2.4.)
(2.4.)
где знак плюс соответствует случаю, когда направление
э.д.с. совпадает с направлением тока, а знак минус, если э.д.с. направлено
навстречу направлению тока.
2.4 Методы расчета цепей постоянного тока
.4.1 Применение законов Кирхгофа к
расчету цепей
В теории электрических цепей различают задачи двух
родов: задачи анализа и синтеза цепей. Под анализом цепи подразумевается
определение электрических величин или их отношений при заданных схеме и
параметрах цепи. Под синтезом цепи понимается обратная задача, а именно подбор
схемы и параметров цепи по заданным соотношениям электрических величин, которые
обычно задаются в функции от частоты или времени. В отличие от задач анализа
цепей, имеющих, как правило, однозначные решения, задачи синтеза цепей могут
иметь несколько или множество решений. Настоящая глава посвящена методам
анализа цепей. Нахождение электрических величин при заданных схеме и параметрах
цепи возможно непосредственным решением уравнений, выражающих первый и второй
законы Кирхгофа для данной цепи. Положим, что в схеме, содержащей р
ветвей и q узлов, заданными являются источники напряжения, а искомыми -
токи в ветвях. Cледовательно, число неизвестных равно числу ветвей. По первому
закону Кирхгофа может быть записано q-1 независимых уравнений; уравнение
для последнего q-го узла является следствием предыдущих q-1
уравнений. Действительно, ввиду того, что каждая ветвь связывает между собой
два узла, ток каждой ветви входит в уравнения, записанные для q узлов,
дважды. Поэтому если просуммировать q уравнений, то получится тождество
вида 0=0. Следовательно, одно из этих уравнений является зависимым. Узлы, для
которых записываются независимые уравнения по первому закону Кирхгофа,
называются независимыми узлами.
Из сказанного следует, что из общего числа q
узлов любые q-1 узлов являются независимыми, а оставшийся последний узел
является зависимым. По второму закону Кирхгофа может быть записано р-q+1
независимых уравнений. Объясняется это тем, что если ко всем ветвям применить
закон Ома, то получится р уравнений вида 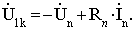 (2.5)
Здесь
(2.5)
Здесь 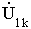 - напряжение между узлами i и k;
- напряжение между узлами i и k;
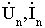 - ЭДС источника и ток в n-й ветви между узлами i
и k;
- ЭДС источника и ток в n-й ветви между узлами i
и k;
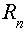 - сопротивление той же ветви.
- сопротивление той же ветви.
В системы уравнений вида (2.5) входят p
неизвестных токов 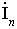 и q-1 неизвестных напряжении
и q-1 неизвестных напряжении 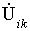 , если из этой системы исключить q-1
напряжений, то останутся р-q+1 уравнений, связывающих ЭДС источников с
падениями напряжений на сопротивлениях и выражающих второй закон Кирхгофа.
, если из этой системы исключить q-1
напряжений, то останутся р-q+1 уравнений, связывающих ЭДС источников с
падениями напряжений на сопротивлениях и выражающих второй закон Кирхгофа.
Таким образом, расчет электрической цепи с помощью
первого и второго законов Кирхгофа сводится к решению (q-1)+(р-q+1)=p
уравнений - по числу ветвей.
Контуры, для которых уравнения, записываемые по
второму закону Кирхгофа, являются независимыми, называются независимыми
контурами.
Для того чтобы уравнения по второму закону Кирхгофа, а
следовательно, и сами контуры, были независимыми, достаточно, чтобы каждый
последующий контур отличался от предыдущего хотя бы одной новой ветвью.
На рис. 2.3 в виде примера показана электрическая
схема с числом ветвей 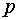 =6 и числом узлов
=6 и числом узлов 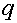 = 4.
Соответственно, число уравнений по первому закону Кирхгофа равно 4-1=3 и по
второму закону Кирхгофа 6-4+1=3. В этой схеме независимыми являются любых три контура.
= 4.
Соответственно, число уравнений по первому закону Кирхгофа равно 4-1=3 и по
второму закону Кирхгофа 6-4+1=3. В этой схеме независимыми являются любых три контура.
Рис. 2.3
2.4.2 Метод контурных токов
Метод контурных токов заключается в том, что вместо
токов в ветвях на основании второго закона Кирхгофа определяются так называемые
контурные токи, замыкающиеся в контурах.
На рис. 2.4. в виде примера показана двухконтурная
электрическая цепь, в которой искомыми являются контурные токи 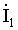 и
и 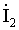 ,
замыкающиеся в контурах. Токи в сопротивлениях
,
замыкающиеся в контурах. Токи в сопротивлениях 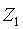 и
и 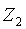 равны соответствующим контурным токам.
равны соответствующим контурным токам.
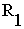
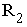
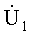
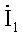
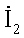
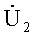
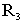
Рис. 2.4. Иллюстрация метода контурных токов
Ток в сопротивлении 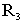 ,
являющемся общим для двух контуров, равен разности контурных.
,
являющемся общим для двух контуров, равен разности контурных.
Число уравнений, записываемых для контурных токов по
второму закону Кирхгофа, равно числу независимых контуров, т.е. для
электрической схемы с числом узлов q и числом ветвей p задача
нахождения контурных токов сведется к решению системы р-q+1
уравнений.
Так как в схеме рис. 4.2 q=3, p=2, то
число уравнений равно 2 (по числу независимых контуров).
Условимся сумму комплексных сопротивлений, входящих в
контур, называть собственным сопротивлением контура, а комплексное
сопротивление, принадлежащее одновременно двум контурам, - общим сопротивлением
этих контуров.
Положительные направления контурных токов задаются
произвольно.
Если направление обхода каждого контура принять
совпадающим с выбранным положительным направлением контурного тока, то при
составлении уравнений по второму закону Кирхгофа падение напряжения от данного
контурного тока в собственном сопротивлении контура следует брать со знаком
плюс.
Падение напряжения от тока смежного контура в
сопротивлении, являющемся общим для двух смежных контуров, следует брать со
знаком минус, если контурные токи в этом сопротивлении направлены встречно, как
это, например, имеет место в схеме рис 2.4, где направление обоих контурных
токов выбрано по ходу часовой стрелки.
Применительно к схеме рис.4.2 собственное
сопротивление контура 1 равно 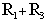 ; сопротивление
R3, принадлежащее одновременно двум контурам, является
общим сопротивлением контуров 1 и 2 и ему при принятом в схеме
рис. 4.2 положительном направлении контурных токов приписывается знак минус.
; сопротивление
R3, принадлежащее одновременно двум контурам, является
общим сопротивлением контуров 1 и 2 и ему при принятом в схеме
рис. 4.2 положительном направлении контурных токов приписывается знак минус.
Если заданная электрическая схема содержит n
независимых контуров, то на основании второго закона Кирхгофа получается
система из n уравнений.
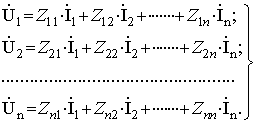 (2.6)
(2.6)
Здесь
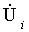 - контурная ЭДС в контуре i, т.е.
алгебраическая сумма ЭДС, действующих в данном контуре; ЭДС, совпадающие по
направлению с направлением обхода, берутся со знаком плюс, а направленные
встречно - со знаком минус:
- контурная ЭДС в контуре i, т.е.
алгебраическая сумма ЭДС, действующих в данном контуре; ЭДС, совпадающие по
направлению с направлением обхода, берутся со знаком плюс, а направленные
встречно - со знаком минус:
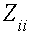 - собственное сопротивление контура i;
- собственное сопротивление контура i;
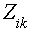 - общее сопротивление контуров i и k.
- общее сопротивление контуров i и k.
В соответствии со сказанным ранее собственное
сопротивление контура берется со знаком плюс, когда направление обхода контура
совпадает с выбранным положительным направлением тока.
Общее сопротивление берется со знаком минус, когда
направление обхода одного контура не совпадает с выбранным положительным
направлением второго.
Решение уравнений (2.7.) относительно искомых
контурных токов может быть найдено с помощью определителей или любым другим
способом.
Так, например, если обозначить через D главный определитель системы уравнений (2.6.) -
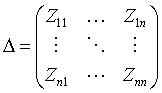 (2.8)
(2.8)
то любой контурный ток (например - второго
независимого контура) может быть найден как
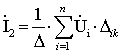 (2.9)
(2.9)
где
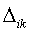 представляет собой тот же определитель системы, в
котором столбец сопротивлений
представляет собой тот же определитель системы, в
котором столбец сопротивлений 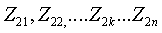 заменен
столбцом соответствующих напряжений
заменен
столбцом соответствующих напряжений 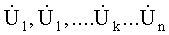 .
.
Использованные выше уравнения, выражающие второй закон
Кирхгофа, записаны в предположении, что источниками электрической энергии
служат источники напряжения.
При наличии в электрической схеме источников тока
последние могут быть заменены эквивалентными источниками напряжения.
Однако если источники тока не имеют проводимостей, то
более целесообразно в этом случае выбрать заданные токи в качестве контурных,
тогда число неизвестных контурных токов и, соответственно, число уравнении
сократится на число заданных токов.
Если ветвь с источником тока является общей ветвью
двух смежных контуров, то в уравнении она учитывается в левой части соотвещего
уравнения в виде неизвестного падения напряжения уравнения на данной ветви.
Дополнительное уравнение к системе (2.6) учитывает зависимость тока источника в
рассматриваемой ветви от контурных токов
смежных ветвей.
2.4.3 Метод наложения
Из общего подхода к расчету токов в разветвленной
электрической цепи, основанного на составлении системы уравнений для отыскания
токов или потенциалов узлов схемы, следует вывод о том, что ток в любом контуре
линейной электрической цепи может быть получен как алгебраическая сумма токов,
вызываемые в этом контуре каждой ЭДС в отдельности.
Метод расчета токов, основанный на
определении токов в одном и том же контуре (или ветви) при поочередном
воздействии ЭДС и последующем алгебраическом сложении этих токов, именуется
методом наложения.
Ввиду того, что напряжения на участках цепи
пропорциональны токам, метод наложения применим и к напряжениям.
При определении частичных слагающих токов по методу
наложения необходимо считать включенными внутренние сопротивления тех
источников напряжения, которые принимаются отсутствующими при вычислении
слагающих токов.
Если в цепи заданы источники ЭДС, т. е. внутренние
сопротивления источников равны нулю, то при определении токов, вызываемых
какой-либо ЭДС, зажимы остальных источников ЭДС "закорачиваются" или,
иначе говоря, источники ЭДС заменяются сопротивлениями, равными нулю.
В свою очередь, в линейной электрической цепи, содержащей
источники тока, узловые напряжения (и, соответственно, напряжения на ветвях)
представляют линейные функции от задающих токов источников.
При определении частичных слагающих узловых напряжений
по методу наложения необходимо считать включенными внутренние проводимости тех
источников тока, которые принимаются отсутствующими при вычислении слагающих
напряжений.
Если источники тока заданы без внутренних
проводимостей, т. е. проводимости их равны нулю, то при пользовании методом
наложения ветви с соответствующим источников тока разрываются, иначе говоря,
источники тока заменяются сопротивлениями, равными бесконечности.
Если в линейной электрической цепи заданными являются
одновременно источники напряжения и источники токов, то метод наложения
применим и в этом случае.
Например, ток в каком-либо контуре данной цепи может
быть получен в результате алгебраического сложения токов, вызываемых в этом
контуре поочередным действием источников напряжения и тока.
При этом отсутствующие источники напряжения заменяются
внутренними сопротивлениями, а отсутствующие источники тока заменяются
внутренними проводимостями источников.
.4.4 Теорема взаимности
Упрощение расчета электрических цепей достигается в
ряде случаев использованием свойства линейных электрических цепей, известного
под названием принципа или теоремы взаимности (обратимости).
Теорема взаимности может быть сформулирована в двух
вариантах - применительно к источникам ЭДС и источникам тока.
Не вдаваясь в детали математического вывода, изложим
эту теорему применительно к источникам ЭДС - если некоторая ЭДС, находящаяся в
каком-либо контуре электрической цепи, вызывает ток в другом контуре данной
цепи, то та же ЭДС, будучи перенесенной во второй контур, вызовет в первом
контурный ток той же величины.
При соответствующем выборе контурных токов ток в ветви
равен контурному току. Поэтому данная теорема справедлива также для токов в
ветвях:
если источник тока, заданный в
каком-либо узле электрической цепи, обусловливает некоторое напряжение между
какими-либо двумя узлами цепи, то тот же источник тока, будучи включенным между
указанными двумя узлами, обусловит в первом узловое напряжение той же величины.
2.4.5 Теорема компенсации
Справедливость положения, именуемого теоремой
компенсации, вытекает из того, что любая из составных частей падения
напряжения, входящая в уравнение второго закона Кирхгофа, может быть перенесена
в другую сторону уравнения с обратным знаком, т.е. может рассматриваться в
качестве дополнительной ЭДС, направленной навстречу току.
Следовательно, токи в электрической цепи не изменятся,
если сопротивление в любом контуре этой цепи заменить ЭДС, равной по величине
падению напряжения в данном сопротивлении и имеющей направление, обратное току,
протекающему через данное сопротивление.
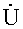
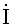
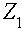
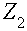
а)
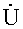
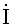
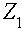
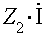
б)
Рис. 2.5 Иллюстрация
теоремы компенсации
Иллюстрацией вышесказанного служит рис. 2.5:
уравнение, записанное для схемы рис 2.5а) по второму закону Кирхгофа
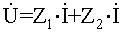 ;
;
может быть представлено в виде
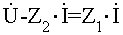 . (2.10.)
. (2.10.)
Такой записи уравнения соответствует схема рис 2.5б),
в которой вместо сопротивления Z2 включена ЭДС равная Z2×I,
направленная противоположно току I. Данная теорема справедлива и для
разветвленных электрических цепей.
2.4.6 Теорема об эквивалентном
источнике
С помощью теоремы об эквивалентном источнике сложная
электрическая схема с произвольным числом источников электрической энергии
приводится к схеме с одним источником, благодаря чему расчет электрической цепи
упрощается.
Существует два варианта теоремы об эквивалентном
источнике: вариант с источником напряжения и вариант с источником тока.
.4.7 Теорема об эквивалентном
источнике напряжения
ток в любой ветви m-n линейной электрической цепи не
изменится, если электрическую цепь, к которой приключена данная ветвь, заменить
эквивалентным источником напряжения. ЭДС этого источника должна быть равна
напряжению на зажимах разомкнутой ветви m-n, а внутреннее сопротивление
источника должно равняться сопротивлению пассивной электрической цепи между
зажимами m и n при разомкнутой ветви.
Данная теорема доказывается следующим образом: в ветвь
m-n вводятся две равные по величине и противоположно направленные ЭДС Umn,
при условии, что Umn равно напряжению между зажимами m-n
при разомкнутой ветви.
2.4.8 Теорема об эквивалентном источнике
тока
ток в любой ветви m-n линейной электрической цепи не
изменится, если электрическую цепь, к которой приключена данная ветвь, заменить
эквивалентным источником тока. Ток этого источника должна быть равен току,
протекающему между зажимами замкнутой ветви m-n, а внутренняя
проводимость источника должна равняться проводимости пассивной электрической
цепи между зажимами m и n при разомкнутой ветви.
2.4.9 Замена параллельных ветвей,
содержащих различные элементы, одной
Рассмотрим участок сложной цепи, содержащий
параллельно включенные ветви (см. рис.2.6a).

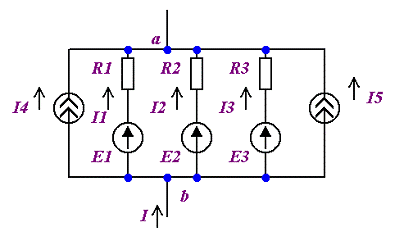
а) б)
Рисунок 2.6.
Необходимо заменить на ветвь, содержащую Rэ
и Eэ, полностью эквивалентную схеме на рисунке 2.6а. В
соответствии с первым законом Кирхгофа:
I=I1+I2+I3+I4+I5,
а
I1=(E-Uab)/R1=(E1-Uab)g1,2=(E2-Uab)g2,
....
In=(En-Uab)gn.
Следовательно,
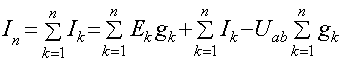 (2.11.)
(2.11.)
Для рисунка 2.6-б:
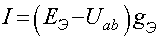 (2.12)
(2.12)
Так как равенство токов, вычисленных по (2.11) и по
(2.12), должно выполняться при любых значениях Uab, то :
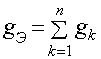 , следовательно,
, следовательно,
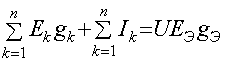
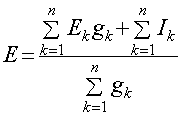 (2.13.)
(2.13.)
Если в ветви нет э.д.с., то Ek=0.
Если э.д.с. имеет направление, обратное изображенному на рисунке, то Ek
берется со знаком минус.
2.4.10 Метод узловых потенциалов
В соответствии с законом Ома, если известны потенциалы
узлов, то можно вычислить ток, протекающий по ветвям, соединяющим эти узлы.
Таким образом, неизвестными могут быть потенциалы узлов, метод расчета
электрических цепей, где неизвестными являются узловые потенциалы, называется
методом узловых потенциалов.
Число неизвестных потенциалов узлов равно числу узлов
минус 1, так как потенциал любого узла можно принять равным нулю. Рассмотрим
участок схемы.(рис.2.7.)
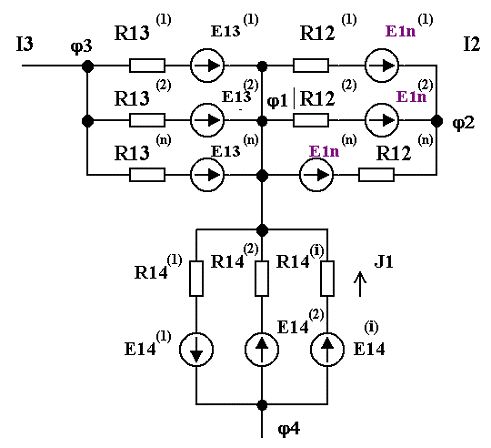
Рисунок 2.7
Исходя из изложенного в предыдущем разделе, сумма
токов ветвей между узлами 1, 2 равна:
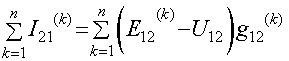
Сумма токов ветвей между узлами 3 и 1:
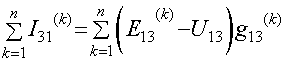
Сумма токов ветвей между узлами 4 и 1:
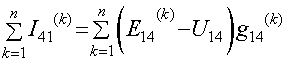
Т.к. U12=j1-j2,
U13=j1-j3,
U14=j1-j4, то,
подставляя U12 в полученные выражения, имеем:

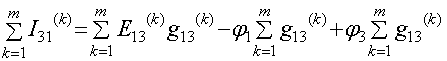
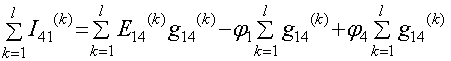
Просуммируем полученные уравнения, т.к. согласно
первого закона Кирхгофа сумма токов в узле равна нулю, то:
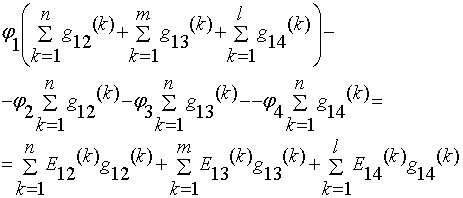
Обозначим:
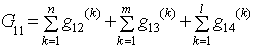 - собственная проводимость узла;
- собственная проводимость узла;
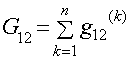 взаимная проводимость между узлами 1 и 2;
взаимная проводимость между узлами 1 и 2;
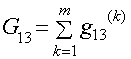 - взаимная проводимость между узлами 1 и 3;
- взаимная проводимость между узлами 1 и 3;
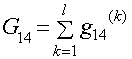 - взаимная проводимость между узлами 1 и 4;
- взаимная проводимость между узлами 1 и 4;
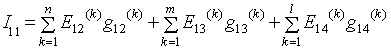 - узловой ток узла 1.
- узловой ток узла 1.
В выражении для узлового тока э.д.с. берется со
знаком “+”, если она направлена к узлу, и со знаком “-”, если направлена от
узла.
Таким образом, уравнение узловых потенциалов для узла
1 принимает вид:
jG11+j2G12+j3G13+j4G14=I11.
Очевидно, если в схеме n узлов, то можно по
указанному выше правилу составить n-1 уравнений:
jG11+j2G12+j3G13+...+jn-1G1(n-1)=I11;
jG21+j2G22+j3G23+...+jn-1G2(n-1)=I22;
jG31+j2G32+j3G33+...+jn-1G3(n-1)=I33;
....
jG(n-1)1+j2G(n-1)2+j3G(n-1)3+...+jn-1G(n-1)(n-1)=I(n-1)(n-1).
В этих уравнениях :
G12,G13... G1(n-1) - взаимная проводимость между 1 узлом и
остальными (n-1) узлами;
G21 ,G23... G2(n-1) - взаимная проводимость между 2 узлом и
остальными (n-1) узлами;
G31,G32... G3(n-1) - взаимная проводимость между 3 узлом и
остальными (n-1) узлами;
G11,G22... G(n-1)(n-1) - собственная проводимость узлов 1, 2,...,
(n-1) ;
I11, I22, I33,....,I(n-1)(n-1) - узловой ток, вычисленный по изложенному выше
правилу.
Очевидно, если между узлами имеется источник тока, то
его величина прибавляется к узловому току, если он направлен к узлу и
вычитается, если он направлен от узла.
2.5 Преобразование электрических схем постоянного тока
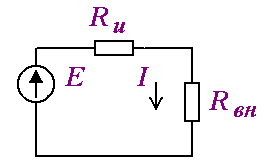
2.5.1 Преобразование реального источника э.д.с. в реальный источник тока
Для схемы на рисунке 2.8. выполним преобразование
схемы, содержащей источник э.д.с., в схему, содержащую источник тока.
Ток в нагрузке Ru :
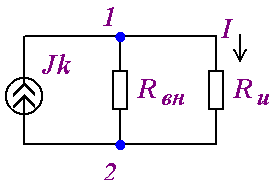
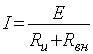
а) б)
Рисунок 2.8.
Для схемы на рисунке 2.8. ток в нагрузке определим
путем замены параллельно соединенного сопротивления эквивалентным. Тогда:
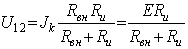 , а ток в
нагрузке:
, а ток в
нагрузке: 
т.е. схемы на рисунке 2.8.а и 2.8.б эквивалентны.
Следовательно, э.д.с. с последовательно соединенным сопротивлением можно
заменить на источник тока, величина которого равна э.д.с., деленная на величину
последовательно включенного сопротивления, и параллельно источнику необходимо
включить это же сопротивление.
.5.2. Преобразование звезды в
треугольник и обратно
Соединение трех сопротивлений только одной клеммой
между собой, как показано на рисунке 2.9-а, называется соединение звездой,
а соединение в замкнутую схему, как показано на рисунке 2.9-б - соединением
в треугольник.
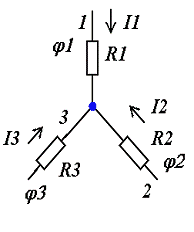
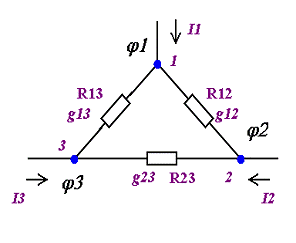
Рисунок 2.9.
В точках 1,2,3 потенциалы j1, j2, j3
которые в обеих схемах соответственно равны, точками 1,2,3 звезда и
треугольник соединяются с остальной частью схемы, не показанной на рисунке.
Очень часто на практике необходимо преобразовать
показанную часть схемы из одного вида в другой. Рассмотрим, как это делается.
Для звезды для узла 0: I1+I2+I3=0,
но
1=(j-j0)g1; I2=(j2-j0)g2; I3=(j3-j0)g3.
Подставив в уравнение для токов узла 0, получим:
jg1+j2g2+j3g3=j0(g1+g2+g3),
или:
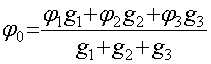
Отсюда вычислим токи I1,I2,I3:
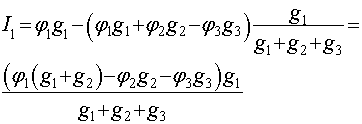
Для треугольника в соответствии с обозначением на
рисунке 2.9-б:
1=
I12-I31=(j-j2)g12-(j3-j)g31=j(g12+g31)-j2g12-j3g31.
Чтобы ток I1 звезды равнялся току
треугольника I1 при любых значенияхj j2
j3 ,
необходимо и достаточно, чтобы в выражениях для токов коэффициенты при j j2
j3 были
равны. Следовательно:
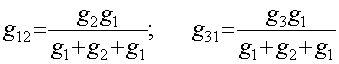
Вычислив токи I1 для треугольника и
звезды и приравняв коэффициенты при j
j2 j3, получим:
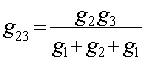
Для обратного преобразования
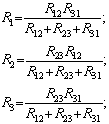
2.6. Активный и пассивный двухполюсник
В любой электрической схеме всегда можно выделить
любую ветвь, тогда остальная часть схемы будет оканчиваться двумя клеммами. Ее
будем изображать прямоугольником с двумя клеммами и называть двухполюсником.
Если внутри прямоугольника содержаться источники э.д.с. или тока, то такой
двухполюсник будем называть активным и обозначать буквой “A”
внутри прямоугольника, в противном случае двухполюсник называется пассивным
и отмечается буквой “П” внутри прямоугольника.
.6.1 Метод эквивалентного генератора
Метод позволяет рассчитать ток любой ветви не
рассчитывая всю цепь. Так как любая ветвь может быть выделена, то расчетная
схема цепи принимает вид, показанный на рисунке 2.10-а.
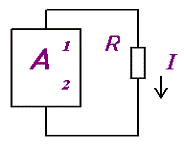
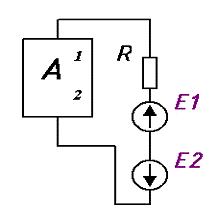
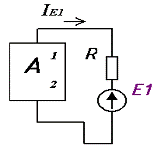
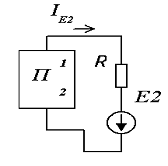
Рисунок 2.10.
Т.е. остальная часть цепи изображена в виде активного
двухполюсника и требуется найти ток в ветви 1-2.
Включим два источника E1 и E2
в ветвь 1-2 навстречу друг другу. E1 и E2
равные по величине (рисунок 2.10-б). Согласно принципа наложения можно
вычислить ток IE=IE1+IE2, как ток,
вызванный э.д.с. E1 и E2 приняв, что э.д.с.
остальных источников равны нулю. IE1 - ток, вызванный э.д.с. E1,
ток IE2 вызван э.д.с. E2. Э.д.с. E1
направлена встречно U12, следовательно, согласно закону
Ома:
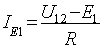
Выберем E1 так, чтобы ток
IE1=0, тогда IE=ЕE2 и схема
может быть представлена, как показано на рисунке 2.10-г, двухполюсник
становится пассивным, так как компенсировано действие внутренних э.д.с.
Относительно зажимов 1,2 этот двухполюсник имеет эквивалентное сопротивление Rэ=Rвн,
тогда:
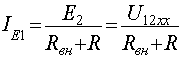
В формуле U12xx- это напряжение Е1,
при котором ток IE1=0 (Е2=Е1),
или иначе - это напряжение холостого хода ( нагрузочная ветвь отключена), таким
образом, двухполюсник на рисунке 2.10-а можно заменить ветвью , содержащей
э.д.с., равную U12xx , и сопротивлением Rвн, или
эквивалентным генератором , э.д.с. которого U12xx , а
внутренне сопротивление Rвн,(см. рис.2.11).
Если закоротить R, то :
Ik=U12xx/Rвн, или Rвн=U12xx/Ik.
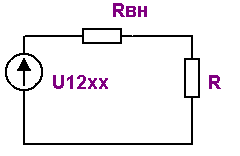
Рисунок 2.11.
Таким образом, можно сформулировать порядок
определения тока ветви методом эквивалентного генератора.
. Разорвать выделенную ветвь и вычислить на ее зажимах
напряжение холостого хода.
. Закоротить выделенную ветвь и определить ток
короткого замыкания Ik.
. Вычислить Rвн=Uxx/Ik.
. Вычислить I=Uxx/(R+Rвн).
.6.2 Передача энергии от активного
двухполюсника нагрузке
Рассмотри энергетические соотношения при передаче
энергии т активного двухполюсника нагрузке. Очевидно, ток в нагрузке I=Uxx/(Rвн+R)
, а мощность, выделяемая в нагрузке:
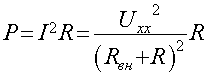
Определим условия, когда в нагрузке выделяется
максимально возможная мощность, если R величина переменная. Максимум
мощности соответствует значению k, при котором dP/dR=0, или:
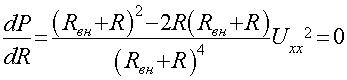
Отсюда R=Rвн. Так как d2P/dR2<0
при R>Rвн и d2P/dR2>0 при
R<Rвн, то в точке R=Rвн - максимум.
Подставив значение R=Rвн в выражение для мощности, получим:
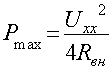
Мощность, выделяемая э.д.с. эквивалентного генератора:
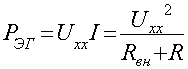
а коэффициент полезного действия:
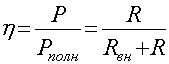
Очевидно, при R=Rвн h=0,5.
Величина h=0,5
недопустимая при передаче энергии. Но при передаче сигналов с помощью
электрического тока (датчики автоматических устройств, речевые сообщения и
т.п.), где основная задача - получить максимальную мощность полезного сигнала -
с таким к.п.д. можно мириться.
В технике управления, радиотехнике выбор оптимального
соотношения R и Rвн называется согласованием
нагрузки.
При передаче энергии от источника э.д.с. по
двухпроводной линии мощность, выделяемую в нагрузке R, можно определить,
воспользовавшись предыдущими доказательствами. Если сопротивление линии считать
внутренним сопротивлением эквивалентного генератора, а э.д.с. источника энергии
Uxx эквивалентного генератора, то:
Рисунок 2.12.
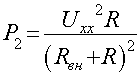
Максимальное значение мощности соответствует значению
тока в нагрузке: I=Uxx/2Rвн, максимальное значение
тока - току короткого замыкания эквивалентного генератора: Imax=Uxx/Rвн,
P2=UxxI-I2R, P1=UxxI. Коэффициент
полезного действия h: h=Р2/P1=1-RI/Uxx.
Зависимости P1,P2,h от тока I показаны на рисунке 2.12.
РАЗДЕЛ 3. ТЕОРИЯ ЦЕПЕЙ ПЕРЕМЕННОГО СИНУСОИДАЛЬНОГО ТОКА
3.1 Основные соотношения в цепях синусоидального тока
3.1.1 Представление синусоидальных функции в виде проекций вращающихся
векторов
Преобладающим видом периодического процесса в
электрических цепях является синусоидальный, характеризующийся тем, что все
напряжения и токи в цепи изменяются синусоидально.
Сложение, вычитание, дифференцирование и интегрирование
синусоидальных функций не нарушают синусоидального закона изменений величин,
что является важным преимуществом их по сравнению со всеми другими
периодическими функциями.
Синусоидальная функция представляет простейший вид
периодической функции. Всякая несинусоидальная периодическая функция может быть
разложена на синусоидальные и постоянную слагающие.
Синусоидальная функция
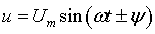 (3.1)
(3.1)
характеризуется амплитудой, частотой и начальной
фазой.
Аргументом функции (3.1) является угол 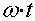 (или, соответственно, время t).
(или, соответственно, время t).
Угловая частота, 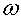 входящая в (3.1), связана с периодом и частотой
соотношением
входящая в (3.1), связана с периодом и частотой
соотношением 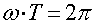 или
или 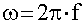 .
.
Величина 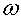 имеет размерность (сек) -1 и
вычисляется в радианах в секунду (рад/сек).
имеет размерность (сек) -1 и
вычисляется в радианах в секунду (рад/сек).
Начальная фаза 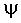 зависит
от выбора начала координат, который выполняется произвольно. Она вычисляется в
тех же единицах, что и аргумент
зависит
от выбора начала координат, который выполняется произвольно. Она вычисляется в
тех же единицах, что и аргумент 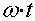 (в
радианах), и определяется величиной смещения синусоиды относительно начала
координат, т. е. измеряется абсциссой, соответствующей точке перехода
отрицательной полуволны в положительную.
(в
радианах), и определяется величиной смещения синусоиды относительно начала
координат, т. е. измеряется абсциссой, соответствующей точке перехода
отрицательной полуволны в положительную.
Косинусоида может рассматриваться как синусоида с
начальной фазой 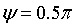 .
.
Таким образом, к синусоидальным функциям в общем
случае причисляются и косинусоидальные функции.
Начальная фаза 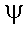 представляет
алгебраическую величину.
представляет
алгебраическую величину.
Угол 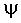 положителен,
когда синусоидальная функция смещена влево относительно начала координат;
будучи, соответственно, отсчитанным влево, он имеет в этом случае положительный
знак:
положителен,
когда синусоидальная функция смещена влево относительно начала координат;
будучи, соответственно, отсчитанным влево, он имеет в этом случае положительный
знак:
Um1 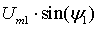
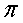
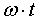
Рис. 3.1
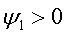
Если синусоидальная функция смещена вправо
относительно начала координат, то угол 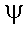 ,
отсчитываемый, соответственно, вправо, имеет отрицательный знак:
,
отсчитываемый, соответственно, вправо, имеет отрицательный знак:
Рис. 3.2
Um2
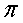
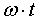
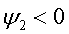
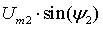
Заданная функция обращается в нуль при значениях
аргумента
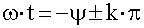 , где k=0,1,2… .
, где k=0,1,2… .
В момент времени 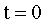 аргумент
аргумент
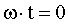 и значение
функции составляет
и значение
функции составляет 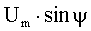 . Это
значение функции равно проекции на вертикальную ось вектора, модуль которого
равен амплитуде
. Это
значение функции равно проекции на вертикальную ось вектора, модуль которого
равен амплитуде 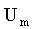 заданной
синусоидальной функции.
заданной
синусоидальной функции.
В зависимости от знака начальной фазы 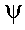 этот вектор в момент времени
этот вектор в момент времени 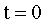 повернут относительно горизонтальной оси на угол
повернут относительно горизонтальной оси на угол 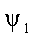 в положительном направлении - против хода часовой
стрелки (рис 3.3,) или на угол
в положительном направлении - против хода часовой
стрелки (рис 3.3,) или на угол 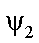 в
отрицательном направлении - по ходу часовой стрелки.
в
отрицательном направлении - по ходу часовой стрелки.
Рис. 3.3
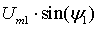
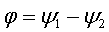
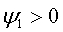
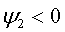
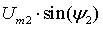
Если вращать в положительном направлении вектор с
угловой скоростью 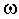 , то с момента времени
, то с момента времени 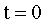 до момента
до момента 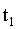 он совершит поворот на угол
он совершит поворот на угол 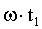 и в момент
и в момент 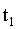 окажется повернутым относительно оси отсчета углов на
угол
окажется повернутым относительно оси отсчета углов на
угол 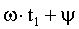 . Здесь, так
же как и выше,
. Здесь, так
же как и выше, 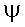 - величина
алгебраическая.
- величина
алгебраическая.
Проекция указанного вектора на вертикальную ось при 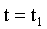 равна
равна 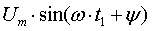 .
.
Сопоставляя рис. 3.1, 3.2 и 3.3, приходим к выводу,
что
в каждый данный момент времени 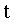 аргументу
аргументу 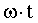 соответствует
значение синусоидальной функции, равное проекции вращающегося вектора на
вертикальную ось.
соответствует
значение синусоидальной функции, равное проекции вращающегося вектора на
вертикальную ось.
Поэтому рассмотрение синусоидальных функций может быть
заменено рассмотрением вращающихся векторов.
Если синусоидальные функции имеют одну и ту же
частоту, то векторы, соответствующие этим функциям, вращаются с одинаковой
угловой частотой, и поэтому углы между ними сохраняются неизменными.
Если полагать, что на рис. 3.1, 3.2 показаны две
синусоидальные функции: 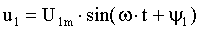 и
и  , имеющие одинаковою угловую частоту
, имеющие одинаковою угловую частоту 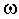 , то рис.3.3
определяет положение двух векторов, соответствующим двум временным кривым.
Кривая
, то рис.3.3
определяет положение двух векторов, соответствующим двум временным кривым.
Кривая 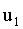 , смещенная влево относительно
, смещенная влево относительно 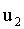 , возрастает
от нуля до своего положительного максимума раньше, чем кривая
, возрастает
от нуля до своего положительного максимума раньше, чем кривая 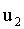 .
.
Поэтому говорят, что 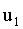 опережает
по фазе
опережает
по фазе 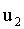 или, что то
же
или, что то
же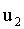 отстает по
фазе от
отстает по
фазе от 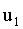 .
.
Разность начальных фаз 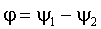 называется
фазовым сдвигом или углом сдвига
называется
фазовым сдвигом или углом сдвига 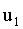 относительно
относительно
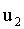 . Этот угол и образуют между собой векторы на
векторной диаграмме рис. 3.3.
. Этот угол и образуют между собой векторы на
векторной диаграмме рис. 3.3.
При равенстве начальных фаз, т. е. при фазовом сдвиге,
равном нулю, говорят, что кривые совпадают по фазе.
Векторы, соответствующие этим кривым, в данном случае
направлены в одну и ту же сторону. При фазовом сдвиге в 180° говорят, что
кривые противоположны по фазе или, что то же, находятся в противофазе.
Соответствующие им векторы направлены в диаметрально противоположные стороны.
Векторное представление синусоидальных функций,
частота которых одинакова, облегчает операции сложения и вычитания этих
функций.
Пусть требуется сложить функции 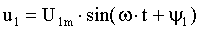 и
и  ,
представленные векторами на рис.3.4. Суммарная кривая
,
представленные векторами на рис.3.4. Суммарная кривая 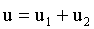 , ординаты которой в каждый данный момент времени
определяются алгебраической суммой соответствующих ординат кривых
, ординаты которой в каждый данный момент времени
определяются алгебраической суммой соответствующих ординат кривых 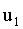 и
и 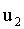 , представляет собой синусоидальную функцию, имеющую
амплитуду
, представляет собой синусоидальную функцию, имеющую
амплитуду 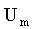 и начальную
фазу
и начальную
фазу 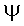 .
.
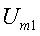
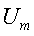
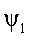
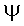
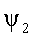
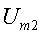
Рис. 3.4 Сложение векторов
Векторное представление синусоидальных функций,
частота которых одинакова, облегчает операции сложения и вычитания этих
функций.
Ввиду того что сумма проекций двух векторов равна
проекции геометрической суммы этих векторов, амплитуда и начальная фаза
результирующей кривой могут быть найдены из векторной диаграммы рис. 3.4;
искомой кривой соответствует вектор, представленный диагональю параллелограмма,
стороны которого равны 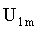 и
и 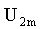 .
.
Согласно рис. 3.4
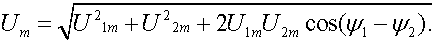 (3.2)
(3.2)
Формула (3.2) может быть получена аналитически, исходя
из уравнения 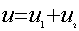 или из выражения
или из выражения
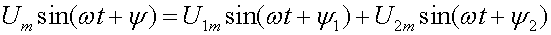
Отсюда следует, что
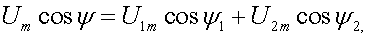 (3.3)
(3.3)
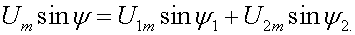 (3.4)
(3.4)
Уравнения (3.3) и (3.4) содержат две неизвестные
величины (Um и Ψ), которые могут быть найдены совместным решением этих
уравнений, которое приводит к выражению (3.2) для амплитуды суммарного
напряжения и к выражению для фазового угла
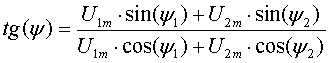 (3.5)
(3.5)
Угол  Ψ может быть также получен непосредственно из векторной диаграммы рис.
2.4.
Ψ может быть также получен непосредственно из векторной диаграммы рис.
2.4.
Вычитание функций 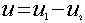 равносильно
сложению
равносильно
сложению 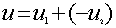 , поэтому в случае вычитания следует заменить в
формулах (3.2) и (3.5) начальную фазу
, поэтому в случае вычитания следует заменить в
формулах (3.2) и (3.5) начальную фазу 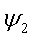 на
на 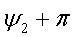 или, что равноценно, на
или, что равноценно, на 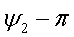 .
.
Определение угла 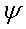 с
помощью выражения (3.5) сводится к нахождению арктангенса, т. е. многозначной
функции. При этом она зависит не только от величины всей дроби (3.5), но и от
знаков числителя и знаменателя в отдельности.
с
помощью выражения (3.5) сводится к нахождению арктангенса, т. е. многозначной
функции. При этом она зависит не только от величины всей дроби (3.5), но и от
знаков числителя и знаменателя в отдельности.
Если числитель и знаменатель положительны, то угол 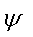 располагается в первой четверти:
располагается в первой четверти: 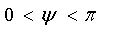 .
.
Если числитель положителен, а знаменатель отрицателен,
то угол 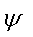 заходит во вторую четверть:
заходит во вторую четверть: 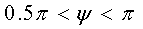 .
.
Если числитель и знаменатель отрицательны, то угол 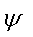 заходит в третью четверть:
заходит в третью четверть: 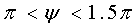
Наконец, если числитель отрицателен, а знаменатель
положителен, то угол 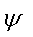 заходит в четвертую четверть:
заходит в четвертую четверть: 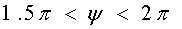 .
.
Вместо положительного угла 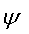 , превосходящего
, превосходящего 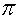 , может
быть взят отрицательный угол
, может
быть взят отрицательный угол 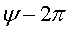 .
.
При пользовании векторной диаграммой с целью
установления фазовых сдвигов или амплитудных значений синусоидальных величин,
имеющих одинаковую частоту, векторная диаграмма может считаться неподвижной
(при равенстве частот углы между векторами не зависят от времени).
Построение векторных диаграмм обычно не связано с
определением мгновенных значений синусоидальных функций; в таких случаях
векторные диаграммы строятся не для амплитуд, а для действующих значений, т. е.
модули векторов уменьшаются по сравнению с амплитудами в 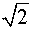 раз.
раз.
При этом векторная диаграмма мыслится неподвижной (не
вращается).
3.1.2 Действующее значение
периодических токов, напряжений и э.д.с.
Во многих случаях на практике необходимо оценить
периодическую функцию тока (э.д.с., напряжения) одной величиной (числом), т.к.
иметь дело с графиками функции неудобно.
Такими величинами можно принять:
среднее значение функции i(t) за
период T;
- средне-квадратичное значение функции i(t) за
период T.
Средние значения за период будем обозначать Iср,Uср,Eср,
согласно определению средней величины:
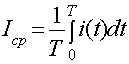
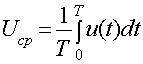
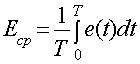
Для синусоидальной функции Iср=0, Uср=0,
Eср=0.
Среднеквадратичные величины будем обозначать большими буквами без индекса:
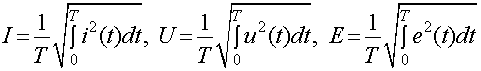
Рисунок 3.5.
Действующие значения имеют определенный физический
смысл. Для связи действующих значений с физическим процессом определим мощность
в цепи переменного тока, содержащей сопротивление r (смотри рис. 3.5).
Зависимость мощности, выделяемой на сопротивлении:
(t)=u(t)*i(t)=i2(t)r.
Найдем среднее значение мощности, выделяемой за
период.
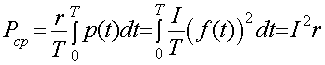
Таким образом, действующее значение тока является
мерой для определения потребляемой мощности (энергии). Из выражения для Pср
видно, что величина Pср не зависит от формы тока. Аналогичные
выводы можно сделать и для U и E.
3.2 Элементы электрической цепи переменного синусоидального
тока
.2.1 Сопротивление
На схемах будем изображать так же, как и сопротивление
в цепи постоянного тока, а обозначать буквой r. Очевидно, если i(t)=Imsinwt, то ur(t)=rImsinwt. Переходя к действующим значениям, получим:
Векторная диаграмма U,I для сопротивления:
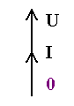
Рисунок 3.6.
3.2.2 Емкость
Согласно определению тока:
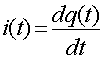 или
или 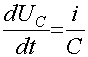
Следовательно,
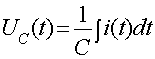
Если i(t)=Imsinwt:
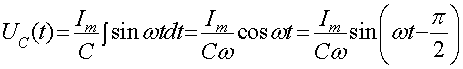
Действующее значение:
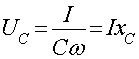
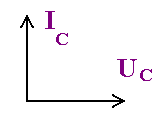
Величина xc=1/Cw называется емкостным
реактивным сопротивлением.
Рисунок 3.7.
Следовательно, вектор напряжения на емкости отстает от
вектора тока через емкость на угол p/2.
.2.3 Индуктивность
Под индуктивностью понимаем отношение
потокосцепления самоиндукции yL к току
через индуктивность. Э.д.с. самоиндукции:
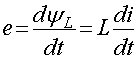
где L - индуктивность, в Гн.
Чтобы уравновесить э.д.с. самоиндукции к индуктивности
необходимо приложить напряжение UL.
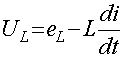
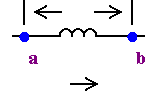
Рисунок 3.8.
Следовательно, для цепи на рисунке 3.8. имеем:
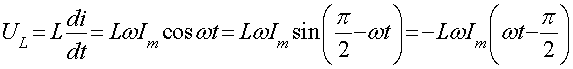
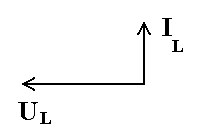
Рисунок 3.9.
Переходя к действующим значениям, полу чим:
L=xL*I,
где xL=Lw-индуктивное реактивное сопротивление.
Векторная диаграмма напряжения UL и
тока i показана на рисунке 3.9.
3.2.4 Последовательное соединение r,
L, C
Рассмотрим цепь, состоящую из r, L, C (рис.
3.10.).
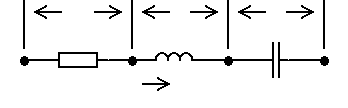
Рисунок 3.9.
Если известен ток i, то векторная диаграмма
напряжений соответствует рис. 3.11.
(для определенности принято, что UL > UC)
,
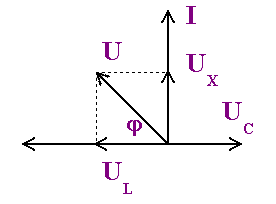
U=UL+UC+Ur.
Рисунок 3.11.
Сложив геометрически вектора UL, UC,
Ur, получаем U.
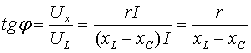
Величину х=xL-xC далее будем
азывать реактивным сопротивлением, а треугольник Ur,
ULC, U- треугольником напряжений.
Величина 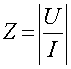 - модуль
полного сопротивления цепи.
- модуль
полного сопротивления цепи.
Так как
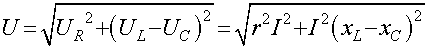
то:
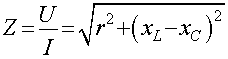
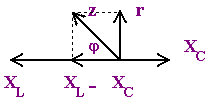
Рисунок 3.12.
Очевидно, если изобразить сопротивления векторами, то
векторная диаграмма примет вид рис. 3.12.
Треугольник, образованный векторами r, xL-xC,
Z, называют треугольником сопротивлений. Как следует из построений,
треугольник сопротивлений и треугольник напряжений подобны.
Подводя итоги, можно отметить, что в цепи, содержащей r,
L, C, ток отстает от напряжения U на угол j, если xL>xC , и опережает напряжение U
на угол j, если xL<xC.
3.2.5 Параллельное соединение r, L, C
Проводимость - величина, обратная сопротивлению.
На участке цепи, изображенном на рисунке 2.10, показаны три параллельные ветви,
первая ветвь содержит только проводимость g, вторая ветвь - емкость С,
третья - индуктивность L.
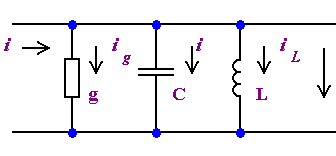
Рисунок 3.13.
Сумма токов равна i. Известно, что:

Тогда:
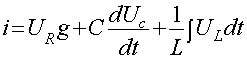
К цепи приложено синусоидальное напряжение U=Umsinwt. Решение
будем искать в виде: i(t)=Imsin(w t-j), тогда:
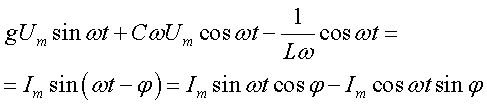
Это решение справедливо для любого значения wt.
При wt=0:
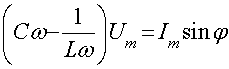 (1)
(1)
При w t=p/2:
m=Imcosj (2)
Возведем обе части уравнений (1) и (2) в квадрат и
просуммируем, получим:
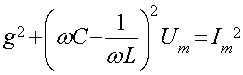
или:
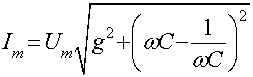
Разделив обе части уравнений (1) и (2) друг на друга,
получаем:
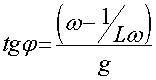
Величину Сw далее
будем называть реактивной емкостной проводимостью, а величину -1/Lw - реактивной
индуктивной проводимостью. В расчетах реактивную индуктивную проводимость
учитывают со знаком “-”.
3.2.6 Мощность в цепи синусоидального
тока
Если напряжение и ток в цепи синусоидальны, а именно
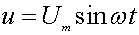 и
и 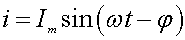 , то мгновенная мощность
, то мгновенная мощность
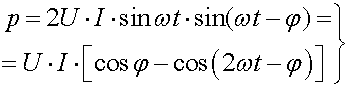 (3.26)
(3.26)
Выражение (3.26) показывает, что мгновенная мощность
состоит из двух частей: постоянной величины 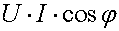 и
синусоидальной-,
и
синусоидальной-,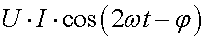 , имеющей удвоенную частоту по сравнению с частотой
напряжения и тока. Следовательно, скорость поступления энергии в цепь
синусоидального тока не постоянна.
, имеющей удвоенную частоту по сравнению с частотой
напряжения и тока. Следовательно, скорость поступления энергии в цепь
синусоидального тока не постоянна.
Средняя мощность за период, называемая активной
мощностью, равна постоянной слагающей выражения (377.26), так как среднее
значение синусоидальной слагающей, совершающей за период Т два цикла,
равно нулю, т.е.
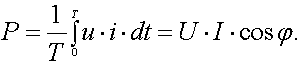 (3.27)
(3.27)
Активная мощность измеряется в ваттах (вт).
Множитель cos(φ) носит название коэффициента мощности. Как видно из
(3.27), активная мощность равна произведению действующих значений напряжения и
тока на коэффициент мощности.
Коэффициент мощности cos(φ) приемника электрической энергии зависит от угла
полного сопротивления данного приемника; чем ближе угол φ к нулю, тем ближе cos(φ) к единице и, следовательно, тем большая при заданных
значениях U и I активная мощность пере дается источником
приемнику.
Повышение коэффициента мощности промышленных
электрических установок представляет важную технике экономическую задачу.
Преобразования (3.27) позволяют получить другие
выражение активной мощности:
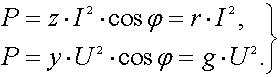 (3.28)
(3.28)
Активная мощность может быть также выражена через
активную составляющую тока
(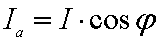 ) или напряжения (
) или напряжения (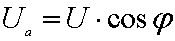 ):
):
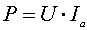 (3.29)
(3.29)
или
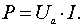 . (3.30)
. (3.30)
Ниже рассматриваются три характерных случая: цепь с
активным сопротивлением; реактивная цепь; смешанная цепь.
3.2.7 Цепь с активным сопротивлением
(φ=0)
При cos(φ) = 1 имеем
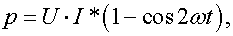 (3.31)
(3.31)
т. е. мгновенная мощность колеблется с удвоенной
угловой частотой (2ω) около среднего значения. Мгновенная мощность все
время положительна: энергия поступает от источника к приемнику и возврата энергии
в источник не происходит. Вся энергия, поступающая в приемник, преобразуется в
тепло.
3.2.8 Реактивная цепь (j=±0,5×p)
При cosφ=0
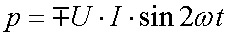 (3.32)
(3.32)
верхний знак относится к случаю индуктивной цепи (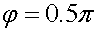 ) ,
) ,
а нижний - к случаю емкостной цепи (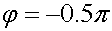 ).
).
Через каждую четверть периода знак мгновенной мощности
изменяется: приемник то запасает энергию (р>0), то расходуетт ее,
возвращая источнику (р < 0).
В случае индуктивной цепи энергия магнитного поля
достигает максимума 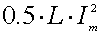 в момент перехода тока в индуктивности через
амплитудное значение; затем она убывает и обращается в нуль при токе, равном
нулю.
в момент перехода тока в индуктивности через
амплитудное значение; затем она убывает и обращается в нуль при токе, равном
нулю.
Соответственно, в случае емкостной цепи энергия
электрического поля достигает максимума 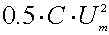 при
амплитудном значении напряжения на емкости; затем она убывает и обращается в
нуль при напряжении равном нулю.
при
амплитудном значении напряжения на емкости; затем она убывает и обращается в
нуль при напряжении равном нулю.
Таким образом, происходят колебания энергии между
источником и приемником, причем электромагнитная энергия не преобразуется в
другие виды энергии, например в тепловую, и активная мощность равна нулю (Р
= 0).
В индуктивной цепи мгновенная мощность равна скорости
изменения энергии магнитного поля, а в емкостной цепи мгновенная мощность равна
скорости изменения анергии электрического поля.
3.2.9 Смешанная цепь
В виде примера рассмотрим случай активно-индуктивной
цепи.
Нa основании (2.26)
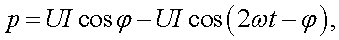
причем 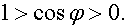
Таким образом, мгновенная мощность колеблется с
удвоенной угловой частотой (2ω) около
оси, отстоящей от оси абсцисс на 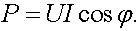
Хотя мгновенная мощность принимает отрицательные
значения, когда и и i имеют разные знаки, однако в течение
большей части периода она положительна и, соответственно, положительные площади
кривой p(t) преобладают над отрицательными.
В результате средняя мощность за период, т.е. активная
мощность Р>0.
В электрических системах, в которых источниками
электрической энергии являются генераторы переменного тока, энергия получается
от первичных двигателей, приводящих генераторы во вращение.
В радиотехнике, где синусоидальные колебания создаются
с помощью электронных устройств, энергия получается от источников постоянного
тока, питающих ламповые генераторы и другие устройства.
Амплитуда синусоидальной составляющей мгновенной
мощности равна произведению действующих значений напряжения и тока
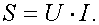 (3.33)
(3.33)
Эта величина носит название полной (кажущейся)
мощности и измеряется в вольт-амперах (ва). Таким образом,
коэффициент мощности равен отношению активной мощности к полной.
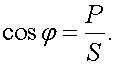
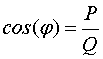 (3.34)
(3.34)
При расчетах электрических цепей пользуются также
понятием реактивной мощности:
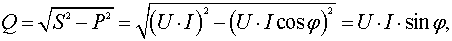 (3.35)
(3.35)
измеряемой в вольт-амперах реактивных (вар).
Очевидно, что 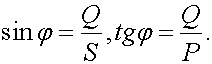 (3.36)
(3.36)
Простые преобразования дают выражения реактивной
мощности в виде:
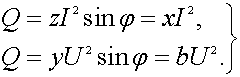 (3.37)
(3.37)
Реактивная мощность может быть также выражена через
реактивную составляющую тока (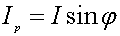 ) или
напряжения (
) или
напряжения (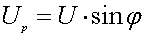 ):
):
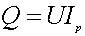 ;
; 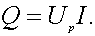 (3.38)
(3.38)
В соответствии с принятым ранее правилом знаков для
угла φ величина реактивной мощности положительна при
отстающем токе (индуктивная нагрузка) и отрицательна при опережающем токе
(емкостная нагрузка).
Реактивная мощность пассивной цепи равна алгебраической
сумме реактивных мощностей для индуктивностей и емкостей, входящих в
состав данной цепи,
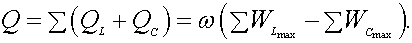 (3.39)
(3.39)
В общем случае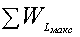 и
и 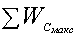 превышают вдвое средние значения, относительно
которых с частотой 2ω
совершают синусоидальные колебания
суммарные мгновенные значения энергии магнитных и, соответственно,
электрических полей [80].
превышают вдвое средние значения, относительно
которых с частотой 2ω
совершают синусоидальные колебания
суммарные мгновенные значения энергии магнитных и, соответственно,
электрических полей [80].
В сложной электрической цепи, состоящей из
сопротивлений, индуктивностей и емкостей, токи в индуктивностях, так же как и
напряжения на емкостях, могут не совпадать по фазе. Поэтому в такой цепи 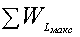 и
и 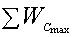 превышают
максимумы энергии, периодически запасаемые в магнитных и электрических полях.
превышают
максимумы энергии, периодически запасаемые в магнитных и электрических полях.
На основании вышеприведенных зависимостей можно
реактивные сопротивление и проводимость цепи выразить как функции 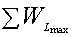 и
и 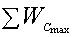 :
:
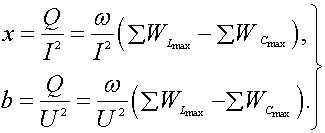 (3.40)
(3.40)
В случае равенства 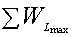 =
=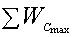 реактивные сопротивление и проводимость, так же как и
реактивная мощность на зажимах цепи, равны нулю, т.е. в цепи имеет место
резонансное явление: происходит непрерывное перераспределение энергии
электрических и магнитных полей, и вся энергия, поступающая от источника,
расходуется в активном сопротивлении цепи, т.е. преобразуется в тепловую
энергию.
реактивные сопротивление и проводимость, так же как и
реактивная мощность на зажимах цепи, равны нулю, т.е. в цепи имеет место
резонансное явление: происходит непрерывное перераспределение энергии
электрических и магнитных полей, и вся энергия, поступающая от источника,
расходуется в активном сопротивлении цепи, т.е. преобразуется в тепловую
энергию.
3.2.10 Баланс мощностей
Из закона сохранения энергии следует, что для любой
электрической цепи соблюдается закон баланса активных мощностей:
активная мощность, генерируемая
источниками, равна активной суммарной мощности, потребляемой нагрузкой.
В свою очередь, можно показать, что и сумма отдаваемых
реактивных мощностей равна сумме потребляемых реактивных мощностей.
Если воспользоваться комплексной формой записи токов,
напряжений и мощностей, то можно доказать, что
сумма комплексных мощностей,
потребляемых во всех ветвях электрической цепи равна нулю; следовательно, также
равны нулю в отдельности алгебраические суммы действительных и мнимых частей
комплексных мощностей.
Иначе говоря, равна нулю как алгебраическая сумма
потребляемых во всех ветвях цепи активных мощностей, так и алгебраическая сумма
потребляемых реактивных мощностей.
3.2.11 Треугольник мощностей
После ввода понятий о активной, реактивной и полной
мощности имеем:
P=UIcosj=UIa=UaI=I2r=U2g,=UIsinj=UIp=UpI=I2x=U2b,
(3.41)
S=UI=IU=I2z=U2y.
Т.е. P, Q, S пропориональны величинам r, x,
z, причем коэффициент пропорциональности равен I2, а
также пропорциональны g, b, y, коэффициент пропорциональности в
последнем случае равен U2. Отсюда следует, что если умножить
стороны треугольника сопротивлений на I2, то в
соответствующем масштабе получим треугольник мощностей. Очевидно, что
треугольник мощностей мы также получим, когда умножим каждую сторону
треугольника проводимостей на U2.
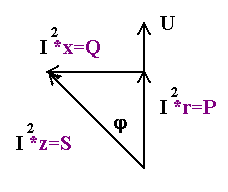
x>0 b>0

j>0 j<0
) б)
Рисунок 3.14.
На рисунке 3.14 показано построение треугольника
мощностей на базе треугольников сопротивлений и проводимостей. Очевидно также,
что для источника э.д.с. справедливо:
P=EIcosj=EIa=EaI=I2r=E2g,
Q=EIsinj=EIp=EpI=I2x=E2b,
(3.42)
S=EI=IE=I2z=E2y.
3.2.12 Эквивалентные параметры и их экспериментальное определение
На практике приходится встречаться с электрическими
цепями значительно более сложными, чем рассмотренные выше. Физические процессы,
происходящие в цепях, рассмотренных выше, несколько идеализированны, например,
не учтены такие явления, как поверхностный эффект, вихревые токи.
Сами элементы цепи тоже являются не чистыми
сопротивлениями, индуктивностями, емкостями. Например, реальная катушка
индуктивности имеет и активное сопротивление - сопротивление провода, которым
она намотана, между витками имеется некоторая емкость.
Конденсатор также содержит сопротивление, соединенные
провода между обкладками и выводами.
Поэтому реальную цепь мы заменяем часто эквивалентными
параметрами - полным, активным и реактивным сопротивлением или полной, активной
и реактивной проводимостью.
Если известно, что напряжение и ток в цепи имеют
синусоидальный характер, то под эквивалентным полным сопротивлением цепи
мы будем понимать отношение U/I, под эквивалентным активным сопротивлением
цепи - отношение средней потребляемой мощности к I2, под эквивалентным
реактивным сопротивлением будем понимать величину, вычисленную по формуле:
=±Öz2-r2 .
Аналогично, полная эквивалентная проводимость -
это отношение I/U, эквивалентная активная проводимость - y=P2/U2
и эквивалентная реактивная проводимость:
b=±Öy2-g2 .
Вопрос определения знака x и b, если не
известен характер цепи, рассмотрим ниже.
Для экспериментального определения z, r, x и y,
g, b необходимо включить последовательно с цепью амперметр, параллельно
цепи подключить вольтметр и измерить ваттметром мощность, потребляемую цепью.
Вычислить z и r, x. Для определения знака х можно,
например, включить последовательно с исследуемой цепью конденсатор, реактивное
сопротивление которого »2х.
Тогда, если цепь имела индуктивный характер, то ток станет равным I’, в
соответствии с круговой диаграммой на рис. 3.15а, т.е. по величине не
изменится. Если цепь имела емкостной характер, то в соотвествии с круговой
диаграммой ток значительно уменьшится. В первом случае необходимо принять х
с плюсом, во втором - с минусом.
U U
U I Ia
Ia
I’ I I
j j1
j‘ j
j
а) б)
Рисунок 3.15.
Две цепи эквивалентны друг другу, если они имеют
одинаковые z, x, r и y, b, g. По величинам x и b,
если x>0 и b>0, можно определить эквивалентную
индуктивность, или, если x<0 и b>0 - эквивалентную емкость.
При этом следует иметь в виду, что эквивалентные параметры зависят от
параметров всех элементов цепи, поэтому эквивалентная индуктивность,
вычисленная по x и r, не равна эквивалентной индуктивности,
вычисленной по b и g. Доказательство этого положения в следующем
параграфе.
3.2.13 Зависимости, связывающие эквивалентные сопротивления и
проводимости
Используя выражения для cos(j) и sin(j), найдем:
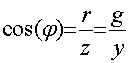
 (3.43)
(3.43)
Так как Z=U/I , а Y=I/U, то z=1/y.
Следовательно, можно выразить проводимость цепи через сопротивления:
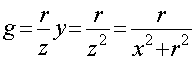
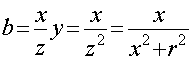 (3.44)
(3.44)
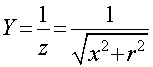
Аналогично выразим сопротивления через проводимости:
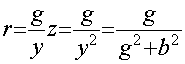
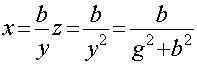 (3.45)
(3.45)
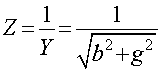
Таким образом, только Z и Y являются
параметрами, обратными друг другу; r и x зависят от всех
проводимостей цепи, а b и g - от всех сопротивлений цепи.
Рассмотрим две эквивалентные цепи (рис. 3.16):
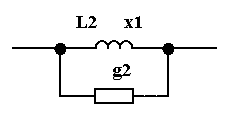
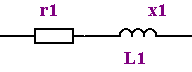
а) б)
Рисунок 3.16.
1=1/(wL1), b2=1/(wL2). (3.46)
В соответствии с правилами вычисления r и x
по g и b имеем:
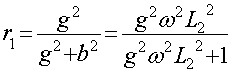
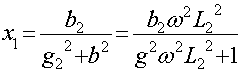 (3.47)
(3.47)
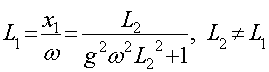
т.е. уже на этом простом примере видно, что
эквивалентные параметры первой цепи зависят от двух эквивалентных параметров
второй цепи.
3.2.14 Применение комплексных чисел
Расчеты электрических цепей переменного тока в
тригонометрической форме или с помощью векторных диаграмм применяются на
практике только в случае относительно простых схем, не содержащих большого
числа контуров и источников, индуктивных связей и т.п.
По мере усложнения электрических схем возникают
значительные трудности производства расчетов в тригонометрической форме или с
помощью векторных диаграмм, и возникает острая потребность в расчетном методе,
позволяющем алгебраическим путем рассчитывать электрические цепи переменного
тока.
Таким удобным расчетным методом является метод
комплексных амплитуд (комплексный или символический метод),
основанный на применении комплексных чисел. Этот метод является по существу
“алгеброй” современной электротехники и радиотехники, в то время как метод
векторных диаграмм является их “геометрией”,
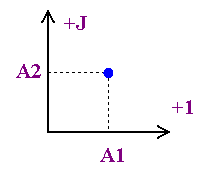
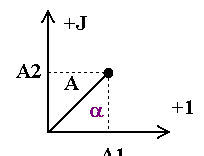
Известно, что комплексное число изображается на
комплексной плоскости точкой, причем в прямоугольной системе координат осью
абсцисс служит действительная, а осью ординат-мнимая ось.
a) б)
Рис. 3.17 Геометрическое изображение
комплексного числа
Так, на рис. 3.17а точка с координатами 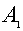 и
и 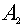 изображает
комплексное число
изображает
комплексное число
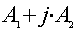 , где
, где 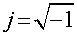 .
.
Комплексное число можно условно обозначать через
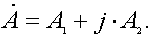 (3.48)
(3.48)
Выражение (2.6) представляет собой алгебраическую
форму записи комплексного числа.
Как известно, каждая точка на комплексной плоскости
определяется радиус-вектором этой точки, т.е. вектором, начало которого совпадает
с началом координат, а конец находится в точке, соответствующей заданному
комплексному числу (рис. 2.4,б).
Пользуясь полярной системой координат, записываем
комплексное число
в так называемой показательной форме:
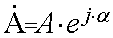 (3.49)
(3.49)
Здесь 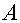 -
модуль,
-
модуль, 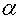 - аргумент или фаза.
- аргумент или фаза.
С учетом того, что
 ;
;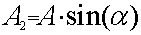 ,
получаем
,
получаем
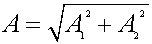 ;
; 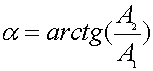 (3.50)
(3.50)
Соответственно, тригонометрическая форма записи
комплексного числа имеет вид:
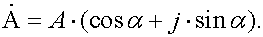 (3.51)
(3.51)
Два комплексных числа считаются равными, если равны
отдельно их действительные и мнимые части. Геометрически это означает равенство
векторов, изображающих комплексные числа.
Понятия “большее и “меньше” применимы только к
координатам комплексных чисел, модулям, фазам, тогда как для самих комплексных
чисел эти понятия не существуют.
Удобство применения той или иной формы записи
комплексных чисел зависит в каждом отдельном случае от тех математических
операций, которые надлежит произвести над комплексными числами.
Так, при сложении или вычитании комплексных величин
пользуются алгебраической (или тригонометрической) формой записи комплексного
числа:
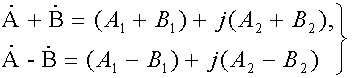 (3.52)
(3.52)
В геометрической интерпретации для получения вектора,
изображающего сумму или разность комплексных чисел, следует сложить или вычесть
векторы, изображающие эти числа, по правилу действий над векторами.
При умножении или делении комплексных величин наиболее
удобно пользоваться показательной формой записи комплексного числа.
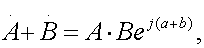 (3.53)
(3.53)
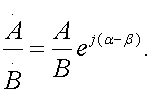 (3.54)
(3.54)
Как видно из (2.10) и (2.11), модуль произведения
равен произведению модулей сомножителей, аргумент произведения равен сумме их
аргументов; модуль частного равен частному модулей делимого и делителя,
аргумент частного равен разности их аргументов.
В геометрической интерпретации вектор, изображающий
произведение 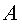 на В, получается поворотом вектора А против
часовой стрелки на угол β (аргумент
вектора В) и умножением его на В.
на В, получается поворотом вектора А против
часовой стрелки на угол β (аргумент
вектора В) и умножением его на В.
Соответственно, вектор, изображающий частное от
деления А на В, получается поворотом A по часовой стрелке
на угол β и делением его на В.
Два комплексных числа (или вектора) называются взаимно
сопряженными, если их модули равны, а аргументы равны по величине и обратные по
знаку; иначе говоря, сопряженные комплексные числа отличаются друг от друга
только знаком мнимой части:
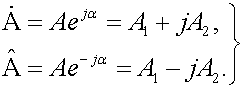 (3.55)
(3.55)
В геометрической интерпретации точки, изображающие
сопряженные числа, расположены симметрично относительно действительной оси.
Сопряженные комплексные числа обладают тем важным
свойством, что про изведение их дает действительное число, равное квадрату
модулей сомножителей:
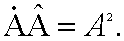 (3.56)
(3.56)
Иначе говоря, точки, изображающие произведение
сопряженных комплексных чисел, располагаются по действительной оси.
При пользовании алгебраической формой записи
комплексных чисел произведение двух комплексных чисел имеет вид
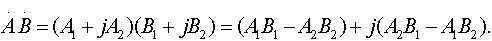 (3.57)
(3.57)
Соответственно, деление двух комплексных чисел,
произведенное с помощью умножения и деления числителя и знаменателя на
сопряженный знаменатель, дает
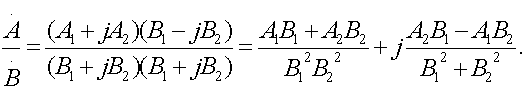 (3.58)
(3.58)
Выражение (2.14), равное выражению (2.10), отличается
от него большим числом операций. То же следует сказать и в отношении выражений
(2.15) и (2.11).
Возведение комплексного числа в степень -1 (обращение
комплексного числа) представляет частный случай деления:
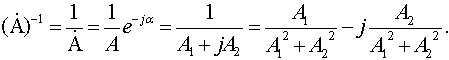 (3.59)
(3.59)
При возведении комплексного числа в степень или
извлечении корня удобна показательная форма записи:
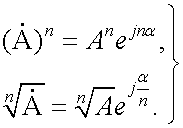 (3.60)
(3.60)
Ранее была показана возможность представления
синусоидальных функций с помощью вращающихся векторов. Вектор, конец которого
вращается в положительную сторону (против часовой стрелки) с угловой скоростью ω, аналитически может быть выражен следующим образом:
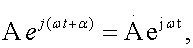 (3.61)
(3.61)
где 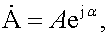 -
комплексная амплитуда представляющая данный вектор в момент t=0.
-
комплексная амплитуда представляющая данный вектор в момент t=0.
Множитель 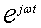 является
оператором вращения: умножение комплексной амплитуды на
является
оператором вращения: умножение комплексной амплитуды на 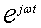 означает поворот вектора А на угол ω×t в
положительную сторону.
означает поворот вектора А на угол ω×t в
положительную сторону.
Комплексная функция может быть выражена в
тригонометрической форме
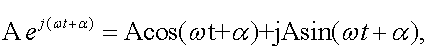 (3.62)
(3.62)
т.е. всякая синусоидальная функция A sin (ω×t + α) может рассматриваться как мнимая часть комплексной
функции, взятая без множителя j, что условно математически записывается так:
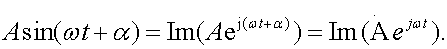 (3.63)
(3.63)
Символ Im (imaginary) означает, что берется
мнимая часть комплексной функции, без множителя j.
Аналогично косинусоидальная функция может быть в
случае необходимости представлена как действительная часть комплексной функции
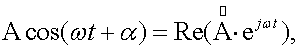 (3.64)
(3.64)
где символ Re (real) означает, что берется
действительная часть комплексной функции.
Между различными формами записи комплексных чисел или
изображающих векторов существуют очевидные соотношения, которые для наглядности
сведены в таблицу 3.1.
Замена синусоидальных функций a(t)
комплексными числами и изображающими их векторами A позволяет перейти от
тригонометрических функций времени к алгебраическим. При этом исходные
синусоидальные функции времени можно считать оригиналами, а комплексные числа и
векторы их изображениями или символами. Поэтому метод расчета
электрических цепей, использующий такое представление функций называется
символическим.
Любой математической операции в области оригиналов
будет соответствовать некоторая операция в области изображений. Без доказательства
сведем в таблицу основные математические операции над оригиналами и
изображениями, представляя последние в двух формах: аналитической и
графической, т.е. в виде аналитических выражений и соответствующих операций с
векторами.
При операциях с комплексными числами и изображающими
их векторами большую роль играют числа, модуль которых равен единице. Они
называются операторами поворота. Наиболее распространенными
операторами поворота являются числа 1, j , -1 и -j . Результаты
умножения произвольного комплексного числа A на эти числа показаны в
таблице 3.
Для исследования взаимных отношений различных величин,
векторы токов, напряжений и ЭДС строятся совместно на одной комплексной
плоскости и такая совокупность векторов называется векторной диаграммой.
Таблица 3.1.
|
Формы записи
|
Am = p + jq
|
Am=Am(cosya+jsinya)
|
Am = Am e jy a
|
|
Am = p + jq
|
-
|
p= Amcosy a q= Amsiny a
|
p= Amcosy a q= Amsiny a
|
Am =Am(cosya+jsinya) 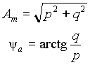 -Am
= Am
-Am
= Am
Am
= Am e jy a 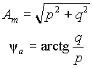 Am = Am
Am = Am
Любой математической операции в области оригиналов
будет соответствовать некоторая операция в области изображений. Без
доказательства сведем в таблицу основные математические операции над оригиналами
и изображениями, представляя последние в двух формах: аналитической и
графической, т.е. в виде аналитических выражений и соответствующих операций с
векторами.
Таблица 3.2.
|
Оригинал
|
Изображение
|
|
a(t)=Amsin(w t+y a)
|
A=p+jq=Ae jya
|
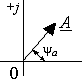
|
|
C× a(t)=С× Amsin(w t+y a)
|
C× A=C(p+jq)=C× Ae jya
|
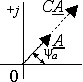
|
|
b(t)=a1(t)+a2(t)
|
B=A1+A2= =(p1+p2)+j(q1+q2)
|
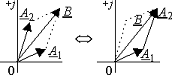
|
|
b(t)=a1(t)a2(t)
|
B=A1 A2=
=(p1 p2)+j(q1
q2)
|
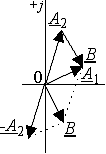
|
|
b(t)=a1(t)× a2(t)
|
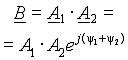 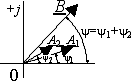
|
|
|
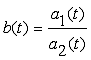 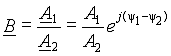 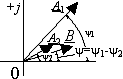
|
|
|
|
b(t)=[a(t)]n
|
B=An= Ane jna
|
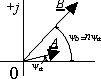
|
|
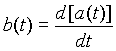 B=jw A= w × Ae j(y a+p /2) B=jw A= w × Ae j(y a+p /2)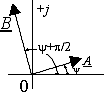
|
|
|
|
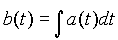 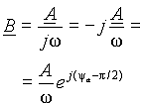 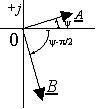
|
|
|
При операциях с комплексными числами и изображающими
их векторами большую роль играют числа, модуль которых равен единице. Они
называются операторами поворота. Наиболее распространенными
операторами поворота являются числа 1, j , -1 и -j . Результаты
умножения произвольного комплексного числа A на эти числа показаны в
таблице 3.3.
Таблица 3.3.
|
E
|
E× A
|
|
1
|
ej0
|
Ae jy
|
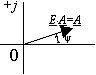
|
|
j
|
ejp /2
|
Ae j(y +p /2)
|
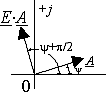
|
|
-1
|
ejp
|
Ae j(y ± p )
|
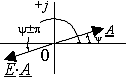
|
|
-j
|
e jp /2
|
Ae j(y - p /2)
|
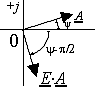
|
3.2.15 Законы Ома и Кирхгофа в
комплексной форме
Рассмотрим применение комплексного метода к случаю
последовательного и параллельного соединения элементов r, L, С.
3.2.16 Последовательное соединение r,
L, С
Положим, что в уравнении напряжений
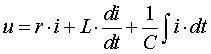 (3.65)
(3.65)
заданными являются параметры r, L, С и
синусоидальное напряжение 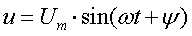 на зажимах цепи, а искомой величиной является ток i.
на зажимах цепи, а искомой величиной является ток i.
Ввиду того, что здесь рассматривается установившийся
режим в цепи с синусоидальным однофазным током, решение данного
дифференциального уравнения будем искать в форме синусоидальной функции
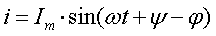 (3.66)
(3.66)
Пусть в соответствии с предыдущим параграфом заданное
синусоидальное напряжение символизируется комплексной функцией
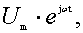 а искомый синусоидальный ток i - комплексной
функцией
а искомый синусоидальный ток i - комплексной
функцией  .
.
Комплексные амплитуды напряжения и тока равны,
соответственно,
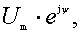 и
и 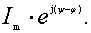
Переписав дифференциальное уравнение (3.65) и
пользуясь правилами коммутативности операций сложения, дифференцирования и
интегрирования относительно символической операции Im, преобразуем полученное
уравнение с учетом того обстоятельства, что при интегрировании функции 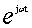 постоянная интегрирования должна быть опущена, так как
в рассматриваемом здесь установившемся режиме электрические заряды или
напряжения на емкостях представляют синусоидальные функции, не содержащие
постоянных слагаемых. В результате преобразований можно получить следующее
алгебраическое комплексное уравнение, выражающее второй закон Кирхгофа для
комплексных амплитуд
постоянная интегрирования должна быть опущена, так как
в рассматриваемом здесь установившемся режиме электрические заряды или
напряжения на емкостях представляют синусоидальные функции, не содержащие
постоянных слагаемых. В результате преобразований можно получить следующее
алгебраическое комплексное уравнение, выражающее второй закон Кирхгофа для
комплексных амплитуд
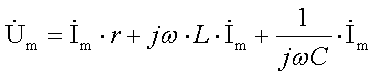 (3.67)
(3.67)
Выражение
 (3.68)
(3.68)
представляет собой комплексное сопротивление
рассматриваемой электрической цепи.
Следовательно, равенства
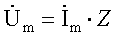 и
и 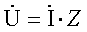 (3.69)
(3.69)
выражают закон Ома для комплексных амплитуд и для
комплексных действующих значений.
Комплексное сопротивление Z представлено в
выражении (3.68) в алгебраической форме.
Та же величина, записанная в тригонометрической и
показательной формах, имеет вид:
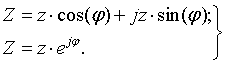 (3.69)
(3.69)
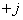
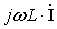
Векторная диаграмма для случая
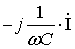
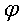 последовательного соединения
последовательного соединения
элементов r, L, С.
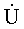
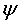
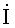
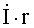
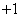
Следует заметить, что уравнение (3.67) можно
рассматривать как алгебраическую интерпретацию векторной диаграммы рис. 3.18,
вычерченной на комплексной плоскости, где:
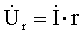 - падение напряжения в активном сопротивлении r
(совпадает по фазе с током
- падение напряжения в активном сопротивлении r
(совпадает по фазе с током 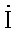 );
);
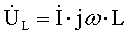 - падение напряжения в индуктивном сопротивлении,
опережающее ток на угол 90o;
- падение напряжения в индуктивном сопротивлении,
опережающее ток на угол 90o;
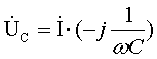 - падение напряжения в емкостном сопротивлении,
отстающее от тока на угол 90o.
- падение напряжения в емкостном сопротивлении,
отстающее от тока на угол 90o.
Аналогичные выводы и построения векторной диаграммы
могут быть произведены для случая параллельного соединения элементов r, L,
С.
Мощность в комплексной форме.
Полная мощность может быть записана в комплексной
форме.
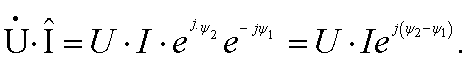 (3.71)
(3.71)
Отсюда следует, что
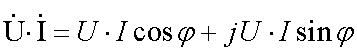 (3.72)
(3.72)
или, что то же,
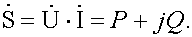 (3.73)
(3.73)
Таким образом, комплексная величина 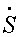 имеет действительную часть, равную активной мощности,
и мнимую часть, равную реактивной мощности; она носит название мощности в
комплексной форме или комплексной мощности и может быть представлена графически
на комплексной плоскости. Модуль
имеет действительную часть, равную активной мощности,
и мнимую часть, равную реактивной мощности; она носит название мощности в
комплексной форме или комплексной мощности и может быть представлена графически
на комплексной плоскости. Модуль 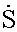 равен
полной мощности.
равен
полной мощности.
3.2.17 Условие передачи источником
максимума мощности приемнику
На практике часто возникает необходимость подбора
сопротивления нагрузки таким образом, чтобы при заданном сопротивлении
источника обеспечивалась передача приемнику максимума активной мощности.
Обозначим сопротивление источника напряжения через 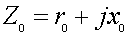 , а сопротивление нагрузки - через
, а сопротивление нагрузки - через 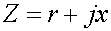 .
.
Активная мощность, потребляемая нагрузкой, равна
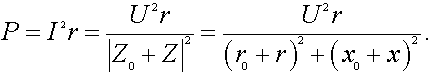 (3.74)
(3.74)
Если изменять реактивное сопротивление x, то
очевидно, при любом значении r ток и, соответственно, активная мощность
достигают наибольшей величины при 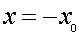 .
.
При этом
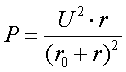 (3.75)
(3.75)
Найдем теперь условие максимума функции (2.44) в
предположении, что r - переменная величина, т.е. из условия 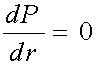 .
.
Следовательно, получается дополнительное условие - 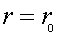 .
.
На основании найденных равенств заключаем, что
условием передачи источником максимума активной мощности приемнику является
равенство
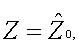 (3.76)
(3.76)
где  -
комплексное сопротивление, сопряженное с
-
комплексное сопротивление, сопряженное с 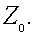
Подстановка дает максимальное значение полной мощности
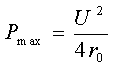 (3.77)
(3.77)
Таким образом, передача максимума полной мощности в
нагрузку достигается при равенстве полных сопротивлений нагрузки и источника.
При этом передаваемая мощность тем больше, чем больше разнятся углы
сопротивлений Z и Zо.
Условия передачи максимума активной или полной
мощности широко используются в радиотехнике, проводной связи, электроавтоматике
и приборостроении.
В энергетических же системах, генерирующих и
потребляющих большие мощности, стремятся к получению высоких КПД генераторов,
что имеет место при сопротивлениях нагрузок, значительно превышающих
сопротивления генераторов.
3.3 Резонанс в электрических цепях синусоидального
переменного тока
Явление резонанса относится к наиболее важным с
практической точки зрения свойствам электрических цепей. Оно заключается в том,
что электрическая цепь, имеющая реактивные элементы обладает чисто резистивным
сопротивлением.
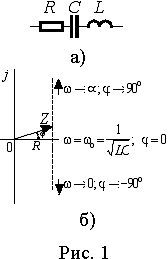
Общее условие резонанса для любого двухполюсника можно
сформулировать в виде Im[Z]=0 или Im[Y]=0, где Z и Y
комплексное сопротивление и проводимость двухполюсника. Следовательно, режим резонанса
полностью определяется параметрами электрической цепи и не зависит от внешнего
воздействия на нее со стороны источников электрической энергии.
Для определения условий возникновения
режима резонанса
в электрической цепи нужно:
· найти ее комплексное сопротивление
или проводимость;
· выделить мнимую часть и приравнять
нулю.
Все параметры электрической цепи, входящие в
полученное уравнение, будут в той или иной степени влиять на характеристики
явления резонанса.
Уравнение Im[Z]=0 может иметь несколько корней
решения относительно какого-либо параметра. Это означает возможность
возникновения резонанса при всех значениях этого параметра, соответствующих
корням решения и имеющих физический смысл.
В электрических цепях резонанс может рассматриваться в
задачах:
· анализа этого явления при вариации
параметров цепи;
· синтеза цепи с заданными резонансными
параметрами.
Электрические цепи с большим количеством реактивных
элементов и связей могут представлять значительную сложность при анализе и
почти никогда не используются для синтеза цепей с заданными свойствами, т.к.
для них не всегда возможно получить однозначное решение. Поэтому на практике
исследуются простейшие двухполюсники и с их помощью создаются сложные цепи с
требуемыми параметрами.
Простейшими электрическими цепями, в которых может
возникать резонанс, являются последовательное и параллельное соединения
резистора, индуктивности и емкости. Соответственно схеме соединения, эти цепи
называются последовательным и параллельным резонансным контуром.
Наличие резистивного сопротивления в резонансном контуре по определению не
является обязательным и оно может отсутствовать как отдельный элемент
(резистор). Однако при анализе резистивным сопротивлением следует учитывать по
крайней мере сопротивления проводников.
Последовательный резонансный контур представлен на
рис. 3.19 а). Комплексное сопротивление цепи равно
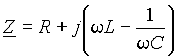 . (3.78)
. (3.78)
Условием <E:Мои документыE@TOE1" l >
резонанса из выражения (3.78) будет
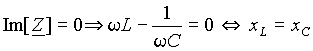 . (3.79)
. (3.79)
Таким образом, резонанс в цепи наступает независимо от
значения резистивного сопротивления R когда индуктивное сопротивление xL
= w L равно емкостному xC
= 1/(w C) . Как следует из выражения
(3.79), это состояние может быть получено вариацией любого их трех параметров -
L, C и w ,
а также любой их комбинацией.
При вариации одного из параметров условие резонанса
можно представить в виде
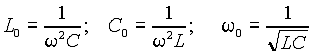 . (3.80)
. (3.80)
Все величины, входящие в выражение (3.80)
положительны, поэтому эти условия выполнимы всегда, т.е. резонанс в
последовательном контуре можно создать
· изменением индуктивности L при
постоянных значениях C и w ;
· изменением емкости C при постоянных
значениях L и w ;
· изменением частоты при
постоянных значениях L и C.
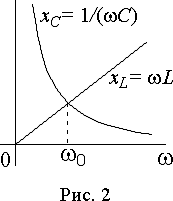
Наибольший интерес для практики представляет вариация
частоты. Поэтому рассмотрим процессы в контуре при этом условии.
При изменении частоты резистивная составляющая
комплексного сопротивления цепи Z остается постоянной, а реактивная
изменяется. Поэтому конец вектора Z на комплексной плоскости
перемещается по прямой параллельной мнимой оси и проходящей через точку R
вещественной оси (рис. 3.19 б) <E:Мои документыE@TOE1" l >). В
режиме резонанса мнимая составляющая Z равна нулю и Z = Z
= Zmin = R , j = 0 , т.е. полное
сопротивление при резонансе соответствует минимальному значению.
Индуктивное и емкостное сопротивления изменяются в
зависимости от частоты так, как показано на рис. 2. При частоте стремящейся к
нулю xC ® µ , xL ®0 , и j
® 90° (рис. 3.19б) <E:Мои документыE@TOE1" l >). При бесконечном
увеличении частоты - xL ® µ , xC ®0 , а j ® 90° . Равенство сопротивлений xL и xC
наступает в режиме резонанса при частоте w0 .
Рассмотрим теперь падения напряжения на элементах
контура. Пусть резонансный контур питается от источника, обладающего свойствами
источника ЭДС, т.е. напряжение на входе контура u = const, и пусть ток в
контуре равен i=Imsinw t.
Падение напряжения на входе уравновешивается суммой напряжений на элементах
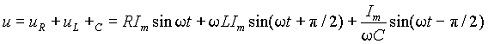 .(3.81)
.(3.81)
Переходя от амплитудных значений к действующим, из
выражения (3.81) получим напряжения на отдельных элементах контура
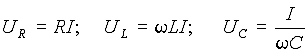 , (3.82)
, (3.82)
а при резонансной частоте
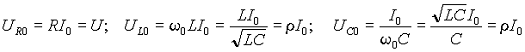 ,(3.83)
,(3.83)
где  -
величина, имеющая размерность сопротивления и называемая волновым или
характеристическим сопротивлением контура.
-
величина, имеющая размерность сопротивления и называемая волновым или
характеристическим сопротивлением контура.
Следовательно, при резонансе
· напряжение на резисторе равно
напряжению на входе контура;
· напряжения на реактивных элементах
одинаковы и пропорциональны волновому сопротивлению контура;
· соотношение напряжения на входе
контура (на резисторе) и напряжений на реактивных элементах определяется
соотношением резистивного и волнового сопротивлений.
Отношение волнового сопротивления к резистивному r /R = Q, называется добротностью
контура, а величина обратная D=1/Q - затуханием.
Таким образом, добротность числено равна отношению напряжения на реактивном
элементе контура к напряжению на резисторе или на входе в режиме резонанса.
Добротность может составлять несколько десятков единиц и во столько же раз
напряжение на реактивных элементах контура будет превышать входное. Поэтому
резонанс в последовательном контуре называется резонансом напряжений.
Рассмотрим зависимости напряжений и тока в контуре от
частоты. Для возможности обобщенного анализа перейдем в выражениях (3.82) к
относительным единицам, разделив их на входное напряжение при резонансе U=RI0
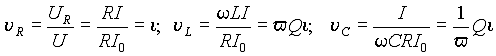 , (3.84)
, (3.84)
где i =I/I0, u k=Uk/U, v = w /w 0 - соответственно ток, напряжение и
частота в относительных единицах, в которых в качестве базовых величин приняты
ток I0, напряжение на входе U и частота w 0 в режиме резонанса.
Абсолютный и относительный ток в контуре равен:
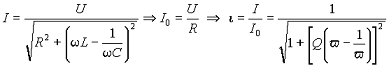 . (3.85)
. (3.85)
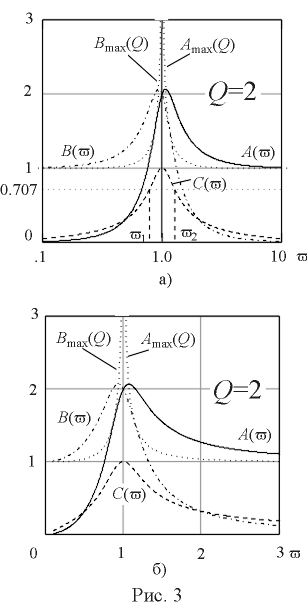
Из выражений (3.84) и (3.85) следует, что характер
изменения всех величин при изменении частоты зависит только от добротности
контура. Графическое представление их при Q=2 приведено на рис. 3.21 в
логарифмическом (а) и линейном (б) масштабах оси абсцисс.
На рис. 3.21 кривые A(v), B(v) и C(v) соответствуют напряжению на
индуктивности, емкости и резисторе или току в контуре. Кривые A(v)=uL(v) и
B(v)=uC(v) имеют максимумы, напряжения в которых определяются
выражением
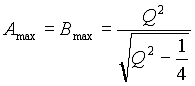 , (3.86)
, (3.86)
а относительные частоты максимумов равны
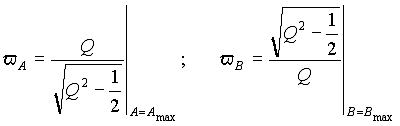 (3.87)
(3.87)
При увеличении добротности Q ® µ Amax = Bmax ® Q, а v 1 ® 1.0 и v 2 ®
1.0.
С уменьшением добротности максимумы кривых u L(v ) и u С(v ) смещаются от резонансной
частоты, а при Q2 < 1/2 исчезают, и кривые относительных
напряжений становятся монотонными.
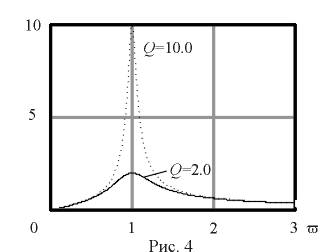
Напряжение на резисторе и ток в контуре имеют при
резонансной частоте максимум равный 1,0. Если на оси ординат отложить
абсолютные значения тока или напряжения на резисторе, то для различных значений
добротности они будут иметь вид, показанный на рис. 3.22. В целом они дают
представление о характере изменения величин, но удобнее делать сопоставление в
относительных единицах.
На рис. 3.23 представлены кривые рис. 3.22 в
относительных единицах. Здесь видно, что увеличение добротности влияет на
скорость изменения тока при изменении частоты.
Можно показать, что разность относительных частот,
соответствующих значениям относительного тока 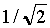 , равна
затуханию контура D=1/Q =v 2
v 1.
, равна
затуханию контура D=1/Q =v 2
v 1.
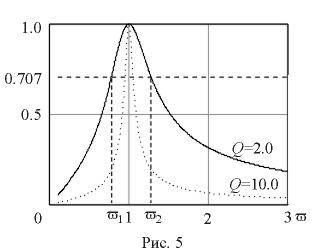
Перейдем теперь к анализу зависимости фазового сдвига
между током и напряжением на входе контура от частоты. Из выражения (3.78) угол
равен
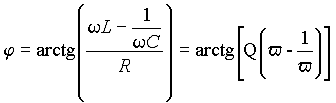 . (3.89)
. (3.89)
Как и следовало ожидать, значение j определяется добротностью контура.
Графически эта зависимость для двух значений добротности показана на рис. 3.24
.
При уменьшении частоты значение фазового сдвига
стремится к значению 90° , а при увеличении к +90° , проходя через нулевое значение при
частоте резонанса. Скорость изменения функции j (v ) определяется добротностью контура.
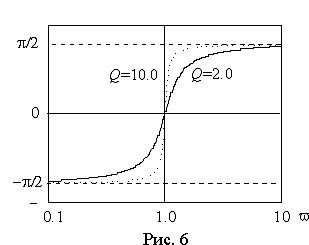
Последовательный резонансный контур может питаться
также от источника электрической энергии, обладающего свойствами источника
тока, т.е. обеспечивающего постоянный ток в нагрузке. Выражения (3.82) остаются
справедливыми и в этом случае, но ток в них будет константой. Поэтому
постоянным будет падение напряжения на резисторе UR = RI
= const. Разделив все напряжения на это базовое значение, получим представление
их в относительных единицах в виде
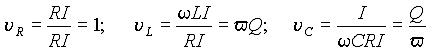 . (3.90)
. (3.90)
В выражении (3.90) добротность также есть отношение
волнового сопротивления к резистивному Q=r /R .
Общее относительное падение напряжения на входе
контура является гипотенузой прямоугольного треугольника напряжений, поэтому
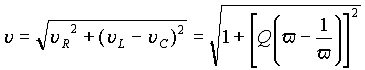 . (3.91)
. (3.91)
Функции uL(v )
и uС(v ) монотонны, а u(v )
имеет минимум u =1.0 при
резонансной частоте, когда uL(v ) uС(v ) = 0. В случае стремления относительной частоты к
бесконечности и к нулю, напряжения на одном из реактивных элементов стремится к
бесконечности. При резонансной частоте они одинаковы и их отношение ко входному
напряжению равно добротности..
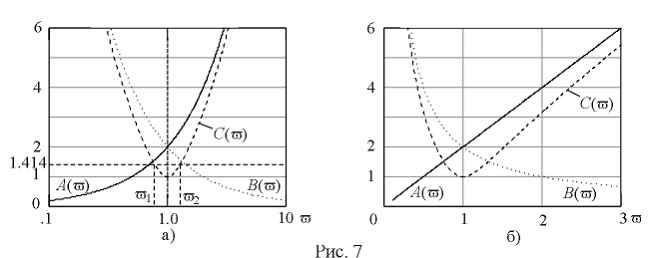
Графическое представление функций u L(v )=A(v ), u С(v )=B(v ) и u(v)=С(v ) при добротности Q=2 дано на
рис. 3.25 в логарифмическом (а) и линейном (б) масштабах оси частот.
Для функции u (v)=С(v) можно показать, что разность относительных частот v 1 и v
2 , соответствующих значениям 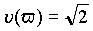 , равна затуханию контура D=1/Q=v 2 v 1.
, равна затуханию контура D=1/Q=v 2 v 1.
Фазовые характеристики контура при питании от
источника тока ничем не отличаются от характеристик режима питания от источника
ЭДС (Рис.3.24).
Сопоставляя частотные характеристики при питании
последовательного резонансного контура от источника тока с характеристиками при
питании его от источника ЭДС, можно сделать следующие выводы:
· частотные характеристики напряжений и
тока контура принципиально отличаются друг от друга, т.к. при питании от
источника ЭДС сумма напряжений остается постоянной и происходит только их
перераспределение между элементами, а при питании от источника тока падения
напряжения на каждом элементе формируются независимо;
· режимы резонанса для обоих случаев полностью
идентичны;
· фазовые частотные характеристики для
обоих случаев также идентичны.
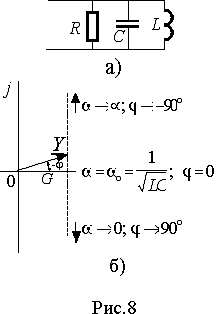
Режим резонанса можно создать также при параллельном
соединении R, L и C (рис. 3.26а)). Такая цепь называется параллельным
резонансным контуром. В этом случае условие <E:Мои
документыE@TOE1" l > резонанса удобнее сформулировать для мнимой части
комплексной проводимости в виде
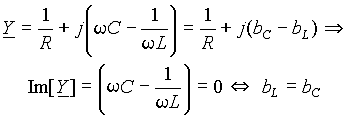 (3.92)
(3.92)
Следовательно, для параллельного контура возможны те
же вариации параметров, что и для последовательного и выражения для них будут
идентичными
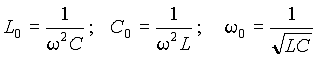 . (3.93)
. (3.93)
При изменении частоты питания изменяется только мнимая
составляющая вектора комплексной проводимости Y , поэтому его конец
перемещается на комплексной плоскости по прямой параллельной мнимой оси и
проходящей через точку G=1/R , соответствующую вещественной
составляющей проводимости (рис. 3.26 б)). При частоте резонанса модуль вектора
минимален, а при стремлении частоты к нулю и бесконечности, его значение
стремится к бесконечности. При этом угол сдвига фаз между током и напряжением j на входе контура стремится к 90° при w ® 0 и к 90°
при w ® µ .
Для параллельного соединения токи в отдельных
элементах можно представить через проводимости и общее падение напряжения U
в виде
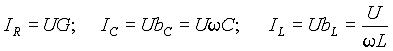 . (3.94)
. (3.94)
Пусть в режиме резонанса падение напряжения на входе
контура равно U0, тогда токи в отдельных элементах будут
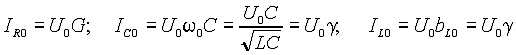 ,(3.95)
,(3.95)
где 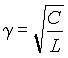 - волновая
или характеристическая проводимость контура. Как следует из выражений
(3.95), при резонансе токи в реактивных элементах одинаковы, а входной ток
равен току в резисторе R. Отношение Q=g /G называется добротностью, а величина обратная D=1/Q -
затуханием параллельного резонансного контура. Таким образом, добротность равна
отношению токов в реактивных элементах контура к току на входе или в резисторе.
В электрических цепях добротность может достигать значений в несколько десятков
единиц и во столько же раз токи в индуктивности и емкости будут превышать
входной ток. Поэтому резонанс в параллельном контуре называется
резонансом токов.
- волновая
или характеристическая проводимость контура. Как следует из выражений
(3.95), при резонансе токи в реактивных элементах одинаковы, а входной ток
равен току в резисторе R. Отношение Q=g /G называется добротностью, а величина обратная D=1/Q -
затуханием параллельного резонансного контура. Таким образом, добротность равна
отношению токов в реактивных элементах контура к току на входе или в резисторе.
В электрических цепях добротность может достигать значений в несколько десятков
единиц и во столько же раз токи в индуктивности и емкости будут превышать
входной ток. Поэтому резонанс в параллельном контуре называется
резонансом токов.
Падение напряжения на входе контура U при
питании его от источника, обладающего свойствами источника тока и формирующего
ток с действующим значением I, будет равно
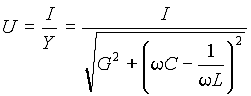 . (3.96)
. (3.96)
Отсюда, напряжение на входе в режиме резонанса U0
= I/G . Тогда ток в контуре - I=U0G.
Перейдем к относительным единицам в выражениях (3.95) и (3.97), приняв в
качестве базовых значений напряжение на входе при резонансе и ток контура,
выраженный через это напряжение. Тогда получим
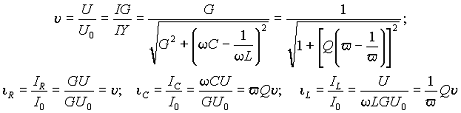 .(3.97)
.(3.97)
Выражения (3.97) полностью совпадают с выражениями
(3.84) и (3.85) <E:Мои документыE@TOE1" l > для частотных
характеристик последовательного контура, если в них относительные токи и
напряжения поменять местами. Следовательно, характеристики рис. 3 <E:Мои
документыE@TOE1" l >.21 будут связаны с выражениями (3.97) следующим
образом: A(v)=iС(v); B(v)=iL(v) и C(v)=i R(v)=u (v ). Для относительных токов iС , iL
и iR справедливыми будут также все закономерности отмеченные
для относительных напряжений последовательного контура.
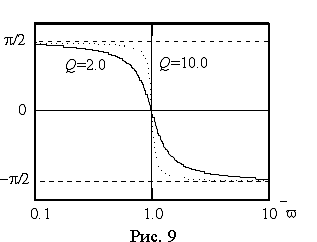
Из выражения (3.92) рассмотренную выше качественно
фазовую частотную характеристику можно представить аналитически в виде
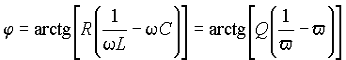
т.е. она совпадает с характеристикой последовательного
контура, но имеет противоположный знак.
Допустим теперь, что параллельный контур питается от
источника со свойствами источника ЭДС. В режиме резонанса входной ток также
будет равен току через резистор - I0=U/R=UG.
Соотнесем все выражения (3.94) с этим током, приняв его за базовую
величину. Тогда
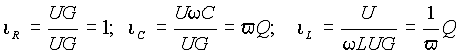 . (3.98)
. (3.98)
Относительный входной ток можно определить,
пользуясь тем, что в треугольнике токов он является гипотенузой
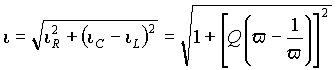 . (3.99)
. (3.99)
Выражения (19) и (20) для относительных токов
совпадают с выражениями (3.90) и (3.91) <E:Мои документыE@TOE1" l >
для относительных напряжений последовательного контура. Следовательно, на рис.
<E:Мои документыE@TOE1" l >3.25 -
i C(v )=A(v ), i L(v )=B(v ) и i R(v )= i (v )=C(v ).
Сравнивая частотные характеристики при питании
параллельного резонансного контура от источника тока с характеристиками при
питании его от источника ЭДС, можно сделать выводы аналогичные тем, которые
были сделаны для последовательного контура:
частотные характеристики токов и напряжения контура
принципиально отличаются друг от друга, т.к. при питании от источника тока
сумма токов остается постоянной и происходит только их перераспределение между
элементами, а при питании от источника ЭДС токи в каждом элементе формируются
независимо;
· режимы резонанса для обоих случаев
полностью идентичны;
· фазовые частотные характеристики для
обоих случаев также идентичны.
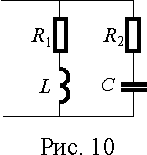
Параллельный резонансный контур может содержать
резистивные сопротивления (рис. 3.27). В этом случае комплексные проводимости
ветвей будут равны
1=G1+jB1; Y2=G2+jB1
,
а общая проводимость
= Y1 + Y2= G1+G2+j(B1+B2)
.
Условием резонанса будет:
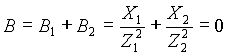
Раскрывая выражение через параметры цепи, получим
 ,
,
откуда резонансная частота w р -
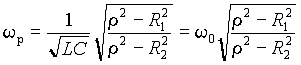 , (3.100)
, (3.100)
где 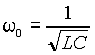 -
резонансная частота в простейшем параллельном контуре (рис. 3.26 а) <E:Мои
документыE@TOE1" l >), а
-
резонансная частота в простейшем параллельном контуре (рис. 3.26 а) <E:Мои
документыE@TOE1" l >), а  -
волновое сопротивление простейшего параллельного контура.
-
волновое сопротивление простейшего параллельного контура.
Анализ выражения (3.100) показывает, что при разных
резистивных сопротивлениях R1 ¹ R2 резонанс
возможен только, если оба сопротивления одновременно больше или меньше r . В
противном случае выражение под корнем отрицательно, резонансная частота мнимая
и не имеет физического смысла.
Если R1 = R2, то w р = w 0, т.е. резонанс наступает при той
же частоте, что и в простейшем контуре без потерь (рис. 3.26 а)).
Однако при этом условии возможен вариант, когда R1
= R2 = r . В этом случае подкоренное выражение в (3.100)
становится неопределенным (0/0) и требуется его дополнительный анализ.
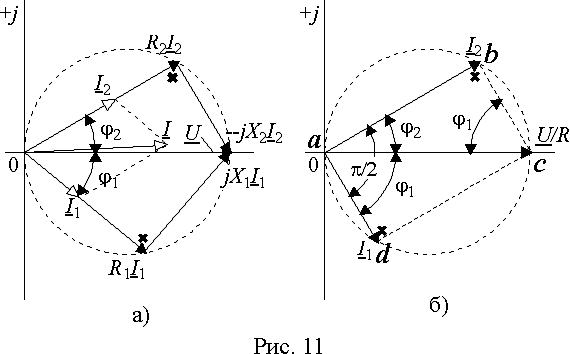
Ветви контура соединены параллельно и общее падение
напряжения на них одинаково и равно сумме падений напряжения на элементах
ветви. При любых изменениях частоты угол между напряжением на резисторе и
реактивном элементе составляет 90 и т.к. сумма их постоянна и равна
входному напряжению, то геометрическим местом точек конца вектора падения
напряжения на резисторе будет полуокружность (рис. 3.28 а)). Причем, векторы
ветви с индуктивностью будут вписываться в нижнюю полуокружность, а ветви с
емкостью - в верхнюю. Входной ток I равен сумме токов ветвей I1
и I2 и резонанс наступает, если его направление совпадает с
вектором входного напряжения U.
Разделим комплексные числа, соответствующие векторам
напряжений рис. 3.28 а), на R = R1 = R2
= r и построим векторную диаграмму токов для режима резонанса
(рис. 3.28 б)), т.е. так, чтобы сумма векторов I1 и I2
была равна U/R. Параллелограмм abcd имеет два противоположных
прямых угла, поэтому два других угла j 1 + j 2 = p /2 . То, что сумма углов j 1 и j 2 равна 90° доказывается
также и тем, что
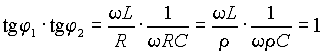 .
.
Таким образом, при любой частоте векторы токов I1
и I2 образуют прямоугольник, вершины которого расположены на
окружности, а диагональю является вектор U/R. Отсюда следует, что при
всех частотах входной ток одинаков, совпадает по направлению с напряжением и
полное сопротивление цепи чисто резистивное и равно r
.
РАЗДЕЛ 4. МНОГОФАЗНЫЕ ЦЕПИ
.1 Понятие о многофазных электрических системах и цепях.
Совокупность электрических цепей, в которых действуют
электродвижущие силы одной и той же частоты, но отличающиеся друг от друга по
фазе, называют многофазной системой электрических цепей, а число цепей,
входящих в систему, называют числом фаз многофазной системы.
Совокупность э.д.с., действующих в многофазной
системе, называют многофазной системой электродвижущих сил, а
совокупность токов, протекающих в этих ветвях - многофазной системой токов.
Примером многофазной системы электрических цепей могут
быть цепи промышленных предприятий, где используются трехфазные системы э.д.с.
и токов. Если цепи, образующие систему, электрически не связаны между собой, то
система несвязанная, в противном случае - связанная. В
дальнейшем для упрощения записи многофазные системы электрических цепей мы
будем называть многофазными цепями. Если комплексы полных сопротивлений всех
фаз одинаковы, то многофазная цепь - симметричная, если комплекс Z
хотя бы одной фазы отличается от остальных значений Z, то многофазная
цепь - несимметричная.
4.2 Симметричные многофазные системы с э.д.с
Многофазную систему э.д.с., напряжений или токов
называют симметричной, если модули всех э.д.с., напряжений или токов равны
между собой, а каждая э.д.с. (напряжение или ток) отстает по фазе от предыдущей
на один и тот же угол, равный 2p/m, где m - число фаз системы. Пусть, например, э.д.с. E1,
E2,..., Em образуют симметричную систему. Тогда:
|E1|=|E2|=...=|Em|, и y1-y2=y3-y2=...=ym-1-ym=ym-y1=2p/m.
То есть э.д.с. образуют симметричную звезду. Отсюда
следует, что
E1+E2+E3+...+Em=0.
Для трехфазной системы, которая является основной
схемой электроснабжения промпредприятий, имеем:
e1=Emsin(wt+y), E1=E=Eejy,2=Emsin(wt+y-2p/3), E2=Eme-j2p/3=Eej(y-2p/3),3=Emsin(wt+y-4p/3), E3=Eme-j4p/3=Eej(y-4p/3).
Обозначим ej2p/3=a=-1/2+jÖ3, тогда a2=ej4p/3=-1/2-jÖ3/2 и 1+a+a2=0 и a4=a.
Тогда для симметричной трехфазной системы:
E1=E, E2=Ea2,
E3=aE,
так как e-j2p/3=ej4p/3=a2, ej2p/3=e-j4p/3=a.
Для симметричной трехфазной системы векторная
диаграмма э.д.с. и Е1+Е2+Е3 показаны на
рисунке 4.1.
Рисунок 4.1.
4.3. Уравновешенные и
неуравновешенные многофазные системы.
Рассмотрим симметричную m-фазную многофазную систему.
Э.д.с. k-той фазы:
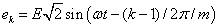
ток k-той фазы:
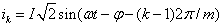 ,
,
мгновенная мощность k-той фазы:
Pk=ikek=2IEsin(wt-(k-1)p/m)sin(wt-j-(k-1)2p/m)=
=EIcosj-EIcos(2wt-j-2(k-1)2p/m),
суммарная мощность многофазной системы:
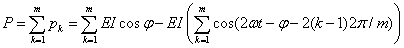
Изображая слагаемые последней суммы векторами при m>2,
мы получим симметричную звезду, а сумма векторов симметричной звезды равна 0.
Таким образом, мгновенное значение мощности
симметричной многофазной системы при m>2 равно нулю. Такие системы
называются уравновешенными.
4.4 Связывание многофазных систем
Существует два основных способа связывания многофазных
систем: звездой и многоугольником. Такое соединение выполняется
как для э.д.с., так и для нагрузок. Соединение звездой показано на рисунке 4.2.
При соединении звездой однополярные клеммы источников э.д.с. соединяются
вместе. Общая точка э.д.с. называется нейтральной точкой.
Провода, идущие от других клемм источников э.д.с.,
называются линейными. Провод, идущий от нейтральной точки, называется нейтральным
(или нулевым).
Аналогично звездой соединяются нагрузочные
сопротивления.
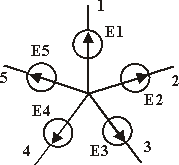
Рисунок 4.2
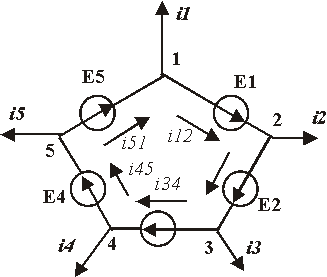
Рисунок 4.3.
При соединении многоугольником провод от источника
э.д.с. соединяется с клеммой следующего источника э.д.с. другой полярности,
таким образом, получается замкнутый многоугольник. Провода, идущие от точек соединения
э.д.с. - линейные.
Разность потенциалов между линейным проводом и
нейтральной точкой называется фазным напряжением, а разность потенциалов
между линейными проводами называют линейным напряжением.
Токи, текущие по линейным проводам - линейные токи.
Токи, текущие по сторонам многоугольника, называются фазными токами. Для
звезды линейный ток равен фазному.
На рисунке 4.4. показан один из вариантов соединения
источников э.д.с. и нагрузки в трехфазной системе.
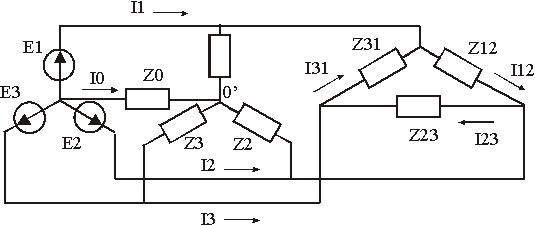
Рисунок 4.4.
Для единообразия далее направление линейных токов
будем выбирать направление от источников э.д.с. к нагрузке. А в нейтральном
проводе направление ток можно выбирать произвольно.
При соединении звездой для линейных напряжений (см.
рис.4.2) имеем:
U12=U1-U2,
U23=U2-U3, ..., Um1=Um-U1.
При соединении многоугольником для линейных токов
имеем:
i1=im1-i1,
i2=i12-i23, ..., im=im1-im-1,m.
В симметричной системе для синусоидальных токов и
напряжений эти же равенства в комплексной форме:
U12=U1-U2,
U23=U2-U3, ..., Um1=Um-U1;1=Im-I1,
I2=I12-I23, ..., Im=Im1-Im-1,m.
При соединении звездой Iл=Iср.
Из рис.4.5 следует, что:
л=2Uсрsinp/m.
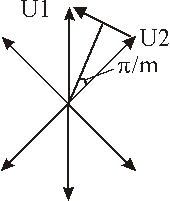
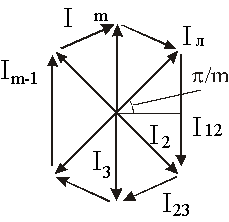
Рисунок 4.5.
Рисунок 4.6.
Для трехфазной системы:
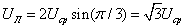
При соединении многоугольником Uл=Uср.
Из рис.4.6.:
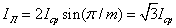
Пользуясь полученными соотношениями, определим при
соединении звездой или многоугольником суммарную мощность системы:
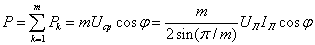
В частности, для трехфазной системы:
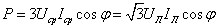
Аналогично, реактивная мощность:
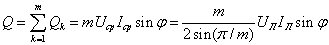
для трехфазной системы:
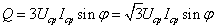
Следовательно, расчет симметричной многофазной системы
сводится к расчету однофазной системы.
4.5 Соединение звездой и треугольником в трехфазной системе
В трехфазной симметричной системе (рис.4.4) по
нейтральному проводу течет ток, равный сумме линейных токов: i0=i1+i2+i3=0,
поэтому нейтральный провод можно не прокладывать.
Расчет цепи при отсутствии взаимоиндуктивности
сводится к расчету токов и напряжений одной фазы. Для определения токов и
напряжений в остальных фазах их сдвигают по отношению к расчетной фазе на 2kp/m градусов, где k - очередность k-той фазы по
отношению к расчетной.
Предварительно, если имеется соединение нагрузки
разными способами, то производят замену соединений к одному виду. При замене
звезды сопротивлений на эквивалентный треугольник (см. рис.3.7.а, б
проводимости треугольника:
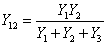 ,
, 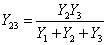 ,
, 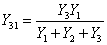
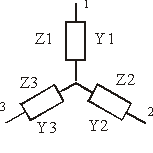
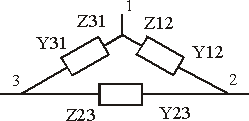
а) б)
Рисунок 4.7.
При замене треугольника эквивалентной звездой:
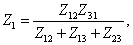
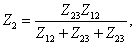
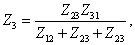
4.6 Расчет несимметричных трехфазных цепей при отсутствии
взаимоиндуктивности
Пусть источники э.д.с. и нагрузка соединены звездой
(рис.3.8). Если нагрузка несимметрична, то между точками ОО’ будет существовать
разность потенциалов и по нейтральному проводу будет течь ток:
IО=IA+IB+IC.
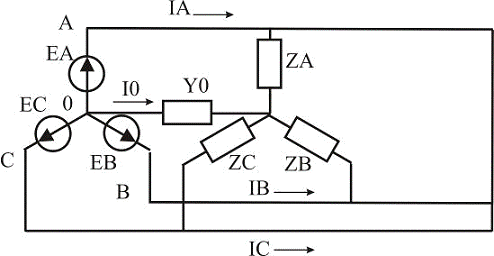
Рисунок 4.8.
Падение напряжения на нулевом проводе: UOO’=IOYO.
Откуда из уравнений по второму закону Кирхгофа для трех контуров получаем:
IA=(UA-UOO’)YA,B=(UB-UOO’)YB,C=(UC-UOO’)YC,
откуда:
O=UAYO+UBYB+UCYC-UOO’(YA+YB+YC).
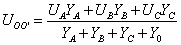
Если нейтральный провод отсутствует, то YO=0,
а:
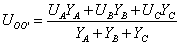
4.7. Симметричные составляющие трехфазной системы
Выше было показано, что под симметричной системой
э.д.с. и токов понимают такую систему из неравных по модулю величин, у которых
все последующие величины отстают от предыдущих на угол 2p/m.
Введем множитель q, то есть угол между
соседними величинами 2pq/m, и если q - целое число, то, давая q
значения от 0 до m-1, мы получим все возможные типы многофазных
систем. Больше всего нас интересуют значения q: 0, 1, -1.
При q=1 - это известная нам симметричная
система, когда каждый последующий в принятой нумерации вектор за предыдущим.
Если q=-1, то векторы следуют друг за другом в порядке, обратном
принятой нумерации. Системы при q=1 называют прямыми системами
или системами с прямым порядком следования фаз, а при q=-1 называют обратными
системами или системами с обратным порядком следования фаз.
При q=0 векторы совпадают друг с другом, такие
системы называют системами нулевой последовательности или нулевыми системами.
Рассмотрим эти системы для трехфазного источника. При q=1
между фазами A, B, C угол 2p/3, между фазами B и C - 2p/3
(рис.3.8а) и между фазами и А - -2p/3. При q=-1
(рис.3.8б) между фазами А и В угол -2p/3, между В
и С - -2p/3, между С
и А угол 2p/3. При q=0 (рис.4.9в) фазный сдвиг равен нулю,
поэтому векторы совпадают по направлению.
а) б) в)
Рисунок 4.9
Рассмотрим случай, когда в цепи нет вращающихся машин,
и покажем, что любую несимметричную трехфазную систему можно разложить на три
указанные составляющие, то есть :
А=А0+А1+А2,
В=В0+В1+В2,
С=С0+С1+С2,
где А0, В0, С0
- составляющие нулевой последовательности;
А1, В1, С1 - составляющие прямой
последовательности;
А2, В2, С2 - составляющие обратной
последовательности.
Для определения этих составляющих необходимы еще шесть
уравнений. Напомним, что буквой а обозначен вектор, равный ej2p/3. Присоединим к трем уравнениям еще
шесть:
В0=А0, В1=а2А1,
В2=аА1,
С0=А0, С1=аА1,
С2=а2А1,
а2=ej4p/3, a3=ej2p=1, a4=a, 1+a+a2=0.
Тогда имеем:
А=А0+А1+А2,
В=В0+В1+В2,
С=С0+С1+С2.
Вычислим сумму и учтем, что А0=В0=С0:
3А0=А+В+С.
Умножим второе уравнение на а, третье - на а2
и , суммируя последние уравнения, найдем:
А+аВ+а2С=А0+а2А0+аА0+А1+а3А1+а3А1+А2+А2а2+А2а=
=А0(1+а+а2)+3А1+А2(1+а+а2),
или: 3А1=А+аВ+а2С.
Умножим второе уравнение на а2, а
третье - на а и, просуммировав систему, получим:
А+а2В+аС=А0+а2А0+аА0+а4А1+а2А1+А1+А2+а3А2+а3А2=
=А0(1+а+а2)+А1(1+а+а2)+3А2, или: 3А2=А+а2В+аС.
Таким образом получим:
А0=1/3(А+В+С),
А1=1/3(А+аВ+а2С),
А2=1/3(А+а2В+аС).
Если система не имеет нулевого провода, то сумма
линейных напряжений равна нулю, откуда А0=0, то есть при
соединении источников в треугольник получаем, что внутри треугольника нет
напряжения нулевой последовательности.
При соединении звездой сумма токов всегда равна нулю.
Следовательно, в этом случае нет токов нулевой последовательности.
Рассмотрим участок трехфазной четырехпроводной цепи,
где полные сопротивления всех фаз одинаковы и взаимные индуктивности любой из
двух фаз между собой одинаковы, равны между собой и взаимные индуктивности
между любой из фаз и нейтральным проводом и включенными в него элементами цепи,
то есть участок трехфазной цепи полностью симметричен.
Однако токи, протекающие по этой цепи, образуют
несимметричную систему, которую можно разложить на симметричные составляющие I0,
I1, I2. Пусть в цепи существуют только I1
и I2. Как для прямой, так и для обратной последовательности
цепь симметрична и ток в нейтральном проводе равен нулю. При это комплексы
эквивалентного сопротивления цепи будут одинаковы, то есть Z1=Z2.
Токи нулевой последовательности замыкаются через нулевой провод, поэтому Z0=Z1=Z2.
Но все составляющие Z0 образуют симметричную систему, поэтому
падение напряжения на участке цепи также образует систему, которую можно
разложить на симметричные составляющие U0=I0Z0,
U1=I1Z1, U2=I2Z2.
Указанные равенства выражают независимость составляющих в симметричной
трехфазной системе. Следует отметить, что если нагрузкой служит электрическая
машина, то в связи с наличием вращающейся магнитной системы Z1¹Z2 даже при симметрии электрической и
магнитной систем электрической машины.
В качестве примера рассмотрим применение метода
симметричных составляющих для расчета однофазного к.з. в симметричной
трехфазной системе.
Пусть нагрузка питается от трехфазного генератора
через линию с сопротивлением в каждой фазе (рис.3.9). Генератор несимметричный,
поэтому Е0=0, Е1=Е1, Е2=0.
Цепь до места короткого замыкания симметрична, а Ua, Ub,
Uc, Ia, Ib, Ic несимметричны и,
разлагая их на симметричные составляющие I0, I1, I2
, независимо от вида короткого замыкания получим:
0=I0Z0+U0,
E1=I1Z1+U1,
=I2Z2+U2.
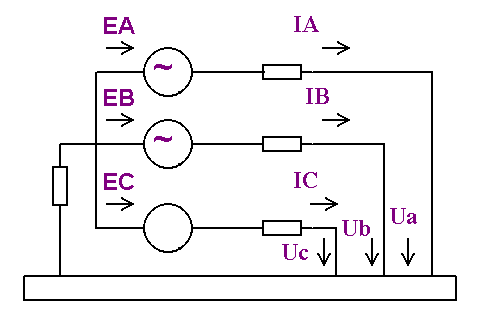
Рисунок 4.10.
При составлении этих уравнений использован принцип
независимости симметричных составляющих, однако, например, короткое замыкание
одной из фаз нарушает симметрию цепи. Предположив, что линия замкнута на еще
один генератор, у которого Ea=-Ua, Eb=-Ub,
Ec=-Uc. При таком анализе цепь остается симметричной
и принцип независимости симметричных составляющих можно применять.
Мы имеем три уравнения, в которых 6 неизвестных.
Остальные уравнения для определения неизвестных могут быть получены при
следующих рассуждениях: при однофазном к.з. Ua=0, Ib=0
и Ic=0 по сравнению с током к.з. на фазе а.
Поэтому Ua=0=U0+U1+U2.
Суммируя три первых уравнения, получим:
1=I0Z0+I1Z1+I2Z2.
Откуда, так как Ib=0, Ic=0,
то из формул для разложения Ia,b,c на симметричные
составляющие, получим: I0=I1=I2=1/3Ia.
Следовательно:
E=1/3Ia(Z0+Z1+Z2), или:
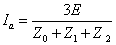
имметричные составляющие напряжений Ua,
Ub, Uc:
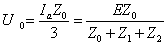
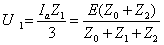
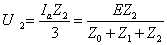
После чего по формулам перехода от симметричных
составляющих к системе Ua, Ub, Uc
определяются последние величины.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1.
Л.Р. Нейман, К.С.
Демирчан. «Энергия», Ленинградское отделение, 1967г.
2.
Теоретические
основы электротехники. А.А.Бессонов. Издательство «Высшая школа», Москва, 1967
г.
3.
К.М. Поливанов.
Теоретические основы электротехники. Издательство «Энергия», Москва-Ленинград,
1965 г.
4.
Г.И. Атабеков.
Теоретические основы электротехники. Издательство «Энергия», Москва, 1970 г.
5.
Сборник задач по
теоретическим основам электротехники. Под редакцией А.А. Бессонова. Москва,
«Высшая школа», 1988 г.