Комплексные сопротивления
Реферат
КОМПЛЕКСНЫЕ
СОПРОТИВЛЕНИЯ
МЕТОД КОМПЛЕКСНЫХ АМПЛИТУД
Для вычисления колебаний тока и напряжения в
различных цепях переменного тока удобно пользоваться символическим методом, в
котором гармонические колебания разных физических величин представляют в виде
комплексных величин. Этот метод значительно упрощает вычисления, и поэтому его
широко применяют для расчета цепей переменного тока.
Известно, что
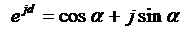 ,
,
где α -
вещественное число, а j=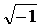 .
.
Поэтому всякое комплексное число
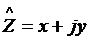
можно представить в показательной
форме
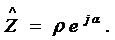
При этом вещественная часть 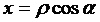 ,
,
мнимая часть 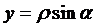 ,
,
и наоборот.
Модуль комплексного числа
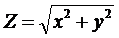 ;
; 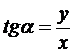
α - аргумент
комплексного числа.
Если α
изменяется со временем по закону
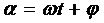 ,
,
то 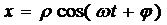 ,
,  , это два колебания с амплитудой ρ и начальной
фазой φ.
, это два колебания с амплитудой ρ и начальной
фазой φ.
Оба эти колебания можно выразить при
помощи одного комплексного выражения
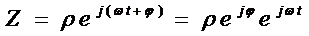
Если берём только вещественную
часть, получим колебания x, а если мнимую, то у. При сложении
колебаний проще пользоваться правилами сложения комплексных чисел.
Поставим в соответствие колебанию 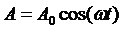 (его как
ранее будем называть базисным) комплексное число
(его как
ранее будем называть базисным) комплексное число 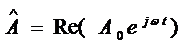 , а колебанию
, а колебанию 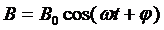 комплексное
число
комплексное
число 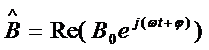 . В
дальнейшем для того, чтобы не загромождать запись, знак действительной части
при записи мы будем опускать, но подразумевать его наличие. Это внесет
некоторые ограничения на операции с комплексными числами, которые ставятся в
соответствие колебаниям. С этими числами можно будет проводить линейные операции
(сложение, вычитание), но нельзя будет проводить нелинейные операции
(умножение, возведение в степень и др.). Поставленные в соответствие колебаниям
комплексные числа приобретут вид
. В
дальнейшем для того, чтобы не загромождать запись, знак действительной части
при записи мы будем опускать, но подразумевать его наличие. Это внесет
некоторые ограничения на операции с комплексными числами, которые ставятся в
соответствие колебаниям. С этими числами можно будет проводить линейные операции
(сложение, вычитание), но нельзя будет проводить нелинейные операции
(умножение, возведение в степень и др.). Поставленные в соответствие колебаниям
комплексные числа приобретут вид
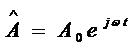 ,
,
 .
.
Величина 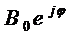 называется
комплексной амплитудой числа. Комплексная амплитуда несёт в себе информацию,
как об амплитуде колебания
называется
комплексной амплитудой числа. Комплексная амплитуда несёт в себе информацию,
как об амплитуде колебания 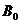 , так и о его фазе φ.
, так и о его фазе φ.
Для базисного колебания комплексная
амплитуда чисто действительное число, так как в этом колебании начальная фаза
равна нулю. В общем виде её можно записать
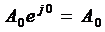
Если комплексная амплитуда записана
в алгебраической форме:

то амплитуда колебания 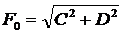 , а тангенс
угла фазового сдвига:
, а тангенс
угла фазового сдвига: 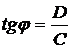 .
Экспоненциальная форма записи:
.
Экспоненциальная форма записи: 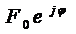 .
.
Если частота ω одинакова
для всех рассматриваемых колебаний, то множитель 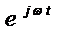 можно опустить и определять
гармоническое колебание лишь с помощью комплексной амплитуды
можно опустить и определять
гармоническое колебание лишь с помощью комплексной амплитуды 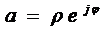 , её модуль ρ - амплитуда
гармонического колебания, аргумент φ - начальная фаза.
, её модуль ρ - амплитуда
гармонического колебания, аргумент φ - начальная фаза.
Представление колебаний с помощью
комплексных выражений тесно связано с векторными диаграммами.

Если на плоскости ввести две взаимно
перпендикулярные оси X и Y, и по оси Х откладывать вещественную часть х
комплексного числа, а по оси Y мнимую часть jy, то число Z будет изображаться
вектором на этой плоскости. Длина этого вектора - модуль комплексного числа,
а угол - аргумент.
Рассмотрим описание произвольного участка цепи
переменного тока с помощью этого метода.
Пусть ток, текущий через участок 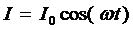 . Ставим в
соответствие току комплексное число
. Ставим в
соответствие току комплексное число 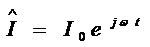 . Напряжение на этом участке
. Напряжение на этом участке  . Ставим
напряжению в соответствие комплексное число
. Ставим
напряжению в соответствие комплексное число 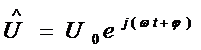 . Преобразуем последнее выражение
. Преобразуем последнее выражение 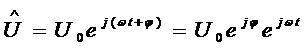 . Числа
. Числа  и
и 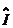 в случае
описания линейных цепей прямо пропорциональны друг другу:
в случае
описания линейных цепей прямо пропорциональны друг другу: 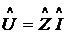 .
Коэффициент пропорциональности
.
Коэффициент пропорциональности 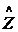 , являющийся в общем случае
комплексным, носит название импеданса этого участка цепи или его комплексного
сопротивления. Можно записать, что
, являющийся в общем случае
комплексным, носит название импеданса этого участка цепи или его комплексного
сопротивления. Можно записать, что 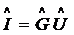 . Коэффициент пропорциональности
. Коэффициент пропорциональности  называется
комплексной проводимостью этого участка цепи или её адмитансом.
называется
комплексной проводимостью этого участка цепи или её адмитансом.
Рассмотрим теперь по отдельности
каждый из видов нагрузок в цепи переменного тока.
Если по электрической цепи течёт
переменный ток 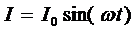 , то,
поставив ему в соответствие комплексную величину, можно записать
, то,
поставив ему в соответствие комплексную величину, можно записать 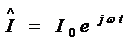 .
.
Напряжение на активном сопротивлении
будет
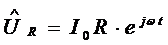 ,
,
его комплексная амплитуда
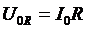
будет вещественной; сдвига фаз между
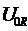 и
и 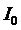 нет.
нет.
Напряжение на индуктивности
опережает по фазе ток на 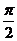 , поэтому
, поэтому
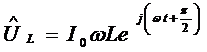 ,
,
его комплексная амплитуда
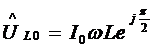 .
.
При этом 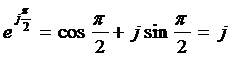 .
.
Следовательно
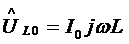 .
.
Напряжение на конденсаторе отстаёт
от тока на 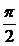 , поэтому
, поэтому
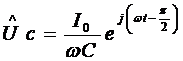 .
.
Амплитуда напряжения
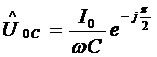 .
.
Так как
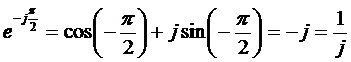 ,
,
то
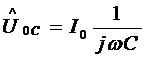 .
.
Надо отметить, что, пользуясь
комплексными выражениями гармонических колебаний, можно производить сложение
нескольких колебаний одинаковой частоты. Для этого надо сложить комплексные
амплитуды этих колебаний. Модуль полученного комплексного выражения даёт
фактическую амплитуду результирующего колебания, а его аргумент - начальную
фазу.
Рассмотрим это на примере цепи,
состоящей из последовательно соединённых сопротивления, конденсатора и
индуктивности. Напряжение на концах этой цепи равно сумме трёх напряжений,
комплексные амплитуды которых нами ранее получены, то есть
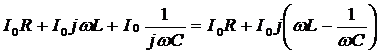 .
.
Модуль этого выражения есть
амплитуда напряжения
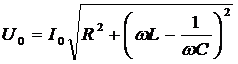 , (*)
, (*)
начальная фаза 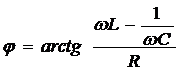 .
.
Выражение (*) есть не что иное, как
закон Ома для последовательной цепи переменного тока. Величина 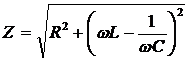 называется
полным сопротивлением цепи, R - активное сопротивление, а величина
называется
полным сопротивлением цепи, R - активное сопротивление, а величина

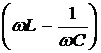 - реактивное сопротивление.
- реактивное сопротивление.
Применение комплексных величин для
расчётов цепей переменного тока можно упростить, если ещё раз ввести понятие о
комплексном сопротивлении. Комплексное сопротивление участка цепи есть
отношение комплексной амплитуды напряжения к амплитуде силы тока, т. е.
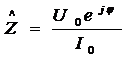
Для активного сопротивления
Для индуктивного сопротивления
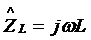 .
.
Для ёмкостного сопротивления
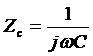 .
.
Величина 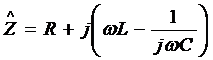 называется
комплексным сопротивлением или импедансом рассмотренной последовательной цепи
переменного тока.
называется
комплексным сопротивлением или импедансом рассмотренной последовательной цепи
переменного тока.
Чтобы найти сопротивление для
разветвленной цепи переменного тока, нужно в этой цепи мысленно заменить каждую
индуктивность 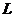 на её
комплексное сопротивление
на её
комплексное сопротивление 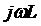 , каждую
ёмкость С- на
, каждую
ёмкость С- на 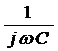 , а все
активные сопротивления оставить без изменений. Затем с указанными комплексными
сопротивлениями нужно произвести те же операции, что и при вычислении
сопротивления для постоянного тока, складывая при последовательном соединении
сопротивления, а при параллельном - их обратные величины. Полученная в
результате этого комплексная величина
, а все
активные сопротивления оставить без изменений. Затем с указанными комплексными
сопротивлениями нужно произвести те же операции, что и при вычислении
сопротивления для постоянного тока, складывая при последовательном соединении
сопротивления, а при параллельном - их обратные величины. Полученная в
результате этого комплексная величина 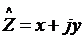 и будет представлять собой полное
комплексное сопротивление цепи (импеданс). Её вещественная часть
и будет представлять собой полное
комплексное сопротивление цепи (импеданс). Её вещественная часть 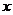 есть
активное сопротивление, а мнимая часть
есть
активное сопротивление, а мнимая часть 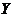 - реактивное сопротивление.
- реактивное сопротивление.
Модуль импеданса
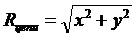
даёт величину полного сопротивления
цепи, а аргумент импеданса даёт угол φ;
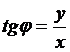 .
.
комплексный амплитуда сопротивление напряжение
ПРИМЕРЫ НАХОЖДЕНИЯ СОПРОТИВЛЕНИЯ ДЛЯ
РАЗВЕТВЛЕННЫХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА
Пример №1.
Цепь состоит из активного
сопротивления 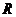 ,
параллельно которому присоединён конденсатор
,
параллельно которому присоединён конденсатор 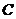 .
.

Импеданс конденсатора 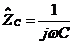 , активного
сопротивления
, активного
сопротивления 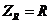 . По правилу
нахождения полного сопротивления при параллельном соединении для импедансов
. По правилу
нахождения полного сопротивления при параллельном соединении для импедансов
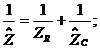
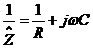 ;
; 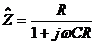 .
.
Чтобы избавиться от комплексности в
знаменателе, умножим числитель и знаменатель на величину 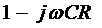 :
:
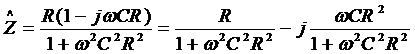 , т.е.
, т.е.
привели к виду 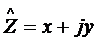 .
.
Полное сопротивление цепи - модуль
комплексного сопротивления:
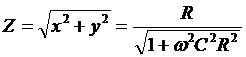 ,
,
а сдвиг по фазе между током и
напряжением
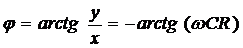 .
.
Угол φ
отрицателен, значит, напряжение отстаёт по фазе от тока.
Пример №2

Цепь содержит две параллельные ветви, в одной из
которых последовательно соединены ёмкость С и активное сопротивление R, в
другой ветви катушка индуктивности L с активным сопротивлением r. Найти полное
сопротивление цепи.
Импеданс верхней ветви
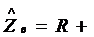 1/jωС.
1/jωС.
Импеданс нижней ветви
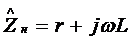 .
.
Импеданс двух параллельных ветвей
цепи
 или
или 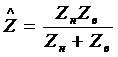 .
.
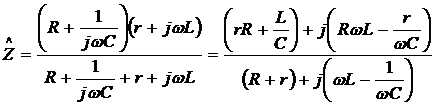
Умножим числитель на 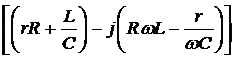 , а
знаменатель на
, а
знаменатель на 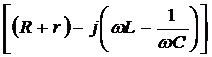 и извлечём
квадратный корень, получим модуль комплексного сопротивления
и извлечём
квадратный корень, получим модуль комплексного сопротивления 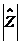
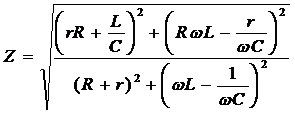 .
.
Если использовать эту формулу для нахождения
сдвига фаз между полным током и напряжением на концах цепи, надо учесть, что
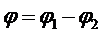 ,
, 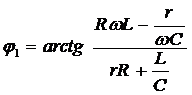 ,
, 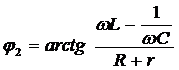 .
.
Если некоторая комплексная величина
представляет собой дробь
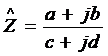 ,
,
то модуль этой величины и её
аргумент могут быть найдены двумя методами. Первый метод заключается в
приведении дроби к виду 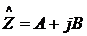 и тогда
модуль
и тогда
модуль 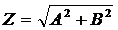 , аргумент
, аргумент 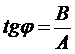 . Для этого
знаменатель и числитель умножаем на величину
. Для этого
знаменатель и числитель умножаем на величину 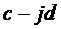 , комплексно-сопряженную
знаменателю:
, комплексно-сопряженную
знаменателю:
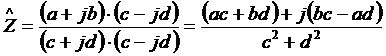 .
.
Модуль этой величины
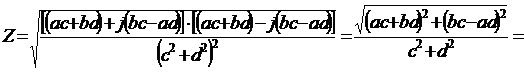
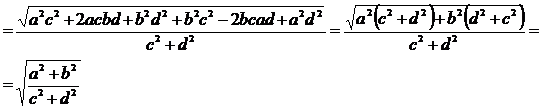 (1)
(1)
Аргумент 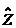 в этом
случае будет
в этом
случае будет
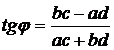 (2)
(2)
Второй метод заключается в том, что
отдельно находим модуль числителя и модуль знаменателя, т.е.
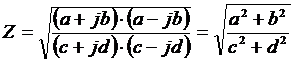 , что совпадает с (1).
, что совпадает с (1).
Но в зтом случае сложнее находится
аргумент:
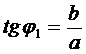 ;
; 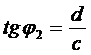 ;
; 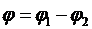 .
.
Докажем это:
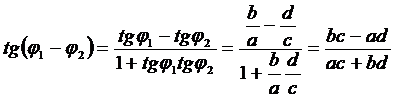 , что совпадает с (2).
, что совпадает с (2).
Пример №3.
Резонанс токов
Вернёмся вновь к резонансу токов и попробуем
подсчитать резонансную частоту, используя метод, с которым мы познакомились
ранее.

Избавившись от комплексности в знаменателе,
получим:
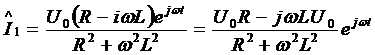 .
.
Аналогично для тока 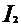 :
:
 .
.
Ток генератора I описывается
комплексным числом
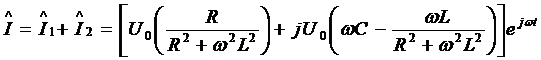 .
.
Резонанс тока наступает тогда, когда
ток генератора синфазен с его напряжением, а это означает, что мнимая часть
числа 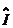 должна
зануляться
должна
зануляться
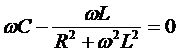 ;
;
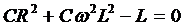 ;
;
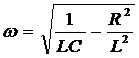 .
.
Когда R=0:
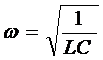 .
.
ПРАВИЛА КИРХГОФА ДЛЯ ПЕРЕМЕННЫХ
ТОКОВ
К переменным токам без всяких
изменений применимо первое правило Кирхгофа, согласно которому, алгебраическая
сумма мгновенных значений токов в узле электрической цепи равна нулю:
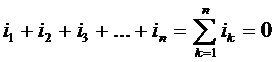 .
.
Мгновенные значения этих токов можно
представить в виде вещественных или мнимых частей комплексных выражений
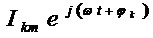 ,
,
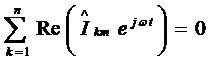 ;
; 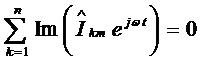 .
.
Так как равенство 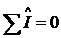 справедливо
при подстановке вместо мгновенных значений вещественных или мнимых частей
комплексных выражений
справедливо
при подстановке вместо мгновенных значений вещественных или мнимых частей
комплексных выражений 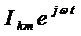 , оно должно
быть справедливым при подстановке вместо мгновенных значений токов самих
комплексных выражений. Тогда первое уравнение Кирхгофа для комплексных
амплитудных значений токов в комплексной форме:
, оно должно
быть справедливым при подстановке вместо мгновенных значений токов самих
комплексных выражений. Тогда первое уравнение Кирхгофа для комплексных
амплитудных значений токов в комплексной форме:
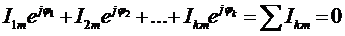 .
.
Подобное равенство можно записать и
для действующих значений токов.
Таким образом, первый закон Кирхгофа
можно сформулировать так: алгебраическая сумма комплексных выражений токов в
ветвях, связанных общим узлом, равна нулю.
Для доказательства справедливости
второго закона Кирхгофа в комплексной форме запишем для произвольного
замкнутого контура уравнение, составленное согласно второму закону Кирхгофа для
мгновенных значений э.д.с. 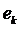 и напряжений с учётом заданных и
выбранных положительных направлений этих величин:
и напряжений с учётом заданных и
выбранных положительных направлений этих величин:
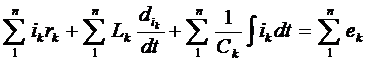 ,
,
где k - номер
ветвей, образующих замкнутый контур.
При синусоидальных э.д.с.
генераторов и линейной цепи все мгновенные значения э.д.с., напряжений и токов
можно представить в виде вещественных или мнимых частей комплексных величин: 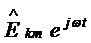 ,
, 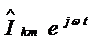 .
.
Так как уравнение Кирхгофа останется
справедливым при подстановке вместо мгновенных значений напряжений, токов и
э.д.с. вещественных частей этих комплексных величин или соответственно мнимых
их частей, оно останется справедливым и при подстановке самих комплексных
величин. Отметим, что амплитудные значения токов, э.д.с. и их начальные фазы не
являются функциями времени и могут быть вынесены за знаки производных и
интегралов. После подстановки получим
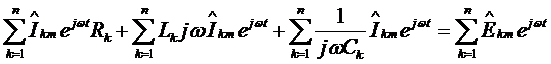
Обе части равенства разделим на 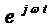 :
:
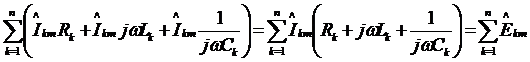
Если комплексное сопротивление
каждой ветви контура обозначить буквой 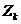 , последнее уравнение примет более
простой вид:
, последнее уравнение примет более
простой вид:

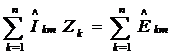 ,
,
здесь 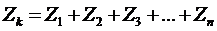 при последовательном соединении
отдельных элементов.
при последовательном соединении
отдельных элементов.
Для действующих значений можно
записать
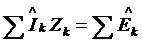 .
.
Это и есть математическое выражение второго
закона Кирхгофа в комплексной форме.
Во всяком замкнутом контуре алгебраическая сумма
комплексных выражений напряжений на отдельных элементах контура равна
алгебраической сумме комплексных выражений э.д.с., действующих в этом контуре.
РАСЧЕТ ЦЕПЕЙ МЕТОДОМ КОМПЛЕКСНЫХ ВЕЛИЧИН
ЗАДАЧА 1
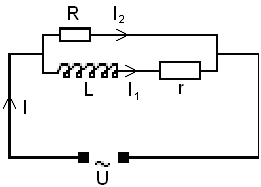
Параллельно соединенные реостат R=60
Ом и дроссель ( L = 0.05 Гн, r
= 20 Ом ) присоединенные к сети переменного тока частоты 50 Гц. По дросселю
идет то 4 А. Какой ток идет по реостату и какой ток поступает из сети.
Дано:
R = 60 Ом
L = 0,05 Гн
r = 20 Ом
ν = 50 Гц
I1 = 4 A
I2 - ?
I - ?
Прежде всего, надо начертить электрическую
схему, обозначить токи и задать их направление.
Найдем импеданс
цепи, состоящей из двух параллельных ветвей.
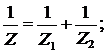
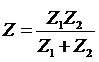 ;
; 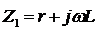 ;
; 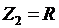 ;
;
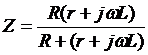 .
.
Комплексное значение полного тока
будет по закону Ома для полной цепи
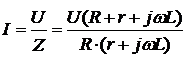
По закону Ома для участка цепи,
содержащей R:
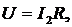
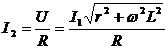 ,
,
т.к. для участка цепи, содержащей
дроссель:
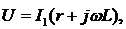

Учитывая это:
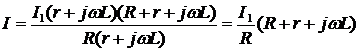
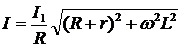
При вычислениях учесть, что 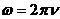 . Вычислим :
. Вычислим :
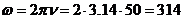 (Гц)
(Гц)
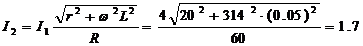 (А).
(А).
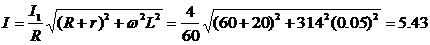 (А).
(А).
ЗАДАЧА 2
К сети переменного тока (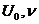 )
присоединены параллельно конденсатор С и дроссель (L,r).
Определить токи в элементах схемы и полный ток.
)
присоединены параллельно конденсатор С и дроссель (L,r).
Определить токи в элементах схемы и полный ток.
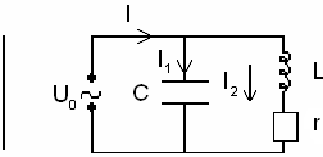
Начертим электрическую схему,
зададим токи и их направление.
Полный ток:
Дано:

L
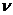
r
C
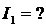
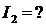
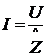 ;
; 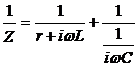 ;
;
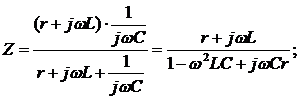
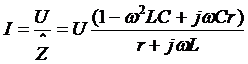 ;
;
По закону Ома для участков цепи:
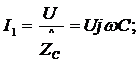
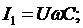
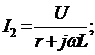
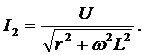
Полный ток можно получить, если
написать
по первому закону Кирхгофа:
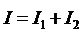 ,
,
тогда
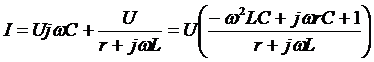 ,
,

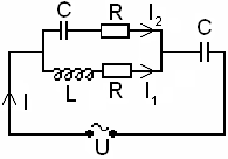
ЗАДАЧА 3
Найти токи на участках цепи
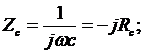
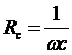
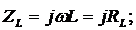
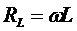
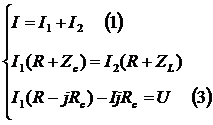 или
или 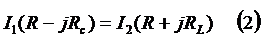
из (3) 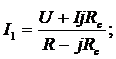
из (2) 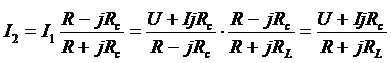 ,
,
подставим в (1)
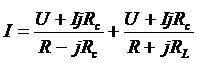
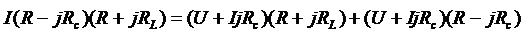 ,
,
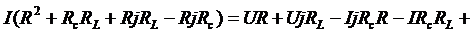
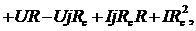
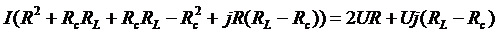 ,
,
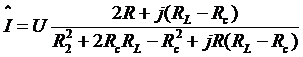 ,
,
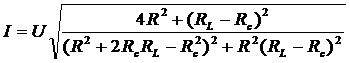 .
.
МЕТОД КОНТУРНЫХ ТОКОВ
Для сложных разветвленных цепей
переменного тока применим также метод контурных токов, согласно которому в
каждом из независимых контуров цепи протекает свой контурный ток. При этом
число неизвестных токов уменьшается до числа независимых контуров. Контурные
токи удовлетворяют уравнения Кирхгофа.
Однако составление контурных
уравнений несколько сложнее, чем составление уравнений при непосредственном
использовании уравнений Кирхгофа. Рассмотрим цепь, изображенную на рисунке.
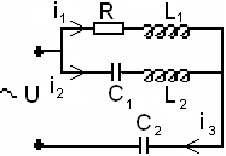
На рисунке обозначены токи и заданы
их направления.
С помощью уравнений Кирхгофа можно
написать 
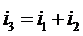 .
.
Для верхнего контура 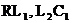
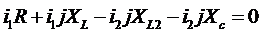
Для контура С1 L 2 C 2:
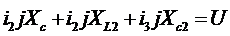
При этом надо учесть:
1) что направление обхода контура в нашем
случае выбрано по часовой стрелке;
2) если выбранное ранее направление тока
совпадает с направлением обхода, ток берется со знаком « плюс », в противном случае
со знаком «минус».
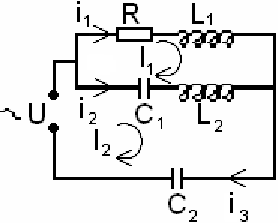
Решим эту же задачу методом
контурных токов. Выберем два независимых контура и положительные направления
контурных токов 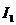 и
и 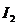 согласно
рисунку и составим уравнения Кирхгофа.
согласно
рисунку и составим уравнения Кирхгофа.
Для контура 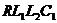 :
:
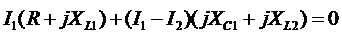
Для контура  :
:
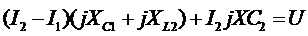 .
.
Приведем подобные слагаемые:
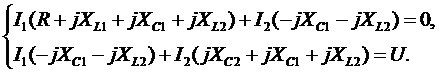
или 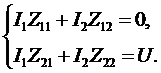
Здесь обозначили 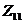 -
собственное сопротивление первого контура,
-
собственное сопротивление первого контура, 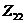 - собственное сопротивление второго
контура; кроме того, оба контура связаны сопротивлениями
- собственное сопротивление второго
контура; кроме того, оба контура связаны сопротивлениями 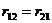 и общей
ветвью.
и общей
ветвью.
Можно составить определитель:
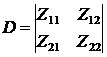
Для нахождения токов 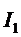 или
или  надо в этом
определителе заменить соответственно первый или второй столбец, на столбец
состоящий из свободных членов, тогда:
надо в этом
определителе заменить соответственно первый или второй столбец, на столбец
состоящий из свободных членов, тогда:

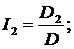
где 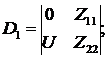
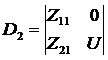
В принципе, все элементы
определителя можно написать для заданной цепи, не составляя предварительно
уравнений Кирхгофа. Нужно отметить, что если производить дальнейшие выкладки в
общем виде, получаются очень громоздкие уравнения. Поэтому дальнейшие расчеты
лучше производить, подставляя числовые значения.
Зададим для приведенной схемы
следующие значения:
R = 4 Oм, 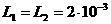 Гн,
Гн, 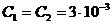 ф,
ф, 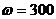 Гц.
Гц.
Тогда
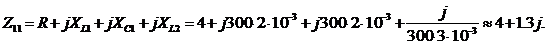
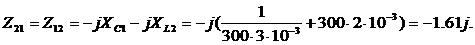
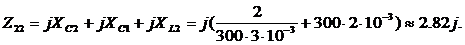

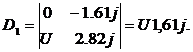
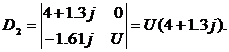
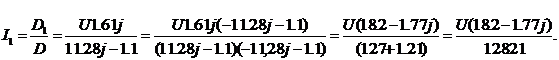
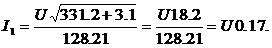
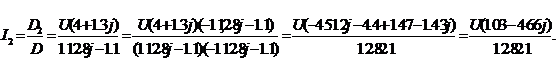
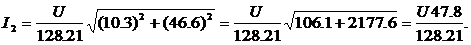
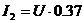 .
.
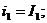
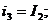
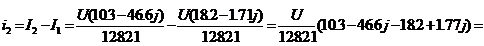
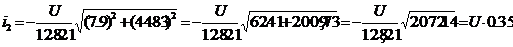
Литература
Волынский
В.А. и др. Электротехника /Б.А. Волынский, Е.Н. Зейн, В.Е. Шатерников: Учеб.
пособие для вузов. - М.: Энергоатомиздат, 2011. - 528 с., ил.
Касаткин
А.С., Немцов М.В. Электротехника: Учеб. пособие для вузов. - 4-е изд., перераб.
- М.: Энергоатомиздат, 2003. - 440 с., ил.
Основы
промышленной электроники: Учебник для неэлектротехн. спец. вузов /В.Г.
Герасимов, О М. Князьков, А Е. Краснопольский, В.В. Сухоруков; под ред. В.Г.
Герасимова. - 3-е изд., перераб. и доп. - М.: Высш. шк., 2006. - 336 с., ил.
Электротехника
и электроника в 3-х кн. Под ред. В.Г. Герасимова Кн.1. Электрические и магнитные
цепи. - М.: Высшая шк. - 2006 г.
Электротехника
и электроника в 3-х кн. Под ред. В.Г. Герасимова Кн.2. Электромагнитные
устройства и электрические машины. - М.: Высшая шк. - 2007 г.