Линейные электрические цепи при несинусоидальных периодических токах
Задача 1

Согласно варианту задания составляем
электрическую схему трехфазной цепи (рис. 1)
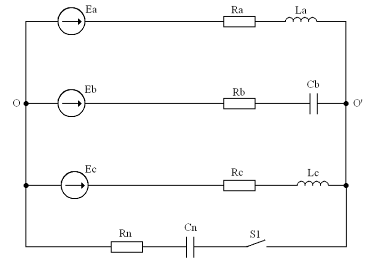
Рис. 1
1. Мгновенные значения ЭДС
генератора
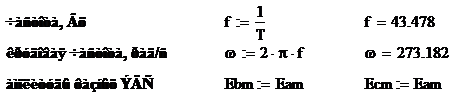
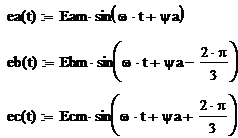
2. Мгновенные значения линейных
напряжений генератора
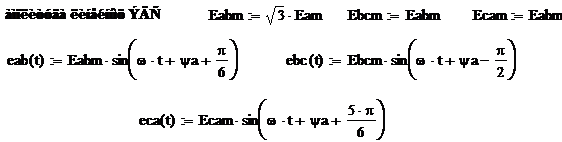
3. Комплексы действующих значений
фазных и линейных напряжений генератора
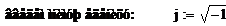
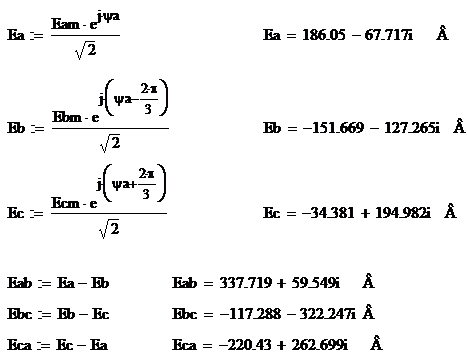
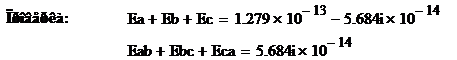
Расчет комплексов фазных и линейных
ЭДС генератора выполнен правильно.
Построим векторную диаграмму фазных
и линейных ЭДС на комплексной плоскости (рис. 2)
Вектора фазных и линейных ЭДС
образуют симметричные трехфазные системы, что подтверждает правильность их
расчета.
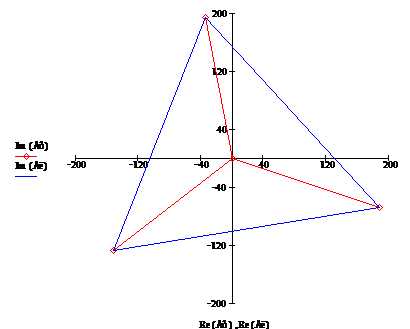
Рис. 2
4. Расчет цепи при условии, что
сопротивление нулевого провода Zn=0
. Комплексные значения фазных токов
нагрузки.
Индуктивные сопротивления фаз
нагрузки, Ом
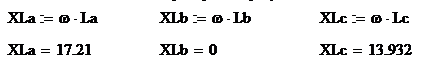
Емкостные сопротивления фаз
нагрузки, Ом
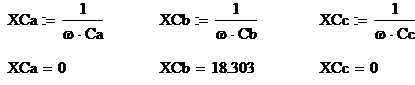
Комплексные сопротивления и
проводимости фаз нагрузки:
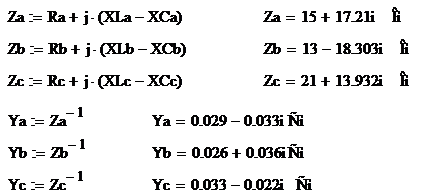
Комплексные фазные токи нагрузки:
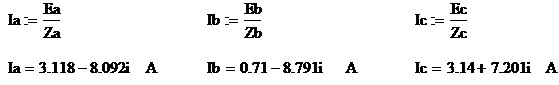
Действующие значения фазных токов
нагрузки, А
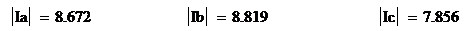
. Комплексный ток в нулевом проводе

Действующее значение тока в нулевом
проводе нагрузки, А
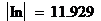
Построим векторную диаграмму токов
на комплексной плоскости (рис. 3)
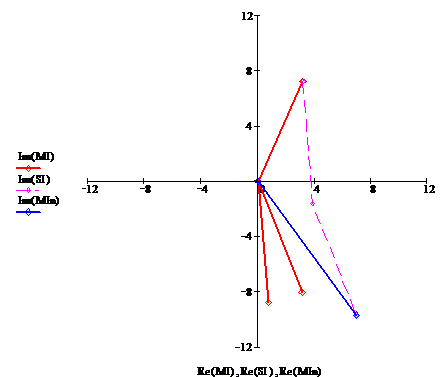
Рис. 3
Сумма токов в узле равна току в
нулевом проводе, что подтверждает правильность расчетов токов.
. Определение полной S и активной P
мощности нагрузки сопряженный комплекс тока:
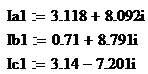
Полная мощность нагрузки:
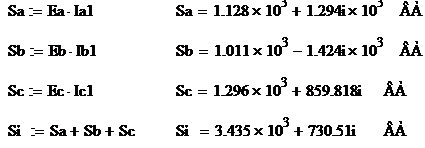
Модуль полной мощности нагрузки:
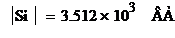
Активная мощность нагрузки:

5. Расчет цепи при условии, что
система не имеет нулевого провода (ключ S1 разомкнут)
. Определение фазных напряжений на
нагрузке
Напряжение между нулевыми точками
генератора и нагрузки, В:
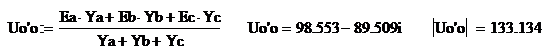
Комплексы фазных напряжений на
нагрузке:
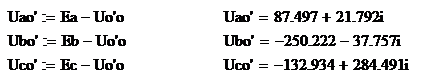
Действующие значения фазных
напряжений на нагрузке, В:
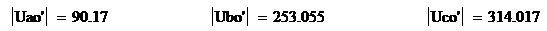
. Определение токов в фазах нагрузки

Действующие значения токов в фазах
нагрузки, А:
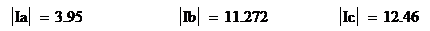
Проверка расчетов по первому закону
Кирхгофа:
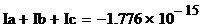
Расчет комплексов фазных токов
выполнен правильно.
Построим векторную диаграмму токов
на комплексной плоскости (рис. 4)
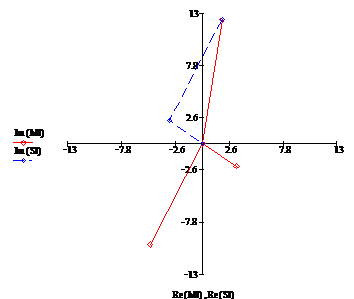
Рис. 4
Сумма токов в узле равна нулю, что подтверждает
правильность расчетов токов.
. Ток в нулевом проводе отсутствует так как:
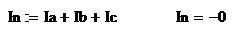
. Для построения
векторно-топографической диаграммы найдем падения напряжений на активных и
реактивных сопротивлениях нагрузки:

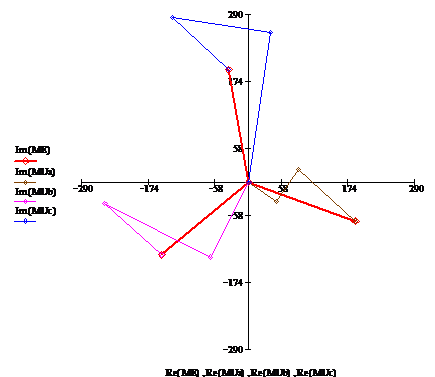
Рис. 5
Проверка по второму закону Кирхгофа:
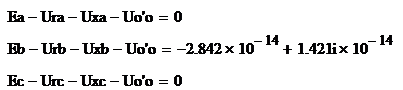
Расчет падений напряжений на
активных и реактивных сопротивлениях нагрузки выполнен правильно.
6. Расчет цепи при условии, что
нулевой провод имеет сопротивление Zn (согласно варианту задания)
. Определение напряжение на нулевом проводе
Индуктивное сопротивление нулевого провода, Ом:
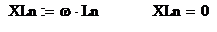
Емкостное сопротивление нулевого
провода, Ом:
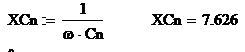
Комплексное сопротивление и
проводимость нулевого провода:
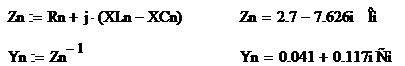
Напряжение на нулевом проводе Uo'o,
В:
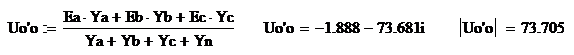
. Определение фазных напряжений на
нагрузке
Комплексы фазных напряжений на
нагрузке, В:

Действующие значения фазных
напряжений на нагрузке, В:
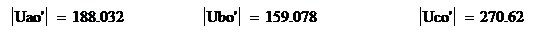
. Определение фазных токов нагрузки
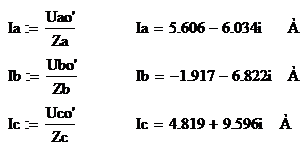
Действующие значения токов в фазах
нагрузки, А:
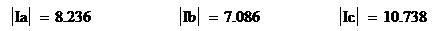
. Определение тока в нулевом проводе
по первому закону Кирхгофа:

по закону Ома:
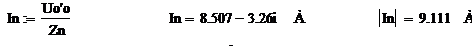
Проверка расчетов по первому закону
Кирхгофа:
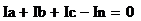
Расчет комплексов фазных токов
выполнен правильно.
7. Расчет цепи при условии, что
нулевой провод в трехфазной системе разомкнут, а фазы нагрузки пересоединены со
звезды на треугольник с ветвями Zab, Zbc и Zca (рис. 6)
электрический цепь генератор
напряжение
1. Определение фазных токов нагрузки
Комплексные проводимости и сопротивления ветвей
треугольника:
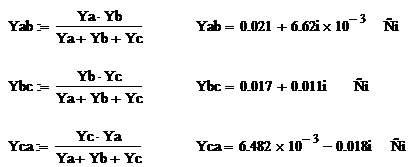
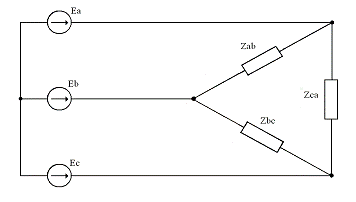
Рис. 6

Фазные токи нагрузки:
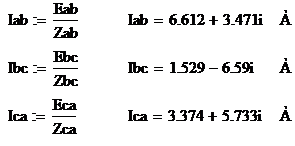
Действующие значения фазных токов
нагрузки, А:
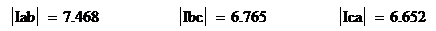
. Определение линейных токов
нагрузки
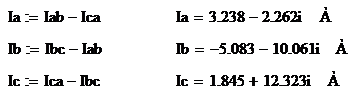
Действующие значения линейных токов
нагрузки, А:
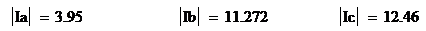
3. Векторные диаграммы токов и напряжений
Построим векторную диаграмму фазных и линейных
токов на комплексной плоскости (рис. 7)
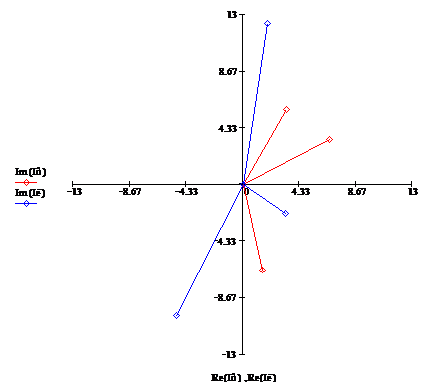
Рис. 7
Построим векторную диаграмму напряжений на
комплексной плоскости (рис. 8)
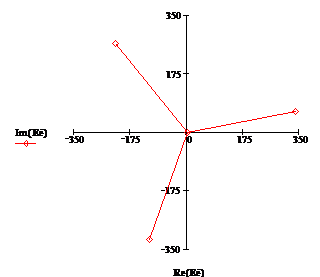
Рис. 8
. Определение полной S и активной P
мощности нагрузки сопряженный комплекс тока:
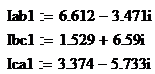
Полная мощность нагрузки:

Модуль полной мощности нагрузки:
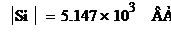
Активное сопротивление при
соединении нагрузки треугольником:
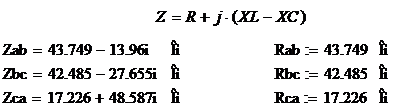
Активная мощность нагрузки:

Задача 2

В соответствии заданным графом схемы на рис. 9
приведена расчетная электрическая цепь.
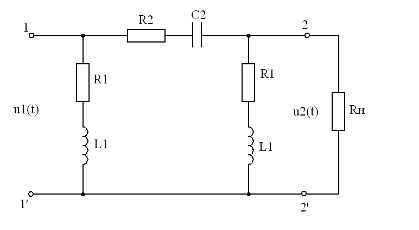
Рис. 9
Круговая частота основной гармонической u1(t),
рад/с:
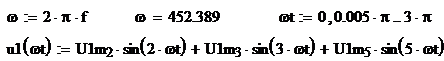
На рис. 10 приведены графики
заданных гармоник и суммарная кривая u1(wt)
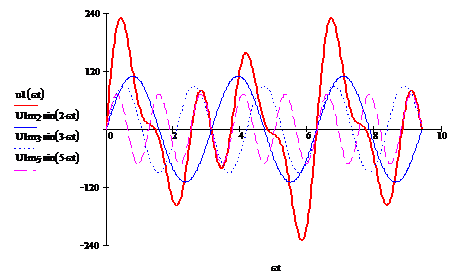
Рис. 10
Определяем комплексный коэффициент передачи в
общем виде.
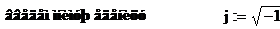
Находим реактивные и полные
сопротивления схемы для заданных гармоник u1(wt), Ом:

Комплексные коэффициенты передачи,
их модули и аргументы в радианах
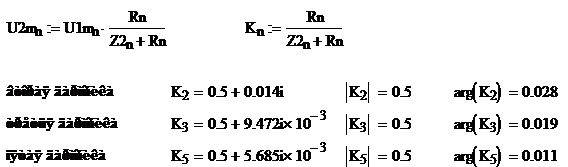
На рис. 11 приведены зависимости модуля
и аргумента коэффициентов передачи для заданных гармоник u1(ωt)
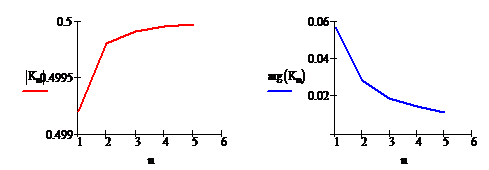
Рис. 11
Определяем амплитуды и начальные
фазы заданных гармоник напряжения на выходе u2(wt):
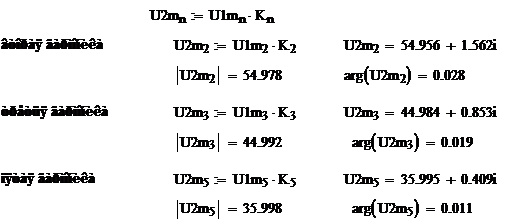
Представим выходное напряжение u2(t)
в виде гармонического ряда
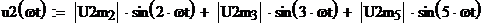
На рис. 12 приведены графики
заданных гармоник и суммарная кривая u2(ωt).
Определим действующее значение
напряжения на нагрузке
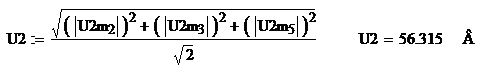
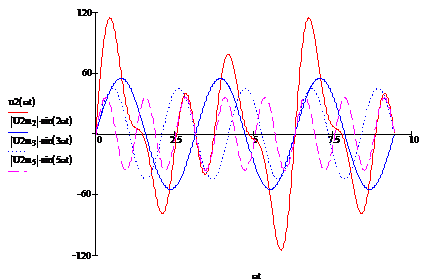
Рис. 12