Электрическая сеть
Содержание
Введение
. Теоретическое описание метода
. Расчет режимов электрической сети
.1 Исходные данные
.2 Схема замещения сети
.3 Определение узловых напряжений
сети
. Текст программы
Список литературы
Введение
Методы линейных уравнений установившегося режима
можно разделить на две группы: точные (или прямые) и итерационные (или
приближенные).
Точными или прямыми методами называются такие,
которые в предположении, что все вычисления ведутся точно (без округлений)
позволяют получить точные значения неизвестных в результате конечного числа
операций. Практически все вычисления ведутся с округлениями, поэтому и значения
неизвестных, полученных точным методом, будут содержать погрешности. Точными
методами являются метод Гаусса и решение линейных уравнений установившегося
режима с помощью обратной матрицы.
Итерационными или приближенными методами
называют такие, которые даже в предположении, что вычисления ведутся без
округлений, позволяют получить решение системы уравнений лишь с заданной
точностью. Точное решение системы в случае применения итерационных методов
может быть получено теоретически как результат бесконечного итерационного
процесса. Эти методы не всегда сходятся при решении линейных уравнений
установившегося режима.
1. Теоретическое описание метода
Простая итерация и метод Зейделя - простейшие из
итерационных методов. Рассмотрение простой итерации важно для понимания сути
применения итерационных методов расчета установившихся режимов электрических
систем.
Для определенности вначале ограничимся системой
уравнений третьего порядка.
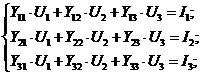 (1.1)
(1.1)
где 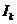 -
задающий ток
-
задающий ток 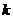 -го узла,
-го узла, 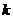 =1,2,3;
=1,2,3;
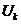 - неизвестное
узловое напряжение, т.е. напряжение между
- неизвестное
узловое напряжение, т.е. напряжение между 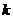 -м
узлом и балансирующим, совпадающим с базисным по
-м
узлом и балансирующим, совпадающим с базисным по 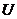 ;
;
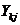 - (при
- (при 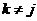 )
- взаимная проводимость узлов
)
- взаимная проводимость узлов 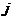 и
и 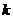 ;
;
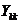 - собственная
проводимость узла
- собственная
проводимость узла 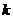 . Взаимная
проводимость узлов
. Взаимная
проводимость узлов 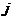 и
и 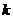 равна
взятой с обратным знаком сумме проводимостей ветвей, соединяющих эти узлы.
равна
взятой с обратным знаком сумме проводимостей ветвей, соединяющих эти узлы.
Предполагая, что диагональные элементы 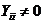 ,
,
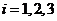 ,
разрешим первое уравнение системы (1.1) относительно
,
разрешим первое уравнение системы (1.1) относительно 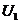 ,
второе - относительно
,
второе - относительно 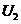 , а третье -
относительно
, а третье -
относительно 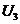 . Тогда получим
систему, эквивалентную (1.1):
. Тогда получим
систему, эквивалентную (1.1):

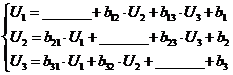 (1.2)
(1.2)
 (1.3)
(1.3)
Зададим начальные приближения неизвестных 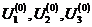 .
Подставляя их в первые части системы (1.2), получаем первые приближения
.
Подставляя их в первые части системы (1.2), получаем первые приближения 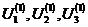 .
Вычисление первого приближения неизвестных соответствует первому шагу
итерационного процесса. Полученные первые приближения могут быть таким же
образом использованы для получения вторых, третьих и последующих приближений.
Используя значения переменных, полученных на предыдущем,
.
Вычисление первого приближения неизвестных соответствует первому шагу
итерационного процесса. Полученные первые приближения могут быть таким же
образом использованы для получения вторых, третьих и последующих приближений.
Используя значения переменных, полученных на предыдущем, 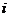 -м
шаге, можно получить
-м
шаге, можно получить 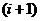 -е приближение
неизвестных:
-е приближение
неизвестных:
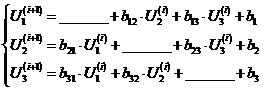 (1.4)
(1.4)
Введем матрицу и вектор-столбцы:
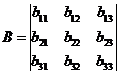 ,
, 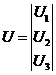 ,
,
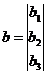 .
.
Диагональные элементы матрицы 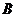 равны
нулю, т.е.
равны
нулю, т.е. 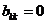 , а недиагональные
элементы (т.е.
, а недиагональные
элементы (т.е. 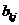 при
при 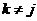 )
совпадают с коэффициентами систем (1.2) и (1.4). Учитывая правило умножения и
сложения матриц, систему (1.2) можно записать в матричной форме:
)
совпадают с коэффициентами систем (1.2) и (1.4). Учитывая правило умножения и
сложения матриц, систему (1.2) можно записать в матричной форме:
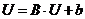 (1.5)
(1.5)
Аналогично итерационное выражение (1.4) можно
записать в матричном виде:
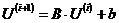 (1.6)
(1.6)
Элементы матрицы 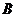 -
безразмерные величины, а элементы вектора
-
безразмерные величины, а элементы вектора 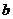 имеют
размерность напряжений.
имеют
размерность напряжений.
Итерационный процесс, определяемый выражениями
(1.4) и (1.6), называется простой итерацией.
Метод Зейделя представляет собой незначительную
модификацию простой итерации. Основная его идея в отличие от простой итерации
заключается в том, что найденное (i+1)-е
приближение (k-1)-го напряжения
сразу же используется для вычисления следующего, k-го
напряжения. Т.е. полученное (i+1)-е
значение напряжения сразу же используется для вычисления (i+1)-го
значения напряжений.
Для сети переменного тока комплексные уравнения
узловых напряжений представляются в виде системы действительных уравнений.
Затем к полученной системе действительных уравнений применяется метод Зейделя.
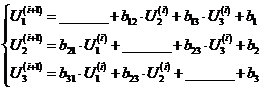 (1.7)
(1.7)

По методу простой итерации 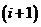 -е
приближение
-е
приближение 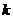 -го
напряжения
-го
напряжения 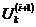 для системы
n-го порядка
вычисляется по следующему выражению:
для системы
n-го порядка
вычисляется по следующему выражению:
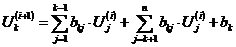 (1.8)
(1.8)
По методу Зейделя 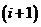 -е
приближение k-го
напряжения
-е
приближение k-го
напряжения 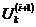 вычисляется
так:
вычисляется
так:
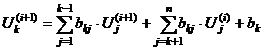 (1.9)
(1.9)
2. Расчет режимов электрической сети
.1 Исходные данные
Дана схема электрической сети (вариант 2),
состоящей из четырех узлов (рис.2.1). Данные проводов представлены в табл.2.1.
Нужно найти узловые напряжения методом Зейделя.
Рисунок 2.1- Схема электрической сети
Таблица 2.1 - Данные проводов
|
№
ветви
|
Длина,
км
|
Марка
провода
|
x0, Ом/км
|
r0, Ом/км
|
|
1-2
|
80
|
АС-400/51
|
0,42
|
0,075
|
|
1-4
|
85
|
АС-300/39
|
0,429
|
0,098
|
|
4-3
|
75
|
АС-500/64
|
0,413
|
0,06
|
.2 Схема замещения сети
Рис.2.2 Схема замещения
Составим уравнения узловых напряжений в виде
(2.1) и (2.2) для электрической сети, схема замещения которой приведена на
рис.2.2.
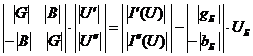
где 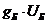 и
и 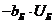 - вектор-столбцы, имеющие вид,
аналогичный (2.4);
- вектор-столбцы, имеющие вид,
аналогичный (2.4); 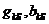 - активная
и реактивная взаимные проводимости узлов
- активная
и реактивная взаимные проводимости узлов 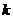 -го и балансирующего.
-го и балансирующего.
При задании нагрузки постоянной
мощностью, ток вычисляется по формуле:
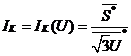
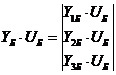 (2.4)
(2.4)
В схеме на рисунке 2.2 - четыре линии
электропередачи, узел 1 - генераторный, 2, 3 и 4 - нагрузочные узлы.
Сопротивления линий следующие:
 Ом;
Ом;
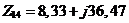 Ом;
Ом;
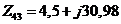 Ом;
Ом;
Узел 1 принят в качестве
балансирующего и базисного, напряжение 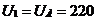 кВ. В узлах 2, 3 и 4 мощности
задаются вводом с клавиатуры, в данном случае они приняты равными 10Вт и -10ВАр
для Р и Q
соответственно.
кВ. В узлах 2, 3 и 4 мощности
задаются вводом с клавиатуры, в данном случае они приняты равными 10Вт и -10ВАр
для Р и Q
соответственно.
По заданным сопротивлениям ветвей
вычисляем их проводимости, Ом-1, по формулам:
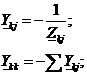 (2.5)
(2.5)
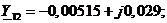

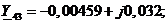
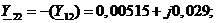
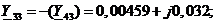
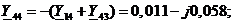
Матрица для четырехузловой сети:
 (2.6)
(2.6)
Для схемы на рисунке 2.2 матрица проводимостей:
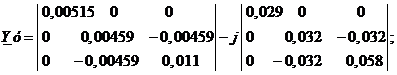
Вектор узловых напряжений:
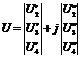 (2.7)
(2.7)
Запишем систему уравнений установившегося
режима, сформировав матрицу коэффициентов следующим образом:
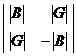 (2.8)
(2.8)
Такое формирование матрицы удобно с точки зрения
решения полученных уравнений итерационными методами, сходимость которых
улучшается, если диагональные элементы доминируют, т.е. по абсолютной величине
больше всех остальных элементов в строке.
В этом случае уравнение запишется в виде:
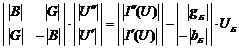 (2.9)
(2.9)
Запишем систему узловых напряжений в виде:
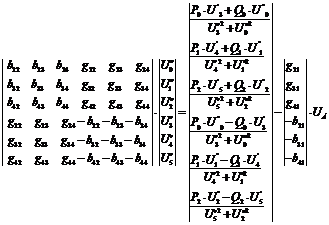 (2.10)
(2.10)
Перемножаем матрицы:
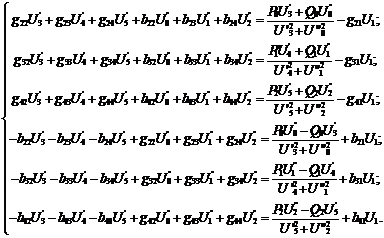 (2.11)
(2.11)
Если подставить значения активных и реактивных
составляющих проводимостей, узловых токов и базисного напряжения, то получим в
матричном виде:

Принимаем начальное приближение
узловых напряжений:
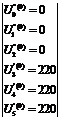
Первые приближения 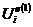 и
и 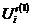 определим
решая систему уравнений.
определим
решая систему уравнений.
Расчет произведен на ЭВМ. Расчет
произведен с заданной точностью по напряжениям 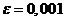 кВ.
кВ.
Результат 1-й итерации:
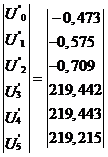
Ответ получен на 16-й итерации:
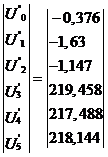
3. Текст программы
электрический сеть напряжение
матрица
Список литературы
1. Мельников Н.А.
Электроэнергетические системы и сети. Учеб. Пособие для электроэнергетических
специальностей вузов. Изд. 2-е. М.: Энергия, 1975.
2. Электротехнический
сравочник: в 3 т. Под общей редакцией И.Н. Орлова (гл. ред.) и др. 7-е изд.,
испр. и доп. - М.: Энергоатомиздат, 1985.
. Самарский А.А., Гулин А.В. Численные
методы: Учеб. Пособие для вузов. - М.: Наука. Гл. ред. физ-мат. лит., 1989.
. Идельчик В.И. Электрические
системы и сети: Учебник для вузов, М. Энергоиздат, 1989.