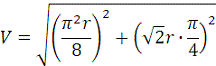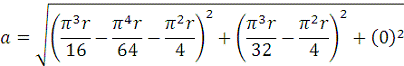Положительное направление отсчёта - по
ходу часовой стрелки, если смотреть навстречу оси z.
Положительным направлением вращения
считается направление против хода часовой стрелки, если смотреть с
положительного конца O1 оси вращения OO1.
. Абсолютную скорость точки M.
|
№ варианта
|
Закон вращения
|
Закон относительного значения
|
|
2-2-1 (14 - 2 - 25)
|
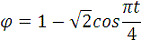
|
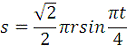
|
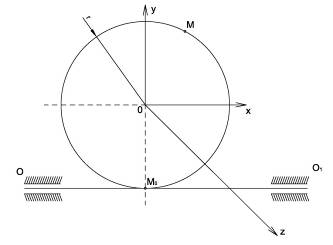
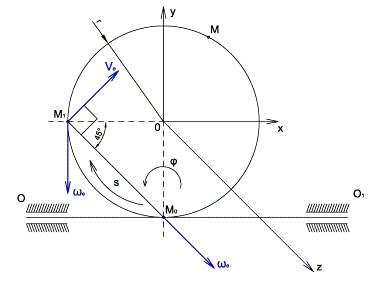
РЕШЕНИЕ:
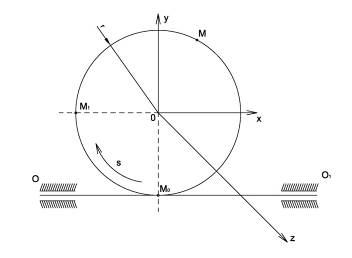
Будем считать, что в
заданный момент времени плоскость чертежа совпадает с плоскостью диска.
Положение точки М на диске определяется расстоянием 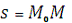
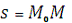 .
.
При,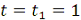 с:
с: 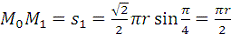 .
Найдем угол, на который повернулся радиус при движении точки М по
окружности:
.
Найдем угол, на который повернулся радиус при движении точки М по
окружности: 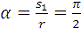 рад.
рад.
Абсолютную скорость точки М
найдем как геометрическую сумму относительной и переносной скоростей: 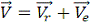
Модуль относительной скорости 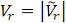
где 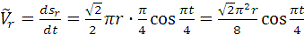
При 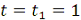 с:
с: 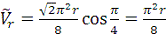 ;
; 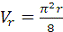
Положительный знак у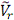 показывает, что вектор
показывает, что вектор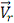 направлен в сторону положительных значений
направлен в сторону положительных значений 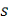 , перпендикулярно радиусу окружности, то есть вертикально вниз.
, перпендикулярно радиусу окружности, то есть вертикально вниз.
Модуль переносной скорости 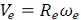 , где
, где 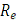 -
радиус окружности, описываемой той точкой тела, с которой в данный момент
совпадает точка М,
-
радиус окружности, описываемой той точкой тела, с которой в данный момент
совпадает точка М,
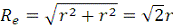
 -
модуль угловой скорости тела:
-
модуль угловой скорости тела:

При 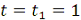 с:
с: 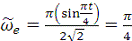
Таким образом, модуль переносной
скорости при 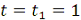 с равен
с равен
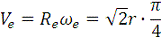
Вектор 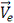 направлен перпендикулярно радиусу
направлен перпендикулярно радиусу 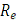 в сторону вращения.
в сторону вращения.
Модуль абсолютной скорости точки М
находим способом проекций:
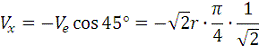
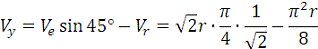
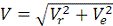 или
или 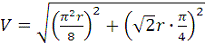
точка скорость ускорение векторный
Абсолютное ускорение точки равно
геометрической сумме относительного, переносного и кориолисова ускорений: 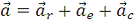 , или в развернутом виде
, или в развернутом виде 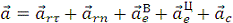
Модуль относительного касательного
ускорения 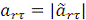
где 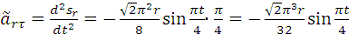
При 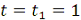 с:
с: 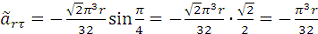 ;
; 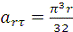
Отрицательный знак 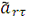
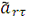 показывает, что вектор
показывает, что вектор 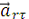
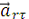 направлен в сторону
отрицательных значений
направлен в сторону
отрицательных значений 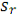
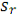 , перпендикулярно
радиусу окружности, то есть вертикально вверх. Знаки
, перпендикулярно
радиусу окружности, то есть вертикально вверх. Знаки 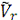
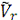 и
и 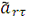
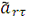 не одинаковы;
следовательно, относительное движение точки М замедленное.
не одинаковы;
следовательно, относительное движение точки М замедленное.
Относительное нормальное
ускорение 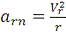 ,
то есть при
,
то есть при 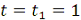 с:
с:
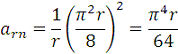
Вектор 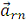 направлен
к центру диска, то есть горизонтально вправо.
направлен
к центру диска, то есть горизонтально вправо.
где 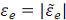 -
модуль углового ускорения диска:
-
модуль углового ускорения диска:
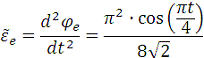
При 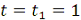 с:
с:
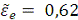
Таким образом, получаем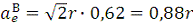
Модуль переносного
центростремительного ускорения 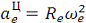 или
или
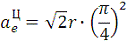
Вектор 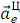 направлен
к центру вращения
направлен
к центру вращения
Кориолисово ускорение 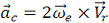
Модуль кориолисова
ускорения 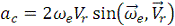 , где
, где 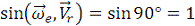
С учетом найденных выше
значений 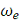 и
и
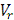 получаем
при
получаем
при 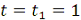 с:
с:
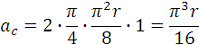
Вектор 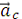
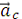 направлен согласно
правилу векторного произведения, то есть перпендикулярно одновременно векторам
направлен согласно
правилу векторного произведения, то есть перпендикулярно одновременно векторам 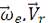
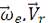 , в ту сторону, откуда
поворот от
, в ту сторону, откуда
поворот от 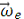
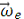 к
к 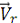
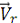 виден против хода
часовой стрелки, то есть вдоль оси x влево.
виден против хода
часовой стрелки, то есть вдоль оси x влево.
Модуль абсолютного
ускорения точки М находим способом проекций:
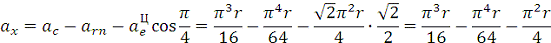
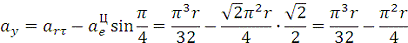
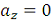

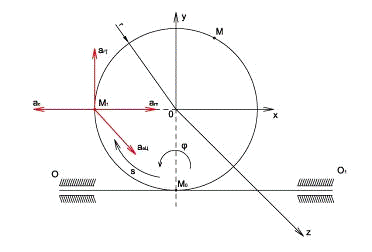
ОТВЕТ: