Современная теория управления
Конспект
лекций
«СОВРЕМЕННАЯ
ТЕОРИЯ УПРАВЛЕНИЯ»
Лекция №1. Модели объектов управления
Математические (аналитические) модели широко
используются при изучении разнообразных процессов в науке и технике, экономике,
в сфере социальных явлений. Известный шведский ученый Леннарт Льюнг пишет в
своей книге «Идентификация систем»: «Формирование моделей на основе результатов
наблюдений и исследование их свойств - вот, по существу, основное содержание
науки. Модели («гипотезы», «законы природы», «парадигмы» и т.п.) могут быть
более или менее формализованными, но все обладают той главной особенностью, что
связывают наблюдения в некую общую картину». А вот высказывание известного
специалиста в области автоматического управления Р. Калмана: «Теория управления
не занимается исследованием реального мира, а лишь математическими моделями
определенных аспектов реального мира».
Математические модели используются при синтезе
систем управления, при анализе различных вариантов развития событий во многих
сферах человеческой деятельности, при составлении прогнозов (например,
составлении прогноза погоды или формировании экономического прогноза изменений
цен на нефть).
Необходимо помнить, что объект моделирования, в
соответствии с терминологией Канта, есть «вещь в себе» - он не доступен для
непосредственного познания. Нам доступны лишь его отдельные фрагменты,
полученные с помощью ощущений (измерений), которые можно сложить в единую
картину только путем синтеза модели. Модель - это «вещь для нас», с ее помощью
мы можем прогнозировать поведение объекта и затем сравнить результаты прогноза
с реальной действительностью. Поскольку модель всегда проще объекта, прогноз и
реальность никогда идеально не совпадают между собой. Обычно создание модели
представляет собой итерационный процесс. Вначале создается простая, но неточная
модель. Затем она совершенствуется.
Базовым понятием математического моделирования
является понятие системы. Система является абстрактным (математическим) образом
реального объекта, а значит - это эквивалент понятия математической модели. Она
представляет собой совокупность взаимосвязанных элементов, представляющих
единое целое. Свойства системы могут отсутствовать у составляющих ее элементов.
Система имеет входы и выходы (рис. 1.1.).
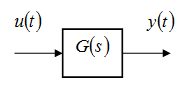
Рис. 1.1. Система с одним входом и одним выходом
Если система не имеет входов, то внешний мир не
имеет возможности воздействовать на нее. Если система не имеет выходов, то она
не воздействует на окружающий мир. Система, которая не имеет ни входов, ни
выходов, практически не существует в реальном мире. Поэтому такие системы
никогда не рассматриваются в приложениях.
Системой можно назвать процесс
решения любой задачи. При этом входами будут являться исходные данные, выходами
- результаты, а целью - правильное решение. В формальном смысле система
задается парой множеств 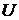 и
и 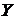 (
(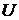 - множество
входов,
- множество
входов, 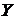 - множество
выходов) и отношением на
- множество
выходов) и отношением на 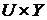 , которое
определяет зависимость между входами и выходами.
, которое
определяет зависимость между входами и выходами.
Соединение систем также является
системой и задается отношением. Например, последовательное соединение систем 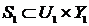 ,
, 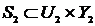 есть
отношение:
есть
отношение: 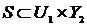 . Таким
образом, можно определять сколь угодно сложные системы, исходя из простых.
. Таким
образом, можно определять сколь угодно сложные системы, исходя из простых.
Любой системе присущи два основных
атрибута: целостность и структурированность.
Целостность (единство) означает, что
система отделена от внешней среды; среда может оказывать на нее действие
(акцию) через входы и воспринимать отклик (реакцию) на эти действия через
выходы.
Структурированность означает, что
система разделена внутри на несколько подсистем, связанных и взаимодействующих
между собой так же, как целая система взаимодействует с внешней средой.
Третье свойство, присущее системе, -
целенаправленность - требует задания некоторой цели, достижение которой говорит
о правильной работе системы.
Функционирование системы - это
процесс, разворачивающийся во времени, т. е. множества возможных входов и
выходов U, Y - это
множества функций времени. Система называется функциональной (определенной),
если каждой входной функции u(t) соответствует
единственная выходная функция y(t). В
противном случае система называется неопределенной. Неопределенность обычно
возникает из-за неполноты информации о внешних условиях работы системы. Важным
свойством, присушим реальным системам, является причинность. Она означает, что
если входные функции 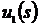 и
и 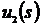 совпадают
при
совпадают
при 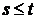 , т.е.
, т.е. 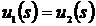 при
при 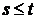 , то
соответствующие выходные функции удовлетворяют условию
, то
соответствующие выходные функции удовлетворяют условию 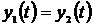 , т.е.
«настоящее не зависит от будущего при заданном прошлом».
, т.е.
«настоящее не зависит от будущего при заданном прошлом».
Индивидуальные свойства системы
описываются на языке математики. Например, на рис. 1.1 свойства системы заданы
в виде передаточной функции 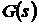 .
.
Аналитическими моделями различных
объектов реального мира являются математические уравнения.
Динамические системы описываются с
помощью дифференциальных уравнений, статические системы - с помощью
алгебраических. Входы системы 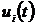 (
(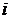 - текущий номер входа) входят в
дифференциальные уравнения как известные функции времени, а выходы
- текущий номер входа) входят в
дифференциальные уравнения как известные функции времени, а выходы 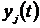 (
(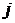 - текущий
номер выхода) - как неизвестные функции времени - они определятся путем решения
данной системы уравнений.
- текущий
номер выхода) - как неизвестные функции времени - они определятся путем решения
данной системы уравнений.
Числовые величины, связанные с
системой, делятся на переменные и параметры. Переменные описывают изменяющееся
состояние системы.
Параметры - это величины, которые
можно считать постоянными на промежутке времени наблюдения за работой системы.
В математическом смысле - это постоянные коэффициенты в дифференциальном или
алгебраическом уравнении, которое является моделью объекта. Значения переменных
и параметров определяют количественную информацию о системе. Оставшаяся
информация, т. е. качественная, определяет структуру системы.
Типовым приемом построения
математических моделей системы является параметризация - выбор в качестве
моделей семейства функций, зависящих от конечного (обычно небольшого)
количества чисел - параметров.
Пример 1.1. Построим аналитическую
модель электронной схемы, изображенной на рис. 1.2.
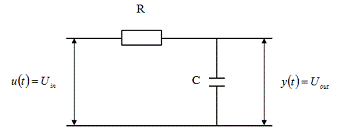
Рис. 1.2. 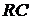 -цепь
-цепь
В данной системе входным сигналом
является входное напряжение 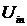 , а выходным сигналом - выходное
напряжение
, а выходным сигналом - выходное
напряжение 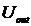 . Для
составления модели воспользуемся известными физическими законами. Согласно
закону Ома протекающий через резистор ток равен
. Для
составления модели воспользуемся известными физическими законами. Согласно
закону Ома протекающий через резистор ток равен
 ,(1.1)
,(1.1)
где  - величина сопротивления резистора.
- величина сопротивления резистора.
Конденсатор имеет в цепи постоянного
тока бесконечно большое сопротивление. Если же приложить к нему переменное
напряжение, то он будет периодически перезаряжаться и в цепи потечет ток.
Мгновенное значение тока определяется выражением
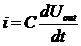 ,(1.2)
,(1.2)
где 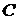 - величина емкости конденсатора.
- величина емкости конденсатора.
Приравнивая правые части уравнений
(1.1) и (1.2), получим
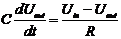 .(1.3)
.(1.3)
Уравнение (1.3) равносильно
линейному дифференциальному уравнению первого порядка
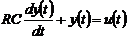 ,(1.4)
,(1.4)
где 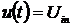 , а
, а 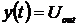 .
.
Уравнение (1.4) является
аналитической моделью электрической схемы, изображенной на рис. 1.2. Если
задать входной сигнал 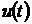 как
известную функцию времени, то, решив уравнение (1.4) при заданных начальных
условиях, получим выходной сигнал
как
известную функцию времени, то, решив уравнение (1.4) при заданных начальных
условиях, получим выходной сигнал 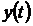 как функцию времени. Другими словами,
уравнение (1.4) позволяет нам моделировать реакцию системы на различные входные
сигналы. Поэтому оно и называется моделью. Произведение
как функцию времени. Другими словами,
уравнение (1.4) позволяет нам моделировать реакцию системы на различные входные
сигналы. Поэтому оно и называется моделью. Произведение 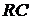 , имеющее
размерность времени, является параметром данной системы.
, имеющее
размерность времени, является параметром данной системы.
Если полученная модель представляет
собой линейное дифференциальное уравнение с постоянными коэффициентами (как в
данном случае), то в качестве модели также используют его изображение по
Лапласу. Изображение по Лапласу уравнения (1.4) выглядит следующим образом
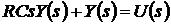 ,(1.5)
,(1.5)
где 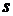 - комплексный параметр
преобразования Лапласа,
- комплексный параметр
преобразования Лапласа,  и
и 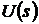 -
изображения по Лапласу функций
-
изображения по Лапласу функций 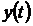 и
и 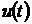 соответственно.
соответственно.
Уравнение (1.5) является
алгебраическим, а не дифференциальным - в этом его преимущество. Мы можем
вынести изображение  за скобки и
найти отношение изображения выходного сигнала системы к изображению входного,
которое называется передаточной функцией системы
за скобки и
найти отношение изображения выходного сигнала системы к изображению входного,
которое называется передаточной функцией системы 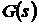 .
.
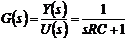 .(1.6)
.(1.6)
По виду передаточной функции (1.6)
можно установить, что моделируемая система является апериодическим звеном с
единичным статическим коэффициентом усиления и постоянной времени, равной 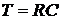 . Определим
реакцию такой системы на ступенчатый входной сигнал. Для этого найдем оригинал
изображения
. Определим
реакцию такой системы на ступенчатый входной сигнал. Для этого найдем оригинал
изображения 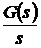 .
.
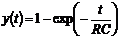 .(1.7)
.(1.7)
График функции, описываемой
уравнением (1.7) для случая, когда 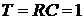 , показан на рис. 1.3.
, показан на рис. 1.3.
График показывает, что в ответ на
ступенчатый входной сигнал система переходит в новое состояние не сразу, а
спустя некоторое время. Приблизительно оно равно: 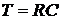 (точнее,
спустя промежуток времени
(точнее,
спустя промежуток времени 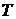 выход
системы составляет 63 % от величины выходного сигнала в установившемся режиме).
выход
системы составляет 63 % от величины выходного сигнала в установившемся режиме).
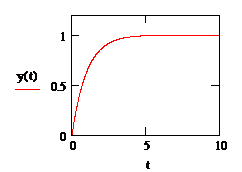
Рис. 1.3. Переходная функция апериодического
звена
Положив в (1.6) 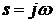 , где
, где 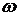 - частота
гармонических колебаний,
- частота
гармонических колебаний, 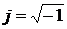 - мнимая
единица, получим частотную функцию
- мнимая
единица, получим частотную функцию
 ,(1.8)
,(1.8)
где 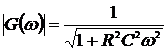 - модуль и
- модуль и 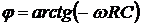 - аргумент
частотной функции.
- аргумент
частотной функции.
Амплитудно-частотная (АЧХ) и
фазово-частотная (ФЧХ) характеристики данной системы показаны на рис. 1.4.
Графики 1.4 показывают, что электрическая схема
на рис. 1.2 является фильтром низких частот, причем гармонические сигналы
передаются с задержкой по фазе.
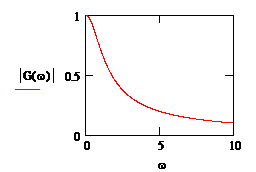
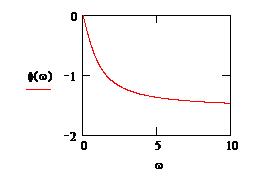
Рис. 1.4. АЧХ и ФЧХ апериодического звена
Пример 1.2. Построим аналитическую модель
электронной схемы, изображенной на рис. 1.5.
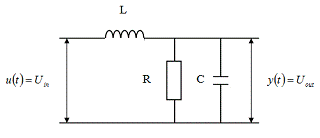
Рис. 1.5. 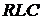 -цепь
-цепь
Здесь резистор включен параллельно
конденсатору и добавлена катушка индуктивностью 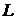 . Падение напряжения на катушке
определяется выражением
. Падение напряжения на катушке
определяется выражением
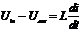 ,(1.9)
,(1.9)
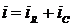 , (1.10)
, (1.10)
где 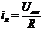 - ток, протекающий через резистор,
- ток, протекающий через резистор,
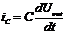 - ток, протекающий через
конденсатор. На основании (1.9) и (1.10) можем записать
- ток, протекающий через
конденсатор. На основании (1.9) и (1.10) можем записать
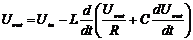 .
.
После преобразований получим
линейное дифференциальное уравнение второго порядка, являющееся математической
моделью схемы, изображенной на рис. 1.5.
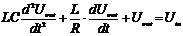 .(1.11)
.(1.11)
В общепринятых обозначениях
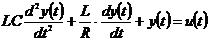 .(1.12)
.(1.12)
Уравнение в изображениях: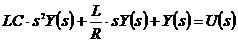 - позволит
найти передаточную функцию
- позволит
найти передаточную функцию
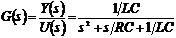 .(1.13)
.(1.13)
Передаточная функция линейной
системы второго порядка в общем случае записывается следующим образом
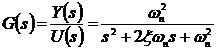 ,(1.14)
,(1.14)
где 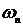 - частота собственных колебаний
системы,
- частота собственных колебаний
системы,
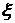 - коэффициент демпфирования
системы. Сравнивая формулы (1.13) и (1.14), получим:
- коэффициент демпфирования
системы. Сравнивая формулы (1.13) и (1.14), получим:
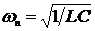 ,
, 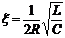 .
.
На рис. 1.6 показаны реакции
линейной системы второго порядка на ступенчатый сигнал при различных
коэффициентах демпфирования (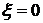 ;
; 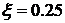 ;
; 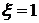 ). График получен в системе MATLAB.
). График получен в системе MATLAB.
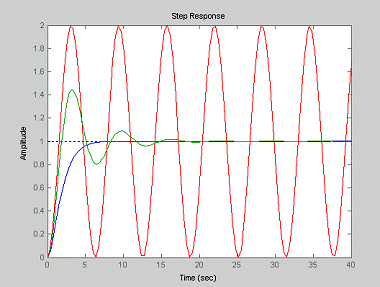
Рис. 1.6. Реакции системы второго порядка на
ступенчатый сигнал при различных коэффициентах демпфирования
Если коэффициент демпфирования равен
нулю, то реакцией системы на ступенчатый сигнал будут бесконечные гармонические
колебания. Они возникнут в изображенной на рис. 1.5 электрической схеме в том
случае, когда сопротивление резистора будет равно бесконечности. Если 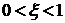 , то
колебания станут затухающими. Если
, то
колебания станут затухающими. Если 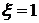 , то колебаний вообще не будет
(случай критического демпфирования).
, то колебаний вообще не будет
(случай критического демпфирования).
Пример 1.3. Построим аналитическую
модель механической системы, изображенной на рис. 1.7.
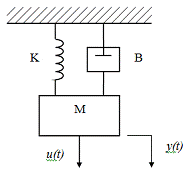
Рис. 1.7. Механическая система
перемещения
Предполагаем, что движение возможно
только в одном направлении - вдоль оси y(t). Никакое
движение в поперечном направлении не допускается. На тело массы М действует три
силы: внешняя сила, сила трения и сила упругости. Согласно принципу д’Аламбера,
к ним нужно добавить силу инерции и результат приравнять нулю. В результате
получим дифференциальное уравнение:
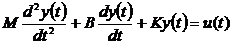 ,(1.15)
,(1.15)
где В - коэффициент трения,
К - коэффициент упругости.
Это дифференциальное уравнение
является моделью механической системы, изображенной на рис. 1.7. Сравнив его с
уравнением (1.12), можно заметить, что они отличаются только коэффициентами.
Коэффициенту LC
соответствует коэффициент М, коэффициенту 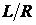 - коэффициент В, единице соответствует
коэффициент К.
- коэффициент В, единице соответствует
коэффициент К.
Передаточная функция механической
системы равна
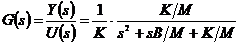 .(1.16)
.(1.16)
Частота собственных колебаний
механической системы равна 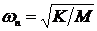 , а коэффициент демпфирования:
, а коэффициент демпфирования: 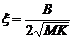 .
.
Рассмотренные примеры показывают,
что различные объекты реального мира могут описываться одинаковыми моделями.
Лекция №2. Классификация
аналитических моделей
Все многообразие имеющихся типов
аналитических моделей можно классифицировать по нескольким основным признакам:
линейные - нелинейные; статические - динамические; стационарные -
нестационарные; дискретные - непрерывные; детерминированные - стохастические -
нечеткие; сосредоточенные - распределенные и т.д.
Математическая модель системы
называется статической, если значение выхода y(t)
зависит от значения входа u(t)
только в тот же момент времени t.
Символически это свойство записывается так:
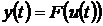 .(2.1)
.(2.1)
Уравнение (2.1) не дифференциальное,
а алгебраическое. Мы можем рассматривать алгебраическое уравнение как частный
случай дифференциального, в котором все производные неизвестной функции
(выходного сигнала системы y(t)) равны
нулю. В простейшем случае линейной системы:
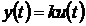 , (2.2)
, (2.2)
где  - коэффициент усиления. Кроме явных
функциональных зависимостей, статические модели могут задаваться неявно, в виде
уравнения или системы:
- коэффициент усиления. Кроме явных
функциональных зависимостей, статические модели могут задаваться неявно, в виде
уравнения или системы:  . Это
уравнение должно быть однозначно разрешимо относительно y(t).
Статическими моделями пользуются, когда в рамках поставленной задачи
инерционностью и «памятью» реальной системы можно пренебречь. Это возможно при
выполнении ряда условий:
. Это
уравнение должно быть однозначно разрешимо относительно y(t).
Статическими моделями пользуются, когда в рамках поставленной задачи
инерционностью и «памятью» реальной системы можно пренебречь. Это возможно при
выполнении ряда условий:
. система устойчива, т.е.
переходные процессы после скачкообразного изменения входов затухают. Конечное
время затухания с заданной точностью обозначим через 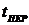 ;
;
. входы меняются медленно,
т.е. 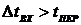 , где
, где 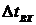 - время
между изменениями входных воздействий;
- время
между изменениями входных воздействий;
. выходы измеряются редко,
т.е. 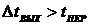 , где
, где 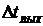 - промежутки
между измерениями выходных величин.
- промежутки
между измерениями выходных величин.
В динамических, моделях значение y(t) может
зависеть от всего прошлого (предыстории) входного процесса:  .
.
Динамические модели позволяют учесть
наличие «памяти», инерционности системы. Математическим аппаратом описания
динамических систем являются дифференциальные, разностные уравнения, конечные
автоматы, случайные процессы.
Система называется стационарной,
если ее реакция на заданное входное воздействие не зависит от того, в каком
промежутке времени осуществляется этот опыт. Это условие удовлетворяется в том
случае, если все параметры дифференциального уравнения, являющегося моделью
системы, остаются неизменными во времени. Если параметры изменяются со
временем, то система является нестационарной.
Пример 2.1. Система, моделью которой
служит линейное уравнение с постоянными коэффициентами, например следующее:
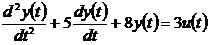 ,(2.3)
,(2.3)
- является стационарной. А модель
следующего вида:
 ,(2.4)
,(2.4)
является нестационарной.
Понятие стационарности системы, как
и понятие ее статичности является относительным (если быть предельно строгим -
все системы нестационарные и динамические). Предположим, что постоянная времени
объекта равна нескольким секундам, а ощутимые изменения параметров можно
обнаружить лишь через месяц. Такую систему при определенных условиях можно
рассматривать как стационарную. Однако при изменении характера решаемых задач
такое допущение может стать недопустимым.
Лекция №3. Линейные непрерывные
модели
Универсальным средством математического описания
объектов, непрерывно изменяющихся во времени, являются дифференциальные
уравнения. Если дифференциальное уравнение линейное, то такая модель называется
линейной. Если моделью объекта является линейное уравнение с постоянными
коэффициентами, то наиболее часто системы задаются в виде рациональных
передаточных функций
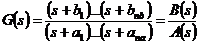 ,(3.1)
,(3.1)
где 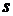 - комплексный параметр
преобразования Лапласа,
- комплексный параметр
преобразования Лапласа, 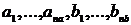 -
коэффициенты (вещественные или комплексные).
-
коэффициенты (вещественные или комплексные).
Иногда в системе имеет место
задержка сигнала на величину 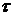 (так называемое - транспортное
запаздывание). Тогда в уравнение (3.1) нужно добавить сомножитель
(так называемое - транспортное
запаздывание). Тогда в уравнение (3.1) нужно добавить сомножитель 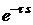 :
:
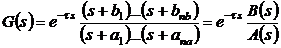 (3.2)
(3.2)
Конечное множество чисел: 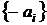 (
(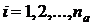 ) называется
полюсами, а множество
) называется
полюсами, а множество 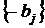 (
(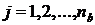 ) - нулями
системы (3.1). Система является устойчивой, если действительная часть всех
полюсов отрицательна. В противном случае - система неустойчивая. Комплексные
нули и полюса образуют пары комплексно сопряженных чисел.
) - нулями
системы (3.1). Система является устойчивой, если действительная часть всех
полюсов отрицательна. В противном случае - система неустойчивая. Комплексные
нули и полюса образуют пары комплексно сопряженных чисел.
Пример 3.1. Если система имеет
полюс: 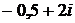 , то она
также имеет и полюс:
, то она
также имеет и полюс: 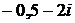 . Подобных
пар может быть несколько. Если система имеет только комплексные полюса (или/и
нули), то их количество четно.
. Подобных
пар может быть несколько. Если система имеет только комплексные полюса (или/и
нули), то их количество четно.
Символ 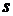 допускает
различную трактовку. Либо это оператор дифференцирования:
допускает
различную трактовку. Либо это оператор дифференцирования:  , тогда
, тогда
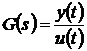 , (3.3)
, (3.3)
где 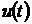 - входной и
- входной и 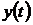 - выходной
сигналы системы.
- выходной
сигналы системы.
Либо 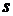 - это комплексная переменная
(параметр преобразования Лапласа), тогда
- это комплексная переменная
(параметр преобразования Лапласа), тогда
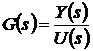 ,(3.4)
,(3.4)
где 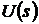 и
и  - преобразования Лапласа входного
- преобразования Лапласа входного 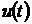 и выходного
и выходного
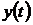 - сигналов
соответственно.
- сигналов
соответственно.
Числитель и знаменатель передаточной
функции (3.1) можно представить в виде полиномов степеней 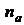 и
и 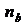 :
:
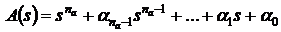 , (3.5а)
, (3.5а)
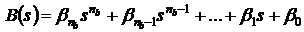 , (3.5б)
, (3.5б)
где 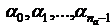 - коэффициенты, зависящие от
полюсов,
- коэффициенты, зависящие от
полюсов,
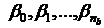 - коэффициенты, зависящие от нулей
передаточной функции.
- коэффициенты, зависящие от нулей
передаточной функции.
Пример 3.2. Передаточная функция
линейной системы первого порядка с транспортным запаздыванием имеет вид:
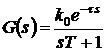 ,(3.6)
,(3.6)
где  - статический коэффициент усиления,
- статический коэффициент усиления,
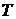 - постоянная времени.
- постоянная времени.
Пример 3.3. Передаточная функция
линейной системы второго порядка с транспортным запаздыванием имеет вид:
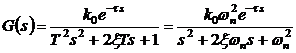 ,(3.7)
,(3.7)
где 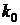 - статический коэффициент усиления,
- статический коэффициент усиления,
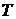 - постоянная времени,
- постоянная времени,
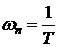 - частота собственных колебаний
системы,
- частота собственных колебаний
системы,
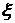 - коэффициент демпфирования.
- коэффициент демпфирования.
В среде программирования «MATLAB» передаточные
функции задаются с помощью специальной команды. С помощью «MATLAB» легко
решаются многие задачи, связанные с моделированием систем.
Пример 3.4. Предположим, нам
необходимо найти нули и полюса передаточной функции
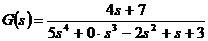 .
.
В «MATLAB» эта задача
решается с помощью следующей программы (тут же приводится и результат):
G=tf([4 7], [5 0 -2 1
3]);(G)=
.7500(G)
ans =
.6992 + 0.6004i
.6992 - 0.6004i
.6992 + 0.4663i
.6992 - 0.4663i
Как можно видеть два полюса
рассматриваемой системы имеют положительные действительные части. Значит, такая
система неустойчива.
Уравнение (3.3) с учетом (3.1) можно
записать следующим образом
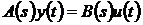 .
.
Или по другому
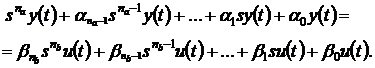
Поскольку в данном случае символ 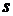 означает
дифференциальный оператор, то приходим к линейному дифференциальному уравнению
означает
дифференциальный оператор, то приходим к линейному дифференциальному уравнению
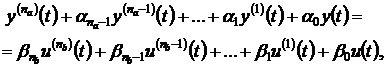 (3.8)
(3.8)
где 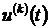 и
и 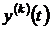 - производные
- производные  -го порядка
функций
-го порядка
функций 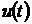 и
и 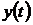 соответственно.
Это дифференциальное уравнение с постоянными коэффициентами является одной из
форм математической модели системы (3.1). Если в системе имеет место
транспортное запаздывание, то дифференциальное уравнение линейной системы
выглядит следующим образом
соответственно.
Это дифференциальное уравнение с постоянными коэффициентами является одной из
форм математической модели системы (3.1). Если в системе имеет место
транспортное запаздывание, то дифференциальное уравнение линейной системы
выглядит следующим образом
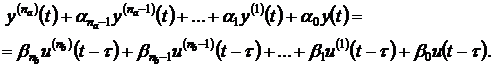 (3.9)
(3.9)
Решение уравнений (3.8) и (3.9)
имеет следующий вид
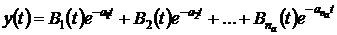 ,
,
где функции 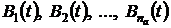 - зависят
от формы входного сигнала. Видно, что если полюса передаточной функции
- зависят
от формы входного сигнала. Видно, что если полюса передаточной функции 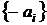 имеют
отрицательные действительные части, то при
имеют
отрицательные действительные части, то при  функция
функция 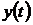 стремится к
конечному значению.
стремится к
конечному значению.
Пример 3.5. Дифференциальное
уравнение линейной системы первого порядка имеет вид:
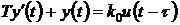 . (3.10)
. (3.10)
Начальные условия предполагаются
нулевыми:  .
.
Пример 3.6. Дифференциальное
уравнение линейной системы второго порядка имеет вид:
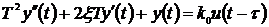 , (3.11)
, (3.11)
Начальные условия также
предполагаются нулевыми:  ,
, 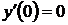 .
.
Уравнение (3.6) можно переписать так
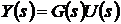 .(3.12)
.(3.12)
Оригиналом уравнения (3.10) является
свертка
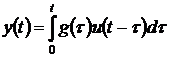 ,(3.13)
,(3.13)
где  - импульсная весовая функция (
- импульсная весовая функция ( ). Эта
функция также является моделью системы. Уравнение (3.13) позволяет рассчитывать
выходной сигнал системы по известному входному сигналу и импульсной весовой
функции.
). Эта
функция также является моделью системы. Уравнение (3.13) позволяет рассчитывать
выходной сигнал системы по известному входному сигналу и импульсной весовой
функции.
Пример 3.7. Импульсная весовая
функция линейной системы первого порядка имеет вид:
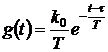 .(3.14)
.(3.14)
Реакция системы на ступенчатый
входной сигнал описывается функцией
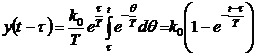 .(3.15)
.(3.15)
Пример 3.8. Импульсная весовая
функция линейной системы второго порядка имеет вид:
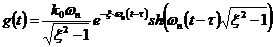 .(3.16)
.(3.16)
Реакция системы на ступенчатый
входной сигнал описывается функцией
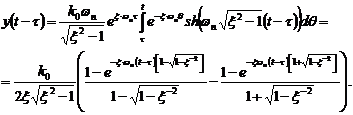 (3.17)
(3.17)
В среде программирования «MATLAB» реакция
системы с передаточной функцией 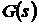 на ступенчатый входной сигнал
рассчитывается с помощью команды step(G).
на ступенчатый входной сигнал
рассчитывается с помощью команды step(G).
Пример 3.9. Определим реакцию на
ступенчатое воздействие системы второго порядка с передаточной функцией
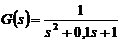 .
.
В командном окне наберем программу:
=tf([1], [1 0.1 1]);(G)
линейный дискретный
управление модель
В результате получим график,
показанный на рис. 3.1.
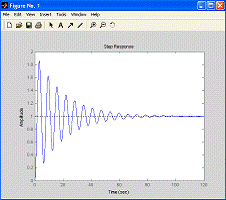
Рис. 3.1. Реакция системы второго
порядка на ступенчатый входной сигнал
Поскольку в уравнениях (3.6) и
(3.12) 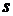 -
понимается как комплексная переменная, то можем записать
-
понимается как комплексная переменная, то можем записать
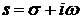 ,
,
где  - действительная и
- действительная и 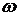 - мнимая
часть переменной
- мнимая
часть переменной 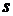 (
(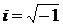 - мнимая
единица). Если
- мнимая
единица). Если 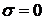 , то
, то 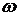 можно
трактовать как частоту колебаний гармонических сигналов и тогда формула (3.1)
описывает частотную характеристику линейной системы. Тогда вместо передаточной
функции мы получаем частотную функцию:
можно
трактовать как частоту колебаний гармонических сигналов и тогда формула (3.1)
описывает частотную характеристику линейной системы. Тогда вместо передаточной
функции мы получаем частотную функцию:
 ,(3.18)
,(3.18)
где 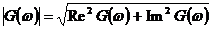 ,
, 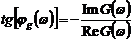 .
.
Функция 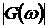 называется
амплитудной частотной характеристикой, а
называется
амплитудной частотной характеристикой, а 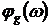 - фазовой частотной характеристикой
системы (3.1). Графики этих функций в логарифмических координатах называются
диаграммной Боде.
- фазовой частотной характеристикой
системы (3.1). Графики этих функций в логарифмических координатах называются
диаграммной Боде.
Пример 3.10. Амплитудная и фазовая
частотные характеристики системы первого порядка имеют вид:
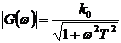 ,(3.19а)
,(3.19а)
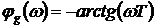 .(3.19б)
.(3.19б)
Пример 3.11. Амплитудная и фазовая
частотные характеристики системы второго порядка имеют вид:
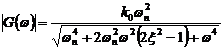 ,(3.20а)
,(3.20а)
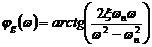 .(3.20б)
.(3.20б)
В «MATLAB» диаграмму
Боде системы с передаточной функцией G(s)
рассчитывают с помощью команды bode(G).
Пример 3.12. Получим диаграмму Боде
для системы второго порядка с передаточной функцией 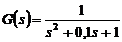 .
.
В результате получим график,
показанный на рис. 3.2.
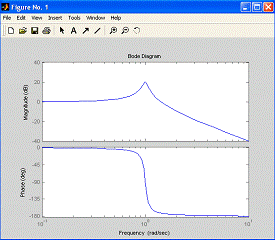
Рис. 3.2. Диаграмма Боде системы
второго порядка
Как можно видеть, амплитудная
характеристика имеет экстремум на частоте свободных колебаний системы. На этой
же частоте наблюдается и резкое изменение фазовой характеристики. При
увеличении коэффициента демпфирования 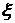 экстремум будет уменьшаться, а при
значении
экстремум будет уменьшаться, а при
значении 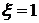 кривая
амплитудной характеристики станет абсолютно гладкой.
кривая
амплитудной характеристики станет абсолютно гладкой.
Заменив в формуле (2.12) 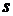 на
на 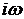 , получим
следующее выражение
, получим
следующее выражение
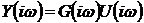 , (3.21)
, (3.21)
где 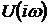 и
и 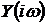 - комплексные спектры входного и
выходного сигналов.
- комплексные спектры входного и
выходного сигналов.
Можно записать и так
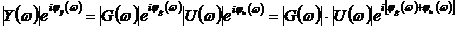 ,(3.22)
,(3.22)
где 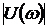 ,
, 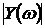 ,
,  ,
, 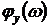 - амплитудные и фазовые спектры
входного и выходного сигналов. Из выражения (3.22) следует
- амплитудные и фазовые спектры
входного и выходного сигналов. Из выражения (3.22) следует
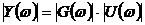 ,(3.23а)
,(3.23а)
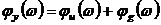 .(3.23б)
.(3.23б)
В приложениях используется понятие
спектральной плотности сигнала, которое имеет физический смысл спектра мощности
(интенсивности колебаний)
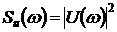 ,
,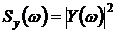 .
.
С учетом (3.23а) можем записать
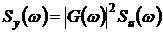 .(3.24)
.(3.24)
Частотная характеристика 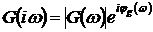 является
одной из возможных форм описания линейной системы (3.1). Она однозначно
определяет все ее свойства.
является
одной из возможных форм описания линейной системы (3.1). Она однозначно
определяет все ее свойства.
Лекция №4. Линейные модели в
пространстве состояний
В середине прошлого столетия в
широкое употребление вошла еще одна форма линейной модели: модель в
пространстве состояний (State Space model). Такая
модель описывает связь между входными и выходными сигналами в виде системы
дифференциальных уравнений первого порядка посредством введения
вспомогательного вектора состояния 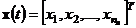 .
.
Ранее мы рассматривали линейную
модель в виде обыкновенного дифференциального уравнения с постоянными коэффициентами
(или в виде передаточной функции).
Такую модель достаточно просто
перевести в модель в пространстве состояний. Рассмотрим уравнение (3.8).
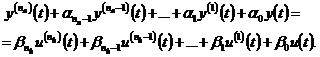
Этому уравнению соответствует
следующая передаточная функция
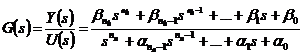 .(4.1)
.(4.1)
Взамен дифференциального уравнения и
передаточной функции (4.1) можно записать систему дифференциальных уравнений
первого порядка
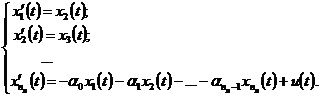 (4.2а)
(4.2а)
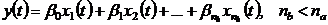 .(4.2б)
.(4.2б)
Справедливость такого преобразования
легко доказывается переходом к изображениям по Лапласу для всех уравнений
системы. При этом учитываем, что: 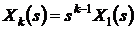 ,
,  .
.
Если модель в пространстве состояний
описывают механическую систему, то компоненты вектора состояний могут иметь
физический смысл координаты материальной точки, ее скорости и ускорения. В
общем случае вектор состояния не обязательно должен иметь наглядный физический
смысл, входов может быть несколько, выходной сигнал - зависеть от всех
компонент вектора состояний и даже от вектора входных сигналов:
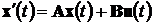 ,(4.3а)
,(4.3а)
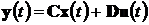 .(4.3б)
.(4.3б)
Здесь 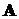 - квадратная матрица размером (
- квадратная матрица размером (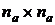 );
); 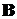 - матрица
размером (
- матрица
размером (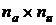 ),
),  -
размерность вектора входных сигналов;
-
размерность вектора входных сигналов; 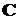 - матрица размером (
- матрица размером (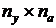 ),
), 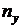 -
размерность вектора выходных сигналов;
-
размерность вектора выходных сигналов;  - матрица размером (
- матрица размером (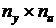 ).
).
Выражения (4.3а) и (4.3б) являются
математической моделью линейной системы в пространстве состояний. Уравнение
(4.3а) называется уравнением состояния, а уравнение (4.3б) - уравнением
наблюдения.
Пример 4.1. Для системы первого
порядка возможна следующая конфигурация:
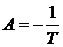 ,
,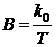 ,
,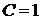 ,
,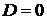 .
.
Пример 4.2. Для системы второго
порядка возможна такая конфигурация:
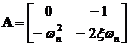 ,
,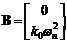 ,
,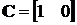 ,
,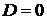 .
.
Корни 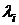 уравнения
уравнения
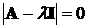 (4.4)
(4.4)
где 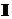 - единичная матрица, называются
собственными числами матрицы
- единичная матрица, называются
собственными числами матрицы 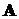 , а векторы
, а векторы 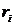 , найденные
из матричного уравнения
, найденные
из матричного уравнения
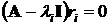 ,(4.5)
,(4.5)
называются собственными векторами
матрицы 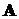 .
Собственные числа равны полюсам системы, записанной в виде (3.1). Уравнение
(4.4), с помощью которого определяются собственные числа (полюса) системы,
называется характеристическим.
.
Собственные числа равны полюсам системы, записанной в виде (3.1). Уравнение
(4.4), с помощью которого определяются собственные числа (полюса) системы,
называется характеристическим.
Пример 4.3. Для системы первого
порядка единственное собственное число равно 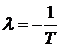 (величина, обратная времени, имеет
физический смысл частоты). Для системы второго порядка
(величина, обратная времени, имеет
физический смысл частоты). Для системы второго порядка  , где
, где 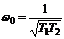 - частота
собственных колебаний системы,
- частота
собственных колебаний системы, 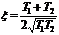 - коэффициент демпфирования,
собственные числа этой матрицы равны полюсам системы
- коэффициент демпфирования,
собственные числа этой матрицы равны полюсам системы
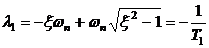 ,
,
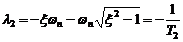 .
.
Собственные векторы равны
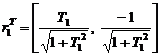 ,
,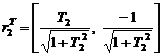 .
.
В «MATLAB»
предусмотрена возможность определения передаточной функции по модели, заданной
в пространстве состояний.
Пример 4.4. Задана модель в пространстве
состояний, имеющая следующие матрицы:
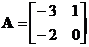 ,
,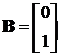 ,
,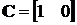 ,
, 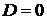 .
.
Этот результат на первый взгляд
кажется обескураживающим. Мы не получили исходные матрицы, как, возможно,
ожидалось. Тем не менее, это правильное решение. Дело в том, что одной и той же
передаточной функции соответствуют различные комбинации матриц 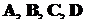 . Другими
словами, любому объекту соответствует бесчисленное количество моделей в
пространстве состояний.
. Другими
словами, любому объекту соответствует бесчисленное количество моделей в
пространстве состояний.
Данный факт можно объяснить
следующим образом. С помощью преобразования Лапласа выразим передаточную
функцию линейной системы через матрицы модели в пространстве состояний:
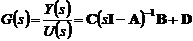 .(4.6)
.(4.6)
Предположим, что мы внесли изменения
в матрицу 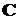 .
Соответствующими изменениями в матрицах
.
Соответствующими изменениями в матрицах 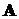 и
и 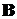 можно добиться того, что
передаточная функция, определяемая выражением (4.6) останется прежней. Убедимся
в этом с помощью следующей программы.
можно добиться того, что
передаточная функция, определяемая выражением (4.6) останется прежней. Убедимся
в этом с помощью следующей программы.
=[-3 -0.5; 4 0];=[0.5; 0];=[0 0.5];
h=ss(A, B,
C, 0);
Введем новый вектор состояния  той же
размерности, что и
той же
размерности, что и 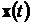 , элементы
которого представляют собой линейные комбинации компонент вектора
, элементы
которого представляют собой линейные комбинации компонент вектора 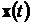 :
:
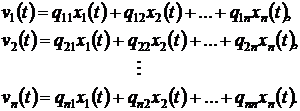
То же самое можно представить в
матричной форме
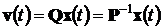 ,(4.7)
,(4.7)
где матрица 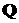 - обратная
некоторой матрице
- обратная
некоторой матрице 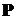 . Следовательно,
вектор состояния
. Следовательно,
вектор состояния 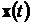 можно
выразить как
можно
выразить как
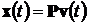 ,(4.8)
,(4.8)
где 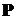 - так называемая матрица
преобразования базиса.
- так называемая матрица
преобразования базиса.
Преобразование одного вектора
состояния в другой изменяет внутреннюю структуру системы (модель состояния), но
не затрагивает соотношение между входом и выходом (передаточную функцию). Такой
тип преобразования называется преобразованием подобия.
Рассмотрим модель системы в
пространстве состояний:
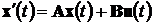 .
.
Применив преобразование подобия
(4.8), получим:
 .
.
Решая это уравнение относительно 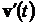 , получим
модель системы с вектором состояния
, получим
модель системы с вектором состояния  .
.
 .
.
Уравнение для выходной переменной
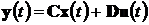 ,
,
с учетом преобразования подобия
(4.8) принимает вид
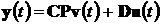 .
.
В общем случае для многомерной
системы с вектором состояния  можем записать
можем записать
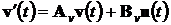 ,(4.9а)
,(4.9а)
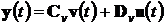 ,(4.9б)
,(4.9б)
где  ,
, 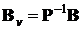 ,
, 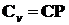 ,
, 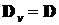 .
.
Пример 4.5. Задана система в
пространстве состояний со следующими матрицами:
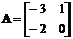 ,
,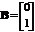 ,
,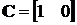 .
.
Необходимо определить матрицы 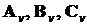 , если
матрица преобразования базиса равна:
, если
матрица преобразования базиса равна:
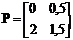 .
.
Эту задачу можно решить в системе «MATLAB» следующим
образом. Соответствующая программа и результат ее выполнения имеют вид:
Av=inv(P)*A*P=inv(P)*B
Если выбрать другую матрицу 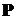 , то получим
новую модель, то есть, для каждой матрицы преобразования, которая имеет себе
обратную, будет существовать своя модель. Выбор той или иной модели зависит от
конкретных обстоятельств: например, желания проектировщика иметь в качестве
переменных состояния естественные физические величины, существование датчиков,
способных измерить данные физические величины. В связи с рассмотренной
особенностью моделей в пространстве состояний возникает вопрос: что следует
понимать под состоянием системы? Можно дать следующее определение: состояние
системы в любой момент времени
, то получим
новую модель, то есть, для каждой матрицы преобразования, которая имеет себе
обратную, будет существовать своя модель. Выбор той или иной модели зависит от
конкретных обстоятельств: например, желания проектировщика иметь в качестве
переменных состояния естественные физические величины, существование датчиков,
способных измерить данные физические величины. В связи с рассмотренной
особенностью моделей в пространстве состояний возникает вопрос: что следует
понимать под состоянием системы? Можно дать следующее определение: состояние
системы в любой момент времени  - это количество информации,
которое вместе со всеми входными переменными однозначно определяет поведение
системы при всех
- это количество информации,
которое вместе со всеми входными переменными однозначно определяет поведение
системы при всех 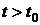 .
.
Лекция №5. Дискретные модели
Дискретной называется система, которая может
переходить из одного состояния в другое только в определенные моменты времени.
Дискретные системы распространены очень широко. Например, цифровой компьютер
является дискретной системой. Если модель непрерывной системы является
дифференциальное уравнение, то моделью дискретной системы является разностное
уравнение. Дискретные системы можно представить также в пространстве состояний
или с помощью передаточной функции. Предположим, что мы используем компьютер
для управления неким объектом (рис. 5.1).
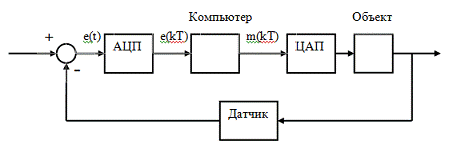
Рис. 5.1. Цифровая система управления
Поскольку компьютер является
цифровым устройством, работающим в реальном времени, он может принимать
информацию в дискретные моменты времени. Пусть эти моменты отстоят друг от
друга на постоянную величину 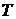 . Этот интервал времени называется
шагом дискретизации.
. Этот интервал времени называется
шагом дискретизации.
Тогда сигнал, поступающий в
компьютер, можно представить в виде числовой последовательности 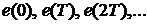 , которую мы
обозначим как
, которую мы
обозначим как 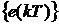 . Очень
часто параметр
. Очень
часто параметр 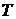 опускают, и
тогда обозначение превращается в
опускают, и
тогда обозначение превращается в 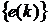 .
.
Выходной сигнал также является
числовой последовательностью 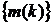 . Компьютер обладает памятью,
поэтому мы можем запоминать входные и выходные сигналы в прошедшие моменты
времени. Линейное разностное уравнение с постоянными коэффициентами
. Компьютер обладает памятью,
поэтому мы можем запоминать входные и выходные сигналы в прошедшие моменты
времени. Линейное разностное уравнение с постоянными коэффициентами 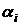 и
и 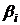
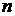 -го порядка
выглядит следующим образом
-го порядка
выглядит следующим образом
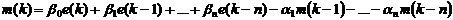 . (5.1)
. (5.1)
Порядок уравнения определяет
«глубину памяти» системы.
В рассматриваемом нами случае
разностное уравнение (5.1) описывает динамику регулятора, в качестве которого
используется цифровой компьютер. Однако оно может служить и моделью объекта,
если тот является линейной дискретной системой.
Решить разностное уравнение означает
найти последовательность 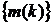 . Такую
последовательность называют решетчатой функцией. Существует три основных метода
решения линейных разностных уравнений с постоянными коэффициентами. Первый
(классический) метод состоит в нахождении общего и частного решений подобно
тому, как это делается при классическом решении линейных дифференциальных уравнений.
Этот метод мы рассматривать не будем. Второй метод является рекуррентным; он
используется при решении разностных уравнений с помощью цифрового компьютера.
Мы рассмотрим его на примере.
. Такую
последовательность называют решетчатой функцией. Существует три основных метода
решения линейных разностных уравнений с постоянными коэффициентами. Первый
(классический) метод состоит в нахождении общего и частного решений подобно
тому, как это делается при классическом решении линейных дифференциальных уравнений.
Этот метод мы рассматривать не будем. Второй метод является рекуррентным; он
используется при решении разностных уравнений с помощью цифрового компьютера.
Мы рассмотрим его на примере.
Пример 5.1. Получим решение
следующего разностного уравнения
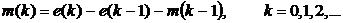
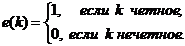
Причем, 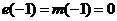 . Решения
для
. Решения
для 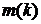 можно
получить, положив сначала в разностном уравнении
можно
получить, положив сначала в разностном уравнении 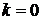 , затем
, затем 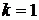 , затем
, затем 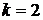 и т.д. В
результате получим
и т.д. В
результате получим
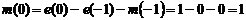
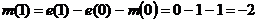
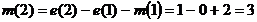
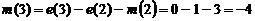
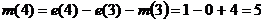
Используя этот метод, можно определить
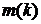 для любых
значений
для любых
значений  . При
больших значениях
. При
больших значениях  подобная
процедура очень трудоемка, поэтому лучше выполнить ее на компьютере. Последний
пример для
подобная
процедура очень трудоемка, поэтому лучше выполнить ее на компьютере. Последний
пример для 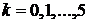 решается с
помощью следующей программы «MATLAB»:
решается с
помощью следующей программы «MATLAB»:
mkminus1=0;
ekminus1=0; ek=1;k=0:5=ek-ekminus1-mkminus1;
[k ek
mk]=mk;=ek;=1-ek;
В этой программе ekminus1
соответствует значению 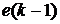 , ek -
значению
, ek -
значению 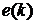 , mkminus1 -
значению
, mkminus1 -
значению 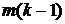 , а mk -
значению
, а mk -
значению 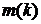 .
.
В качестве второго примера
применения рекуррентного метода решения разностных уравнений рассмотрим
численное интегрирование дифференциального уравнения по методу Эйлера. Дано
дифференциальное уравнение первого порядка:
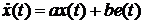 .
.
Для малого значения 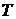 производную
производную
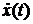 можно
представить как
можно
представить как
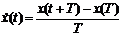 .
.
Тогда дифференциальное уравнение
приближенно примет вид:
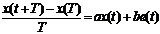 .
.
Переходя к дискретному времени 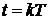 , получим
разностное уравнение
, получим
разностное уравнение
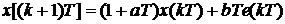 .
.
Таким образом, интегрирование
дифференциального уравнения методом Эйлера сводится к получению разностного
уравнения. Вообще любой метод численного интегрирования может быть сведен к
разностному уравнению и запрограммирован для решения на цифровом компьютере.
Третий метод решения линейных
разностных уравнений с постоянными коэффициентами основан на использовании 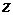 -преобразования,
которое эквивалентно преобразованию Лапласа для непрерывных систем. Рассмотрим
следующее разностное уравнение
-преобразования,
которое эквивалентно преобразованию Лапласа для непрерывных систем. Рассмотрим
следующее разностное уравнение 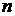 -го порядка, считая входную
последовательность
-го порядка, считая входную
последовательность 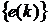 известной
известной
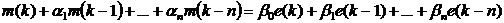 .(5.2)
.(5.2)
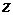 -преобразование данного уравнения
выглядит следующим образом:
-преобразование данного уравнения
выглядит следующим образом:
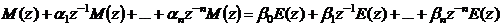 (5.3)
(5.3)
где 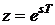 - параметр
- параметр 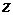 -преобразования,
-преобразования,
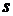 - параметр
преобразования Лапласа,
- параметр
преобразования Лапласа,
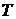 - шаг дискретизации,
- шаг дискретизации,
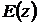 - изображение входного сигнала,
- изображение входного сигнала,
 - изображение выходного сигнала.
- изображение выходного сигнала.
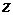 -преобразование основано на теореме
операционного исчисления о запаздывании. Если
-преобразование основано на теореме
операционного исчисления о запаздывании. Если 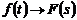 , то
, то 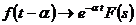 .
.
Уравнение (5.3) можно переписать
следующим образом
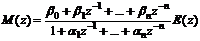 .(5.4)
.(5.4)
Поскольку 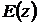 известно,
то
известно,
то 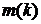 можно
найти, применив обратное
можно
найти, применив обратное 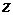 -преобразование
к выражению (5.4).
-преобразование
к выражению (5.4).
Пример 5.2. Рассмотрим разностное
уравнение из предыдущего примера
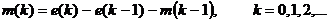
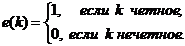
Найдем 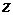 -преобразование
этого уравнения
-преобразование
этого уравнения
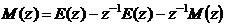 .
.
Отсюда следует
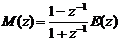 .
.
Изображение входного сигнала можно
представить в виде
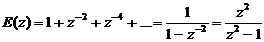 .
.
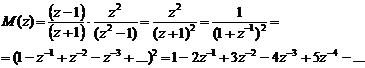
Решетчатая функция равна
коэффициентам полученного ряда
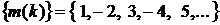 .
.
В программе имитационного
моделирования «Simulink», которая является частью языка технического
программирования «MATLAB», модель дискретной системы
задается в виде рациональной передаточной функции
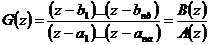 ,(5.4)
,(5.4)
где 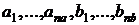 - коэффициенты (вещественные или
комплексные).
- коэффициенты (вещественные или
комплексные).
Пример 5.3. Дискретная система
первого порядка (инерционное звено) имеет передаточную функцию
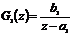 ,(5.5)
,(5.5)
где 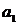 и
и 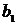 - коэффициенты (
- коэффициенты (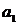 - полюс
системы).
- полюс
системы).
Пример 5.4. Дискретная система
второго порядка имеет передаточную функцию
 ,(5.6)
,(5.6)
где  и
и 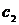 - полюса системы,
- полюса системы, 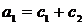 ,
,  .
.
Пример 5.5. Построим в «MATLAB» модель
дискретной системы второго порядка, показанной на рис. 5.2. На рис. 5.3
приведена реакция этой системы на ступенчатый входной сигнал.
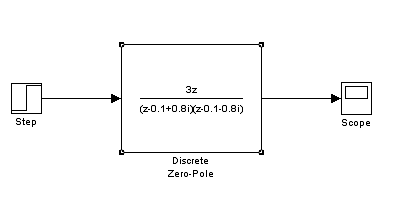
Рис. 5.2. Устойчивая дискретная
система второго порядка
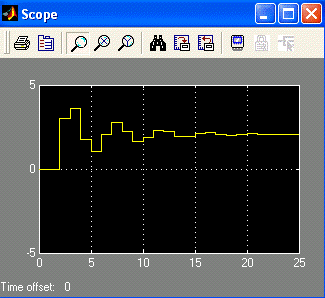
Рис. 5.3. Реакция устойчивой дискретной системы
второго порядка на ступенчатый входной сигнал
Пример 5.6. Построим в «MATLAB»
модель дискретной системы второго порядка, показанной на рис. 5.4. На рис. 5.5
приведена реакция этой системы на ступенчатый входной сигнал.
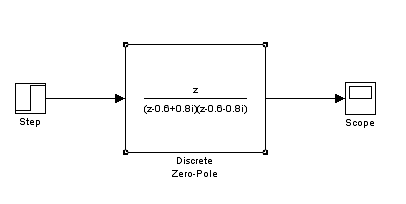
Рис. 5.4. Неустойчивая дискретная система
второго порядка
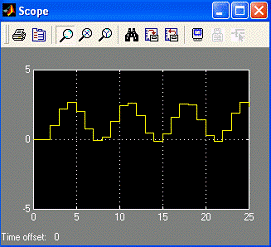
Рис. 5.5. Реакция неустойчивой дискретной
системы второго порядка на ступенчатый входной сигнал
Дискретная система, также как и непрерывная,
может быть представлена в пространстве состояний:
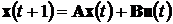 - уравнение
состояния;
- уравнение
состояния;
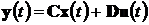 - уравнение наблюдения, где
- уравнение наблюдения, где
· 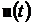 - входной сигнал;
- входной сигнал;
· 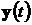 - выходной сигнал;
- выходной сигнал;
· 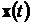 - вектор состояний;
- вектор состояний;
· A, B, C, D -
параметрические матрицы.
Пример 5.7. Система первого порядка может быть
описана такими параметрами:
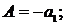
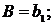
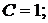
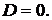 (5.4)
(5.4)
Пример 5.8. Система второго порядка
может иметь следующие матрицы:
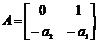 ;
; ;
; ;
;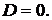 (5.5)
(5.5)
Лекция №6. Нелинейные модели
Моделями нелинейных динамических
систем являются нелинейные дифференциальные (или конечноразностные - для
дискретных объектов) уравнения. Нелинейным дифференциальным уравнением
называется такое уравнение, в котором хотя бы одна производная неизвестной
функции 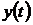 или сама
эта функция представлена во второй либо более высокой степени. Арсенал
нелинейных моделей значительно богаче, чем линейных. Практически каждая
нелинейная система имеет свое индивидуальное математическое описание.
или сама
эта функция представлена во второй либо более высокой степени. Арсенал
нелинейных моделей значительно богаче, чем линейных. Практически каждая
нелинейная система имеет свое индивидуальное математическое описание.
Пример 6.1. Уравнение движения
вертикально стартующей ракеты записывается в виде
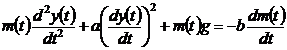 ,(6.1)
,(6.1)
где 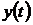 - высота ракеты над точкой старта,
- высота ракеты над точкой старта,
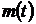 - мгновенная масса ракеты,
- мгновенная масса ракеты,
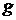 - ускорение свободного падения,
- ускорение свободного падения,
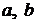 - положительные коэффициенты.
- положительные коэффициенты.
Первый член левой части уравнения
имеет физический смысл силы инерции, второй - силы сопротивления воздуха,
третий - силы тяжести. Правая часть уравнения пропорциональна тяге реактивного
двигателя. В этом уравнении нелинейность определяется квадратичной зависимостью
скорости ракеты.
Нелинейное дифференциальное
уравнение может быть представлено в виде системы дифференциальных уравнений
первого порядка. Это нелинейная модель в пространстве состояний.
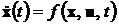 ,(6.2а)
,(6.2а)
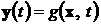 ,(6.2б)
,(6.2б)
где 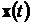 -
- 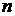 -мерный вектор состояния,
-мерный вектор состояния,
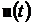 -
- 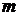 -мерный вектор управления,
-мерный вектор управления,
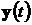 -
- 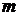 -мерный вектор выходных переменных,
-мерный вектор выходных переменных,
 и
и 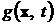 - нелинейные вектор-функции.
Зависимость этих функций от
- нелинейные вектор-функции.
Зависимость этих функций от  отражает действие возмущений. Как и
в системе (4.2) уравнение (6.2а) называется уравнением состояния, а (6.2б) -
уравнением наблюдения.
отражает действие возмущений. Как и
в системе (4.2) уравнение (6.2а) называется уравнением состояния, а (6.2б) -
уравнением наблюдения.
Пример 6.2. Преобразуем уравнение
(6.1) в модель в пространстве состояний. Для этого введем замену переменных: 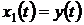 ,
, 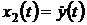 ,
, 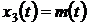 ,
,  . В
результате получим
. В
результате получим
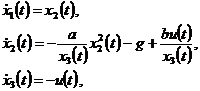 (6.3а)
(6.3а)
 .(6.3б)
.(6.3б)
Здесь (6.3а) - векторное уравнение
состояния, а (6.3б) - уравнение наблюдения. Как можно видеть, не все уравнения
этой системы нелинейные.
Динамические нелинейные системы с
гладкими нелинейностями описываются с помощью рядов Вольтерра (Вито Volterra (3.5.1860,
Анкона, - 11.10.1940, Рим) итальянский математик, профессор университетов в
Пизе, Турине, Риме, член национальной академии деи Линчеи в Риме). Построение
рядов Вольтерра заключается в следующем. Представим нелинейную систему в виде
двух последовательно соединенных блоков - линейного и нелинейного (рис. 6.1).
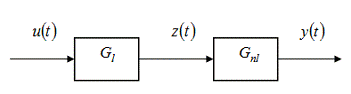
Рис. 6.1. Представление нелинейной
системы в виде последовательного соединения линейного и нелинейного звеньев
Выходной сигнал линейного звена
может быть представлен в виде интеграла свертки
 .(6.4)
.(6.4)
Так как выходной сигнал системы
является функцией  , то,
раскладывая
, то,
раскладывая 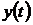 в ряд по
степеням
в ряд по
степеням 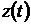 , получим
, получим
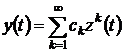 .(6.5)
.(6.5)
Подставляя (6.4) в (6.5), приходим к
выражению
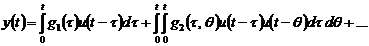 ,(6.6)
,(6.6)
которое и определяет ряд Вольтерра.
В уравнении (6.6) используются обозначения: 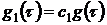 ;
; 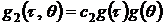 и т.д.
и т.д.
Пример 6.3. Преобразуем уравнение
(6.1) в ряд Вольтерра. Для простоты перейдем от неизвестной функции 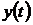 к функции
к функции 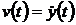 , имеющей
смысл скорости движения ракеты.
, имеющей
смысл скорости движения ракеты.
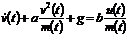 .(6.7)
.(6.7)
Определив функцию 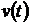 , мы можем
найти и функцию
, мы можем
найти и функцию 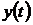 по формуле
по формуле
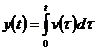 .(6.8)
.(6.8)
Вначале проведем линеаризацию
уравнения (6.7) в окрестности произвольно выбранной точки  . В момент
времени
. В момент
времени  скорость
ракеты будет равна
скорость
ракеты будет равна 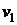 , а ее масса
-
, а ее масса
- 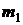 . Введем
новую переменную
. Введем
новую переменную 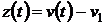 , (
, (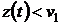 ). Тогда
вместо (6.7) можем записать
). Тогда
вместо (6.7) можем записать
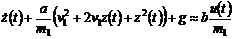 (6.9)
(6.9)
Поскольку приращение скорости 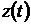 в
окрестности точки
в
окрестности точки  гораздо
меньше
гораздо
меньше 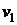 , то членом
, то членом 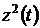 можно
пренебречь. В результате получим линейное дифференциальное уравнение
можно
пренебречь. В результате получим линейное дифференциальное уравнение
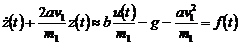 .(6.10)
.(6.10)
Функция  описывает
изменяющуюся во времени сумму приложенных к ракете сил (сила тяги реактивного
двигателя минус вес ракеты, минус сопротивление воздуха). Эта функция может
рассматриваться в качестве преобразованного управляющего воздействия, поскольку
она однозначно зависит от функции
описывает
изменяющуюся во времени сумму приложенных к ракете сил (сила тяги реактивного
двигателя минус вес ракеты, минус сопротивление воздуха). Эта функция может
рассматриваться в качестве преобразованного управляющего воздействия, поскольку
она однозначно зависит от функции 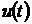 . Решением линейного уравнения
первого порядка (6.10) является свертка
. Решением линейного уравнения
первого порядка (6.10) является свертка
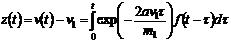 .(6.11)
.(6.11)
Точность данного результата
постепенно снижается при удалении от точки  . Если мы хотим иметь более точное
решение, то должны учесть нелинейность исходного уравнения (6.7). Мы можем
этого добиться с помощью ряда Вольтерра.
. Если мы хотим иметь более точное
решение, то должны учесть нелинейность исходного уравнения (6.7). Мы можем
этого добиться с помощью ряда Вольтерра.
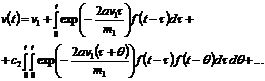 (6.12)
(6.12)
Обычно нелинейные уравнения решаются
численно на компьютере. Для этого исходное дифференциальное уравнение
преобразуют в конечно-разностное уравнение путем перехода от непрерывной модели
к дискретной.
Пример 6.4. Преобразуем уравнение
(6.7) в конечно-разностное уравнение. Для этого представим производную  в виде
разности:
в виде
разности:
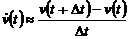 ,(6.13)
,(6.13)
где  - шаг дискретизации. Получим
конечно-разностное уравнение
- шаг дискретизации. Получим
конечно-разностное уравнение
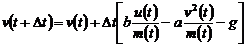 .(6.14)
.(6.14)
Поскольку  , можем
записать:
, можем
записать:
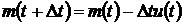 .(6.15)
.(6.15)
Используя начальное условие 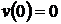 и задав
закон изменения входного управляющего сигнала
и задав
закон изменения входного управляющего сигнала 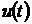 , получим решение
конечно-разностного уравнения (6.14) путем организации итерационного процесса:
, получим решение
конечно-разностного уравнения (6.14) путем организации итерационного процесса:

На рис. 6.2. показаны результаты численного
решения уравнения (6.7) с использованием конечно-разностных уравнений (6.14) и
(6.15). Как можно видеть, реакция системы на ступенчатое входное воздействие
качественно подобна реакции хорошо демпфированной линейной системы второго
порядка. Сразу после запуска ускорение ракеты растет. Однако при увеличении
скорости возрастает также сила сопротивления воздуха, поэтому при постоянном
управляющем воздействии ускорение достигает максимального значения и затем
начинает уменьшаться. Как известно, для выхода на околоземную орбиту ракете
необходимо достичь первой космической скорости. Оптимальная стратегия
управления должна заключаться в том, чтобы достичь этой скорости без превышения
определенного уровня ускорения, которое может губительно сказаться на здоровье
космонавтов. Расход топлива при этом должен быть минимальным.

Рис. 6.2. Результаты численного решения
нелинейного уравнения (6.7) при ступенчатом входном воздействии
Необходимо отметить, что модель (6.7) не
учитывает падения давления воздуха с набором высоты. Поэтому она верно
описывает движение ракеты только в приповерхностном слое атмосферы.
В нелинейных системах вид и качество переходного
процесса существенно зависят от величины входного воздействия и начальных
условий. Увеличение входного воздействия приводит к качественному изменению
переходного процесса: из устойчивого он становится неустойчивым. Изменение
начальных условий также может приводить к существенному отличию в переходных
процессах, например, к возникновению незатухающих колебаний.
Существенная особенность нелинейных систем
заключается в том, что к ним неприменим принцип суперпозиции. Реакцию
нелинейных систем на несколько произвольных внешних воздействий нельзя
рассматривать как сумму составляющих на каждое воздействие отдельно, поскольку
эта реакция зависит от величины входного воздействия и начальных условий.
Характерной особенностью нелинейных систем
является возможность возникновения в них автоколебаний, т.е. таких собственных
периодических процессов, параметры которых (частота и фаза) не зависят от
начальных условий. В нелинейной системе может быть несколько состояний
равновесия, к которым в зависимости от величины начальных условий и входных
воздействий стремятся переходные процессы.
Обычно используют комбинированное описание
нелинейных систем, при котором звенья, уравнения которых допускают
линеаризацию, образуют линейную часть системы, а устройства, поведение которых
описывают нелинейные уравнения, составляют ее нелинейную часть. Часто в
комбинированной системе нелинейные элементы имеют статическую нелинейность, при
которой зависимость между входным и выходным сигналами записывается в виде
алгебраического уравнения.
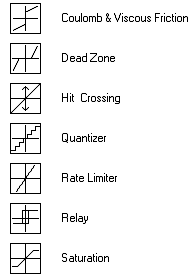
Рис. 6.3. Нелинейные звенья
На рис. 6.3 приведены примеры типовых
статических нелинейных звеньев, используемые в программе «Simulink»
языка технических вычислений «MatLab».
Coulomb & Viscour
Friction (Колебания
Коломбо-Вискура) - расщепляет сигнал на ряд сигналов, колеблющихся в
определенном диапазоне; Dead
Zone (Мертвая зона) -
заменяет значение входного сигнала, лежащее в заданном диапазоне, нулем; Hit
Crossing (Обнаружено
пересечение) - позволяет идентифицировать момент времени, когда входной сигнал
«пересекает» некоторое значение: при появлении такой ситуации на выходе блока
формируется единичный импульсный сигнал; Quantizer
(Квантование сигнала) - преобразует непрерывный сигнал в дискретный; Rate
Limiter (Ограничитель
уровня) - имеет переходный процесс в виде прямой линии (если амплитуда
синусоидального сигнала превысит определенное значение, сигнал на выходе
приобретает треугольную форму); Relay
(Реле) - имитирует работу реле с гистерезисом, если входной сигнал превысит
некоторое пороговое значение, то на выходе блока формируется «разрешающий»
сигнал; Saturation
(Насыщение) - выходной сигнал не может превысить заданный уровень.
Ввиду сложности нелинейных систем на практике
часто используют приближенные способы их описания. К подобным способам
относится метод гармонической линеаризации. В англоязычной литературе его
называют методом описывающей функции.
Этот метод применим к системам, которые содержат
только одну нелинейность. Система такой конфигурации изображена на рис. 6.4.
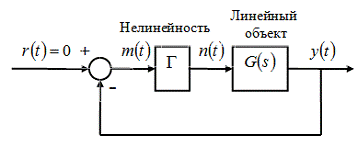
Рис. 6.4. Вариант нелинейной системы
Как можно видеть, входной сигнал системы равен
нулю. Такую систему называют свободной. Если к тому же она является
стационарной, то такую систему называют автономной. Предположим, что входной сигнал
нелинейности является синусоидальным.
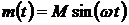 .(6.16)
.(6.16)
Тогда в установившемся режиме сигнал
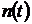 будет
периодическим, но несинусоидальным. Такой сигнал можно представить в виде ряда
Фурье:
будет
периодическим, но несинусоидальным. Такой сигнал можно представить в виде ряда
Фурье:
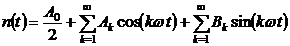 .(6.17)
.(6.17)
Коэффициенты ряда Фурье определяются
выражениями
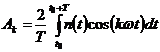 ,(6.18)
,(6.18)
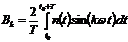 ,(6.19)
,(6.19)
где  - произвольный момент времени. Мы
ограничимся случаем, когда
- произвольный момент времени. Мы
ограничимся случаем, когда  ; это справедливо, если нелинейность
симметрична относительно амплитуды входного сигнала.
; это справедливо, если нелинейность
симметрична относительно амплитуды входного сигнала.
Предположим также, что 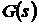 соответствует
фильтру низких частот, так что
соответствует
фильтру низких частот, так что 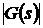 имеет малые значения для высших
гармоник сигнала
имеет малые значения для высших
гармоник сигнала 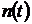 по
сравнению с его значением для основной частоты. Тогда выходной сигнал
по
сравнению с его значением для основной частоты. Тогда выходной сигнал 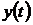 можно
записать в виде
можно
записать в виде
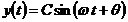 .(6.20)
.(6.20)
Это допущение лежит в основе метода
описывающей функции. Высшими гармониками в 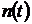 тогда можно пренебречь, поскольку
они оказывают очень малое влияние на
тогда можно пренебречь, поскольку
они оказывают очень малое влияние на 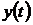 . В результате сигнал
. В результате сигнал 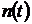 можно
аппроксимировать выражением
можно
аппроксимировать выражением
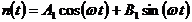 .(6.21)
.(6.21)
Используем следующее представление
 ;
; .
.
Теперь можем записать
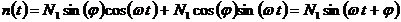 .(6.22)
.(6.22)
Преобразование Лапласа аппроксимации
сигнала 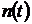 выглядит
следующим образом
выглядит
следующим образом
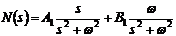 .(6.23)
.(6.23)
Преобразование Лапласа сигнала 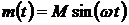 :
:
 .(6.24)
.(6.24)
Отношение изображений  имитирует
«передаточную функцию» нелинейного звена.
имитирует
«передаточную функцию» нелинейного звена.
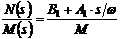 .(6.25)
.(6.25)
Имитация «частотной функции» имеет
следующий вид:
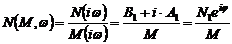 .(6.26)
.(6.26)
Мы получили приближенное описание
нелинейного звена с помощью комплексного коэффициента усиления 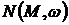 , который,
собственно, и называется описывающей функцией.
, который,
собственно, и называется описывающей функцией.
Описывающая функция 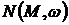 в общем
случае зависит как от амплитуды, так и от частоты входной синусоиды.
в общем
случае зависит как от амплитуды, так и от частоты входной синусоиды.
Лекция №7. Цель управления. Методы
синтеза регуляторов
Системы управления делят на два
класса. Если целью системы является поддержание постоянного значения физической
переменной при наличии возмущений, то ее называют системой регулирования.
Примером может служить система регулирования скорости генераторов переменного
тока в компаниях-производителях электроэнергии. Такая система должна обеспечивать
постоянное значение скорости генераторов, чтобы частота генерируемого
напряжения была равна 50 Гц, независимо от величины нагрузки.
Ко второму классу относятся следящие
системы, или сервомеханизмы. Примером следящей системы может служить система
управления роботом, когда его рука должна воспроизводить некоторую заданную
траекторию в пространстве.
Известный специалист в области
теории автоматического управления Р. Калман дает следующее определение цели
управления: «Цель управления состоит в том, чтобы изменить динамику поведения
физической системы в соответствии с желаниями человека».
Эта цель достигается с помощью
регулятора - элемента системы управления, предназначенного для изменения
динамики системы. На рис. 7.1 показана замкнутая система управления, в которую
включен регулятор.
Регулятор проектируют под конкретный
объект. Чтобы спроектировать регулятор, необходимо иметь модель объекта
(например, в виде передаточной функции). Известны три способа синтеза
регулятора: 1) синтез с помощью корневого годографа; 2) синтез в частотной
области; 3) синтез с помощью современной теории управления (метод назначения
полюсов).
Метод корневого годографа позволяет
разместить в заданных точках два доминирующих полюса системы. Однако положение
остальных полюсов остается неопределенным, что является главным недостатком
этого метода.
Частотные методы очень хороши в
практическом применении, большинство систем управления проектируются именно на
основе различных модификаций этих методов. Отличительной их особенностью
является робастность (дословно «грубость» по-английски), что означает
нечувствительность характеристик замкнутой системы к небольшим погрешностям
модели реальной системы. Эта особенность имеет существенное значение по причине
сложности построения точной модели реальной системы, а также в связи с тем, что
многим системам присущи различного рода нелинейности, осложняющие их анализ и
синтез.

Рис. 7.1. Замкнутая система управления
Метод корневого годографа и частотные методы
называют классическими, или традиционными. В последние годы были разработаны
новые методы синтеза регуляторов, которые принято называть методами современной
теории управления. Современная теория позволяет реализовать заданное положение
всех полюсов передаточной функции замкнутой системы. Расплатой за размещение
всех полюсов является необходимость в точной модели объекта управления и
необходимость в измерении многих переменных в системе. Поскольку методы
современной теории управления в большей степени зависимы от точности модели в
процессе синтеза регулятора, чем частотные методы, то они применяются очень
редко и не всегда приводят к успеху. Однако следует ожидать, что в будущем
современные методы станут более практичными и получат широкое применение.
Корневой годограф - это траектории корней
характеристического уравнения (полюсов передаточной функции) замкнутой
системы при изменении какого-либо параметра системы.
Для изучения метода корневого
годографа будем рассматривать систему общего вида, изображенную на рис. 7.2,
где  -
передаточная функция объекта управления, H(s) -
передаточная функция обратной связи,
-
передаточная функция объекта управления, H(s) -
передаточная функция обратной связи, 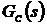 - передаточная функция регулятора.
- передаточная функция регулятора.

Рис. 7.2. Система для изучения
метода корневого годографа
Вначале мы зададим передаточную
функцию регулятора следующим образом: 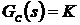 , где
, где 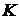 - константа, коэффициент усиления (
- константа, коэффициент усиления (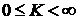 ). Такой
регулятор называется пропорциональным (П-регулятор). Тогда замкнутая система
будет иметь передаточную функцию
). Такой
регулятор называется пропорциональным (П-регулятор). Тогда замкнутая система
будет иметь передаточную функцию
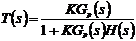 .(7.1)
.(7.1)
Характеристическое уравнение
соответственно равно
 .(7.2)
.(7.2)
Корни характеристического уравнения
являются полюсами системы. Если изменить величину параметра K, то полюса
также поменяют свои значения. При непрерывном изменении K полюса
будут двигаться на комплексной плоскости по определенной траектории.
В общем случае передаточная функция
разомкнутой системы равна: 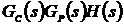 . Корневой годограф можно построить
с помощью программы MATLAB. Для этого нужно набрать команду: rlocus(F(s)), где
. Корневой годограф можно построить
с помощью программы MATLAB. Для этого нужно набрать команду: rlocus(F(s)), где  («root locus» - по
английски означает «корневой годограф»).
(«root locus» - по
английски означает «корневой годограф»).
Пример 7.1. С помощью MATLAB построить
корневой годограф замкнутой системы, если разомкнутая система имеет вид
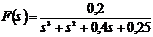 .
.
Решение. Запустив программу MATLAB, набираем
следующие команды:
F=tf([0.2],
[1 1 0.4 0.25]);(F)
Результат показан на рис. 7.3.
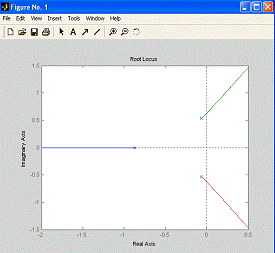
Рис. 7.3. Корневой годограф для
системы из примера
Из рисунка видно, что
характеристическое уравнение замкнутой системы имеет три корня: один
вещественный и два комплексно-сопряженных. Помеченные крестиками точки соответствую
значению параметра K=0. Как можно видеть, при увеличении
параметра комплексные полюса пересекают мнимую ось, так что действительные
части их становятся положительными, а замкнутая система - неустойчивой. Таким
образом, чтобы система оставалась устойчивой, значение K должно быть
небольшим.
Заметим, что корневой годограф
всегда симметричен относительно вещественной оси.
Пример 7.2. Применение метода
корневого годографа рассмотрим на практическом примере синтеза системы
управления положением спутника. Входом модели является момент  ,
развиваемый двигателем, а выходом - угловое положение спутника
,
развиваемый двигателем, а выходом - угловое положение спутника  . Уравнение
объекта имеет вид:
. Уравнение
объекта имеет вид:  - второй
закон Ньютона. Передаточная функция соответственно равна:
- второй
закон Ньютона. Передаточная функция соответственно равна: 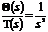 . Примем
передаточную функцию обратной связи равной единице:
. Примем
передаточную функцию обратной связи равной единице: 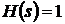 , а
передаточную функцию регулятора:
, а
передаточную функцию регулятора: 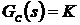 . Тогда разомкнутая система будет
иметь вид:
. Тогда разомкнутая система будет
иметь вид: 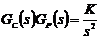 . А
замкнутая соответственно:
. А
замкнутая соответственно:
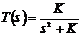 .(7.3)
.(7.3)
Система (7.3) является системой
второго порядка с частотой собственных колебаний 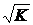 и коэффициентом демпфирования,
равным нулю. Ее полюса равны:
и коэффициентом демпфирования,
равным нулю. Ее полюса равны: 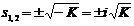 . Поскольку
. Поскольку 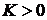 , то это
чисто мнимые полюса. Корневой годограф замкнутой системы показан на рис. 7.4.
, то это
чисто мнимые полюса. Корневой годограф замкнутой системы показан на рис. 7.4.
Как можно видеть, замкнутая система
при всех K>0
находится на границе устойчивости. Следовательно, угловое положение спутника  будет
изменяться по синусоидальному закону при любых значениях K. Совершенно
очевидно, что такая структура системы является неприемлемой.
будет
изменяться по синусоидальному закону при любых значениях K. Совершенно
очевидно, что такая структура системы является неприемлемой.
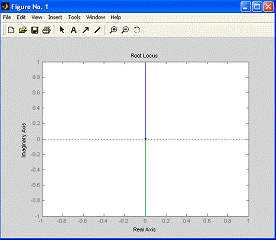
Рис. 7.4. Корневой годограф системы
с П-регулятором
Чтобы получить работоспособную
систему, воспользуемся ПД-регулятором: 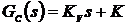 . Обычно говорят, что в такой
системе использована обратная связь по скорости, или по производной. Тогда
разомкнутая система имеет вид
. Обычно говорят, что в такой
системе использована обратная связь по скорости, или по производной. Тогда
разомкнутая система имеет вид
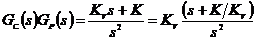 .(7.4)
.(7.4)
Введение обратной связи по скорости
позволяет изменить коэффициент усиления до значения 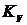 и добавить
в передаточную функцию разомкнутой системы нуль:
и добавить
в передаточную функцию разомкнутой системы нуль: 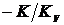 . Если разомкнутая система имеет вид
. Если разомкнутая система имеет вид
 , то
замкнутая соответственно
, то
замкнутая соответственно
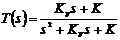 .(7.5)
.(7.5)
Система (7.5) является системой
второго порядка с частотой собственных колебаний 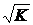 и коэффициентом демпфирования,
равным
и коэффициентом демпфирования,
равным 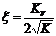 . Если
. Если 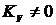 , то
, то 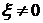 и
переходный процесс будет затухающим. Полюса системы (7.5) равны:
и
переходный процесс будет затухающим. Полюса системы (7.5) равны:
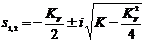 .(7.6)
.(7.6)
Введем обозначения:
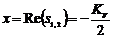 ,
,
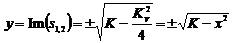 .
.
Поскольку мы имеем теперь не один, а
два параметра 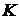 и
и 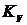 , возникает
вопрос, какой из них следует считать переменной величиной, чтобы получить
корневой годограф замкнутой системы? Важны не абсолютные значения этих величин,
а соотношение между ними, то есть, параметр
, возникает
вопрос, какой из них следует считать переменной величиной, чтобы получить
корневой годограф замкнутой системы? Важны не абсолютные значения этих величин,
а соотношение между ними, то есть, параметр
 .(7.7)
.(7.7)
Заметим, что параметр  равен
абсолютному значению нуля системы. Для полюсов можно записать:
равен
абсолютному значению нуля системы. Для полюсов можно записать: 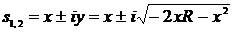 . Тогда:
. Тогда: 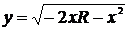 . Возведя
. Возведя 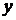 в квадрат,
получим:
в квадрат,
получим: 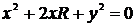 . Прибавив к
левой и правой частям уравнения слагаемое
. Прибавив к
левой и правой частям уравнения слагаемое 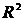 , приходим к формуле круга,
смещенного влево от начала координат на величину
, приходим к формуле круга,
смещенного влево от начала координат на величину  :
:
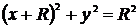 .(7.8)
.(7.8)
Корневой годограф такой системы
изображен на рис. 7.5.
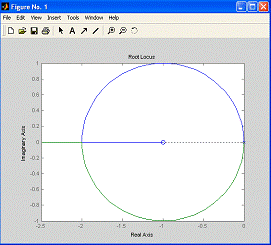
Рис. 7.5. Корневой годограф системы
с ПД-регулятором
На основании данного корневого
годографа можно сделать вывод, что замкнутая система управления с
ПД-регулятором будет устойчивой при всех 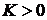 и
и 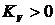 . Поскольку теперь имеются два
варьируемых параметра
. Поскольку теперь имеются два
варьируемых параметра 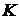 и
и 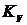 , то корни
характеристического уравнения системы могут быть размещены в любых точках левой
полуплоскости комплексной плоскости.
, то корни
характеристического уравнения системы могут быть размещены в любых точках левой
полуплоскости комплексной плоскости.
Пример 7.3. Замкнутая система
управления описывается передаточной функцией (7.5). Найти значение 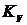 ,
обеспечивающее критическое демпфирование
,
обеспечивающее критическое демпфирование 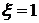 , если частота собственных колебаний
замкнутой системы
, если частота собственных колебаний
замкнутой системы 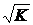 должна быть
равна единице.
должна быть
равна единице.
Решение. 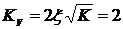 . График
переходной функции системы с такими параметрами показан на рис. 7.6.
. График
переходной функции системы с такими параметрами показан на рис. 7.6.
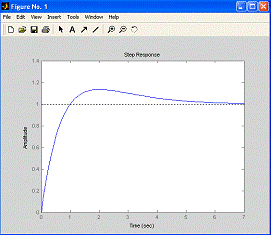
Рис. 7.6. График переходной функции
Лекция №8. Требования к
проектируемой системе управления
К проектируемой системе управления
обычно предъявляют следующие требования:
) система должна быть устойчивой,
запас устойчивости не должен быть ниже заданных норм;
) точность в установившемся режиме
должна быть высокой;
) переходная функция должна иметь
приемлемые характеристики;
) чувствительность к изменению
параметров должна быть низкой;
) способность компенсировать
возмущения, напротив, должна быть высокой.
). Запас устойчивости. В теории
управления помимо понятия устойчивости систем, которая может либо быть, либо не
быть, существует понятие относительной устойчивости. Из двух устойчивых
линейных систем одна может быть более устойчивой, а другая - менее устойчивой.
Относительная устойчивость системы определяется величиной двух параметров:
запасом устойчивости по модулю и запасом устойчивости по фазе.
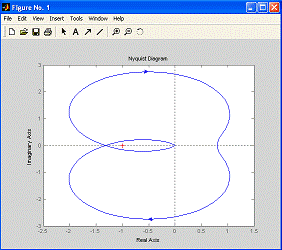
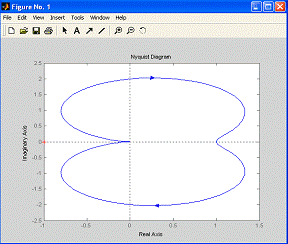
Рис. 8.1. Диаграммы Найквиста
неустойчивой (а) и устойчивой (б) систем
Запас устойчивости системы можно
определить с помощью диаграммы Найквиста или с помощью диаграммы Боде.
Диаграмма Найквиста позволяет определить устойчивость замкнутой системы по ее
частотным характеристикам в разомкнутом состоянии. На рис. 8.1 показаны
диаграммы Найквиста двух разных систем. Левая (а) соответствует системе,
которая в замкнутом виде является неустойчивой («петля» охватывает красный крестик,
находящийся в точке (-1, 0) - это критерий устойчивости Найквиста). Правая (б)
- системе, которая в замкнутом виде устойчивая («петля» не охватывает красный
крестик).
Если информация о передаточной
функции разомкнутой системы  уже введена в программу, то
диаграмму Найквиста можно получить с помощью команды: nyquist(G).
уже введена в программу, то
диаграмму Найквиста можно получить с помощью команды: nyquist(G).
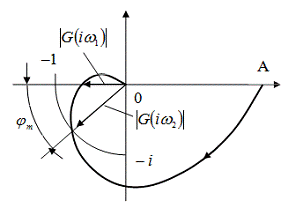
Рис. 8.2. Определение запасов
устойчивости по диаграмме Найквиста
На рис. 8.2 показана нижняя часть
диаграммы Найквиста системы, устойчивой в замкнутом состоянии. Диаграмма
представляет собой график частотной функции 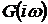 разомкнутой системы в полярных
координатах. Каждая точка жирной линии соответствует определенной частоте
разомкнутой системы в полярных
координатах. Каждая точка жирной линии соответствует определенной частоте 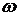 . Точка, для
которой
. Точка, для
которой 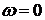 , помечена
буквой «А», стрелкой указано направление возрастания частоты. Длина отрезка,
проведенного от начала координат до произвольной точки диаграммы, равна модулю
частотной функции
, помечена
буквой «А», стрелкой указано направление возрастания частоты. Длина отрезка,
проведенного от начала координат до произвольной точки диаграммы, равна модулю
частотной функции 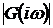 , а угол
между отрезком и горизонтальной осью координат равен фазе частотной функции
, а угол
между отрезком и горизонтальной осью координат равен фазе частотной функции 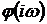 .
.
Напомним, что частотная функция 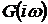 получается
из передаточной функции
получается
из передаточной функции 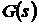 путем
замены аргумента. Вместо параметра преобразования Лапласа
путем
замены аргумента. Вместо параметра преобразования Лапласа 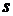 используется
аргумент:
используется
аргумент: 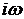 , где
, где 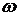 - круговая
частота гармонических колебаний,
- круговая
частота гармонических колебаний, 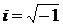 - мнимая единица.
- мнимая единица.
Очевидно, что запасом устойчивости
обладают только устойчивые системы. На рис. 8.2 видно, что точка пересечения
графиком горизонтальной линии с координатой: 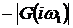 находится правее «роковой» точки
-1, так что данная система устойчива. Запас устойчивости по модулю в абсолютных
единицах определяется выражением:
находится правее «роковой» точки
-1, так что данная система устойчива. Запас устойчивости по модулю в абсолютных
единицах определяется выражением: 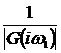 , а запас по фазе - равен углу
, а запас по фазе - равен углу  (см. рис.
8.2).
(см. рис.
8.2).
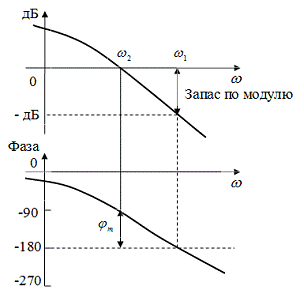
Рис. 8.3. Определение запасов
устойчивости по диаграмме Боде
Запасы устойчивости по модулю и по
фазе замкнутой системы можно определить также с помощью диаграммы Боде (рис.
8.3). Запас по модулю определяется на частоте, при которой  . Эта
частота на диаграмме Боде (рис. 8.3) обозначена как
. Эта
частота на диаграмме Боде (рис. 8.3) обозначена как  . Запас по модулю
принято выражать в децибелах, то есть, как
. Запас по модулю
принято выражать в децибелах, то есть, как 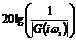 . Запас по фазе определяется на
частоте
. Запас по фазе определяется на
частоте 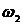 , на которой
, на которой
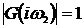 (или 0 дБ).
Запас по фазе
(или 0 дБ).
Запас по фазе  есть
разность между
есть
разность между 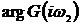 и
и 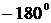 , как
показано на рисунке.
, как
показано на рисунке.
Запасы устойчивости необходимы для
того, чтобы иметь приемлемый вид переходной функции. Второй мотив стремления к
большим запасам устойчивости связан с неточностью моделирования. Поскольку
модели, на основе которых решается задача синтеза, в какой-то степени являются
неточными, то запасы устойчивости можно рассматривать также как гарантию
безопасной работы системы.
Эмпирическим путем установлено, что
запас по модулю в 8 дБ (что соответствует абсолютному значению в 2,51) обычно
является достаточным для систем управления, тогда как запас в 5 дБ (абсолютное
значение 1,78) недостаточен. Аналогично, запас по фазе 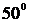 обычно
оказывается приемлемым, а запас
обычно
оказывается приемлемым, а запас 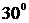 недостаточен.
недостаточен.
). Точность в установившемся режиме.
Точность работы системы управления в установившемся режиме достигается с
помощью следующего правила. Частотная функция замкнутой системы определяется
выражением
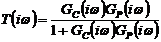 .(8.1)
.(8.1)
Если на некоторой
частоте  коэффициент
усиления разомкнутой системы
коэффициент
усиления разомкнутой системы 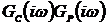 достаточно велик, то коэффициент
усиления замкнутой системы приблизительно равен единице. Таким образом, чтобы
ошибка была малой на некоторых частотах, соответствующий коэффициент усиления
разомкнутой системы должен быть достаточно большим. Если мы сумеем
спроектировать систему, имеющую большой коэффициент усиления в широком
диапазоне частот, то эта система очень хорошо будет отслеживать сигналы, спектр
которых расположен в этом диапазоне.
достаточно велик, то коэффициент
усиления замкнутой системы приблизительно равен единице. Таким образом, чтобы
ошибка была малой на некоторых частотах, соответствующий коэффициент усиления
разомкнутой системы должен быть достаточно большим. Если мы сумеем
спроектировать систему, имеющую большой коэффициент усиления в широком
диапазоне частот, то эта система очень хорошо будет отслеживать сигналы, спектр
которых расположен в этом диапазоне.
). Переходная функция. На рис. 8.4
показана типичная переходная функция системы при наличии пары доминирующих
полюсов. Основными параметрами, которые могут представлять интерес, являются:
время нарастания 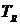 ,
максимальное значение переходной функции
,
максимальное значение переходной функции 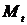 (или перерегулирование в
процентах), и время установления
(или перерегулирование в
процентах), и время установления  .
.
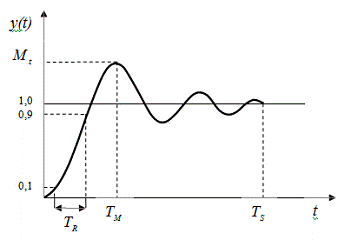
Рис. 8.4. Типичная переходная
функция
Время нарастания  тесно
связано с полосой пропускания замкнутой системы. В общем случае, если нам нужно
уменьшить время нарастания, скажем, в 2 раза, то необходимо приблизительно в 2
раза увеличить полосу пропускания замкнутой системы. Если мы хотим уменьшить
время установления
тесно
связано с полосой пропускания замкнутой системы. В общем случае, если нам нужно
уменьшить время нарастания, скажем, в 2 раза, то необходимо приблизительно в 2
раза увеличить полосу пропускания замкнутой системы. Если мы хотим уменьшить
время установления  , то полюсы
передаточной функции замкнутой системы необходимо сдвинуть влево на
, то полюсы
передаточной функции замкнутой системы необходимо сдвинуть влево на 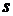 -плоскости,
уменьшив таким образом постоянные времени. Сдвиг полюсов замкнутой системы
влево приводит также к увеличению полосы пропускания. Следовательно, чтобы
сократить длительность переходного процесса в системе, необходимо увеличить ее
полосу пропускания.
-плоскости,
уменьшив таким образом постоянные времени. Сдвиг полюсов замкнутой системы
влево приводит также к увеличению полосы пропускания. Следовательно, чтобы
сократить длительность переходного процесса в системе, необходимо увеличить ее
полосу пропускания.
Перерегулирование в переходной
функции связано с резонансом замкнутой системы, который проявляется в виде
максимума ее амплитудно-частотной характеристики (см. рис. 8.5).
Замкнутая система может обладать
резонансными свойствами, только если запасы устойчивости являются малыми.
Следовательно, для уменьшения перерегулирования необходимо увеличивать запасы
устойчивости. Перерегулирование обычно более чувствительно к запасу
устойчивости по фазе, чем по модулю. Требования к ограничению влияния
резонансных свойств могут быть заданы в виде процентного перерегулирования
переходной функции, в виде максимально допустимого значения
амплитудно-частотной характеристики замкнутой системы, отмеченного как 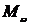 на рис.
8.5, или в виде запаса устойчивости по фазе.
на рис.
8.5, или в виде запаса устойчивости по фазе.

Рис. 8.5. Частотная характеристика замкнутой
системы
). Чувствительность. Обычно параметры объекта
управления изменяются в зависимости от температуры, влажности, срока службы и
т.д. Чувствительность передаточной функции замкнутой системы к изменению
передаточной функции объекта, представленная в зависимости от частоты,
описывается выражением
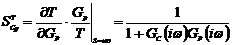 .(8.2)
.(8.2)
Отсюда видно, что для того, чтобы
эта чувствительность была малой в заданном диапазоне частот, модуль частотной
функции разомкнутой системы в этом диапазоне должен быть достаточно большим.
Обычно это стремятся сделать путем увеличения коэффициента усиления в контуре.
Но это, в свою очередь, уменьшает запасы устойчивости, поэтому, как правило,
приходится искать компромисс между низкой чувствительностью и достаточными
запасами устойчивости.
). Компенсация возмущений. Модель
замкнутой системы при наличии возмущений представлена на рис. 8.6.

Рис. 8.6. Система при наличии
возмущений
На этом рисунке 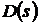 обозначает
возмущение (случайный нежелательный входной сигнал). Например, это может быть
восходящий поток воздуха, действующий на пассажирский авиалайнер. Выходной
сигнал такой системы может быть записан в виде
обозначает
возмущение (случайный нежелательный входной сигнал). Например, это может быть
восходящий поток воздуха, действующий на пассажирский авиалайнер. Выходной
сигнал такой системы может быть записан в виде
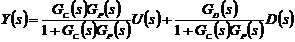 .(8.3)
.(8.3)
Для того чтобы уменьшить влияние
возмущения на выход, необходимо сделать коэффициент усиления разомкнутой
системы 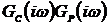 достаточно
большим в диапазоне частот, занимаемом возмущениями
достаточно
большим в диапазоне частот, занимаемом возмущениями 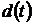 . Если это
невозможно, то коэффициент усиления разомкнутой системы должен быть сделан как
можно большим в как можно большем диапазоне частот. Однако это приводит к
уменьшению запасов устойчивости.
. Если это
невозможно, то коэффициент усиления разомкнутой системы должен быть сделан как
можно большим в как можно большем диапазоне частот. Однако это приводит к
уменьшению запасов устойчивости.
Лекция № 9. Синтез ПИД-регулятора
Регуляторы в системах
автоматического управления в общем случае бывают различными. Однако чаще всего
используется ПИД-регулятор, осуществляющий пропорционально-интегрально-дифференциальный
закон управления. Передаточная функция ПИД-регулятора имеет вид
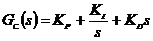 .(9.1)
.(9.1)
Интегральная составляющая
соответствует отставанию по фазе, а дифференциальная составляющая - опережению по
фазе. Следовательно, интегральная составляющая играет роль в области низких
частот: 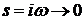 , а
дифференциальная составляющая - в области высоких частот:
, а
дифференциальная составляющая - в области высоких частот: 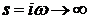 . Диаграмма
Боде для ПИД-регулятора представлена на рис. 9.1.
. Диаграмма
Боде для ПИД-регулятора представлена на рис. 9.1.
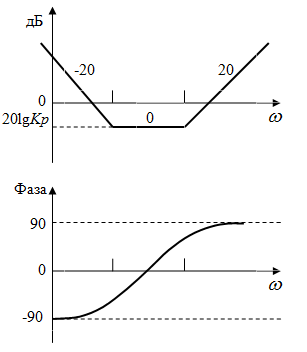
Рис. 9.1. Диаграмма Боде для
ПИД-регулятора
Пропорциональный канал регулятора
образует на выходе составляющую, которая является функцией текущего состояния
системы. Поскольку выход интегратора зависит от входного сигнала во все
предшествующие моменты времени, то эта составляющая выходного сигнала
регулятора определяется прошлым состоянием системы. Она не может измениться
мгновенно и поэтому характеризует инерционность системы. Выход дифференциатора
пропорционален скорости изменения входного сигнала, поэтому данный канал можно
рассматривать в качестве предсказателя будущего состояния системы.
Дифференциальная составляющая выхода регулятора способствует улучшению вида
переходного процесса в системе, сокращая его длительность. Однако, если входной
сигнал «засорен» высокочастотным шумом, то это предсказание может привести к
нежелательным результатам. Итак, ПИД-регулятор можно рассматривать как
устройство, вырабатывающее сигнал, являющийся функцией прошлого, настоящего и
прогнозируемого будущего состояния системы.
Диаграмма Найквиста для
скорректированной системы при частоте 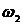 проходит через точку
проходит через точку  , где
, где  - запас по
фазе. Иначе говоря
- запас по
фазе. Иначе говоря
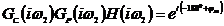 .(9.2)
.(9.2)
Если аргумент функции 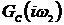 обозначить
через
обозначить
через  , то
согласно (9.2):
, то
согласно (9.2):
 .(9.3)
.(9.3)
Из (9.1) и (9.2) следует
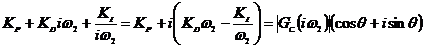 ,(9.4)
,(9.4)
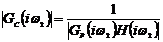 .(9.5)
.(9.5)
Приравняв в (9.4) действительные
части, получим:
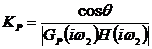 ,(9.6)
,(9.6)
а приравняв мнимые части:
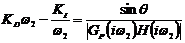 .(9.7)
.(9.7)
Частоту 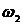 можно
рассчитать, считая заданным время установления
можно
рассчитать, считая заданным время установления 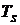 :
:
 .(9.8)
.(9.8)
Соотношение (9.8) является точным
только для типовой системы второго порядка. Для систем более высокого порядка
оно может служить лишь приближением, причем иногда даже очень грубым.
Коэффициент  задается,
исходя из требований к качеству системы в установившемся режиме.
задается,
исходя из требований к качеству системы в установившемся режиме.
На рис. 9.1 видно, что фазовый
сдвиг, создаваемый регулятором на частоте 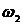 , может быть как положительным, так
и отрицательным, а модуль частотной функции
, может быть как положительным, так
и отрицательным, а модуль частотной функции 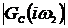 может быть как больше, так и меньше
единицы. Поэтому единственным ограничением на выбор частоты
может быть как больше, так и меньше
единицы. Поэтому единственным ограничением на выбор частоты 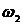 является
то, что абсолютное значение угла
является
то, что абсолютное значение угла  должно быть меньше, чем
должно быть меньше, чем 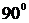 .
.
Коэффициенты  и
и  являются
взаимозависимыми. Если увеличить
являются
взаимозависимыми. Если увеличить  , то и
, то и  также надо
будет увеличить. Увеличение
также надо
будет увеличить. Увеличение  может иметь два последствия.
Во-первых, в систему вносится большее отставание по фазе, поэтому переходная
функция будет иметь большее перерегулирование и более длительное время
установления. Во-вторых, система может стать условно устойчивой, т.е. система
остается устойчивой, но она может потерять устойчивость как при увеличении, так
и при уменьшении коэффициента усиления.
может иметь два последствия.
Во-первых, в систему вносится большее отставание по фазе, поэтому переходная
функция будет иметь большее перерегулирование и более длительное время
установления. Во-вторых, система может стать условно устойчивой, т.е. система
остается устойчивой, но она может потерять устойчивость как при увеличении, так
и при уменьшении коэффициента усиления.
Некоторые часто встречающиеся
нелинейности эффективно уменьшают коэффициент усиления при больших входных
сигналах. Одной из наиболее распространенных нелинейностей является
нелинейность типа «ограничение». При малых входных сигналах такой элемент
работает в линейном режиме и имеет коэффициент усиления К. Однако при больших
входных сигналах элемент насыщается и его эквивалентный коэффициент усиления
падает. Если такой элемент входит в состав условно устойчивой системы, то при
больших сигналах система может стать неустойчивой.
Пример 9.1. Осуществим синтез
ПИД-регулятора для системы, которая в разомкнутом состоянии имеет передаточную
функцию
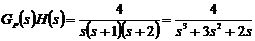 .
.
Исходные параметры, определяющие
требование к системе, следующие: запас по фазе 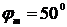 , время установления
, время установления  с.
с.
Решение: Вначале определим частоту,
на которой обеспечивается необходимый запас по фазе:
 .
.
С помощью «MATLAB» определим
модуль и аргумент передаточной функции 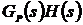 :
:
w2=1.7;=tf([4],
[1 3 2 0]);=evalfr(Gp, i*w2);=abs(Gpiw2), phase=angle(Gpiw2)*180/pi
В результате выполнения программы
получим:
mag =0.4545
phase =170.1010
Согласно (9.3):
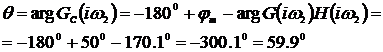
С помощью (9.6) находим
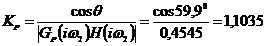 .
.
Формула (9.7) позволяет найти сумму:
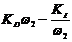 .
.
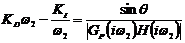 .
.
Чтобы подобрать оптимальные значения
коэффициентов  и
и  , сравним
реакции замкнутой системы на ступенчатый входной сигнал при следующих значениях
коэффициента
, сравним
реакции замкнутой системы на ступенчатый входной сигнал при следующих значениях
коэффициента  : 0,005;
0,05; 0,5. Для этого используем программу «MATLAB»:
: 0,005;
0,05; 0,5. Для этого используем программу «MATLAB»:
=[0.005 0.05 0.5]; phim=50;
w2=1.7;=tf([0 0 0 4], [1 3 2 0]);
for
k=1:3=evalfr(Gp,
i*w2);mag=abs(Gpiw2);=-pi+phim/57.296-angle(Gpiw2);=cos(theta)/Gpiw2mag;=sin(theta)/(w2*Gpiw2mag)+KI(k)/w2^2;
[KP, KI(k),
KD]=tf([0 KD KP KI(k)], [0 0 1 0]);=minreal(Gc*Gp/(1+Gc*Gp));(T), pause
[Gm, Pm,
Wcg, Wcp]=margin...
(Gc*Gp), pause
В результате расчетов получим, что
если  , то
, то 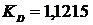 ; если
; если 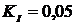 , то
, то 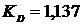 ; если
; если 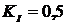 , то
, то 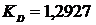 . Запас
устойчивости по фазе во всех трех случаях одинаков и на частоте
. Запас
устойчивости по фазе во всех трех случаях одинаков и на частоте  равен
49,9998 градусам. Переходные функции замкнутой системы для различных значений
коэффициента
равен
49,9998 градусам. Переходные функции замкнутой системы для различных значений
коэффициента  показаны на
рис. 9.2.
показаны на
рис. 9.2.
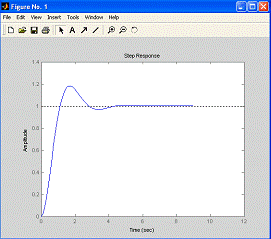
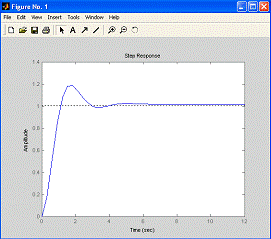
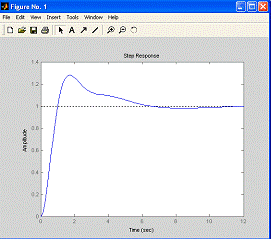
Рис. 9.2. Переходные функции
замкнутой системы
Графики показывают, что время
установления в 4 секунды обеспечивается только при  . Поэтому
окончательно принимаем значения коэффициентов:
. Поэтому
окончательно принимаем значения коэффициентов: 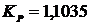 ;
;  ;
; 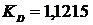 . Таким образом, синтезированный
регулятор имеет передаточную функцию:
. Таким образом, синтезированный
регулятор имеет передаточную функцию:
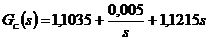 .
.
Построим диаграммы Боде для исходной
системы и для системы с регулятором. Для этого в системе «MATLAB» необходимо
набрать следующую программу:
KP=1.1035; KI=0.005; KD=1.1215;
Gp=tf([4],
[1 3 2 0]);=tf([KD KP KI], [1 0]);=Gp*Gc;(Gp), hold on
bode(Gpc), hold on
Полученные диаграммы показаны на
рис. 9.3.

Рис. 9.3. Диаграмма Боде исходной
системы (синяя линия) и системы с регулятором (зеленая линия)
Как можно видеть, регулятор повысил
коэффициент усиления на низких частотах и расширил полосу пропускания
разомкнутой системы. А главное - увеличил запасы устойчивости по модулю и по
фазе.
Лекция № 10. Синтез системы в
пространстве состояний
Классические процедуры синтеза
основаны на использовании передаточной функции, синтез путем размещения полюсов
основан на использовании модели в переменных состояния. Модель линейной
непрерывной системы в переменных состояния имеет вид:
 (10.1)
(10.1)
Мы ограничимся случаем систем с
одним входом и одним выходом, поэтому 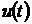 ,
, 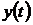 - это скалярные переменные.
Предположим, что вход системы, обозначаемый как
- это скалярные переменные.
Предположим, что вход системы, обозначаемый как  , равен нулю (см. рис. 10.1).
, равен нулю (см. рис. 10.1).

Рис. 10.1. Синтез системы на основе
размещения полюсов
В общем случае вход объекта
управления 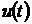 является
функцией переменных состояния
является
функцией переменных состояния
 .(10.2)
.(10.2)
Это уравнение называют законом
управления. При синтезе путем размещения полюсов закон управления определяется
как
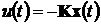 ,(10.3)
,(10.3)
где 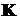 есть вектор постоянных
коэффициентов размерности
есть вектор постоянных
коэффициентов размерности 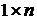 . Далее мы
покажем, что этот закон управления позволяет разместить все полюсы замкнутой
системы в любых заданных точках. Закон управления можно записать в виде:
. Далее мы
покажем, что этот закон управления позволяет разместить все полюсы замкнутой
системы в любых заданных точках. Закон управления можно записать в виде:
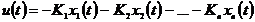 .(10.4)
.(10.4)
Отсюда видно, что сигнал,
поступающий на вход объекта, представляет собой линейную комбинацию всех
переменных состояния.
Задача синтеза заключается в
определении желаемого положения корней характеристического уравнения системы и
нахождении коэффициентов 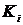 ,
обеспечивающих заданное размещение корней.
,
обеспечивающих заданное размещение корней.
Поскольку вход системы равен нулю,
то ее назначение сводится к тому, чтобы поддерживать равной нулю выходную
переменную. На практике система подвержена влиянию возмущений, которые
стремятся сделать выход объекта отличным от нуля. Цель обратной связи - вернуть
значение выходной переменной (и всех переменных состояния) к нулю определенным,
наперед заданным, образом. Система такого типа (при входном сигнале, равном
нулю) обычно называется регулятором состояния.
Сначала мы рассмотрим метод
размещения полюсов на примере, а затем сформулируем общие принципы процедуры
синтеза.
Пример 10.1. В примере 7.2 мы
получили передаточную функцию, описывающую движение спутника в виде: 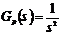 . Уравнения
состояния можно записать так
. Уравнения
состояния можно записать так
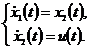 (10.5)
(10.5)
В матричном виде они будут выглядеть
следующим образом
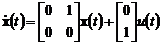 .(10.6)
.(10.6)
Уравнение наблюдения:
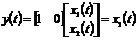 .(10.7)
.(10.7)
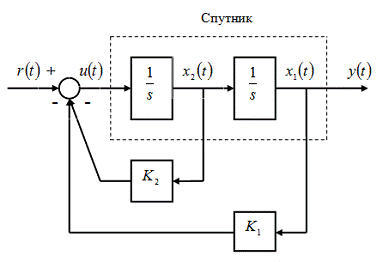
Рис. 10.2. Схема моделирования
системы управления спутником
В соответствии с формулой (10.4) и
рис. 10.2 сигнал на входе объекта равен
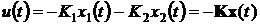 .(10.8)
.(10.8)
Уравнения состояния для замкнутой
системы имеют вид
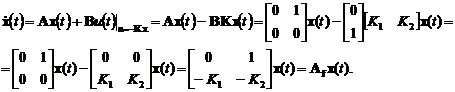
Матрица  - это
матрица коэффициентов замкнутой системы. Характеристическое уравнение замкнутой
системы имеет вид
- это
матрица коэффициентов замкнутой системы. Характеристическое уравнение замкнутой
системы имеет вид
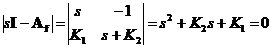 .(10.9)
.(10.9)
Предположим, что условия синтеза
системы требуют, чтобы два корня характеристического уравнения были расположены
в точках 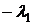 и
и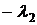 .
.
Присвоив желаемому
характеристическому уравнению обозначение 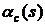 , запишем:
, запишем:
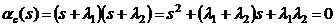 .(10.10)
.(10.10)
Синтез заключается в выборе таких
коэффициентов 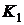 и
и 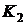 в уравнении
(10.9), которые равнялись бы соответствующим коэффициентам в уравнении (10.10).
Таким образом
в уравнении
(10.9), которые равнялись бы соответствующим коэффициентам в уравнении (10.10).
Таким образом
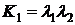 ,
,
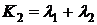 .
.
Из этого примера следует, что
надлежащим выбором коэффициентов обратной связи можно разместить корни
характеристического уравнения модели системы (полюсы передаточной функции
замкнутой системы) в любых заданных точках на 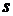 -плоскости. Заметим, что если
-плоскости. Заметим, что если 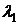 и
и 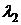 являются
комплексными, то
являются
комплексными, то 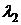 должен быть
комплексно-сопряженным корню
должен быть
комплексно-сопряженным корню 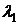 . Поэтому коэффициенты
. Поэтому коэффициенты 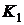 и
и 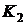 всегда
вещественны.
всегда
вещественны.
Теперь изложим общие принципы
синтеза. Для линейной стационарной системы уравнения состояния объекта имеют
вид:
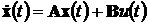 . (10.11)
. (10.11)
Закон управления выбирается так, что
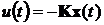 . (10.12)
. (10.12)
Подставляя (10.12) в (10.11),
получим
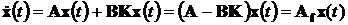 , (10.13)
, (10.13)
где 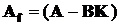 есть матрица коэффициентов
замкнутой системы. Тогда можно записать характеристическое уравнение замкнутой
системы
есть матрица коэффициентов
замкнутой системы. Тогда можно записать характеристическое уравнение замкнутой
системы
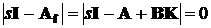 . (10.14)
. (10.14)
Предположим, что по условиям синтеза
корни характеристического уравнения должны иметь значения  . Обычно
исходят из следующего условия:
. Обычно
исходят из следующего условия:
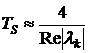 ,
,
где 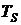 - время установления переходных
процессов в системе. Из всех полюсов в качестве
- время установления переходных
процессов в системе. Из всех полюсов в качестве 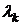 выбирается тот, у которого модуль
действительной части имеет наименьшее значение. Желаемое характеристическое
уравнение системы тогда можно записать в виде
выбирается тот, у которого модуль
действительной части имеет наименьшее значение. Желаемое характеристическое
уравнение системы тогда можно записать в виде
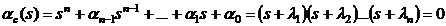 .(10.15)
.(10.15)
В соответствии с процедурой синтеза
путем размещения полюсов необходимо найти такую матрицу 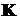 , чтобы
выражения (10.14) и (10.15) были равны друг другу
, чтобы
выражения (10.14) и (10.15) были равны друг другу
 .(10.16)
.(10.16)
Это уравнение содержит 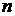 неизвестных
неизвестных
 .
Приравнивая в этом уравнении коэффициенты при одинаковых степенях
.
Приравнивая в этом уравнении коэффициенты при одинаковых степенях 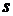 , мы получим
, мы получим
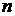 уравнений
относительно
уравнений
относительно 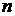 неизвестных.
Эти уравнения являются линейными. Решив их, мы получим элементы матрицы
неизвестных.
Эти уравнения являются линейными. Решив их, мы получим элементы матрицы  .
.
В 1972 году Аккерман вывел формулу
для вычисления матрицы  :
:
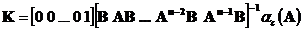 ,(10.17)
,(10.17)
где 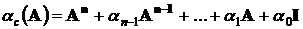 - матричный полином, образованный
путем использования коэффициентов желаемого характеристического уравнения
- матричный полином, образованный
путем использования коэффициентов желаемого характеристического уравнения 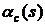 .
.
Матрица 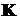 может быть
вычислена на компьютере по формуле (10.17). В «MATLAB» матрица
может быть
вычислена на компьютере по формуле (10.17). В «MATLAB» матрица 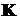 вычисляется
с помощью команды:
вычисляется
с помощью команды:
K=acker(A, B, Pp).
Операндами этой команды являются
матрицы A и B из
уравнения состояния системы, а также Pp -
вектор-строка желаемого расположения полюсов системы управления.
Пример 10.2. Вначале аналитически
рассчитаем элементы матрицы 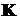 по формуле Аккермана для системы
управления положением спутника. Модель системы в переменных состояния имеет вид
по формуле Аккермана для системы
управления положением спутника. Модель системы в переменных состояния имеет вид
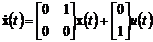 .
.
Значит: 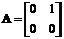 ,
, 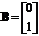 ,
,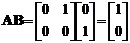 .
.
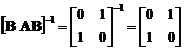 .
.
Образуем матричный полином
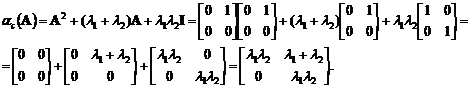
Применим формулу Аккермана
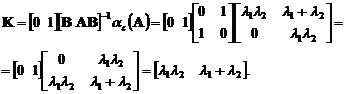
Пример 10.3. На рис. 10.3 приведена
схема практической реализации системы управления спутником. Предположим, что по
условиям синтеза необходимо получить критически демпфированную систему со
временем установления 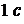 . Поскольку
время установления приблизительно в четыре раза больше постоянной времени
объекта, постоянная времени равна:
. Поскольку
время установления приблизительно в четыре раза больше постоянной времени
объекта, постоянная времени равна: 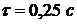 . Следовательно, два полюса должны
быть расположены в точке
. Следовательно, два полюса должны
быть расположены в точке 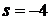 , то есть:
, то есть: 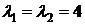 .
.
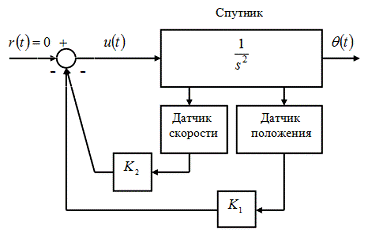
Рис. 10.3. Система управления
спутником
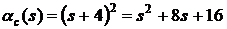 .
.
На основании предыдущего примера
требуемые коэффициенты обратной связи равны
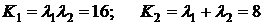 .
.
Соответствующая передаточная функция
замкнутой системы равна
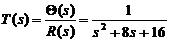 .
.
С помощью следующей программы мы
можем рассчитать реакцию системы на начальные условия 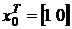 , при
коэффициентах демпфирования
, при
коэффициентах демпфирования 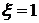 и (для сравнения)
и (для сравнения) 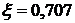 .
.
A=[0 1; 0
0]; B=[0; 1]; C=[1 0]; D=0;=[-4 -4];=acker(A, B, Pp)p1=ss((A-B*K), B, C,
D);=[-4+4*i -4-4*i];=acker(A, B, Pp), pausep2=ss((A-B*K), B, C, D);(e10p1, [1;
0]), hold on(e10p2, [1; 0]), hold on
Результат расчетов показан в виде
графика на рис. 10.4.

Рис. 10.4. Реакция системы на
начальные условия
Синяя линия соответствует 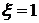 , а зеленая
, а зеленая 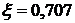 . В
последнем случае корни характеристического уравнения должны быть равны
. В
последнем случае корни характеристического уравнения должны быть равны 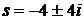 , и
, и
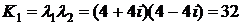 ,
,
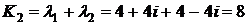 .
.
Как можно видеть, выходной сигнал
при 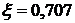 затухает
гораздо быстрее и имеет очень малое перерегулирование. Этим объясняется
популярность выбора значения
затухает
гораздо быстрее и имеет очень малое перерегулирование. Этим объясняется
популярность выбора значения 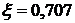 для доминирующих полюсов системы.
для доминирующих полюсов системы.
Из последнего примера, казалось бы,
следует, что мы можем выбрать вещественную часть корней сколь угодно большой,
чтобы повысить быстродействие системы. В модели системы мы действительно можем
это сделать. Однако для того, чтобы уменьшить постоянную времени объекта,
необходимо увеличивать коэффициент обратной связи. И это не случайно, так как
чтобы увеличить скорость реакции объекта, на его вход должен поступать большой
сигнал. А если возрастают амплитуды сигналов в системе, то велика вероятность
того, что она перейдет в нелинейный режим работы. При очень больших сигналах
практически любая реальная система будет работать как нелинейная.
Следовательно, линейная модель, которая использовалась при синтезе, больше не
будет точно отображать поведение реальной системы и ее истинные характеристики.
Лекция №11. Оценка состояния и
синтез наблюдателя
Если все переменные состояния
объекта могут быть измерены, то говорят, что в системе существует полная
обратная связь по состоянию. Во многих системах второго порядка используется
обратная связь и по положению, и по скорости. Следовательно, они являются
системами с полной обратной связью по состоянию. Однако известно много систем,
которые невозможно точно описать системами первого или второго порядков. В
большинстве таких систем невозможно измерить все переменные состояния, однако
их можно оценить в результате наблюдения за поведением объекта. На рис. 11.1
приведена блок-схема процесса оценки состояния.

Рис. 11.1. Оценка состояния
Устройство оценки состояния
называется наблюдателем. Наблюдатель получает информацию о входах и выходах
системы. На основании этой информации он формирует оценку неизвестного
состояния системы. Наблюдатель имеет ту же динамику, что и сама система. Его
моделью является следующее дифференциальное уравнение первого порядка
 .(11.1)
.(11.1)
Для простоты мы рассматриваем
систему с одним входом и одним выходом, поэтому 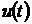 и
и 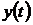 - скалярные величины. Однако
наблюдатель можно построить и для более сложных систем со многими входами и
выходами. Матрицы
- скалярные величины. Однако
наблюдатель можно построить и для более сложных систем со многими входами и
выходами. Матрицы 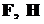 и
и  должны быть
выбраны таким образом, чтобы вектор
должны быть
выбраны таким образом, чтобы вектор 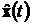 давал точную оценку
давал точную оценку 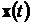 . Тогда в
системе управления вектор
. Тогда в
системе управления вектор 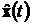 используется
для формирования сигнала обратной связи
используется
для формирования сигнала обратной связи 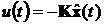 .
.
Уравнения для определения матриц 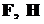 и
и 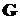 могут быть
получены разными способами. Мы воспользуемся методом передаточной функции.
Передаточная функция от входа
могут быть
получены разными способами. Мы воспользуемся методом передаточной функции.
Передаточная функция от входа 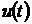 к переменной состояния наблюдателя
к переменной состояния наблюдателя 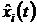 должна быть
равна передаточной функции от
должна быть
равна передаточной функции от 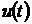 к переменной состояния
к переменной состояния 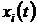 для всех
для всех 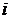 , то есть
, то есть
 .(11.2)
.(11.2)
Преобразование Лапласа уравнений
состояния и наблюдения
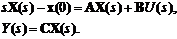
Игнорируя начальные условия, решим
эти уравнения относительно 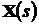 :
:
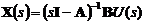 .(11.3)
.(11.3)
Преобразуя по Лапласу уравнение
наблюдателя (11.1) и игнорируя начальные условия, получим
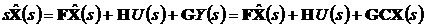 .(11.4)
.(11.4)
Отсюда, учитывая (11.3), выразим 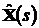
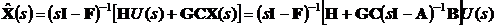 .
.
Из равенства передаточных функций
(11.2) следует
 .
.
Группируя коэффициенты при члене 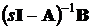 , получим
, получим
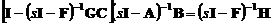 .
.
Затем из левой стороны этого
уравнения вынесем 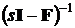 в качестве
сомножителя
в качестве
сомножителя
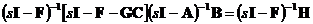 .
.
Теперь можем записать
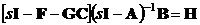 .
.
Окончательно получим
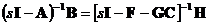 .
.
Это уравнение удовлетворяется, если
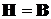 ,(11.5)
,(11.5)
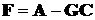 .(11.6)
.(11.6)
Теперь уравнение наблюдателя (11.1)
мы можем записать в следующем виде
 ,(11.7)
,(11.7)
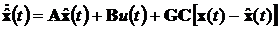 .(11.8)
.(11.8)
Из уравнения (11.8) следует, что
если ошибка 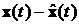 будет равна
нулю, уравнение наблюдателя переходит в уравнение системы.
будет равна
нулю, уравнение наблюдателя переходит в уравнение системы.
Матрица  выбирается
так, чтобы переходный процесс в наблюдателе заканчивался быстрее, чем
переходный процесс в системе. Эмпирически установлено, что наблюдатель должен
обладать быстродействием, в 2-4 раза превышающим быстродействие системы.
выбирается
так, чтобы переходный процесс в наблюдателе заканчивался быстрее, чем
переходный процесс в системе. Эмпирически установлено, что наблюдатель должен
обладать быстродействием, в 2-4 раза превышающим быстродействие системы.
Теперь перейдем к вопросам синтеза
наблюдателей состояния. Из уравнения (11.7) следует, что характеристическое
уравнение наблюдателя имеет вид
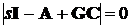 .(11.9)
.(11.9)
Основной метод синтеза наблюдателя
состоит в том, чтобы сделать его в 2-4 раза более быстродействующим, чем
замкнутая система. Следовательно, мы можем выбрать такое характеристическое
уравнение наблюдателя, которое содержит информацию о желаемом быстродействии:
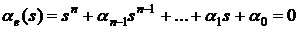 . (11.10)
. (11.10)
Тогда матрица  должна
удовлетворять уравнению
должна
удовлетворять уравнению
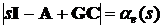 (11.11)
(11.11)
Отметим сходство данной задачи с
синтезом системы путем размещения полюсов. Поэтому для синтеза наблюдателей
состояния также может быть использована формула Аккермана. В итоге получим
следующий результат:
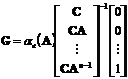 .(11.12)
.(11.12)
Выражение (11.12) позволяет
вычислить матрицу 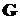 по
заданному характеристическому полиному наблюдателя
по
заданному характеристическому полиному наблюдателя  и известным
матрицам
и известным
матрицам  и
и 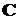 .
.
Пример 11.1. Проведем синтез
наблюдателя для системы управления спутником. Уравнения состояния и наблюдения
объекта имеют вид
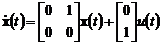 ,
,
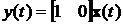 .
.
В примере 10.3 был синтезирован
регулятор, удовлетворяющий характеристическому уравнению
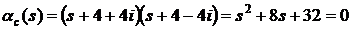 ,
,
который обеспечивал постоянную
времени замкнутой системы 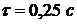 и параметр
и параметр 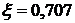 . Теперь мы
синтезируем наблюдатель, который обладал бы критическим демпфированием с
постоянной времени
. Теперь мы
синтезируем наблюдатель, который обладал бы критическим демпфированием с
постоянной времени 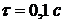 . Таким
образом,
. Таким
образом,
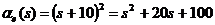 .
.
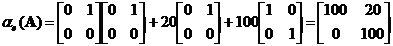 .
.
 ,
,
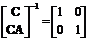 .
.
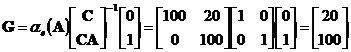 .
.
На этом синтез наблюдателя завершен.
Эта процедура может быть выполнена с помощью следующей программы «MATLAB»:
A=[0 1; 0
0]; B=[0; 1]; C=[1 0]; D=0;=[-10 -10];=acker(A', C', Pe); G=Gt'
В этой программе для вычисления
коэффициентов наблюдателя используются инструкция acker и
транспонированные матрицы, так как
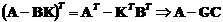 .
.
Следовательно, в инструкции acker 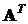 заменяет
заменяет 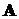 ,
, 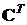 заменяет
заменяет 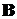 , а
результатом является
, а
результатом является 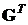 .
.
Пример 11.2. В данном примере мы
рассмотрим реализацию закона управления с помощью наблюдателя состояния,
использовав результаты примеров 10.3 и 11.1 соответственно. В примере 10.3 была
найдена матрица коэффициентов, позволяющая разместить полюсы замкнутой системы
в точках 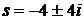 :
:
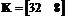 ,
,
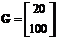 .
.
В соответствии с (11.7) уравнения
наблюдателя имеют вид
 ,
,
поскольку теперь 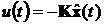 . В
последнем уравнении
. В
последнем уравнении

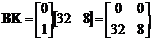 .
.
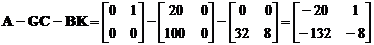 .
.
В результате регулятор-наблюдатель
описывается следующими уравнениями
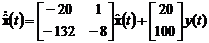 ,
,
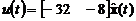 .
.
В этих уравнениях 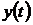 является
входом, а
является
входом, а 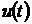 - выходом
наблюдателя. Данная задача решается с помощью следующей программы «MATLAB»:
- выходом
наблюдателя. Данная задача решается с помощью следующей программы «MATLAB»:
A=[0 1; 0
0]; B=[0; 1]; C=[1 0]; D=0;p4=ss(A, B, C, D);=[-4+4*i -4-4*i];=acker(A, B,
Pp)=[-10 -10];=acker(A', C', Pe); G=Gt'=reg(e10p4, K, G), pause=-tf(rsys),
Gp=tf(e10p4), G01=Gec*Gp, pause
[gm, pm, wg,
wp]=margin(G01)
В этой программе объединены две
предыдущие программы и использована функция reg (от слова
регулятор), которая вычисляет матрицы системы с регулятором-наблюдателем. Затем
мы переходим к моделям регулятора и объекта управления в виде передаточных
функций и определяем для замкнутой системы запасы устойчивости по модулю и по
фазе.
Литература
1. Чаки Ф. Современная теория
управления: нелинейные, оптимальные и адаптивные системы. - М:. Мир, 1975. -
423 с.
2. Филлипс Ч., Харбор Р.
Системы управления с обратной связью. - М.: Лаборатория Базовых Знаний, 2001. -
616 с.
. Савин М.М., Елсуков В.С.
Пятина О.Н. Теория автоматического управления. - Ростов н/Д: Феникс, 2007. -
469 с.
. Ивахненко А.Г. Долгосрочное
прогнозирование и управление сложными системами. - К.: Техніка,
1975. - 311 с.
. Калман Р., Фалб П., Арбиб
М. Очерки по математической теории систем. - М.: Мир, 1971. - 399 с.
. Васильев В.И. и др.
Многоуровневое управление динамическими объектами. М.: Наука, 1987. - 309 с.
. Цвиркун А.Д. Основы синтеза
структуры сложных систем. М.: Наука, 1982. - 200 с.