Определение параметров цепи

Определение параметров цепи

1. Расчёт несимметричной трёхфазной цепи

Задание:

1) определить токи и напряжения на всех участках схемы;

) составить баланс активных мощностей;

) построить в масштабе векторную диаграмму токов и топографическую диаграмму напряжений;

) разложить полученную систему токов генераторов на симметричные составляющие аналитически и графически.

Исходные данные

четырехполюсник трехфазный цепь генератор

Таблица 1. Числовые значения для задачи 1.

Рис. 1. Схема к задаче 1.

. Определим токи и напряжения на всех участках схемы.

Для этого преобразуем «звезду» сопротивлений 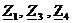 в эквивалентный треугольник 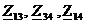 (рис. 2).

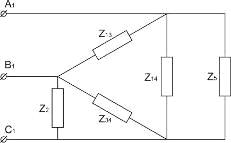
Рис. 2. Расчётная схема. Эквивалентный треугольник Z₁₃, Z₃₄, Z₁₄

Для эквивалентности преобразования таких схем необходимо соблюсти стандартное требование: токи и напряжения в непреобразованной части цепи должны остаться неизменными, что означает, что сопротивление между любой парой точек должны быть одинаковыми как при соединении «треугольник», так и при соединении «звезда», поэтому определим эквивалентные сопротивления треугольника по формулам:

, ,

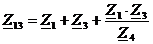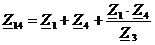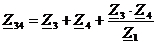
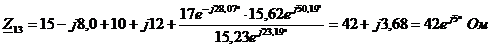
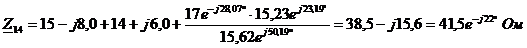
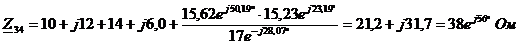
Определим эквивалентное сопротивление 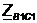, Ом параллельного соединения сопротивлений 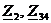 по формуле:

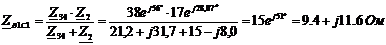
Определим эквивалентное сопротивление 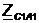, Ом параллельного соединения сопротивлений 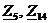 по формуле:

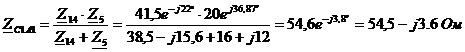
Преобразуем в треугольник сопротивлений 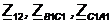(рис. 3)

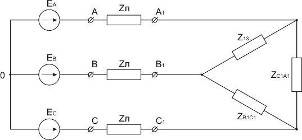
Рис. 3 Схема соединения сопротивлений «треугольником»

Преобразуем треугольник сопротивлений 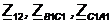(рис. 3) в эквивалентную «звезду» 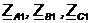 (рис. 4).

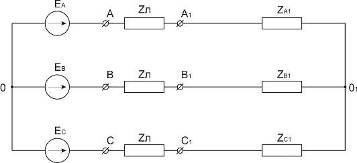
Рис. 4 Схема соединения сопротивлений «звездой»

Определим сопротивления «звезды» 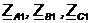 по формулам:

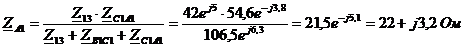
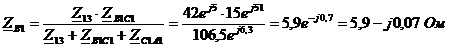
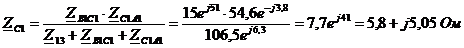
Находим комплексные сопротивления 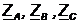, Ом и комплексные проводимости фаз 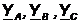, См, по формулам:

;

;

;

;

;

.

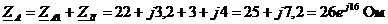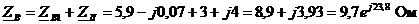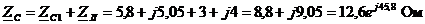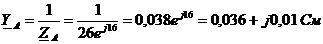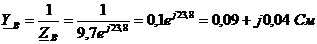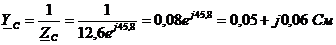Далее задачу решаем методом двух узлов. Запишем фазные напряжения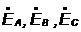 в комплексном виде:

;

;

.

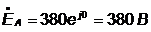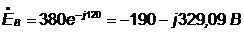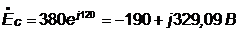Определим смещение нейтрали 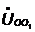 В по формуле:

,

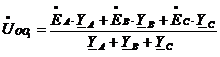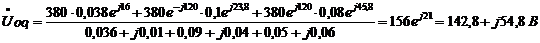
Находим линейные токи 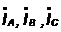, А по формулам:

;

;

.

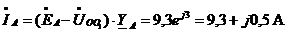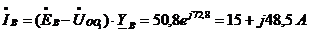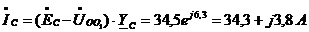Находим фазные напряжения нагрузки 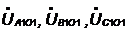, В по формулам:

;

;

.

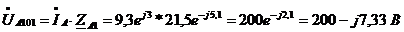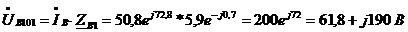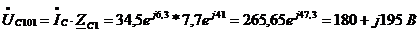Находим линейные напряжения нагрузки 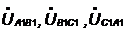, В по формулам:

;

.

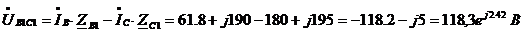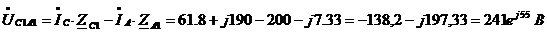Находим падение напряжений в 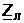 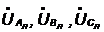, В по формулам:

;

;

.

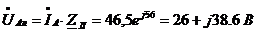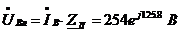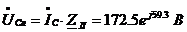Находим токи на всех участках цепи 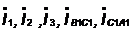, А по формулам:

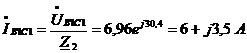
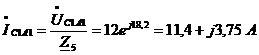
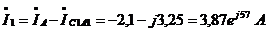
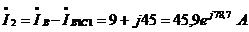
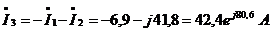
. Составим баланс активных мощностей. Уравнение баланса активных мощностей имеет вид:

;

;

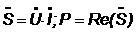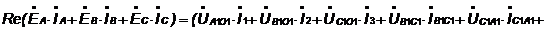
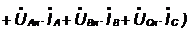Правая часть уравнения: ;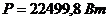

Левая часть уравнения: .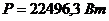

Таким образом, обе части уравнения приблизительно равны, т.е. баланс мощностей выполняется.

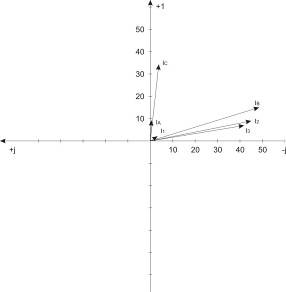
Рис. 5. Векторная диаграмма токов

3. Построим векторную диаграмму токов (рис. 5) и топографическую диаграмму напряжений (рис. 6).

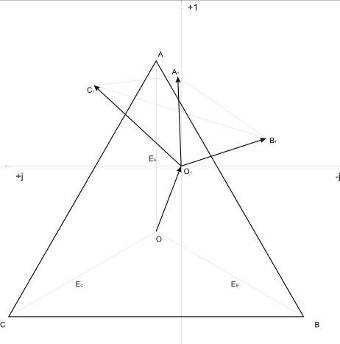
Рис. 6. Топографическая диаграмма напряжений

2. Расчет линейного пассивного четырехполюсника

Задание:

Для электрической схемы, представленной на рис. 1, выполнить следующее:

1) определить сопротивление холостого хода 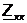 и короткого замыкания  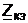четырехполюсника;

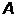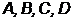) по найденным сопротивлениям найти коэффициенты четырехполюсника в форме  (т.е. коэффициенты  или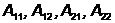) и проверить соотношение между ними ();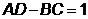

) определить напряжение 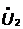, токи 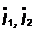, мощности 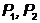и КПД 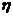четырехполюсника при значениях напряжения 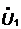 и активном сопротивлении нагрузки 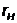 (подключено к клеммам 2-2’);

) определить характеристическое сопротивление четырехполюсника 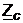и проверить его расчетами, приняв сопротивление нагрузки ;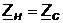

) постоянную передачи 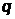 четырехполюсника.

Список использованных источников

1.   1. Атабеков, Г.И. Теоретические основы электротехники. Ч. 1. / Г.И. Атабеков. - М.: Энергия, 1978

2.      Бессонов, Л.А. Сборник задач по теоретическим основам электротехники / Л.А. Бессонов [и др.]. - М.: Высшая школа, 1975

.        Бессонов, Л.А. Теоретические основы электротехники / Л.А. Бессонов. - М.: Высшая школа, 2006

4.   Гольдик, О.Е. Программированное изучение теоретических основ электротехники / О.Е. Гольдик, А.Е. Каплянский, Л.С. Полотовский. - М.: Высшая школа, 1978

5.   Зевеке, Г.Б. Основы теории цепей / Г.Б. Зевеке [и др.]. - М.: Энергия, 1975

6.      Каплянский, А.Е. Теоретические основы электротехники / А.Е. Каплянский, А.П. Лысенко, Л.С. Полотовский. - М.: Высшая школа, 1972

7.   Матханов, П.Н. Основы анализа электрических цепей. Линейные цепи / П.Н. Матханов. - М.: Высшая школа, 1981

8.      Матханов, П.Н. Основы анализа электрических цепей. Нелинейные цепи / П.Н. Матханов. - М.: Высшая школа, 1977

9.   Нейман, Л.Р. Теоретические основы электротехники. Т. 1. / Л.Р. Нейман, К.С. Демирчин. - М.: Энергия, 1975

10. Поливанов, К.М. Теоретические основы электротехники. Ч. 1. / К.М. Поливанов. - М.: Энергия, 1972

11.    Теоретические основы электротехники. Т. 1 / под ред. П.А. Ионкина. - М.: Высшая школа, 2004

.        Шебес, М.Р. Теория линейных электрических цепей в упражнениях и задачах / М.Р. Шебес. - М.: Высшая школа, 1975