Бифуркационная динамика систем

Бифуркационная динамика систем

Лабораторная работа

Бифуркационная динамика систем

Ход работы:

.        Пусть на изолированном острове летом выводятся насекомые численностью Х_i, которые откладывают яйца и умирают. Из яиц на следующий год выводятся новые насекомые численностью Х_{i +1.} Очевидно, численность потомства Х_{i +1} должна зависеть от численности родительского поколения Х_i и от каких-то дополнительных факторов. Эта зависимость учитывается уравнением:

Х_{i +1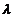} =  (N - Х_{i )},

Где 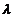> 0 - некоторый параметр (т.е. постоянная в условиях рассмотрения величина), N - максимально возможная численность популяции.

Для унификации уравнения численность популяции нормируют по отношению к предельной величине, что математически оформляется делением обеих частей равенства на N²:

Х_{i +1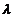}^* = ^* Х_i^*(1 - Х_i^*),

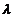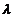Где Х_i^* = Х_i/N Х_{i +1}^*= Х_{i +1}/ N ^*= N

2.      Пусть 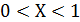 и 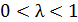. Тогда 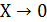. Зададим 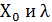в заданных пределах и рассчитаем 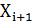и занесем в таблицу результаты.

λ=0,4 X₀=0,5

Анализ табличных результатов показывает, что популяция сокращается.

.        Зададим значение λ большее в интервале .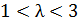

λ=2

Как видно, в данном случае популяция не возрастает, а стремится по численности к некоторому предельному значению 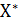. Этот предел для каждого λ может быть рассчитан аналитическим путем решения уравнения

.

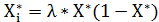Уравнение имеет два решения:

.

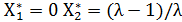Первое решение реализуется (т.е. существует устойчиво) при малых 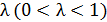, а второе для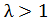, т.к. условиям задачи по должно быть .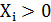

.        Зададим λ еще большее значение .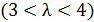

λ=3,5

В этом случае динамика численности популяции заметно усложняется: возникают два ее предельных (стационарных) значения, причем сама численность колеблется, попеременно приближаясь то к одному, то к другому пределу.

.        Построим график зависимости стационарных состояний численности от параметра скорости роста (.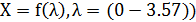

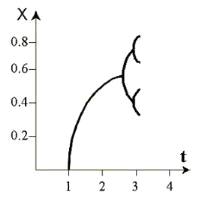
популяция особь бифуркационный

Второе критическое значение 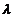₂ = 3.4 соответствует раздвоению каждой из ветвей решения, т.е. стационарных значений становится не два, а четыре.

Контрольные вопросы.

1.      N-максимальная численность, которой может достичь популяция. Численность популяции на конкретной территории не может увеличиваться бесконечно, так как на всех особей не хватит пропитания. Как только численность популяции начнет приближаться к N, между особями начнется конкуренция за территорию, борьба за выживание. Путем естественного отбора некоторые особи погибнут, и численность популяции уменьшится и будет меньше N.

.        При 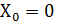динамика популяции будет нулевой. Такая популяция существовать не будет.