Исследование математической модели популяционной динамики
ИССЛЕДОВАНИЕ
МАТЕМАТИЧЕСКОЙ МОДЕЛИ ПОПУЛЯЦИОННОЙ ДИНАМИКИ
Работа посвящена исследованию актуальной задачи
математического моделирования в биологии. Исследуемая модель взаимодействия
видов типа конкуренция хищника за жертву представляет собой систему нелинейных
обыкновенных дифференциальных уравнений. Все выводы, сделанные на основе
качественного анализа модели, подтверждены численными экспериментами.
Постановка задачи
Модель типа конкуренция хищника за жертву - это
модификация модели Лотки-Вольтерра, описывающей динамику численности двух
популяций, взаимодействующих по принципу хищник-жертва. Конкуренция хищника за
жертву учитывается системой:
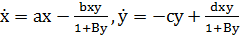 , (1)
, (1)
где х и у - плотности
популяции жертвы и хищника соответственно,
а - скорость размножения популяции жертвы в
отсутствие хищника,- удельная скорость потребления популяцией хищника популяции
жертвы при единичной плотности обеих популяций,
с
- естественная смертность хищника,/b - коэффициент переработки потребленной
хищником биомассы жертвы в собственную биомассу,функция, описывающая
зависимость скорости выедания жертв от плотности популяций жертвы и хищника.
Поставим
перед собой задачу качественного исследования динамики решений системы (1) при
различных соотношениях между значениями параметров системы.
Исследование модифицированной модели
Проведем качественный анализ системы (1). Для
этого исходную модель
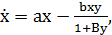 (2)
(2)
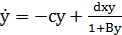 ,
,
заменой переменных t=t/a,
x=au/d,
y=av/b
приведем к виду:
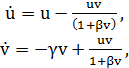 (3)
(3)
где β=αВ/b.
Качественное исследование предполагает
исследование системы на устойчивость. Для этого найдем положение равновесия
системы (3), приравняв правую часть к нулю:
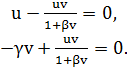 (4)
(4)
Получаем точки А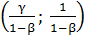 и В(0;0) - это особые точки.
и В(0;0) - это особые точки.
Исследуем на устойчивость точку А по первому
приближению. Линеаризуем систему (2), и, составив матрицу Якоби, найдем
соответствующие собственные значения:
Для того, чтобы установить устойчивость или
неустойчивость решения, рассмотрим несколько случаев, зависимых от знака
дискриминанта.
В первом случае при 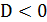 ,
где
,
где 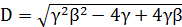 ,
собственные числа
,
собственные числа
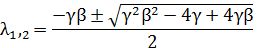
являются комплексными. По классификации особых
точек линейных систем на плоскости следует, что нулевое решение устойчиво и
особая точка типа «устойчивый фокус». (Рисунок 1.)
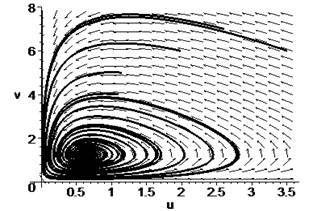
Рисунок 1. Устойчивый фокус.
В следующем случае при 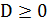 и
и
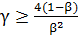 собственные
числа
собственные
числа
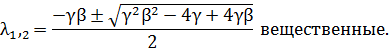
Нулевое решение устойчиво при 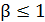 .Заметим,
что по смысловому значению
.Заметим,
что по смысловому значению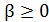 , т.е. оно лежит на
интервале
, т.е. оно лежит на
интервале 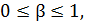 следовательно,
особая точка типа «устойчивый узел». (Рисунок 2.)
следовательно,
особая точка типа «устойчивый узел». (Рисунок 2.)
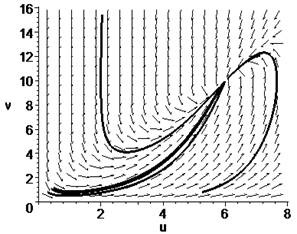
Рисунок 2. Устойчивый узел.
Третий случай определен при 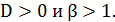 Данное
условие выполняется при
Данное
условие выполняется при 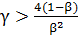 , откуда следует,
что
, откуда следует,
что 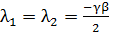 вещественные.
вещественные.
Нулевое решение А (-10,-10) неустойчивое типа
«седло». Но данное решение нам неинтересно, т.к. по смысловому условию задачи
решение положительно. (Рисунок 3.)
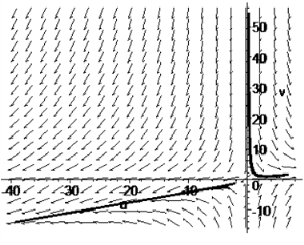
Рисунок 3. Седло.
В четвертом случае при 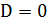 и
при
и
при 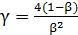 ,
откуда следует, что
,
откуда следует, что
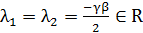 ,
,
Нулевое решение А (16,2) устойчиво типа
«устойчивый дикритический узел».
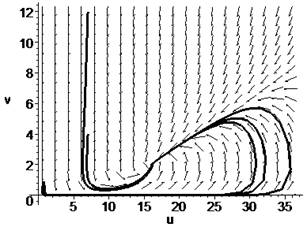
Рисунок 4. Дикритический узел.
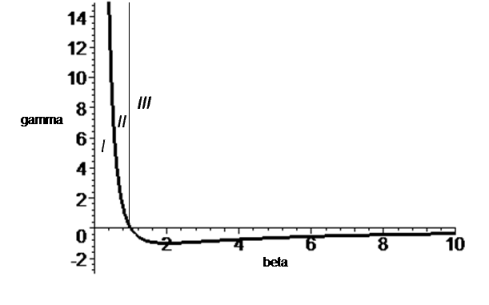
Рисунок 5. График зависимости γ от β.
Область I, согласно проведенным исследованиям,
соответствует случаю 1, в котором особая точка является устойчивым фокусом.
Область II, согласно проведенным исследованиям,
соответствует случаю 2 , при 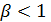 в котором особая
точка является устойчивым узлом.
в котором особая
точка является устойчивым узлом.
Области III, согласно проведенным исследованиям,
соответствуют случаю 3, в котором особая точка неустойчива типа седло.
Область IV (сам график), согласно проведенным
исследованиям, соответствует случаю 4, в котором особая точка является
устойчивым дикритическим узлом.
Исследуем на устойчивость точку В по первому
приближению.
Подставим значение точки равновесия В 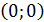 и
получим матрицу:
и
получим матрицу:
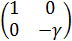 (7)
(7)
Собственные значения матрицы (7):
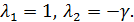
Получаем, что
а) При 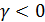 и
и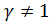 нулевое решение неустойчиво типа неустойчивый узел.
нулевое решение неустойчиво типа неустойчивый узел.
б) При 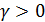 нулевое
решение неустойчиво типа седло.
нулевое
решение неустойчиво типа седло.
в) При 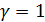 нулевое
решение неустойчиво типа неустойчивый диакритический узел.
нулевое
решение неустойчиво типа неустойчивый диакритический узел.
Но по смысловому значению 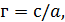 значит
значит
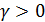 и
возможны случаи б) и в).
и
возможны случаи б) и в).
Итак, при 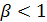 нетривиальное
равновесие существует и устойчиво. По мере роста параметра
нетривиальное
равновесие существует и устойчиво. По мере роста параметра 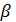 равновесие
существует и устойчиво. По мере роста параметра
равновесие
существует и устойчиво. По мере роста параметра 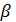 равновесные
численности популяций хищника и жертвы растут. Неравенство
равновесные
численности популяций хищника и жертвы растут. Неравенство 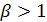 отвечает
ситуации, когда скорость роста популяции жертвы всегда, при любой сколь угодно
большой плотности популяции хищника, больше скорости выедания. Популяция жертвы
неограниченно растет, нетривиальное равновесие отсутствует [1].
отвечает
ситуации, когда скорость роста популяции жертвы всегда, при любой сколь угодно
большой плотности популяции хищника, больше скорости выедания. Популяция жертвы
неограниченно растет, нетривиальное равновесие отсутствует [1].
математический моделирование дифференциальный хищник
Заключение
Цель данной работы заключалась в исследовании
модифицированной модели Лотки-Вольтерра типа конкуренция хищника за жертву. При
качественном исследовании была проведена линеаризация исходной системы, найдены
все возможные точки покоя и определены их типы. В результате построена
бифуркационная диаграмма, отражающая смену динамических режимов системы.
Проведенные исследования данной работы совпадают с результатами работ
А.Д.Базыкина [1].
Литература
1.
Базыкин А.Д. Нелинейная динамика взаимодействующих популяций.- Москва - Ижевск:
Институт компьютерных исследований, 2003, 368 с.
. Ризниченко Г.Ю,
Математические модели в биофизике и экологии. - Москва -Ижевск: Институт
компьютерных исследований, 2003, 184 с.
. Ризниченко Г.
Ю.Лекции по математическим моделям в биологии. [Электронный ресурс] /
Г.Ю.Ризниченко. - Режим доступа: http: //bourabai.kz/cm/lect06.htm/
.
Филиппов А.Ф. Сборник задач по дифференциальным уравнениям. Ижевск, 2000. - 176
с.