Модель популяции с нижней критической плотностью
Реферат на тему:
«Модель популяции
с наименьшей критической численностью»
Выполнила
ст. гр. БМЗС-61
Саблина А.В.
Проверил
Лазуренко Р.Р.
г. Ростов-на-Дону
 2011
г.
2011
г.
Оглавление.
Введение. 3
1. Моделирование как метод познания. Основные
определения. 5
2. Основные модели роста популяций. 9
3. Модель популяции с наименьшей критической
численностью.. 15
Заключение. 22
Список литературы. 23
Введение.
На
разных уровнях развития живой материи продукционные процессы проявляют себя
по-разному, но их феноменологическое описание всегда включает рождение, рост,
взаимодействие с внешней средой, в том числе с другими особями своего вида или
других видов, смерть особей. Именно это обстоятельство позволяет применять
сходный математический аппарат для описания моделей роста и развития у таких,
казалось бы, удаленных друг от друга по лестнице уровней организации живой
материи, как клеточная популяция и сообщество видов в экосистеме.
Описание
изменения численности популяции во времени составляет предмет популяционной
динамики. Популяционная динамика является частью биологии математической,
наиболее продвинутой в смысле формального математического аппарата, своего рода
"математическим полигоном" для проверки теоретических идей и
представлений о законах роста и эволюции биологических видов, популяций,
сообществ. Возможность описания популяций различной биологической природы
одинаковыми математическими соотношениями обусловлена тем, что с динамической
точки зрения, рост и отбор организмов в процессе эволюции происходит по
принципу "Кинетического совершенства" (Шноль, 1979)
Преимущества
математического анализа любых, в том числе популяционных, процессов, очевидны.
Математическое моделирование не только помогает строго формализовать знания об
объекте, но иногда (при хорошей изученности объекта) дать количественное
описание процесса, предсказать его ход и эффективность, дать рекомендации по
оптимизации управления этим процессом. Это особенно важно для биологических
процессов, имеющих прикладное и промышленное значение - биотехнологических
систем, агробиоценозов, эксплуатируемых природных экосистем, продуктивность
которых определяется закономерностями роста популяций живых организмов,
представляющих собой "продукт" этих биологических систем.
Объект – некоторая часть окружающего нас мира,
которая может быть рассмотрена как единое целое. Примеры объектов – дерево,
мяч, ПК, программа, сосед за партой. Для идентификации объектов служит имя,
определяющее его свойства. Свойство – совокупность признаков объекта, по
которым его можно отличить от других объектов.
Модель – упрощенное подобие реального объекта
(процесса), созданного человеком для определенного применения (цели).
Модели бывают: материальные (натурные) и информационные
(описание объекта моделирования в определенной форме), делятся на статические и
динамические.
Типы моделей – табличные (объекты и их свойства
представлены в виде списка, их значения размещаются в ячейках прямоугольной
таблицы), иерархические (отражающие процесс классификации – биология,
файловая структура…) – вид Граф, сетевые (сложная структура связи
между элементами – сотовая телефонная связь, Интернет).
Моделирование – это метод познания,
состоящий в создании иисследование моделей.
Процесс разработки моделей и их
исследование на компьютере можно разделить на несколько основных этапов.
На первом этапе исследования объекта или процесса обычно
строится описательная информационная модель. Такая модель выделяет
существенные, с точки зрения целей проводимого исследования, параметры объекта,
а несущественными параметрами пренебрегает.
На втором этапе создается формализованная модель,
т.е. описательная информационная модель записывается с помощью какого-либо
формального языка. В такой модели с помощью формул, уравнений, неравенств и
т.д. фиксируются формальные соотношения между начальными и конечными значениями
свойств объектов, а также накладываются ограничения на допустимые значения этих
свойств.
На третьем этапе необходимо формализованную информационную
модель преобразовать в компьютерную модель, т.е. выразить ее на понятном
для компьютера языке. Существуют два принципиально различных пути построения
компьютерной модели:
· построение алгоритма
решения задачи и его кодирование на одном из языков программирования;
· построение
компьютерной модели с использованием одного из приложений (электронных таблиц,
СУБД и т.д.).
Четвертый этап исследования информационной модели состоит в
проведении компьютерного эксперимента. Если компьютерная модель
существует в виде программы на одном из языков программирования, ее нужно
запустить на выполнение и получить результаты.
Если компьютерная модель исследуется в приложении, например,
в электронных таблицах, можно провести сортировку или поиск данных, построить
диаграмму или график и т.д.
Пятый этап состоит в анализе полученных результатов и
корректировке исследуемой модели. В случае различия результатов, полученных
при исследовании информационной модели, с измеряемыми параметрами реальных
объектов, можно сделать вывод, что на предыдущих этапах построения модели были
допущены ошибки или неточности.
Метод построения математических моделей — метод
математического познания действительности изучаемых реальных объектов или
объектов, уже описанных в других областях знаний, с целью их более глубокого
изучения и решения всех, возникающих в этих реальных ситуациях задач с помощью
математического аппарата.
Математическая модель — это приближённое
описание какого-нибудь класса явлений, выраженное на языке какой-нибудь
математической теории (с помощью системы алгебраических уравнений и неравенств,
дифференциальных или интегральных уравнений, функций, системы геометрических
предложений, векторов и т.п.).[1]
Математическое моделирование — описание анализируемого
объекта внешнего мира с помощью математической символики.
Как алгоритм математической деятельности метод
математического моделирования содержит три этапа:
1. построение
математической модели объекта (явления, процесса);
2. исследование
полученной модели, т. е. решение полученной математической задачи средствами
математики;
При этом должны соблюдаться следующие требования:
1. модель
должна адекватно отражать наиболее существенные (с точки зрения определенной
постановки задачи) свойства объекта, отвлекаясь от несущественных его свойств;
2. модель
должна иметь определенную область применимости, обусловленную принятыми при её
построении допущениями;
3. модель
должна позволять получать новые знания об изучаемом объекте.
После того как математическая модель построена, возможны два
случая:
1. полученная
конкретная модель принадлежит к уже изученному в математике классу моделей и
тогда математическая задача решается уже известными методами;
2. эта модель
не укладывается ни в одну из известных схем (классов) моделей, разработанных в
математике, и тогда возникает внутри математическая проблема исследования
нового класса моделей, что приводит к дальнейшему развитию одной из
существующих математических теорий или к появлению новой.
Это развитие математических теорий находит затем применение
к изучению той области знаний, в которой возникла исходная задача, а также и
других объектов реального мира, приводящих к математическим объектам того же
класса.
2.1. Модель неограниченного роста численности популяции.
Все живые организмы теоретически способны к очень быстрому увеличению
численности. При неограниченных ресурсах и отсутствии гибели от болезней, хищников
и т.п. даже при низкой исходной численности популяция любого вида за
сравнительно короткий срок может так вырасти, что покроет весь земной шар
сплошным слоем.
Способность к увеличению численности за данный промежуток времени называют биотическим
потенциалом вида.[2]
У разных видов биотический потенциал разный: у крупных млеко питающихся
численность может возрастать в год лишь в 1,05 - 1,1 раза, а у мелких насекомых
(рачков, дафний) численность в год может возрасти в 1010-1030 раз. А у бактерий
и одноклеточных водорослей еще быстрее. Во всех этих случаях, при идеальных
условиях численность будет расти в геометрической прогрессии, и график
изменения численности будет представлять собой экспоненту. Рост численности в
геометрической прогрессии называется экспоненциальным ростом.
В лабораторных условиях наблюдать экспоненциальный рост можно в популяциях
дрожжей, водоросли хлореллы, бактерий на начальных стадиях роста.
В природе экспоненциальный рост наблюдается при вспышках саранчи, непарного
шелкопряда и других насекомых. Экспоненциально может расти численность
животных, заселенных в новую местность, где у них мало врагов и много пищи (классический
пример - рост численности кроликов, завезенных в Австралию).
Во всех этих случаях экспоненциальный рост наблюдается в течение коротких
промежутков времени, после чего скорость роста численности снижается.
2.2. Модель Мальтуса (рождаемость - смертность)
В популяциях микроорганизмов удельная скорость роста зависит от скорости
деления клеток. Исходные клетки делятся на дочерние, что и определяет прирост
численности.
В популяциях многоклеточных организмов удельная скорость роста зависит от
рождаемости и смертности. [3]
Рождаемость характеризует частоту появления новых особей в популяции. Различают
рождаемость абсолютную и удельную. Абсолютная рождаемость - число
особей, появившихся в популяции за единицу времени. Удельная рождаемость
выражается в числе особей на особь в единицу времени. Например, для популяции
человека как показатель удельной рождаемости обычно используют число детей,
родившихся в год на 1000 человек.
Смертность (абсолютная и удельная) характеризует скорость
убывания численности популяции, вследствие гибели особей от хищников, болезней,
старости и т.д.
Используя такие параметры модели изменения численности популяции, австрийский
священник Мальтус опубликовал в 1802 году результаты своих исследований,
основанных на данных о росте населения в американских колониях. Приведем его
рассуждения:
Пусть в популяции с начальной численностью N особей за промежуток времени dt
появляется dNновых особей. Если число вновь появившихся особей прямо
пропорционально N и dt, то имеем уравнение dN=r*dt*N. Разделив обе части на dt,
получим:
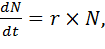 (1)
(1)
где dN/dt - абсолютная скорость роста численности , r - биотический потенциал.
Решением уравнения (1) будет
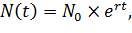 (2)
(2)
В дискретном виде это уравнение можно записать так:
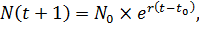 (3)
(3)
2.3. Модель Ферхюльста (рождаемость и смертность с учетом роста численности)
Как правило, численность популяции зависит не только от рождаемости и
смертности, но и от ограниченности пищевых и других ресурсов. Вскоре за созданием
модели Мальтуса, бельгийский математик Ферхюльст задался вопросом: будет ли
население Бельгии расти неограниченно? Ответом на этот вопрос было создание
новой модели динамики численности популяции при ограниченных ресурсах,
описываемой следующим уравнением:
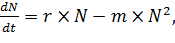 (4)
(4)
где r
- удельная скорость роста численности,
N - численность популяции,
m - число встреч членов популяции, при котором они могут конкурировать за
какой-либо ресурс.
Уравнение это отличается от уравнения экспоненциального роста (уравнения
Мальтуса) выражением m*N2, которое как раз и отражает ограниченность
ресурсов.
Перепишем уравнение (4) так:
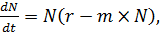 (5)
(5)
Выражение в скобках - это удельная скорость роста популяции. Причем чем больше
численность популяции (N), тем меньше скорость роста. Если в правой части
уравнения вынести за скобки выражение r:
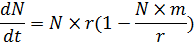 и обозначить m/r за 1/K,
то уравнение (4) можно переписать так:
и обозначить m/r за 1/K,
то уравнение (4) можно переписать так:
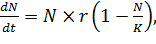 (6)
(6)
При малых N значением N/K можно пренебречь, и тогда рост численности идет по
экспоненциальному закону, при возрастании N и неизменном K рост численности
будет замедляться, и при N близком кК рост остановится. ВеличинуК называют емкостью
среды. Она отражает возможности среды обитания предоставить популяции
нужные для ее роста ресурсы.
Уравнение (6) графически отображается в виде S-образной кривой. Эта кривая
называется логистической кривой, а рост численности, соответствующий уравнению
(6) - логистическим.
Исследуя кривую, можно сказать, что максимальная скорость роста достигается,
когда численность равна K/2. В некоторый момент численность стабилизируется и
остается постоянной величиной.
Популяции, существующие в условиях ограниченных ресурсов, часто хорошо
подчиняются правилам логистического роста. Например, когда овцы были завезены в
Тасманию, рост их стада описывался логистической кривой.
Но правила логистического роста приложимы не ко всем случаям. Например, у
размножающихся половым путем видов, при слишком малой численности мала
вероятность встреч особей разного пола и размножение может вообще прекратиться.
Для реализации модели в среде электронных таблиц уравнение (6) следует
представить в дискретном виде:
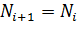 ×r×(1−
×r×(1−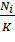 ),(7)
),(7)
где Ni - численность популяции в i-й момент времени;
r - удельная скорость роста популяции (рождаемость/ смертность);
К - емкость среды.
От уравнения Ферхюльста отталкиваются ученые, подразделяющие воспроизводство на
два отдельных принципа или стратегии:
1.R-стратегия - это почти ничем не регулируемое размножение. Смертность
у таких видов огромна, но даже она не спасает популяцию от чрезмерного
разрастания, в связи с чем эти виды то и дело проходят стандартную процедуру: популяционный
взрыв, коллапс, стабилизация.
Как только концентрация вида становится чрезмерной, начинает страдать кормовая
база, распространяются инфекции, повышается уровень внутривидовой агрессии, не
хватает места, включаются механизмы паники - вариантов коллапса бывает много.
Но все они приводят к уничтожению большинства животных. Лемминги, несущиеся
толпами в море, саранча, устилающая своими телами южные города... После
коллапсов идет период относительно благополучной стабилизации, когда опять
можно безнаказанно размножаться. Потом все повторяется заново.
2.К-стратегии придерживаются почти все крупные млекопитающие и
большинство видов птиц. Она заставляет вид самостоятельно контролировать свою
численность разными способами. Самые популярные - воздержание и умерщвление
потомства.
Воздержание обычно выбирают звери-одиночки (тигры, барсуки, зяблики,
медведи...). Для них характерно наличие собственных "охотничьих
угодий" - территории, которая контролируется одной особью или супружеской
парой. Молодые животные, которые пока не нашли пару, придерживаются целибата,
т.к. право на размножение нужно заслужить.
Стадным или стайным животным больше присущ метод уничтожения нежелательного
потомства. Незадолго перед родами у самок включается механизм "проверки
популяции". Если обилие тел сородичей вдруг вызывает у мамы беспокойство,
если она не может находить себе качественный корм, если условия для выращивания
детенышей она оценивает как неблагоприятные. Шансы на то, что она не сожрет
детенышей или не бросит их на произвол судьбы, очень невысокие.
Но нужно добавить, что К-стратегия не является панацеей - если по каким-то
причинам она не срабатывает, то стандартный набор взрыв-коллапс-стабилизация постигает
и вид с К-стратегией.
Человек изначально носитель К-стратегии. Но т.к. мы принадлежим к виду, который
ухитряется искусственно увеличивать базу своих ресурсов, наша популяция почти
всегда находится в ситуации "перед взрывом". Мы же почти всегда
умудрялись держать свою популяцию на пределе, за что периодически попадаем на
голод, войну или мор - три основных внешних регулятора, работающих по принципу R-стратегии.
В рассмотренных моделях прирост численности (биомассы)
популяции представлен линейным членом, пропорциональным численности. Строго
говоря, это соответствует лишь тем популяциям, размножение которых происходит
путем самооплодотворения (микроорганизмы). Если же в основе размножения лежит
скрещивание, предполагающее встречи между особями разных полов одного и того же
вида, то прирост будет тем выше, чем больше количество встреч между особями, а
последнее пропорционально второй степени N. [4] Таким
образом, для разнополой популяции в условиях неограниченных ресурсов можно
записать:
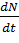 =r×
=r×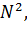 (8)
(8)
Уравнение (8) хорошо описывает тот факт, что при низких
плотностях популяций скорость размножения резко падает, так как вероятность
встречи двух особей разных полов уменьшается при понижении плотности популяции
пропорционально квадрату плотности. Однако при больших плотностях популяций
скорость размножения лимитирует уже не число встреч особей противоположного
пола, а число половозрелых самок в популяции. Кроме того, важно учесть время, в
течение которого может состояться оплодотворение. Если это время больше
времени, в течение которого особь способна к размножению, то популяция
вымирает.
Пусть Т – среднее время между двумя последующими
оплодотворениями, τ – среднее время вынашивания плода, постоянное для
каждого вида, tср – среднее время, в течение
которого может состояться оплодотворение:
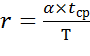 =
=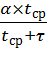 ,(9)
,(9)
где α – коэффициент пропорциональности, tср – величина, уменьшающаяся при возрастании
плотности популяции:tср = β/N, β = const.
Тогда,
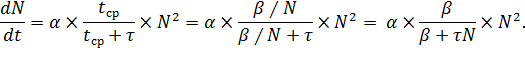
Таким образом, уравнение, учитывающее фактор разнополости и
количество самок, готовых к оплодотворению, имеет вид:
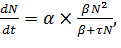 (10)
(10)
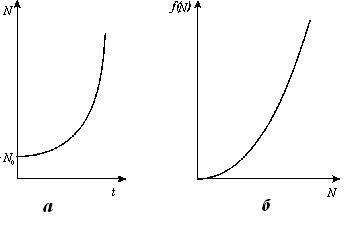
Графики численности в зависимости от времени (рис. 1 а) и
скорости размножения как функции численности (рис. 1б) для уравнения (10)
представлены на рис. 1.
В действительности плотность популяции не должна опускаться ниже некоторой
критической величины. При падении плотности популяции ниже критической среднее
время, в течение которого может состояться оплодотворение, становится больше
времени жизни отдельной особи, точнее, времени, в течение которого особь
способна к размножению. В этом случае популяция вымирает.[5]
|
|
|
Рис. 1. а - график зависимости численности от
времени и б - скорости размножения как функции численности для уравнения (10)
|
Этот эффект может быть учтен, если в формулу (10) ввести
член, пропорциональный численности популяции с коэффициентом γи
описывающий смертность. Зависимость скорости роста популяции от ее численности
при этом примет вид:
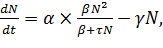 (11)
(11)
Уравнение (11) имеет два стационарных решения: 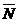 1=0 и
1=0 и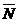 2=
2=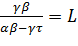 (значения параметров модели задаются
такими, чтобы величина L была положительной).
(значения параметров модели задаются
такими, чтобы величина L была положительной).
Исследуем устойчивость стационарных состояний графическим
методом. Для этого необходимо определить знак функции:
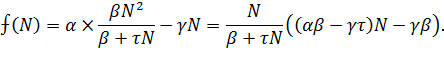
Знаменатель функции положителен при положительных значениях N, меняет знак при прохождении через значение N = - β/τ. Числитель меняет знак при
прохождении через стационарные точки 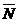 1,2 .В
результате имеем
1,2 .В
результате имеем 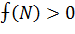 при N>
при N>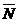 2 = L,
в области 0 <N<Lфункция
2 = L,
в области 0 <N<Lфункция
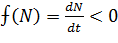 (рис. 1 а). При прохождении через точку
(рис. 1 а). При прохождении через точку 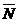 1=0 скорость роста популяции
модели (11) меняет знак с «плюса» на «минус», что означает устойчивость
стационарного состояния
1=0 скорость роста популяции
модели (11) меняет знак с «плюса» на «минус», что означает устойчивость
стационарного состояния 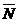 1. При
прохождении точки
1. При
прохождении точки 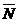 2
2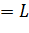 скорость роста меняет знак с «минуса»
на «плюс», что позволяет сделать вывод о неустойчивости этого стационарного
состояния.
скорость роста меняет знак с «минуса»
на «плюс», что позволяет сделать вывод о неустойчивости этого стационарного
состояния.
В случае, когда начальная численность популяции лежит в
пределах от 0 до L, скорость ее роста
отрицательна, т.е. популяция вымирает. Если же начальная численность больше L – популяция неограниченно растет. Величина Lполучила название нижняя критическая численность
(плотность). График зависимости численности популяции, описываемый моделью (11)
от времени представлен на рис. 2 б.
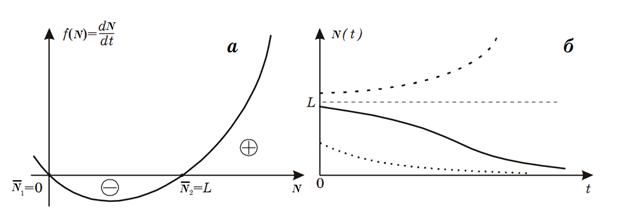
Рис. 2. Модель популяции с наименьшей критической
численностью. Зависимости скорости роста популяции от ее размера (а) и динамика
численности популяции (б).
Величина нижней критической плотности L различна для разных
видов. Наблюдения биологов показали, что это всего лишь одна пара особей на
тысячу квадратных километров в случае ондатр и сотни тысяч особей для
американского странствующего голубя. Заранее трудно было предугадать, что столь
многочисленный вид перешел через критическую границу своей численности и
обречен на вырождение. Однако это произошло, несмотря на все усилия по охране
этих птиц.
Для голубых китов критическая граница общей численности
оказалась равной десяткам - сотням. Хищническое истребление этих гигантских
животных привело к тому, что их осталось слишком мало в Мировом океане. И хотя
охота на них запрещена, надежд на восстановление популяции голубых китов
практически нет.
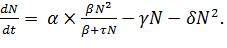 (12)
(12)
Данное нелинейное уравнение, обладающее «триггерными»
свойствами, в 1985 г. предложил А.Д.Базыкин. [6]
Уравнение имеет три стационарных значения:
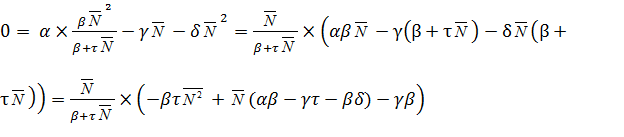 .
.
Это нулевое решение 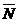 1=0, а также два значения,
обращающих в ноль квадратный трехчлен:
1=0, а также два значения,
обращающих в ноль квадратный трехчлен: 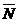 2=
L’ и
2=
L’ и 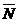 3 = K’.Значения численности L’
и K’ являются критическими:
3 = K’.Значения численности L’
и K’ являются критическими: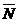 2 = L
– минимально возможная численность,
2 = L
– минимально возможная численность, 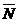 3 = K’ – максимально возможная (параметры модели α,β,
τ, γ, δ выбирают такими, чтобы величины L’ и K’ были
положительными). Устойчивость стационарных состояний проверим, аналогично
предыдущему случаю, графическим методом. Функция
3 = K’ – максимально возможная (параметры модели α,β,
τ, γ, δ выбирают такими, чтобы величины L’ и K’ были
положительными). Устойчивость стационарных состояний проверим, аналогично
предыдущему случаю, графическим методом. Функция 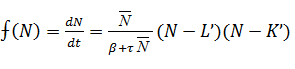 модели (12) в положительной области
значений переменной N меняет знак с «плюса» на
«минус» при переходе через
модели (12) в положительной области
значений переменной N меняет знак с «плюса» на
«минус» при переходе через 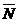 1=0 (это
стационарное состояние устойчиво), затем с «минуса» на «плюс» в точке
1=0 (это
стационарное состояние устойчиво), затем с «минуса» на «плюс» в точке 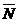 2 = L’
(неустойчивое стационарное значение) и, наконец, опять с «плюса» на «минус» в
точке
2 = L’
(неустойчивое стационарное значение) и, наконец, опять с «плюса» на «минус» в
точке 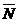 3 = K’(устойчивое
стационарное значение) (рис.3 а). График зависимости численности популяции,
описываемый моделью (12) от времени представлен на рис. 3 б.
3 = K’(устойчивое
стационарное значение) (рис.3 а). График зависимости численности популяции,
описываемый моделью (12) от времени представлен на рис. 3 б.
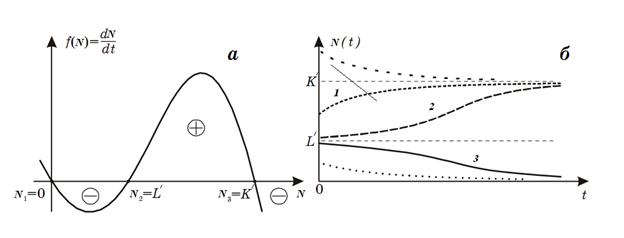
Рис. 3. Модель популяции с нижней и верхней
критическими границами численности. Зависимость скорости роста популяции от ее
размера (а) и динамика численности популяции (б).
При любых промыслах особый интерес представляет величина
нижней критической границы, при переходе через которую популяция уже не сможет
восстановиться. Модель позволяет дать некий методический рецепт определения не
самой критической границы, но степени близости к ней численности вида.
Обратимся к рис. 3 б. Пусть численность вида в начальный момент времени была
близка к максимально возможной. При t = 0 происходит одноразовое выбивание
популяции. Если численность осталась значительно больше критической,
восстановление происходит сначала быстро, а затем с монотонным замедлением
(кривая 1). Если же оставшаяся популяция близка к критической точке,
восстановление происходит сначала очень медленно, численность популяции надолго
"застревает" вблизи критической точки, а затем уже, "набрав
силы", более быстро приближается к стационарному уровню (кривая 2). Таким
образом, наблюдая реакцию системы на возмущение, можно предсказать приближение
ее к опасным границам.
Математические модели - не только средство для количественного описания
явлений. Модель сложной системы - это математический образ, позволяющий
формализовать и обобщить в терминах теории представления о многочисленных
свойствах и характеристиках сложной системы. Расширение понятийного и образного
круга не меньше чем количественные расчеты представляет собой ценный результат
междисциплинарных исследований с применением аппарата математики и физики для
изучения живых систем. В этом смысле популяционная динамика занимает особое
место. При всей ограниченности "числа особей", как характеристики
вида или сообщества, значение термина "численность" имеет четкий и
универсальный смысл.
Описанная математическая
модель популяции с наименьшей критической численностью имеет огромную
практическую ценность, так как помогает определить, в каком состоянии
(устойчивом или нет) будет находиться популяция в определенный промежуток
времени, а также позволяет предсказать приближение размера популяции к опасным
границам, дальше которых идет вырождение.
1. ая
биофизика взаимодействующих популяций. М., Наука, 1985, 165 с.