Математические основы финансов
Математические
основы финансов
План
I.
Понятие временной стоимости денег
II.
Базовые понятия финансовой математики
2.1
Антисипативный и декурсивный методы начисления процентных ставок
2.2
Эквивалентность процентных ставок
2.3
Учет инфляционного обесценения денег
2.4
Аннуитеты
2.5
Дивиденды и проценты по ценным бумагам. Доходность по операциям с ценными
бумагами
Литература
I. Понятие временной стоимости денег
стоимость процентный
ставка доходность
Временная стоимость денег (англ. time value of
money) - одно из самых важнейших понятий в финансах. Отцом понятия является
Леонардо Фибоначчи; разработал он его в 1202 году. Временная стоимость денег
гласит, что деньги должны приносить прибыль; таким образом сумма сейчас стоит
больше, чем эта же сумма потом, т.к. вложенная сейчас сумма принесет прибыль
потом.
Для того чтобы лучше понять временную стоимость
проведем несложные расчеты:
Возьмем к примеру два человека: Серик и Берик.
Исходная сумма (англ. present value) составит 5 000 $. Серик решил взять эти
деньги потом, через пять лет, А Берик сейчас и положил их допустим на депозит
под 12% годовых, допустим, под простую ставку. Посчитаем реальную стоимость
денег Серика на данный момент с учетом того, что он решил взять деньги через
пять лет. Конечно, в нашем примере, мы можем посчитать лишь виртуальную
исходную сумму Серика, т.к. сейчас он ничего не получал. Но вычисление исходной
суммы (пусть и виртуальной) позволит нам понять, сколько Серик получил бы
сейчас, если бы он был мудрым, как Берик, чтобы получить в конце периода
наращенную сумму в 5000. Иными словами, сколько надо иметь сейчас, чтобы
вложить и через пять лет получить 5000? Годовая процентная ставка в нашем
примере неизменна и составляет 12%.
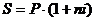
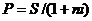 = 5000/(1+0,12·5) = 5000/1,6 = 3125
= 5000/(1+0,12·5) = 5000/1,6 = 3125
Таким образом, получается, что выбор
второго варианта (сумма потом) просто равен получению 3125 сейчас. Теперь
главный вопрос: что лучше, 3125 сейчас или 5000 потом? То есть взять 5000
потом, это то же самое, что взять 3125 сейчас. И это даже с учетом того, что мы
не учитываем инфляцию.. Базовые понятия финансовой математики
Проценты - доход от предоставления
капитала в долг в различных формах (ссуды, кредиты), либо от инвестиций
производственного или финансового характера.
Процентная ставка - величина,
характеризующая интенсивность начисления процентов.
Наращение первоначальной суммы долга
- это увеличение суммы долга за счет присоединения начисленных процентов
(дохода).
Множитель (коэффициент) наращения -
величина, показывающая, во сколько раз вырос первоначальный капитал.
Период начисления - промежуток
времени, за который начисляют проценты (получается доход).
Интервал начисления - минимальный
период, по прошествии которого происходит начисление процентов.
Декурсивный метод начисления
(ссудный процент) - проценты начисляются в конце каждого интервала начисления.
Ссудный процент представляет собой отношение начисленной суммы за определенный
интервал к сумме, имеющейся на начало данного интервала.
Антисипативный способ начисления
(учетная ставка) - проценты начисляются в начале каждого интервала начисления.
Учетная ставка представляет собой отношение суммы дохода, выплачиваемого за
определенный интервал начисления к величине наращенной суммы, полученной по
прошествии этого интервала.
Простая процентная ставка -
процентная ставка применяется к одной и той же первоначальной денежной сумме в
течение всего периода начисления.
Сложная процентная ставка - по
прошествии каждого интервала начисления в следующем интервале проценты
начисляются к сумме долга и начисленных за предыдущие интервалы процентов.
Возьмем для понимания декурсивный метод
начисления по простой ставке. Допустим, взят кредит на сумму 10 000 $, на срок
36 месяцев, при простой годовой ссудной ставке 10%.
То есть S= 10000*(1+3*0,1) = 10000* 1,3=13000
Проценты это разница между вложенным капиталом и
наращенной суммой - 3000
Процентная ставка - 10%
Наращение первоначальной суммы 13 000
Коэффициент наращения 1,3
Период - 36 месяцев
Интервал начисления - 1 год
2.1 Антисипативный и декурсивный методы
начисления процентных ставок
|
ПРОСТАЯ
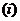 СЛОЖНАЯ СЛОЖНАЯ
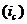
|
|
|
Наращенная
сумма 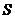
|
ДЕКУРСИВНАЯ 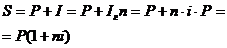
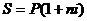
В
случае если на разных интервалах начисления применяются различные процентные
ставки, то используется следующая формула:
В
конце первого интервала:
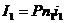
В
конце первого интервала:
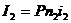 и т.д.,
и т.д.,
следовательно,
общая сумма процентного дохода будет равна:
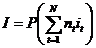
И
наращенная сумма будет составлять:
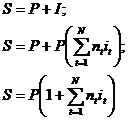
При
начислении сложной ссудной ставки используется принцип начисления на сумму
долга+проценты начисленные в предыдущих интервалах, или иными словами
начисления «процентов на проценты»:
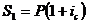 (в первый
год)
(в первый
год)
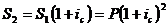 (во второй
год)
(во второй
год)
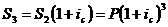 (в третий
год)
(в третий
год)
и
т.д.
В
конце периода начисления наращенная сумма составит:
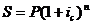
Или
при интервале начисления отличным от года(квартал, месяц, день):
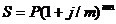
При
непрерывном наращивании процентов, то есть когда m стремится к бесконечности
(срок неограничен), а продолжительность интервала начисления стремится к нулю,
т.е. интервал начисления неограничен:
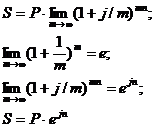
В
случае если процентные ставки разные в различные интервалы начисления, то:
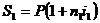
на
первом интервале начисления;
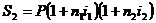 на втором
интервале; и т.д.
на втором
интервале; и т.д.
тогда
наращенная сумма на конец периода составит::
Операция
дисконтирования 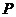
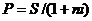
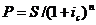
|
|
|
Коэффициент
наращения 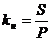
|
|
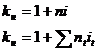 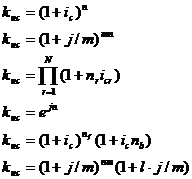
|
|
|
Определение
срока (периода 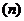 ) )
|
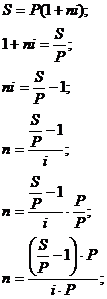
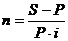
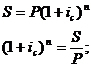
Для
нахождения неизвестной данной находящейся в степени находим натуральные
логарифмы:
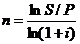
или
в случае сложной ставки с интервалом начисления отличным от года:
|
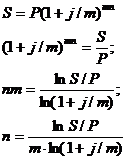
|
|
|
|
Определение
процентной ставки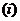
|
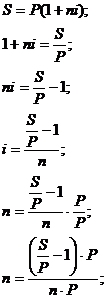
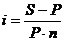
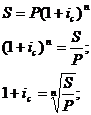
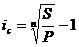
в
случае сложной ставки с интервалом начисления отличным от года:
|
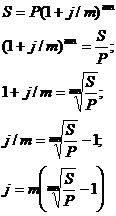
|
|
|
|
|
Правило
69/72 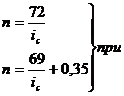 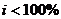
|
|
Наращенная
сумма 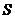
|
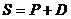 ;
;
где
«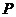 » фактически
получаемая сумма, а «
» фактически
получаемая сумма, а «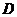 » дисконт
взимаемый в самом начале интервала, тогда:
» дисконт
взимаемый в самом начале интервала, тогда:
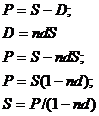 При
начислении сложной учетной ставки так же используется принцип начисления на
сумму долга+проценты, начисленные в предыдущих интервалах, или иными словами,
начисления «процентов на проценты»:
При
начислении сложной учетной ставки так же используется принцип начисления на
сумму долга+проценты, начисленные в предыдущих интервалах, или иными словами,
начисления «процентов на проценты»:
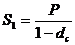
по
прошествии первого интервала; 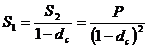
по
прошествии второго интервала;
и
т.д.
аналогично
случаю сложных ссудных процентов наращенная сумма на конец периода составит:
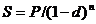
И
в случае интервала начисления отличного от года:
|
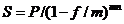
|
|
|
|
Сумма
дисконта 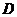
|
|
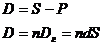
|
|
Операция
дисконтирования 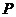
|
|
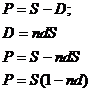 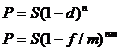
|
|
Коэффициент
наращения 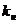
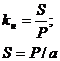
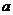 -коэффициент
дисконтирования;
-коэффициент
дисконтирования;
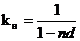
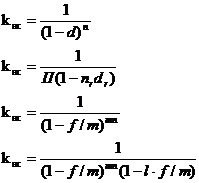
в
случае если число интервалов начисления не представляет собой точное число:
|
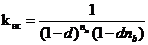
|
|
|
|
Определение
срока (периода 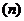 ) )
|
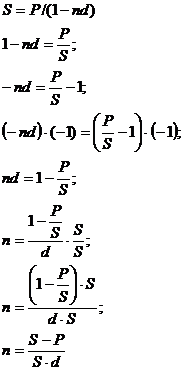
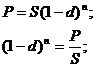
Для
нахождения неизвестной данной находящейся в степени находим натуральные
логарифмы:

В
случае интервала начисления отличным от года:
|
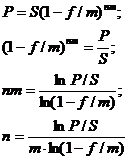
|
|
|
|
Определение
процентной ставки
|
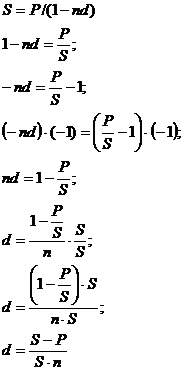
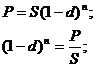
Избавляемся
от степени путем возведения обеих частей в 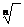 ;
;
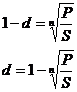
Или
в случае интервала начисления отличным от года аналогично:
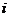 - относительная величина
ссудной ставки %
- относительная величина
ссудной ставки %
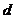 - относительная величина
учетной ставки %
- относительная величина
учетной ставки %
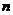 - период начисления
- период начисления
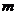 - интервал начисления
- интервал начисления
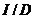 - общая сумма процентных денег на
период начисления
- общая сумма процентных денег на
период начисления
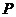 - первоначальный
капитал/денежная сумма
- первоначальный
капитал/денежная сумма
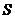 - наращенная сумма
- наращенная сумма
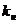 - коэффициент наращения
- коэффициент наращения
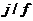 - номинальная годовая ставка
- номинальная годовая ставка
.2 Эквивалентность процентных ставок
Эквивалентные процентные ставки -
это такие процентные ставки разного вида, использование которых дают одинаковые
финансовые результаты при одинаковых начальных условиях.
) Эквивалентность простых учетных и
ссудных ставок
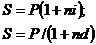
При условии одинаковых условий, т.е.
срока, первоначальной суммы, эквивалентная процентная ставка определяется:
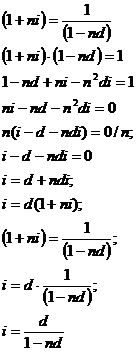
В случае определения эквивалентной
учетной ставки:
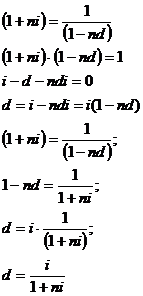
) Эквивалентность простых и сложных
ссудных ставок
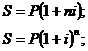
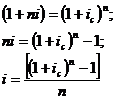
В случае если дана простая ссудная
ставка, а необходимо определить эквивалентную ей сложную учетную ставку, то:
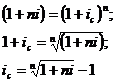
В том случае, если интервал
начисления по сложной ссудной ставке отличен от года, то простая ссудная ставка
определяется следующим образом:
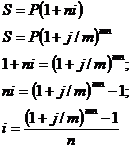
В случае противоположном этому, когда дана
простая ссудная ставка процентов, а необходимо определить эквивалентную ей
сложную ссудную ставку с интервалом начисления отличным от года, то
используется следующее уравнение эквивалентности:
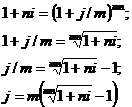
3) Если необходимо определить
сложную ссудную ставка с интервалом начисления в 1 год, эквивалентную сложной
ссудной ставке, но с иным интервалом начисления, отличным от года, то
используется следующее уравнение эквивалентности:
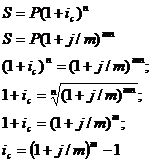
Данная ставка именуется эффективной
ставкой сложных процентов.
) Эквивалентность сложных учетной и
ссудной ставки
При определении данной сложной
учетной ставки эквивалентная сложная ссудная ставка будет определяться как:
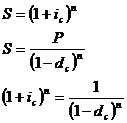
Возводим обе части уравнения в 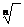 :
:
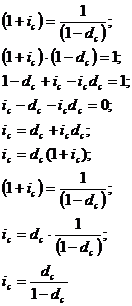
В ином случае, когда дана сложная
ссудная ставка процентов, а необходимо определить эквивалентную ей сложную
учетную ставку процентов, то используется следующая формула:
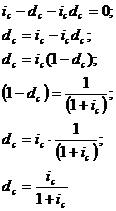

5) Уравнивающая ставка. Рассмотрим
случай, когда нам нужно определить что выгодней заплатить большую сумму, но
позже, или меньшую сумму, но раньше. Т.е. при условии, что 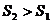 и
и 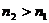 , необходимо
узнать что выгодней нам, заплатить
, необходимо
узнать что выгодней нам, заплатить 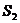 через
через 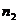 , или
заплатить меньшую сумму
, или
заплатить меньшую сумму 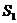 , но раньше,
через
, но раньше,
через 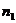 . Т.е. для
принятия такого решения, нужно определить современные величины этих значений. И
в таких случаях определяется уравнивающая ставка, которая выражает тот случай,
когда современные величины обоих значений совпадут т.е.
. Т.е. для
принятия такого решения, нужно определить современные величины этих значений. И
в таких случаях определяется уравнивающая ставка, которая выражает тот случай,
когда современные величины обоих значений совпадут т.е. 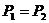 :
:
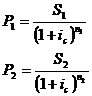 ;
;
Тогда определим уравнивающую ставку,
удовлетворяющую условию 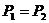 :
:
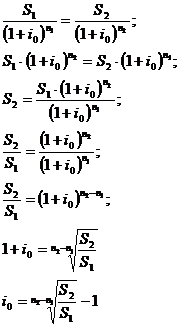
т.е. при всех 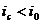 , или
сложной ставке меньшей, чем уравнивающая, будет выгодней взять меньшую сумму на
меньший срок, а в случае
, или
сложной ставке меньшей, чем уравнивающая, будет выгодней взять меньшую сумму на
меньший срок, а в случае 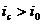 следует
использовать вариант с большей суммой и на больший срок.
следует
использовать вариант с большей суммой и на больший срок.
2.3 Учет инфляционного обесценения денег
Темп инфляции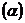

Наращенная сумма с учетом инфляции
будет равна:
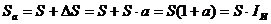
Индекс инфляции 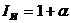
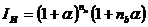 в случае, если период начисления
нецелое число;
в случае, если период начисления
нецелое число;
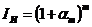 в случае, если задан уровень
инфляции за интервал меньше года.
в случае, если задан уровень
инфляции за интервал меньше года.
Формула Фишера:
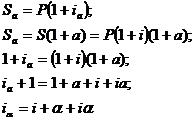
Значение 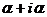 является
величиной, которую необходимо прибавить к реальной ставке доходности для
компенсации инфляционных потерь.
является
величиной, которую необходимо прибавить к реальной ставке доходности для
компенсации инфляционных потерь.
Ссудные ставки с учетом инфляции
Простая ссудная ставка с учетом
инфляции:
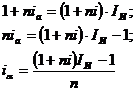
Сложная ссудная ставка процентов с
погодичным интервалом начисления с учетом инфляции:
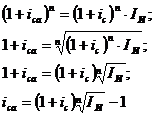
Сложная ссудная ставка процентов с
интервалом начисления, отличным от года, с учетом инфляции:
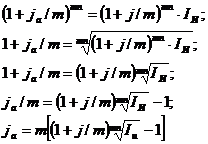
Учетные ставки с учетом инфляции
Простая учетная ставка с учетом
инфляции:
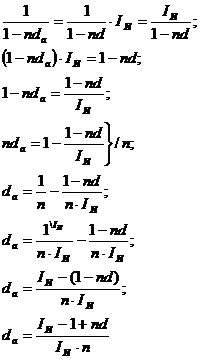
Сложная учетная ставка процентов с
погодичным интервалом начисления с учетом инфляции:
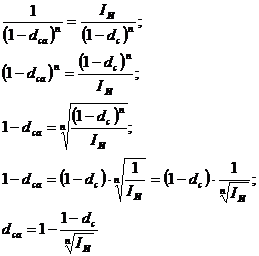
Сложная учетная ставка процентов с
интервалом начисления, отличным от года, с учетом инфляции:
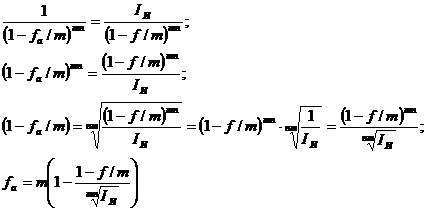
.4 Аннуитеты
Аннуитет (финансовая рента) - поток
однонаправленных платежей с равными интервалами между последовательными
платежами в течение определенного количества лет.
Аннуитет постнумерандо
(обыкновенный) - платежи осуществляются в конце интервалов
Наращенная сумма всего аннуитета:
Сумма первого платежа, на который
будут начисляться проценты, составит:
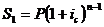 ;
;
Для второго платежа проценты будут
начисляться на один год меньше:
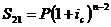 ; и т.д.
; и т.д.
На последний платеж, произведенный в
конце n-го года, проценты уже не начисляются:
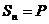 ; тогда общая наращенная сумма будет
составлять сумму всех платежей
; тогда общая наращенная сумма будет
составлять сумму всех платежей 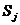 :
:
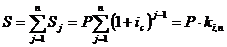 т.е.:
т.е.:
Используем математическую формулу
для суммы членов геометрической прогрессии:
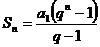
Где 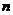 сумма членов геометрической
прогрессии или общее количество платежей, первый член прогрессии
сумма членов геометрической
прогрессии или общее количество платежей, первый член прогрессии 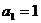 , а
, а 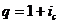 , тогда:
, тогда:
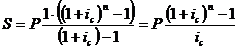
Т.е. коэффициент наращения для
аннуитета постнумерандо составляет:
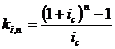
Современное значение каждого платежа
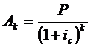
Следовательно, современная величина
всего аннуитета:
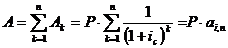
Снова используем формулу определения суммы
членов геометрической прогрессии:
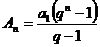 ;
;
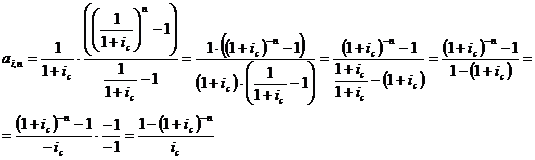
То есть современная величина всего
аннуитета 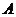 составит
составит
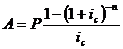
Определим взаимосвязь наращенной и
современной сумм аннуитета:
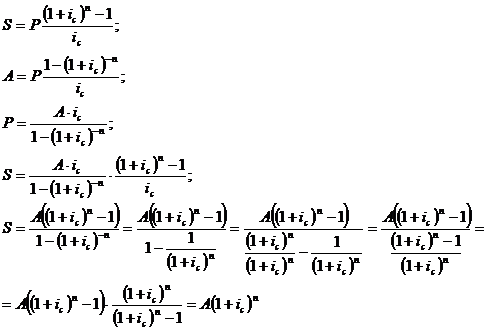
Определение размера очередного
платежа:
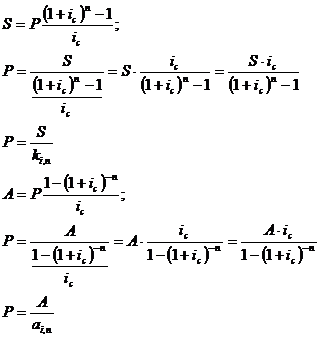
Срок аннуитета:
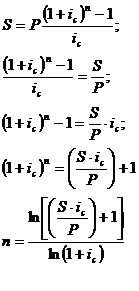
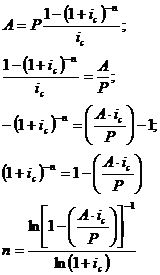
Для определения аннуитета
пренумерандо нужно формулы наращенной суммы или современной стоимости аннуитета
постнумерандо умножать на  :
:
Коэффициент наращения для аннуитета
пренумерандо составит:
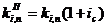
И соответственно коэффициент
приведения для аннуитета пренумерандо:
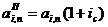
Каждая современная величина
аннуитета пренумерандо 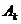 будет
больше на
будет
больше на 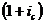 , т.к.
дисконтирование аннуитета постнумерандо по заданной ставке
, т.к.
дисконтирование аннуитета постнумерандо по заданной ставке 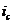 проводиться
на один раз меньше, чем у аннуитета пренумерандо. Т.е. современная величина
всего аннуитета пренумерандо составит:
проводиться
на один раз меньше, чем у аннуитета пренумерандо. Т.е. современная величина
всего аннуитета пренумерандо составит:
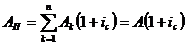
Вечные аннуитеты (когда срок
аннуитета 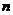 не
ограничен):
не
ограничен):
Постнумерандо: 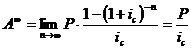
Пренумерандо: 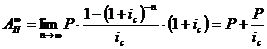
При увеличении аннуитета с каждым
интервалом на определенную величину 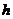 ,
,
т.е. платежи представят собой
следующий ряд:
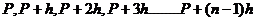
Наращенная сумма всего аннуитета
тогда составит:
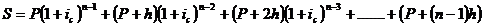
Умножим обе части на 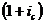
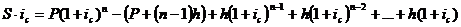
Видно, что часть равенства
представляет собой сумму членов геометрической прогрессии, где 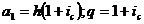 отсюда мы
получаем:
отсюда мы
получаем:
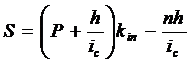
Найдем современное значение
аннуитета А:
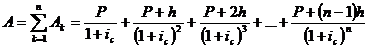 ,
,
Умножим обе части на 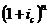 , тогда
получим:
, тогда
получим:
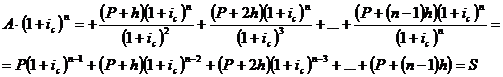
Т.е. верна формула взаимосвязи
наращенной и современной сумм аннуитета:
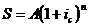 , откуда:
, откуда:
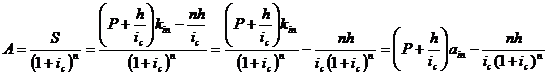
Конверсия аннуитетов, т.е. изменение
начальных параметров аннуитета, после которого новый аннуитет был бы
эквивалентен данному, то есть их современные величины равны к одному и тому же
моменту времени:
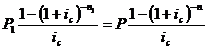 , тогда:
, тогда:
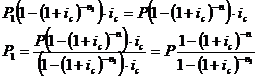
.5 Дивиденды и проценты по ценным бумагам.
Доходность по операциям с ценными бумагами
Долговые ценные бумаги обычно имеют
фиксированную процентную ставку и являются обязательством выполнить полную
сумму долга с процентами на определенную дату в будущем. По дисконтным долговым
ценным бумагам доход представляет собой скидку с номинала.
Долевые ценные бумаги представляют
собой непосредственную долю держателя в реальной собственности и обеспечивают
получение дивиденда в неограниченное время
Расчет доходности по облигациям:
Курс облигаций:
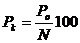
Доход по облигации
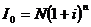

Ссудная ставка, эквивалентная доходу
по облигациям:
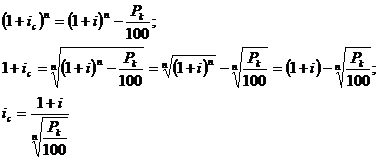
Расчет доходности по акциям
Валовый доход от покупки акций
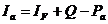 который состоит из:
который состоит из:
Доход от дивидендов: 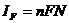 (срок *
величина дивидендов * номинал)
(срок *
величина дивидендов * номинал)
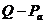 -разница между покупной и продажной
ценами акции
-разница между покупной и продажной
ценами акции
Ссудная ставка, эквивалентная доходу
от акции
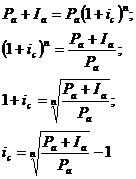
Литература
1. Андрюшин
С., Кузнецова В. Приоритеты денежно-кредитной политики центральных банков в
новых условиях // Вопросы экономики. - 2011. - № 6. - С. 57 - 59.
. Ануреев
С.В. Денежно-кредитная политика, диспропорции и кризисы. - М.: Кнорус, 2009. -
448 с.
. Баликоев
В.З. Общая экономическая теория. - М.: Омега-Л, 2011. - 688 с.
. Гусейнов
Р.М., Семенихина В.А. Экономическая теория. - М.: Омега-Л, 2009. - 448 с.
. Жученко
О.А. Инструменты денежно-кредитной политики и их использование // Вестник
государственного гуманитарного университета. - 2009. - № 3. - С. 65 - 73.
. Коршунов
Д.А. О построении модели общего равновесия для экономики России // Деньги и
кредит. - 2011. - № 2. - С. 56 - 67.
. Криворотова
Н.Ф., Урядова Т.Н. Актуальные проблемы денежно-кредитной политики России //
Terra Economicus. - 2012. - № 3. - С. 24 - 26.
. Лукша
Н. Инфляция и денежно-кредитная политика // Экономико-политическая ситуация в
России. - 2012. - № 12. - С. 9 - 11.
. Малхасян
А.М. Направления совершенствования денежно-кредитной политики Российской
Федерации // Финансы и кредит. - 2012. - № 43. - С. 51 - 62.
. Матовников
М.Ю. К вопросу об инструментах денежно-кредитной политики // Деньги и кредит. -
2012. - № 1. - С. 32 - 34.
. Милюков
А.И., Пенкин С.А. Денежно-кредитная политика как фактор роста российской
экономики // Банковское дело. - 2011. - № 9. - С. 21 - 24.
. Улюкаев
А.В. Новые вызовы денежно-кредитной политики // Деньги и кредит. - 2012. - №
11. - С. 3 - 5.
. Экономическая
теория / Под ред. В.Д. Камаева. - М.: Владос, 2007. - 592 с.
. Экономическая
теория / Под ред. Е.Н. Лобачевой. - М.: Юрайт, 2011. - 522 с.