Синтез систем автоматического управления
Литературный обзор методов синтеза
систем автоматического управления
Под синтезом системы автоматического
управления понимается направленный расчет, имеющий конечной целью отыскание
рациональной структуры системы и установление оптимальных величин параметров ее
отдельных звеньев. По отношению к основе синтеза в настоящее время имеются
разные точки зрения.
Синтез можно трактовать как
инженерную задачу, сводящуюся к такому построению системы, при котором
обеспечивается выполнение технических требований к ней. Подразумевается, что из
многих возможных решений инженер, проектирующий систему, будет выбирать те,
которые являются оптимальными с точки зрения существующих конкретных условий и
требований к габаритам, весу, простоте, надежности и т. п.
Иногда в понятие инженерного синтеза
вкладывается еще более узкий смысл и рассматривается синтез, имеющий целью
определение вида и параметров корректирующих средств, которые необходимо
добавить к некоторой неизменяемой части системы (объект с управляющим
устройством), чтобы обеспечить требуемые динамические качества.·
При инженерном синтезе системы
автоматического управления необходимо обеспечить, во-первых, требуемую точность
и, во-вторых, приемлемый характер переходных процессов.
В настоящее время для целей синтеза
широко используются вычислительные машины, однако также эффективно применяются
и расчетные методы проектирования. Среди расчетных методов синтеза САУ, прежде
всего, следует выделить корневые методы, метод корневых годографов, метод
стандартных переходных характеристик, а также метод логарифмических амплитудных
характеристик. Все перечисленные методы широко применяются на практике. В
данной работе производится синтез САУ наиболее простым корневым методом,
разработанным Соколовым Т. Н.
Определение передаточных функций по
задающему и возмущающему воздействиям
Передаточная функция первого звена:
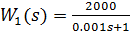
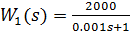
Передаточная функция
второго звена:
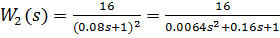
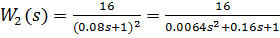
Передаточная функция
третьего звена:
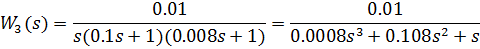
Передаточная функция
разомкнутой системы:
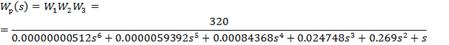
Передаточная функция
замкнутой системы:
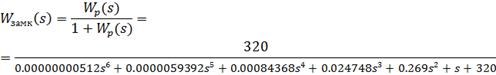
Передаточная функция
разомкнутой системы по возмущению:
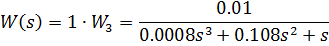
Передаточная функция
замкнутой системы по возмущению:
Передаточная функция
замкнутой системы относительно ошибки по возмущающему воздействию:
Передаточная функция
замкнутой системы относительно ошибки по задающему воздействию:
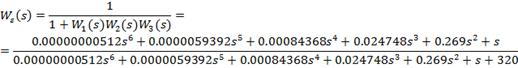
Построение модели
исследуемой САУ в среде MatLab(Simulink)
Рис. 1. Модель
нескорректированной исследуемой системы
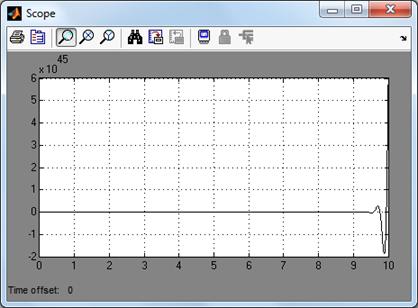
Рис. 2. Переходная
характеристика нескорректированной исследуемой системы
Из рисунка 2 видно, что
система неустойчива. Следовательно, на данном этапе нельзя определить
показатели качества.
Оценка устойчивости
замкнутой нескорректированной системы регулирования по критерию Гурвица
система автоматическое
управление синтез
Критерий разработан для
анализа устойчивости САУ в форме определителей, составляемых из коэффициентов
характеристического уравнения.
Найдем
характеристическое уравнение системы:
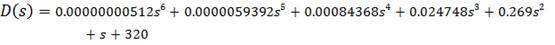
Составим определитель
Гурвица:
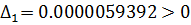
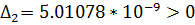
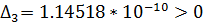
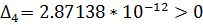
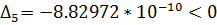
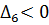
Так как определители
Гурвица не имеют одинаковые знаки со знаком первого коэффициента
характеристического уравнения, то система неустойчива.
Оценка устойчивости
замкнутой системы по критерию Михайлова
Годограф характеристического
вектора, т.е. кривую, которую описывает характеристический вектор при изменении
частоты от 0 до +∞, называют кривой Михайлова. При аn>0 кривая
Михайлова начинается в положительной вещественной полуоси.
Критерий Михайлова: для
того чтобы система была устойчива, необходимо и достаточно, чтобы при а0>0
ее кривая Михайлова, начинаясь с положительной вещественной полуоси,
последовательно обходила n квадрантов в положительном направлении (против
часовой стрелки).
Характеристическое
уравнение замкнутой системы:
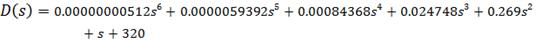
В системе MatLab
построим годограф Михайлова:
=[0.00000000512
0.0000059392 0.00084368 0.024748 0.269 1 320]; den=[1]; w=0.0001:0.01:10;
=freqs(num,den,w);=real(APK); v=imag(APK); (u,v); grid
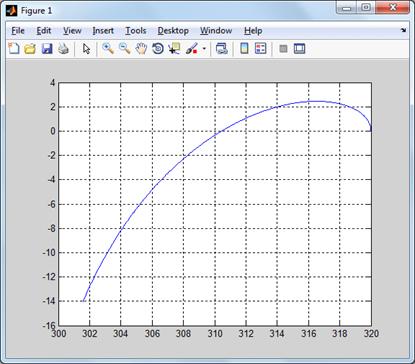
Рис. 3. Годограф
Михайлова нескорректированной системы
По рис. 3 можно сделать
вывод, что система неустойчива, так как годограф Михайлова при изменении
частоты от 0 до +∞, начав движение из точки, лежащей на положительной
вещественной полуоси, не проходит последовательно 6 квадрантов.
Определение устойчивости
САУ по критерию Найквиста
Критерий позволяет
судить об устойчивости замкнутой системы по виду АФХ разомкнутой системы.
Передаточная функция
разомкнутой системы:
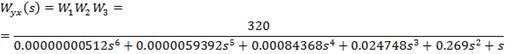
Построим АФХ в среде
MatLab:
=tf([320],[0.00000000512
0.0000059392 0.00084368 0.024748 0.269 1]); nyquist(sys); grid
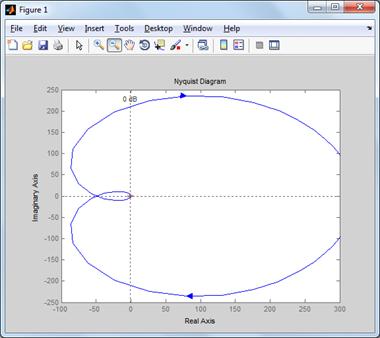
Рис. 4.АФХ разомкнутой
нескорректированной системы
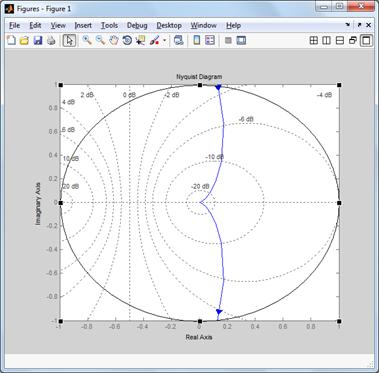
Рис. 5. АФХ разомкнутой
системы (увеличенный вариант)
Так как АФХ разомкнутой
системы охватывает точку (-1;j0), то система неустойчива.
Оценка запаса
устойчивости замкнутой системы по ЛАХ и ЛФХ разомкнутой системы
Передаточная функция
разомкнутой системы:
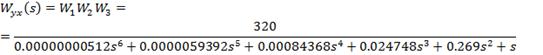
Текст программы:
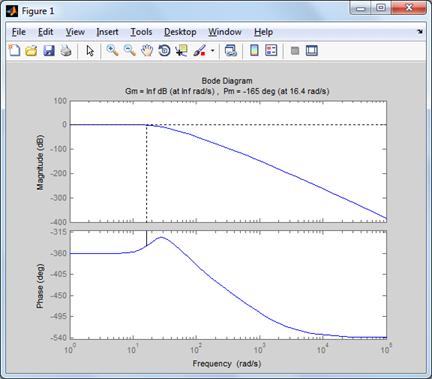
Рис.6. АФХ и ЛФХ
разомкнутой САУ
Поскольку в области
положительной ЛАЧХ присутствуют переходы ЛФЧХ через прямые ±π(2i+1),
где i=0,1,2…, согласно критерию Найквиста для ЛЧХ замкнутая САУ
неустойчива.
Получение корректирующего
устройства, обеспечивающего заданные показатели качества работы системы по
методу Соколова
Определим разность
порядков знаменателя (n1) и числителя (m1) передаточной функции замкнутой
нескорректированной системы (n1− m1).
Передаточная функция
замкнутой системы:
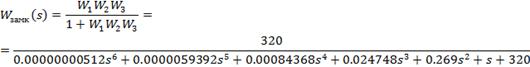=0; n1=6
Формируем желаемую
передаточную функцию замкнутой системы, на основе нормированных передаточных
функций
Определяем порядок
астатизма: ν=1.
Для астатизма первого
порядка нормированная передаточная функция имеет следующий вид:
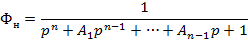
Найдем порядок числителя
и знаменателя нормированной передаточной функции:
m=ν−1=0=(n1−m1)+ν−1=6
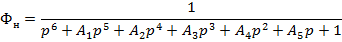
Выбираем коэффициенты
нормированной передаточной функции для максимальной степени устойчивости.
Подставим из таблицы коэффициенты и получим:
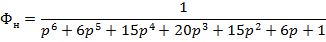
Построим модель
нормированной передаточной функции в Simulink и определим время ее переходного
процесса
Рис. 7. Модель
нормированной передаточной функции
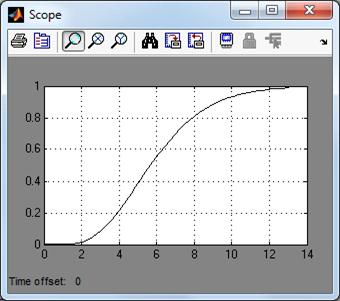
Рис. 8. Переходной
процесс нормированной передаточной функции
Перейдем от
нормированной к желаемой передаточной функции на основании теоремы масштабов
преобразования Лапласа с использованием следующих соотношений:
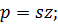
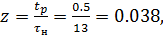
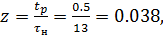
где−аргумент
нормированной передаточной функции;−комплексный аргумент Лапласа;−коэффициент
масштаба времени;−заданное время регулирования;
τн−время
регулирования нормированной передаточной функции.
Определим желаемую
передаточную функцию:
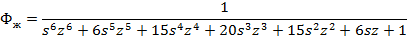
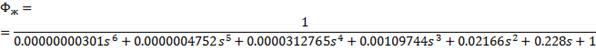
Построим модель желаемой
передаточной функции в Simulink:
Рис. 9. Модель желаемой
системы
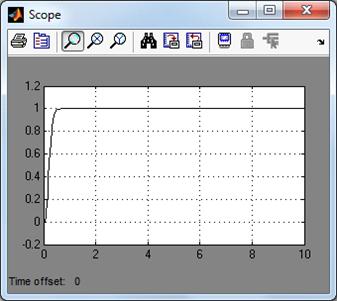
Рис. 10. Переходная
характеристика желаемой системы
Определим корректирующее
устройство
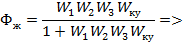
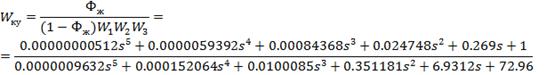
Построим модель
скорректированной системы в Simulink:
Рис. 11. Модель
скорректированной системы при последовательном включении КУ
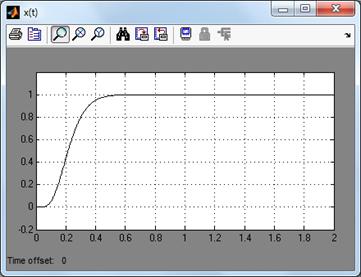
Рис. 12. Переходной
процесс скорректированной передаточной функции
Разделим корректирующее
устройство на два−параллельное и последовательное. Параллельное
корректирующее устройство определим через критерий Гурвица:
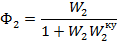
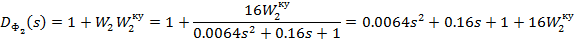
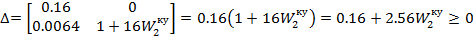
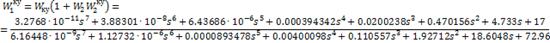
Аппроксимируем
передаточную функцию корректирующего устройства:
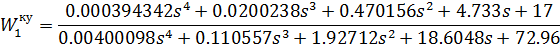
Составление структурной
схемы скорректированной системы, оценка запаса устойчивости, определение
показателей качества и точности
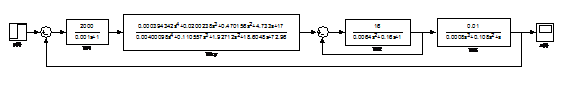
Рис. 13. Модель
скорректированной системы
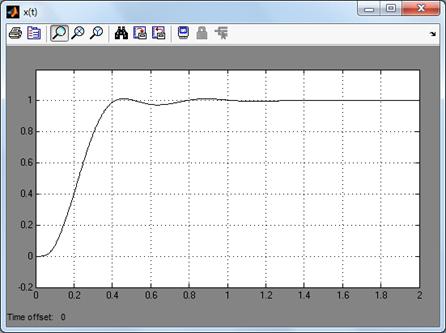
Рис. 14. Переходной
процесс скорректированной системы
Из переходного процесса
видно, что система устойчива. Определим показатели качества из рис. 14:
Время регулирования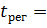 
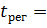0.33с
Перерегулирование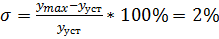 
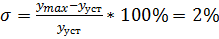
Передаточная функция
замкнутой системы по ошибке:
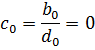
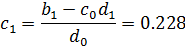
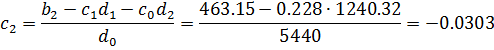
Передаточная функция
разомкнутой скорректированной системы:
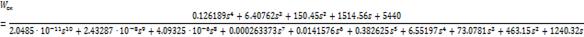
Характеристическое
уравнение разомкнутой скорректированной САУ:
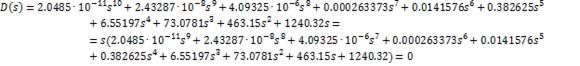
То есть система в
разомкнутом состоянии обладает астатизмом I порядка, и среди корней этого
уравнения есть нулевой. Поэтому согласно теореме Ляпунова, система находится на
границе устойчивости.
По критерию Найквиста
для астатичных систем, для устойчивости замкнутой САУ необходимо и достаточно,
чтобы АФХ разомкнутой системы, дополненная дугой бесконечного радиуса до
положительной полуоси, не охватывала точку с координатами (-1; j0). АФХ
разомкнутой системы построена в Matlab.
=tf([0.126189 6.40762
150.45 1514.56 5440], [0.000000000020485 0.0000000243287 0.00000409325
0.000263373 0.014157 0.382625 6.55197 73.0781 463.15 1240.32 0]);(sys); grid
axis([-1 1 -1 1])
Рис. 15. АФХ разомкнутой
скорректированной системы
По рис. 15 видно, что
АФХ разомкнутой системы не охватывает точку (-1; j0), следовательно, замкнутая
САУ устойчива.
Найдены запасы
устойчивости замкнутой системы. Запас устойчивости по модулю h=0.65. Запас
устойчивости по фазе φ=60°.
Построение кривой
D-разбиения в плоскости одного параметра
Для исследования
скорректированной системы на области устойчивости методом D-разбиения в
плоскости одного параметра в структуру САУ введен дополнительный коэффициент
усиления K (рис.16).
Рис.16. Структурная
схема скорректированной системы с коэффициентом усиления
Передаточная функция
замкнутой скорректированной системы:
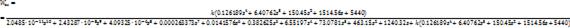
Характеристическое
уравнение:
=>
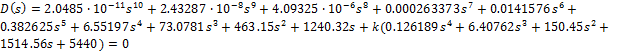
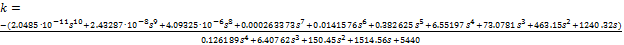
=[0.000000000020485
0.0000000243287 0.00000409325 0.000263373 0.014157 0.382625 6.55197 73.0781
463.15 1240.32 0]; =[0.126189 6.40762 150.45 1514.56 5440]; w=-150:0.01:150;
=freqs(num,den,w); u=real(APK); v=imag(APK); (u,v); grid
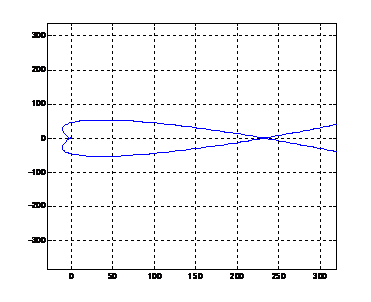
Рис. 17. Кривая
D-разбиения в плоскости одного параметра
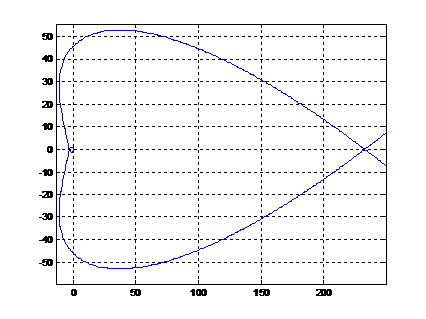
Рис. 17.1. Кривая
D-разбиения в плоскости одного параметра (увеличенное)
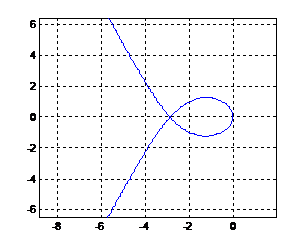
Рис. 17.2. Кривая
D-разбиения в плоскости одного параметра (увеличенное)
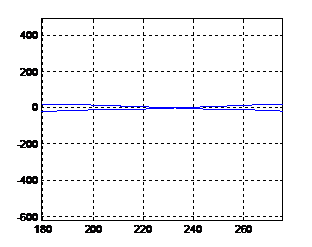
Рис. 17.2. Кривая
D-разбиения в плоскости одного параметра (увеличенное)
Область I является
претендентом на область устойчивости. Чтобы установить является ли данная
область областью устойчивости, выбрано значение из этой области k=−1. При
этом характеристическое уравнение примет вид:
Коэффициенты
характеристического уравнения:
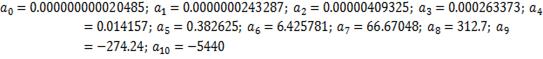
Для определения
устойчивости по критерию Гурвица написана следующая программа:
isa(D, 'lti')
[B, D] = tfdata(D,
'v');= 1; length(D(:)) < 4= NaN; Mnrs = NaN;any(D(:) <= 0)= 0;= D(:);=
length(D) - 1; % Размеры матрицы Гурвица= [zeros(n-1, 1); D(end:-1:1);
zeros(n-2, 1)];= zeros(n, n); % Заготовка матрицы Гурвица= zeros(n-2, 1); %
Вектор миноровi = 1:n(:, i) = A((n - i)*2 + 1:3*n - 2*i); i = 2:n-1(i-1) =
det(Mtrx(1:i,1:i));any([D(:); Mnrs(:)] <= 0)= 0;
Вызвана следующая функция:
>> [A, B, C] =
raus_gur([0.000000000020485 0.0000000243287 0.00000409325 0.000263373 0.0141576
0.382625 6.425781 66.67048 312.7 -274.24 -5440])=0=1.0e-012 *
.0942
.0000
.0000
.0000
.0000
.0000
.0007
.6611=1.0e+003 *1
through 8
.0000 0.0000 0.0004
0.0667 -0.2742 0 0 0
.0000 0.0000 0.0000
0.0064 0.3127 -5.4400 0 0
0.0000 0.0000 0.0004
0.0667 -0.2742 0 0
0.0000 0.0000 0.0000
0.0064 0.3127 -5.4400 0
0 0.0000 0.0000 0.0004
0.0667 -0.2742 0
0 0.0000 0.0000 0.0000
0.0064 0.3127 -5.4400
0 0 0.0000 0.0000 0.0004
0.0667 -0.2742
0 0 0.0000 0.0000 0.0000
0.0064 0.3127
0 0 0 0.0000 0.0000
0.0004 0.0667
0 0 0 0.0000 0.0000
0.0000 0.00649 through 10
0
0
0
0
0
0
0
.4400 0
.2742 0
.3127 -5.4400
Так как A=0, то система
неустойчива. Проверим на устойчивость II область. Для этого примем k=1. Тогда
характеристическое уравнение примет вид:
Коэффициенты
характеристического уравнения:
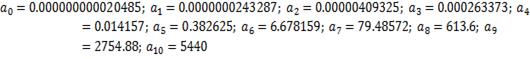
Вызвана следующая
функция:
>> [A, B, C] =
raus_gur([0.000000000020485 0.0000000243287 0.00000409325 0.000263373 0.0141576
0.382625 6.678159 79.48572 613.5 2754.88 5440])=1=1.0e-012 *
.0942
.0000
.0000
.0000
.0000
.0000
.7048=1.0e+003 *1
through 8
.0000 0.0000 0.0004
0.0795 2.7549 0 0 0
.0000 0.0000 0.0000
0.0067 0.6135 5.4400 0 0
0.0000 0.0000 0.0004
0.0795 2.7549 0 0
0.0000 0.0000 0.0000
0.0067 0.6135 5.4400 0
0 0.0000 0.0000 0.0004
0.0795 2.7549 0
0 0.0000 0.0000 0.0000
0.0067 0.6135 5.4400
0 0 0.0000 0.0000 0.0004
0.0795 2.7549
0 0 0.0000 0.0000 0.0000
0.0067 0.6135
0 0 0 0.0000 0.0000
0.0004 0.0795
0 0 0 0.0000 0.0000
0.0000 0.00679 through 10
0
0
0
0
0
0
0
.4400 0
.7549 0
.6135 5.4400
Так как A=1, то система
устойчива. Вектор В содержит значения диагональных определителей кроме первого
элемента и последнего определителя, так как значение внешнего определителя
всегда будет иметь тот же знак, что и предыдущий. Согласно методу Гурвица,
чтобы система была устойчива, все эти определители должны оказаться
положительными.
Матрица С − сам
определитель Гурвица.
Следовательно, при k=1
САУ устойчива. Поскольку САУ устойчива при значении параметра k, выбранного из
области−претендента, то эта область является областью устойчивости.
Исследование условий
возникновения периодических движений в нелинейной системе
Построена модель
исследуемой САУ с нелинейным элементом типа насыщение (модель представлена на
рис. 20):
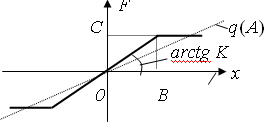
Рис 18. Нелинейный
элемент типа насыщение
Для нелинейности типа
насыщение, при A≥B:
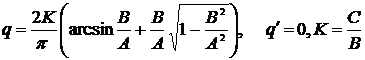
В соответствии с
заданием B=C=1.
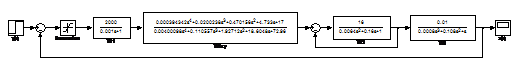
Рис. 19. Модель
нелинейной САУ
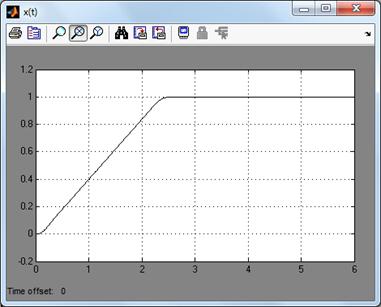
Рис.20. Переходная
характеристика нелинейной системы
Из переходной
характеристики видно, что система является устойчивой.
Поскольку линейная часть
системы устойчива, проверку САУ на наличие автоколебаний осуществлена методом
Гольдфарба с помощью системы Matlab. Для этого построены годографы линейной
Wл(jω) и нелинейной Zн(A) частей САУ.
=[0.126189 6.40762
150.45 1514.56 5440]; =[0.000000000020485 0.0000000243287 0.00000409325
0.000263373 0.0141576 0.382625 6.55197 73.0781 463.15 1240.32 0];
w=-100:0.1:100;=freqs(num,den,w); u=real(APK);v=imag(APK);=0; for a=0.1:0.1:50,
k=k+1;=-1/(2/pi*(asin(0.1/a)+(0.1/a)*sqrt(1-0.01/(a*a))));(k)=real(q);
v1(k)=imag(q); end(u,v,u1,v1)
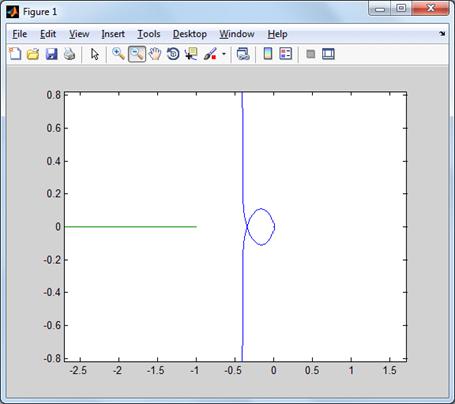
Рис. 21. АФХ линейной и
нелинейной части
По рис. 21 видно, что
АФХ линейной и нелинейной части не пересекаются, что указывает на отсутствие
периодических движений.
Анализ абсолютной
устойчивости нелинейной системы
Анализ абсолютной
устойчивости проведен по методу Попова. Согласно этому методу в системе Matlab
построен модифицированный годограф W*(jω), у
которого вещественная часть: U*(jω)=Re(W(jω)), а
мнимая часть: V*(jω)= ωIm(W(jω)).
Передаточная функция
разомкнутой скорректированной системы:
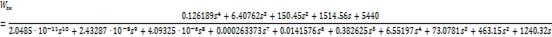
=1; w=0; u=[];
v=[];w<=100,s=j*w;=(0.126189*s^4+6.40762*s^3+150.45*s^2+1514.56*s+544)/(0.000000000020485*s^10+0.0000000243287*s^9+0.00000409325*s^8+0.000263373*s^7+0.0141576*s^6+0.382625*s^5+6.55197*s^4+73.0781*s^3+463.15*s^2+1240.32*s)(k)=real(f);v(k)=imag(f)*w;=w+0.01;k=k+1;(u,v);grid
Для нелинейного звена
типа насыщения (рис. 18) K=C/B=1.
Поскольку через точку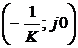
,
соответствующую точке (-1, j0) можно провести прямую так, чтобы
модифицированный годограф W*(jω) находился справа
от нее (рис. 22) и не пересекался с ней, то исследуемая САУ абсолютно
устойчива.
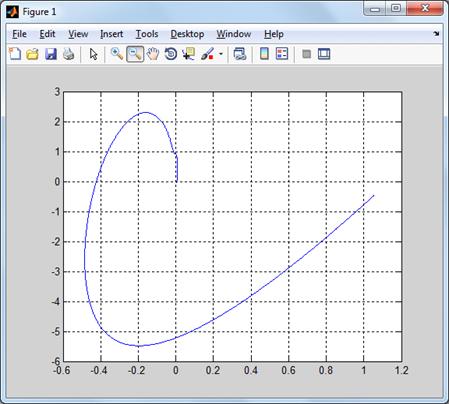
Рис. 22.
Модифицированный годограф W*(jω)
Заключение
В данной работе проведен
анализ заданной САУ на устойчивость различными методами, выявлена
неустойчивость исходной системы.
Методом Соколова Т.Н.
синтезированы корректирующие устройства с целью получения САУ, соответствующей
заданным требованиям. Проведен анализ скорректированной САУ на устойчивость,
определены запасы устойчивости и показатели качества и точности, которые
соответствуют заданным требованиям: перерегулирование σ=2%,
время регулирования tрег=0,33 с.
В скорректированную САУ
введен нелинейный элемент типа «насыщение», в результате чего получена
нелинейная САУ. Методом Гольдфарба определено отсутствие автоколебаний в
нелинейной САУ, методом Попова установлено, что исследуемая САУ абсолютно
устойчива.
Список использованной
литературы
1. Методические указания к курсовой работе по дисциплине
"Теория управления" для студентов специальности 210100 -
"Управление и информатика в технических системах" Уфимск. гос. авиац.
техн. ун-т; Сост. Б.Г. Ильясов, Л.А. Болотовская. Уфа, 1998.- 24 с.
. Бесекерский В.А., Попов Б.П. Теория систем автоматического
управления. - М. Наука, 1976. - 605 с.