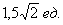Исследование функции
1. Исследовать функцию и построить ее график
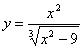
Решение
. Область определения.
Все предусмотренной формулой функции операции, кроме деления, - т.
е. операции сложения и возведения в натуральную степень - выполняются при любых
значениях аргумента х, а деление возможно, если делитель не равен нулю. Поэтому
данная функция определена, если знаменатель задающей ее дроби не равен нулю:
если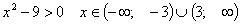 
, Таким образом, 
.
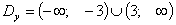2) Точки пересечения с осями координат:
С осью ОХ т. е. у=0: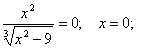 
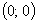- точка пересечения с осою ОХ.
С осью ОУ т. е. х=0: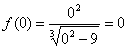 
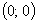- точка пересечения с осою ОУ.
) Исследуем на четность нечетность. Проверим выполнимость
равенств: если f(-x) = f(x), то
функция четная, если f(-x) = - f(x), то функция нечетная, при х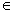
D(y). Если равенства не выполняются, то функция ни четная ни
нечетная.
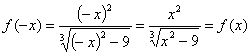
Функция четная.
) Исследуем на наличие асимптот.
Вертикальные асимптоты.
Поскольку вертикальные асимптоты следует искать лишь в точках
разрыва данной функции, единственным «кандидатом» в нашей задаче является
прямая х=-3 и х=3.
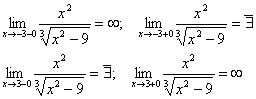
Следовательно х=-3 и х=3 точки разрыва 2-го рода и х=-3 и х=3 -
вертикальные ассимпноты.
Наклонные и горизонтальные асимптоты.
Уравнение наклонной асимптоты графика функции 
имеет вид
где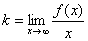 
; 
.
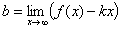В частности, получается, что если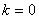 
, а 
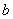при этом существует, по этим формулам
находится горизонтальная асимптота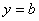 
.
Выясним наличие наклонных асимптот.
;
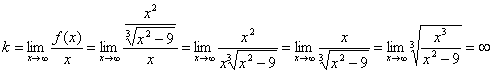Наклонных асимптот нет.
. Найдем экстремумы и интервалы монотонности. Действуем по
следующей схеме.
Вычислим первую производную данной функции:
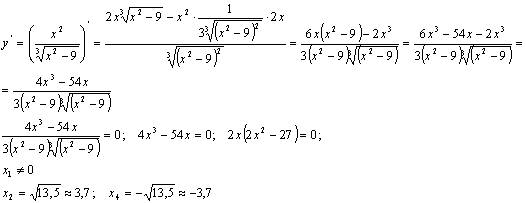
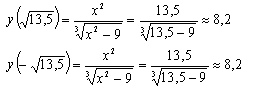
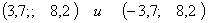- точки подозрительные на экстремум.
Исследуем поведение функции справа и слева от подозрительных
точки и точек в которых функция не существует.
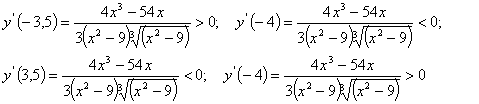
Значит на промежутке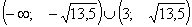
функция убывает, а на промежутке и 
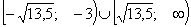функция возрастает.
Занесем полученные данные в таблицу:
у 
т.
min
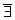
т.
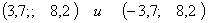- точка минимума.
6. Найдем интервалы выпуклости функции и точки перегиба.
Для этого поступаем так.
Вычислим вторую производную данной функции:
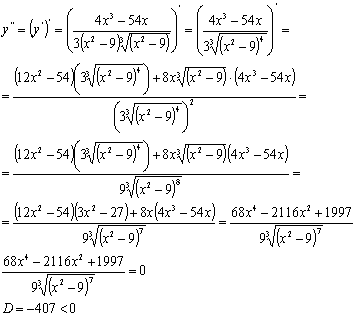
(0; 0) - точек подозрительная на перегиб нет.
Исследуем поведение функции справа и слева от точек в которых
функция не существует.
2. Задание 2
Найти площадь фигуры, ограниченной графиками функций
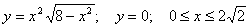
Решение
Сделаем чертеж:
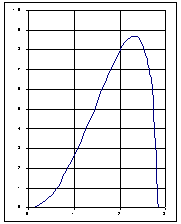
Вычислим площадь полученной области с пределами интегрирования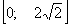 
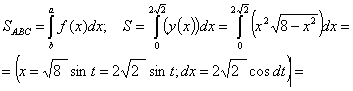
Ответ: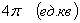 
3. Задание 3
. Вычислить длину дуги кривой, заданной уравнением
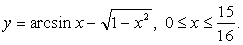
Решение
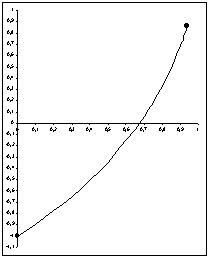
Вычислим длину дуги кривой по формуле:
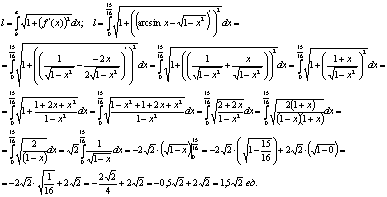
Ответ: 