Исследование функции. Вычисление производных функции
Федеральное
агентство связи
Сибирский
Государственный Университет Телекоммуникаций и Информатики
Межрегиональный
центр переподготовки специалистов
Контрольная
работа
По
дисциплине: Математический анализ
Выполнил: Калинин Максим
Проверил: Агульник Ольга Николаевна
Новосибирск,
2015 г
1. Найти пределы
а)
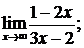 б)
б) 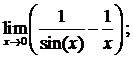 в)
в) 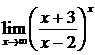 .
.
Решение.
Воспользуемся
формулами:
 (19)
(19)
 (20)
(20)
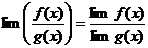 (21)
(21)
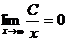 (22)
(22)
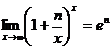 (23).
(23).
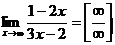 -
воспользуемся тождественными преобразованиями: разделим числитель и знаменатель
выражения на
-
воспользуемся тождественными преобразованиями: разделим числитель и знаменатель
выражения на 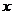 .
.
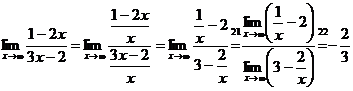 .
.
Поскольку
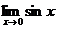 ~
~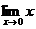 , то
, то 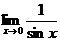 ~
~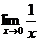 , тогда
, тогда
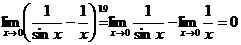 .
.
в)
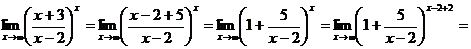
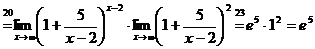
Ответ:
а) 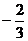 , б) 0, в)
, б) 0, в)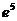 .
.
.
Найти производные 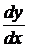 данных функций
данных функций
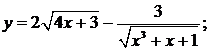 б)
б) 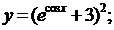
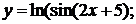 г)
г) 
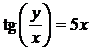 .
.
Решение.
Свойства
производной:
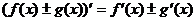 (24)
(24)
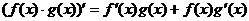 (25)
(25)
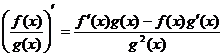 (26)
(26)
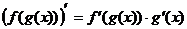 (27)
(27)
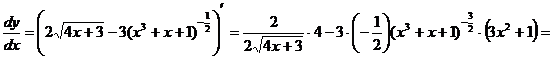
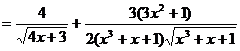 .
.
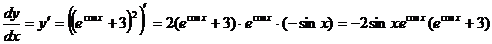 .
.
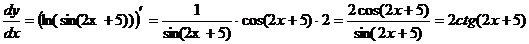 .
.
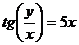 -
функция задана неявно.
-
функция задана неявно.
Продифференцируем
обе части равенства:
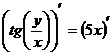 ;
;
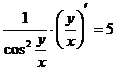 ;
;
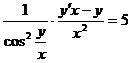 ;
;
Выразим
производную 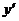 :
:
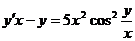 ;
;
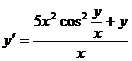 ;
;
 .
.
Ответ:
а) 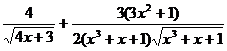 ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
3.
Исследовать методами дифференциального исчисления функцию 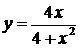 . Используя результаты исследования, построить её
график
. Используя результаты исследования, построить её
график
Решение.
Схема исследования функции
.
Найдем область определения функции: 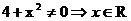 . Точек
разрыва нет. 2. Проверим, не является ли функция четной или нечетной; проверим
также, не является ли она периодической.
. Точек
разрыва нет. 2. Проверим, не является ли функция четной или нечетной; проверим
также, не является ли она периодической.
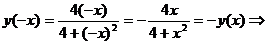 функция
нечетная, ее график симметричен относительно начала координат, непериодическая
функция
нечетная, ее график симметричен относительно начала координат, непериодическая
.
Найдем точки пересечения графика функции с осями координат.
Пересечение
с 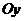 :
: 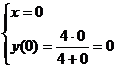 точка
точка 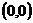
Пересечение
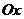 :
: 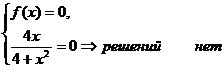 .
.
.
Найдем производную функции и ее критические точки.
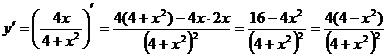
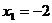 ,
, 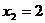 - критические точки.
- критические точки.
5.
Найдем промежутки монотонности и экстремумы функции.
Определим
знак производной на каждом из интервалов методом частных значений:
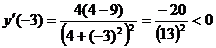 ,
, 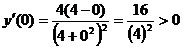 ,
,
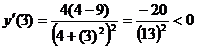 .
.
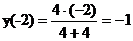 ,
, 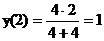 .
.
Табл.1.
Значит
 при
при 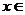 (-2;2),
(-2;2), 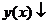 при
при 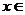
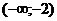 и
и 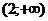
точка
минимума 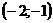 ; - точка максимума
; - точка максимума 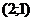 .
.
.
Найдем вторую производную, ее нули и интервалы знакопостоянства.
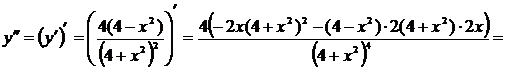
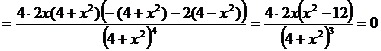 .
.
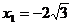 ,
, 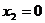 ,
, 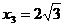 .
.
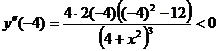 ,
, 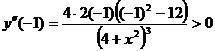 ,
, 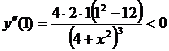 ,
, 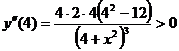
Табл.2.
В
интервалах, где 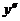 < 0 , то есть при
< 0 , то есть при 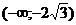 и
и 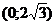 график функции выпуклый, а где
график функции выпуклый, а где 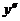 >0 -
>0 - 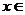
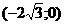 и
и 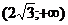 - вогнутый.
- вогнутый.
.
Найдем асимптоты.
Уравнения
наклонных асимптот  , где
, где 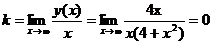 , тогда
наклонных асимптот не существует.
, тогда
наклонных асимптот не существует.
Горизонтальная
асимптота 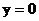 (ось
(ось 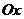 )
)
График
данной функции имеет вид:
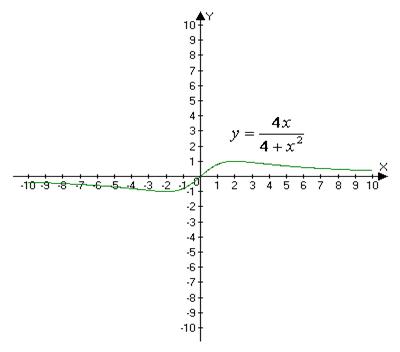
Рис.3.
4.
Дана функция 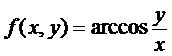 . Найти все её частные производные второго порядка
. Найти все её частные производные второго порядка
Решение.
Для
вычисления частных производных будем пользоваться правилом: все переменные,
кроме той, по которой дифференцируем, считаем постоянными. Тогда учитывая (24)
- (27). Найдем вначале производные первого порядка.
 -
считаем
-
считаем 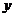 постоянной, а
постоянной, а 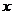 -
переменной.
-
переменной.
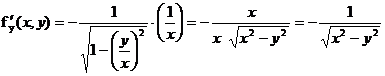 - считаем
- считаем
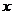 постоянной, а
постоянной, а 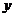 -
переменной.
-
переменной.
Найдем
производные второго порядка:
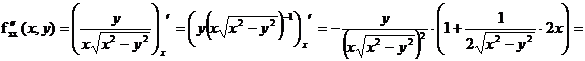
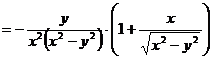 -
дифференцируем
-
дифференцируем 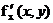 по
по 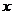 , считая
, считая 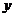 постоянной.
постоянной.
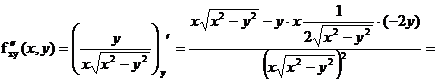
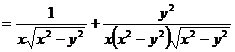 -
дифференцируем
-
дифференцируем 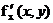 по
по 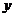 , считая
, считая 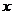 постоянной.
постоянной.
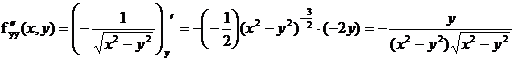 -
дифференцируем
-
дифференцируем 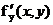 по
по 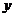 , считая
, считая 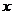 постоянной.
постоянной.
Ответ:
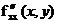
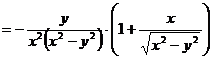 ,
,
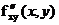
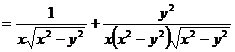 ,
, 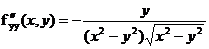 .
.
. Найти неопределенные интегралы
а)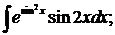 б)
б)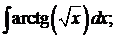
в)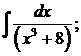 г)
г)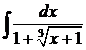 .
.
Решение.
Воспользуемся
свойствами интеграла:
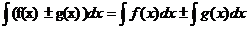 (28)
(28)
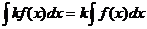 . (29)
. (29)
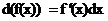 (30) -
внесением под знак дифференциала необходимой переменной.
(30) -
внесением под знак дифференциала необходимой переменной.
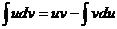 (31)
(31)
Воспользуемся
формулой понижения степени 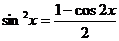 , тогда
, тогда
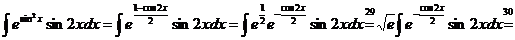
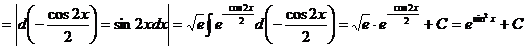 .
.
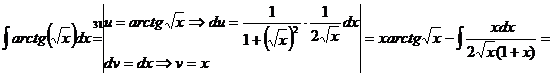
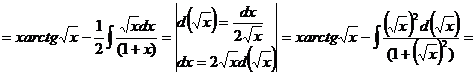

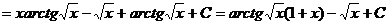
Разложим
подынтегральную функцию на простейшие дроби и воспользуемся формулами
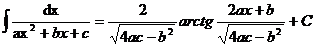 , если
, если 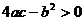 (32)
(32)
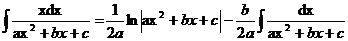 (33).
(33).
экстремум
дробь монотонность подынтегральный
Воспользуемся для разложения методом неопределенных коэффициентов:
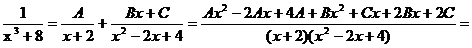
 получим
систему:
получим
систему: 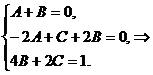
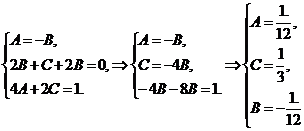 . Тогда
. Тогда
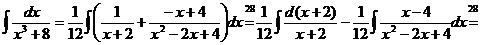
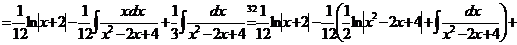
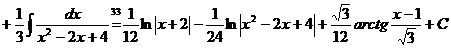 .
.
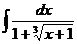 -
выполним замену переменной
-
выполним замену переменной 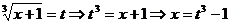 , тогда
, тогда 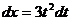 .
.
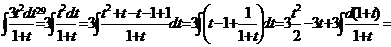
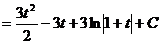 .
.
Выполним
обратную замену, тогда 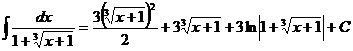 .
.
Ответ:
а) 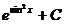 , б)
, б) 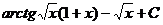 , в)
, в) 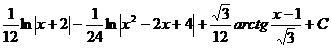 , г)
, г) 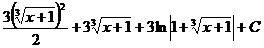 .
.
Список
использованной литературы
1. Выгодский М.Я. Справочник по высшей
математике. 8-е изд. - М.: Наука, 1966 - 872 с.
2. Демидович Б.П.. Сборник задач и
упражнений по математическому анализу. - М.: Наука, 1972 - 544 с.
3. Задачи и упражнений по
математическому анализу для втузов.: Учебное пособие для студентов высших техн.
учебн. заведений/под. ред. Б.П. Демидовича. - М.; ООО «Издательство Астрель» ,
2004 - 495с.
4. Запорожец Г.И. Руководство к решению
задач по математическому анализу. 4-е изд. - М.: Высшая школа, 1966 - 460 с.
5. Пискунов Н.С. Дифференциальное и
интегральное исчисления для втузов, Том 2 -М. :Наука, 1985. - 560с.
6. Справочник по математике для
экономистов/В.Е. Барбаумов, В.И. Ермаков, Н.Н. Кривенцова и др.; Под ред. В.И.
Ермакова. - М.: Высшая школа, 1987. - 336 с.