Производная функции и ее приложения
Контрольная
работа
Тема:
Производная
функции и ее приложения
Содержание
1.
Производная и дифференциал функции
1.1
Основные определения и теоремы
.2
Техника дифференцирования
.3
Дифференциал функции
.4
Производные и дифференциалы высших порядков
.
Приложения производных
.1
Применение производных к вычислению пределов
.2
Исследование функции на монотонность и точки локального экстремума
.3
Исследование функции на направление выпуклости и точки перегиба
.4
Задачи на наибольшее и наименьшее значения
.
Полное исследование функции и построение эскиза ее графика
.1
Асимптоты графика функции
.2
Полное исследование функции
Литература
1. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
ФУНКЦИИ
1.1 Основные определения и теоремы
Дадим сначала понятие производной функции
Определение 1.1
Пусть 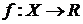 ,
, 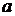 - точка сгущения Х,
- точка сгущения Х, 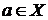 . Если
существует предел отношения приращения функции
. Если
существует предел отношения приращения функции 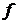 в точке
в точке 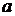 к
приращению аргумента, при условии, что приращение аргумента стремится к нулю,
то величина этого предела называется производной функции
к
приращению аргумента, при условии, что приращение аргумента стремится к нулю,
то величина этого предела называется производной функции 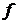 в точке
в точке 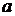 и обозначается
и обозначается
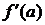 или
или 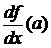 .
.
То есть
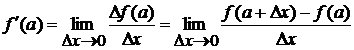 . (1)
. (1)
Так как предел в правой части
формулы (1) может не существовать, а в случае существования быть конечным или
бесконечным, то в зависимости от этого функции делятся на дифференцируемые и не
дифференцируемые в заданной точке.
Определение 1.2
Пусть 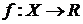 ,
, 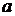 - точка сгущения Х,
- точка сгущения Х, 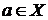 . Функция
. Функция 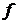 называется
дифференцируемой в точке
называется
дифференцируемой в точке 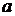 тогда и
только тогда, когда у нее существует конечная производная в точке
тогда и
только тогда, когда у нее существует конечная производная в точке 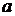 , то есть
существует конечный предел
, то есть
существует конечный предел
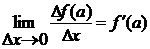
Теорема 1.1 Критерий
дифференцируемости функции
Пусть 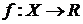 ,
, 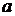 -точка сгущения Х,
-точка сгущения Х, 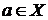 . Функция
. Функция 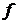 является
дифференцируемой в точке
является
дифференцируемой в точке 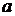 тогда и
только тогда, когда ее приращение в точке
тогда и
только тогда, когда ее приращение в точке 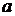 может быть представлено в виде:
может быть представлено в виде:
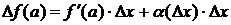 ,
,
где 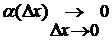
Определение 1.3
Пусть функция 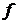 дифференцируема
в точке
дифференцируема
в точке 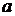 . Тогда,
согласно критерию дифференцируемости функции в точке
. Тогда,
согласно критерию дифференцируемости функции в точке
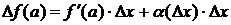 ,
,
где 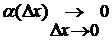
Главная, линейная относительно 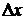 часть
приращения функции
часть
приращения функции 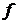 в точке
в точке 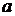 называется
дифференциалом функции
называется
дифференциалом функции 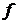 в точке
в точке 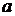 и
обозначается
и
обозначается
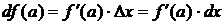 ,
,
где 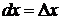
Теорема 1.2 Об арифметических
операциях с дифференцируемыми функциями
Пусть функции 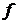 и
и 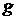 дифференцируемы
в точке
дифференцируемы
в точке 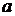 . Тогда
функции
. Тогда
функции 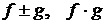 и
и 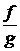 (при
условии, что
(при
условии, что 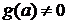 )
дифференцируемы в точке
)
дифференцируемы в точке 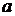 , причем
, причем
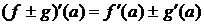
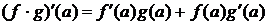
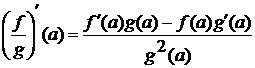 .
.
Используя определение производной
(формулу (1)) и теорему 1.2, можно вывести производные основных элементарных
функций, которые мы и приведем далее.
Таблица производных основных
элементарных функций
1)  8)
8) 
) 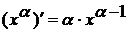 9)
9) 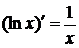
) 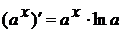 10)
10) 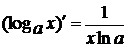
) 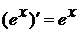 11)
11) 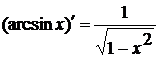
) 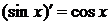 12)
12) 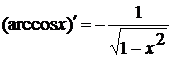
) 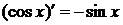 13)
13) 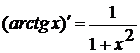
) 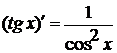 14)
14) 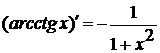
Теорема 1.3 О производной сложной
функции
Пусть 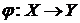 и дифференцируема в точке
и дифференцируема в точке 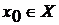 ; пусть
; пусть 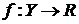 и
дифференцируема в точке
и
дифференцируема в точке 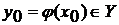 . Тогда
функция
. Тогда
функция 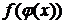 дифференцируема
в точке
дифференцируема
в точке 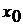 и
и 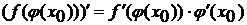 .
.
1.2 Техника дифференцирования
На практике для того чтобы найти
производную заданной функции (продифференцировать функцию), необходимо знать
таблицу производных основных элементарных функций, приведенную выше и правила
дифференцирования, содержащиеся в теоремах 1.2 и 1.3. Выделим последние еще
раз:
Правила дифференцирования
1) 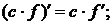
) 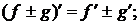
) 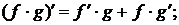
) 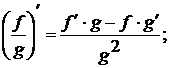
5) 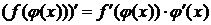 .
.
Рассмотрим ряд примеров для того, чтобы
разобрать технику дифференцирования.
Пример 1.1 Найти
производную:
а) 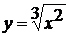 ; б)
; б) 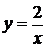 ; в)
; в) 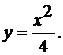
Решение. а) Для того
чтобы продифференцировать функцию, содержащую корень любой степени, необходимо
корень записать в виде степени. В нашем случае 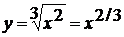 . Тогда далее для дифференцирования
можно использовать формулу (2) из таблицы производных (c
. Тогда далее для дифференцирования
можно использовать формулу (2) из таблицы производных (c 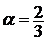 ), получим
), получим
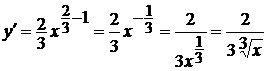 ;
;
б) во втором и третьем примерах
функции представляют собой дробь. Так как формула дифференцирования дроби самая
«громоздкая», то лучше ее применять в том случае, когда дробь «полная»
(неизвестное 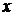 содержится
и в числителе, и в знаменателе). Но во втором примере неизвестное содержится
только в знаменателе, поэтому проще эту функцию для дифференцирования представить
так:
содержится
и в числителе, и в знаменателе). Но во втором примере неизвестное содержится
только в знаменателе, поэтому проще эту функцию для дифференцирования представить
так: 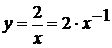 . И тогда
функция представляет собой число 2, умноженное на функцию
. И тогда
функция представляет собой число 2, умноженное на функцию 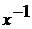 . А значит,
для дифференцирования такой конструкции применим правило дифференцирования 1)
(производная константы, умноженной на функцию). Согласно этой формуле
. А значит,
для дифференцирования такой конструкции применим правило дифференцирования 1)
(производная константы, умноженной на функцию). Согласно этой формуле
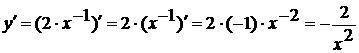 ;
;
в) Так как в этом случае функция
также представляет собой «неполную» дробь, то проще ее представить в виде:
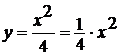
И тогда снова имеем дело с
конструкцией «константа , умноженная на функцию», и применяя правило
дифференцирования 1) и формулу 2) из таблицы производных, получим:
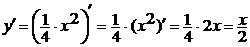
Пример 1.2 Найти производную
функции:
а) 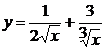 ; б)
; б) 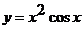 ; в)
; в) 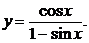
Решение. а) Для того
чтобы продифференцировать функцию, являющуюся комбинацией нескольких функций,
нужно установить, что собой представляет исходная функция: алгебраическую
сумму, произведение, дробь или сложную функцию. Для этого нужно установить
какая операция выполняется последней в задании функции. В данном примере
последняя операция - сложение дробей 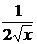 и
и  . Значит сначала нужно применить
правило дифференцирования суммы (формула 2). Имеем
. Значит сначала нужно применить
правило дифференцирования суммы (формула 2). Имеем
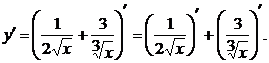
Далее осталось найти производные 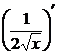 и
и 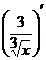 . Аналогично
рассуждениям примера 1.1 б) и в) видно, что обе дроби, оставшиеся для
дифференцирования «неполные», поэтому удобнее их представить в виде:
. Аналогично
рассуждениям примера 1.1 б) и в) видно, что обе дроби, оставшиеся для
дифференцирования «неполные», поэтому удобнее их представить в виде:
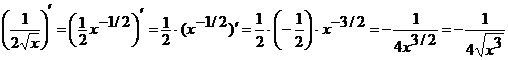 ,
,
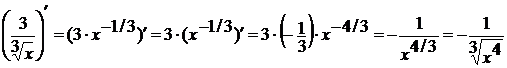
Тогда окончательно имеем:
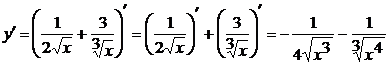
б) Последняя операция, выполняющаяся
в этом примере - умножение 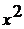 и
и 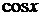 , значит необходимо применить
формулу (3) - правило дифференцирования произведения, получим:
, значит необходимо применить
формулу (3) - правило дифференцирования произведения, получим:
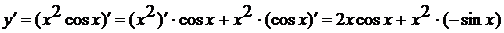
в) В этом примере последняя операция
- деление. Заметим, что в этом случае дробь «полная» (неизвестное 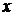 содержится
и в числителе, и в знаменателе), значит, следует применить правило
дифференцирования (4) (правило дифференцирование дроби). Тогда получим
содержится
и в числителе, и в знаменателе), значит, следует применить правило
дифференцирования (4) (правило дифференцирование дроби). Тогда получим
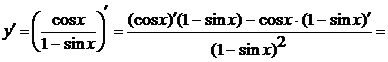
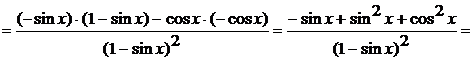
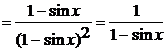
Пример 1.3 Найти
производную функции:
а) 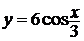 ; б)
; б) 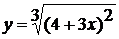 ; в)
; в) 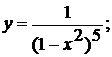
г) 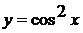 ; д)
; д) 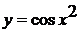 ; е)
; е) 
ж) 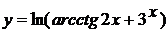 ; з)
; з) 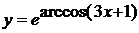 ; и)
; и) 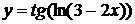 .
.
Решение. а)
Определяем последнюю операцию, выполняемую в этом примере. Это умножение числа
6 на функцию 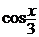 . Поэтому
применим сначала формулу (1) из правил дифференцирования, получим
. Поэтому
применим сначала формулу (1) из правил дифференцирования, получим
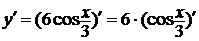
Далее, для того чтобы найти
производную функции 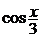 нужно снова
определить последнюю операцию, выполняемую в этом выражении. Это взятие
косинуса от
нужно снова
определить последнюю операцию, выполняемую в этом выражении. Это взятие
косинуса от 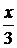 .
Следовательно, имеем дело со сложной функцией, для дифференцирования которой
нужно применить формулу (5). Согласно этой формуле сначала нужно
продифференцировать внешнюю функцию, то есть косинус (
.
Следовательно, имеем дело со сложной функцией, для дифференцирования которой
нужно применить формулу (5). Согласно этой формуле сначала нужно
продифференцировать внешнюю функцию, то есть косинус (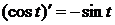 ), и
приписать ей тот аргумент, что и был, то есть
), и
приписать ей тот аргумент, что и был, то есть 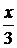 , а затем умножить на производную
внутренней функции.
, а затем умножить на производную
внутренней функции.
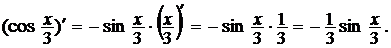
Таким образом, получим
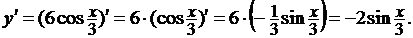
б) Снова имеем дело со сложной функцией.
Последняя операция в данном выражении - это извлечение кубического корня,
поэтому начинаем дифференцирование с него. Для этого, как уже отмечалось в
примере 1.1 а), представить корень в виде степени:
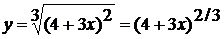
Теперь последняя операция -
возведение в степень 2/3. Значит нужно дифференцировать эту функцию как
степенную (формула (2) из таблицы производных
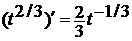 ,
,
роль t в ней
играет выражение (4+3x)), а затем умножить на производную
внутренней функции (4+3x ).
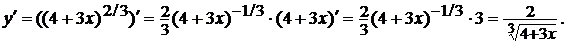
в) В этом примере функция
представляет собой дробь (последнее действие деление), но дробь «не полная» так
как неизвестное содержится только в знаменателе. Поэтому такую функцию удобно
для дифференцирования сначала представить в виде:
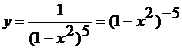
Тогда эту функцию следует дифференцировать также
как и предыдущую, получим:
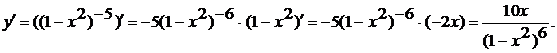
г) Последняя операция в этом примере
- возведение в квадрат функции cos x.
Следовательно, нужно начать дифференцирование со степени, то есть применить
формулу (2) из таблицы производных (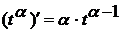 , роль t в нашем
случае будет играть cos x, а
, роль t в нашем
случае будет играть cos x, а 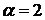 ). Получим
). Получим
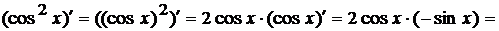
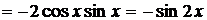
д) В этом примере порядок действий
таков: сначала х возводится в квадрат, а затем от полученного выражения берется
косинус (сложная функция). Поэтому начинаем дифференцировать с последней
операции, для этого применяем формулу (6) из таблицы производных, а затем
умножаем на производную аргумента (согласно правилу дифференцирования сложной
функции):
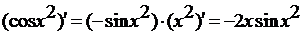
е) Здесь по порядку действий сначала
х возвели в куб, далее взяли от полученного выражения синус, а потом все
возвели в квадрат (сложная функция). Итак, последняя операция - возведение во
вторую степень выражения 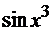 . Значит
сначала применяем формулу (2) из таблицы производных
. Значит
сначала применяем формулу (2) из таблицы производных 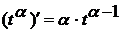 (роль t в ней будет
играть
(роль t в ней будет
играть 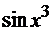 ):
):
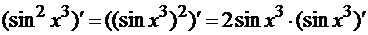
Чтобы найти 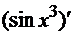 , нужно
начать дифференцирование опять с последней операции - теперь это взятие синуса
от
, нужно
начать дифференцирование опять с последней операции - теперь это взятие синуса
от 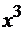 . Используем
формулу (5) из таблицы производных:
. Используем
формулу (5) из таблицы производных: 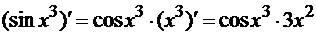 . Тогда
. Тогда
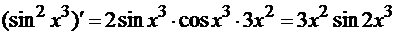
ж) Здесь последняя операция - взятие
натурального логарифма от выражения ( ) (сложная функция). Поэтому
используем формулу дифференцирования сложной функции: сначала находим
производную от натурального логарифма (формула (9) из таблицы производных, роль
аргумента функции логарифм, играет сейчас
) (сложная функция). Поэтому
используем формулу дифференцирования сложной функции: сначала находим
производную от натурального логарифма (формула (9) из таблицы производных, роль
аргумента функции логарифм, играет сейчас 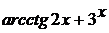 ).
).
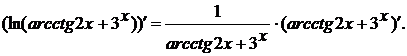
Чтобы найти 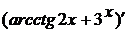 , снова
определяем последнюю операцию в этом выражении - это сложение
, снова
определяем последнюю операцию в этом выражении - это сложение 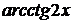 и
и 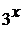 . Значит,
используем правило дифференцирования суммы:
. Значит,
используем правило дифференцирования суммы:
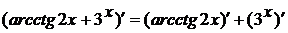
Далее используем формулы производных
арккотангенса и показательной функции (соответственно формулы (14) и (3) из
таблицы производных). Имеем
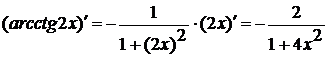 , а
, а 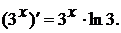
Тогда, окончательно,
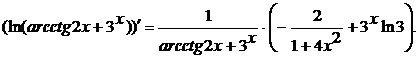
з) Последняя операция - возведение е
в степень 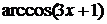 (сложная
функция). Поэтому по правилу дифференцирования сложной функции, находим
производную сначала от внешней функции (
(сложная
функция). Поэтому по правилу дифференцирования сложной функции, находим
производную сначала от внешней функции (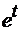 формула (4) из таблицы производных,
роль t будет
играть
формула (4) из таблицы производных,
роль t будет
играть 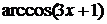 ) и умножаем
полученный результат на производную внутренней функции, то есть на производную
) и умножаем
полученный результат на производную внутренней функции, то есть на производную 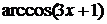 .
.
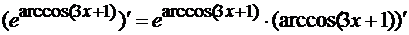
Для нахождения 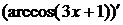 определяем
последнюю операцию в данном выражении. Это взятие арккосинуса от 3х+1. Значит,
применим формулу (12) из таблицы производных для дифференцирования арккосинуса:
определяем
последнюю операцию в данном выражении. Это взятие арккосинуса от 3х+1. Значит,
применим формулу (12) из таблицы производных для дифференцирования арккосинуса:
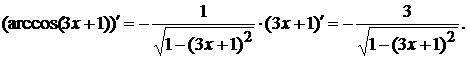
Окончательно
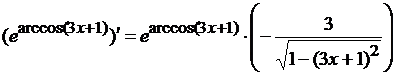
и) Здесь последовательно выполняются
три операции: 1) из 3 вычитается 2х, 2) берется натуральный логарифм от
полученной разности, 3) от всего полученного выражения берется тангенс (сложная
функция). Поэтому дифференцируем как всегда ее с последнего действия, то есть
находим производную тангенса (формула (7) из таблицы производных), затем
дифференцируем натуральный логарифм, и, наконец, многочлен 3-2х.
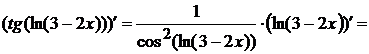
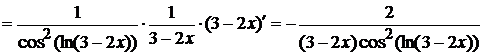
Пример 1.4 Найти
производную функции 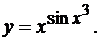
Решение. Заметим,
что у этой функции неизвестное х содержится и в основании степени, и в
показателе (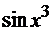 ). Как уже
отмечалось в [5], такая функция называется показательно-степенной, и формулы
для ее дифференцирования в таблице производных нет. Поэтому, как и ранее, при
работе с такими функциями их нужно представить на основании основного
логарифмического тождества в виде показательной функции:
). Как уже
отмечалось в [5], такая функция называется показательно-степенной, и формулы
для ее дифференцирования в таблице производных нет. Поэтому, как и ранее, при
работе с такими функциями их нужно представить на основании основного
логарифмического тождества в виде показательной функции:
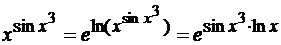
Тогда последняя операция -
возведение е в степень  (сложная
функция). Значит, используем сначала формулу (4) из таблицы производных:
(сложная
функция). Значит, используем сначала формулу (4) из таблицы производных:
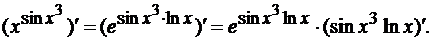
Для нахождения 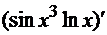 определим
последнюю операцию, выполняющуюся в этом выражении. Это умножение
определим
последнюю операцию, выполняющуюся в этом выражении. Это умножение 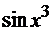 на
на 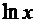 .
Следовательно, используем далее правило дифференцирования произведения:
.
Следовательно, используем далее правило дифференцирования произведения:
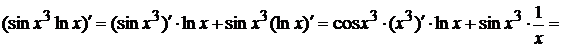
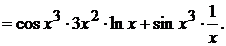
Тогда окончательно имеем
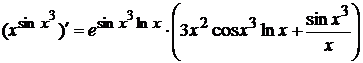
Пример 1.5 Найти
производную функции
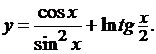
Решение. Определяем
последнюю операцию, выполняемую в этом выражении. Это сложение 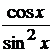 и
и 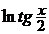 .
Следовательно, применим сначала формулу дифференцирования суммы:
.
Следовательно, применим сначала формулу дифференцирования суммы:
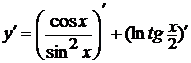
Первое слагаемое - частное двух
функций. Используя правило дифференцирования дроби, получим
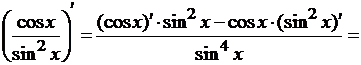
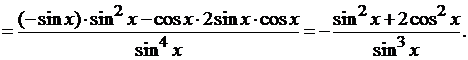
Последняя операция в выражении 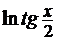 - это
взятие натурального логарифма от
- это
взятие натурального логарифма от 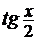 (сложная функция), следовательно,
действуем по правилу дифференцирования сложной функции, то есть сначала
применяем формулу (9), а затем (7) из таблицы производных. Имеем
(сложная функция), следовательно,
действуем по правилу дифференцирования сложной функции, то есть сначала
применяем формулу (9), а затем (7) из таблицы производных. Имеем
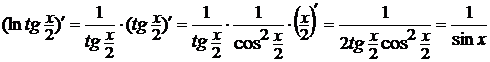
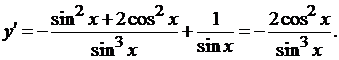
1.3 Дифференциал функции
Согласно определению 1.3, дифференциал функции -
это главная часть приращения функции. Он находится по формуле
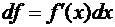
То есть, для того чтобы найти
дифференциал функции, нужно найти ее производную и умножить полученное на  . Если
требуется вычислить дифференциал в конкретной точке, то найденную
предварительно производную необходимо вычислить в этой точке и умножить
полученное число на
. Если
требуется вычислить дифференциал в конкретной точке, то найденную
предварительно производную необходимо вычислить в этой точке и умножить
полученное число на  .
.
Пример 1.6 Найти
дифференциал функции 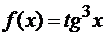 .
.
Решение. Найдем
сначала производную заданной функции:
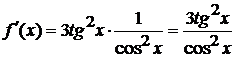
Тогда 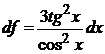
Пример 1.7 Вычислить
дифференциал функции 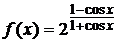 в точке
в точке 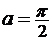 .
.
Решение. Найдем
сначала производную заданной функции в произвольной точке:
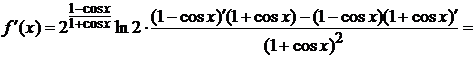
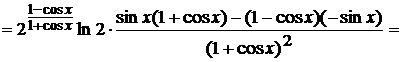
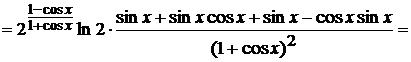
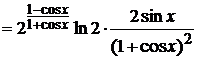
Вычислим теперь значение производной
в точке 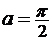 :
:
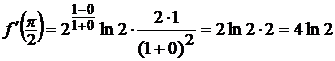
Тогда 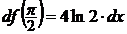 .
.
.4 Производные и дифференциалы
высших порядков
Пусть  дифференцируема на множестве Х (то
есть, дифференцируема в каждой точке этого множества). Тогда на множестве Х определена
функция
дифференцируема на множестве Х (то
есть, дифференцируема в каждой точке этого множества). Тогда на множестве Х определена
функция 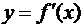 . Если
функция
. Если
функция 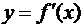 дифференцируема
на Х, то говорят, что функция
дифференцируема
на Х, то говорят, что функция  дважды дифференцируема на Х и
производная от функции
дважды дифференцируема на Х и
производная от функции 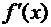 называется
производной второго порядка функции
называется
производной второго порядка функции  , то есть
, то есть 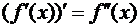 , а
дифференциал от дифференциала функции
, а
дифференциал от дифференциала функции  называется дифференциалом второго
порядка функции
называется дифференциалом второго
порядка функции  :
:
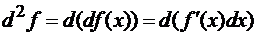 .
.
Если х независимая переменная, то
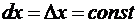
и 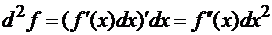
Производную от производной второго
порядка называют третьей производной функции  :
:
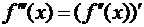 ,
,
а 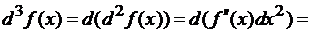
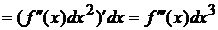
Этот процесс можно продолжать и
дальше.
Пример 1.8 Найти вторую
производную функции
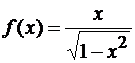 в точке
в точке 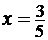
Решение. Найдем сначала
первую производную заданной функции. Так как требуется найти вторую производную
 , то
полученную первую производную нужно будет продифференцировать еще раз. Чтобы
это было сделать проще, необходимо
, то
полученную первую производную нужно будет продифференцировать еще раз. Чтобы
это было сделать проще, необходимо 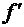 упростить.
упростить.
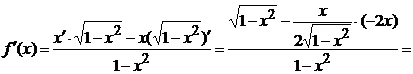
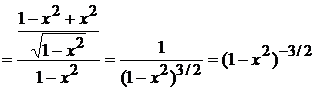
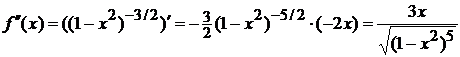
Подставим 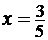 в
полученную вторую производную, получим:
в
полученную вторую производную, получим:
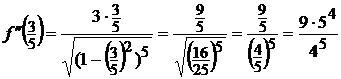
Пример 1.9 Найти
дифференциал второго порядка функции
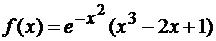
Решение
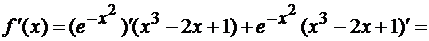
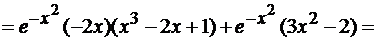
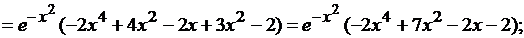
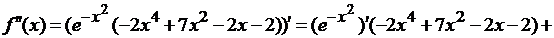
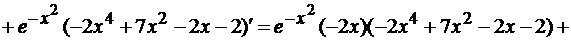
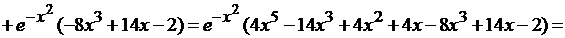
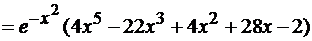 .
.
Тогда 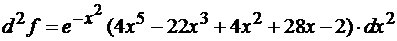 .
.
2. ПРИЛОЖЕНИЯ ПРОИЗВОДНЫХ
.1 Применение производных к
вычислению пределов.
Напомним, что при вычислении
пределов функций ответ не всегда можно дать сразу. Часто возникают
неопределенности типа 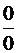 ,
, 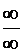 ,
, 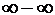 ,
, 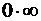 и другие.
Основные методы раскрытия этих неопределенностей мы разбирали в пособии [5]. Но
нужно отметить, что не всякий предел можно вычислить при помощи описанных там
подходов или решение можно существенно облегчить, применяя производные. Это
можно делать на основании следующей теоремы:
и другие.
Основные методы раскрытия этих неопределенностей мы разбирали в пособии [5]. Но
нужно отметить, что не всякий предел можно вычислить при помощи описанных там
подходов или решение можно существенно облегчить, применяя производные. Это
можно делать на основании следующей теоремы:
Теорема 2.1 Правило Лопиталя
Пусть 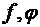 определены на
определены на 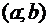 и
удовлетворяют следующим условиям:
и
удовлетворяют следующим условиям:
) 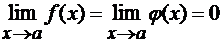 или
или 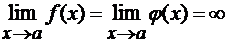 ;
;
) 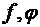 дифференцируемы на
дифференцируемы на 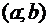 ;
;
) 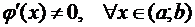 .
.
Тогда если существует предел
отношения производных функций  и
и 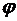 , то существует предел отношения
самих этих функций и эти пределы равны. То есть, если
, то существует предел отношения
самих этих функций и эти пределы равны. То есть, если
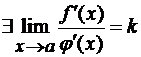 , то
, то 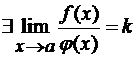
Итак, согласно теореме 2.1 правило
Лопиталя непосредственно можно применять для вычисления пределов в случае
неопределенностей 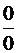 и
и 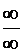 , при этом
нужно найти производные числителя и знаменателя отдельно (не путать правило
Лопиталя с правилом дифференцирования дроби!).
, при этом
нужно найти производные числителя и знаменателя отдельно (не путать правило
Лопиталя с правилом дифференцирования дроби!).
Замечание 2.1
Правило Лопиталя можно применять
неоднократно, пока сохраняется неопределенность.
Пример 2.1 Применяя
правило Лопиталя, вычислить предел
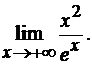
Решение. При 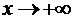 и
числитель, и знаменатель дроби стремятся к
и
числитель, и знаменатель дроби стремятся к 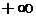 , а, следовательно, имеем дело с
неопределенностью
, а, следовательно, имеем дело с
неопределенностью 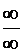 . Чтобы
раскрыть эту неопределенность, применим правило Лопиталя. Это можно сделать,
так как и остальные условия теоремы выполнены (функции, стоящие в числителе и
знаменателе дифференцируемы на
. Чтобы
раскрыть эту неопределенность, применим правило Лопиталя. Это можно сделать,
так как и остальные условия теоремы выполнены (функции, стоящие в числителе и
знаменателе дифференцируемы на 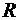 ,
, 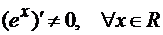 ). Следовательно,
). Следовательно,
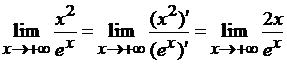
Итак, после применения правила
Лопиталя, получили дробь, числитель и знаменатель которой по-прежнему стремятся
к 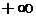 ,
следовательно, снова неопределенность
,
следовательно, снова неопределенность 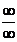 . Значит, правило Лопиталя можно
применить теперь уже к этому выражению, получим
. Значит, правило Лопиталя можно
применить теперь уже к этому выражению, получим
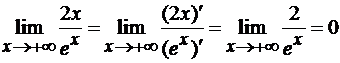
Окончательно имеем
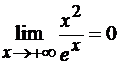
Замечание 2.2 При других
типах неопределенности, отличных от  и
и  , правило Лопиталя сразу применять
нельзя. Необходимо сначала провести тождественные преобразования исходного
выражения, которые привели бы к неопределенности
, правило Лопиталя сразу применять
нельзя. Необходимо сначала провести тождественные преобразования исходного
выражения, которые привели бы к неопределенности 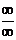 или
или 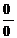 .
.
Пример 2.2 Применяя
правило Лопиталя, вычислить предел 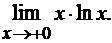
Решение. При 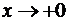 первый
множитель стремится к нулю, а
первый
множитель стремится к нулю, а 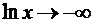 (вспомните график логарифмической
функции). Значит, имеем дело с неопределенностью
(вспомните график логарифмической
функции). Значит, имеем дело с неопределенностью 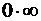 . Согласно замечанию 2.2, необходимо
выполнить преобразования, которые приведут к неопределенности
. Согласно замечанию 2.2, необходимо
выполнить преобразования, которые приведут к неопределенности 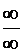 или
или 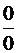 . То есть
требуется из произведения сделать дробь. Это возможно, для этого нужно один из
множителей «опустить» в знаменатель. Получим
. То есть
требуется из произведения сделать дробь. Это возможно, для этого нужно один из
множителей «опустить» в знаменатель. Получим
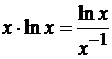
Обратите внимание на то, что
«опускать» в знаменатель, вообще говоря, можно любой множитель, но с учетом
того, что при применении правила Лопиталя знаменатель придется
дифференцировать, лучше переносить тот множитель, производная которого
находится проще (в нашем случае проще дифференцировать 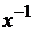 , чем
, чем 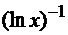 ). Итак,
проведя вышеуказанные преобразования, получили дробь, у которой
). Итак,
проведя вышеуказанные преобразования, получили дробь, у которой
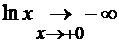 и
и 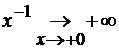
То есть пришли к неопределенности  . Теперь
можно применять правило Лопиталя:
. Теперь
можно применять правило Лопиталя:
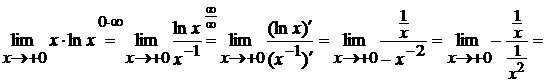
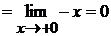
Замечание 2.3
После применения правила Лопиталя,
перед тем как проверить ушла ли неопределенность, часто бывает полезно
упростить полученное выражение, как мы сделали в предыдущем примере.
Пример 2. 3 Вычислить
предел, применяя правило Лопиталя
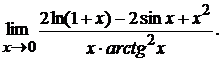
Решение. При  и
числитель, и знаменатель дроби стремятся к нулю. Имеем неопределенность
и
числитель, и знаменатель дроби стремятся к нулю. Имеем неопределенность 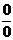 . Можно
применять правило Лопиталя. Но, заметим, что в знаменателе стоит произведение,
и при его дифференцировании мы получим уже довольно сложное выражение
. Можно
применять правило Лопиталя. Но, заметим, что в знаменателе стоит произведение,
и при его дифференцировании мы получим уже довольно сложное выражение
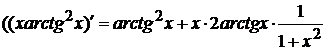 )
)
И если после одного применения
правила Лопиталя неопределенность не уйдет, то придется его применять еще раз,
то есть дифференцировать полученное выражение, которое еще усложнится. Поэтому
перед каждым применением правила Лопиталя рекомендуется упростить функцию за
счет перехода к эквивалентным, если это возможно, а уж затем дифференцировать.
Так в данной ситуации можно существенно упростить решение примера, если в
знаменателе перейти к эквивалентным:
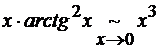
Неопределенность от этого не
«уйдет», но дифференцировать станет намного проще.
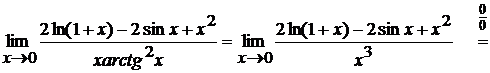
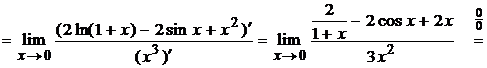
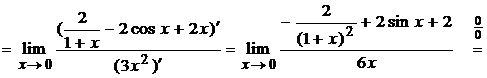
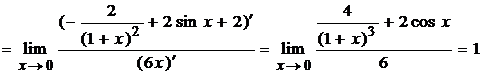
Пример 2.4 Вычислить
предел, применяя правило Лопиталя
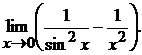
Решение. При  дроби
дроби 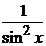 и
и 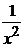 стремятся к
бесконечности. Следовательно, имеем неопределенность
стремятся к
бесконечности. Следовательно, имеем неопределенность 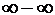 . А значит
нужно провести преобразования, чтобы получить неопределенность
. А значит
нужно провести преобразования, чтобы получить неопределенность 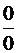 или
или 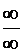 . Для этого
приведем выражение к общему знаменателю
. Для этого
приведем выражение к общему знаменателю
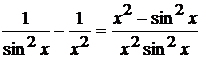
В полученной дроби числитель и
знаменатель стремятся к нулю при  . То есть пришли к неопределенности
. То есть пришли к неопределенности 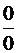 , и теперь
можно применять правило Лопиталя. Но снова заметим, что можно существенно
упростить решение, перейдя к эквивалентным в знаменателе:
, и теперь
можно применять правило Лопиталя. Но снова заметим, что можно существенно
упростить решение, перейдя к эквивалентным в знаменателе:
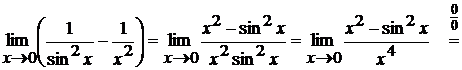
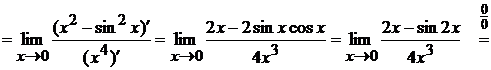
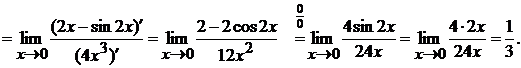
В предпоследнем равенстве мы снова перешли к
эквивалентным
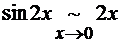
Итак, при вычислении пределов с
помощью правила Лопиталя полезно соблюдать порядок действий, приведенный ниже.
1) Проверить есть ли неопределенность и если да,
то какого она типа.
2) Перейти к неопределенности 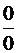 или
или 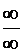 , если она
другая.
, если она
другая.
) Перейти к эквивалентным,
если это возможно.
) Применить правило Лопиталя.
) Упростить полученное
выражение.
) Перейти к пункту 1), и
далее действовать по циклу, пока не уйдет неопределенность.
производный дифференциал функция
предел экстремум
2.2 Исследование функции на
монотонность и точки локального экстремума
Определение 2.1
Функция 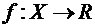 называется
возрастающей (убывающей) на множестве Х, если
называется
возрастающей (убывающей) на множестве Х, если 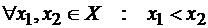 выполняется неравенство
выполняется неравенство
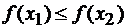 (
(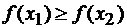 ).
).
Возрастающие и убывающие функции
называются монотонными. Если два последних неравенства в определении 2.1
строгие, то функцию  называют
строго возрастающей (строго убывающей) на множестве Х. Строго возрастающие и
строго убывающие функции называют строго монотонными.
называют
строго возрастающей (строго убывающей) на множестве Х. Строго возрастающие и
строго убывающие функции называют строго монотонными.
Использовать определение 2.1 для
исследования функции на монотонность неудобно, так как невозможно перебрать все
точки из множества Х и проверить их на выполнение первого или второго
неравенства. Проще исследовать функцию на монотонность можно при помощи
производной на основании следующих теорем.
Теорема 2.2 Критерий монотонности
функции
Пусть функция  непрерывна
на промежутке Х и дифференцируема внутри Х. Для того чтобы функция
непрерывна
на промежутке Х и дифференцируема внутри Х. Для того чтобы функция  возрастала
(убывала) на промежутке Х необходимо и достаточно чтобы
возрастала
(убывала) на промежутке Х необходимо и достаточно чтобы
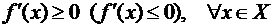
Определение 2.2
Пусть функция 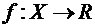 ,
, 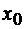 - точка
сгущения множества Х,
- точка
сгущения множества Х, 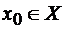 . Точка
. Точка 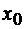 называется
точкой локального минимума (максимума) функции
называется
точкой локального минимума (максимума) функции  , если
, если
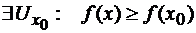
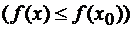 ,
, 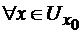
Точки локального минимума и
максимума функции объединены понятием локального экстремума.
Иными словами точка локального
минимума (максимума) - это точка, в которой функция принимает самое маленькое
(большое) значение по сравнению со значениями в близлежащих точках.
Использовать определение 2.2 для
нахождения точек локального экстремума функции неудобно, так как сначала надо
найти нужную окрестность точки 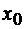 , а затем перебрать все точки из
этой окрестности и проверить их на выполнение первого или второго неравенств. И
снова значительно упростит задачу исследование при помощи производной.
, а затем перебрать все точки из
этой окрестности и проверить их на выполнение первого или второго неравенств. И
снова значительно упростит задачу исследование при помощи производной.
Теорема 2.3 Необходимое условие
локального экстремума
Пусть функция 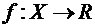 ,
, 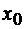 - точка
локального экстремума функции
- точка
локального экстремума функции  . Если
. Если  дифференцируема
в точке
дифференцируема
в точке 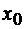 , то
, то 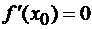 .
.
Из теоремы 2.3 следует, что если
функция дифференцируема в точке 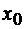 и
и 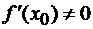 , то эта точка автоматически не
может быть экстремальной. Поэтому точками локального экстремума могут быть лишь
те точки, в которых производная функции
, то эта точка автоматически не
может быть экстремальной. Поэтому точками локального экстремума могут быть лишь
те точки, в которых производная функции  равна нулю, либо точки, в которых
равна нулю, либо точки, в которых  не
дифференцируема. Так, например, для функции
не
дифференцируема. Так, например, для функции 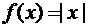 точка
точка 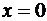 является
точкой локального минимума (вспомните ее график), но функция не дифференцируема
в этой точке.
является
точкой локального минимума (вспомните ее график), но функция не дифференцируема
в этой точке.
Определение 2.3
Точки, в которых производная функции
равна нулю и те точки, в которых функция не дифференцируема, называются
критическими или подозрительными на экстремум.
Почему только подозрительными на
экстремум? Ответ на этот вопрос дадут следующие примеры.
Пример 2.5
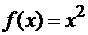
Найдем производную этой функции: 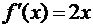 . Вычислим
ее значение в точке
. Вычислим
ее значение в точке 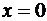 :
: 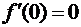 .
.

Х = 0
Вспомнив график этой функции,
заметим, что точка 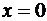 является
точкой минимума. Итак, получили, что
является
точкой минимума. Итак, получили, что 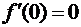 и точка
и точка 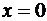 является
точкой экстремума.
является
точкой экстремума.
Пример 2.6
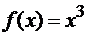
Найдем производную этой функции: 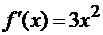 . Вычислим
ее значение в точке
. Вычислим
ее значение в точке 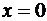 :
: 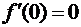 .
.
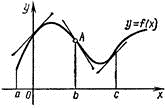
Х = 0
Вспомнив график этой функции,
заметим, что точка 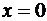 не является
точкой экстремума, так как в любой окрестности этой точки функция принимает
значения и большие, чем в
не является
точкой экстремума, так как в любой окрестности этой точки функция принимает
значения и большие, чем в 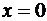 , и меньшие.
Итак, несмотря на то, что
, и меньшие.
Итак, несмотря на то, что 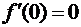 , точка
, точка 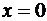 не является
точкой экстремума.
не является
точкой экстремума.
Таким образом, из примеров видно,
что условие равенства нулю производной функции  в точке
в точке 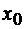 еще не
гарантирует наличие в ней экстремума (он может быть как в примере 2.5, а может
и не быть как в примере 2.6). Поэтому равенство нулю производной в точке
является только необходимым, но не достаточным условием локального экстремума.
Чтобы теперь из множества точек, подозрительных на экстремум, выбрать те,
которые окажутся экстремальными, применим достаточное условие локального
экстремума.
еще не
гарантирует наличие в ней экстремума (он может быть как в примере 2.5, а может
и не быть как в примере 2.6). Поэтому равенство нулю производной в точке
является только необходимым, но не достаточным условием локального экстремума.
Чтобы теперь из множества точек, подозрительных на экстремум, выбрать те,
которые окажутся экстремальными, применим достаточное условие локального
экстремума.
Теорема 2.4 Достаточное условие
локального экстремума
Пусть функция  непрерывна
на множестве Х,
непрерывна
на множестве Х, 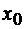 -
критическая точка функции
-
критическая точка функции  и
и  дифференцируема
в некоторой проколотой окрестности точки
дифференцируема
в некоторой проколотой окрестности точки 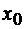 . Если при переходе через точку
. Если при переходе через точку 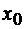 слева на
право,
слева на
право, 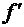 меняет знак
с «+» на «˗» (с «˗» на «+»), то точка
меняет знак
с «+» на «˗» (с «˗» на «+»), то точка 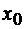 является точкой локального
максимума (минимума) функции
является точкой локального
максимума (минимума) функции  .
.
Итак, подводя итог всему
вышесказанному, составим алгоритм исследования функции на монотонность и точки
локального экстремума.
Алгоритм исследования функции на
монотонность и точки локального экстремума
1) Найти область определения
функции  .
.
) Найти производную функции  .
.
) Найти критические точки.
) Определить знак 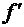 на
промежутках, на которые критические точки разбили область определения.
на
промежутках, на которые критические точки разбили область определения.
) Сделать выводы на основании
достаточного условия о наличии экстремумов в критических точках.
Пример 2.7 Найти
интервалы монотонности и точки локального экстремума функции
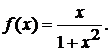
Решение. Найдем
сначала область определения:
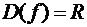
Далее найдем производную этой
функции:
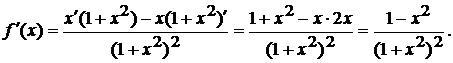
Теперь нужно найти критические
точки, то есть точки, в которых производная равна нулю, либо не существует. Так
как производная представляет собой дробь, то нас будут интересовать точки, где
дробь равна нулю, то есть нули числителя, и точки, в которых дробь не
определена - нули знаменателя. Чтобы найти такие точки, продолжим
преобразовывать найденную производную с целью разложить на множители числитель
и знаменатель:
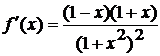
Теперь видно, что числитель
обращается в ноль в двух точках: 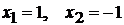 , а знаменатель не обращается в ноль
ни при каких х. Значит, имеем две критические точки
, а знаменатель не обращается в ноль
ни при каких х. Значит, имеем две критические точки 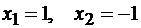 . Согласно
необходимому условию локального экстремума, только они могут претендовать на
роль экстремальных. Выясним, имеет ли заданная функция экстремумы в этих
точках, и если да, то какого типа. Применим достаточное условие локального
экстремума. Для этого на числовую ось нанесем область определения функции
. Согласно
необходимому условию локального экстремума, только они могут претендовать на
роль экстремальных. Выясним, имеет ли заданная функция экстремумы в этих
точках, и если да, то какого типа. Применим достаточное условие локального
экстремума. Для этого на числовую ось нанесем область определения функции  (в нашем
случае это будет вся числовая ось) и отметим критические точки, попавшие в
область определения
(в нашем
случае это будет вся числовая ось) и отметим критические точки, попавшие в
область определения 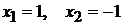 . Разобьем
область определения на интервалы:
. Разобьем
область определения на интервалы: 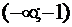 ,
, 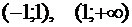 . И определим знак производной на
каждом из этих интервалов. Знаки можно расставить автоматически следующим
образом:
. И определим знак производной на
каждом из этих интервалов. Знаки можно расставить автоматически следующим
образом:
) Знаки начинаем расставлять
с правого промежутка (можно подстановкой, например, вычислить значение
производной в точке 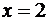 :
: 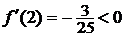 ).
Следовательно, на промежутке
).
Следовательно, на промежутке 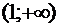
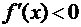 и по критерию монотонности это
означает, что функция
и по критерию монотонности это
означает, что функция  убывает на
этом промежутке.
убывает на
этом промежутке.
) Далее определяем знаки
производной в оставшихся промежутках. При переходе через точку знак меняется,
если множитель, обращающийся в ноль в этой точке, стоит в нечетной степени.
Если степень четная - знак не меняется. В точке 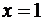 множитель
множитель 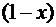 обращается
в ноль.
обращается
в ноль.
Степень этого множителя первая,
нечетная. Значит, при переходе через точку 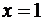 производная меняет знак (на
промежутке
производная меняет знак (на
промежутке 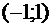
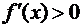 ). При
переходе через точку
). При
переходе через точку 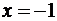 знак
знак 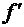 снова
меняется, так как множитель
снова
меняется, так как множитель 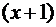 , обращающийся в ноль в этой точке,
также стоит в нечетной степени. Значит,
, обращающийся в ноль в этой точке,
также стоит в нечетной степени. Значит,
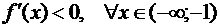 .
.

 ˗˗˗ + ˗˗˗
˗˗˗ + ˗˗˗

 -1 1
-1 1
Таким образом, имеем:  возрастает
на
возрастает
на 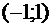 ,
,  убывает на
убывает на 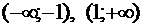 ; точка
; точка 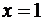 является
точкой локального максимума, а
является
точкой локального максимума, а 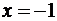 - точка локального минимума функции
- точка локального минимума функции
 .
.
Далее возрастание или не убывание
функции  на
промежутке Х будем обозначать
на
промежутке Х будем обозначать 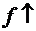 на Х, а убывание или не возрастание
-
на Х, а убывание или не возрастание
- 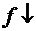 на Х.
на Х.
Пример 2.8 Найти
интервалы монотонности и точки локального экстремума функции
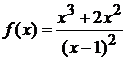
Решение. Найдем
сначала область определения:
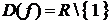
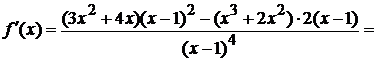
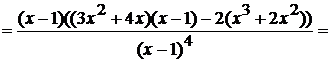
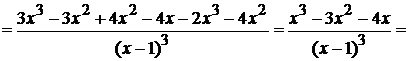
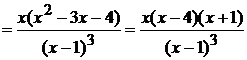
Критические точки, как уже
обсуждалось в предыдущем примере, это нули числителя и знаменателя 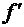 . То есть
точки
. То есть
точки 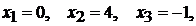
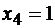 . На оси ОХ
отметим область определения функции (точка
. На оси ОХ
отметим область определения функции (точка 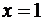 -«выколотая»). Нанесем критические
точки, попавшие в область определения функции. Знак
-«выколотая»). Нанесем критические
точки, попавшие в область определения функции. Знак 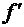 в крайнем
правом интервале «+», так как, например,
в крайнем
правом интервале «+», так как, например,
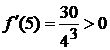
Далее знаки будут чередоваться, так
как все множители стоят в нечетных степенях.
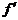 +
+  ˗˗˗ + ˗˗˗
+
˗˗˗ + ˗˗˗
+

 -1 0 1
4
-1 0 1
4
Таким образом, получим:
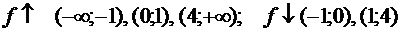 ;
;
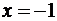 - точка локального максимума,
- точка локального максимума, 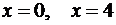 - точки
локального минимума функции
- точки
локального минимума функции  . Точка
. Точка 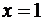 , несмотря
на то, что
, несмотря
на то, что 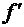 меняет знак
при переходе через нее, не является точкой локального экстремума, так как она
не входит в область определения функции
меняет знак
при переходе через нее, не является точкой локального экстремума, так как она
не входит в область определения функции  .
.
2.3 Исследование функции на
направление выпуклости и точки перегиба
Определение 2.4
Пусть функция  непрерывна
на
непрерывна
на 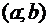 . Говорят,
что график функции обращен выпуклостью вверх (вниз), если хорда, соединяющая
любые две точки графика, лежит не выше (не ниже) куска графика, соединяющего
эти точки.
. Говорят,
что график функции обращен выпуклостью вверх (вниз), если хорда, соединяющая
любые две точки графика, лежит не выше (не ниже) куска графика, соединяющего
эти точки.
Исследовать функцию на направление
выпуклости по определению получится, только если известен ее график. В других
случаях определять направление выпуклости снова можно при помощи производной.
Теорема 2.5 Достаточное условие
направления выпуклости функции
Пусть функция  дважды
дифференцируема на
дважды
дифференцируема на 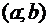 . Если
. Если
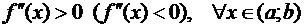 ,
,
то график функции  обращен
выпуклостью вниз (вверх) на
обращен
выпуклостью вниз (вверх) на 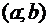 .
.
Пусть функция  непрерывна
на
непрерывна
на 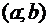 и
и 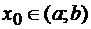 . Точка
. Точка 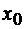 называется
точкой перегиба графика функции
называется
точкой перегиба графика функции  , если при переходе через нее график
меняет свое направление выпуклости.
, если при переходе через нее график
меняет свое направление выпуклости.
И снова, этим определением можно
воспользоваться, только если перед глазами имеется график исследуемой функции.
Поэтому применим производную к исследованию на перегиб.
Теорема 2.6 Необходимое условие
точки перегиба
Пусть функция 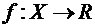 ,
, 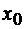 - точка
перегиба графика функции
- точка
перегиба графика функции  . Если
. Если  дважды
дифференцируема в точке
дважды
дифференцируема в точке 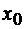 , то
, то 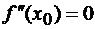
Из теоремы 2.6 следует, что если
функция дважды дифференцируема в точке 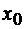 и
и 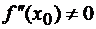 , то эта точка автоматически не
может быть точкой перегиба. Поэтому точками перегиба могут быть лишь те точки,
в которых вторая производная функции
, то эта точка автоматически не
может быть точкой перегиба. Поэтому точками перегиба могут быть лишь те точки,
в которых вторая производная функции  равна нулю, либо точки, в которых
равна нулю, либо точки, в которых  не имеет
второй производной.
не имеет
второй производной.
Определение 2.6
Точки, в которых вторая производная
функции равна нулю и те точки, в которых функция не дифференцируема дважды,
называются подозрительными на перегиб.
Можно привести примеры, показывающие,
что условие равенства нулю второй производной в точке является необходимым, но
не достаточным (приведите такие примеры). Значит, необходимо условие,
позволяющее отсортировать из множества точек, подозрительных на перегиб, те,
которые действительно являются перегибами. Такое условие содержит следующая
теорема.
Теорема 2.7 Достаточное условие
точки перегиба
Пусть функция  непрерывна
на
непрерывна
на 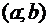 и дважды
дифференцируема на
и дважды
дифференцируема на 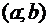 , быть может
кроме точки
, быть может
кроме точки 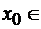
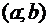 (
(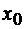 - точка подозрительная на перегиб).
Если при переходе через точку
- точка подозрительная на перегиб).
Если при переходе через точку 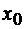 ,
, 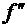 меняет знак, то точка
меняет знак, то точка 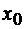 является
точкой перегиба графика функции
является
точкой перегиба графика функции  .
.
Заменив в алгоритме исследования
функции на монотонность и точки локального экстремума 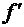 на
на 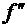 , получим
алгоритм исследования функции на направление выпуклости и точки перегиба.
, получим
алгоритм исследования функции на направление выпуклости и точки перегиба.
Пример 2.9 Определить
направления выпуклости графика функции 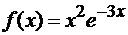 , найти точки перегиба.
, найти точки перегиба.
Решение. Область
определения функции: 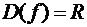 . Для
исследования на направление выпуклости и точки перегиба нужна вторая
производная функции
. Для
исследования на направление выпуклости и точки перегиба нужна вторая
производная функции  . Найдем
сначала первую:
. Найдем
сначала первую:
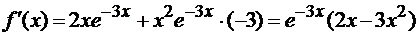
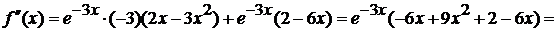
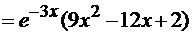 .
.
Напомним, что точками
подозрительными на перегиб являются нули второй производной и точки, в которых
она не определена. Чтобы их найти разложим 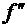 на множители. Для этого найдем
корни квадратного трехчлена
на множители. Для этого найдем
корни квадратного трехчлена
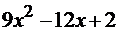
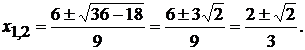
Тогда
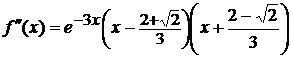
Так как 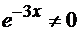 ни при
каких х из области определения, то точками подозрительными на перегиб будут две
точки
ни при
каких х из области определения, то точками подозрительными на перегиб будут две
точки 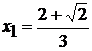 ,
, 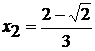 . Отметим на
числовой оси область определения, и нанесем на ось точки подозрительные на
перегиб, попавшие в область определения. Определяем знак
. Отметим на
числовой оси область определения, и нанесем на ось точки подозрительные на
перегиб, попавшие в область определения. Определяем знак 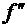 на
получившихся промежутках. На
на
получившихся промежутках. На 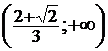 можно определить подстановкой, что
можно определить подстановкой, что 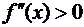 . Далее
знаки будут чередоваться.
. Далее
знаки будут чередоваться.

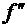 + ˗˗˗
+
+ ˗˗˗
+

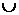
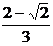
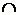
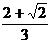
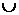
Следовательно, график функции
направлен выпуклостью вверх на 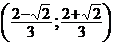 , выпуклостью вниз на
, выпуклостью вниз на 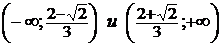 . Точки
. Точки 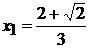 и
и 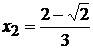 являются
точками перегиба графика функции.
являются
точками перегиба графика функции.
Далее выпуклость вниз функции  на
промежутке Х будем обозначать
на
промежутке Х будем обозначать 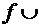 на Х, выпуклость вверх -
на Х, выпуклость вверх - 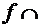 на Х.
на Х.
.4 Задачи на наибольшее и наименьшее
значения
Пусть функция  непрерывна
на отрезке
непрерывна
на отрезке 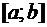 . Требуется
найти точки, в которых функция достигает самое большое и самое маленькое свое
значение на отрезке
. Требуется
найти точки, в которых функция достигает самое большое и самое маленькое свое
значение на отрезке 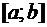 . Такая
задача всегда имеет решение, согласно теореме Вейерштрасса.
. Такая
задача всегда имеет решение, согласно теореме Вейерштрасса.
Теорема 2.8 Вейерштрасса
Пусть функция  непрерывна
на отрезке
непрерывна
на отрезке 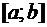 . Тогда она
ограничена на этом отрезке и достигает своего наибольшего и наименьшего
значения, то есть найдутся точки
. Тогда она
ограничена на этом отрезке и достигает своего наибольшего и наименьшего
значения, то есть найдутся точки 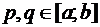 такие, что
такие, что
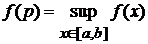 ,
, 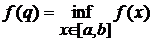 .
.

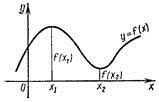
а х1 х2 х3
b
Рис. 1
По рис. 1 , видно, что наибольшее и
наименьшее значения функция достигает в точках х3 и а
соответственно. То есть наибольшее и наименьшее значения могут достигаться либо
в точках локального экстремума, лежащих внутри отрезка, либо на концах отрезка.
Так как точки локального экстремума находятся среди критических точек функции  , и по рис.1
видно, что значение функции в точке локального максимума (в точке х1
) может быть меньше, чем значение в точке локального минимума в точке х2,
то не важно знать: является ли найденная критическая точка максимумом или
минимумом (важно значение функции в этой точке). Учитывая эти рассуждения,
имеем следующий алгоритм решения задачи.
, и по рис.1
видно, что значение функции в точке локального максимума (в точке х1
) может быть меньше, чем значение в точке локального минимума в точке х2,
то не важно знать: является ли найденная критическая точка максимумом или
минимумом (важно значение функции в этой точке). Учитывая эти рассуждения,
имеем следующий алгоритм решения задачи.
Алгоритм нахождения наибольшего и
наименьшего значения функции
1) Найти производную функции  .
.
) Найти критические точки
функции  , попавшие в
интервал
, попавшие в
интервал 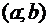 .
.
) Найти значения функции в
этих точках и на концах отрезка.
) Выбрать из полученных
значений самое большое и самое маленькое.
Пример 2.10 Найти
наибольшее и наименьшее значения функции
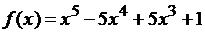 на отрезке [-1;2].
на отрезке [-1;2].
Решение. Найдем
производную заданной функции:
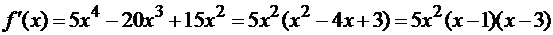
Очевидно, что критическими точками
будут
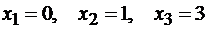
Нас интересуют только те из них,
которые попали внутрь заданного отрезка [-1;2]. Это точки 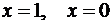 . Осталось
вычислить значения функции в этих точках и на концах отрезка и выбрать из них
наибольшее и наименьшее:
. Осталось
вычислить значения функции в этих точках и на концах отрезка и выбрать из них
наибольшее и наименьшее:
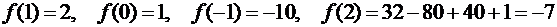
Таким образом
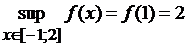 ,
,
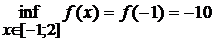 .
.
3. ПОЛНОЕ ИССЛЕДОВАНИЕ ФУНКЦИИ И
ПОСТРОЕНИЕ ЭСКИЗА ЕЕ ГРАФИКА
.1 Асимптоты графика функции
Определение 3.1
Асимптота графика функции 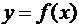 - это прямая,
к которой график функции неограниченно приближается при удалении точки по
графику в бесконечность.
- это прямая,
к которой график функции неограниченно приближается при удалении точки по
графику в бесконечность.
Асимптоты бывают вертикальными,
наклонными и, как частный случай последних - горизонтальными.
Утверждение 3.1
Прямая 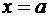 является
вертикальной асимптотой графика функции
является
вертикальной асимптотой графика функции 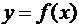 при
при 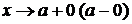 , если соответствующий односторонний
предел в точке а равен бесконечности, то есть
, если соответствующий односторонний
предел в точке а равен бесконечности, то есть
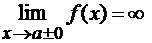
Замечание 3.1
График функции 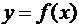 может иметь
вертикальную асимптоту
может иметь
вертикальную асимптоту 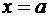 , если точка
а является точкой разрыва 2-го рода функции
, если точка
а является точкой разрыва 2-го рода функции  f либо если точка а лежит на конце
области определения функции, но сама в область определения не входит, то есть
область определения функции имеет вид
f либо если точка а лежит на конце
области определения функции, но сама в область определения не входит, то есть
область определения функции имеет вид 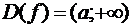 (или
(или  , или
, или 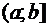 и т.д.).
и т.д.).
Пример 3.1 а)
Рассмотрим функцию
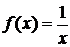
Область определения ее
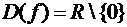
Точка 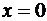 является точкой разрыва 2-го рода
заданной функции, так как, например,
является точкой разрыва 2-го рода
заданной функции, так как, например,
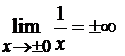
Следовательно, прямая 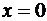 является
вертикальной асимптотой графика функции
является
вертикальной асимптотой графика функции
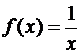 при
при 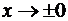 .
.
б) Рассмотрим функцию 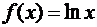 . Область
определения ее
. Область
определения ее 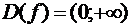 . Согласно
замечанию 3.1 в точке
. Согласно
замечанию 3.1 в точке 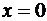 может быть
вертикальная асимптота у графика рассматриваемой функции. Проверим это. Для
этого вычислим односторонний предел функции при
может быть
вертикальная асимптота у графика рассматриваемой функции. Проверим это. Для
этого вычислим односторонний предел функции при 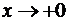 :
: 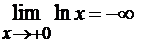 . Следовательно, прямая
. Следовательно, прямая 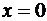 является
вертикальной асимптотой графика заданной функции.
является
вертикальной асимптотой графика заданной функции.
Утверждение 3.2
Пусть 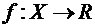 и
и 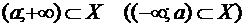 . Для того чтобы прямая
. Для того чтобы прямая 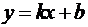 была
наклонной асимптотой графика функции
была
наклонной асимптотой графика функции 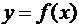 при
при 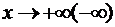 , необходимо и достаточно, чтобы
выполнялись условия:
, необходимо и достаточно, чтобы
выполнялись условия:
1) существует конечный
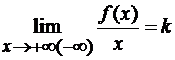 ;
;
2) существует конечный
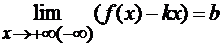 .
.
Замечание 3.2
Если предел в первом условии
утверждения 3.2 окажется равным нулю, а второй предел существует и конечен, то
график функции будет иметь при 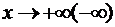 горизонтальную асимптоту
горизонтальную асимптоту 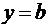 .
.
Пример 3.2 Найдем
наклонные асимптоты графика функции
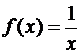
Для этого найдем оба предела из
утверждения 3.2:
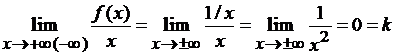
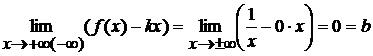
Так как оба предела существуют,
конечны и 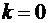 , то график
рассматриваемой функции имеет горизонтальную асимптоту
, то график
рассматриваемой функции имеет горизонтальную асимптоту 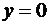 при
при 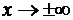 .
.
Пример 3.3 Найти все
асимптоты графика функции
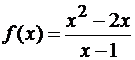
Решение. Определим
сначала, есть ли у графика функции вертикальные асимптоты. Для этого найдем
область определения функции:
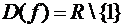
Точка 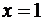 является точкой разрыва 2-го рода,
так как
является точкой разрыва 2-го рода,
так как
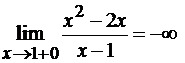
Следовательно, прямая 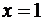 является
вертикальной асимптотой графика заданной функции. Проверим теперь наличие у
графика наклонных асимптот.
является
вертикальной асимптотой графика заданной функции. Проверим теперь наличие у
графика наклонных асимптот.
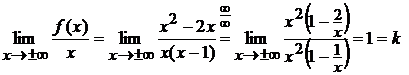
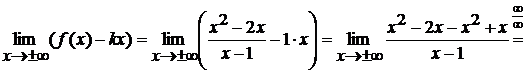
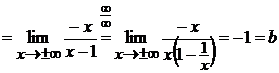
Таким образом, имеем, прямая 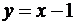 является
наклонной асимптотой графика заданной функции при
является
наклонной асимптотой графика заданной функции при 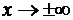 .
.
Замечание 3.3
В некоторых случаях пределы
из утверждения 3.2 приходится вычислять отдельно при 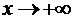 и при
и при 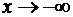 .
.
3.2 Полное исследование функции
Полное исследование функции с
построением эскиза ее графика проводится по следующему плану.
План исследования функции
1. Найти область определения функции.
2. Исследовать функцию на непрерывность.
Указать точки разрыва (если они есть) и их характер, сделать вывод о
вертикальных асимптотах. Исследовать функцию на наличие наклонных асимптот.
. Исследовать функцию на четность,
нечетность, периодичность и сделать вывод о графике.
. Найти точки пересечения графика с осями
координат, указать промежутки знакопостоянства.
. Исследовать функцию на монотонность и
точки локального экстремума.
. Найти промежутки направления выпуклости
и точки перегиба.
. Составить сводную таблицу данных
исследования и построить эскиз графика.
Пример 3.4 Провести
полное исследование и построить эскиз графика функции
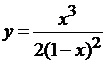
Решение. 1)
Область определения этой функции
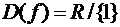
) Функция представляет собой
отношение двух многочленов, следовательно, она непрерывна как частное
непрерывных функций в своей области определения. Так как точка 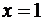 является
точкой сгущения области определения, но ей не принадлежит, то она является
точкой разрыва. Исследуем характер разрыва. Для этого найдем односторонние
пределы при
является
точкой сгущения области определения, но ей не принадлежит, то она является
точкой разрыва. Исследуем характер разрыва. Для этого найдем односторонние
пределы при 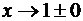 :
:
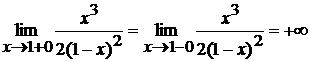
Следовательно, точка 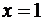 является
точкой разрыва 2-го рода, и прямая
является
точкой разрыва 2-го рода, и прямая 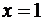 - вертикальная асимптота графика
функции. Проверим заданную функцию на наличие наклонных асимптот. Рассмотрим
для этого
- вертикальная асимптота графика
функции. Проверим заданную функцию на наличие наклонных асимптот. Рассмотрим
для этого
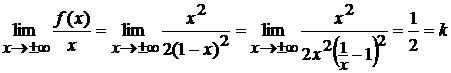
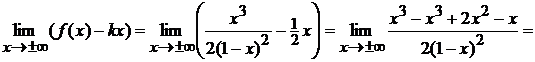
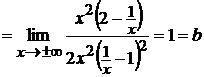
Значит, прямая 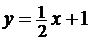 является
наклонной асимптотой графика функции при
является
наклонной асимптотой графика функции при 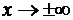 .
.
3) Рассматриваемая функция не является ни
четной, ни нечетной, так как область определения не является множеством,
симметричным относительно нуля. Функция не периодическая, так как из области
определения исключена только одна точка (если бы функция была бы периодической,
то все точки вида
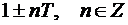 ,
,
где Т - величина периода, так же не входили бы в
область определения).
4) Найдем точки пересечения с
осью ОХ. Для этого нужно положить 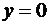 . Получим:
. Получим:
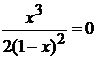
Отсюда 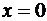 .
Следовательно, точка пересечения с осью ОХ имеет координаты (0;0). Чтобы найти
точку пересечения с
.
Следовательно, точка пересечения с осью ОХ имеет координаты (0;0). Чтобы найти
точку пересечения с 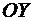 , нужно
положить
, нужно
положить 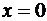 . Тогда
. Тогда 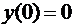 . То есть
график функции пересекает оси в начале координат. Промежутки знакопостоянства
функции:
. То есть
график функции пересекает оси в начале координат. Промежутки знакопостоянства
функции:
1

˗˗˗ + +
) Исследуем функцию на монотонность и точки
локального экстремума:
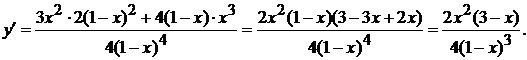
Критическими являются точки 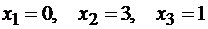
 0 1 3
0 1 3

 + + ˗˗
+
+ + ˗˗
+
Точка 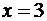 является точкой локального минимума
и
является точкой локального минимума
и 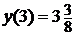 .
.
6) Найдем направления выпуклости графика функции
и точки перегиба:
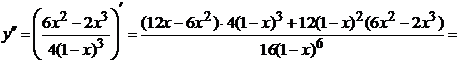
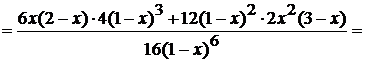
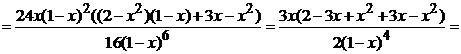
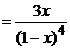
Точки 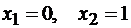 являются точками подозрительными на
перегиб.
являются точками подозрительными на
перегиб.
) Сведем все исследования в
одной таблице. Для этого укажем поведение функции на промежутках, на которые
область определения разбивается «особыми» точками, к которым отнесем точки
разрыва, точки пересечения с осью ОХ, точки экстремума и точки перегиба. У нас
таких точек три: 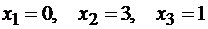 .
.
 ˗˗˗ +
+
˗˗˗ +
+


 0
0  1
1
Точка 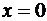 является точкой перегиба
является точкой перегиба
|
х
|
(-∞;0)
|
0
|
(0;1)
|
1
|
(1;3)
|
3
|
(3;+∞)
|
|
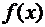 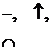 Точка перегиба,
точка пересечения с осями Точка перегиба,
точка пересечения с осями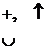 Точка разрыва
2-го рода Точка разрыва
2-го рода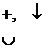 Лок. Min. Лок. Min.
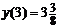 
|
|
|
|
|
|
|
|
Построение графика начинаем с нанесения асимптот

Литература
1.
Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. М.: Наука, 1975
(и более поздние издания).
.
Фоменко С.В. Математический анализ (учебное пособие). Г. Ростов-на-Дону, 2011.
.
Минорский В.П. Сборник задач по высшей математике. М.: Наука, 1987 (и более
поздние издания).
.
Налбандян Ю.С., Спинко Л.И. Контрольные задания по математическому анализу.
Методические указания для студентов заочного отделения экономического
факультета РГУ. Часть 1. Ростов-на-Дону 2009 г.
.
Ляликова Е.Р., Спинко Л.И. Функции: предел и непрерывность. Методическое
пособие для студентов 1-го курса направлений «Экономика», «Прикладная
информатика в экономике» экономического факультета ЮФУ. Ростов-на-Дону 2012 г.