Исчисление функции одного переменного

Исчисление функции одного переменного

РОССИЙСКАЯ ФЕДЕРАЦИЯ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

ФГБОУ ВПО «ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

ИНСТИТУТ ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ

СПЕЦИАЛЬНОСТЬ «Экономика»

Контрольная работа

По дисциплине: Математический анализ

Введение в анализ и дифференциальное исчисление функции одного переменного

Задание 1.

Вычислить предел

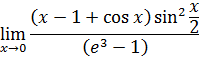
Решение.

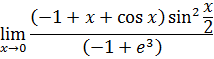
Выносим константу за скобки:

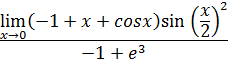
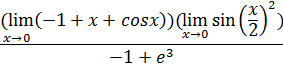
Предел константы является постоянным, предел суммы равен сумме пределов:

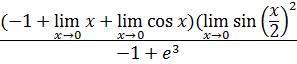
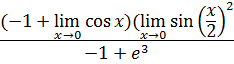
Предел x, при x стремящимся к 0, равен 0.

Предел cos x, при x стремящимся к 0, равен 1.

Ответ: 0.

Задание 2.

Найти асимптоты функции

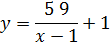
По определению асимптоты:

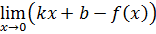
Находим коэффициент k:

,

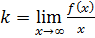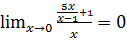
Находим коэффициент b:

,

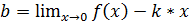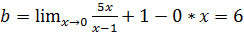
Получаем уравнение горизонтальной асимптоты:

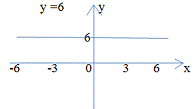
Рис. 1

Ответ: y=6; x=0.

Задание 3.

Определить глобальные экстремумы:

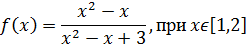
Решение.

Находим первую производную функции:

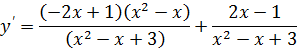
или

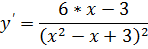
Приравниваем ее к нулю:

,

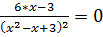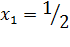
Вычисляем значения функции на концах отрезка:

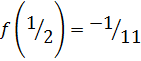
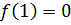
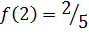
Ответ: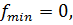  

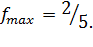
Задание 4.

Исследовать на монотонность, найти локальные экстремумы и построить эскиз графика функции

Решение.

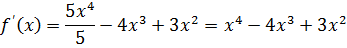
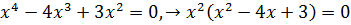
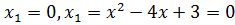
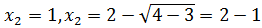
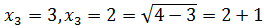
Рис. 2

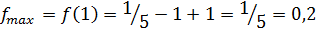
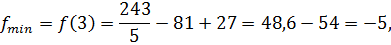
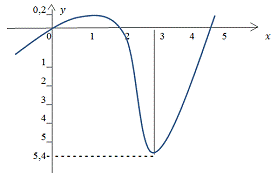
Рис. 3

Задание 5.

Найти промежутки выпуклости и точки перегиба функции

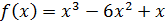
Решение.

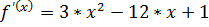
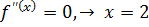
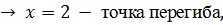
т.к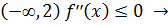. на  на 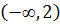 выпуклость вверх,

т.к. на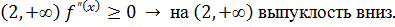

Дифференциальное исчисление функций и его приложение

Задание 1.

Провести полное исследование свойств и построить эскиз графика функции

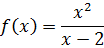
Решение.

Область определения функции:

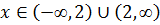
Пересечение с осью абсцисс :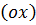

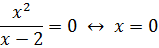
Пересечение с осью ординат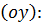

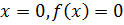
Поведение функции в граничных точках области определения:

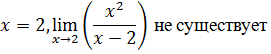
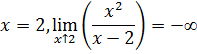
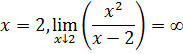
Поведение функции на бесконечности:

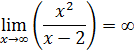
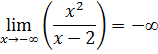
Наклонная асимптота функции:

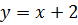
Исследование функции на четность/нечетность:

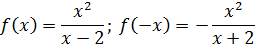
Функция является ни четной, ни нечетной.

Производная функции равна:

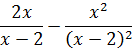
Нули производной: ,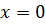

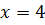
Функция возрастает на:

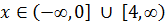
Функция убывает на:

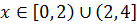
Минимальное значение функции:

Максимальное значение функции:

Построение графика функции:

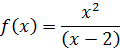
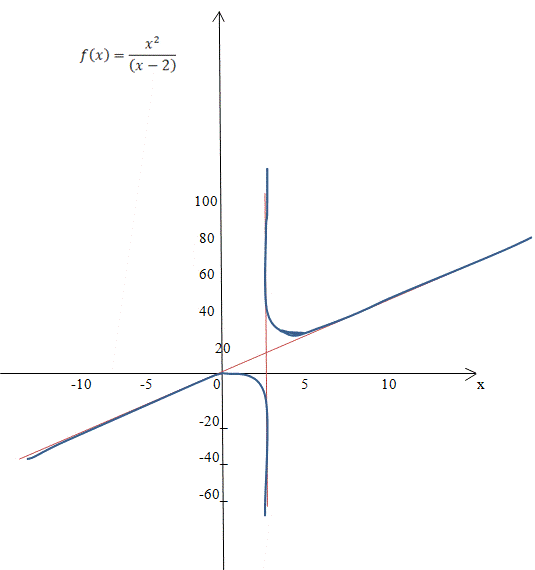
Рис. 4

Задание 2.

Найти локальные экстремумы функции

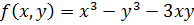
Решение.

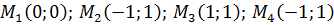
В точке

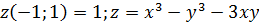
Найдем частные производные:

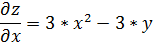
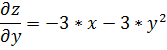
Решим систему уравнений:

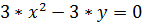
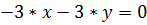
Получим:

а) Из первого уравнения выражаем 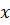 и подставляем во второе уравнение:

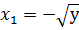
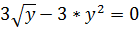
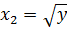
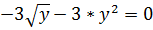
Откуда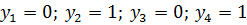

Данные значения подставляем в выражение для 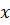. Получаем:

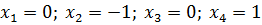
б) Из первого уравнения выражаем 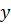 и подставляем во второе уравнение:

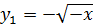
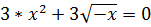
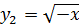
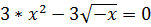
Откуда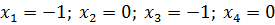

Данные значени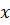я  подставляем в выражение для 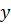. Получаем:

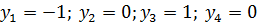
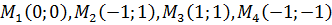
Найдем частные производные второго порядка.

, ,

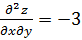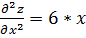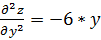
Вычислим значения этих частных производных второго порядка в критических точках 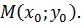Вычислим значение для точки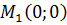

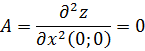
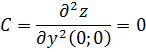
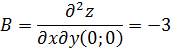
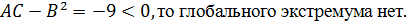
Вычисляем значения для точки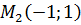

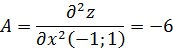
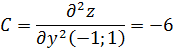
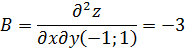
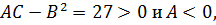
Вычисляем значения для точки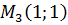

.

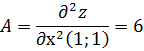
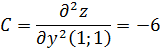
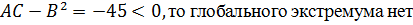Вычисляем значения для точки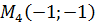

:

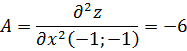
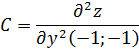
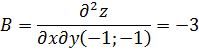
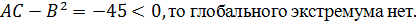
В точке 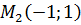 имеется максимум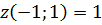

Задание 3.

Определить экстремумы функции

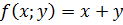, если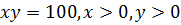

Решение.

Задача сводится к нахождению прямоугольника, имеющего наибольший/наименьший полупериметр при заданной площади. Известно, что среди прямоугольников с заданным периметром наибольшей площадью обладает квадрат. Поэтому наименьшим полупериметром среди прямоугольников, имеющих 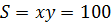 , обладает квадрат, для которого 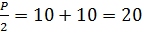 . Прямоугольника с наибольшим полупериметром не существует. Следовательно, функция 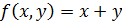 при условии 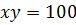 имеет минимум, если 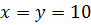, причем 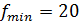. Условного максимума функция не имеет.

Интегральное исчисление функции одного переменного

Задание 1. Найти неопределенный интеграл

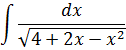
Решение.

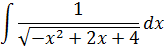
Для подынтегральной функции 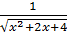 полный квадрат равен:

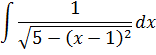
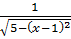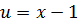Для подынтегральной функции  произведем замену и

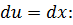
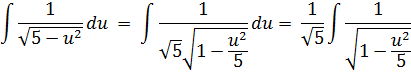
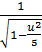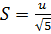Для подынтегральной функции  произведем замену  и

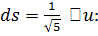
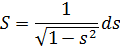
Интегралом 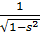 является

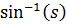
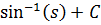
Произведем обратную замену для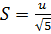

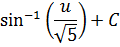
Произведем обратную замену для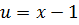

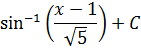
Ответ: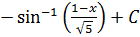

Задание 2.

Найти неопределенный интеграл

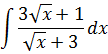
Решение.

Делаем замену переменных:

,

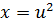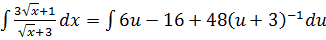
Интеграл суммы есть сумма интегралов:

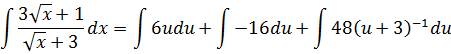
Вынесли константу из-под знака интеграла:

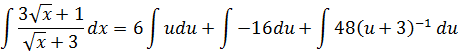
Проинтегрировали степенную функцию:

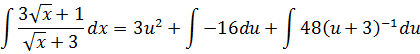
Проинтегрировали константу:

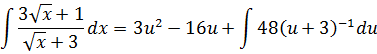
Вынесли константу из-под знака интеграла:

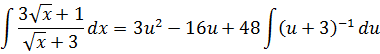
Делаем замену переменных:

,

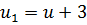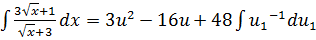
Проинтегрировали степенную функцию:

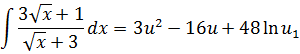
Сделали обратную замену:

Сделали обратную замену:

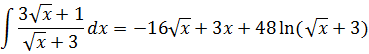
Ответ:

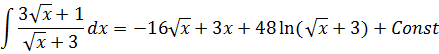
Задание 3.

Найти неопределенный интеграл:

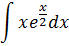
Решение.

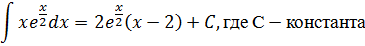
Интегрируем подынтегральную функцию по частям:

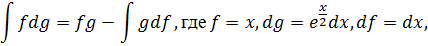
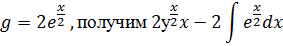
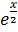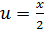В подынтегральной функции  производим замену и

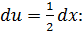
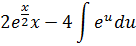
Интегралом 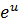 является

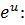
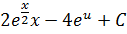
Произведем обратную замену для :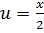

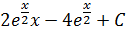
Ответ: .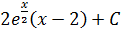

Задание 4.

Вычислить:

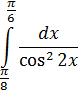
Решение.

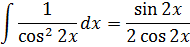
Подставляем пределы интегрирования:

функция переменная интегрирование

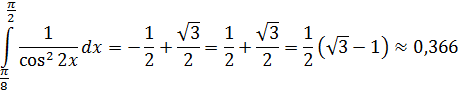
Ответ:

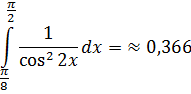
Задание 5.

Определить площадь плоской фигуры, ограниченной кривыми

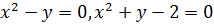
Решение.

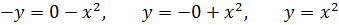
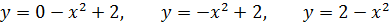
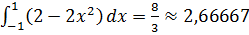
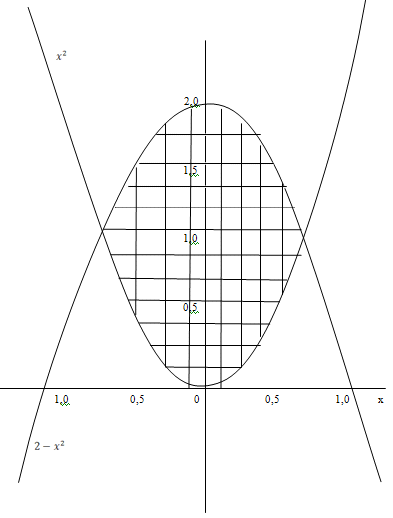
Рис. 5

Список литературы

1. А.П. Девятков, А.А. Макаров, Е.Г. Пыткеев, А.Г. Хохлов. Математика: Математический анализ и линейная алгебра., М., 2011.