Теоретические и методические аспекты изучения темы 'Интегральное исчисление функции нескольких переменных'
Оглавление
Введение
. Тройной
интеграл и его вычисление
.1 Задача о
вычислении массы тела
.2 Тройной
интеграл и условия его существования
.3 Свойства
интегрируемых функций и тройных интегралов
.4 Вычисление
тройного интеграла, распространенного на параллелепипед
.5 Вычисление
тройного интеграла по любой области
.6
Несобственные тройные интегралы
.7
Механические приложения
. Замена
переменных в тройных интегралах
.1
Преобразование пространств и криволинейные координаты
.2 Примеры
.3 Выражение
объема в криволинейных координатах
.4 Замена
переменных в тройных интегралах
.
Методические основы изучения раздела темы «Тройные интегралы» и их применение в
педагогическом вузе
.1
Психолого-педагогические аспекты образования в высшей школе
.2
Методические рекомендации по проведению лекционных занятий с применением
информационных технологий
.3 Разработка
лекционных занятий
.4
Методические рекомендации по проведению практических занятий
.5 Разработка
практических занятий
.6 Применение
новых информационных технологий при изучении практического материала
.7
Обучающе-контролирующая программа по теме “Тройные интегралы”
Заключение
Литература
Приложения
Введение
Реформа российского математического образования высшей школы заключается
в том, что к традиционно изучаемым курсам в математике добавляются новые. Это
ведет к сокращению аудиторных часов, предназначенных для изучения базовых
дисциплин математического блока - в том числе математического анализа.
Потребности современного образования ставят перед методикой преподавания
математики новые задачи. Особенно остро встает вопрос о методике изучения
математического анализа в вузе. Тройной интеграл является одной из важнейших и
объемнейших тем математического анализа. Поэтому необходимо, чтобы материал был
хорошо усвоен студентами. Теоретические и практические исследования по данной
теме являются актуальными и обусловлены потребностями педагогических вузов.
Итак, объектом исследования темы является процесс организации учебной
деятельности при изучении дисциплины «Математический анализ» в педагогическом
вузе.
В качестве предмета исследования выступает методика изучения раздела
математического анализа «Тройные интегралы» в вузах педагогической
направленности.
Научная проблема исследования состоит в поиске наиболее оптимальных
закономерностей при изучении этого вопроса.
Цель данной работы - формирование методического аппарата по изучению темы
“Тройные интегралы”.
Реализация поставленной цели потребовала решения ряда задач, а именно:
. Обосновать и разработать содержание и методику изучения темы «Тройные
интегралы» в педагогическом вузе с учетом возрастных особенностей студентов;
. Создать обучающее-контролирующую программу по данной теме для студентов
второго курса физико-математических факультетов педагогических вузов.
В соответствии с этим гипотеза исследования заключается в том, что
разработанная методика изучения раздела математического анализа «Тройные
интегралы» с использованием новых педагогических и информационных технологий
будет способствовать более успешному формированию знаний, умений и навыков у
студентов педагогических вузов по дисциплине «Математический анализ».
Для достижения цели и поставленных задач были привлечены следующие методы
исследования:
. Теоретический анализ проблемы, определение основных положений исследования;
. Анализ психолого-педагогической, математической, методической
литературы, учебных пособий, работ по истории математики, учебных программ;
. Ознакомление с методическим опытом преподавателей СГПИ.
Практическая значимость исследования квалификационной работы определена
тем, что ее материалы будут полезны:
преподавателям физико-математических факультетов педагогических вузов при
подготовке и проведении лекционных и практических занятий по дисциплине
“Математический анализ”, а также при организации самостоятельной работы
студентов.
студентам при подготовке к практическим занятиям, коллоквиумам,
экзаменам, при написании курсовых и выпускных работ.
1. Тройной интеграл и его вычисление
.1 Задача о вычислении массы тела
Пусть дано некоторое тело (V), заполненное массами, и в каждой его точке
M(x, y, z) известна плотность распределение ρ =
ρ(M)=ρ(x, y, z)
этих масс. Требуется определить всю массу m тела [2].
Для
решения этой задачи разложим тело (V) на ряд частей: (V1), (V2),
… , (Vn) и выберем в пределах каждой из них по точке 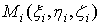 .
.
Примем
приближенно, что в пределах части (Vi) плотность постоянна и равна
как раз плотности 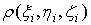 в выбранной точке. Тогда масса
в выбранной точке. Тогда масса 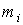 этой части
этой части  приближенно
выразится так:
приближенно
выразится так:
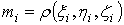 ,
,
масса
же всего тела будет
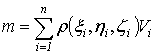 .
.
Если диаметры всех частей стремятся к нулю, то в пределе это приближенное
равенство становиться точным, так что
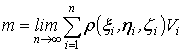 , (1)
, (1)
и задача решена [3].
Видно, что решение задачи и здесь привело к рассмотрению предела
своеобразной суммы - типа интегральных сумм различного вида.
Подобного рода интегральные суммы приходится часто рассматривать в
механике и в физике; они получили название тройных интегралов. В принятых
обозначениях полученный выше результат запишется так [1]:
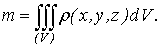 (2)
(2)
.2
Тройной интеграл и условия его существования
При
построении общего определения нового интегрального образования тройного
интеграла - основную роль играет понятие объема тела [1].
С
понятием объема уже знакомы. Условие существования объема для данного тела
заключается в том, чтобы ограничивающая его поверхность имела объем 0 . Только
такие поверхности будем рассматривать, так, что существование объемов во всех
нужных нам случаях тем самым обеспечивается. В частности, в состав указанного
класса поверхностей входят кусочно-гладкие поверхности.
Пусть
теперь в некоторой пространственной области (V) задана функция f(x, y, z).
Разобьем эту область с помощью сети поверхностей на конечное число частей (V1),
(V2), … , (Vn), имеющих соответственно объемы V1,
V2, … ,Vn. В пределах i-го элемента возьмем произвольную
точку 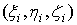 , значение функции в этой точке
, значение функции в этой точке 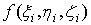 умножим на объем Vi и составим
интегральную сумму
умножим на объем Vi и составим
интегральную сумму
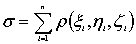 Vi.
Vi.
Конечный
предел I этой суммы, при стремлении к нулю наибольшего из диаметров всех
областей (Vi) и называется тройным интегралом функции f(x, y, z) в
области (V). Он обозначается символом
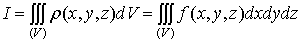 .
.
Конечный предел подобного вида может существовать только для ограниченной
функции. Для такой функции вводятся, кроме интегральной суммы σ,
еще суммы Дарбу:
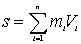 ,
, 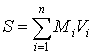 ,
,
где
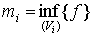 ,
, 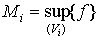 .
.
Обычным
путем устанавливается, что для существования интеграла необходимо и достаточно
условие
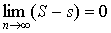 или
или 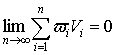 ,
,
где
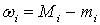 есть колебание функции f в области
есть колебание функции f в области 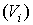 . Заметим, что при существовании интеграла обе суммы
s, S также имеют его своим пределом.
. Заметим, что при существовании интеграла обе суммы
s, S также имеют его своим пределом.
Отсюда
непосредственно следует, что всякая непрерывная функция f интегрируема.
Можно
несколько расширить эти условия, а именно: интегрируема всякая ограниченная
функция, все разрывы которой лежат на конечном числе поверхностей с объемом 0
[3].
Доказательство
этого утверждения основано на следующей лемме:
Если область (V), содержащая поверхность (S) с объемом 0, разложена на
элементарные области, то сумма объемов тех из них, которые задевают поверхность
(S), стремиться к нулю вместе с диаметрами всех частичных областей.
.3 Свойства интегрируемых функций и тройных интегралов
. Существование и величина тройного интеграла не зависят от значений,
принимаемых функцией вдоль конечного числа поверхностей с объемом 0.
2.
Если 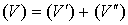 , то
, то 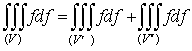 , причем
из существования интеграла слева вытекает уже существование интегралов справа,
и обратно.
, причем
из существования интеграла слева вытекает уже существование интегралов справа,
и обратно.
.
Если k= const, то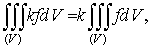 причем из существования интеграла справа следует
существование интеграла слева.
причем из существования интеграла справа следует
существование интеграла слева.
.
Если в области (V) интегрируемы две функции f и g, то интегрируема и функция 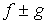 , причем
, причем
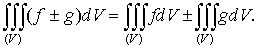
.
Если для интегрируемых в области (V) функции, f и g выполняется неравенство 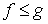 , то
, то
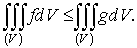
6.
В случае интегрируемости функции 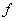 интегрируема
и функция
интегрируема
и функция 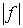 , и имеет место неравенство
, и имеет место неравенство
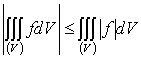 .
.
.
Если интегрируемая в 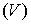 функция
функция 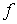 удовлетворяет
неравенству
удовлетворяет
неравенству 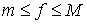 , то
, то 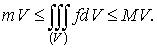
Иными
словами, имеет место теорема о среднем значении
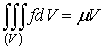
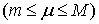 .
.
В
случае непрерывности функции 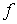 эту
формулу можно написать
эту
формулу можно написать
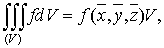 (3)
(3)
где
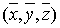 есть некоторая точка области
есть некоторая точка области 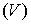 [3].
[3].
Устанавливаем
понятие функции от (трехмерной) области, в частности, аддитивной функции.
Важным
примером такой функции является интеграл по переменной области 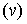 :
:
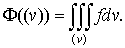 (4)
(4)
Вводится
аналогично прежнему понятие производной функции 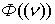 по
области в данной точке
по
области в данной точке 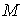 , так называется предел
, так называется предел
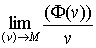
при
стягивании к точке М содержащей ее области 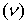 .
.
.
Если подинтегральная функция непрерывна, то производная
Рис.
1.
по
области в точке 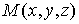 от интеграла (4) будет равна значению подинтегральной
функции в этой точке, т. е.
от интеграла (4) будет равна значению подинтегральной
функции в этой точке, т. е. 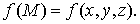
Таким
образом, при сделанном предположении интеграл (4) служит для функции 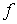 в некотором смысле «первообразной» и, как
доказывается аналогично плоскому случаю, единственной аддитивной первообразной.
в некотором смысле «первообразной» и, как
доказывается аналогично плоскому случаю, единственной аддитивной первообразной.
.4 Вычисление тройного интеграла, распространенного на параллелепипед
Изложение
вопроса о вычислении тройного интеграла начнем с того случая, когда тело, в
котором определена функция 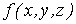 ,
представляет собой прямоугольный параллелепипед
,
представляет собой прямоугольный параллелепипед 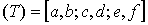 (рис.1),
проектирующийся на плоскость
(рис.1),
проектирующийся на плоскость 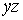 в
прямоугольник
в
прямоугольник 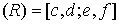 [4].
[4].
Теорема.
Если для функции 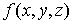 существует тройной интеграл
существует тройной интеграл
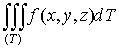 (5)
(5)
и
при каждом постоянном 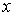 из
из 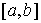 - двойной
интеграл
- двойной
интеграл
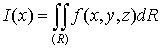 , (6)
, (6)
то
существует также повторный интеграл
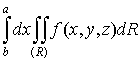 , (7)
, (7)
и
выполняется равенство
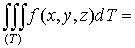
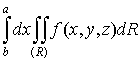 . (8)
. (8)
доказательство: Разделим
промежутки 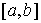 ,
, 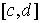 ,
, 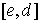 на части с помощью точек
на части с помощью точек
 ,
,
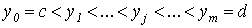 ,
,
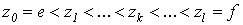 ,
,
тем
самым разложим параллелепипед (Т) на элементарные параллелепипеды
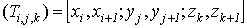
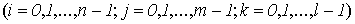
и
одновременно прямоугольник 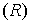 - на
элементарные прямоугольники
- на
элементарные прямоугольники
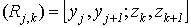
(где
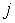 и
и  пробегают
те же значения, что и только что).
пробегают
те же значения, что и только что).
Положив
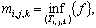
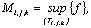
имеем
в силу 1.3, 1.7,
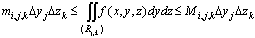
для
всех значений 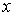 из
из 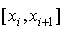 . Фиксируя
произвольное значение
. Фиксируя
произвольное значение 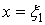 , в этом промежутке, просуммируем подобные неравенства
для всех значений j и k; мы получим неравенства
, в этом промежутке, просуммируем подобные неравенства
для всех значений j и k; мы получим неравенства
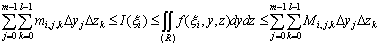 .
.
Наконец,
умножим эти неравенства почленно на 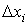 и
просуммируем на этот раз по значку
и
просуммируем на этот раз по значку 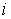 :
:
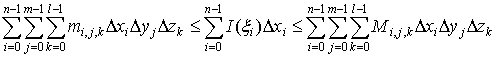 .
.
Крайние
члены представляют собой суммы Дарбу для интеграла (3) и стремятся к нему, как
к пределу, при стремлении к нулю всех разностей 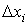 ,
, 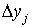 ,
,  . Значит,
к тому же пределу стремится интегральная сумма, стоящая посредине. Этим
доказано одновременно как существование интеграла (7), так и равенство (8).
Если предположить еще существование простого интеграла
. Значит,
к тому же пределу стремится интегральная сумма, стоящая посредине. Этим
доказано одновременно как существование интеграла (7), так и равенство (8).
Если предположить еще существование простого интеграла
 (9)
(9)
при
любых значениях х из 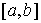 , у из
, у из 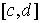 ,то
двойной интеграл в равенстве (8) можно заменить повторным и окончательно
получим:
,то
двойной интеграл в равенстве (8) можно заменить повторным и окончательно
получим:
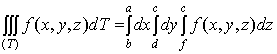 . (10)
. (10)
Таким
образом, вычисление тройного интеграла приводится к последовательному
вычислению трех простых интегралов. Роли переменных 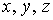 , в формуле (10), разумеется, могут быть произвольно
переставлены.
, в формуле (10), разумеется, могут быть произвольно
переставлены.
Если
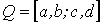 , то
, то
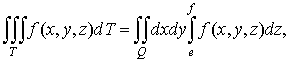 (11)
(11)
И
здесь роли переменных можно переставлять.
В
частности, для случая непрерывной функции 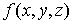 ,очевидно,
имеют место все формулы (8), (10), (11) и им подобные, получающиеся
перестановкой переменных [3].
,очевидно,
имеют место все формулы (8), (10), (11) и им подобные, получающиеся
перестановкой переменных [3].
.5 Вычисление тройного интеграла по любой области
Общий
случаи интеграла, распространенного на тело 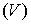 любой
формы, может быть легко приведен к только что рассмотренному. Именно, если
функция
любой
формы, может быть легко приведен к только что рассмотренному. Именно, если
функция 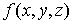 определена в области
определена в области 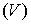 ,то
вместо нее следует лишь ввести, функцию
,то
вместо нее следует лишь ввести, функцию 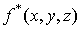 ,
определенную в объемлющем
,
определенную в объемлющем 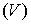 прямоугольном параллелепипеде
прямоугольном параллелепипеде 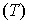 , полагая
, полагая
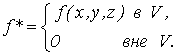
Этим
путем и получаются все приводимые ниже формулы.
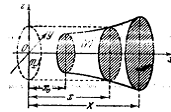
Рис. 2.
Остановимся
на случаях, представляющих наибольший интерес. Пусть тело  содержится между плоскостями
содержится между плоскостями  и
и 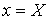 и каждою
параллельною им плоскостью, отвечающей фиксированному значению
и каждою
параллельною им плоскостью, отвечающей фиксированному значению 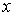
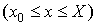 , пересекается по некоторой фигуре, имеющей площадь;
через
, пересекается по некоторой фигуре, имеющей площадь;
через 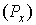 обозначим ее проекцию на плоскость
обозначим ее проекцию на плоскость 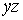 (рис. 2). Тогда
(рис. 2). Тогда
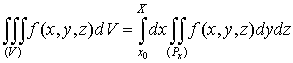 (8*)
(8*)
в
предположении существования тройного и двойного интегралов. Это - аналог
формулы (8).
Пусть,
далее, тело 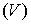 представляет собой «цилиндрический брус»,
ограниченный снизу и сверху, соответственно, поверхностями
представляет собой «цилиндрический брус»,
ограниченный снизу и сверху, соответственно, поверхностями
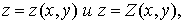
проектирующимися
на плоскость 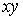 в некоторую фигуру
в некоторую фигуру 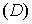 ,
ограниченную кривой
,
ограниченную кривой 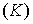 с площадью 0; с боков тело
с площадью 0; с боков тело 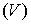 ограничено цилиндрической поверхностью с образующими,
параллельными оси
ограничено цилиндрической поверхностью с образующими,
параллельными оси 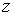 , и с кривой
, и с кривой 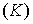 в роли
направляющей. Тогда аналогично формуле (11) имеем
в роли
направляющей. Тогда аналогично формуле (11) имеем
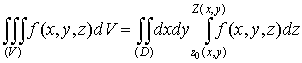 (11*)
(11*)
при
этом предполагается существование тройного интеграла и простого - внутреннего-
интеграла справа [4].
Если
область 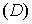 представляет собой криволинейную трапецию,
ограниченную двумя кривыми (рис.14)
представляет собой криволинейную трапецию,
ограниченную двумя кривыми (рис.14) 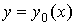 и
и 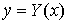
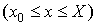 и прямыми
и прямыми 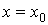 ,
, 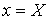 , то тело
, то тело 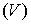 подходит
под оба типа, рассмотренных выше. Заменяя двойной интеграл-то ли в формуле
(8*), то ли в формуле (11*)-повторным, получим
подходит
под оба типа, рассмотренных выше. Заменяя двойной интеграл-то ли в формуле
(8*), то ли в формуле (11*)-повторным, получим
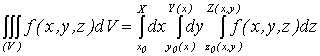 . (10*)
. (10*)
Эта
формула обобщает формулу (10).
Как
и в простейшем случае, который был рассмотрен в предыдущем п°, и здесь
непрерывность функции 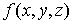 обеспечивает приложимость всех формул (8*), (11 *),
(10*) и им подобных, получающихся из них перестановкой переменных
обеспечивает приложимость всех формул (8*), (11 *),
(10*) и им подобных, получающихся из них перестановкой переменных 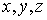 .
.
Рис. 3.
.6 Несобственные тройные интегралы
В случаях, когда область интегрирования простирается в бесконечность или
подинтегральная функция перестает быть ограниченной вблизи особых точек, линий
или поверхностей, несобственный тройной интеграл получается помощью
дополнительного предельного перехода, исходя из собственного интеграла.
Несобственные тройные интегралы также являются необходимо абсолютно
сходящимися. Это обстоятельство сводит весь вопрос о существовании и вычислении
таких интегралов к случаю положительной (неотрицательной) подинтегральной
функции [2].
.7 Механические приложения
Естественно,
что все геометрические и механические величины, связанные с распределением масс
в пределах некоторого тела  в
пространстве, в принципе выражаются на этот раз тройными интегралами,
распространенными на тело
в
пространстве, в принципе выражаются на этот раз тройными интегралами,
распространенными на тело  .Здесь также проще всего пользоваться принципом
"суммирования бесконечно малых элементов" [1].
.Здесь также проще всего пользоваться принципом
"суммирования бесконечно малых элементов" [1].
Обозначим
через 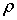 плотность распределения масс в произвольной точке
тела
плотность распределения масс в произвольной точке
тела 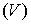 ; она является функцией от координат точки; эту
функцию мы будем всегда предполагать непрерывной. Суммируя элементы массы
; она является функцией от координат точки; эту
функцию мы будем всегда предполагать непрерывной. Суммируя элементы массы 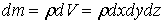 , для величины всей массы будем иметь
, для величины всей массы будем иметь
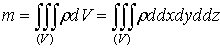 (12)
(12)
Исходя из элементарных статических моментов
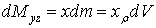 ,
,  ,
, 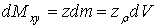
найдем
самые статические моменты:
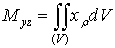 ,
, 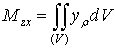 ,
,  , (13)
, (13)
а
по ним -и координаты центра тяжести:
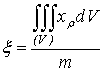 ,
, 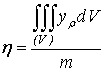 ,
, 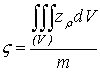 . (14)
. (14)
В
случае однородного тела, 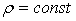 , получаем проще:
, получаем проще:
 ,
, 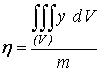 ,
,  .
.
Сами собой понятны и формулы для моментов инерции относительно осей
координат:
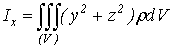 ,
, 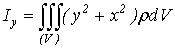 ,
, 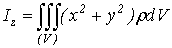 (15)
(15)
или относительно координатных плоскостей:
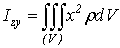 ,
,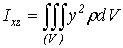 ,
, 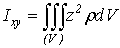 . (16)
. (16)
Наконец,
пусть массы, заполняющие тело  ,
оказывают притяжение на точку
,
оказывают притяжение на точку 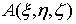 (массы
1) по закону Ньютона. Сила притяжения со стороны элемента
(массы
1) по закону Ньютона. Сила притяжения со стороны элемента 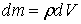 массы имеет на оси координат проекции
массы имеет на оси координат проекции
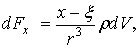
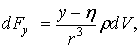
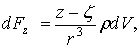
где
расстояние элемента (или точки, в которой мы считаем сосредоточенной его массу)
от точки 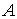 . Суммируя, для проекций полной силы
. Суммируя, для проекций полной силы 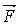 притяжения на оси координат получим
притяжения на оси координат получим
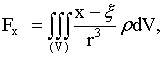
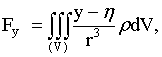
 (17)
(17)
Аналогично определяется и потенциал нашего тела на точку:
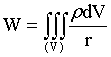 . (18)
. (18)
Если
точка 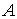 лежит вне тела, то все эти интегралы оказываются
собственными. В этом случае можно дифференцировать интеграл
лежит вне тела, то все эти интегралы оказываются
собственными. В этом случае можно дифференцировать интеграл 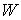 по любой из переменных
по любой из переменных 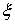 ,
, 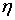 ,
, 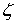 под
знаком интеграла на основании соображений, сходных с теми, которыми
пользовались в отношении простых интегралов. В результате мы и получим, что
под
знаком интеграла на основании соображений, сходных с теми, которыми
пользовались в отношении простых интегралов. В результате мы и получим, что
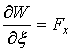 ,
, 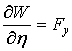 ,
, 
В
случае же, когда точка 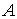 сама принадлежит телу
сама принадлежит телу 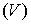 , в этой
точке
, в этой
точке 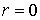 , и подинтегральные функции в (17) и (18) вблизи нее
перестают быть ограниченными [1].
, и подинтегральные функции в (17) и (18) вблизи нее
перестают быть ограниченными [1].
2.
Замена переменных в тройных интегралах
.1
Преобразование пространств и криволинейные координаты
Идеи, развитые в связи с преобразованием плоских областей, естественно
переносятся и на случай пространственных областей.
Пусть
имеем пространство, отнесенное к системе прямоугольных координат 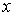
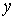
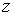 , и
другое пространство с системой координат
, и
другое пространство с системой координат 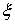
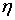
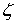 .
Рассмотрим две замкнутые области
.
Рассмотрим две замкнутые области 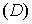 и
и 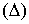 в этих пространствах ограниченные соответственно
поверхностями
в этих пространствах ограниченные соответственно
поверхностями  и
и 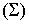 , которые
всегда будем предполагать кусочно-гладкими. Допустим, что эти области связаны
между собой взаимно однозначным непрерывным соответствием, которое
осуществляется формулами:
, которые
всегда будем предполагать кусочно-гладкими. Допустим, что эти области связаны
между собой взаимно однозначным непрерывным соответствием, которое
осуществляется формулами:
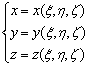 (19)
(19)
При
этом, необходимо, точкам поверхности 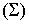 отвечают
именно точки поверхности
отвечают
именно точки поверхности  , и наоборот [1].
, и наоборот [1].
Пусть
функции (19) имеют в области 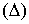 непрерывные
частные производные; тогда и якобиан
непрерывные
частные производные; тогда и якобиан
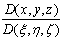 (20)
(20)
также
является непрерывной функцией в 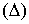 . Здесь
будем считать, что этот определитель всегда отличен от нуля, сохраняя
определенный знак.
. Здесь
будем считать, что этот определитель всегда отличен от нуля, сохраняя
определенный знак.
Если
в области 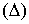 взять кусочно- гладкую поверхность:
взять кусочно- гладкую поверхность:
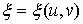 ,
, 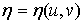 ,
, 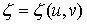 (21)
(21)
(предполагая,
что параметры изменяются в некоторой области 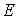 на
плоскости
на
плоскости  ), то формулы (19) преобразуют ее в кусочно-гладкую же
поверхность в области
), то формулы (19) преобразуют ее в кусочно-гладкую же
поверхность в области 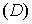 . Эта поверхность будет иметь уравнения
. Эта поверхность будет иметь уравнения
 . (22)
. (22)
Ограничимся
случаем гладкой поверхности (20): на ней особых точек нет, так что определяем:
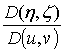 ,
, 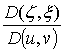 ,
, 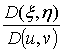 (23)
(23)
одновременно
в нуль не обращаются. Проверке подлежит лишь отсутствие особых точек и на
поверхности (21).
Имеем линейные равенства относительно величин (22):
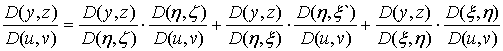 ,
,
 ,
,
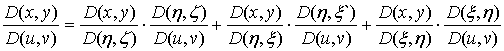 [2].
[2].
Определитель,
составленный из коэффициентов при этих величинах, т.e. из алгебраических
дополнений к элементам определителя (20), по известной теореме алгебры равен
квадрату этого последнего и, следовательно, вместе с ним отличен от нуля. Если
бы левые части написанных равенств в какой-нибудь точке 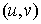 одновременно обратились а нуль, то нулями были бы и
все три определителя (23), что противоречило бы допущению.
одновременно обратились а нуль, то нулями были бы и
все три определителя (23), что противоречило бы допущению.
Числа
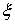 ,
, 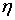 ,
, 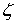 однозначно характеризующие положение точки в
пространстве
однозначно характеризующие положение точки в
пространстве 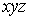 , называются криволинейными координатами этой точки.
Точки пространства
, называются криволинейными координатами этой точки.
Точки пространства 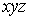 , для которых одна из этих координат сохраняет
постоянное значение, образуют координатную поверхность. Всего будет
существовать три семейства таких координатных поверхностей; через каждую точку
области
, для которых одна из этих координат сохраняет
постоянное значение, образуют координатную поверхность. Всего будет
существовать три семейства таких координатных поверхностей; через каждую точку
области 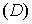 проходит по одной поверхности каждого семейства [3].
проходит по одной поверхности каждого семейства [3].
Впрочем,
все это будет так лишь в предположении строгой однозначности соответствия между
областями 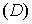 и
и 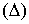 . На
практике эта однозначность часто нарушается.
. На
практике эта однозначность часто нарушается.
.2
Примеры
)
Цилиндрические координаты представляют соединение полярных координат в
плоскости  с обычной декартовой аппликатой
с обычной декартовой аппликатой 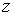 (рис.4). Формулы, связывающие их с декартовыми, имеют
вид
(рис.4). Формулы, связывающие их с декартовыми, имеют
вид
 ,
, 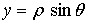 ,
, 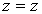 (24)
(24)
Эти формулы отображают область
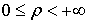 ,
, 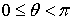 ,
, 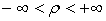
на
все пространство 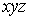 . Отметим, однако, что прямая
. Отметим, однако, что прямая 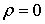 ,
, 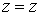 отображается
в одну точку
отображается
в одну точку  ; этим нарушается взаимная однозначность соответствия
[2].
; этим нарушается взаимная однозначность соответствия
[2].
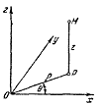
Рис.
4.
Координатные поверхности в рассматриваемом случае будут:
а)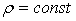 - цилиндрические поверхности с образующими,
параллельными оси
- цилиндрические поверхности с образующими,
параллельными оси 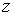 ; направляющими для них служат окружности на плоскости
; направляющими для них служат окружности на плоскости
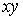 с центром в начале;
с центром в начале;
б)
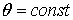 - полуплоскости, проходящие через ось
- полуплоскости, проходящие через ось 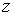 ;
;
в)
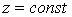 - плоскости, параллельные плоскости
- плоскости, параллельные плоскости 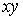 .
.
Якобиан
преобразования:
 .
.
Исключая
случай 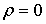 , якобиан сохраняет положительный знак.
, якобиан сохраняет положительный знак.
)
Сферические координаты, называемые иначе полярными координатами в пространстве,
связаны с декартовыми формулами:
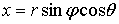 ,
, 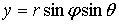 ,
, 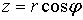 ,
,
Где
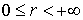 ,
, 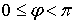 ,
, 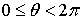 .
.
Геометрический
смысл величин 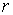 ,
, 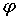 ,
, 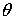 ясен из puc.5:
ясен из puc.5: 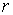 есть
радиус вектор
есть
радиус вектор 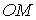 , соединяющий начало(полюс) с данной точкой
, соединяющий начало(полюс) с данной точкой 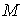 ;
;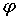 - угол, составляемый с осью координат
- угол, составляемый с осью координат 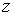 (полярной осью);
(полярной осью); 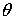 - угол,
составляемый с осью
- угол,
составляемый с осью 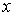 проекцией
проекцией 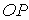 (перпендикулярную
к полярной оси) [1].
(перпендикулярную
к полярной оси) [1].
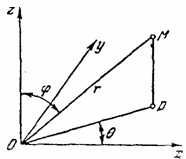
Рис.5.
В
этом случае снова сталкиваемся с нарушением взаимной однозначности
соответствия: плоскость 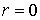 пространства
пространства 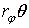 отображается
в начало координат
отображается
в начало координат 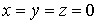 , прямая
, прямая 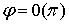 ,
, 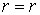 отображается в одну точку
отображается в одну точку 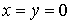 ,
, 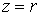 .
.
Координатные поверхности составляют три семейства:
а)
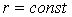 - концентрические сферы с центром в начале координат;
- концентрические сферы с центром в начале координат;
б)
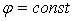 - круговые конусы, осью которых служит ось
- круговые конусы, осью которых служит ось 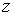 ;
;
в)
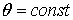 - полуплоскости, проходящие через ось
- полуплоскости, проходящие через ось 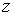 .
.
Якобиан
этого преобразования:
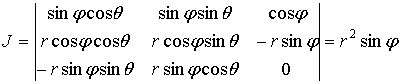 .
.
Якобиан
сохраняет знак плюс, за исключением упомянутых выше случаев, когда 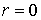 , либо
, либо 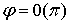 , и
якобиан обращается в нуль [4].
, и
якобиан обращается в нуль [4].
)
Преобразование пространства самого в себя по формулам:
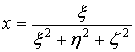 ,
, 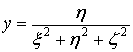 ,
, 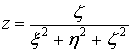
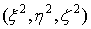 однозначно
обратимо:
однозначно
обратимо:
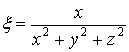 ,
, 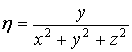 ,
, 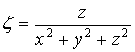 .
.
Оно
называется инверсией [5].
)
Эллиптические координаты. Рассмотрим семейство софокусных и соосновных
поверхностей второго порядка:
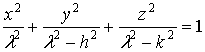
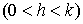 ,
,
состоящее
из эллипсоидов (при 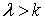 ), однополостных гиперболоидов (при
), однополостных гиперболоидов (при 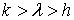 ) и, наконец, двуполостных гиперболоидов (при
) и, наконец, двуполостных гиперболоидов (при 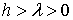 ).
).
Через
каждую точку 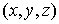 пространства, не лежащую на координатах плоскостях,
проходит по одной поверхности каждого типа. Действительно, левая часть
уравнения, получаемого из (24):
пространства, не лежащую на координатах плоскостях,
проходит по одной поверхности каждого типа. Действительно, левая часть
уравнения, получаемого из (24):
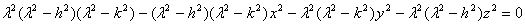 ,
,
имеет
знак минус при 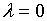 , знак плюс при
, знак плюс при  , снова
знак минус при
, снова
знак минус при 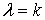 и, наконец, знак плюс при больших
и, наконец, знак плюс при больших 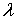 . Отсюда следует, что уравнение имеет три положительных
корня: один
. Отсюда следует, что уравнение имеет три положительных
корня: один 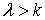 (что отвечает эллипсоиду), второй
(что отвечает эллипсоиду), второй 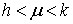 , (он дает однополостный гиперболоид), третий
, (он дает однополостный гиперболоид), третий 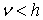 (двуполостной гиперболоид) [1].
(двуполостной гиперболоид) [1].
Используя
свойства корней написанного выше уравнения, которое мы можем рассматривать как
кубическое уравнение относительно 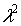 , а
именно:
, а
именно:
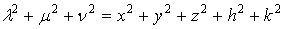 ,
,
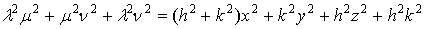 ;
;
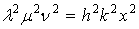 ,
,
найдем:
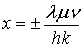 ,
,  ,
,
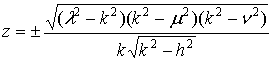 .
.
Если
ограничиться первым координатным октантом, то в этих формулах надлежит
сохранить лишь положительные знаки. Числа 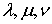 можно
рассматривать, как криволинейные координаты точек этого угла. Их и называют
эллиптическими координатами. Три семейства координатных поверхностей - это и
будут семейства эллипсоидов, однополостных и двуполостных гиперболоидов, о
которых была речь выше.
можно
рассматривать, как криволинейные координаты точек этого угла. Их и называют
эллиптическими координатами. Три семейства координатных поверхностей - это и
будут семейства эллипсоидов, однополостных и двуполостных гиперболоидов, о
которых была речь выше.
Якобиан преобразования имеет вид:
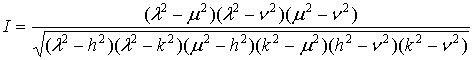 [3].
[3].
2.3
Выражение объема в криволинейных координатах
Возвращаясь
к предположениям и обозначениям п° 1.1, поставим себе задачей выразить объем
(ограниченного) тела 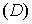 в пространстве
в пространстве 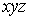 . Иным
интегралом, распространенным на соответствующее тело
. Иным
интегралом, распространенным на соответствующее тело 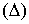 в пространстве
в пространстве 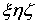 .
.
Искомый
объем выражается, прежде всего поверхностным интегралом второго типа: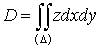 ,распространенным на внешнюю сторону поверхности
,распространенным на внешнюю сторону поверхности  . Отсюда постараемся перейти к обыкновенному двойному
интегралу.
. Отсюда постараемся перейти к обыкновенному двойному
интегралу.
Будем
исходить из параметрических уравнений (21) поверхности (23)(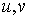 изменяются в области
изменяются в области 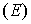 на
плоскости
на
плоскости 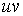 ). Тогда уравнения (22) выразят, очевидно, поверхность
). Тогда уравнения (22) выразят, очевидно, поверхность
 .
.
Полагая
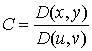 , имеем:
, имеем: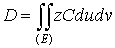 .
.
При
этом интеграл берется со знаком плюс, если ориентация поверхности  , связанная с рассмотрением внешней ее стороны
соответствует ориентации плоскости
, связанная с рассмотрением внешней ее стороны
соответствует ориентации плоскости  , что
всегда можно предположить [1].
, что
всегда можно предположить [1].
Так
как  зависят от
зависят от  через
посредство переменных
через
посредство переменных 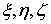 , то, по известному свойствy функциональных
определителей:
, то, по известному свойствy функциональных
определителей:
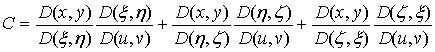 .
.
Подставляя
выражение  в полученный выше интеграл, найдем:
в полученный выше интеграл, найдем:
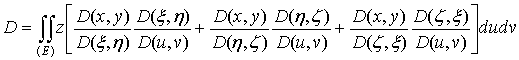 . (25)
. (25)
Сопоставим
этот интеграл с поверхностным интегралом второго типа, распространенным на
внешнюю сторону поверхности  :
:
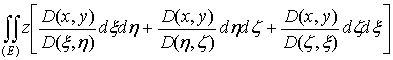 . (26)
. (26)
Если
его преобразовать, исходя из параметрических уравнений (21) к обыкновенному
двойному интегралу придем как раз к интегралу (24). Единственное различие между
этими интегралами может заключаться лишь в знаке: если ориентация плоскости 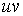 соответствует ориентации поверхности
соответствует ориентации поверхности 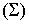 , связанной с рассмотрением внешней ее стороны, то
интегралы равны, в противном же случае они разнятся знаками [1].
, связанной с рассмотрением внешней ее стороны, то
интегралы равны, в противном же случае они разнятся знаками [1].
Наконец,
от интеграла (26) по формуле Остроградского можно перейти к тройному интегралу
по области 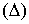 :
:
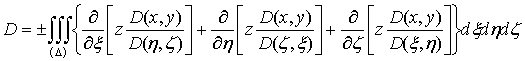 .
.
Подинтегральное
выражение равно:
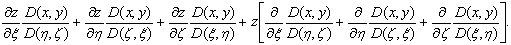

Сумма,
стоящая здесь в первой строке, равна якобиану:
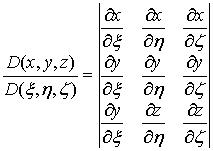 ,
,
в
чем легко убедиться, разлагая этот определитель по элементам последней строки;
сумма же в квадратных скобках, как показывает непосредственное вычисление,
равна нулю. Таким образом, приходим к формуле:
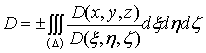 .
.
Если
вспомнить, что по предположению якобиан сохраняет знак, который он сообщает и
интегралу, то станет ясно (так как здесь считаем 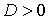 ), что
знак перед интегралом должен совпасть со знаком якобиана. Это дает нам право
переписать полученный результат в окончательной форме:
), что
знак перед интегралом должен совпасть со знаком якобиана. Это дает нам право
переписать полученный результат в окончательной форме:
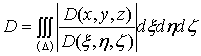 (27)
(27)
или,
обозначая якобиан для краткости через 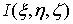 :
:
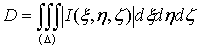 . (27*)
. (27*)
Подинтегральное
выражение
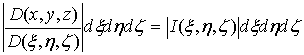
обычно
называют элементом объема в криволинейных координатах [4].
.7
Замена переменных в тройных интегралах
С помощью выражения объема в криволинейных координатах нетрудно
установить и общую формулу замены переменных в тройных интегралах.
Пуста
между областями 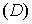 и
и 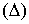 пространств
пространств
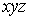 и
и 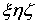 cyществует соответствие, охарактеризованное в п0
2.1. Считая соблюденными все условия, при которых была выведена формула (26),
покажем теперь, что имеет место следующее равенство
cyществует соответствие, охарактеризованное в п0
2.1. Считая соблюденными все условия, при которых была выведена формула (26),
покажем теперь, что имеет место следующее равенство
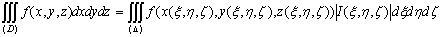 (28)
(28)
где
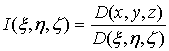 , вполне похожее формуле замены переменных в двойных
интегралах. При этом функцию
, вполне похожее формуле замены переменных в двойных
интегралах. При этом функцию 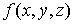 предполагаем
непрерывной или, самое большее, допускающей разрывы вдоль конечного числа
кусочно-гладких поверхностей (но во всяком случае сохраняющей ограниченность).
Таким образом, существование обоих интегралов в равенстве (28) не вызывает
сомнений; нужно установить лишь самое равенство [2].
предполагаем
непрерывной или, самое большее, допускающей разрывы вдоль конечного числа
кусочно-гладких поверхностей (но во всяком случае сохраняющей ограниченность).
Таким образом, существование обоих интегралов в равенстве (28) не вызывает
сомнений; нужно установить лишь самое равенство [2].
Разложив
кусочно-гладкими поверхностями области 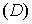 и
и 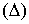 на (соответствующие друг другу) элементарные части
на (соответствующие друг другу) элементарные части 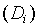 и
и 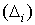
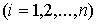 , применим к каждой паре областей
, применим к каждой паре областей 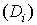 ,
, 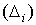 формулу
(25); получим
формулу
(25); получим
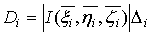 , (29)
, (29)
где
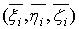 есть некоторая точка области
есть некоторая точка области 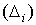 не зависящая от выбора. Возьмем соответствующую точку
не зависящая от выбора. Возьмем соответствующую точку
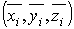 области
области 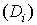 , т. е.
положим
, т. е.
положим
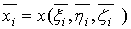 ,
, 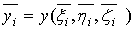 ,
, 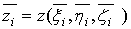 , (30)
, (30)
и
составим интегральную сумму для первого из интегралов (28):
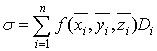 .
.
Подставив
сюда вместо 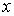 ,
, 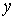 ,
, 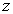 выражения (30), а вместо
выражения (30), а вместо 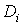 -выражение (28), придем к сумме
-выражение (28), придем к сумме
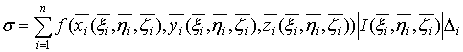 ,
,
которая,
очевидно, уже является интегральной суммой для второго из интегралов (28).
Устремим
к нулю диаметры областей 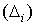 , вследствие чего в силу непрерывности соответствия
устремятся к нулю и диаметры областей
, вследствие чего в силу непрерывности соответствия
устремятся к нулю и диаметры областей 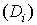 . Сумма
. Сумма 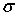 должна стремиться одновременно к обоим интегралам,
откуда и следует требуемое равенство.
должна стремиться одновременно к обоим интегралам,
откуда и следует требуемое равенство.
Как и в случае двойных интегралов формула (28) имеет место и при
нарушении сформулированных выше при доказательстве формулы (26) предположений в
отдельных точках или вдоль конечного числа кусочно-гладких линий и
поверхностей, лишь бы якобиан сохранял ограниченность.
Можно пойти дальше при расширении условий применимости формулы (28),
допуская и несобственные интегралы. Подчеркнем еще раз, что при указанных там
условиях формула имеет место в предположении существования одного из интегралов
(28), существование другого отсюда уже будет вытекать [2].
В заключение упомянем, что формулы (26) и (28) могли быть написаны и без
знака абсолютной величины при якобиане. Для этого чтобы иметь право на это,
следовало бы ввести понятие об ориентированном теле (в связи с ориентированием
его границы), затем в зависимости от его ориентации приписывать тот или другой
знак его объему и распространенному на тело интегралу.
3. Методические основы изучения раздела темы“Тройные интегралы и их
приложения” и их применение в педагогическом вузе
.1 Психолого-педагогические аспекты образования в высшей школе
В настоящее время нет, пожалуй, более спорной проблемы в педагогике и
психологии высшей школы, чем проблема воспитания студентов. “Надо ли
воспитывать взрослых людей?”, “Стоит ли и корректно ли это делать?” Ответ на эти
вопросы зависит от того, как понимать воспитание. Если его понимать как
воздействие на личность с целью формирования нужных воспитателю, вузу, обществу
качеств, то ответ может быть только отрицательным. Если как создание условий
для саморазвития личности в ходе вузовского обучения, то ответ должен быть
однозначно положительным.
Зачем нужен преподаватель в вузе, только ли как
носитель и «передатчик» информации? Но как раз в этом качестве он значительно
уступает многим другим источникам информации, таким, например, как книги и
компьютеры. Вуз служит не только и может быть не столько для передачи
специальных знаний, сколько для развития и воспроизведения особого культурного
слоя, важнейшим элементом которого является и сам специалист. Специалиста как
представителя определенной культуры характеризует не только специфический набор
знаний и умений, но и определенное мировоззрение, жизненные установки и
ценности, особенности профессионального поведения и т.п. Поэтому он не только
передает студенту знания и профессиональные умения, а приобщает его к
определенной культуре, и чтобы эта культура развивалась и воспроизводилась,
необходимы живые люди, живое человеческое общение [28].
Воспитывать - это в значительной степени означает
строить систему взаимоотношений между людьми. В современной педагогике (и еще
более явно в психологии) начинает преобладать подход к воспитанию не как к
целенаправленному формированию личности, в соответствии с выбранным идеалом, а
как к созданию условий для саморазвития личности.
Положения гуманистической психологии запрещают любые
прямые воздействия на личность какие бы цели (воспитательные или
терапевтические) они не преследовали. Не имеем также права заранее решать за
человека, каким ему быть, ибо каждый имеет право и должен сам прожить свою
жизнь, не перекладывая на других ответственность за тот выбор, за те решения,
которые ему приходится принимать. Уникальность и неповторимость каждой личности
составляют богатство всего общества, и всякое искусственное ограничение
свободного проявления и развития личности подрывает ее творческие потенции
[25].
Сам способ существования личности есть постоянный
выход за пределы самой себя, стремление к росту и развитию, направление
которого воспитатель не может предугадать заранее и он не имеет права принимать
сколько-нибудь ответственные решения за воспитуемого, какими бы само собой
разумеющимися эти решения не казались ему. Самый главный прием воспитания - это
принятие человека таким, какой он есть, без прямых оценок и наставлений. Только
в этом случае будет ее сохраняться у воспитателя контакт с воспитуемым, что
является естественным условием плодотворного взаимодействия обоих участников
воспитательного процесса.
Означает ли это, что воспитатель должен занимать
пассивную позицию в отношении тех выборов и принципиальных решений, которые
принимает его воспитанник? Разумеется, нет. Главная задача воспитателя -
раскрыть перед воспитуемым широкое поле выборов, которое часто не открывается
самим ребенком, подростком, юношей из-за его ограниченного жизненного опыта,
недостатка знаний и неосвоенности всего богатства культуры. Раскрывая такое
поле выборов, воспитатель не должен, да и не может скрыть своего оценочного
отношения к тому или иному выбору. Следует избегать только слишком однозначных
и директивных способов выражения этих оценок, всегда сохраняя за воспитанником
право на самостоятельное принятие решения, в противном случае ответственность
за любые последствия принятых решений он с себя снимет и переложит на
воспитателя [28].
Другое принципиальное требование к организации
процесса воспитания состоит в неизменно
уважительном отношении к личности воспитуемого как полноценного и равноправного
партнера любой совместной деятельности. Идея равенства, партнерства и взаимного
уважения друг к другу лежит в основе так называемой педагогики сотрудничества,
принципы которой совершенно неоспоримы в вузовском обучении. Как утверждают
многие крупные ученые и педагоги, основатели больших научных школ, наибольший
учебный и воспитательный эффект достигается в таких ситуациях, когда учитель и
ученик вместе решают задачу, ответ на которую не знает ни тот ни другой. В этом
случае феномен партнерства и сотрудничества выражен максимально.
Другая важнейшая задача воспитания - помощь
воспитуемому в выработке индивидуального стиля жизни, индивидуального стиля
деятельности и общения. Для решения такой задачи преподавателю необходимо
владеть некоторыми навыками и методиками психодиагностики, а также вооружить
студентов приемами самопознания. Важнейшее значение имеет знание
психологических и психофизиологических особенностей студентов, определяемых их
социальным статусом, возрастом и характером основной деятельности [25].
Часто преподаватели руководствуются индифферентными
представлениями о студентах как об устройствах по переработке информации,
которые слушают лекции, читают учебники, выполняют задания и, когда это
требуется, демонстрируют эти знания на зачетах и экзаменах. Иногда это приводит
к безличным и неадекватным требованиям, с которыми студенты просто не могут
справиться. Для того, чтобы при построении программы учесть возможности и
потребности студентов, нужно хорошо их знать. Успешная учебная деятельность
студента зависит не только от степени владения приемами интеллектуальной
деятельности; она обусловлена также личностными параметрами учебной
деятельности - устойчивой системой отношений студента к окружающему миру и к
самому себе.
На какие же вопросы следует обращать внимание в связи
с необходимостью учета возрастных особенностей и индивидуальных различий
студентов в воспитательно-образовательном процессе вуза? Современные студенты -
это прежде всего молодые люди в возрасте 18-25 лет. Этот возраст определяется
как поздняя юность или ранняя зрелость. Отсутствие единого термина уже говорит
о сложности, неоднозначности психологических характеристик этого периода жизни.
Очень важно иметь в виду, что человек непрерывно эволюционирует как единое
целое, так что ни одну сторону его жизни нельзя понять в отрыве от других
сторон. Возьмем, например, такой, казалось бы не имеющий отношения к педагогической
ситуации параметр, как физическое развитие молодых людей. Студенческий возраст
характеризуется наивысшим уровнем таких показателей, как мышечная сила,
быстрота реакции, моторная ловкость, скоростная выносливость и др. Как принято
говорить - это возраст физического совершенства человека. Большинство
спортивных рекордов установлено именно в этом возрасте. Однако, как
свидетельствуют данные Всемирной организации здравоохранения, именно студенты
характеризуются худшими показателями физиологических функций в своей возрастной
группе. Они лидируют по числу больных гипертонией, тахикардией, диабетом,
нервно-психическими нарушениями. Причины этого, как показывают исследования,
кроются в том, что в процессе вузовского обучения студенты испытывают сильное
психическое напряжение, часто разрушительное для здоровья [28].
Преподаватель должен учитывать, что эти нагрузки
особенно велики в периоды контроля и оценивания. Но именно здесь часто
совершается одна из грубейших педагогических ошибок: негативную оценку результатов
усвоения учебной программы преподаватель переносит на оценку личности студента
в целом, давая студенту знать с помощью мимики, жестов, а то и в словесной
форме, что он неумен, ленив, безответствен и т.п. Заставляя студента переживать
негативные эмоции, преподаватель оказывает прямое влияние на физическое
состояние и здоровье студента.
Учеба в вузе требует больших затрат времени и энергии,
что обуславливает некоторую задержку социального становления студентов по
сравнению с другими группами молодежи. Этот факт часто порождает у
преподавателей ошибочное представление о студентах как социально незрелых
личностях, нуждающихся в постоянной опеке, снисходительном отношении. Сам того
не осознавая преподаватель в этом случае как бы ставит планку, ограничивает
уровень, до которого студент, по его представлению, может развить свои личные
качества, в данном случае ответственность, инициативность, самостоятельность.
Воспитуемый (в данном случае студент) неосознанно воспринимает такую программу
и, что особенно огорчительно, внутренне принимает ее. Человеку свойственно
легко адаптироваться к заниженным требованиям: в этих условиях способности
студента не только не развиваются, но и часто деградируют.
Отношение же педагога к студенту как к социально
зрелой личности, напротив, как бы отодвигает планку, раскрывает новые
горизонты, тем самым не ограничивая возможности развития личности, а усиливая
их своей верой, внутренней поддержкой [28].
Как правило, именно в студенческом возрасте достигают
максимума в своем развитии не только физические, но и психологические свойства,
и высшие психические функции: восприятие, внимание, память, мышление, речь,
эмоции и чувства. Этот факт позволил Б.Г.Ананьеву сделать вывод о том, что
данный период жизни максимально благоприятен для обучения и профессиональной
подготовки. В этот период происходит активное формирование индивидуального
стиля деятельности. Преобладающее значение в познавательной деятельности
начинает приобретать абстрактное мышление, формируется обобщенная картина мира,
устанавливаются глубинные взаимосвязи между различными областями изучаемой
реальности.
Если преподаватель не развивает именно эти
способности, у студента может закрепиться навык полумеханического запоминания
изучаемого материала, что ведет к росту показной эрудиции, но тормозит развитие
интеллекта. Результаты специальных обследований показывают, что у большинства
студентов уровень развития таких интеллектуальных операций, как сравнение,
классификация, определение весьма невысок. Преподавателю зачастую приходится
прилагать большие усилия, чтобы преодолеть школярское отношение к учебе:
ориентацию только на результат интеллектуальной деятельности и равнодушие к
самому процессу движения мысли [25].
Лишь немного более половины студентов повышают
показатели интеллектуального развития от первого курса к пятому, и как правило
такое повышение наблюдается у слабых и средних студентов, а лучшие студенты
часто уходят из вуза с тем же уровнем интеллектуальных способностей, с которым
пришли.
Важнейшая способность, которую должен приобрести
студент в вузе, - это собственно способность учиться, которая радикальным
образом скажется на его профессиональном становлении, ибо определяет его
возможности в послевузовском непрерывном образовании. Научиться учиться важнее,
чем усвоить конкретный набор знаний, которые в наше время быстро устаревают.
Еще важнее способность самостоятельного добывания знаний, основанная на
творческом мышлении.
Особенно бурно в период вузовского обучения идет
развитие специальных способностей. Студент впервые сталкивается со многими
видами деятельности, являющимися компонентами его будущей профессии, поэтому на
старших курсах необходимо уделять особое внимание диалоговым формам общения со
студентами, в частности, в процессе выполнения ими курсовых и дипломного проектов,
прохождения практик и т.п.
Эмоциональная сфера в студенческом возрасте приходит к
некоторому уравновешенному состоянию, «успокаиваясь» после своего бурного
развития и брожения в подростковый период. Но определенные отголоски прошедших
«бурь» иногда дают себя знать, особенно у студентов с задержками личностного
развития, т.е. страдающих инфантилизмом. Часто может наблюдаться
гипертрофированная и несколько абстрактная неудовлетворенность жизнью, собой и
другими людьми. При неадекватном педагогическом воздействии такие состояния
могут стать причиной деструктивных тенденций в поведении. Но при обращении
энергии этого эмоционального состояния на решение сложной и значимой для
студента задачи неудовлетворенность может стать стимулом к конструктивной и плодотворной
работе [29].
Выраженный и часто подчеркнутый рационализм в
обращении преподавателей со студентами негативно сказывается на развитии их
эмоциональной сферы в целом. Поэтому преподавателю необходимо сознательно
следить за тем, не переходит ли опасную черту почти неизбежный дисбаланс
рационального и эмоционального в стиле его общения со студентами. В этом случае
без некоторой, пусть порой даже искусственно добавляемой, эмоциональной
теплоты, эффективность его работы со студентами может сильно снизиться даже при
ее очень высоком содержательном уровне. Без принятия таких мер у преподавателя
самого могут возникнуть эмоциональные перегрузки, еще более усиливающие
трудности нахождения верного эмоционального тона в общении со студентами.
Самая главная особенность юношеского возраста (включая
и позднюю юность) состоит в осознании человеком своей индивидуальности,
неповторимости, в становлении самосознания и формировании «образа Я». Образ
«Я», - это социальная установка, отношение личности к себе, включающее три
взаимосвязанных компонента: познавательный, эмоциональный и поведенческий. За
последние десятилетия произошел сдвиг пика становления самосознания с возраста
17-19 лет на 23-25 лет. Становление самосознания актуализирует проявление
важнейших и часто противоречивых потребностей юношеского возраста - в общении,
уединении, в достижениях и др.
Потребность в достижении, если она не находит своего
удовлетворения в основной для студента учебной деятельности, закономерно
смещается на другие сферы жизни - в спорт, бизнес, общественную деятельность,
хобби, или в сферу интимных отношений. Но человек обязательно должен найти для
себя область успешного самоутверждения, в противном случае ему грозит уход в
болезнь, невротизация или уход в криминальную жизнь [28].
И здесь ответственна роль преподавателя как первого
эксперта, дающего студенту «обратную связь» о результатах его исследовательской
работы. Своими оценками он может неосторожно убить у студента всякую надежду и,
соответственно, желание утверждаться на ниве науки и подтолкнуть его к выбору
других сфер жизни для самоутверждения и удовлетворения потребности в
достижении.
Благоприятное положение студента в окружающей его
среде содействует нормальному развитию его личности. Не должно быть
существенного расхождения между самооценкой и оценкой, получаемой студентом от
значимых для него людей (референтной группы), к которым обязательно должен
относиться и преподаватель. В этом случае он может помочь студенту в
преодолении неблагоприятного соотношения самооценки, ожидаемой оценки и оценки,
исходящей от референтной группы. Это можно сделать, целенаправленно,
организовав такую педагогическую ситуацию, чтобы студент предстал перед
значимыми для него «другими» в выгодном свете и получил положительную оценку,
что приведет к повышению ожидаемой оценки, улучшит его психологическое
состояние и сделает более благоприятной позицию личности в целом.
Заключая разговор об условиях успешной воспитательной
работы, следует напомнить изложенные в начале параграфа общие положения о
сущности воспитания как о создании благоприятных условий для самовоспитания
человека путем раскрытия перед ним поля возможных выборов и их последствий, при
том, что окончательное решение всегда должен принимать сам воспитуемый.
Важнейшим условием внимания студента к тому, что раскрывает перед ним
преподаватель выступает безусловное принятие студента преподавателем и
признания за ним права на любой выбор без того, чтобы быть отвергнутым [28].
Развитие творческого мышления в процессе обучения и воспитания
Предложенные ниже рекомендации должны быть использованы в вузовском
обучении, или преподаватель может их использовать в своей консультационной
работе со студентами.
1.
Одно из первых
педагогических требований, предъявляемых к процессу обучения с точки зрения
развития творческого мышления состоит в том, чтобы ни в коем случае не
подавлять интуицию обучаемого.
2.
Вторая
рекомендация состоит в формировании у студентов уверенности в своих силах, веры
в свою способность решить задачу.
3.
В процессе
обучения желательно в максимальной степени опираться на положительные эмоции.
4.
Необходимо
всемирно стимулировать стремление учащегося к самостоятельному выбору целей,
задач и средств их решения.
5.
Следует в
довольно широких пределах поощрять склонность к рискованному поведению.
6.
Важнейшая задача
- не допускать формирования конформного мышления, бороться с соглашательством и
ориентацией на мнение большинства.
7.
Развивать
воображение и не подавлять склонность к фантазированию, даже если оно иногда
граничит с “выдаванием” выдумки за истину.
8.
Формировать
чувствительность к противоречиям , умение обнаруживать и сознательно
формировать их.
9.
Чаще использовать
в обучении задачи так называемого открытого типа, когда отсутствует одно
правильное решение, которое остается только найти или угадать.
10. Шире применять проблемные методы
обучения, которые стимулируют установку на самостоятельное или с помощью
преподавателя открытие нового знания, усиливает веру студента в свою
способность к таким открытиям.
11. Весьма полезным для развития
творческого мышления является обучение специальным эвристическим приемам
решения задач различного типа.
12. Важнейшим условием творчества
студентов является совместная с преподавателем исследовательская деятельность
13. Наконец, самая главная, тринадцатая
заповедь, - всячески поощрять стремление человека любого возраста быть самим
собой, его умение слушать свое “Я” и действовать в соответствии с его
“советами”. Для этого на всех этапах обучения преподаватель должен не просто
декларировать свое уважение к личности ученика, но и реально чувствовать,
переживать непреходящую и ни с чем не сравнимую ценность каждой живой личности.
Изучение познавательных процессов у студентов
Для исследования познавательных процессов в студенческом возрасте виды
памяти, как правило, изменяются мало, во всяком случае - не улучшаются, если
для этого не проводится специальных упражнений. Да и сами такие упражнения вряд
ли в состоянии существенно улучшить или долгое время поддерживать на высоком
уровне кратковременную и оперативную память, так как, во-первых, оба вида
памяти с возрастом ухудшаются по естественным причинам; во-вторых потому, что
они, как непродуктивные мало используются в жизни взрослым человеком. Гораздо
большая нагрузка приходится на долговременную память, а также на произвольную
память, логическую и опосредованную кратковременную и оперативную память.
В студенческом возрасте нет, как правило, особой необходимости вновь
повторно возвращаться к психодиагностике объема внимания и отдельно оценивать
такие свойства внимания, как распределение и переключение. Гораздо важнее иметь
интегральные характеристики внимания и портативную методику, которая позволяет
их оценивать. Желательно, в частности, иметь два комплексных показателя
внимания: продуктивность и устойчивость, распределение и переключение. Кроме
того, целесообразно в методике, оценивающей эти свойства внимания, заменить
симмульный материал.
Психологические закономерности профессионального развития студентов
Студент-первокурсник (как, впрочем, и любой другой человек, попадает в
новую для него ситуацию) начинает свою студенческую жизнь с использования для
решения новых образовательных задач старых, проверенных временем школьных
способов учебной деятельности, причем использует их скорее всего механически,
поскольку слабо осознает реальную ситуацию профессионального развития и
фактически ее не принимает, т.е. она не является руководством к действию.
В ходе реализации школьного опыта студент сталкивается с определенными
трудностями и достигает даже относительно невысоких учебных результатов путем
высокого напряжения своих энергических возможностей. Именно низкая
результативность обучения при высоких энергозатратах заставляет его задуматься
о правильности, адекватности используемых им способов обучения и в конечном
счете побуждает к поиску новых способов учебной деятельности, соответствующих
требованиям высшей школы. Осознание такой необходимости приходит к студенту в
конце 1-го - начале 2-го года обучения. Этот момент следует считать
критическим, так как он связан с принятием студентом конкретной ситуации
профессионального развития и началом нового этапа становления профессионала
[25].
Невысокая успеваемость у студентов 2-го курса указывает на то, что в это
время учебная деятельность фактически отсутствует (старые школьные ее формы
отвергнуты, а новые еще не сформировались), и все внимание студента
сосредоточено на выработке новых способов учебно-познавательной активности.
Становление новой учебно-академической формы учебной деятельности завершается в
конце 2-го курса, что и приводит к резкому скачку академической успеваемости и
обученности на 3-м курсе.
На 4-м курсе социальная ситуация профессионального развития изменяется:
из учебно-академической она превращается в учебно-профессиональную. Новая
ситуация актуализируется в ходе педагогической практики, в рамках которой
студент сталкивается не с учебно-познавательными, а с профессиональными
задачами. Решая их, студент убеждается, что накопленные на 1-3-м курсах
фундаментальные знания требуют преобразования в форму, удобную для передачи
школьникам. Снижения академической успеваемости на 4-м курсе свидетельствует о
том, что студент активно сосредоточен на преобразовании академических знаний,
на включении их в качестве предметных в структуру профессиональной
деятельности.
На 4-м курсе происходит дифференциация форм активности студента. С одной
стороны, начинает складываться система профессионально-педагогической
деятельности в форме учебно-профессиональной, а с другой - учебно-академическая
деятельность меняет свою направленность: из средства накопления фундаментальных
знаний она превращается в средство формирования профессиональной деятельности,
окончательное становление которой происходит на стадии самостоятельной работы в
школе [25].
Таким образом, можно выделить следующую последовательность становления
системы профессионально-педагогической деятельности: школьная форма учебной
деятельности - мораторий (выработка новых форм деятельности) -
учебно-академическая форма деятельности - мораторий (выработка новых форм
деятельности и смена ориентации) - учебно-профессиональная форма деятельности и
учебно-академическая как средство ее формирования - профессиональная
деятельность.
Становление профессиональной идентичности. Студент-первокурсник до
определенного момента продолжает еще ощущать себя школьником, т.е. некоторое
время является носителем школьной идентичности. Психологически это проявляется
в том, что он поступил в вуз, не может осознать себя студентом , у него сохраняются
школьные привычки, он оценивает все происходящее с позиции школьника, ему еще
неуютно и непривычно в роли студента.
Осознавать архаичность и непродуктивность школьной идентичности студент
начинает уже на 1-м курсе, чему способствует общение со старшекурсниками и
более продвинутыми товарищами по группе, усвоение требований преподавателей
вуза и другие средства вхождения в новую социальную роль. Преодоление школьной
идентичности затрудняется из-за отсутствия у студента адекватной Я-концепции,
реальных представлений о жизни и деятельности студенчества и т.д. К концу 2-го
курса у студентов накапливается “критическая масса” опыта студенческой жизни,
что позволяет ему окончательно преодолеть школьную идентичность и ощутить себя
студентом. Становление студенческой идентичности в основном завершается к 3-му
курсу, что с формирования системы профессиональной деятельности сопровождается
ростом большинства самооценочных показателей, фиксацией социального статуса
индивида в группе и стиля студенческой жизнедеятельности.
На 3-м курсе окончательно складывается личность студента как субъекта
учебно-академической деятельности. Иначе говоря, на 3-м курсе индивид
становится настоящим студентом и по делам, и по мировоззрению, по отношению к
себе и к учебе, системе ценностей и интересов, способу одеваться, общаться,
проводить свободное время и т.д.
Однако на 4-5 курсах (в зависимости от типа вуза) под влиянием
производственной (педагогической) практики и все большей ориентации студентов
на послевузовскую жизнь у них начинает складываться собственно профессиональная
идентичность. Об этом свидетельствует, в частности, изменение отношения
студентов к учебным предметам. Читаемые курсы, отдельные их разделы студенты
все в большей и большей степени оценивают с профессиональной точки зрения, т.е.
пригодятся они или нет в будущей работе. В это же время студент принимает
окончательное решение о том, связывать ли свою дальнейшую судьбу со школой или
нет [32].
Формирование профессиональной идентичности к концу обучения в вузе у большинства
студентов не завершается, поэтому многие студенты - пятикурсники не верят в
себя как в профессионалов и не считают себя таковыми. Это состояние они
переживают как неготовность к самостоятельной деятельности, как ощущение страха
перед будущим вообще и профессиональными перспективами в частности. Возможно,
именно по этой причине у студентов 5-го курса профессиональная самооценка
существенно снижается. Завершение формирования ПИ происходит в период
самостоятельной профессиональной деятельности в школе.
Итак, выделяются следующие этапы становления ПИ: школьная
идентичность-мораторий (поиски новых форм идентичности) - студенческая
идентичность-мораторий (уточнение старых и поиск новых форм идентичности) -
учебно-профессиональная идентичность - профессиональная идентичность [25].
Развитие профессиональной направленности. Профессиональное развитие
студентов связано также с формированием и преобразование структуры мотивов,
которые как внутренние источники активности личности определяют процесс ее
профессионального становления. В целом основу детерминации данного процесса
составляет комплекс как внешних, так и внутренних по отношению к индивиду
факторов, которые образуют социальную ситуацию профессионального развития.
Установлено, что профессиональное развитие студента определяется тремя
группами мотивов: учебно-познавательными, профессиональными и мотивами
жизненного пути, которые действуют на всех этапах обучения в вузе, образуя
единый комплекс, но удельный вес каждой группы мотивов в общей структуре
мотивации деятельности студента может изменяться [32].
Так, на 1-м курсе ведущая роль отводится мотивации жизненного пути,
поскольку высокий уровень удовлетворенности студента собой, профессией и учебой
нельзя объяснить результативностью обучения (она низкая), стабильностью
положения в группе (она недостаточная), определенностью своего положения в
плане точности профессионального выбора. Причина этого заключается в росте
уважения студента к себе как субъекту жизненного пути, впервые решившему важную
жизненную проблему-выбор профессии и поступление в вуз. Студент осознает, что
далеко не всем удалось решить данную проблему, и эта “избранность” порождает
особого рода эйфорию, которая проявляется в росте самооценок и
удовлетворенности собой.
Возможно, что рост самоуважения и возникающее на его основе состояние
“эмоционального благодушия” маскируют реальные проблемы учебной деятельности,
вследствие чего замедляется процесс становления адекватных форм учебной
деятельности, и откладывается на более позднее время обретение студентами
академической идентичности.
В конечном счете все возрастающие учебно-академические требования и
невысокие результаты обучения при больших затратах сил и времени заставляют
студента обратить внимание на проблемы своего профессионального развития. Это
приводит к тому, что учебно-познавательная мотивация начинает доминировать и
именно она “запускает” процессы поиска и освоения новых форм учебной
деятельности, процессы осознания и принятия себя в качестве студента вуза.
Результаты “включения” данной формы мотивации не заставляют себя долго ждать:
уже в конце 2-го - начале 3-го курса обнаруживается резкий рост успеваемости,
обученности, показатели удовлетворенности и учебно-профессиональных самооценок
[28].
Относительно резкое падение академической успеваемости у студентов 4-го
курса не является результатом снижения их обученности и обучаемости. Главная
причина заключается в смене ведущей мотивации у студентов: под влиянием
педагогической практики у них начинает меняться отношение к осваиваемым в вузе
предметам, так как они понимают, что фундаментальные, теоретические и
практические знания, которые им преподают в вузе, - необходимое, но
недостаточное условие для решения задач профессиональной деятельности.
В ходе практики студенты убеждаются в том, что далеко не все знания,
получаемые ими в вузе, нужны в реальной практической деятельности, а если и
нужны, то не в той форме, в какой они усваиваются в процессе обучения. Эти
“открытия” существенно повышают учебную избирательность студентов при освоении
отдельных предметов, “запускают” механизмы преобразования академических знаний
и умений в собственно профессиональные. Иначе говоря, начиная с 4-го курса,
большинство студентов осмысливает процесс обучения в вузе с позиций требований
профессиональной деятельности, что, несомненно, означает актуализацию
собственно профессиональной мотивации, превращение ее в ведущий фактор
внутренней активности личности.
Относительно отношения внешних и внутренних факторов детерминации
профессионального развития студентов можно сказать следующее. Несмотря на
важную роль мотивов как внутренних источников активности личности, ведущая роль
в структуре детерминации профессионального развития студентов все-таки
отводится внешним факторам, т.е. меняющимся учебно-профессиональным требованиям;
именно они динамизируют и проблематизируют ситуацию, стимулируют процесс
обучения и задают основные его ориентиры. Студенты активно относятся к
предъявляемым требованиям; демонстрируют разнообразные способы их усвоения,
которые определяются индивидуальными возможностями студентов, их
познавательными потребностями и опытом. Однако творчество студентов не входит
за рамки данных требований, а лишь обеспечивает максимально возможное их
освоение и приспособление к ним [32].
Ведущая роль мотивации в процессе профессионального развития в полной
мере проявляется только после окончания вуза, на начальных этапах
самостоятельного трудового пути специалиста, когда основные нормативные
требования усвоены.
Периодизация профессионального развития. С учетом объективного содержания
социальной ситуации профессионального развития (ССПР) процесс профессионального
развития в педагогическом вузе, преподавание в котором ведется по традиционной
для нашей страны пятилетней модели, делится на два периода:
. Учебно-академический, охватывающий 1-3-й курсы; его специфика
заключается в том, что она в прямой или косвенной форме предъявляет требования
к уровню фундаментальной подготовки студентов, к способу учебно-познавательной
деятельности, к качествам личности студента. Новообразованиями данного периода
являются становление личности студента, преодоление школьной и обретение
студенческой идентичности; формирование академической формы учебной
деятельности и структуры познавательных способностей, необходимых для ее
реализации;
. Учебно-профессинальный, включающий конец 3-го, а также 4-й и 5-й курсы,
когда ССПР предъявляет к личности и деятельности студента в основном
профессиональные требования. Ведущими новообразованиями этого периода являются
актуализация профессиональной мотивации, становление элементов системы
профессионально-педагогической деятельности и переориентация
учебно-академической деятельности на ее формирования, обретение элементов
профессиональной идентичности, становление структуры профессионального
интеллекта.
Каждый из выделенных периодов делится на ряд фаз, анализ содержания
которых раскрывает нормативную специфику принятия ССПР и особенности
профессионального развития студентов [32].
Учебно-академический период.
Фаза 1 (охватывает в основном 1-й курс обучения в вузе). Для данной фазы
характерны самая низкая академическая успеваемость и практически самые высокие
показатели идентичности. Преобладают школьная идентичность и школьные формы
учебной деятельности. Реальные проблемы профессионального развития маскируются
состоянием эйфории, вызванной высоким уровнем самоуважения в связи с
поступлением в вуз. Реальная ССПР осознается студентами слабо и фактически не
принимается как руководство к действию.
Фаза 2 (2-й курс). Студент принимает реальную ССПР и скорее всего
осознает необходимость изменения своей идентичности и способов учебной
деятельности. Этому способствует кризис профессионального развития, который
возникает в конце 1-го - начале 2-го курса и свидетельствует об осознании
студентами реальных противоречий развития данного периода. Внимание студентов
обращено на совершенствование самого себя, что и объясняет невысокую
успеваемость и обученность, которая ниже, чем на 1-м курсе.
Фаза 3(3-й курс). Все требования ССПР учебно-академического периода
студентами в основном реализуется, о чем свидетельствует резкий рост
успеваемости и идентичности. Кризис профессионального развития завершается,
студент обретает адекватную идентичность, у него формируется система
учебно-академической деятельности, складывается соответствующая структура
интеллекта. Можно считать, что 3-м курсе заканчивается формирование личности
студента как субъекта учебно-академической деятельности [32].
Учебно-профессиональный период.
Фаза 1 (конец 3-го - 4-й курс). Происходит смена ССПР, но благодаря
накопленному опыту и сильной обратной связи в ходе педагогической практики она
осознается и принимается студентами достаточно быстро. Во время этой фазы
студент переживает второй кризис профессионального развития, острота которого
существенно зависит от степени преемственности фундаментальной и
профессионально-методической подготовки. Студент вновь обращается к решению
задач саморазвития, поиску элементов профессиональной идентичности,
формированию системы профессиональной деятельности, перестройке фундаментальных
знаний, встраиванию учебно-академической деятельности в структуру
профессиональной и т.д. Резкое снижение успеваемости студентов является одним
из главных показателей их направленности на саморазвитие.
Фаза 2 (5-й курс). Кризис профессионального развития завершается. У
студентов складываются основы профессиональной идентичности, начинает
профессионализироваться интеллект, формируется система учебно-профессиональной
деятельности, которая в дальнейшем преобразуется в профессиональную. Вместе с
тем происходит активация мотивации жизненного пути, которая способствует росту
тревожности в связи с неопределенностью будущей профессиональной деятельности.
Формируется профессиональная готовность, начинается внутренняя работа по
подготовке к вступлению в самостоятельную профессиональную жизнь [32].
.2 Методические рекомендации по проведению лекционных занятий с
применением информационных технологий
Лекционный материал по теме «Тройные интегралы» приходится на конец 2-го
курса и создает теоретическую основу для всех видов учебной деятельности по
математическому анализу. К концу 2-го курса у студентов накапливается
“критическая масса” опыта студенческой жизни, что позволяет ему окончательно
преодолеть школьную идентичность и ощутить себя студентом. Контроль усвоения
студентами части лекционного материала обеспечивают коллоквиумы.
Резкое сокращение аудиторного времени на изучение курса «Математический
анализ» ставит задачу усиления самостоятельной работы студентов по проработке
важнейших разделов курса. На лекции преподаватель может успеть лишь в тезисной
форме изложить основные вопросы курса. Все остальное изучение материала ложится
на плечи студентов в виде их самостоятельной работы. Становление новой
учебно-академической формы учебной деятельности завершается в конце 2-го курса,
что и приводит к резкому скачку академической успеваемости и обученности на 3-м
курсе. Процесс профессионального развития в педагогическом вузе делится на два
периода, один из них - учебно-академический, охватывающий 1-3-й курсы; его
специфика заключается в том, что она в прямой или косвенной форме предъявляет
требования к уровню фундаментальной подготовки студентов, к способу
учебно-познавательной деятельности, к качествам личности студента.
Новообразованиями данного периода являются становление личности студента,
преодоление школьной и обретение студенческой идентичности; формирование
академической формы учебной деятельности и структуры познавательных
способностей, необходимых для ее реализации. Поэтому возникает возможность
использования самостоятельной работы студентов [32].
В процессе изучения курса предусматриваются следующие виды
самостоятельной работы студентов над изучаемым материалом:
) проработка и осмысление лекционного материала;
) работа с учебниками и учебными пособиями по лекционному материалу;
) подготовка к практическим занятиям по рекомендуемой литературе;
) работа с обучающее-контролирующей программой по теме «Тройные
интегралы».
Ряд тем и вопросов курса отведены для самостоятельной проработки
студентами. Количество и содержание этих вопросов зависит от степени
усвояемости студентами лекционного материала. Если лектор чувствует, что
материал лекции хорошо понимается и усваивается аудиторией достаточно, то
сложность лекции можно повысить, а темп чтения можно ускорить, чтобы дать студентам
больше интересного материала, что может несколько сократить объем
самостоятельной работы.
С другой стороны у лектора появляется возможность расширить круг
изучаемых проблем, дать на самостоятельную проработку новые интересные вопросы.
Ориентировочный перечень самостоятельно рассматриваемых студентами вопросов
приводится в «Методических указаниях к самостоятельной проработке
теоретического материала»[25]. Там же приводится перечень рекомендуемой
литературы, которую необходимо использовать для усвоения отмеченных вопросов.
Студент должен разобраться в указанной литературе и письменно изложить кратко и
доступно для себя основное содержание материала. Преподаватель проверяет
качество усвоения самостоятельно проработанных вопросов на практических
занятиях, контрольных работах, коллоквиумах и во время экзамена. Затем
корректирует изложение материала и нагрузку на студентов.
Таким образом, использование самостоятельной работы студентов дает
возможность значительно активизировать их работу над материалом курса и повысить
уровень их усвоения.
Содержание учебного материала по теме:
“Тройные интегралы ”
Определение тройного интеграла;
Свойства тройного интеграла;
Вычисление тройного интеграла;
Криволинейная система координат (КСК);
Цилиндрическая система координат (ЦСК);
Сферическая система координат (ССК);
Замена переменных в тройных интегралах;
Объем в криволинейных и сферических координатах [24].
Тематическое планирование учебного материала
Тема "Тройные интегралы и их приложения ” входит в четвертый раздел
математического анализа ”Интегральное исчисление для функции нескольких
переменных”, включающего:
Кратные интегралы;
Криволинейные интегралы;
Приложения криволинейных и кратных интегралов.
Примерный тематический план по теме “ Интегральное исчисление
для функции нескольких переменных ”
|
4 семестр
|
Всего часов
|
В том числе аудиторных
|
Самостоят. работа
|
|
|
Всего
|
Лекции
|
Практические занятия
|
Котрольная работа
|
|
|
Кратные интегралы
|
25
|
12,5
|
8
|
4
|
0,5
|
12,5
|
|
Криволинейные интегралы
|
20,5
|
10,25
|
8
|
2
|
0,25
|
10,25
|
|
Приложения криволинейных и
кратных интегралов
|
12,5
|
6,25
|
2
|
4
|
0,25
|
6,25
|
Тематический план по теме
”Тройные интегралы”
|
Всего часов
|
3,25
|
|
Лекции
|
2
|
|
Практические занятия
|
1
|
|
Контрольная работа
|
0,25
|
Тематическое планирование по теме:
”Тройные интегралы”
|
ВИД ЗАНЯТИЯ
|
ТЕМА
|
НОМЕР ЗАНЯТИЯ
|
|
Лекция №1
|
Определение тройного
интеграла. Свойства тройного интеграла. Вычисление тройного интеграла.
Криволинейная система координат.
|
1
|
|
Лекция №2
|
Цилиндрическая система
координат. Сферическая система координат. Замена переменных в тройном
интеграле. Объем в цилиндрических и сферических координатах.
|
2
|
Для успешного формирования теоретических знаний, было
создано электронное пособие по теме «Тройные интегралы ». Оно включает в себя
не только теоретический минимум в виде фондовых лекций, но расширенное изучение
темы [24].
Бурное развитие компьютерных технологий в современном мире
охватило практически все сферы жизнедеятельности общества, в том числе и
образования. Благодаря этому персональный компьютер превратился в мощное
средство образования. Однако это вовсе не означает, что компьютер, берущий на
себя часть функций педагога, способен вытеснить его из процесса обучения.
Наоборот, умелое сотрудничество человека и персонального компьютера в
образовании позволит сделать процесс обучения более эффективным [33].
По сравнению с традиционным для вузов уроком-лекцией, когда преподаватель
излагает тему, а студенты слушают, смотрят, запоминают или конспектируют
учебный материал, лекция, построенная по предлагаемой методике, имеет важное
преимущество - интерактивность. Интерактивность дает студентам возможность
активно вмешиваться в процесс обучения: задавать вопросы, получать более
подробные и доступные пояснения по неясным для них разделам и фрагментам
излагаемого преподавателем учебного материала [32].
Сочетание комментариев преподавателя с информацией подаваемой с помощью
компьютера значительно активизирует внимание студентов к содержанию излагаемого
преподавателем учебного материала и повышает интерес к новой теме. Обучение
становится занимательным и эмоциональным, принося эстетическое удовлетворение
студентам и повышая качество излагаемой преподавателем информации. При этом
существенно изменяется его роль в учебном процессе. Преподаватель эффективнее
использует учебное время лекции, сосредоточив внимание на обсуждении наиболее
сложных фрагментов учебного материала.
Интерактивная лекция сочетает в себе преимущества традиционного способа
обучения под руководством педагога и индивидуального компьютерного обучения.
Компьютер из «учителя» превращается в активного помощника преподавателя. Наряду
с информационно-познавательным содержанием интерактивная лекция имеет
эмоциональную окраску благодаря использованию в процессе ее изложения
компьютерных рисунков [33].
Значительно повышаются требования к квалификации преподавателя. Он должен
обладать необходимым уровнем знания компьютерной техники и владеть навыками
работы с программным обеспечением.
Важным условием проведения интерактивной лекции является также наличие
специализированной аудитории, оснащенной компьютерной техникой и современными
средствами публичной демонстрации визуального и звукового учебного материала.
В процессе изложения лекции преподаватель эпизодически представляет
информацию на слайдах в качестве иллюстрации. Это способствует лучшему усвоению
учебного материала студентами.
Таким образом, участие в процессе обучения одновременно педагога и
компьютера значительно улучшает качество образования. Использование
предложенной методики активизирует процесс преподавания, повышает интерес
студентов к изучаемой дисциплине и эффективность учебного процесса, позволяет
достичь большей глубины понимания учебного материала. С одной стороны,
сотрудничество преподавателя и компьютера делает учебную дисциплину более
доступной для понимания различными категориями студентов, улучшает качество ее
усвоения. С другой - оно предъявляет более высокие требования к уровню
подготовки преподавателя и его квалификации, который должен уже не только
владеть традиционными методиками преподавания, но и уметь модернизировать их в соответствии
со спецификой обучаемых, используя современные достижения науки и техники [32].
Некоторые советы преподавателю по использованию технических средств в
учебном процессе
Как известно, работа с техническими средствами в большей степени, чем
другие виды педагогической деятельности зависит не только от субъективных
усилий преподавателя, но и от совокупности внешних условий его деятельности -
наличия специально оборудованных помещений, технического персонала, позиции
руководства в вопросах использования ТСО в учебном процессе, подготовленности
студентов к использованию технических средств и т.п.
Особенно ответственным и часто вызывающим разного рода
непредвиденные осложнения является использование ТСО в лекционной работе. В то
же время опыт показывает, что при хорошей подготовке и исключении «накладок»
использование в лекции даже простых технических средств предъявления информации
может существенно повысить ее привлекательность для студентов, дидактическую
эффективность, а также снизить нагрузку на голосовой аппарат преподавателя
[28].
Можно привести несколько простых советов, не
основанных на глубоких научных изысканиях, но позволяющих помочь преподавателю
предотвратить почти неизбежные осложнения в его «общении» с техникой на
лекциях. Часто можно наблюдать такую картину, когда преподаватель, сталкиваясь
с теми или иными неполадками, как бы дистанцируется от самой техники и
обслуживающего ее персонала. Типичные реплики в такой ситуации: «Видите, в
каких условиях нам приходится работать», «Как всегда ничего не работает», «В
этом институте даже нормальных мела и тряпки не бывает», «Такие у нас инженеры»
и т.п. А вместе с тем вина за сложившуюся неприятную ситуацию во многом лежит и
на преподавателе, не проверившем, не предупредившем, не ... и т.д.
Следует поступать так.
. До начала семестра необходимо узнать, какие
аудитории и в каком учебном корпусе оснащены ТСО, в каком состоянии они
находятся, кто ведает их обслуживанием, часто ли ими пользуются другие
преподаватели. Полезно вместе с ответственными за техническое состояние
оборудования опробовать его, продемонстрировать свою заинтересованность в том,
чтобы эти средства были приведены в рабочее состояние и хорошо отрегулированы.
Очень полезно проявить здесь настойчивость и сделать тех, от кого это зависит, своими
заинтересованными партнерами.
. Не пользоваться ненадежно работающей или плохо
отрегулированной аппаратурой. Следует убедиться перед занятием в ее
работоспособности лично, не доверяя это никому другому. Если какими-то
материалами приходится пользоваться впервые, предварительно просмотреть и
прослушать их именно в данной аудитории, убедиться, что они хорошо
просматриваются или прослушиваются из любого места в аудитории. Если при этом
обнаружатся сбои или выявится неудовлетворительное качество дидактических
материалов, необходимо воздержаться от их демонстрации: каждый сбой резко
нарушает нормальную работу во время лекции, а при частых сбоях дискредитируется
сама идея использования ТСО.
3. Лекцию опасней перегрузить, чем «недогрузить» демонстрациями, ибо
лектор всегда должен оставаться в центре событий, сохраняя за собой позицию
основного источника информации. Лектор ни в коем случае не должен превращаться
в простого комментатора того, что предъявляется. Все должно обстоять как раз
наоборот: привлекаемые материалы призваны иллюстрировать речь, пояснять
высказанные мысли и идеи.
4. При подготовке дидактических материалов желательно
максимально учитывать психологические законы восприятия и эргономические
требования. При необходимости следует посоветоваться по этому вопросу со
специалистами из соответствующих подразделений вуза [30].
Главное в том, чтобы использование технических средств не выступало
«принудиловкой», навязанной кем-то обязанностью - в этом случае уж точно ничего
хорошего не получится. Только если поверить в их полезность, вложить в работу с
ними не только свой ум, но и кусочек сердца, успех будет гарантирован.
Апробация лекционных занятий
Разработанная методика проведения лекционных занятий была апробирована на
втором курсе факультета математики и информатики СГПИ в феврале 2003 - 2004
учебного года.
Для проведения лекций использовался компьютер с TV - кодером и телевизор
с диагональю экрана 71 см. Текст лекции, увеличенный до 32 шрифта, с
гибкомагнитного диска подавался на экран и озвучивался лектором.
Просмотр конспектов у всего потока студентов показал, что их качество
возросло, это свидетельствует о целесообразности проведения лекции с
применением новых информационных технологий. Кроме того, в 1,5 раза возросла
скорость подачи материала.
При хорошей подготовки и исключении «накладок» использование в лекции
даже простых технических средств предъявления информации может существенно
повысить ее привлекательность для студентов, дидактическую эффективность, а
также снизить нагрузку на голосовой аппарат преподавателя.
.3 Разработка лекционных занятий
Определение тройного интеграла
1.Рассмотрим систему трех уравнений
 ,
,
где
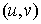 - множество упорядоченных пар
- множество упорядоченных пар  . Когда точка
. Когда точка  пробегает область
пробегает область  , точка с
координатами
, точка с
координатами 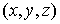 опишет некоторую поверхность в
опишет некоторую поверхность в 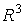 .
.
Это
множество принято называть поверхностью в  и
обозначать
и
обозначать 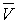 , а систему трех уравнений называют ее параметрическим
представлением,
, а систему трех уравнений называют ее параметрическим
представлением, 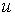 и
и 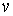 -
параметры, принадлежащие области
-
параметры, принадлежащие области 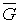 .
.
.Пусть
граница этой поверхности обозначается 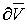 .
.
.Пусть
в замкнутой 3-х мерной области 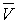 задана
некоторая функция
задана
некоторая функция 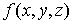 .
.
.Разобьем
эту область 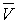 кусочно-гладкими
поверхностями на конечное число измеримых областей
кусочно-гладкими
поверхностями на конечное число измеримых областей 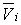 ,
, 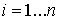 [3].
[3].
.Обозначим
через  диаметр
диаметр  , максимальное расстояние между точками, а
, максимальное расстояние между точками, а 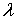 - наибольший из всех диаметров частичной области
- наибольший из всех диаметров частичной области 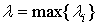 ,
, 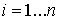 ,
, 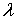 -ранг разбиения области
-ранг разбиения области 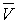 на
частичные области
на
частичные области 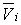 .
.
.Выберем
в каждой частичной области 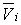 произвольную
точку
произвольную
точку 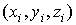 .
.
.Составим
интегральную сумму вида:
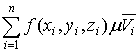 ,
,
где
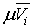 - мера объема (мера Жордано).
- мера объема (мера Жордано).
Определение:
Если при 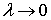 , интегральная сумма стремиться к конечному пределу,
причем он не зависит от способа разбиения тела
, интегральная сумма стремиться к конечному пределу,
причем он не зависит от способа разбиения тела  на
подобласти
на
подобласти 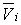 и выбора точек
и выбора точек 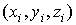 , то
функция
, то
функция 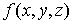 называется интегрируемой по области
называется интегрируемой по области 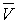 , а сам предел называется тройным интегралом от
функции
, а сам предел называется тройным интегралом от
функции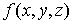 по области
по области 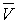 и
обозначается
и
обозначается
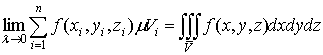 [2].
[2].
Свойства тройного интеграла
1.
Если функция 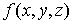 интегрируема по области
интегрируема по области  , то она ограничена на указанной области.
, то она ограничена на указанной области.
.
Если функция 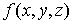 непрерывна по области
непрерывна по области 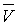 , то она
интегрируема на указанной области.
, то она
интегрируема на указанной области.
.
Если область 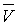 разбита
на две, то тройной интеграл равен сумме тройных интегралов, т.е. если
разбита
на две, то тройной интеграл равен сумме тройных интегралов, т.е. если 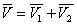 , то
, то
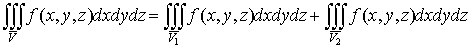 .
.
Существование интегралов в правой части обеспечивает существование
интеграла в левой части и наоборот.
4.
Если 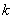 - некоторое действительное число (
- некоторое действительное число ( ), то константу можно выносить из под знака интеграла
), то константу можно выносить из под знака интеграла 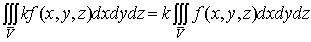 . Если f - интегрируема, то и функция
. Если f - интегрируема, то и функция 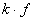 интегрируема, если
интегрируема, если  . Из
существования интеграла в левой части вытекает существование интеграла в правой
части.
. Из
существования интеграла в левой части вытекает существование интеграла в правой
части.
.
Справедлива формула:
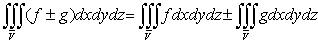 .
.
Существование
интегралов в правой части влечет существование интеграла в левой части.
.
Если 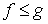
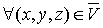 и они
интегрируемы на
и они
интегрируемы на 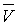 , то
, то
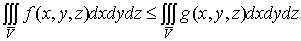 .
.
.
Если f интегрируема на  (т.е. есть предел частичных сумм), то и модуль от нее
интегрируем и справедлива формула
(т.е. есть предел частичных сумм), то и модуль от нее
интегрируем и справедлива формула
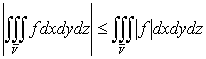 [1].
[1].
.
Теорема о среднем: Если 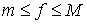 на
на 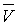 и f -
интегрируема, то
и f -
интегрируема, то 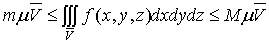 , m- наименьшее значение, M- наибольшее по области
, m- наименьшее значение, M- наибольшее по области 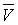 , где
, где 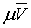 - мера Жордано.
- мера Жордано.
Следствия
8 свойства:
.Обе
части разделим на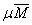 , получим
, получим  , где
, где 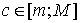 .
.
.Если
кроме указанных условий теоремы о среднем функция 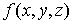 непрерывна в любой точке области
непрерывна в любой точке области 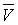 , то справедливо утверждение
, то справедливо утверждение
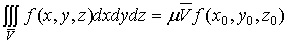 ,
,
где
точка 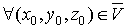 .
.
.
Если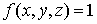 , то
, то 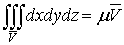 [2].
[2].
Вычисление тройного интеграла
1 случай. Область имеет следующий вид:
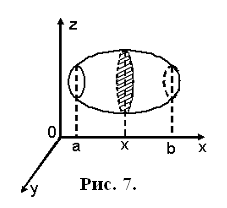
В
данном случае считают, что  -
измеряемое сечение, функция
-
измеряемое сечение, функция 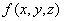 определена
на
определена
на 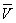 и интегрируема на нем. При таких условиях тройной
интеграл будет определяться по формуле:
и интегрируема на нем. При таких условиях тройной
интеграл будет определяться по формуле:
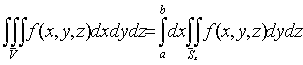 .
.
Замечание:
Считается, что 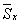 - измеримая область
- измеримая область 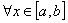 с гладкой
границей.
с гладкой
границей.
случай.
Задана на 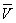 непрерывная функция
непрерывная функция 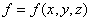 .
.
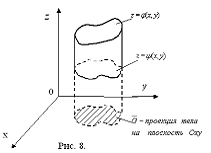
При
таких условиях 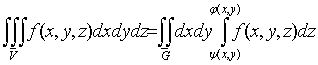 .
.
случай.
Если область 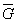 имеет специальный вид (дополнение ко второму случаю).
имеет специальный вид (дополнение ко второму случаю).
Тройной
интеграл будет определяться по формуле:
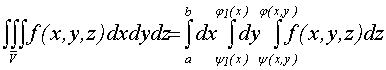 .
.
случай.
Объем тела вращения. В плоскости Oxy задан график функции 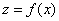 . Его вращением относительно оси Ox получается тело
вращения
. Его вращением относительно оси Ox получается тело
вращения 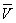 .
.
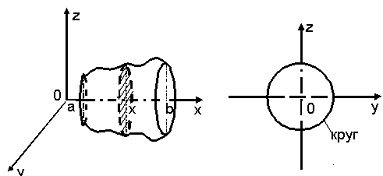
1.
Воспользуемся формулой 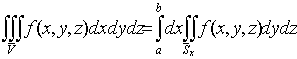 .
.
.
Так как 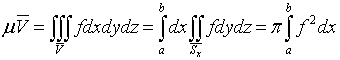 .
.
Криволинейная система координат в  R3
R3
1.Рассмотрим
2 пространства 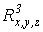 и
и 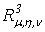 ,
, 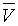 содержится в
содержится в 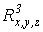 ,
, 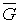 содержится в
содержится в 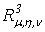 (рис.12
- 13).
(рис.12
- 13).
.Пусть
векторное поле 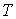 осуществляет преобразование пространства
осуществляет преобразование пространства 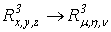
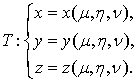
.Пусть
это векторное поле удовлетворяет всем необходимым условиям преобразования
областей, т.е.
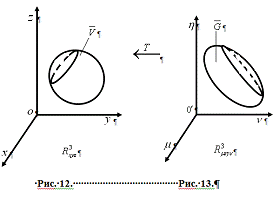
а)
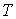 непрерывно дифференцируемо в области
непрерывно дифференцируемо в области  , а это значит, что функции
, а это значит, что функции 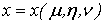 ,
, 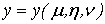 ,
, 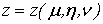 , непрерывно дифференцируемы в области
, непрерывно дифференцируемы в области 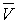 .
.
б)
Поле 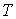 устанавливает взаимно однозначные соответствия между
устанавливает взаимно однозначные соответствия между  и между
и между 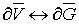 .
.
в)
Функциональный определитель или якобиан поля 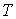 отличен
от нуля в области
отличен
от нуля в области 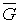 , т.е. сохраняет свой знак в указанной области
, т.е. сохраняет свой знак в указанной области
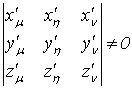 в
области
в
области  .
.
При
таких условиях векторное поле  осуществляет
преобразование областей
осуществляет
преобразование областей  .
.
Теорема:
Если векторное поле 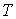 представляет
собой преобразование областей
представляет
собой преобразование областей 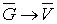 , то
кусочно-гладкая поверхность, лежащая в области
, то
кусочно-гладкая поверхность, лежащая в области 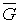 преобразуется
в кусочно-гладкую поверхность, лежащую в области
преобразуется
в кусочно-гладкую поверхность, лежащую в области 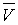 .
.
1. Как и в случае двух переменных эта теорема позволяет трактовать
преобразование 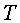 как переход от ПДСК к КСК.
как переход от ПДСК к КСК.
. Криволинейные координаты в трехмерном пространстве будут уже
являться криволинейными координатными поверхностями.
. И сетка будет задаваться криволинейными поверхностями [1].
. Координатные поверхности в КСК могут быть заданы параметрически
следующим образом:
а)
зафиксируем 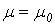 , тогда пространство
, тогда пространство 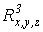 будет задаваться
будет задаваться
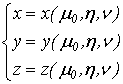
где
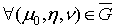 , а
, а 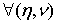 является
параметром при создании этой кривой поверхности.
является
параметром при создании этой кривой поверхности.
б)
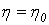
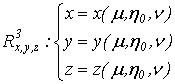
где
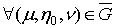 , а
, а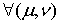 является
параметром.
является
параметром.
в)
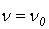
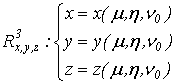
где
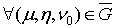 , а
, а 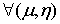 является параметром.
является параметром.
.Уравнение
связи из ПДСК в КСК имеет вид:
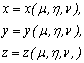
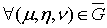 .
.
Аналогично записывается уравнение связи из КСК в ПДСК [2].
Цилиндрическая система координат
1.
Векторное поле 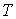 в данном случае задается
в данном случае задается

где
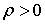 ,
, 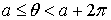 ,
,  .
.
.
Пусть дана точка 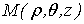 .
.
.
Спроектируем ее на плоскость  , т.е.
найдем
, т.е.
найдем 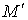 .
.
.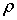 называется полярным радиусом,
называется полярным радиусом, 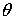 - полярный угол.
- полярный угол.
.Для
получения взаимно однозначного соответствия между ЦСК и ПДСК нужно вырезать ось
 :
: 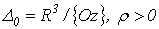 .
.
.
Уравнение связи ЦСК с ПДСК имеет вид: 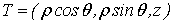 . Такая
система координат называется цилиндрической, т.к. одна из ее координатных
поверхностей является цилиндром.
. Такая
система координат называется цилиндрической, т.к. одна из ее координатных
поверхностей является цилиндром.
.
Координатные поверхности в ЦСК:
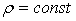 -
цилиндры,
-
цилиндры, 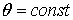 -
полуплоскости,
-
полуплоскости,  - плоскости.
- плоскости.
.
Функциональный определитель в ЦСК имеет вид:
 ,
,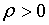 [3].
[3].
Сферическая система координат
1.Векторное
поле 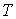 в данном случае задается
в данном случае задается
где
 ,
,  ,
, 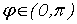 .
.
.ССК
организована в пространстве 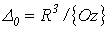 .
.
.Уравнение
связи ССК с ПДСК имеет вид: 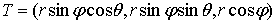 .
.
.Координатные
поверхности в ЦСК:
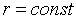 - сфера,
- сфера,
 -
круговой конус,
-
круговой конус,  - полуплоскость.
- полуплоскость.
.Функциональный
определитель в ССК имеет вид:
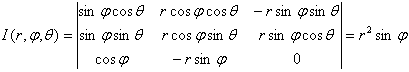 ,
,
 [3].
[3].
Замена переменных в тройном интеграле
1.Пусть
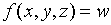 непрерывна в замкнутой области
непрерывна в замкнутой области 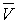 с кусочно-гладкой границей.
с кусочно-гладкой границей.
.Пусть
векторное поле 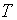 осуществляет преобразование пространства
осуществляет преобразование пространства
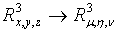 , в
котором
, в
котором 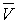 содержится в
содержится в 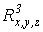 , а
, а 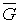 содержится в
содержится в 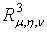 и
и 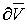 - кусочно-гладкая граница одного поля,
- кусочно-гладкая граница одного поля, 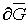 - другого.
- другого.
.Пусть
области 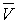 и
и 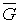 -
ограниченные области, т.е. они будут измеримы по Жордано - кубируемы (имеют
объемы).
-
ограниченные области, т.е. они будут измеримы по Жордано - кубируемы (имеют
объемы).
.При
всех указанных условиях будет справедлива формула:
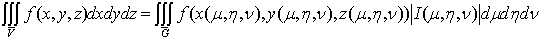 .
.
Доказательство:
.Разобьем
область  на подобласти кусочно-гладкими поверхностями
на подобласти кусочно-гладкими поверхностями  .
.
.Тогда
область  разобьется
кусочно-гладкими границами на частичные области
разобьется
кусочно-гладкими границами на частичные области 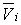 ,
, 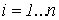 .
.
.Составим
интегральную сумму такого рода
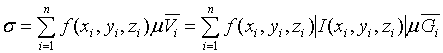 ,
,
так
как
и
на основании 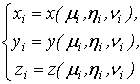 справедливы формулы
справедливы формулы
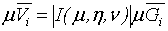 .
.
Интегральную
сумму можно переписать в таком виде
. .
.
.Если
перейти к пределу при 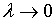 от левой части формулы п.3 и от правой части п.4, то
получится требуемое выражение, ч.т.д [2].
от левой части формулы п.3 и от правой части п.4, то
получится требуемое выражение, ч.т.д [2].
Объем в ЦСК и ССК
1.В ЦСК объем вычисляется по формуле:
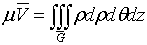 .
.
.
В ССК объем вычисляется по формуле:
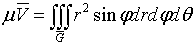 [1].
[1].
.4 Методические рекомендации по проведению практических занятий
тройной интеграл педагогический студент
При изучении курса «Математический анализ» студенты часть материала
должны проработать самостоятельно. Роль самостоятельной работы велика.
Планирование самостоятельной работы студентов по курсу «Математический
анализ» необходимо проводить в соответствии с уровнем подготовки студентов к
изучаемому курсу. Самостоятельная работа студентов распадается на два
самостоятельных направления: на изучение и освоение теоретического лекционного
материала, и на освоение методики решения задач по математическому анализу
[24].
В помощь студенту здесь могут быть рекомендованы фондовые лекции, которые
разрабатывает ведущий преподаватель курса. Фондовые лекции представлены в
распечатанном и набраны в электронном видах. При всех формах самостоятельной
работы студент может получить разъяснения по непонятным вопросам у
преподавателя на индивидуальных консультациях в соответствии с графиком
консультаций. Студент может также обратиться к рекомендуемым преподавателем
учебникам, учебным пособиям и обучающе - контролирующей программе (см. глава 2,
§7), в которых теоретические вопросы изложены более широко и подробно, чем на
лекциях и с достаточным обоснованием.
Консультация - активная форма учебной деятельности в педагогическом вузе.
Консультацию предваряет самостоятельное изучение студентом литературы по
определенной теме. Качество консультации зависит от степени подготовки
студентов и остроты поставленных перед преподавателем вопросов.
Основной частью самостоятельной работы студента
является его систематическая подготовка к практическим занятиям. Студенты
должны быть нацелены на важность качественной подготовки к таким занятиям. При
подготовке к практическим занятиям студенты могут пользоваться разработанными «Методическими
рекомендациями к практическим занятиям» по курсу «Математический анализ» и
задачниками. Кроме того, можно воспользоваться электронным пособием по теме
“Тройные интегралы” (раздел ПРАКТИЧЕСКОЕ ЗАНЯТИЕ). Планы практических занятий и
заданий к ним приведены в «Методических рекомендациях к практическим
занятиям»[23].
При подготовке к практическим занятиям студенты должны освоить вначале
теоретический материал по новой теме занятия, с тем, чтобы использовать эти
знания при решении задач. Затем просмотреть объяснения решения примеров, задач,
сделанные преподавателем на предыдущем практическом занятии, разобраться с
примерами, приведенными лектором по этой же теме. Решить заданные примеры. Если
некоторые задания вызвали затруднения при решении, попросить объяснить
преподавателя на очередном практическом занятии или консультации.
Темы практических занятий и задания к ним сообщаются студенту
заблаговременно для самостоятельной подготовки.
Для того, чтобы учебный процесс проходил наиболее эффективно, студентам
необходимо вырабатывать и развивать у себя систему знаний и умений, которые
отражают меру интеллектуального развития:
·
в конкретном
видеть общее;
·
из общего
выделять конкретное;
·
видеть внутри - и
межпредметные связи относительно различных научных понятий, методов и т.д.;
·
осознание
единства и целостности научной картины мира;
·
умение соотносить
научные категории с объективной реальностью;
·
понимание
относительного характера знаний и необходимости уточнять их путем
систематического познания;
·
умение
анализировать и обобщать;
·
гибкость
мыслительной деятельности, осознанная устойчивость и самостоятельность
мышления;
·
прочность
имеющихся знаний, умений и навыков, их восстанавливаемость [24].
Для реализации приведенной системы знаний студентам предлагаются
различные средства. В частности, «Методические рекомендации к практическим
занятиям и самостоятельной работе», «Сборник задач по математическому анализу».
Данные методические пособия помогают студентам организовать свою работу
как на практических занятиях, так и при работе во внеаудиторное время.
Сборники задач и методические рекомендации к практическим занятиям
предусматривают разбиение учебного материала на темы, изучение которых
предусмотрено Государственным стандартом и учебной программой по математическому
анализу. Каждое практическое занятие разбито на ряд вопросов, помогающих
студентам самостоятельно работать при подготовке к практическим занятиям и
лекциям. Это такие вопросы как:
1. План занятия. Здесь более подробно
обозначены вопросы, изучаемые в данной теме.
2. Задания. Первая группа заданий
подготавливает студентов к восприятию нового материала. Вторая группа - это
задания по усвоению и закреплению изученного.
3. Вопросы для самоконтроля. Этап
самооценки и самоконтроля является очень важным в процессе самообразовательной
деятельности. Поэтому наличие этого пункта дает возможность студентам оценить
результаты своей работы, соотнести их с базовым уровнем, а так же позволяет
усваивать не только материал практического плана (т.е. методы математического
анализа), но и теоретические аспекты этих методов, т. е. способствует
фундаментализации знаний.
Знания и умения, которые формируются у студентов в ходе изучения
математического анализа, достигают наибольшего эффекта при следующих основных
условиях, эти условия могут быть созданы только при непосредственном участии и
работе самих студентов.
Четкое определение цели деятельности в смысле результата действий и цели
упражнений (т.е. каких показателей действий надо достичь в процессе
упражнений).
1. Ясное представление техники
выполнения действий, т.е. образца, которого следует достичь.
2. Понимание правил и последовательности
выполнения действий направленных на достижение целей.
3. Постоянный самоконтроль качества
действий путем сличения их результатов со сложившимися в представлении или по
зрительно воспринимаемым образцам.
4. Своевременное обнаружение отклонений,
ошибок и брака в действиях при следующих повторениях этих действий.
5. Правильная самооценка успехов в
достижении конкретной деятельности и цели упражнений в смысле совершенствования
осваиваемых действий.
Следовательно, нужны, во - первых, система и последовательность
упражнений; во-вторых, разумное их распределение во времени; в - третьих,
необходима постоянная актуализация в самообразовательной деятельности студентов
по переносу знаний и умений в новую ситуацию; в - четвертых, активизация опыта
по решению задач и преобразования ранее усвоенных способов деятельности и др.
Организационно - управленческие умения, которые необходимы студентам для
самостоятельной деятельности по математическому анализу, особенно во внеучебное
время, и которые повышают готовность к самообразованию:
·
умение намечать и
принимать к исполнению задачи, основные пути поиска и усвоения учебного
материала;
·
навыки планирования
учебного труда, распределения усилий и времени для решения этих задач;
·
умения оценивать
достигнутые результаты и ставить новые задачи [24].
Содержание практических занятий по теме: “Тройные интегралы”
Определение тройного интеграла;
Вычисление тройного интеграла;
Замена переменных в тройных интегралах;
Тройной интеграл в сферических и цилиндрических координатах;
Геометрические приложения тройного интеграла: вычисление объемов тел,
координат центра тяжести [24].
Тематическое планирование практических занятий по теме:”Тройные
интегралы”
|
Практическое
занятие №11
|
Определение тройного
интеграла. Вычисление тройного интеграла. Замена переменных в тройных
интегралах. Тройной интеграл в сферических и цилиндрических координатах.
Геометрические приложения тройного интеграла: вычисление объемов тел.
|
Практическое занятие №11
Тема: Тройной интеграл и его геометрические приложения
План занятия
1. Определение и вычисление тройного
интеграла.
2. Тройной интеграл в сферических и
цилиндрических координатах.
3. Геометрические приложения тройного
интеграла: вычисление объемов тел. Примеры: №№ 937(стр.42,23);№№1, 2
(стр.349,17); №№98,99,100 (стр.24,21); №1 (стр.121,3)
Задания
1. Подготовиться по теме «Криволинейные
интегралы I и II родов».
2. Решить примеры: №№ 933,934,948,949(стр.41-43,
23)
3.
Вопросы для
самоконтроля
4. Дайте определение тройного интеграла.
5. Напишите формулы преобразования
тройного интеграла к сферическим и цилиндрическим координатам.
6. Изобразите сферическую и
цилиндрическую системы координат [23].
Апробация разработанного практического занятия
На факультете математики и информатики Славянского - на - Кубани
государственного педагогического института была проведена апробация
разработанного практического занятия на втором курсе в группах 2002 - м - 1 и
2002 - м - 2 в марте 2003 - 2004 учебного года. Представим таблицу с
полученными результатами при проведении самостоятельной работы.
|
Группа
|
«5»
|
«4»
|
«3»
|
«2»
|
Качественный показатель
|
Абсолютный показатель
|
|
М - 1
|
11%
|
30%
|
37%
|
22%
|
41%
|
78%
|
|
М - 2
|
19%
|
39%
|
30%
|
12%
|
58%
|
89%
|
.5 Разработка практического занятия
Практическое занятие №11
Тема: Тройной интеграл и его геометрические приложения
Тип занятия - практикум, форма занятия представляет собой комбинированную
между коллективной и фронтальной.
Средствами обучения на данном практическом занятии являются: сборник
задач по математическому анализу, рисунки на доске, методические рекомендации
по проведению практических занятий.
При проведении занятия использовались следующие методы обучения -
словесные, наглядные, по дидактической цели - познавательные, по характеру
познавательной деятельности - проблемные.
Цель: при решении упражнений закрепить знания, умения и навыки,
полученные на лекции в области вычисления тройных интегралов по любой области,
с помощью замены переменных, вычисления объемов тел, координат центра тяжести.
Ход занятия:. Организационная часть
Студентам сообщается тема практического занятия, его цель, проводится
проверка присутствующих.. Основная часть
В начале занятия проводится фронтальный опрос с целью проверки
теоретических знаний по изученной теме. Студентам предлагается ответить на
следующие вопросы у доски, выполняя необходимые при ответе записи (у доски
работают 4 студента одновременно).
Вопрос 1. Сформулируйте определение тройного интеграла.
Ответ:
Если при 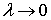 интегральная сумма
интегральная сумма
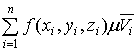
 .
.
Вопрос
2. Написать формулы вычисления тройного интеграла: для 1 и 2 случаев.
Ответ:
.случай.
Область имеет следующий вид:
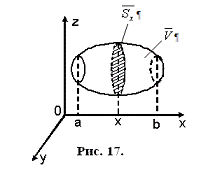
В
данном случае считают, что 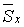 -
измеряемое сечение, функция
-
измеряемое сечение, функция 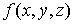 определена
на
определена
на 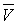 и интегрируема на нем. При таких условиях тройной
интеграл будет определяться по формуле:
и интегрируема на нем. При таких условиях тройной
интеграл будет определяться по формуле:
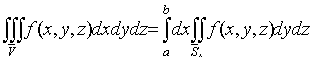 .
.
Замечание:
Считается, что 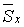 - измеримая область
- измеримая область 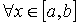 с гладкой
границей.
с гладкой
границей.
случай.
Задана на 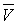 непрерывная функция
непрерывная функция 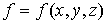 .
.
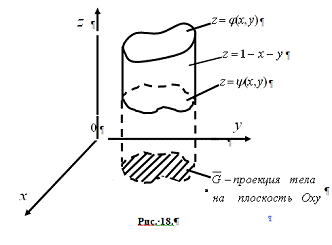
При
таких условиях
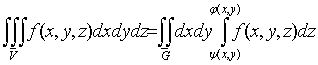 .
.
Вопрос
3. Написать формулы вычисления тройного интеграла: 3 и 4 случай.
Ответ:
3 случай. Если область 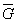 имеет специальный вид (дополнение ко второму случаю).
имеет специальный вид (дополнение ко второму случаю).

Тройной
интеграл будет определяться по формуле:
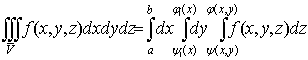 .
.
случай.
Объем тела вращения. В плоскости Oxz задан график функции  . Его вращением относительно оси Ox получается тело
вращения
. Его вращением относительно оси Ox получается тело
вращения  .
.
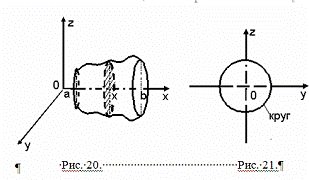
.
Воспользуемся формулой
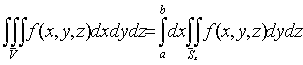 .
.
.
Так как
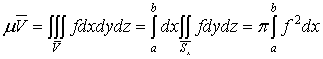 .
.
Вопрос
4. Записать формулу преобразования тройного интеграла к цилиндрическим
координатам.
Ответ:
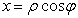 ,
,  ,
, 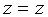
 ,
, 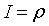
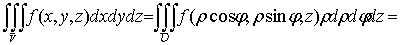
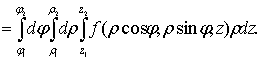
Вопрос
5. Записать формулу преобразования тройного интеграла к сферическим
координатам.
Ответ:
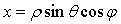 ,
, 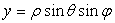 ,
, 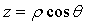 ,
, 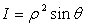
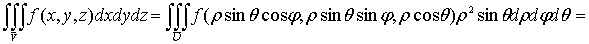
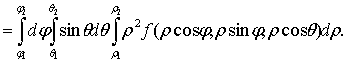
Вопрос
6. Написать формулы вычисления объема.
Ответ:
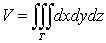 , в ЦСК:
, в ЦСК: 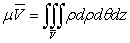 ,
,
в
ССК: 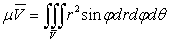 .
.
Преподаватель:
Итак, а теперь перейдем непосредственно к выполнению упражнений.
При
объяснении нового материала преподаватель проводит на доске подробное решение
(с пояснениями) разных упражнений по изучаемой теме.
№1
(Преподаватель у доски) Вычислить 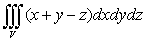 , где
область
, где
область  - параллелепипед, ограниченный плоскостями
- параллелепипед, ограниченный плоскостями  ,
,  ,
, 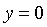 ,
,  ,
,  ,
,  [23].
[23].
Решение:
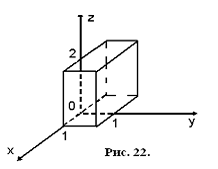
По
формуле вычисления тройного интеграла (случай 3) имеем

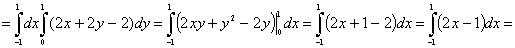
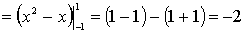 .
.
№2.
(Студент с помощью преподавателя) Вычислить
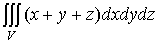 ,
,
где
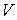 - пирамида, ограниченная плоскостью
- пирамида, ограниченная плоскостью 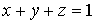 и координатными плоскостями
и координатными плоскостями 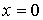 ,
, 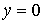 ,
, 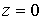 [17].
[17].
Решение:
Для
построения пирамиды найдем проекции на плоскости  ,
, 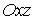 ,
, 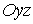 . На
плоскость
. На
плоскость 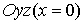 :
: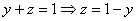 ,
, 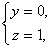
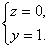
На
плоскость 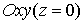 :
: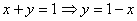 ,
, 
На
плоскость  :
: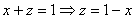 ,
, 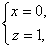
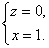
Область
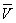 проектируется на
проектируется на  в
треугольник
в
треугольник 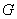 , ограниченный прямыми
, ограниченный прямыми 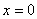 ,
, 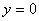 ,
, 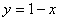 .
.
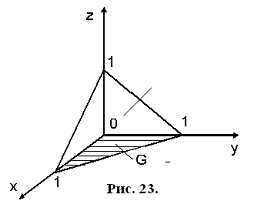
По
формуле вычисления тройного интеграла (случай 3) имеем
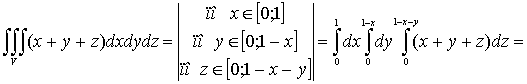
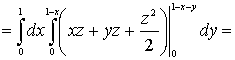
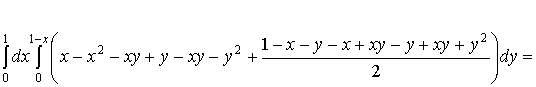
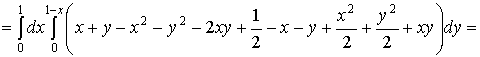

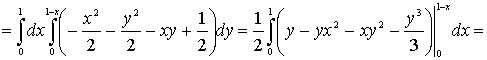
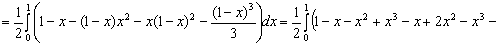
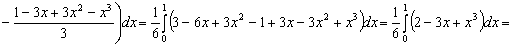
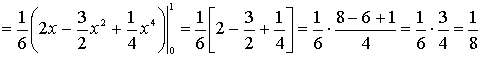 .
.
№3.
(Студент самостоятельно) Вычислить тройной интеграл
 ,
,
где
 - пирамида, ограниченная плоскостью
- пирамида, ограниченная плоскостью  и координатными плоскостями
и координатными плоскостями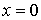 ,
, 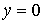 ,
, 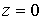 [17].
[17].
Решение:
Найдем
проекцию области 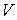 на плоскость
на плоскость  , то есть
, то есть
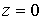 :
: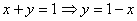 ,
, 
 .
.
На
плоскость 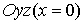 :
: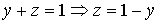 ,
, 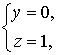
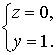 .
.
На
плоскость 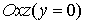 :
: ,
, 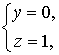
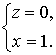 .
.
Проекцией
тела на плоскость  служит треугольник
служит треугольник  ,
образованный прямыми
,
образованный прямыми 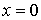 ,
, 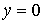 и
и 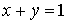 .
.
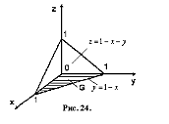
Границами
изменения 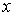 служат числа 0 и 1, а при постоянном
служат числа 0 и 1, а при постоянном 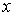 переменная
переменная 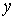 изменяется
от 0 до
изменяется
от 0 до 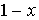 .
.
Если
же фиксированы и 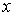 , и
, и 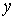 , то
пределами изменения
, то
пределами изменения 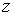 будут 0 и
будут 0 и 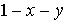 . По
формуле
. По
формуле
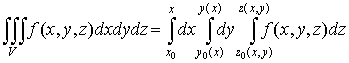 получаем
получаем
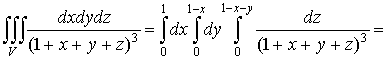
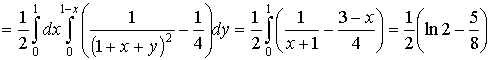 [17].
[17].
Первичное закрепление материала проводится при решении студентами у доски
упражнений, подобных рассмотренным. Остальные решают на месте, сверяя свое
решение с решением у доски.
№4.(Преподаватель
у доски) Вычислить тройной интеграл 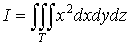 , если
, если 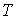 - шар
- шар 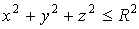 [21].
[21].
Решение:
Перейдем
к сферическим координатам 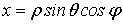 ,
, 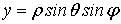 ,
, 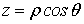 ,
, 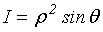 . В
области
. В
области 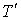 координаты
координаты 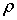 ,
, 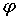 ,
, 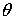 изменяются
так:
изменяются
так:  ,
,  ,
, 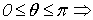
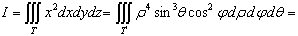
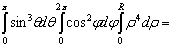
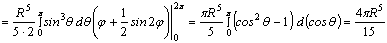 .
.
№5.
Вычислить тройной интеграл 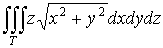 , если
область
, если
область  ограничена цилиндром
ограничена цилиндром  и
плоскостями
и
плоскостями 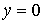 ,
,  и
и  [22].
[22].
Решение:
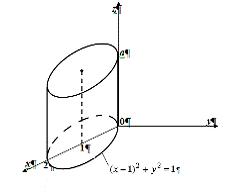
Перейдем
к цилиндрическим координатам: 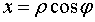 ,
, 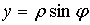 ,
,  ,
, 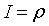 .
.
Уравнение
цилиндра в этих координатах примет вид:
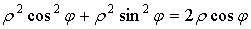 или
или 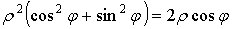 , т.е.
, т.е. 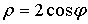 .
.
Следовательно,
в области  координаты
координаты 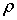 ,
, 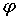 и
и 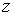 изменяются
так:
изменяются
так:
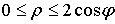 ,
,  ,
, 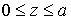 .
.
Поэтому
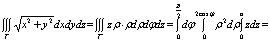

 .
.
Студент
у доски, остальные работают самостоятельно, в конце решения сравнивают
полученный результат
№6.
Вычислить 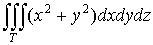 , если область
, если область 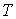 -
верхняя половина шара
-
верхняя половина шара 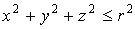 [17].
[17].
Решение:
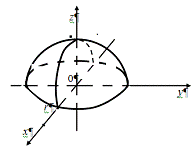
Введем
сферические координаты 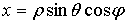 ,
, 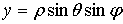 ,
, 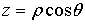 ,
, 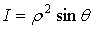 .
.
Новые
переменные изменяются в пределах 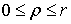 ,
, 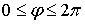 ,
, 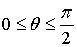 .
.
Таким
образом,
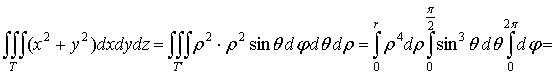
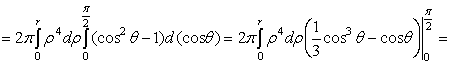
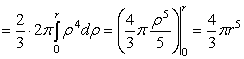 .
.
№7(Преподаватель
у доски) Вычислить объем тела, ограниченного сферой 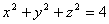 и параболоидом
и параболоидом 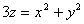 [3].
[3].
Решение:
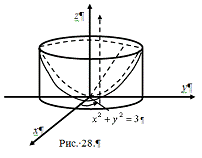
Найдем
проекцию линии пересечения сферы и параболоида на плоскость  . Для этого достаточно из системы уравнений
. Для этого достаточно из системы уравнений 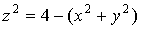 ,
, 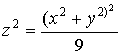 исключить
переменную
исключить
переменную  . В результате получим:
. В результате получим:  или
или
 , откуда
, откуда 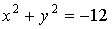 и
и 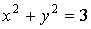 - корни квадратного уравнения.
- корни квадратного уравнения.
Следовательно,
уравнением проекции будет окружность 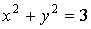 .
.
В
силу симметрии достаточно вычислить объем тела 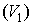 находящегося
в 1 октанте, и результат умножить на 4. Тогда согласно формуле:
находящегося
в 1 октанте, и результат умножить на 4. Тогда согласно формуле: 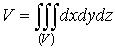 для искомого объема получим
для искомого объема получим 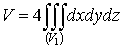
Так
как проекция данного тела  на плоскость
на плоскость  есть
круг
есть
круг  , то для вычисления последнего интеграла целесообразно
перейти к цилинричиским координатам.
, то для вычисления последнего интеграла целесообразно
перейти к цилинричиским координатам.
После
преобразования по формулам: 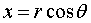 ,
, 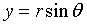 ,
,  уравнения
окружности
уравнения
окружности 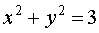 , параболоида
, параболоида 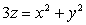 и сферы
и сферы 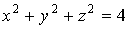 , соответственно принимают вид:
, соответственно принимают вид:  ,
,  и
и 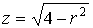 . Из рисунка видно, что в области интегрирования
. Из рисунка видно, что в области интегрирования 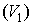 угол
угол 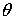 изменяется
от
изменяется
от  до
до 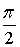 ,
, 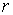 - от
- от  до
до 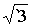 ,
, 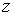 - от
- от 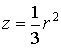 до
до 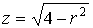 . Поэтому
. Поэтому
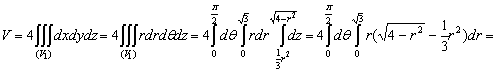
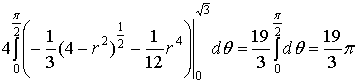 .
.
Преподаватель:
Итак, подведем итог: на сегодняшнем занятии мы с вами познакомились с тройным
интегралом, вычислением его по любой области, научились вычислять тройной
интеграл путем преобразования декартовых координат к цилиндрическим и
сферическим координатам, находить объем тела. Для окончательного закрепления
изученной темы на дом будут заданы аналогичные примеры [23].
Домашнее
задание: сборник задач по математическому анализу для студентов второго курса
факультета математики-информатики. Ч.4.: №933, 934, 949 (стр. 41-43, 23). Ниже
приведены решенные номера домашнего задания.
№933.
Вычислить 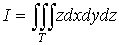 , где область
, где область  определяется
неравенствами
определяется
неравенствами  ,
, 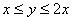 ,
, 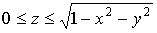 [21].
[21].
Решение:
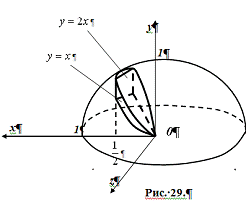
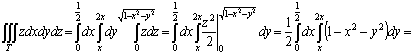
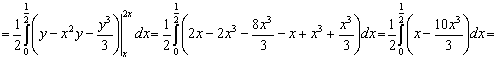
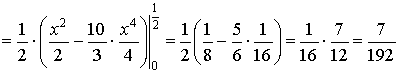 .
.
№934.
Вычислить интеграл  , если область
, если область  ограничена
плоскостями
ограничена
плоскостями 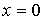 ,
,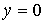 ,
, 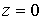 ,
, 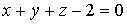 [27].
[27].
Решение:
Область
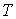 ограничена сверху плоскостью
ограничена сверху плоскостью 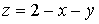 , а снизу плоскостью
, а снизу плоскостью 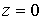 .
Проекцией тела на плоскость
.
Проекцией тела на плоскость  служит
треугольник, образованный прямыми
служит
треугольник, образованный прямыми 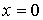 ,
,  ,
,  .
.
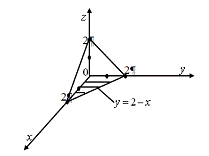
Следовательно,
по формуле вычисления тройного интеграла
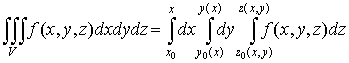
получаем
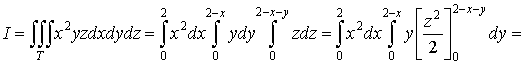
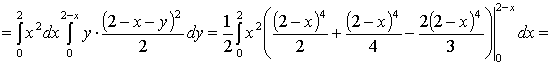
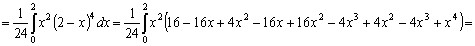
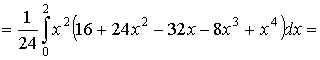
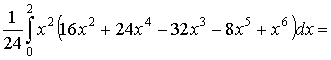
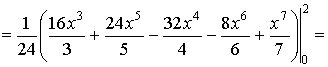
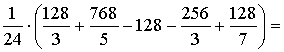
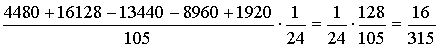 .
.
№949.
Вычислить 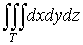 , где область
, где область 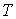 - шар
- шар 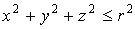 [16].
[16].
Решение:
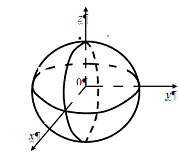
Перейдем
к сферическим координатам 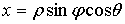 ,
, 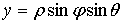 ,
, 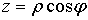 ,
, 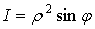 ,
, 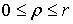 ,
, 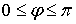 ,
, 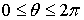 .
.
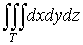
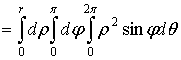
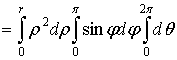
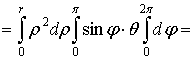
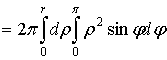
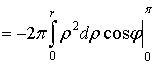
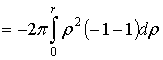
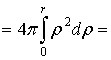
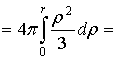
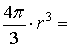
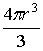 .
.
3.6 Методические рекомендации по использованию информационных технологий
на практических занятиях
Осуществление компьютерного обучения на базе новых
информационных технологий является одним из важных направлений
совершенствования профессиональной подготовки будущих педагогов.
Информационная технология, которая используется при изучении курса
«Математический анализ» включает программированное обучение, экспертные
системы.
Обучающие системы, которые включены в процессе изучения математического
анализа построены в виде электронных учебников и характеризуются следующими
параметрами:
структурная сложность;
содержательная сложность;
информативность;
ясность структуры.
Обучающие программы представляют собой электронные модели учебника, то
есть содержат основные предложения учебника. В тексте учебников выделены
структурные единицы, например, понятия, задачи, вопросы, теоремы, набор этих
структурных единиц определяется предметом и, в частности, представленными в
учебниках темами [25].
Наличие в программе курса «Математического анализа» большого количества
часов, отведённых на практические занятия даёт возможность строить процесс
обучения по данному курсу в соответствии с принципами, на основе которых
применяются информационные технологии (основные принципы дидактики:
наглядность, активность и сознательность, доступность, системность и
последовательность).
Проведение практических занятий в компьютерных классах позволяет
оптимально сочетать такие формы организации учебного процесса, как общие,
групповые и индивидуальные.
Изучение с помощью технических средств позволяет реализовать
дифференцированный подход к обучению [30].
Такие формы организации обучения как лекция, практические занятия в
сочетании с применением информационных технологий позволяет строить учебный
процесс в соответствии с современными тенденциями развития образования, такими
как: усиление роли самостоятельной работы студента, смещение акцента с
преподавания на учение, чем обеспечивается направленность на развитие
самообразовательной деятельности будущих специалистов.
Обучающие программы, как уже отмечалось, имеют модель, эквивалентную
учебнику. Это позволяет организовать изучение как теоретического так и
практического материала. Наличие структурированной системы подачи информации
ведёт к рациональной организации системы контроля за усвоением учебного
материала, наиболее полно реализующую принцип «прозрачного ящика», предполагающий
информационное обеспечение управления [25].
Тестовый контроль, предусмотренный в каждой обучающей программе,
обеспечивает систематическую обратную связь, а так же позволяет преподавателю
своевременно проводить учебные мероприятия по коррекции усвоения знаний.
Применение обучающих программ в процессе изучения курса «Математический
анализ» позволяет проводить контролирующие мероприятия независимо от
применяемых форм, методов и средств обучения, в виде итогового тестирования по
темам как по теоретическому содержанию курса, так и по практическому, то есть
проводить контроль усвоенных знаний, умений и навыков обучаемых.
Наличие обучающих систем обеспечивает значительную экономию учебного
времени как преподавателя, так и студентов. Это достигается тем, что теоретический
и практический материал, который имеется в учебниках, несёт в себе информацию в
сжатой форме и содержит не только базовый материал, но и разделы выходящие за
рамки программы. Таким образом, это способствует как фундаментализации знаний,
так и расширению математического кругозора студентов, а это, в свою очередь,
обеспечивает реализацию принципов профессионально-педагогической направленности
обучения [30].
Исходя из вышеуказанного, можно указать следующие методические
рекомендации к использованию информационных технологий в процессе изучения
курса «Математический анализ»:
) В соответствии с учебной программой курса можно организовать
изучение отдельных тем на практических занятиях в компьютерных классах:) изучение
теоретических вопросов;) изучение практического содержания темы;) комплексное
изучение предлагаемых тем.
) В течение изучения курса можно проводить контрольные мероприятия
по отдельным разделам и темам. Проводиться контроль:
a) усвоения теоретического содержания
темы;
b) уровня сформированности умений и
навыков по решению базовых задач, включённых в обязательные результаты
обучения.
3) На первом занятии преподавателем даются указания к работе с
обучающими программами. После чего студентам предлагается самостоятельно
изучить темы во внеаудиторное время. Контрольные мероприятия преподаватель
может проводить либо с использованием тестовых систем, либо с использованием
других форм (устные и письменные опросы, фронтальные проверки).
По теме «Тройные интегралы» создана обучающе - контролирующая программа
(см. глава 2 §7).
Применение этой программы можно органично вписать в учебный процесс.
3.7 Обучающе-контролирующая программа по теме «Тройные интегралы»
В рамках исследовательской работы разработана обучающе
- контролирующая программа по теме «Тройные интегралы» для студентов и
преподавателей физико-математических факультетов педагогических вузов.
Программа состоит из двух частей: обучающей и контролирующей. Обучающая
часть выполнена в виде электронного пособия по теме «Тройные интегралы». Данное
пособие содержит в себе основные теоретические аспекты данной темы, а также
примеры решения заданий.
Содержание пособия имеет следующий вид:
·
Фондовые лекции
по теме ”Тройные интегралы”
·
Тройной интеграл
и его вычисление;
·
Замена переменных
в тройном интеграле;
·
Практическое
занятие.
Параграфы, представленные в электронном учебнике,
являют собой расширенный материал по соответствующему вопросу фондовых лекций.
Студент может сравнить доказательство той или иной
теоремы, того или иного свойства, вопроса по электронному учебнику и по
фондовым лекциям. И затем в дальнейшем использовать именно тот материал,
который ему легче запомнить для последующего применения на практике.
В разделе Практическое занятие приводятся решенные примеры по данной
теме. При активации того или иного пункта на экран выводится теоретическое
содержание этого пункта. Имеется возможность выйти в главное меню-содержание.
Работа с данным электронным пособием не требует особых знаний в области
программирования и устройства компьютера.
Пособие выполнено в формате html - основном формате
сети Интернет - что придаёт ему простоту в изготовлении и эксплуатации и
допускающем гиперссылки. Это позволяет использовать электронное пособие и его
отдельные материалы для размещения на институтском образовательном сервере.
Другой вариант - размещение пособия на компакт-дисках, в том числе и
перезаписываемых.
Электронное пособие предоставляет большие возможности
для личностной творческой работы. Преподаватель и студенты могут участвовать в
составлении собственного электронного пособия, в добавлении к нему материалов
или заданий без существенных затрат на переиздание. В «бумажных» учебниках
такая возможность не предусмотрена, конструирование студентами личностного
содержания образования затруднено. Максимально, что может сделать студент, это
оставить на полях «бумажного» учебника свои пометки.
Электронное пособие предоставляет возможность внесения
в него изменений педагогом. Ведь преподавателям приходится собирать и приносить
на занятие многочисленные пособия, вырезки и другие материалы, когда изучается
та или иная тема. Здесь же преподаватель может быстро добавить в учебник свежие
данные или те материалы, которые он нашел в других электронных библиотеках,
книгах или в сети Интернет.
Форма такого электронного пособия - блочная. Это означает, что отдельные
блоки могут заменяться, добавляться или изменяться в ходе обучения. В отличие
от «бумажных» учебников замена электронных блоков не сопряжена с существенными
затратами по переизданию.
Контролирующая часть представляет собой тест. В тесте необходимо решить 5
из 25 примеров по данной теме. Количество вариантов ответов пять. На каждый
вопрос время устанавливается в настройках программы 10 - 12 минут, в
зависимости от сложности задания. Ход времени отображается при помощи
индикатора прогресса.
Перед прохождением тестирования пользователю предлагается внести в
отдельную форму-окно свои личные данные: фамилию, имя, отчество, курс и группу.
По завершении теста эти данные могут заноситься в базу данных автоматически, если
в настройках включена соответствующая опция. Кроме того, в базу данных
заносится дата прохождения тестирования и количество правильных ответов.
Для просмотра и управления базой данных результатов предусмотрены
специальные средства отображения информации с удобной системой навигации и
фильтрации. Эти средства позволяют получить всю необходимую информацию о
пользователях, проходивших тестирование, датах прохождения тестирования и
полученных оценках. Имеется возможность сгенерировать запрос к базе данных по
заранее сформированным критериям (фамилия, курс, группа, результат). Наборы
данных можно просматривать, изменять и выводить на печать. Доступ к базе данных
результатов осуществляется только при вводе пароля.
В программе имеется специальный конструктор, при помощи которого можно
создавать и вносить в базу данных новые вопросы тестирования, а также изменять
существующие. В конструкторе, кроме содержания вопроса, определяются такие его
параметры, как количество вариантов ответов, номер правильного варианта, время,
отводимое на вопрос и наличие рисунка к нему.
Программа включает в себя систему настроек, позволяющих изменять
параметры её работы. В окне настроек пользователь имеет возможность установить
следующие параметры:
. Расположение файла электронного пособия. В зависимости от реального
расположения данного файла пользователь может либо выбрать опцию «В одном
каталоге с программой», либо при помощи стандартного для Windows диалогового
окна открытия файлов вручную выбрать нужный файл.
. Количество вопросов тестирования. Данный параметр ограничивается лишь
реальным количеством вопросов, находящихся в базе данных. Установка параметра в
ноль отключает соответствующее тестирование, то есть делает его недоступным для
пользователей.
. Смена пароля. Для осуществления данной операции необходимо ввести
старый пароль.
. Автоматическая запись результатов тестирования в базу данных. Параметр
регулируется двухпозиционным переключателем, с помощью которого включается либо
отключается данная опция.
. Расположение файла базы данных вопросов и результатов тестирования. В
зависимости от реального расположения данного файла пользователь может либо
выбрать опцию «В одном каталоге с программой», либо при помощи стандартного для
Windows диалогового окна открытия файлов выбрать нужный файл, либо вручную
ввести путь к SQL-серверу, на котором хранится искомая база данных. При выборе
последнего варианта необходимо установить параметры подключения к SQL-серверу.
Нажав на соответствующую кнопку, можно проверить установленное таким образом
подключение, после чего программа выведет сообщение о его успешности.
Все данные, которыми оперирует программа, хранятся в защищенных паролями
файлах формата Access 2000. Этими файлами снабжён каждый отдельный экземпляр
программы. Кроме того, программа снабжена файлом формата *.mdf , представляющим
собой базу данных SQL-сервера. Данный файл содержит таблицы вопросов и
результатов тестирования. Это позволяет использовать программу как клиентское
приложение, посредством сети взаимодействующее с базой данных, расположенной на
сервере. Данный вариант наиболее предпочтителен с точки зрения рационального
использования системных ресурсов и централизации хранения данных.
Доступ к данным осуществляется по технологии ADO, обеспечивающей
совместимость со всеми распространёнными версиями ОС Windows и не требующей
установки дополнительного программного обеспечения.
Обучающе - контролирующая программа была разработана с
целью создания благоприятных условий для самообразования студентов II курса
физико-математических факультетов педагогических вузов. Его использование будет
способствовать эффективному и всестороннему изучению раздела математического
анализа «Тройные интегралы».
Апробация разработанной обучающе - контролирующей программы
На факультете математики и информатики Славянского - на - Кубани
государственного педагогического института была проведена апробация
разработанной обучающе - контролирующей программы на втором курсе в группах
2002 - м - 1 и 2002 - м - 2 в апреле 2003 - 2004 учебного года. Представим
таблицу с полученными результатами.
|
Группа
|
«5»
|
«4»
|
«3»
|
«2»
|
Качественный показатель
|
Абсолютный показатель
|
|
М - 1
|
22%
|
36%
|
41,3%
|
0,7%
|
57%
|
92%
|
|
М - 2
|
30%
|
37%
|
22,6%
|
0,4%
|
67%
|
96%
|
Заключение
В данной выпускной квалификационной работе рассмотрены теоретические и
методические аспекты изучения раздела математического анализа «Интегральное
исчисление функции нескольких переменных». В первой главе данной работы
рассмотрены теоретические основы изучения раздела.
Во второй главе изложены методические рекомендации изучения данной темы,
приведены психолого-педагогические аспекты образования в высшей школе,
методические рекомендации по проведению лекционных и практических занятий с
применением новых информационных технологий с целью повышения эффективности
учебной деятельности.
Для проверки знаний и навыков интегрального исчисления студентов, была
создана обучающе - контролирующая программа, содержащая теоретический материал,
который может понадобиться студентам при изучении данной темы, а также тест,
позволяющий проверить у студента навыки интегрирования. Обучающе -
контролирующая программа выполнено таким образом, что возможно дальнейшее
расширение его объема за счет новых вопросов и дополнения исходного материала.
Программа дает студентам восполнить пропущенные лекции, не проводить
продолжительное время в библиотеке за отбором материала. Тест состоит из 5
вопросов, время на каждый вопрос 10 - 12 мин, в зависимости от сложности.
Таким образом, в ходе выполнения этой работы были решены поставленные
задачи, а именно, обосновано и разработано содержание и методика преподавания
темы «Тройные интегралы» в педагогическом вузе с учетом возрастных особенностей
студентов, создана обучающе - контролирующая программа по данной теме для
студентов второго курса физико-математических факультетов педагогических вузов.
Тем самым была реализована цель исследования, заключающаяся в формировании
методического аппарата по изучению рассматриваемой теме.
Разработанная методика проведения лекционных и практических занятий была
апробирована на втором курсе факультета математики и информатики СГПИ 2002-2003
и 2003-2004 учебных годах.
Доклады по теме выпускной квалификационной работы заслушивались на
научно-практических конференциях СГПИ в 2002, 2003 и 2004 годах. Статья по
методике изучения темы «Тройные интегралы» в педагогическом вузе была
опубликована в «Сборнике научных трудов студентов и преподавателей СГПИ» в 2003
году.
Материалы данной работы могут быть полезны студентам математических
факультетов педагогических вузов, а также преподавателям математического
анализа.
1. Учебные материалы для изучения темы
«Тройные интегралы»;
2. Обучающее - контролирующая программа
по данной теме;
3. Методические рекомендации для
преподавателей и студентов педагогических вузов по организации обучения
соответствующего раздела математического анализа с применением новых
информационных технологий с целью повышения эффективности учебной деятельности;
4. Набран электронный конспект лекций
(32 шрифт).
Обучающее - контролирующая программа содержит теоретический материал,
который может понадобиться студентам при изучении данной темы, а также тест,
позволяющий проверить у студента навыки интегрирования. Обучающее -
контролирующая программа выполнена таким образом, что возможно дальнейшее
расширение ее объема за счет новых вопросов и дополнения исходного материала.
Программа дает студентам восполнить пропущенные лекции, не проводить
продолжительное время в библиотеке за отбором материала. Тест состоит из 5
вопросов, время 10 - 12 мин.
Электронный конспект лекций (32 шрифт) обеспечивает:) для студентов:
самостоятельные проработки лекций в случае пропуска занятия;
подготовки к экзаменам, коллоквиумам, контрольным и самостоятельным
работам;
для написания курсовых и выпускных работ;
самостоятельные проработки отдельных вопросов, которые лектором вынесены
на самостоятельное изучение.
в) для преподавателей:
подготовку к лекционным занятиям;
проведение лекционных занятий в компьютерном классе;
организацию самостоятельной работы студентов при подготовке к экзаменам,
коллоквиумам, контрольным и самостоятельным работам [3].
Набранные в электронном виде фондовые лекции по теме «Тройные интегралы»,
содержат необходимый и достаточный для изучения теоретический материал по
данной теме, а именно:
·
Определение
тройного интеграла;
·
Свойства тройного
интеграла;
·
Вычисление
тройного интеграла;
·
Криволинейная
система координат (КСК);
·
Цилиндрическая
система координат (ЦСК);
·
Сферическая
система координат (ССК);
·
Замена переменных
в тройных интегралах;
·
Объем в ЦСК и ССК
[1].
Литература
1. Фихтенгольц
Г. М. Курс дифференциального и интегрального исчисления. Т.1. - СПб: Лань,
1997. - 430с.
. Фихтенгольц
Г. М. Основы математического анализа. Т.2. - СПб: Лань, 1999. - 395с.
. Бохан
Н.А. и др. Курс математического анализа. В 2-х томах-М.: Просвещение, 1965. -
562с.
. Кудрявцев
Л. Д. Курс математического анализа Т.2. - М.: Высшая школа, 1998.- 342с.
. Кудрявцев
В.А., Демидович Б.П. Краткий курс высшей математики.-М.: Наука,1989. 97 - 104с.
. Бугров
Я.С., Никольский С.М. Высшая математика. Дифференциальное и интегральное
исчисление.:учебник для вузов.-4-е изд.., переработка и дополнение. - Ростов
н/Д: издательство «Феникс», 1997. - 512с.
. Бугров
А. С., Никольский С. М. Дифференциальное и интегральное исчисление. - Ростов
н/Д: Феникс, 1997.- 438с.
. Натансон
И. П. Краткий курс высшей математики. - Ч.2. СПб.: Лань, 1997.- 328с.
. Никольский
С. М. Курс математического анализа. Т.1. - М.: Наука, 1973.- 352с.
. Власов
В.Г. Конспект лекций по высшей математике.-М.: Айрис, 1996.-533с.
. Гусак
А. А. Высшая математика. Т.1. - Минск: БГУ, 1976.- 326с.
. Зорич
В. А. Математический анализ. Т.2. - М.: Наука, 1981.- 364с.
. Зорич
В.А. Математический анализ, часть 2,-М.: Наука, Главная редакция
физико-математической литературы,1981.-544 с.
. Коровкин
П. П. Математический анализ. Ч.2. - М.: Просвещение, 1974.- 452с.
. Толстов
Р.П. Элементы математического анализа, т.I-М. 1974.-520с.
. Шипачёв
В. С. Высшая математика. - Высшая школа, 1996.- 364с.
. Шипачёв
В.С. Основы высшей математики / под ред А.Н. Тихонова.- М.: Высш. шк.,
1998.-406с.
. Бермант
Г. Н. Сборник задач по курсу математического анализа. - М.: Наука, 1969.- 378с.
. Давыдов
Н. А., Коровкин П. П., Никольский В. Н. Сборник задач по математическому
анализу. - М.: Просвещение, 1973.- 376с.
. Данко
П. Е. и др. Высшая математика в упражнениях и задачах. Т.1. - М.: высшая школа,
1980.-328с.
. Задачник
по курсу математического анализа. Ч.2. / Под ред. Н. Я. Виленкина. - М.:
Просвещение, 1971.-432с.
. Зиновьева
Л. А. Сборник задач по математическому анализу для студентов второго курса
факультета математики-информатики. Ч.4. - Славянск-на-Кубани: СФАГПИ, 1998.-
48с.
. Зиновьева
Л. А. , Чернышев А.Н. Математический анализ: методические рекомендации к
практическим занятиям и самостоятельной работе для студентов педагогических
вузов (2 курс, 4 семестр).- Славянск - на - Кубани, 2000 - 12с.
. Зиновьева
Л. А. , Чернышев А.Н. Учебная программа курса “ Математичес- кий анализ”
факультета математики-информатики. Ч.3 - Славянск-на-Кубани: СФАГПИ, 1998.-
143с.
. Полат
Е.С. Новые педагогические и информационные технологии в системе образования:
учебное пособие для студентов педагогических вузов и системы повышения
квалификации педагогических кадров.-М.: Академия, 2001.- 272с.
. Райков
Д. А. Одномерный математический анализ. - М.: Высшая школа, 1989.- 432с.
. Сборник
задач и упражнений по математическому анализу / Под ред. Б. П. Демидовича. -
М.: Наука, 1990.- 376с.
. Смирнов
С.Д. Педагогика и психология высшего образования: от деятельности к личности:
учебное пособие для слушателей факультетов и институтов повышения квалификации
преподавателей вузов и аспирантов - М.: АспектПресс,1995.- 271с.
. Зимняя
И.А. Педагогическая психология. - М.: Логос, 2001. - 362с.
. Басова
Н.В. Педагогика и практическая психология. - Ростов н/Д: Издательство “Феникс”,1999.-
346с.
. Самыгин
С.И. Педагогика и психология высшей школы: учебное пособие. - Ростов н/Д:
Издательство “Феникс”,1998.- 517с.
. Шадриков
В.Д. Подготовка учителя математики: инновационные подходы. - М.: Академия,
2002.- 383с.
. Кукушина
В.С. Педагогические технологии: учебное пособие для студентов педагогических
специальностей. - Ростов н/Д: Издательство “МарТ”, 2002.- 320с.