Дифференциальные операции теории поля
Дифференциальные операции теории поля
Введение
Для описания физических величин
удобно использовать понятие поля. Простейшими физическими величинами являются
скаляр и вектор. Их обобщением является тензор. Полное определение тензора мы
дадим в курсе тензорного анализа, а сейчас под тензором будем понимать
физическую величину, которая может быть задана в виде числа (скаляра), вектора,
матрицы или более сложного образования.
Определение 1. В
пространстве (среде) задано поле тензора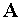 
, если этот тензор
определен в каждой точке пространства
.
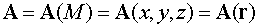В качестве 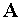можно
выбрать скаляр, вектор или тензор более высокого ранга. Рассмотрим основные
свойства поля и его характеристики.
1. Скалярное поле
Определение 1. Поле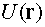 
называется
скалярным, если в каждой точке пространства определено значение скалярной
величины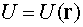 
.
Поле может зависеть
также и от времени
.
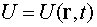Здесь t играет роль параметра. Примеры скалярных полей: температура в
каждой точке сплошной среды, плотность вещества или электрического заряда (как
функция координат точек среды), электрический потенциал,…
Определение 2.
Поверхностью уровня скалярного поля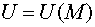 
называется совокупность
точек удовлетворяющих уравнению
,
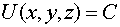где С - некоторая
постоянная.
На плоскости уравнение
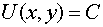
определяет линии уровня.
Выберем в пространстве
некоторое направление l,
которое задается единичным вектором (ортом)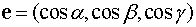 
. Рассмотрим две точки М
и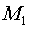 
,
лежащие на этой линии
Определение 3.
Производной от функции 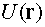по
направлению l называется предел
.
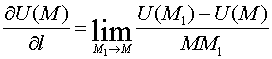Эта величина
характеризует быстроту изменения функции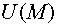 
в направлении 
.
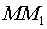Имеем
,
,
, 
,
.
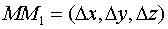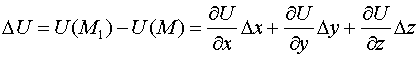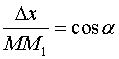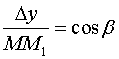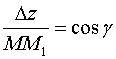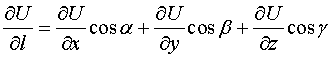
Если направление
задается вектором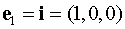 
,
то
.
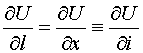Аналогично, для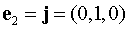 
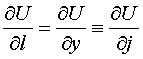
и для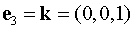 
.
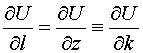Определение 4.
Градиентом скалярной функции 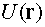называется вектор
.
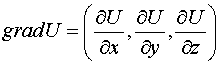В математике часто
используется символ (читается «набла»)
,
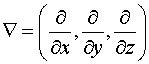который называют
оператором дифференцирования или оператором Гамильтона. С помощью этого
оператора градиент функции может быть записан в виде
.
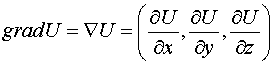Теорема 1. Производная
скалярного поля 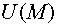в
точке М в направлении орта 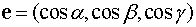равна проекции
градиента поля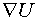 
на
направление орта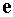 
.
Доказательство.
Производную по направлению, определяемому ортом 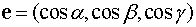, можно записать в виде
скалярного произведения
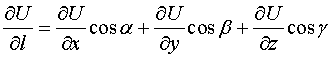
С другой стороны
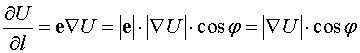
где φ
- угол между векторами е и .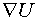
Максимальное значение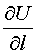 
достигается
при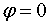 
,
когда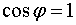 
.
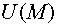Следовательно, градиент функции указывает направление
максимального возрастания этой функции.
2. Векторное поле
Определение 1. Поле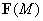 
называется
векторным, если в каждой точке пространства определено значение векторной
величины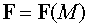 
.
Примеры векторных полей:
напряженность электрического поля, поле скоростей в движущейся среде,
напряженность магнитного поля,…
Определение 2.
Векторными линиями поля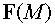 
называются
кривые, касательные в каждой точке которых совпадают с направлениями вектора 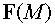в
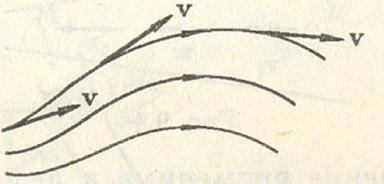
этой точке. На рисунке показано поле скоростей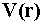 
движущейся жидкости.
В электростатике
векторные линии называют силовыми линиями или линиями напряженности
электрического поля.
Теорема 1. Если задано
векторное поле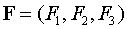 
,
то векторные линии этого поля описываются системой дифференциальных уравнений
.
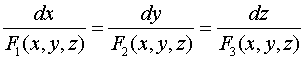Доказательство. На
рисунке в точке М показаны элемент длины векторной линии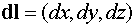 
и
вектор поля .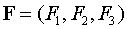
Запишем условие
параллельности двух векторов:
.
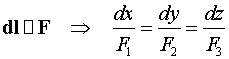Если векторное поле
определяет скорость движения среды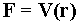 
, то векторные линии
называются линиями тока.
Пример 1. Найти
векторную линию векторного поля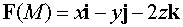 
, проходящую через точку
.
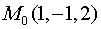Решение. Имеем систему
дифференциальных уравнений
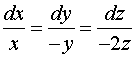
с начальными условиями
.
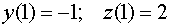Проинтегрируем систему:
,
.
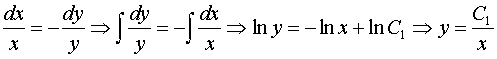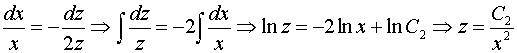Используем начальные
условия:
; 
.
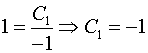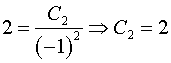Ответ: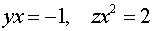 
.
Пример 2. Найти линии
тока плоского потока жидкости, характеризуемого вектором скорости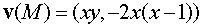 
.
Ответ: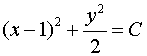 
.
3. Дивергенция и ротор
векторного поля
Рассмотрим векторное
поле ,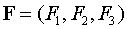
заданное в трехмерном пространстве.
Определение 1.
Дивергенцией векторного поля 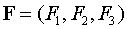называется число,
которое определяется выражением
.
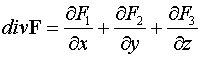При этом предполагается,
что соответствующие частные производные существуют в рассматриваемой точке.
Дивергенцию векторного поля, так же, как и градиент, можно записать, используя
оператор набла
.
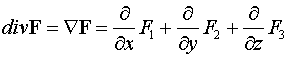Здесь дивергенция
представлена как скалярное произведение векторов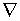 
и F. Отметим без доказательства, что дивергенция описывает плотность
источников, создающих поле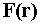 
.
Пример 1. Вычислить
дивергенцию векторного поля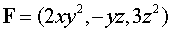 
в точке 
.
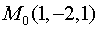Ответ:
.
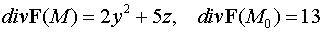Определение 2. Ротором
векторного поля 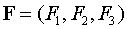называется
вектор, который определяется выражением
.
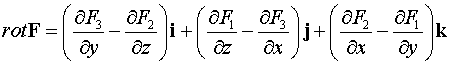Отметим, что в
представленной сумме индексы в соседних слагаемых изменяются согласно правилу
круговой перестановки с учетом правила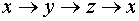 
.
Ротор векторного поля можно
записать с помощью оператора набла
.
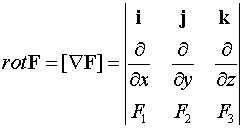Ротор характеризует
тенденцию к вращению или завихрению векторного поля ,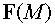
поэтому иногда его называют вихрем и обозначают curlF.
Пример 1. Вычислить
ротор векторного поля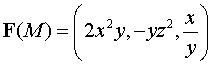 
в
точке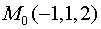 
.
Ответ: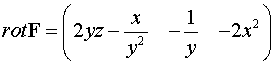 
,
.
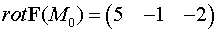Иногда возникает
необходимость вычисления градиента векторного поля .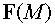
В этом случае вычисляется градиент от каждой компоненты векторного поля. В
результате получается тензор второго ранга, которым и определяется градиент
вектора. Этот тензор можно описать матрицей
.
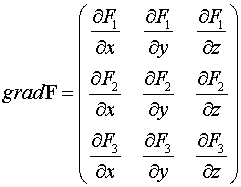Для описания таких
объектов удобно использовать тензорные обозначения
,
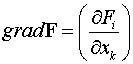полагая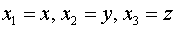 
.
Использование тензорных методов упрощает математические операции над такими
объектами. Детальное изложение аппарата тензорного исчисления дается в курсе
«Основы тензорного анализа», который читается параллельно курсу «Дополнительные
главы высшей математики».
Пример 1. Вычислить
градиент векторного поля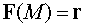 
.
Решение. Для вычислений
используем тензорные обозначения. Имеем
.
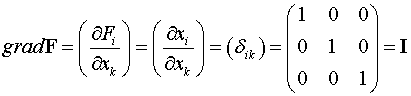Здесь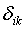 
символ
Кронекера,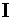 
-
единичная матрица.
Ответ: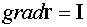 
.
Пример 2. Вычислить
градиент скалярного поля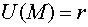 
и
сравнить выражения 
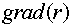и
.
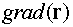4. Некоторые свойства
оператора набла
Ранее мы ввели оператор
векторного дифференцирования
.
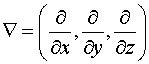С помощью этого
оператора мы записали основные дифференциальные операции в тензорных полях:
,
,
.
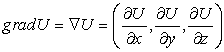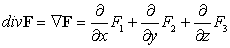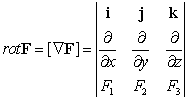Оператор 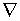является
обобщением оператора дифференцирования и обладает соответствующими свойствами
производной:
) производная суммы
равна сумме производных
;
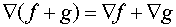) постоянный множитель
можно выносить за знак оператора
.
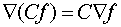В переводе на язык
векторных функций эти свойства имеют вид:
,
,
,
,
,
.
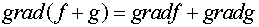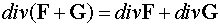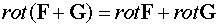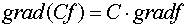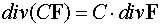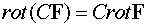Выводятся эти формулы
так же, как и соответствующие формулы для производных функции одной переменной.
Использование оператора
Гамильтона позволяет упростить многие операции, связанные с дифференцированием
в тензорных полях. Однако следует иметь в виду, что этот оператор векторный и с
ним надо обращаться аккуратно. Рассмотрим некоторые применения этого оператора.
При этом соответствующие формулы записываются как с помощью оператора
Гамильтона, так и в обычных обозначениях.
1) 
,
;
) 
,
;
) 
,
) 
,
;
) 
,
.
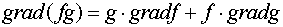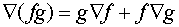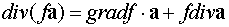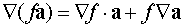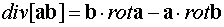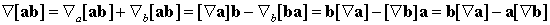
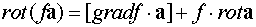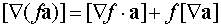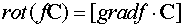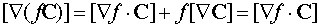Доказательство этих
равенств можно произвести как непосредственным вычислением соответствующих
функций, так и с помощью оператора «набла». Рекомендуется самостоятельно
проверить справедливость записанных равенств двумя методами.
В качестве примера,
показывающего необходимость аккуратного обращения с оператором Гамильтона,
вычислим градиент скалярного произведения двух векторных функций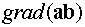 
.
Формально, используя свойства оператора дифференцирования, можно записать
.
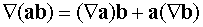Если считать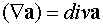 
,
,
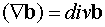то получим неправильный результат
.
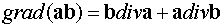Ошибка здесь заключается
в том, что выражение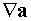 
следует
понимать как 
,
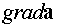т.е. как градиент векторной функции (специального обозначения для этого объекта
нет). Правильным будет выражение
,
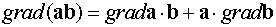где точка означает
свертку тензора с вектором (свертка является обобщением понятия скалярного
произведения). Более удобной здесь является тензорная форма записи
.
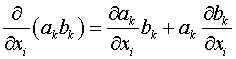Здесь по повторяющимся
индексам производится суммирование от 1 до 3.
скалярный поле дифференцирование
кронекер
1. Тихонов А.Н., Самарский А.А. Уравнения математической физики,
М.: МГУ, 1999, 798 с.
. Кальницкий Л.А., Добротин Д.А., Жевержев В.Ф. Специальный курс
высшей математики для втузов, М.: «Высшая школа», 1976, 390 с.
. Берман Г.Н. Сборник задач по курсу математического анализа, М.:
Наука, 1985, 384 с.
. Все решения к «Сборнику задач по общему курсу физики» В.С.
Волькенштейн, М.: Аст, 1999, книга 1, 430 с., книга 2, 588 с.
. Красильников О.М. Физика. Методическое руководство по обработке
результатов наблюдений. М.: МИСиС, 2002, 29 с.
. Супрун И.Т., Абрамова С.С. Физика. Методические указания по
выполнению лабораторных работ, Электросталь: ЭПИ МИСиС, 2004, 54 с.