Дифференциальные операции в криволинейной системе координат

Дифференциальные операции в криволинейной системе координат

Дифференциальные операции в криволинейной системе координат

1. Градиент

В декартовой системе координат градиент функции 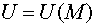 определяется формулой

.

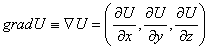При переходе к криволинейной системе координат формула для градиента должна измениться. Найдем выражение для градиента в криволинейной системе координат. Можно записать

.

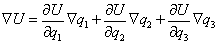Мы получили

.

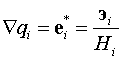Следовательно,

.

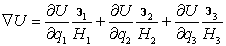Сформулируем полученный результат в виде теоремы.

Теорема 1. В ортогональной криволинейной системе координат градиент скалярного поля 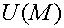 определяется формулой

.

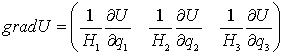Пример 1. Найти выражение для градиента в цилиндрической системе координат.

Решение. Коэффициенты Ламе в цилиндрической системе координат выражаются формулами

.

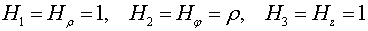Следовательно,

.

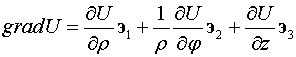Ответ: .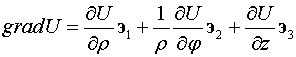

Замечание 1. В полярной системе координат градиент определяется формулой

.

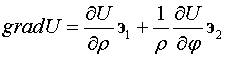Пример 2. Найти выражение для градиента в сферической системе координат.

Решение. Запишем коэффициенты Ламе в сферической системе координат

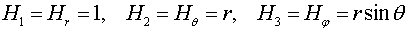
Следовательно,

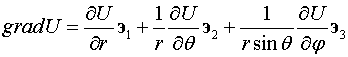
Ответ: .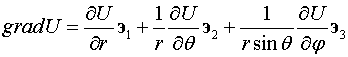

2. Дивергенция

Дивергенция векторного поля 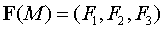 определяется выражением

.

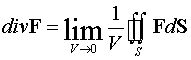В декартовой системе координат для дивергенции получено выражение

.

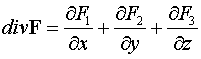В криволинейной системе координат выражение для дивергенции имеет более сложный вид.

Теорема 1. В ортогональной криволинейной системе координат дивергенция векторного поля 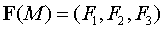 определяется выражением

.

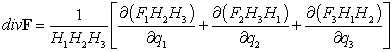Доказательство теоремы производится так же, как и для градиента. Учитывая выражения для интегрального представления дивергенции, можно получить записанную выше формулу.

Пример 1. Найти выражение для дивергенции в цилиндрической системе координат.

Решение. Запишем выражения для коэффициентов Ламе в цилиндрической системе координат:

.

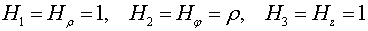Подставляя эти значения в общую формулу для дивергенции, получим

.

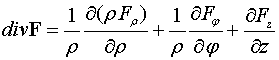Выполняя дифференцирование, эту формулу можно записать в виде

.

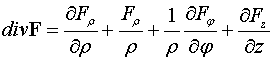Из этой формулы видно, что даже для постоянного в цилиндрической системе координат поля дивергенция может быть отличной от нуля.

Замечание 1. В полярной системе координат дивергенция векторного поля определяется формулой

.

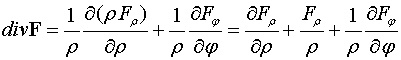Пример 2. Найти выражение для дивергенции в сферической системе координат.

Решение. Учитывая значения коэффициентов Ламе

,

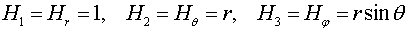получим

.

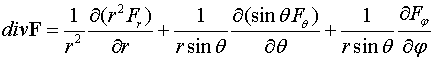. Ротор

Ротор описывает вихревые свойства среды и определяется выражением

.

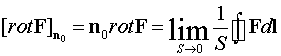В декартовой системе координат для ротора получена формула

.

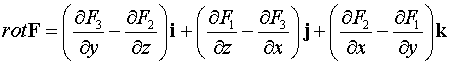Найдем выражение для ротора в криволинейной ортогональной системе координат. Для этого рассмотрим замкнутый контур ABCD.

Его площадь

.

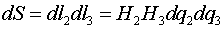Интеграл по замкнутому контуру

.

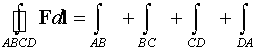Вычислим эти интегралы

,

.

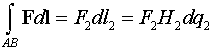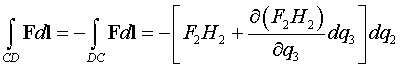Найдем сумму интегралов

.

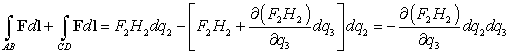Аналогично получим

.

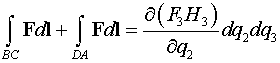Циркуляция определяется выражением

Используя определение ротора

,

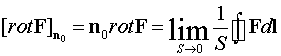получим выражения для компонент, направленных вдоль соответствующих осей

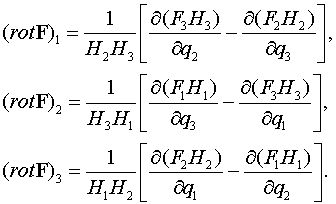
Пример 1. Найти выражение для компонент ротора в цилиндрической системе координат.

Решение. Подставляя в полученные формулы значения коэффициентов Ламе, получим

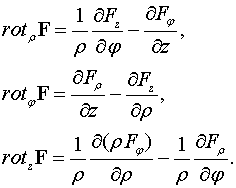
Пример 2. Найти выражение для компонент ротора в сферической системе координат.

Ответ:

.

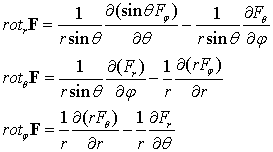4. Оператор Лапласа

Оператор Лапласа определяется выражением

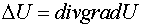
и в декартовой системе координат описывается формулой

.

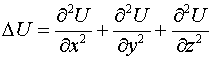Найдем выражение для оператора Лапласа в криволинейной ортогональной системе координат. Для этого запишем градиент и дивергенцию в криволинейной системе координат

,

.

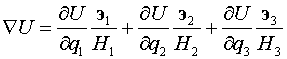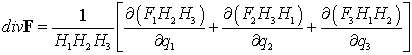Подставляя эти выражения в оператор Лапласа, получим

.

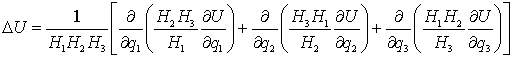Пример 1. Найти выражение для оператора Лапласа в цилиндрической системе координат.

Решение. Подставляя значения коэффициентов Ламе, получим

.

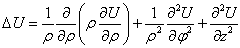Замечание 1. Оператор Лапласа в полярной системе координат определяется формулой

.

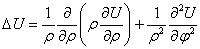Пример 2. Найти выражение для оператора Лапласа в сферической системе координат.

Решение. Подставляя значения коэффициентов Ламе, получим

Ответ:

.

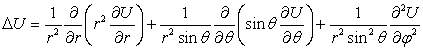5. Уравнение Лапласа

Уравнением Лапласа называют уравнение вида .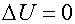

Это уравнение называют уравнением эллиптического типа. Оно часто встречается в задачах, связанных с определением потенциала различных стационарных полей. В частности, задача определения поля температур, электрического потенциала, упругих напряжений и деформаций связана с решением уравнения Лапласа. Отметим, что в математической физике изучают также уравнения гиперболического и параболического типа.

Существует много различных методов решения уравнений эллиптического типа. Среди них можно выделить метод разделения переменных, метод функции источника, теорию потенциала, метод аналитических функций и много других. Рассмотрим несколько простейших задач, не связанных с использованием специальных методов.

Цилиндрическая симметрия. Найдем решение уравнения Лапласа для функции, обладающей цилиндрической симметрией, т.е. не зависящей от полярного угла 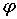 и переменной z. В этом случае уравнение Лапласа, записанное в цилиндрической системе координат, имеет вид

.

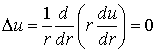Частные производные здесь заменены полными. Из этого уравнения следует

,

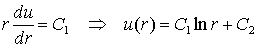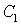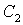где  и - произвольные постоянные, которые можно найти из граничных условий.

Сферическая симметрия. Найдем решение уравнения Лапласа для функции, обладающей сферической симметрией, т.е. не зависящей от углов 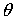 и 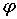. В этом случае уравнение Лапласа, записанное в сферической системе координат, имеет вид

.

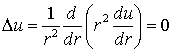Нетрудно найти решение этого уравнения

.

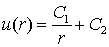Решение уравнения Пуассона рассмотрим на конкретных примерах.

Пример 1. Найти решение уравнения Пуассона 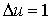 внутри круга радиуса 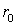, если

Решение. Искомая функция обладает цилиндрической симметрией, поэтому запишем уравнение Пуассона в цилиндрической системе координат в виде

.

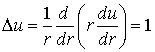Решим это уравнение

.

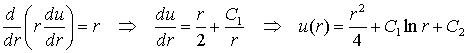градиент криволинейный ламе дифференциальный

Постоянные 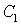 и 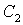 найдем из граничного условия и условия ограниченности функции. Учитывая, что 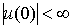, получим . Из условия 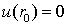 получим

.

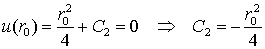Следовательно, имеем окончательный ответ

.

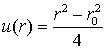Список источников

1. Тихонов А.Н., Самарский А.А. Уравнения математической физики, М.: МГУ, 1999, 798 с.

. Кальницкий Л.А., Добротин Д.А., Жевержев В.Ф. Специальный курс высшей математики для втузов, М.: «Высшая школа», 1976, 390 с.

. Берман Г.Н. Сборник задач по курсу математического анализа, М.: Наука, 1985, 384 с.

. Все решения к «Сборнику задач по общему курсу физики» В.С. Волькенштейн, М.: Аст, 1999, книга 1, 430 с., книга 2, 588 с.

. Красильников О.М. Физика. Методическое руководство по обработке результатов наблюдений. М.: МИСиС, 2002, 29 с.

. Супрун И.Т., Абрамова С.С. Физика. Методические указания по выполнению лабораторных работ, Электросталь: ЭПИ МИСиС, 2004, 54 с.