|
Номер
предприятия
|
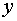 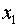 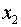 Номер предприятия Номер предприятия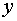 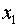 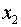
|
|
|
|
|
|
|
|
1
|
6
|
3,5
|
10
|
11
|
10
|
6,3
|
21
|
|
2
|
6
|
3,6
|
12
|
12
|
11
|
6,4
|
22
|
|
3
|
7
|
3,9
|
15
|
13
|
11
|
7
|
23
|
|
4
|
7
|
4,1
|
17
|
14
|
12
|
7,5
|
25
|
|
5
|
7
|
4,2
|
18
|
15
|
12
|
7,9
|
28
|
|
6
|
8
|
4,5
|
19
|
16
|
13
|
8,2
|
30
|
|
7
|
8
|
5,3
|
19
|
17
|
13
|
8,4
|
31
|
|
8
|
9
|
5,3
|
20
|
18
|
14
|
8,6
|
31
|
|
9
|
9
|
5,6
|
20
|
19
|
14
|
9,5
|
35
|
|
10
|
10
|
6
|
21
|
20
|
15
|
10
|
36
|
Требуется:
1. Построить линейную модель множественной
регрессии. Записать стандартизованное уравнение множественной регрессии. На
основе стандартизованных коэффициентов регрессии и средних коэффициентов
эластичности ранжировать факторы по степени их влияния на результат.
2. Найти коэффициенты парной, частной и
множественной корреляции. Проанализировать их.
3. Найти скорректированный коэффициент множественной
детерминации. Сравнить его с нескорректированным (общим) коэффициентом
детерминации.
4. С
помощью 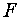 -критерия Фишера оценить статистическую
надежность уравнения регрессии и коэффициента детерминации
-критерия Фишера оценить статистическую
надежность уравнения регрессии и коэффициента детерминации 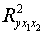 .
.
5. С
помощью частных 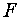 -критериев Фишера оценить целесообразность
включения в уравнение множественной регрессии фактора
-критериев Фишера оценить целесообразность
включения в уравнение множественной регрессии фактора 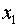 после
после 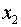 и фактора
и фактора 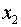 после
после 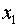 .
.
6. Составить
уравнение линейной парной регрессии, оставив лишь один значащий фактор.
Решение
Для удобства проведения расчетов поместим результаты
промежуточных расчетов в таблицу:
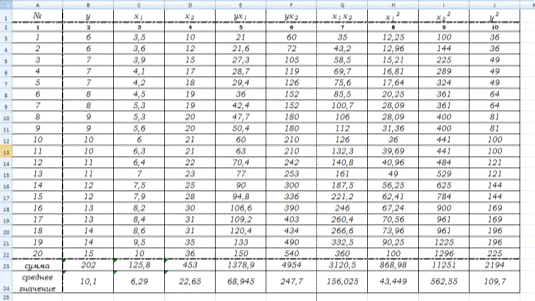
Найдем средние квадратические отклонения признаков:
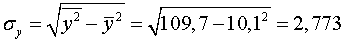 ;
;
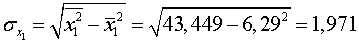 ;
;
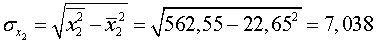 .
.
1. Вычисление параметров линейного уравнения
множественной регрессии.
Для нахождения параметров линейного уравнения множественной
регрессии
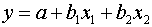
необходимо решить следующую систему линейных уравнений
относительно неизвестных параметров 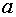 ,
, 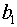 ,
, 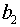 :
:
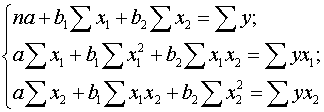
либо воспользоваться готовыми формулами:
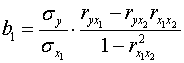 ;
; 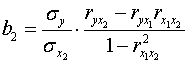 ;
;
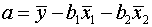 .
.
Рассчитаем сначала парные коэффициенты корреляции:
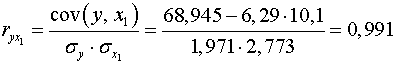 ;
;
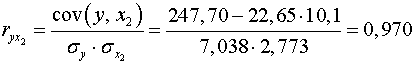 ;
;
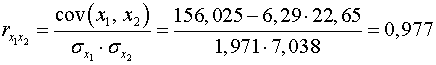 .
.
Находим
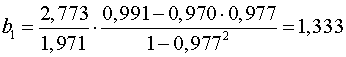 ;
;
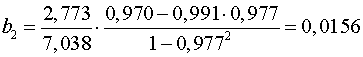 ;
;
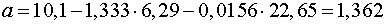 .
.
Таким образом, получили следующее уравнение множественной
регрессии:
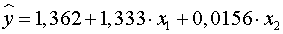 .
.
Коэффициенты 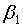 и
и 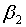 стандартизованного уравнения регрессии
стандартизованного уравнения регрессии 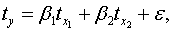 находятся по формулам:
находятся по формулам:
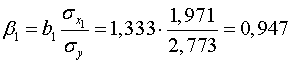 ;
;
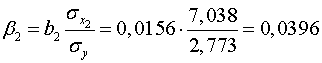 .
.
Т.е. уравнение будет выглядеть следующим образом:
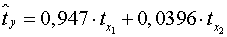 .
.
Так как стандартизованные коэффициенты регрессии можно сравнивать
между собой, то можно сказать, что ввод в действие новых основных фондов
оказывает большее влияние на выработку продукции, чем удельный вес рабочих высокой
квалификации.
Сравнивать влияние факторов на результат можно также при помощи
средних коэффициентов эластичности:
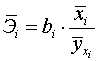 .
.
Вычисляем:
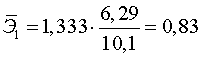 ;
; 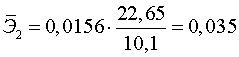 .
.
Т.е. увеличение только основных фондов (от своего среднего
значения) или только удельного веса рабочих высокой квалификации на 1 %
увеличивает в среднем выработку продукции на 0,83 % или 0,035 % соответственно.
Таким образом, подтверждается большее влияние на результат 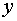 фактора
фактора 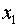 , чем фактора
, чем фактора 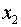 .
.
2. Коэффициенты парной корреляции мы уже нашли:
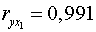 ;
; 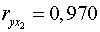 ;
; 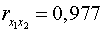 .
.
Они указывают на весьма сильную связь каждого фактора с
результатом, а также высокую межфакторную зависимость (факторы 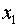 и
и 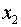 явно коллинеарны, т. к.
явно коллинеарны, т. к. 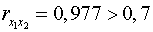 ). При такой сильной межфакторной зависимости рекомендуется один
из факторов исключить из рассмотрения.
). При такой сильной межфакторной зависимости рекомендуется один
из факторов исключить из рассмотрения.
Частные коэффициенты корреляции характеризуют тесноту связи
между результатом и соответствующим фактором при элиминировании (устранении
влияния) других факторов, включенных в уравнение регрессии.
При двух факторах частные коэффициенты корреляции
рассчитываются следующим образом:
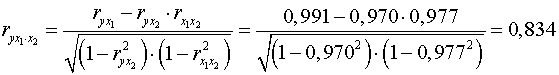 ;
;
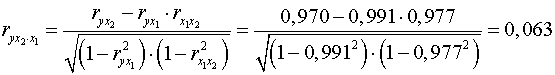 .
.
Если сравнить коэффициенты парной и частной корреляции, то
можно увидеть, что из-за высокой межфакторной зависимости коэффициенты парной
корреляции дают завышенные оценки тесноты связи. Именно по этой причине
рекомендуется при наличии сильной коллинеарности (взаимосвязи) факторов
исключать из исследования тот фактор, у которого теснота парной зависимости
меньше, чем теснота межфакторной связи.
Коэффициент множественной корреляции определить через матрицу
парных коэффициентов корреляции:
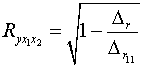 ,
,
где
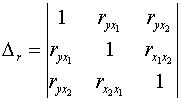
- определитель матрицы парных коэффициентов корреляции;
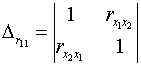
определитель матрицы межфакторной корреляции.
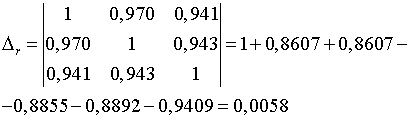 ;
;
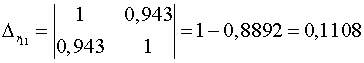 .
.
Коэффициент множественной корреляции
 .
.
Аналогичный результат получим при использовании других
формул:
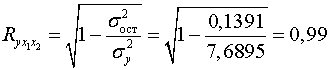 ;
;
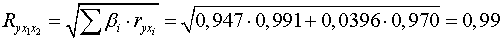 ;
;
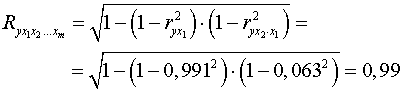 .
.
Коэффициент множественной корреляции показывает на весьма сильную
связь всего набора факторов с результатом.
3. Нескорректированный
коэффициент множественной детерминации 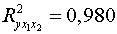 оценивает долю вариации результата за счет представленных в
уравнении факторов в общей вариации результата. Здесь эта доля составляет
оценивает долю вариации результата за счет представленных в
уравнении факторов в общей вариации результата. Здесь эта доля составляет 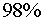 и указывает на весьма высокую степень
обусловленности вариации результата вариацией факторов, иными словами - на
весьма тесную связь факторов с результатом.
и указывает на весьма высокую степень
обусловленности вариации результата вариацией факторов, иными словами - на
весьма тесную связь факторов с результатом.
Скорректированный коэффициент множественной детерминации
определяет тесноту связи с учетом степеней свободы общей и остаточной
дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа
факторов и поэтому может сравниваться по разным моделям с разным числом
факторов. Оба коэффициента указывают на весьма высокую (более 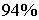 ) детерминированность результата
) детерминированность результата 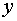 в модели факторами
в модели факторами 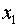 и
и 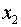 .
.
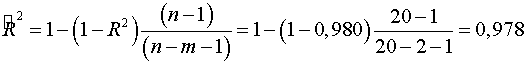
4. Оценку
надежности уравнения регрессии в целом и показателя тесноты связи 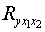 дает
дает 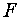 -критерий Фишера:
-критерий Фишера:
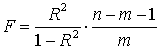 .
.
В нашем случае фактическое значение 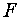 -критерия Фишера:
-критерия Фишера:
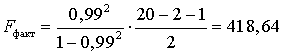 .
.
Получили, что 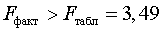 (при
(при 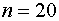 ), т. е. вероятность случайно получить
такое значение
), т. е. вероятность случайно получить
такое значение 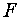 -критерия не превышает допустимый уровень
значимости
-критерия не превышает допустимый уровень
значимости 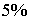 . Следовательно, полученное значение не
случайно, оно сформировалось под влиянием существенных факторов, т. е.
подтверждается статистическая значимость всего уравнения и показателя тесноты
связи
. Следовательно, полученное значение не
случайно, оно сформировалось под влиянием существенных факторов, т. е.
подтверждается статистическая значимость всего уравнения и показателя тесноты
связи 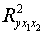 .
.
5. С
помощью частных 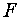 -критериев Фишера оценим целесообразность
включения в уравнение множественной регрессии фактора
-критериев Фишера оценим целесообразность
включения в уравнение множественной регрессии фактора 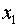 после
после 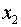 и фактора
и фактора 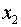 после
после 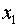 при помощи формул:
при помощи формул:
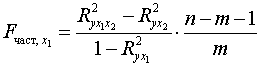 ;
;
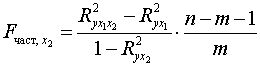 .
.
Найдем 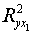 и
и 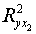 .
.
 ;
;
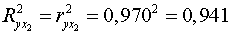 .
.
Имеем
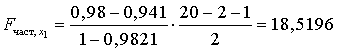 ;
;
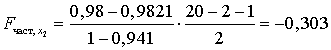 .
.
Получили, что 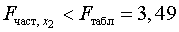 . Следовательно, включение в модель фактора
. Следовательно, включение в модель фактора 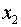 после того, как в модель включен фактор
после того, как в модель включен фактор 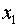 статистически нецелесообразно: прирост
факторной дисперсии за счет дополнительного признака
статистически нецелесообразно: прирост
факторной дисперсии за счет дополнительного признака 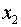 оказывается незначительным,
несущественным; фактор
оказывается незначительным,
несущественным; фактор 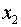 включать в уравнение после фактора
включать в уравнение после фактора 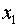 не следует.
не следует.
Если поменять первоначальный порядок включения факторов в модель и
рассмотреть вариант включения 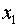 после
после 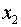 , то результат расчета частного
, то результат расчета частного 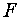 -критерия для
-критерия для 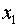 будет иным.
будет иным. 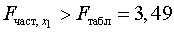 , т. е. вероятность его случайного
формирования меньше принятого стандарта
, т. е. вероятность его случайного
формирования меньше принятого стандарта 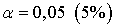 . Следовательно, значение частного
. Следовательно, значение частного 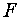 -критерия для дополнительно включенного фактора
-критерия для дополнительно включенного фактора 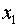 не случайно, является статистически
значимым, надежным, достоверным: прирост факторной дисперсии за счет
дополнительного фактора
не случайно, является статистически
значимым, надежным, достоверным: прирост факторной дисперсии за счет
дополнительного фактора 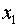 является существенным. Фактор
является существенным. Фактор 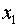 должен присутствовать в уравнении, в том
числе в варианте, когда он дополнительно включается после фактора
должен присутствовать в уравнении, в том
числе в варианте, когда он дополнительно включается после фактора 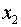 .
.
6. Общий
вывод состоит в том, что множественная модель с факторами 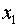 и
и 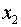 с
с 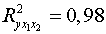 содержит неинформативный фактор
содержит неинформативный фактор 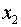 . Если исключить фактор
. Если исключить фактор 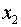 , то можно ограничиться уравнением парной
регрессии:
, то можно ограничиться уравнением парной
регрессии:
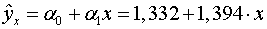 ,
, 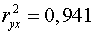 .
.
. Системы эконометрических уравнений
Дана система эконометрических уравнений.
Макроэкономическая модель (упрощенная версия модели Клейна):
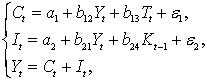
где 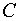 - потребление;
- потребление; 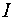 - инвестиции;
- инвестиции; 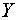 - доход;
- доход; 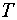 - налоги;
- налоги; 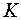 - запас капитала;
- запас капитала; 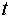 - текущий период;
- текущий период; 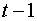 - предыдущий период.
- предыдущий период.
Требуется
1. Применив необходимое и достаточное условие
идентификации, определите, идентифицируемо ли каждое из уравнений модели.
2. Определите метод оценки параметров модели.
3. Запишите в общем виде приведенную форму модели.
Решение
Первое уравнение - функция потребления, второе уравнение -
функция инвестиций, третье уравнение - тождество дохода.
Модель представляет собой систему одновременных уравнений.
Проверим каждое ее уравнение на идентификацию.
Модель включает три эндогенные переменные 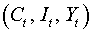 и две предопределенные переменные
(экзогенную переменную -
и две предопределенные переменные
(экзогенную переменную - 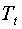 и лаговую переменную -
и лаговую переменную - 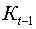 ).
).
Проверим необходимое условие идентификации для каждого из
уравнений модели.
Первое уравнение: 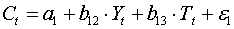 . Это уравнение содержит две эндогенные переменные
. Это уравнение содержит две эндогенные переменные 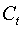 и
и 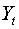 и одну предопределенную переменную
и одну предопределенную переменную 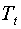 . Таким образом,
. Таким образом, 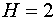 , а
, а 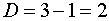 , т. е. выполняется условие
, т. е. выполняется условие 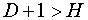 . Уравнение сверхидентифицируемо.
. Уравнение сверхидентифицируемо.
Второе уравнение: 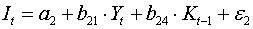 . Оно включает две эндогенные переменные
. Оно включает две эндогенные переменные 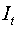 и
и 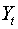 и одну экзогенную переменную
и одну экзогенную переменную 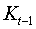 . Выполняется условие
. Выполняется условие 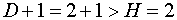 . Уравнение сверхидентифицируемо.
. Уравнение сверхидентифицируемо.
Третье уравнение: 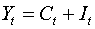 . Оно представляет собой тождество, параметры которого известны.
Необходимости в идентификации нет.
. Оно представляет собой тождество, параметры которого известны.
Необходимости в идентификации нет.
Проверим для каждого уравнения достаточное условие идентификации.
Для этого составим матрицу коэффициентов при переменных модели.
|
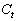 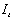 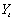  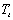
|
|
|
|
|
|
I уравнение
|
-1
|
0
|
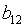 0 0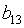
|
|
|
|
II уравнение
|
0
|
-1
|
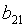 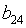 0 0
|
|
|
|
Тождество
|
1
|
1
|
-1
|
0
|
0
|
В соответствии с достаточным условием идентификации ранг
матрицы коэффициентов при переменных, не входящих в исследуемое уравнение,
должен быть равен числу эндогенных переменных модели без одного.
Первое уравнение. Матрица коэффициентов при переменных, не
входящих в уравнение, имеет вид
|
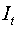 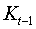
|
|
|
II уравнение
|
-1
|
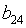
|
|
Тождество
|
1
|
0
|
Ранг данной матрицы равен двум, так как определитель квадратной
матрицы 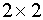 не равен нулю:
не равен нулю:
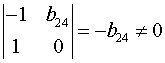 .
.
Достаточное условие идентификации для данного уравнения
выполняется.
Второе уравнение. Матрица коэффициентов при переменных, не
входящих в уравнение, имеет вид
|
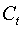 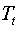
|
|
|
|
I уравнение
|
-1
|
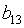
|
|
Тождество
|
1
|
0
|
Ранг данной матрицы равен двум, так как определитель квадратной
матрицы 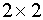 не равен нулю:
не равен нулю:
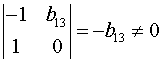 .
.
Достаточное условие идентификации для данного уравнения
выполняется.
Таким образом, все уравнения модели сверхидентифицируемы.
Приведенная форма модели в общем виде будет выглядеть следующим образом:
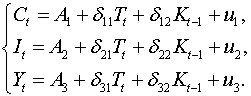
Для оценки параметров необходимо применить двухшаговый
метод наименьших квадратов.
. Временные ряды
корреляция регрессия линейный уравнение
Имеются условные данные об объемах потребления электроэнергии (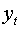 ) жителями региона за 16 кварталов.
) жителями региона за 16 кварталов.
|
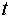 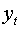 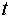 
|
|
|
|
|
1
|
5,8
|
9
|
7,9
|
|
2
|
4,5
|
10
|
5,5
|
|
3
|
5,1
|
11
|
6,3
|
|
4
|
9,1
|
10,8
|
|
5
|
7,0
|
13
|
9,0
|
|
6
|
5,0
|
14
|
6,5
|
|
7
|
6,0
|
15
|
7,0
|
|
8
|
10,1
|
16
|
11,1
|
Требуется:
1. Построить автокорреляционную функцию и сделать
вывод о наличии сезонных колебаний.
2. Построить мультипликативную модель временного
ряда.
3. Сделать прогноз на 2 квартала вперед.
Решение
Построим поле корреляции:
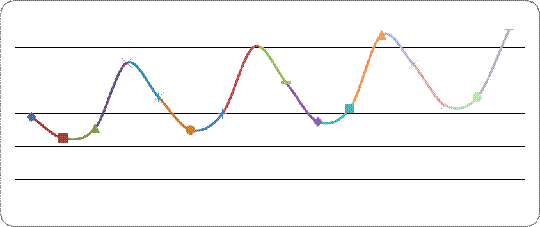
Рис. 1
Уже исходя из графика видно, что значения 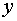 образуют пилообразную фигуру. Рассчитаем
несколько последовательных коэффициентов автокорреляции. Для этого составляем
первую вспомогательную таблицу.
образуют пилообразную фигуру. Рассчитаем
несколько последовательных коэффициентов автокорреляции. Для этого составляем
первую вспомогательную таблицу.
Таблица 2
|
t
|
yt
|
yt-1
|
yt -
y1
|
yt-1 -
y2
|
(yt -
y1) *(yt-1 - y2)
|
(yt-y1)2
|
(yt-1-y2)2
|
|
|
1
|
5,8
|
-
|
-
|
-
|
-
|
-
|
-
|
|
|
2
|
4,5
|
5,8
|
-2,89
|
-1,24
|
3,59
|
8,37
|
1,54
|
|
|
3
|
5,1
|
4,5
|
-2,29
|
-2,54
|
5,83
|
5,26
|
6,45
|
|
|
4
|
9,1
|
5,1
|
1,71
|
-1,94
|
-3,31
|
2,91
|
3,76
|
|
|
5
|
7
|
9,1
|
-0,39
|
2,06
|
-0,81
|
0,15
|
4,24
|
|
|
6
|
5
|
7
|
-2,39
|
-0,04
|
0,10
|
5,73
|
0,00
|
|
|
7
|
6
|
5
|
-1,39
|
-2,04
|
2,84
|
1,94
|
4,16
|
|
|
8
|
10,1
|
6
|
2,71
|
-1,04
|
-2,81
|
7,33
|
1,08
|
|
|
9
|
7,9
|
10,1
|
0,51
|
3,06
|
1,55
|
0,26
|
9,36
|
|
|
10
|
5,5
|
7,9
|
-1,89
|
0,86
|
-1,63
|
3,58
|
0,74
|
|
|
11
|
6,3
|
5,5
|
-1,09
|
-1,54
|
1,68
|
1,20
|
2,37
|
|
|
12
|
10,8
|
6,3
|
3,41
|
-0,74
|
-2,52
|
11,61
|
0,55
|
|
|
13
|
9
|
10,8
|
1,61
|
3,76
|
6,04
|
2,58
|
14,14
|
|
|
14
|
6,5
|
9
|
-0,89
|
1,96
|
-1,75
|
0,80
|
3,84
|
|
|
15
|
7
|
6,5
|
-0,39
|
-0,54
|
0,21
|
0,15
|
0,29
|
|
|
16
|
11,1
|
7
|
3,71
|
-0,04
|
-0,15
|
13,74
|
0,00
|
|
|
Сумма
|
110,9
|
105,6
|
0,00
|
0,00
|
8,85
|
65,61
|
52,54
|
|
|
Среднее
значение
|
7,39
|
7,04
|
-
|
-
|
-
|
-
|
-
|
|
Следует заметить, что среднее значение получается путем
деления не на 16, а на 15, т. к. у нас теперь на одно наблюдение меньше.
Теперь вычисляем коэффициент автокорреляции первого порядка
по формуле (4.1):
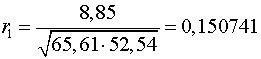 .
.
Составляем вспомогательную таблицу для расчета коэффициента
автокорреляции второго порядка.
Таблица 3
|
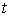
|
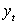
|
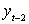
|
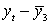
|
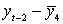
|
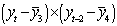
|
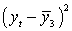
|
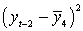
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
|
1
|
5,8
|
-
|
-
|
-
|
-
|
-
|
-
|
|
|
2
|
4,5
|
-
|
-
|
-
|
-
|
-
|
-
|
|
|
3
|
5,1
|
5,80
|
-2,50
|
-1,24
|
3,11
|
6,25
|
1,54
|
|
|
4
|
9,1
|
4,50
|
1,50
|
-2,54
|
-3,81
|
2,25
|
6,47
|
|
|
5
|
7
|
5,10
|
-0,60
|
-1,94
|
1,17
|
0,36
|
3,77
|
|
|
6
|
5
|
9,10
|
-2,60
|
2,06
|
-5,35
|
6,76
|
4,23
|
|
|
7
|
6
|
7,00
|
-1,60
|
-0,04
|
0,07
|
2,56
|
0,00
|
|
|
8
|
10,1
|
5,00
|
2,50
|
-2,04
|
-5,11
|
6,25
|
4,17
|
|
|
9
|
7,9
|
6,00
|
0,30
|
-1,04
|
-0,31
|
0,09
|
1,09
|
|
|
10
|
5,5
|
10,10
|
-2,10
|
3,06
|
-6,42
|
4,41
|
9,35
|
|
|
11
|
6,3
|
7,90
|
-1,30
|
0,86
|
-1,11
|
1,69
|
0,73
|
|
|
12
|
10,8
|
5,50
|
3,20
|
-1,54
|
-4,94
|
10,24
|
2,38
|
|
|
13
|
9
|
6,30
|
1,40
|
-0,74
|
-1,04
|
1,96
|
0,55
|
|
|
14
|
6,5
|
10,80
|
-1,10
|
3,76
|
-4,13
|
1,21
|
14,12
|
|
|
15
|
7
|
9,00
|
-0,60
|
1,96
|
-1,17
|
0,36
|
3,83
|
|
|
16
|
11,1
|
6,50
|
3,50
|
-0,54
|
-1,90
|
12,25
|
0,29
|
|
|
Сумма
|
106,4
|
98,60
|
0,00
|
0,00
|
-30,96
|
56,64
|
52,53
|
|
|
Среднее
значение
|
7,60
|
7,04
|
|
|
|
|
|
|
Следовательно
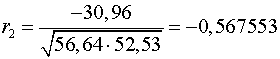 .
.
Аналогично находим коэффициенты автокорреляции более высоких
порядков, а все полученные значения заносим в сводную таблицу.
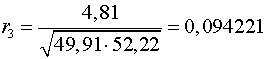
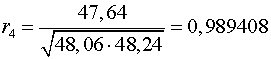
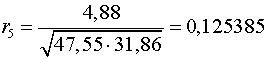
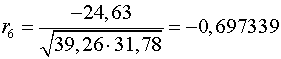
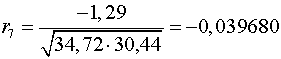
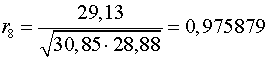
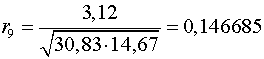
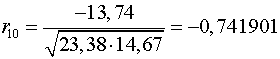
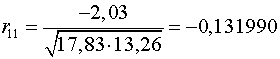
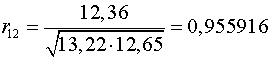
Таблица 4.
|
Лаг
|
|
1
|
0,150741
|
|
2
|
-0,567553
|
|
3
|
0,094221
|
|
4
|
0,989408
|
|
5
|
0,125385
|
|
6
|
-0,697339
|
|
7
|
-0,039680
|
|
8
|
0,975879
|
|
9
|
0,146685
|
|
10
|
-0,741901
|
|
11
|
-0,131990
|
|
12
|
0,955916
|
Коррелограмма:
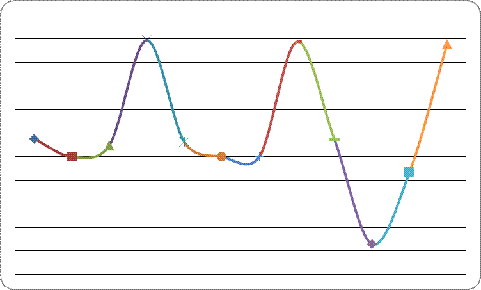
Рис. 2.
Анализ коррелограммы и графика исходных уровней временного
ряда позволяет сделать вывод о наличии в изучаемом временном ряде сезонных
колебаний периодичностью в четыре квартала.
Построим мультипликативную модель временного ряда.
Шаг 1. Проведем выравнивание исходных уровней ряда
методом скользящей средней. Для этого:
.1. Просуммируем уровни ряда последовательно за каждые четыре
квартала со сдвигом на один момент времени и определим условные годовые объемы
потребления электроэнергии (гр. 3 табл. 5).
.2. Разделив полученные суммы на 4, найдем скользящие средние
(гр. 4 табл. 5). Полученные таким образом выровненные значения уже не содержат
сезонной компоненты.
.3. Приведем эти значения в соответствие с фактическими моментами
времени, для чего найдем средние значения из двух последовательных скользящих
средних - центрированные скользящие средние (гр. 5 табл. 5).
Таблица
5.
|
№ квартала, t
|
Объем
потребления энергии, yt
|
Итого за четыре
квартала
|
Скользящая
средняя за четыре квартала
|
Центрированная
скользящая средняя
|
Оценка сезонной
компоненты
|
|
1
|
5,8
|
-
|
-
|
-
|
-
|
|
2
|
4,5
|
24,5
|
6,125
|
-
|
-
|
|
3
|
5,1
|
25,7
|
6,425
|
6,275
|
0,8127
|
|
4
|
9,1
|
26,2
|
6,55
|
6,4875
|
1,4027
|
|
5
|
7
|
27,1
|
6,775
|
6,6625
|
1,0507
|
|
6
|
5
|
28,1
|
7,025
|
6,9
|
0,7246
|
|
7
|
6
|
29
|
7,25
|
7,1375
|
0,8406
|
|
8
|
10,1
|
29,5
|
7,375
|
7,3125
|
1,3812
|
|
9
|
7,9
|
29,8
|
7,45
|
7,4125
|
1,0658
|
|
10
|
5,5
|
30,5
|
7,625
|
7,5375
|
0,7297
|
|
11
|
6,3
|
31,6
|
7,9
|
7,7625
|
0,8116
|
|
12
|
10,8
|
32,6
|
8,15
|
8,025
|
1,3458
|
|
13
|
9
|
33,3
|
8,325
|
8,2375
|
1,0926
|
|
14
|
6,5
|
33,6
|
8,4
|
8,3625
|
0,7773
|
|
15
|
7
|
-
|
-
|
-
|
-
|
|
16
|
11,1
|
-
|
-
|
-
|
-
|
Шаг 2.
Найдем оценки сезонной компоненты как частное от деления фактических уровней
ряда на центрированные скользящие средние (гр. 6 табл. 5). Эти оценки
используются для расчета сезонной компоненты 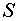 (табл. 6.). Для этого найдем средние за каждый квартал оценки
сезонной компоненты
(табл. 6.). Для этого найдем средние за каждый квартал оценки
сезонной компоненты 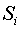 . Считается, что сезонные воздействия за
период взаимопогашаются. В мультипликативной модели это выражается в том, что
сумма значений сезонной компоненты по всем кварталам должна быть равна числу
периодов в цикле. В нашем случае число периодов одного цикла равно 4.
. Считается, что сезонные воздействия за
период взаимопогашаются. В мультипликативной модели это выражается в том, что
сумма значений сезонной компоненты по всем кварталам должна быть равна числу
периодов в цикле. В нашем случае число периодов одного цикла равно 4.
Таблица
6.
|
Показатели
|
№ квартала, i
|
|
I
|
II
|
III
|
IV
|
|
-
|
-
|
0,8127
|
1,4027
|
|
1,0507
|
0,7246
|
0,8406
|
1,3812
|
|
1,0658
|
0,7297
|
0,8116
|
1,3458
|
|
1,0926
|
0,7773
|
-
|
-
|
|
Всего за i-й
квартал
|
3,2091
|
2,2316
|
2,4649
|
4,1297
|
|
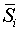 Средняя
оценка сезонной компоненты для i-го квартала, Средняя
оценка сезонной компоненты для i-го квартала,
|
1,0697
|
0,7439
|
0,8216
|
1,3766
|
|
Скорректированная
сезонная компонента, Si
|
1,0666
|
0,7417
|
0,8192
|
1,3725
|
Имеем
 .
.
Определяем корректирующий коэффициент:
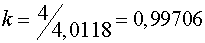 .
.
Скорректированные значения сезонной компоненты 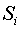 получаются при умножении ее средней
оценки
получаются при умножении ее средней
оценки 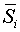 на корректирующий коэффициент
на корректирующий коэффициент 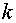 .
.
Проверяем условие равенство 4 суммы значений сезонной компоненты:
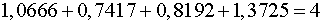 .
.
Шаг 3.
Разделим каждый уровень исходного ряда на соответствующие значения сезонной
компоненты. В результате получим величины 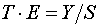 (гр. 4 табл. 7), которые содержат только тенденцию и случайную
компоненту.
(гр. 4 табл. 7), которые содержат только тенденцию и случайную
компоненту.
Таблица
7.
|
t
|
yt
|
Si
|
yt/Si
|
T
|
T*S
|
E=yt/(T*S)
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
1
|
5,8
|
1,0666
|
5,4378
|
5,8475
|
6,2369
|
0,9299
|
|
2
|
4,5
|
0,7417
|
6,0671
|
6,0392
|
4,4793
|
1,0046
|
|
3
|
5,1
|
0,8192
|
6,2256
|
6,2309
|
5,1044
|
0,9991
|
|
4
|
9,1
|
1,3725
|
6,6302
|
6,4226
|
8,8150
|
1,0323
|
|
5
|
7
|
1,0666
|
6,5629
|
6,6143
|
7,0548
|
0,9922
|
|
6
|
5
|
0,7417
|
6,7413
|
6,8060
|
5,0480
|
0,9905
|
|
7
|
6
|
0,8192
|
7,3242
|
6,9977
|
5,7325
|
1,0467
|
|
8
|
10,1
|
1,3725
|
7,3588
|
7,1894
|
9,8675
|
1,0236
|
|
9
|
7,9
|
1,0666
|
7,4067
|
7,3811
|
7,8727
|
1,0035
|
|
10
|
5,5
|
0,7417
|
7,4154
|
7,5728
|
5,6167
|
0,9792
|
|
11
|
6,3
|
0,8192
|
7,6904
|
7,7645
|
6,3607
|
0,9905
|
|
12
|
10,8
|
1,3725
|
7,8689
|
7,9562
|
10,9199
|
0,9890
|
|
13
|
9
|
1,0666
|
8,4380
|
8,1479
|
8,6906
|
1,0356
|
|
14
|
6,5
|
0,7417
|
8,7637
|
8,3396
|
6,1855
|
1,0508
|
|
15
|
7
|
0,8192
|
8,5449
|
8,5313
|
6,9888
|
1,0016
|
|
16
|
11,1
|
1,3725
|
8,0874
|
8,7230
|
11,9723
|
0,9271
|
Шаг 4.
Определим компоненту 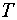 в мультипликативной модели. Для этого
рассчитаем параметры линейного тренда, используя уровни
в мультипликативной модели. Для этого
рассчитаем параметры линейного тренда, используя уровни 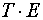 . В результате получим уравнение тренда:
. В результате получим уравнение тренда:
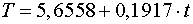 .
.
Подставляя в это уравнение значения 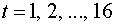 , найдем уровни
, найдем уровни 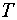 для каждого момента времени (гр. 5 табл. 7.).
для каждого момента времени (гр. 5 табл. 7.).
Шаг 5.
Найдем уровни ряда, умножив значения 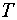 на соответствующие значения сезонной компоненты (гр. 6 табл. 7.).
На одном графике откладываем фактические значения уровней временного ряда и
теоретические, полученные по мультипликативной модели.
на соответствующие значения сезонной компоненты (гр. 6 табл. 7.).
На одном графике откладываем фактические значения уровней временного ряда и
теоретические, полученные по мультипликативной модели.
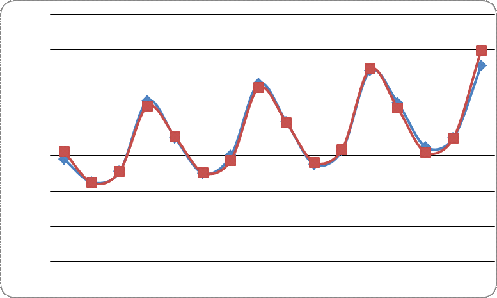
Расчет ошибки в мультипликативной модели производится по
формуле:
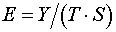 .
.
Для сравнения мультипликативной модели и других моделей временного
ряда можно использовать сумму квадратов абсолютных ошибок 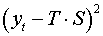 :
:
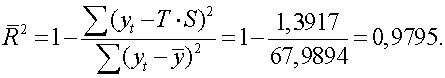
Шаг 6.
Прогнозирование по мультипликативной модели. Прогнозное значение 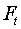 уровня временного ряда в
мультипликативной модели есть произведение трендовой и сезонной компонент. Для
определения трендовой компоненты воспользуемся уравнением тренда
уровня временного ряда в
мультипликативной модели есть произведение трендовой и сезонной компонент. Для
определения трендовой компоненты воспользуемся уравнением тренда
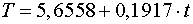 .
.
Получим
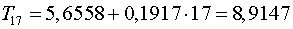 ;
;
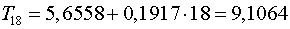 .
.
Значения сезонных компонент за соответствующие кварталы равны: 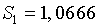 и
и 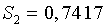 . Таким образом
. Таким образом
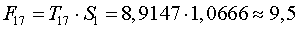 ;
;
 .
.
Т.е. в следующие два квартала следует ожидать следующие объемы
потребления электроэнергии 9,5 и 6,8 соответственно.