Напряжения и токи электрических цепей
Реферат
Напряжения и токи электрических цепей
1. Электрическая цепь
при последовательном соединении элементов с R, L и C
R, L, C - это параметры электрической цепи, причем активное сопротивление
R
характеризует активный (необратимый) процесс преобразования электрической
энергии в другие виды энергии, а индуктивность L и емкость C - обратимый процесс
преобразования энергии электромагнитного поля.

Под действием напряжения
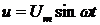 источника
питания в цепи возникает ток i.
Ток создает падения напряжения на элементах цепи:
источника
питания в цепи возникает ток i.
Ток создает падения напряжения на элементах цепи: 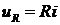 -
на элементе с активным сопротивлением;
-
на элементе с активным сопротивлением; 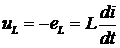 - на элементе с
индуктивностью;
- на элементе с
индуктивностью; 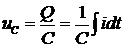 -
на элементе с емкостью. По второму закону Кирхгофа для данной цепи запишем
-
на элементе с емкостью. По второму закону Кирхгофа для данной цепи запишем
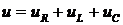 или
или 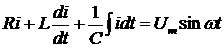
В результате решения
данного уравнения найдем 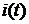 .
.
Найдем частное решение
данного уравнения, то есть ток установившегося режима. Так как правая часть
этого уравнения - синусоидальная функция, то и частное решение следует искать в
виде синусоидальной функции
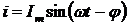 .
.
Функция 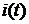 полностью
определена, если известны амплитуда тока Im
и угол сдвига фаз φ между напряжением и током. Найдем эти величины.
полностью
определена, если известны амплитуда тока Im
и угол сдвига фаз φ между напряжением и током. Найдем эти величины.
Как было показано ранее,
напряжение 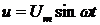 изображается
комплексным числом
изображается
комплексным числом 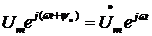 ;
ток
;
ток 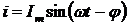 -
комплексным числом
-
комплексным числом 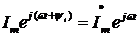 ;
производная
;
производная 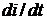 -
комплексным числом
-
комплексным числом 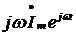 ;
интеграл
;
интеграл 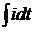 -
комплексным числом
-
комплексным числом 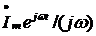 .
.
Перейдем от
дифференциального уравнения к алгебраическому уравнению в комплексной форме
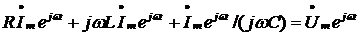 .
.
После преобразования
имеем
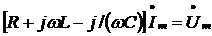
а разделив обе части
уравнения на 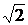 ,
получим аналогичное линейное алгебраическое уравнение для комплексных
действующих значения:
,
получим аналогичное линейное алгебраическое уравнение для комплексных
действующих значения:
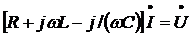
Коэффициент
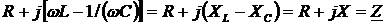
является полным
сопротивлением цепи в комплексной форме. Вещественная составляющая R полного сопротивления равна активному сопротивлению цепи, а
мнимая составляющая X
называется её реактивным сопротивлением. Реактивное сопротивление цепи равно
разности индуктивного и емкостного сопротивлений:
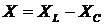 .
.
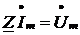 ;
; 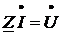 ,
,
откуда комплексное
полное сопротивление
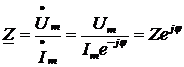 ,
,
где модуль полного
сопротивления
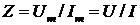 .
.
Таким образом, модуль
полного сопротивления цепи равен отношению модулей действующих значений
напряжения и тока, а аргумент комплексного сопротивления - сдвигу фаз φ
между векторами напряжения и тока.
Модуль полного
сопротивления цепи
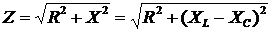
то есть, полное
сопротивление цепи равно корню квадратному из суммы квадратов активного и
реактивного сопротивлений.
Можем найти амплитуду
тока, определяющую функцию 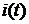
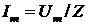 .
.
Теперь, если
воспользоваться равенством
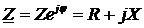 ,
,
можно определить угол
сдвига фаз φ
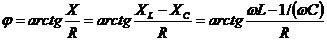 .
.
Таким образом, значение
угла φ зависит от соотношения между реактивным X и активным R
сопротивлениями. Чем больше реактивное сопротивление, тем больше угол φ.
Знак угла φ зависит от соотношения между индуктивным и емкостным
сопротивлениями. Если 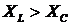 ,
то угол φ положительный и ток можно определить по формуле
,
то угол φ положительный и ток можно определить по формуле 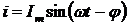 ,
откуда видно, что ток отстает по фазе от напряжения на угол φ.
Если
,
откуда видно, что ток отстает по фазе от напряжения на угол φ.
Если 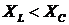 ,
то угол φ отрицательный и ток
,
то угол φ отрицательный и ток 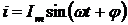 , то есть опережает по
фазе напряжение на угол φ.
, то есть опережает по
фазе напряжение на угол φ.
На рисунке показано, как
изменяются напряжение и ток в цепи с последовательно соединенными активным,
индуктивным и емкостным сопротивлениями при условии 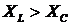 :
:

При построении векторной диаграмм в
качестве начального удобно выбрать вектор тока, так как при последовательном
соединении ток во всех элементах один и тот же. Как было условлено, начальный
вектор совмещаем с положительным направлением мнимой оси (здесь и далее оси
обозначать не будем).

Падения напряжения в комплексной
форме на участке цепи с активным, индуктивным и емкостным сопротивлениями
соответственно
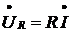 ;
; 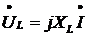 ;
;
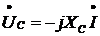 .
.
Вектор 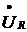 на
участке с активным сопротивлением совпадает по фазе с вектором
на
участке с активным сопротивлением совпадает по фазе с вектором 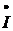 ,
и на векторной диаграмме его проводим в направлении тока. Падение напряжения
,
и на векторной диаграмме его проводим в направлении тока. Падение напряжения 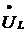 на
участке с индуктивностью опережает ток по фазе на угол π/2,
причем поворачивать вектор надо против часовой стрелки по отношению к вектору
на
участке с индуктивностью опережает ток по фазе на угол π/2,
причем поворачивать вектор надо против часовой стрелки по отношению к вектору 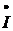 .
Падение напряжения
.
Падение напряжения 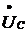 на
участке с емкостью отстает от тока на угол π/2,
причем
на
участке с емкостью отстает от тока на угол π/2,
причем 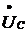 следует
повернуть на угол 90º по направлению вращения часовой стрелки по отношению к вектору
следует
повернуть на угол 90º по направлению вращения часовой стрелки по отношению к вектору 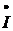 .
.
По второму закону
Кирхгофа можно написать уравнение
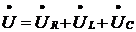 .
.
Для нахождения вектора 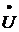 полного
напряжения цепи к концу вектора
полного
напряжения цепи к концу вектора 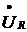 пристраиваем вектор
пристраиваем вектор 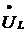 путем
параллельного переноса, а к концу вектора
путем
параллельного переноса, а к концу вектора 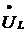 пристраиваем вектор
пристраиваем вектор 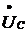 .
Вектор полного напряжения
.
Вектор полного напряжения 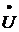 соединяет
начало координат с концом вектора
соединяет
начало координат с концом вектора 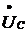 (последнего слагаемого
вектора).
(последнего слагаемого
вектора).
Поскольку векторная
диаграмма построена для случая, когда 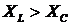 (следовательно, и
(следовательно, и 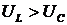 ),
ток в цепи отстает по фазе на угол φ
от полного напряжения, комплексное значение которого
),
ток в цепи отстает по фазе на угол φ
от полного напряжения, комплексное значение которого 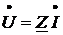 .
.
2. Треугольник
напряжений и сопротивлений
Если электрическая цепь
состоит из последовательно соединенных элементов с активным и реактивным
сопротивлениями, то векторная диаграмма напряжений имеет вид прямоугольного
треугольника. Гипотенуза этого треугольника равна полному напряжению U, а катеты треугольника - активной 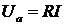 и реактивной Uр
составляющим полного напряжения, причем
и реактивной Uр
составляющим полного напряжения, причем
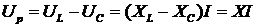
Из треугольников
напряжений можно получить ряд важных соотношений между напряжениями:
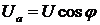 ;
; 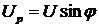
где
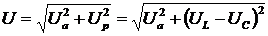 ;
;
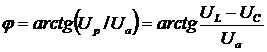 .
.
Если начальный вектор 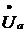 расположен
горизонтально, то при
расположен
горизонтально, то при 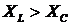 треугольник
напряжений находится сверху от него и снизу при
треугольник
напряжений находится сверху от него и снизу при 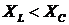 . После деления всех
сторон треугольника напряжений на ток I
получим треугольник сопротивлений, подобный треугольнику напряжений:
. После деления всех
сторон треугольника напряжений на ток I
получим треугольник сопротивлений, подобный треугольнику напряжений:
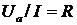 ;
; 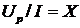 ;
;
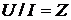 .
.

Из треугольника сопротивлений можно
получить соотношения
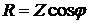 ;
; 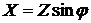 ,
,
а также известные уже равенства
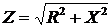 ;
; 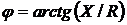 .
.
3. Резонанс напряжений
При последовательном
соединении элементов с R,
L и C ток в цепи
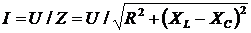 .
.
Из всех возможных
соотношений между индуктивным XL
и емкостным XC
сопротивлениями особый интерес представляет случай, когда эти сопротивления
равны, то есть 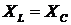 .
В этом случае реактивное сопротивление цепи
.
В этом случае реактивное сопротивление цепи 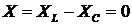 и полное сопротивление
и полное сопротивление  минимально.
Тогда ток в цепи
минимально.
Тогда ток в цепи 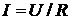 и
при
и
при 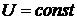 ,
,
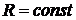 значение
его максимально.
значение
его максимально.
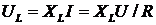 ;
; 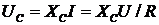 .
.
Таким образом,
напряжения на индуктивном и емкостном элементах могут превышать напряжение сети
в 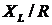 раз,
если
раз,
если 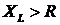 .
Сдвиг по фазе между напряжениями
.
Сдвиг по фазе между напряжениями 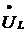 и
и 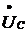 равен
π, то есть эти напряжения находятся в противофазе.
равен
π, то есть эти напряжения находятся в противофазе.
Такой режим цепи при
последовательном соединении с R,
L и C, когда 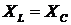 ,
а напряжения на индуктивном (
,
а напряжения на индуктивном (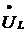 ) и емкостном (
) и емкостном (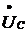 )
элементах, находящихся в противофазе, равны по значению и могут превышать
напряжение всей цепи, носит название режима резонанса напряжений.
)
элементах, находящихся в противофазе, равны по значению и могут превышать
напряжение всей цепи, носит название режима резонанса напряжений.
Векторная диаграмма
напряжений для режима резонанса представлена на рисунке.

Реактивная составляющая
напряжения равна нулю; следовательно, полное напряжение 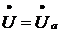 ,
а угол сдвига фаз
,
а угол сдвига фаз 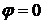 ;
;
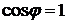 .
.
Активная мощность такой
цепи 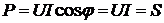 ,
а реактивная
,
а реактивная 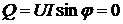 .
Реактивные же мощности индуктивной катушки (
.
Реактивные же мощности индуктивной катушки (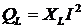 ) и конденсатора (
) и конденсатора (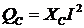 )
не равны нулю: их мгновенные значения в любой момент времени равны между собой,
но обратны по знаку. Происходит непрерывный обмен энергией между магнитным
полем катушки и электрическим полем конденсатора.
)
не равны нулю: их мгновенные значения в любой момент времени равны между собой,
но обратны по знаку. Происходит непрерывный обмен энергией между магнитным
полем катушки и электрическим полем конденсатора.
Равенство индуктивного и
емкостного сопротивлений
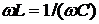
можно добиться, изменяя
угловую частоту ω, индуктивность L
или емкость С. Угловая частота, при которой наступает резонанс напряжений
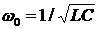 .
.
При этой, резонансной,
частоте ток в цепи достигает максимального значения.
Явление резонанса широко
используют в устройствах радиотехники, телевидения, автоматики и других
электроустройствах. Если электрическая цепь имеет параметры L и C такие, что
резонансной для цепи является частота 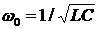 , то ток этой частоты
будет иметь максимальное значение. Поскольку резонансные явления связаны со
значительным увеличением напряжения на элементах с индуктивностью и емкостью,
это может привести к пробою их изоляции.
, то ток этой частоты
будет иметь максимальное значение. Поскольку резонансные явления связаны со
значительным увеличением напряжения на элементах с индуктивностью и емкостью,
это может привести к пробою их изоляции.
4. Электрическая цепь
при параллельном соединении элементов с R,
L и C
К цепи с параллельным
соединением элементов с R,
L и C подводим
напряжение 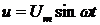 ,
под действием которого в ветвях создают токи
,
под действием которого в ветвях создают токи 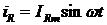 (в ветви с R),
(в ветви с R), 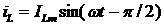 (в
ветви с L),
(в
ветви с L), 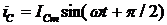 (в
ветви с С).
(в
ветви с С).

Соответственно действующие значения
токов в ветвях
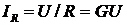 ;
; 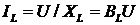 ;
;
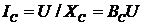
а действующее значение
полного тока
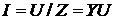 ,
,
где 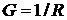 ;
;
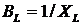 ;
;
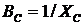 ;
;
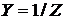 -
активная, индуктивная, емкостная и полная проводимости цепи.
-
активная, индуктивная, емкостная и полная проводимости цепи.
По первому закону
Кирхгофа для данной цепи,
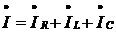 .
.
При построении векторной
диаграммы токов за начальный удобно принять вектор напряжения. Векторы
комплексных токов 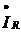 ,
,
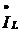 и
и
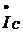 в
ветвях направлены с учетом их сдвига по фазе по отношению к вектору напряжения.
В соответствии с уравнением
в
ветвях направлены с учетом их сдвига по фазе по отношению к вектору напряжения.
В соответствии с уравнением 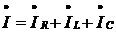 производят
геометрическое сложение векторов токов на комплексной плоскости и находят
вектор полного комплексного тока
производят
геометрическое сложение векторов токов на комплексной плоскости и находят
вектор полного комплексного тока 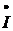 .
.


На предыдущем рисунке
построен треугольник токов OAB,
катеты которого равны активной Iа
и реактивной Iр
составляющим тока, а гипотенуза - полному току I.
Активная составляющая тока совпадает по фазе с напряжением. Реактивная
составляющая тока 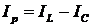 сдвинута
по фазе относительно напряжения на угол π/2.
Если
сдвинута
по фазе относительно напряжения на угол π/2.
Если 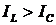 ,
то Iр
отстает по фазе от напряжения на угол π/2,
а полный ток - на угол φ (0≤φ≤π/2).
Если
,
то Iр
отстает по фазе от напряжения на угол π/2,
а полный ток - на угол φ (0≤φ≤π/2).
Если 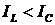 ,
то Iр
опережает напряжение на угол π/2,
а полный ток - на φ (-π/2≤φ≤0).
,
то Iр
опережает напряжение на угол π/2,
а полный ток - на φ (-π/2≤φ≤0).
Из треугольника токов
следует соотношения:
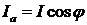 ;
; 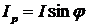 ;
;
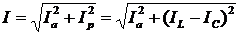 ;
;
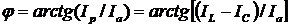 ;
;
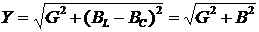 .
.
Таким образом, полная
проводимость цепи равна корню квадратному из суммы квадратов активной G и реактивной 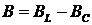 проводимостей.
проводимостей.
Полный ток в цепи при
параллельном соединении элементов с R,
L и C
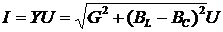 .
.
Поделив стороны
треугольника токов на напряжение U:
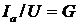 ;
;
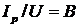 ;
;
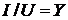 ,
построим треугольник проводимостей, из которого можно получить следующие
соотношения:
,
построим треугольник проводимостей, из которого можно получить следующие
соотношения:
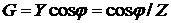 ;
; 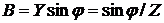 ;
;
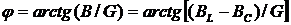 .
.

Полная проводимость цепи в
комплексной форме
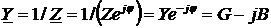 ,
,
где G и B - активная и
реактивная проводимости соответственно.
Как видно из последней
формулы, если угол φ положительный, то есть полный ток имеет индуктивную реактивную
составляющую, то реактивная проводимость в комплексной форме отрицательна, и
наоборот.
Активная и реактивная
мощность цепи
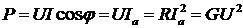
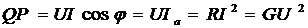
причем реактивная
мощность отдельных ветвей 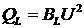 ,
,
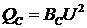 .
.
Полная мощность цепи 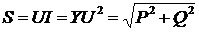 .
.
5. Резонанс токов
В электрической цепи при
параллельном соединении ветвей с R(G), L(BL), C(BC) ток определяется по формуле 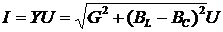 .
.
Особый интерес
представляет случай, когда индуктивная и емкостная реактивные проводимости
равны друг другу. Тогда полная проводимость цепи 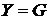 , так как
, так как 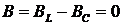 ,
а полный ток
,
а полный ток
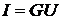
имеет минимальное
значение и только активную составляющую 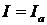 . Следовательно,
. Следовательно, 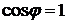 .
.
Токи в ветвях с
проводимостями BL
и BC
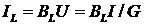 ;
; 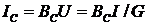 ,
,
то есть равны по
значению (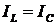 )
и могут превышать полный ток в цепи в
)
и могут превышать полный ток в цепи в 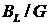 раз, если
раз, если 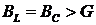 .
Векторная диаграмма токов для рассмотренного случая имеет вид
.
Векторная диаграмма токов для рассмотренного случая имеет вид

Режим цепи при
параллельном соединении элементов с R,
L и C, когда 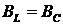 ,
а токи в ветвях с реактивными проводимостями IL
и IC равны по значению и могут превышать
полный ток цепи, называется режимом резонанса токов. Для этого режима
характерно
,
а токи в ветвях с реактивными проводимостями IL
и IC равны по значению и могут превышать
полный ток цепи, называется режимом резонанса токов. Для этого режима
характерно 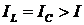 ,
если
,
если 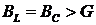 ;
;
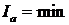 ;
; 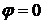 ;
;
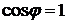 ;
;
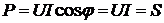 ;
;
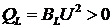 ;
; 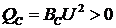 ;
;
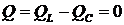 .
.
В режиме резонанса токов
рассматриваемая цепь ведет себя по отношению к источнику питания так, как будто
она состоит только из элементов с активной проводимостью. В действительности же
в параллельных ветвях L и C могут протекать токи, даже превышающие полный ток, протекающий в
источнике питания. Но эти токи всегда противоположны по фазе друг другу. Это
означает, что через каждую четверть периода происходит обмен энергиями между
магнитным полем индуктивной катушки и электрическим полем конденсатора, который
поддерживается напряжением U источника питания.
. Повышение коэффициента
мощности
Только активная составляющая тока
определяет преобразование электроэнергии в другие виды энергии, то есть
позволяет количественно оценить совершаемую работу. Реактивная же составляющая
тока никакой работы не производит. Однако при её наличии увеличивается полный
ток.
Представим электроприемник,
потребляющий активную и индуктивную составляющие тока, схемой последовательного
соединения элементов Rпр и XLпр.


На векторной диаграмме вектор
приемника 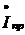 составляет
с вектором напряжения
составляет
с вектором напряжения 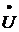 угол φпр, причем
угол φпр, причем
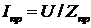 ;
; 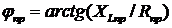 .
.
В отсутствие емкости C, включенный параллельно
с приемником Zпр, ток 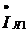 в линии передачи равен току
в линии передачи равен току 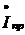 приемника. Если в проводах линии передачи (сопротивление которых R) протекает ток
приемника. Если в проводах линии передачи (сопротивление которых R) протекает ток 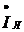 , то теряемая в них мощность
, то теряемая в них мощность 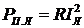 . Так как в данном случае
. Так как в данном случае
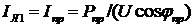 ,
,
то при 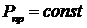 и
и 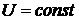 с
уменьшением коэффициента мощности
с
уменьшением коэффициента мощности 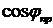 увеличивается ток в линии, а следовательно, и потеря мощности
увеличивается ток в линии, а следовательно, и потеря мощности
Таким образом, для уменьшения потерь
мощности в передающих устройствах необходимо увеличить коэффициент мощности
приемников электроэнергии.
Конденсаторы емкостью C включают параллельно
электроприемнику. Ток 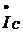 конденсатора
является практически чисто реактивным, опережающим напряжение на угол π/2. Этот ток компенсирует
реактивную индуктивную составляющую тока приемника, в результате чего общая
реактивная составляющая тока уменьшается.
конденсатора
является практически чисто реактивным, опережающим напряжение на угол π/2. Этот ток компенсирует
реактивную индуктивную составляющую тока приемника, в результате чего общая
реактивная составляющая тока уменьшается.
При емкости конденсатора, равной C2, и токе 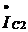 ток в
линии
ток в
линии
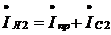 , или
, или 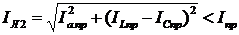 .
.
Угол сдвига фаз φ2 между напряжением 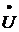 и
током
и
током 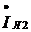 уменьшился, а коэффициент мощности увеличился (
уменьшился, а коэффициент мощности увеличился (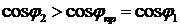 ).
).
С увеличением емкости конденсатора
ток 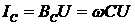 увеличивается так, что при некотором значении емкости C3 можно получить равенство
увеличивается так, что при некотором значении емкости C3 можно получить равенство 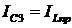 (режим резонанса токов). В этом случае реактивная составляющая
тока приемника ILпр полностью
компенсируется и ток в линии достигает минимального значения, равного активной
составляющей тока приемника Iа.пр. При дальнейшем
увеличении емкости конденсаторов
(режим резонанса токов). В этом случае реактивная составляющая
тока приемника ILпр полностью
компенсируется и ток в линии достигает минимального значения, равного активной
составляющей тока приемника Iа.пр. При дальнейшем
увеличении емкости конденсаторов 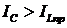 и реактивная составляющая тока в линии, а следовательно, и полный
ток в ней увеличиваются. Наступает режим перекомпенсации, когда реактивная
составляющая тока в линии носит емкостной характер.
и реактивная составляющая тока в линии, а следовательно, и полный
ток в ней увеличиваются. Наступает режим перекомпенсации, когда реактивная
составляющая тока в линии носит емкостной характер.
Следует помнить, что при подключении
конденсаторов потребляемая реактивная индуктивная мощность электроприемника
остается неизменной, но её источником становится батарея конденсаторов,
установленная вблизи приемника. В результате в линии передачи реактивные токи
уменьшаются.
Для обеспечения заданного значения
коэффициента мощности предприятия необходимо устанавливать конденсаторы
определенной мощности или емкости. Если электроприемники имеют мощность 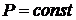 и
и 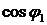 , то
они потребляют из сети реактивную индуктивную мощность
, то
они потребляют из сети реактивную индуктивную мощность 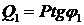 . При заданном значении
. При заданном значении 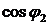 , которое должно обеспечить предприятие (
, которое должно обеспечить предприятие (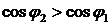 ), потребляемая реактивная мощность
), потребляемая реактивная мощность 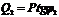 .
.
Разность реактивных мощностей 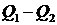 компенсируется емкостной реактивной мощностью конденсаторов
компенсируется емкостной реактивной мощностью конденсаторов
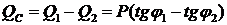 .
.
Реактивную мощность конденсаторов
можно также определить по формуле
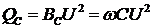 .
.
Приравнивая правые части этих
уравнений, получим
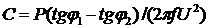 .
.
При этом емкость
выражается в фарадах, если мощность выражена в ваттах, а напряжение - в
вольтах. Для полной компенсации (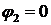 ) необходимо, чтобы
) необходимо, чтобы
электрический напряжение
цепь резонанс
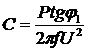 .
.
Литература
1. Алиев И.И. Электротехнический справочник / И.И. Алиев. - 4-е
изд., испр. - М.: РадиоСофт, 2004 или 2006. - 383 с.
. Березкина Т.Ф. Задачник по общей электротехнике с основами
электроники: Учеб. пособие для сред. спец. учеб. заведений / Т.Ф.
. Березкина, Н.Г. Гусев, В.В. Масленников. - 4-е изд., стер. - М.:
Высш. шк., 2001. - 380 с.
. Иванов И.И. Электротехника: Основные положения, примеры и задачи
/ И.И. Иванов, А.Ф. Лукин, Г.И. Соловьев. - Изд. 3-е, стер. - СПб.: Лань, 2004.
- 191 с.
. Владимиров В.С. Уравнения математической физики. М.: Наука,
1976. 2. Владимиров В.С. и др. Сборник задач по уравнениям математической
физики. М.: Наука 1982.
. Годунов С.К. Уравнения математической физики. М.: Наука, 1979.