Анализ линейных электрических цепей в установившемся и переходном режимах
Оглавление
1. Введение
. Задание на курсовую работу
. Расчет простейшей электрической цепи
.1 Схема для анализа. Исходные данные для простейшей
электрической цепи
.2 Метод расчета простейшей электрической цепи
.3 Проверка баланса мощностей в простейшей цепи
.4 Построение векторно-топографической диаграммы
. Расчет сложной электрической цепи
.1 Схема для анализа. Исходные данные для сложной
электрической цепи
.2 Расчет сложной электрической цепи методом контурных токов
.2 Расчет сложной электрической цепи методом узловых
напряжений
.3 Расчет сложной электрической цепи методом эквивалентного
генератора.
.4 Проверка баланса активных реактивных мощностей
.5 Построение векторно-топографической диаграммы
. Расчет трёхфазных электрических цепей
.1 Исходные данные
.2 Расчет симметричного режима трехфазной цепи
.2.1 Построение векторно-топографической диаграммы
.2.2 Расчет мощности в трехфазной цепи
.3 Расчет симметричной трехфазной цепи при воздействии
несинусоидальной ЭДС
.3.1 Расчет входного ЭДС
.4 Анализ трехфазной цепи синусоидального тока методом
симметричных составляющих
. Расчет переходного процесса в электрической цепи
.1 Исходные данные
.2 Расчет переходного процесса в электрической цепи
Заключение
Литература
1. Введение
Целью данной курсовой по разделу «Анализ линейных электрических цепей в
установившемся и переходном режимах» работы является:
· закрепление теоретических знаний и самостоятельное применение их к
анализу электрических цепей;
· выработка навыков и умений в выполнении типового анализа
цепей;
· знакомство с правилами оформления технической документации.
В данной курсовой работе применяются следующие методы расчета и понятия:
· постоянные и переменные токи и напряжения;
· амплитуда и фаза;
· действующие и мгновенные значения токов и напряжений;
· комплексный метод расчета в цепях переменного тока;
· энергия и мощность в цепях переменного тока;
· векторные и топографические диаграммы;
· сложные и простые электрические цепи;
· схема цепи и ее граф;
· законы Кирхгофа;
· методы решения сложных цепей и простых;
· основные свойства и преобразования в электрических цепях;
· принцип суперпозиций;
· свойство взаимности;
· основные свойства трехфазных цепей переменного тока;
· метод несимметричных составляющих;
· методы расчет электрических цепей при переходных процессах.
2. Задание на
курсовую работу
. Анализ простейшей электрической цепи синусоидального тока
. Построить схему простейшей электрической цепи, используя кодировку
ветвей в соответствии с вариантом.
3.
Определить комплексные действующие значения токов по заданным действующим
значениям ЭДС источников и параметрам элементов 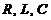 .
.
.
Записать выражения мгновенных значений токов 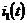 ,
, 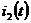 ,
, 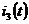 и
построить их графики.
и
построить их графики.
.
Проверить баланс активных и реактивных мощностей.
.
Построить векторную диаграмму токов и топографическую диаграмму напряжений в
одной координатной системе.
.
Определить по векторно-топографической диаграмме действующее значение
напряжения 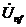 и сдвиг фаз между напряжениями
и сдвиг фаз между напряжениями 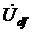 и
и 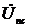 .
.
.
Для исходной схемы найти мгновенное значение напряжения 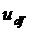 , если ЭДС источника не задана, но известен ток
, если ЭДС источника не задана, но известен ток 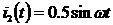 .
.
.
Анализ сложных (разветвлённых) электрических цепей
.
По заданному графу и в соответствии с номером варианта работы построить схему
цепи с числом узлов 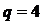 и числом ветвей
и числом ветвей 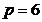 .
.
.
На изображении графа заданной схемы выделить его дуги, назначенные ветвями
дерева на схеме цепи, обозначить базисный узел.
.
Сформировать основные топологические матрицы исследуемой электрической цепи.
Составить с их помощью систему контурных уравнений.
.
Решить полученную систему контурных уравнений и с помощью найденных контурных
токов вычислить токи всех ветвей.
.
Составить систему узловых уравнений. Решить ее и на основе найденных узловых
напряжений вычислить токи ветвей. Полученные результаты сравнить с токами,
найденными по методу контурных токов.
.
В соответствии с индивидуальным заданием, для одной из ветвей найти ток по
теореме об эквивалентном источнике напряжения (или эквивалентном источнике
тока)
.
На основании законов Кирхгофа составить систему независимых алгебраических
уравнений относительно комплексов токов или напряжений ветвей.
.
Проверить правильность решения задачи анализа цепи по выполнению баланса
активных и реактивных мощностей.
.
Построить векторную диаграмму токов ветвей и векторно-топографическую диаграмму
напряжений. В последней показать узловые напряжения и напряжения всех ветвей
схемы.
.
В симметричной трёхфазной цепи определить все мгновенные токи при воздействии
на цепь синусоидальной ЭДС.
.
Построить векторно-топографическую диаграмму.
.
Определить показания ваттметров.
.
Проверить баланс активной мощности.
.
Определить все мгновенные токи при воздействии несинусоидальной ЭДС.
.
Построить график несинусоидальной ЭДС фазы А.
.
Для трехфазной электрической цепи, на входе которой действует симметричная
система ЭДС прямой последовательности определить токи для заданного варианта
продольной или поперечной несимметрии методом симметричных составляющих.
.
Для заданной цепи определить искомый параметр тока или напряжения при
переходном процессе.
.
Построить график искомой величины при переходном процессе.
3. Расчет
простейшей электрической цепи
.1 Схема для
анализа. Исходные данные для простейшей электрической цепи
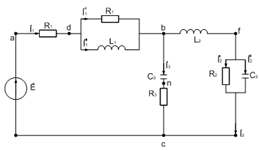
Рис. 1. Схема простейшей электрической цепи
Исходные данные.
Em=10 B R1=2 Oм L1=0.8 мГн C2=159 мкФ
Ψe = -70O R2=2.5 Ом L2=0.99 мГн C3=265 мкФ
ƒ=200 Гц R3=1.5 Ом
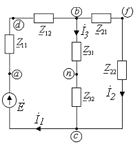
Рис.2. Общий вид рассчитываемой схемы
.2 Метод
расчета простейшей электрической цепи
Вычисляем реактивные сопротивления:
XL1=2
 π
π
 ƒ
ƒ
 L1=2
L1=2
 π
π
 200
200
 0.8
0.8
 10-3=1 Ом
10-3=1 Ом
XL2=2
 π
π
 ƒ
ƒ
 L2=2
L2=2
 π
π
 200
200
 0.99
0.99
 10-3=1.244
Ом
10-3=1.244
Ом
XC2=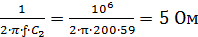
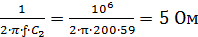
XC3=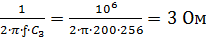
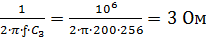
Находим комплексные значения сопротивлений ветвей и всей цепи:
Z1=R1+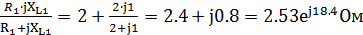
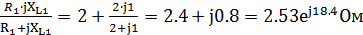
Z2=jXL2+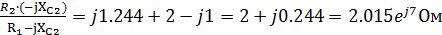
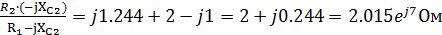
Z3=-jXC3+R3=-j3+1.5=3.354e-j63.4
Ом
Найдем сопротивление параллельных ветвей:
Z23=Z2
 Z3/(Z2+Z3)=2.015ej
Z3/(Z2+Z3)=2.015ej
 3.354e-j63.4/(2+j0.244+1.5-j3)=6.758e-j56.4/(3.5-j2756)=1.517e-j18.2=1.441-j0.474
Ом
3.354e-j63.4/(2+j0.244+1.5-j3)=6.758e-j56.4/(3.5-j2756)=1.517e-j18.2=1.441-j0.474
Ом
Найдем полное сопротивление цепи:
Z23=Z1+Z23=2.4+j0.8+1.441-j0.474=3.841+j0.326=3.855ej4.9
Ом
Находим комплексные действующие значения токов:
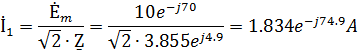
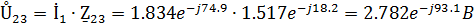
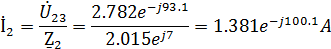
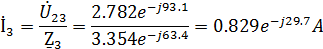
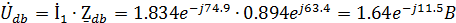
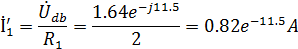
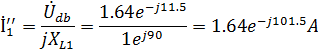
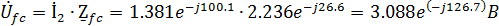
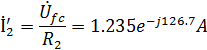
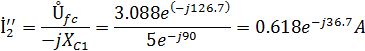
Найдем комплексные действующие значения токов:
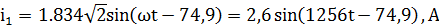
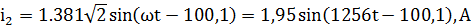
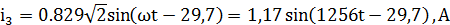
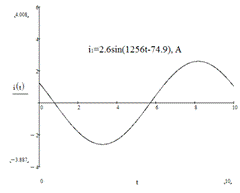
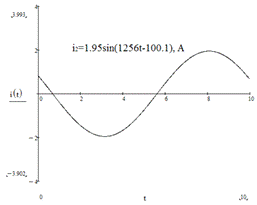
3.3 Проверка
баланса мощностей в простейшей цепи.
Мощность источника
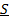
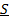 U
U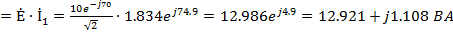
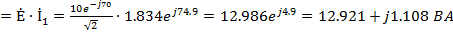

Мощность нагрузки
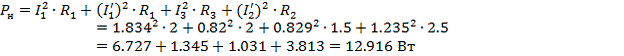
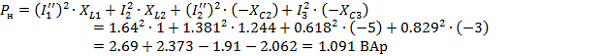
Относительная
ошибка
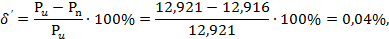
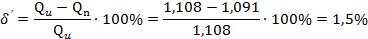
.4 Построение
векторно-топографической диаграммы
Выберем
масштаб токов 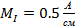
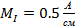 , и
напряжений -
, и
напряжений - 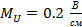
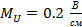 .
.
Полученная
диаграмма приведена в приложении 1. По ней действующее значение напряжения 
 , а сдвиг
фаз между напряжениями
, а сдвиг
фаз между напряжениями 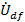
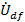 и
и 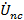
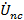 оказался
равным 20°.
оказался
равным 20°.
Находим
мгновенное значение напряжения 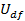
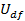 , если
известен ток
, если
известен ток 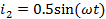
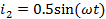
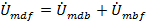
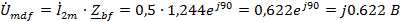
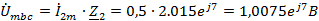
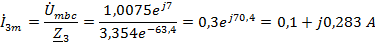
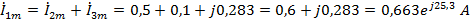
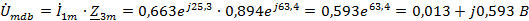
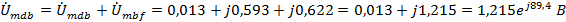
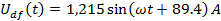
4. Расчет
сложной электрической цепи.
.1 Схема для
анализа. Исходные данные для сложной электрической цепи
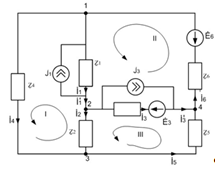
Рис.3. Схема сложной электрической цепи.
Исходные данные:
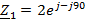
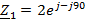 Ом
Ом 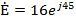
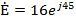 В
В 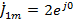
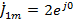 А
А
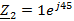
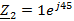 Ом
Ом 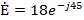
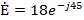 В
В 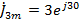
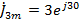 А
А
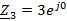
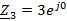 Ом Связи
2,3,6
Ом Связи
2,3,6
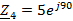
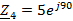 Ом Ветвь
“n” - 2
Ом Ветвь
“n” - 2
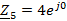
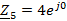 Ом Узел
“0” - 2
Ом Узел
“0” - 2
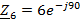
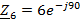 Ом
Ом
Дерево
графа:
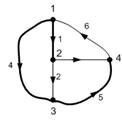
Рис.
4. Граф сложной электрической цепи
.2 Расчет
сложной электрической цепи методом контурных токов
На основании законов Кирхгофа составим систему независимых алгебраических
уравнений относительно токов или напряжений ветвей.
1)
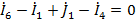
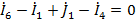
)
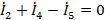
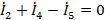
)

I)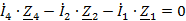
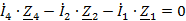
II)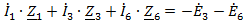
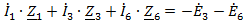
III)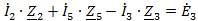
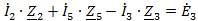
Преобразуем
источники тока в эквивалентные источники ЭДС.
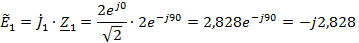
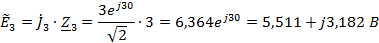
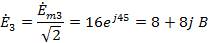
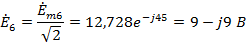
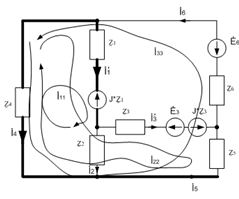
Рис.
5 Преобразованная схема
Составим,
с помощью матриц, систему уравнений подлежащую решения с целью определения
контурных токов.
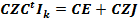
Матрица
основных контуров:
|
1
|
4
|
5
|
2
|
3
|
6
|
|
|
1
|
-1
|
|
1
|
|
|
2
|
|
С =
|
1
|
-1
|
-1
|
|
1
|
|
3
|
|
|
1
|
1
|
|
|
1
|
6
|
Матрицы источников:
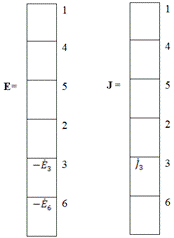
Матрица параметров Z:
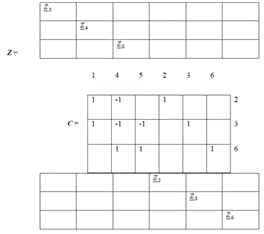

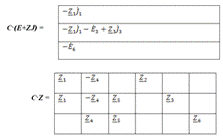

Система уравнений:
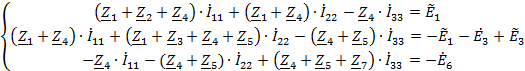
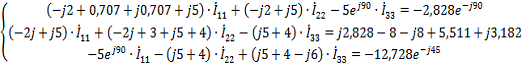
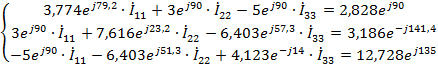
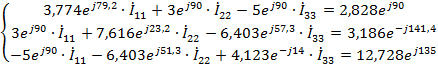
Контурные токи:
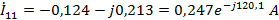
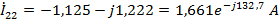
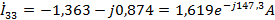
Токи
в ветвях:
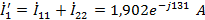
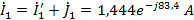
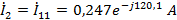
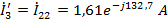
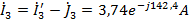

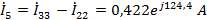
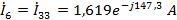
.2 Расчет
сложной электрической цепи методом узловых напряжений
Рассчитаем токи в ветвях методом узловых напряжений.
Преобразуем источники ЭДС в эквивалентные источники тока
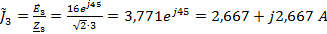
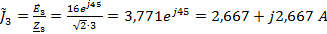
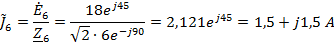
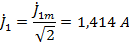
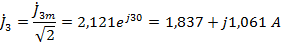
Рассчитаем
проводимости ветвей:
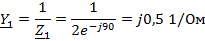
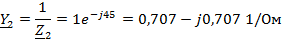
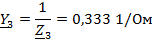
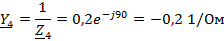
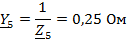
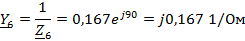
Преобразованная
схема
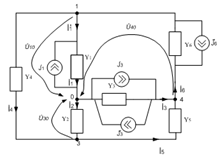
Рис.
6 Преобразованная схема
С
помощью матриц, составим систему уравнений, подлежащую решению с целью
определения узловых напряжений
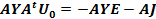
Матрица
интенденции:
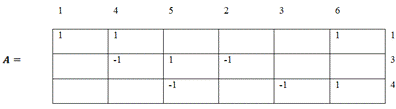
Матрицы
источников
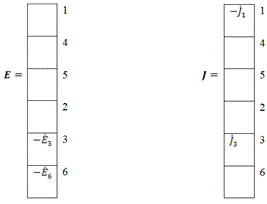
Матрица
параметров 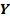
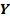
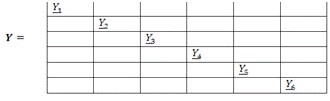
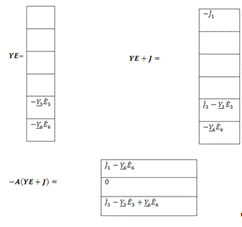
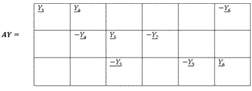
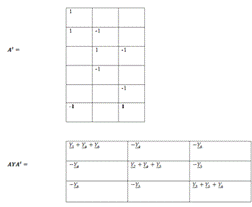
Система
уравнений:
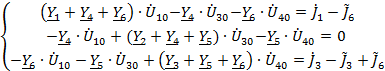
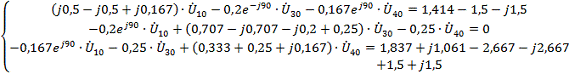
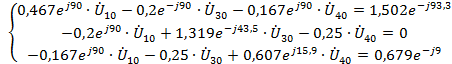
Узловые напряжения:
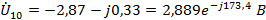
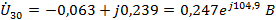
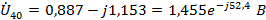
Напряжения
ветвей:
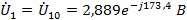
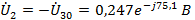

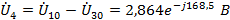
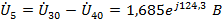
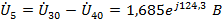
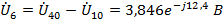
Токи
в ветвях
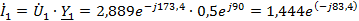
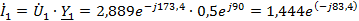 A
A
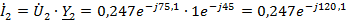
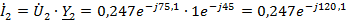 A
A
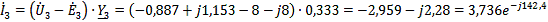
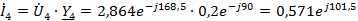
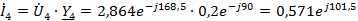 A
A
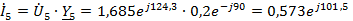
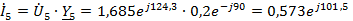 A
A
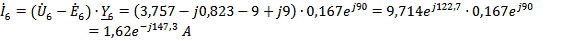
Результаты
расчетов токов двумя методами очень близки.
4.3 Расчет
сложной электрической цепи методом эквивалентного генератора
Определим
ток 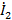
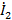 по теореме
об эквивалентном источнике напряжения.
по теореме
об эквивалентном источнике напряжения.
При
определении тока 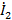
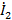 всю
остальную цепь по отношению к этой ветви можно заменить эквивалентным
источником напряжения
всю
остальную цепь по отношению к этой ветви можно заменить эквивалентным
источником напряжения 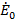
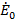 c
внутренним сопротивлением
c
внутренним сопротивлением 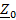
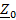 .
.
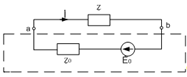
Рис.
7 Схема эквивалентного генератора
Тогда,
искомый ток 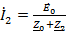
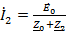 .
.
Чтобы
найти 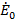
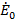 необходимо
разомкнуть ветвь с сопротивлением
необходимо
разомкнуть ветвь с сопротивлением 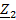
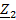 и
вычислить напряжение
и
вычислить напряжение 
 на ее
зажимах, при этом
на ее
зажимах, при этом 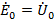
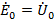 .
.
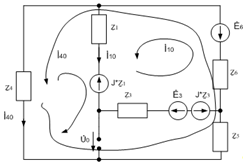
Рис.8
Преобразованная схема
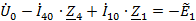
Токи
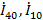
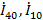 найдем
методом контурных токов.
найдем
методом контурных токов.
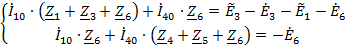
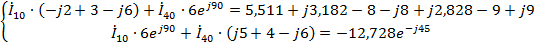
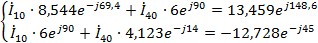
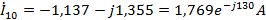
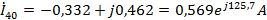
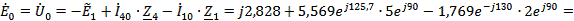
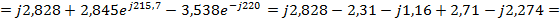
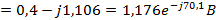
Для
определения 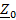
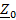 исключаем
все источники цепи и рассматриваем цепь как пассивный двухполюсник по отношению
к зажимам a-b
исключаем
все источники цепи и рассматриваем цепь как пассивный двухполюсник по отношению
к зажимам a-b
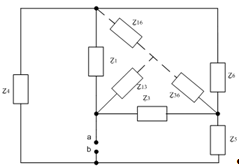
Рис.
9 Преобразованная схема
Преобразуем
треугольник 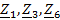
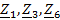 в
эквивалентную звезду
в
эквивалентную звезду
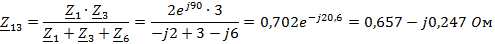
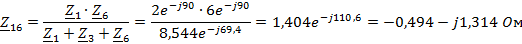
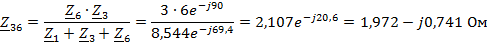
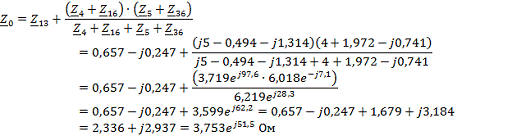
Искомый
ток
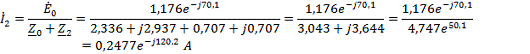
.4 Проверка
баланса активных реактивных мощностей.
Составим баланс активных и реактивных мощностей
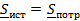
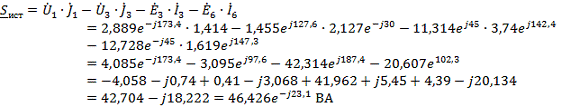
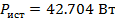
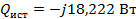
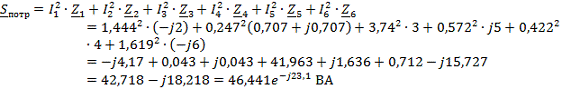
4.5
Построение векторно-топографической диаграммы.
Строим топографическую диаграмму напряжений, сопряженную с векторной
диаграммой токов: приложение 2
5. Расчет
трёхфазных электрических цепей.
.1 Исходные
данные
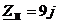 Ом,
Ом, 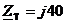 Ом,
Ом,
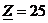 Ом,
Ом, 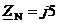 Ом,
Ом,
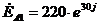 В,
В, 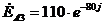 В,
В, 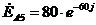 В.
В.
Схема
заданной трехфазной электрической цепи приведена на рис. 1.
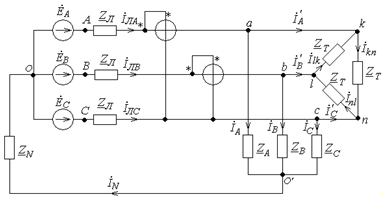
Рис.10.
Схема, рассчитываемой трехфазной ЭЦ
.2 Расчет
симметричного режима трехфазной цепи
Для упрощения расчета данной трехфазной цепи заменим треугольник нагрузки
эквивалентной звездой, где сопротивление плеча равно 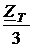 (рис. 2).
(рис. 2).
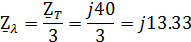
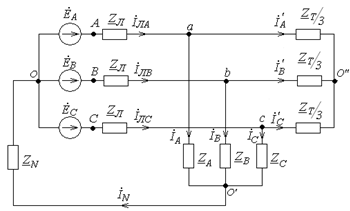
Рис. 11. Преобразованная схема
В полученной схеме вследствие ее симметрии нейтральные точки генератора и
нагрузки могут быть объединены и расчет целесообразно вести для одной фазы,
независимо от других, например, для фазы А.
Выделим фазу А:
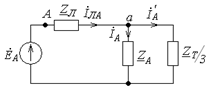
Рис. 12. Расчетная схема для фазы A
Находим токи фазы А:
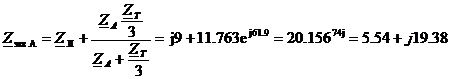 Ом
Ом
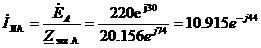 А
А

 A
A
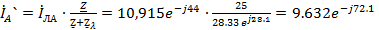
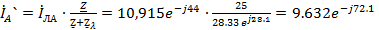 A
A
Токи
фаз В и С:
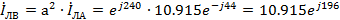
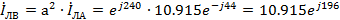 А
А
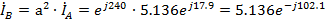
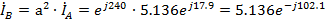 A
A
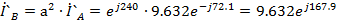
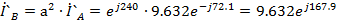 A
A
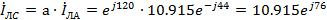
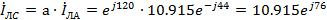 А
А
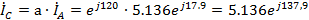
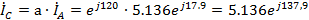 A
A

 A
A
Токи
в фазах треугольника учетом того, что нагрузка симметричная, при указанных на
схеме условных положительных направлениях токов, находим из соотношений:
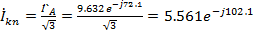
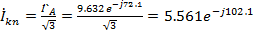 A
A
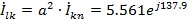
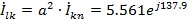 A
A
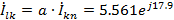
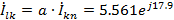 A
A
Мгновенные
токи:
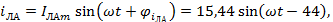
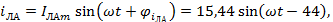 А
А

 A
A

 A
A
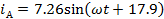
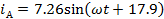 A
A
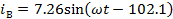
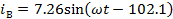 A
A
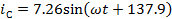
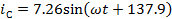 A
A

 A
A
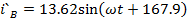
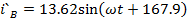 A
A

 A
A
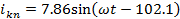
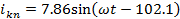 A
A
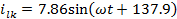
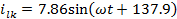 A
A
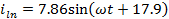
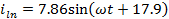 A
A
5.2.1
Построение векторно-топографической диаграммы
На диаграмме сначала строим векторы всех токов. Примем потенциал узла «0»
равным нулю, тогда:
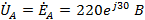
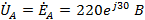
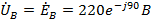
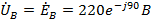
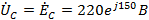
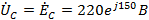
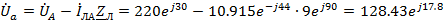
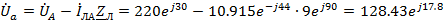 B
B
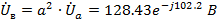
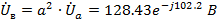
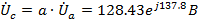
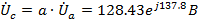
.2.2 Расчет
мощности в трехфазной цепи
В данном случае ваттметры включены в фазы А и В по схеме двух ваттметров,
т.е. Р=РА+РВ.
Определяем показания каждого ваттметра
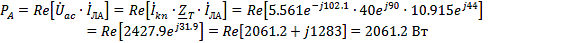
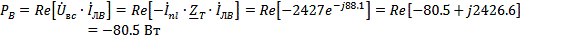
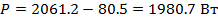
Проверим баланс активной мощности
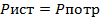
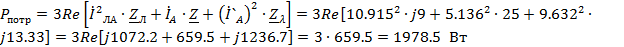
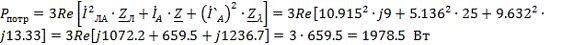
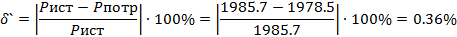
Относительная
ошибка составляет менее 3% что подтверждает правильность расчета.
 5.3
Расчет симметричной трехфазной цепи при воздействии несинусоидальной ЭДС
5.3
Расчет симметричной трехфазной цепи при воздействии несинусоидальной ЭДС
Определить
мгновенные токи 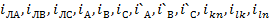
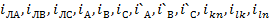 при
воздействии несинусоидальной эдс
при
воздействии несинусоидальной эдс
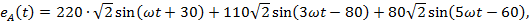
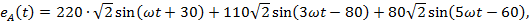 В
В
Так
как нагрузка трехфазной цепи для первой и пятой гармоник является симметричной,
то порядок вычисления токов для каждой из этих гармоник аналогичен порядку
расчета симметричного режима.
Токи
по первой гармонике рассчитаны ранее.
Гармоника
При
расчете токов третьей гармоники необходимо учитывать то положение, что высшие
гармоники, порядок которых кратен трем, образуют систему нулевой
последовательности, т.е. 
 , В, то,
токи фаз А, В, С, также образуя нулевую последовательность, совпадают по фазе и
в нулевом проводе появляется ток утроенной частоты, равный их сумме
, В, то,
токи фаз А, В, С, также образуя нулевую последовательность, совпадают по фазе и
в нулевом проводе появляется ток утроенной частоты, равный их сумме 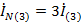
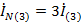
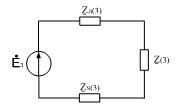
Рис.13.
Расчетная схема третьей гармоники
Рассчитаем
сопротивления для третьей гармоники

 Ом
Ом
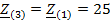
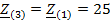 Ом
Ом
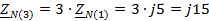
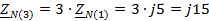 Ом
Ом
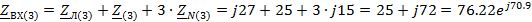
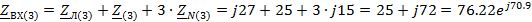 Ом
Ом
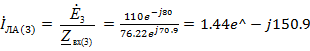
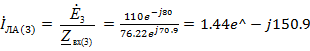 A
A
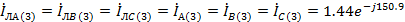
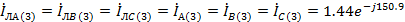 A
A
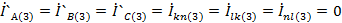
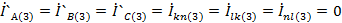 A
A
Гармоника
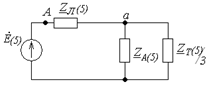
Рис.
14. Расчетная схема для пятой гармоники.
Рассчитаем
сопротивления для пятой гармоники:
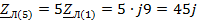
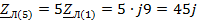 Ом
Ом
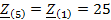
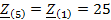 Ом
Ом
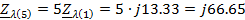
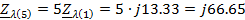 Ом
Ом
Находи
токи фазы А

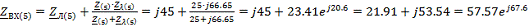 Ом
Ом
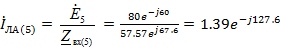
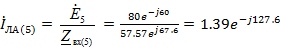 A
A
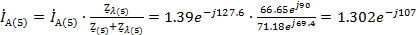
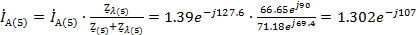 A
A
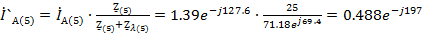
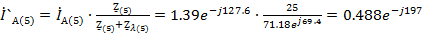 A
A
Токи
фаз В и С
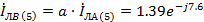
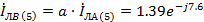 A
A
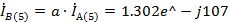
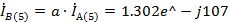 A
A
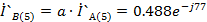
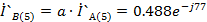 A
A
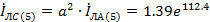
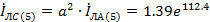 A
A
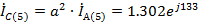
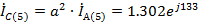 A
A
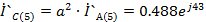
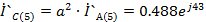 A
A
Токи в фазах треугольника:

 A
A
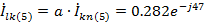
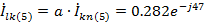 A
A
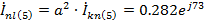
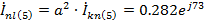 A
A
Мгновенные
токи

 А
А
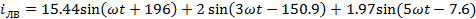
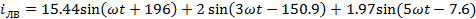 A
A
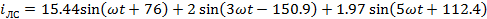
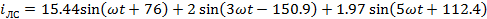 A
A
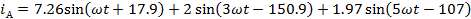
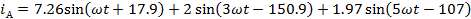 A
A
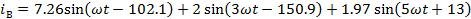
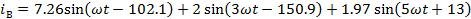 A
A
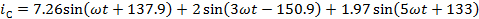
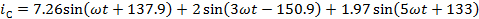 A
A
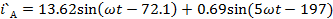
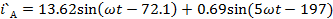 A
A
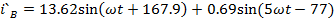
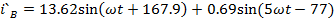 A
A
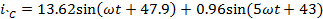
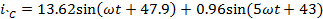 A
A
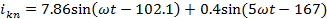
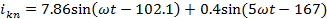 A
A
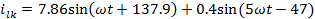
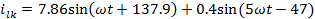 A
A
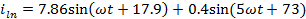
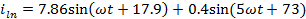 A
A
5.3.1 Расчет
входного ЭДС
Расчет входного ЭДС представляется в виде суммы:
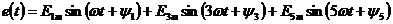
Действующее
значение искомого ЭДС 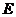 при учете гармоник 1, 3, 5 вычисляется по формуле:
при учете гармоник 1, 3, 5 вычисляется по формуле:
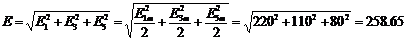 В,
В,
где
действующие значения гармонических составляющих ЭДС 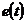 равны:
равны:
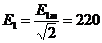 В,
В,
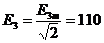 В,
В,
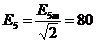 В.
В.
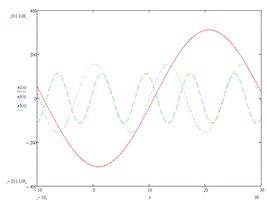
Рис.
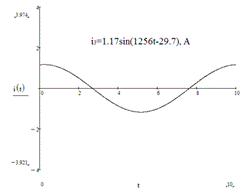
15. Формы ЭДС при первой, третьей и пятой гармониках
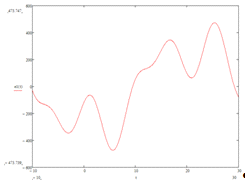
Рис. 16. Форма результирующего, несинусоидального ЭДС
5.4
Анализ трехфазной цепи синусоидального тока методом симметричных составляющих (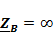
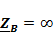 )
)
Метод симметричных составляющих основан на том положении, что любая
несимметричная система токов или напряжений в трехфазной цепи может быть
представлена в виде суммы трех симметричных систем прямой, обратной и нулевой
последовательностей. Если в цепи существуют несимметричные участки, то,
используя принцип компенсации, эти участки заменяют несимметричными источниками
напряжений, которые затем представляют как сумму трех симметричных источников
различных составляющих. После такой замены вся цепь для каждой последовательности
становится симметричной и для неё разноимённые симметричные составляющие токов
и напряжений не зависят друг от друга. Следовательно, дальнейший расчет токов
можно вести относительно симметричных цепей отдельных последовательностей.
Принимая фазу В за основную, составляем расчетные схемы прямой, обратной
и нулевой последовательностей.
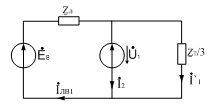 а)
а)
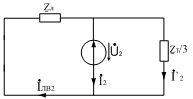 б)
б)
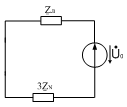 в)
в)
Рис.15. Эквивалентные схемы для а) Прямой, б) обратной, в) нулевой
последовательностей
Для каждой их схем составляем уравнения по второму закону Кирхгофа и три
дополнительных уравнения.
Преобразуем схемы различных последовательностей.
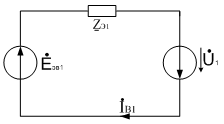 а)
а)
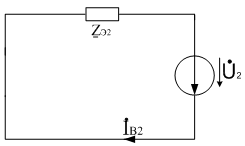 б)
б)
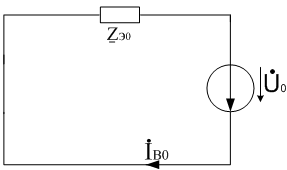 в)
в)
Рис.16. Преобразованные схемы для а) Прямой, б) обратной, в) нулевой
последовательностей.
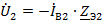
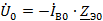
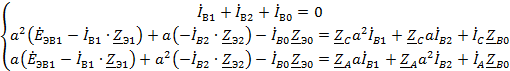
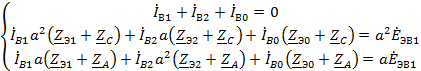
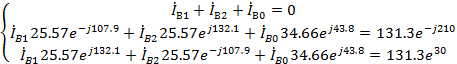
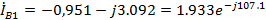
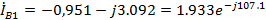 А
А
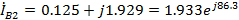
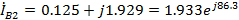 A
A
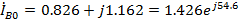
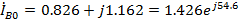 A
A
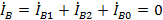
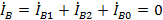 A
A
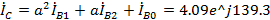
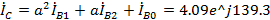 A
A
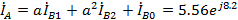
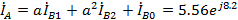 A
A
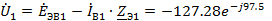
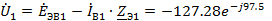 B
B
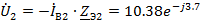
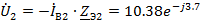 B
B
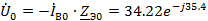
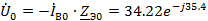 B
B
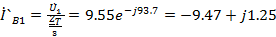
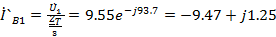 A
A
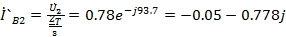
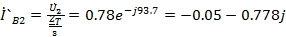 A
A
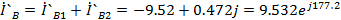
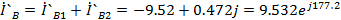
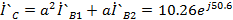
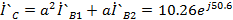 A
A
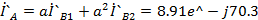
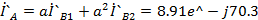 A
A
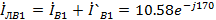
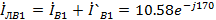 A
A
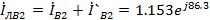
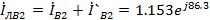 A
A
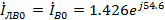
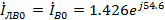 A
A
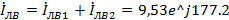
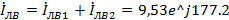 A
A
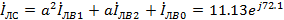
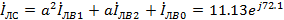 A
A
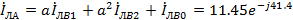
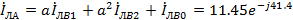 A
A
Мгновенные значения токов:
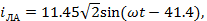
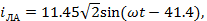 А
А
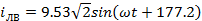
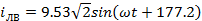 A
A
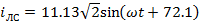
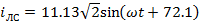 A
A
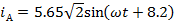
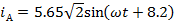 A
A
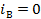
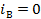 A
A

 A
A

 A
A
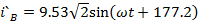
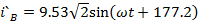 A
A
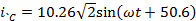
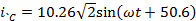 A
A
6. Расчет
переходного процесса в электрической цепи
.1 Исходные
данные
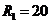 Ом,
Ом, 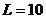 мГн,
мГн,
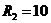 Ом,
Ом, 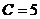 мкФ,
мкФ,
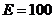 В.
В. 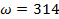
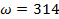 1/С
1/С
Найти
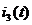
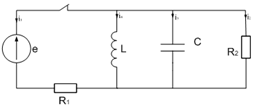
Рис.17.
Исходная схема
Расчет
переходного процесса при действии в электрической цепи постоянной ЭДС
.2 Расчет
переходного процесса в электрической цепи
Классический метод
Рассчитаем независимые начальные условия.
Учтем, что при действии в цепи источника постоянной ЭДС индуктивность L
Имеет нулевое сопротивление(закоротка), а емкость представляет разрыв.
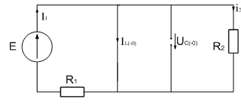
Рис.
18. Схема на момент времени 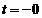
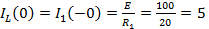
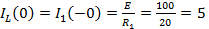 A
A
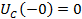
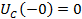 B
B
Таким
образом, имеем независимое начальные условия:
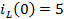
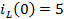 A
A
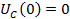
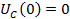 B
B
Рассчитаем
установившийся ток 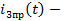
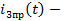 это ток,который
установится в ветви по завершении переходного процесса
это ток,который
установится в ветви по завершении переходного процесса 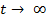
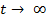
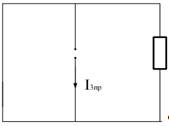
Рис.
19. Схема на момент t=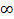
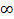
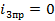
Находим
корни характеристического уравнения.
Для
получения характеристического уравнения составим выражение входного
споротивления 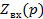
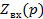 по
отношению к разрыву ветви с емкостью и решим уравнение
по
отношению к разрыву ветви с емкостью и решим уравнение 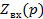
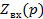 .
Индуктивное сопротивление примем равным за
.
Индуктивное сопротивление примем равным за 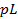
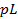 ,
емкостное
,
емкостное 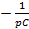
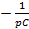
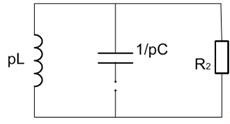
Рис.
20. Пассивная схема.
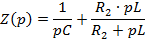
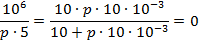
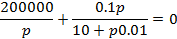
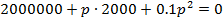
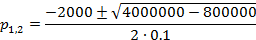
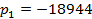
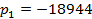
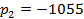
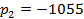
Запишем
выражение свободной составляющей тока 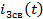
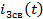 имеем
имеем
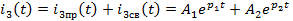
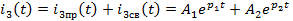
Таким
образом, для тока 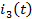
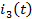 имеем
имеем
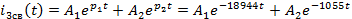
Определим
зависимое начальное условие - значение 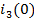
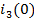 и
и 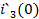
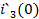
Воспользуемся
послекомутационной схемой цепи при t=0
В
этой схеме индуктивность заменим некой ЭДС, 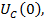
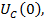 направленным
навстречу току
направленным
навстречу току 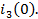
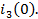 Но т.к.
Но т.к. 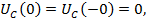
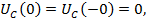 то вместо
источника ЭДС - провод
то вместо
источника ЭДС - провод
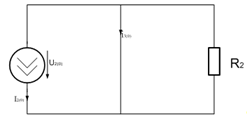
Рис.
21. Схема на момент коммутации (t=0).
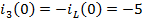
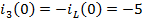 A
A
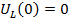
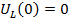 B
B
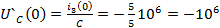
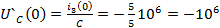 B/c
B/c
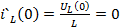
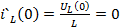 A
A
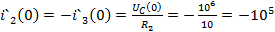
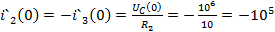 A/c
A/c
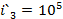
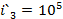 A/c
A/c
Определяем
постоянные интегрирования
Запишем
общий вид искомого решения и его производной
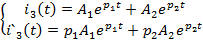
Подставим
в них t = 0
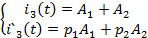
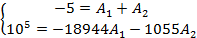
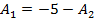
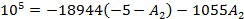
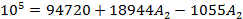
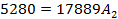
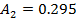
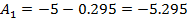
Окончательное
выражение для тока 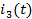
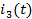 имеет
вид
имеет
вид
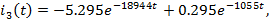
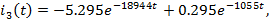 A
A
Строим
график
Форма
тока 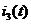 при переходном процессе будет выглядеть следующим
образом:
при переходном процессе будет выглядеть следующим
образом:
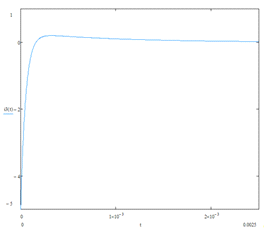
Рис.
22. Форма тока 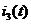 при переходном процессе.
при переходном процессе.
Заключение
Итогами данной курсовой работы является:
· закрепление теоретических знаний и самостоятельное применение их к
анализу электрических цепей;
· выработка навыков и умений в выполнении типового анализа
цепей;
· знакомство с правилами оформления технической документации.
Следует отметить, что все расчеты были выполнены с достаточной точностью
и в пределах максимально допустимой погрешности, а так же были повторно
проверены в программных продуктах Multisim и MathCad.
Литература:
электрический ток
реактивный мощность
1. Л.Р. Нейман, К.С. Демирчан - Теоретические основы
электротехники. Том 1. Санкт-Петербург: «Энергоиздат», 1981г.
2. Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов
- Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М.,
«Энергия», 1975г.
. Т.И. Атабеков - Теоретические основы
электроэнергетики. М.: «Энергия», 1978г.