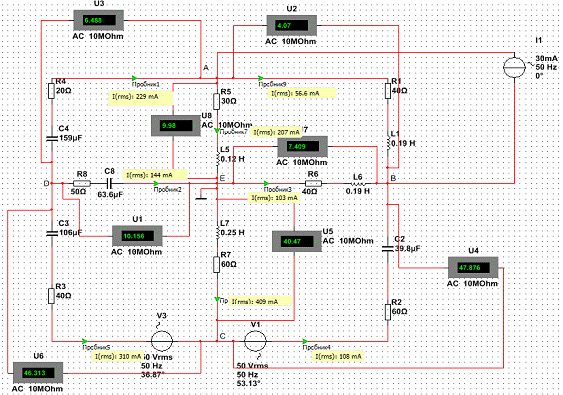
Исследование электрической цепи синусоидального тока
Московский
государственный институт электронной техники
Кафедра
«Электротехники»
Контрольная
работа
Тема
“Исследование электрической цепи синусоидального тока”
по курсу
“Электротехника, электроника и схемотехника. Электротехника”
Выполнил Ильин П.А.
Работу принял Сапожников Б. И.
Москва 2012
Задание 1. Изобразить электрическую схему и ее направленный
граф
|
Z1, Ом
|
Z2, Ом
|
Z3, Ом
|
Z4, Ом
|
Z5, Ом
|
Z6, Ом
|
Z7, Ом
|
Z8, Ом
|
|
40+j60
|
60-j80
|
40-j30
|
20-j20
|
30+j40
|
40+j60
|
60+j80
|
50-j50
|
|
E2, В
|
E3, В
|
J9, мА
|
|
30+j40
|
40+j30
|
30
|
Так как на напряжениях №1,5,6,7 jX>0 то в соответствующих цепях будут содержаться катушки индуктивности,
в цепях №2,3,4,8 - конденсаторы, так как jX<0.
ω = 2 * π * f = 2 * 3.14 * 50 = 314 рад\с
Общие формулы:
L = 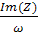 ;
;
C = 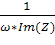 ;
;
Отсюда найдем значения:
L1 = 0,19 Гн
L5 = 0,12 Гн
L6 = 0,19 Гн
L7 = 0,25 Гн
C2 = 3,98*10 -5 Ф
C3 = 1,06*10 -4 Ф
С4 = 1,59*10 -4 Ф
С8 = 6,36*10 -5 Ф
Теперь посчитаем сдвиг фазы ЭДС по формуле
ϕ = arctg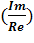 :
:
ϕ1 = arctg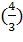 = 0.9 => ϕ1= 53.13 ͦ
= 0.9 => ϕ1= 53.13 ͦ
ϕ2 = arctg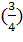 = 0.64 => ϕ1= 36.86 ͦ
= 0.64 => ϕ1= 36.86 ͦ
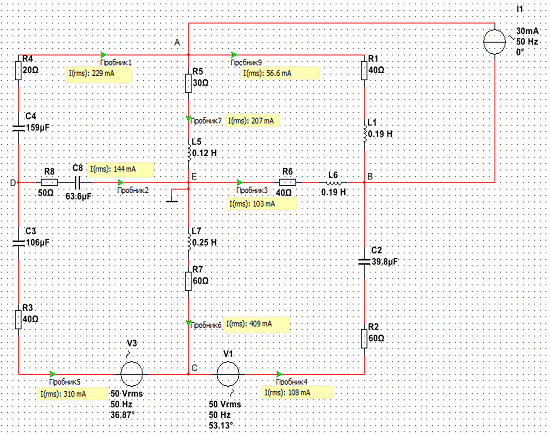
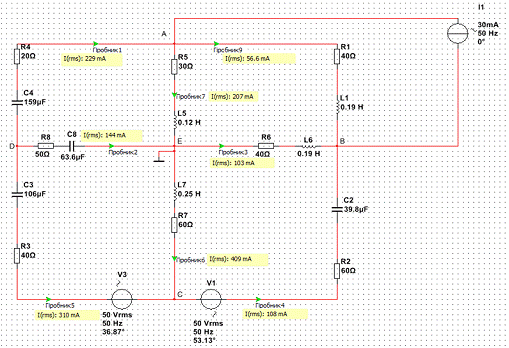
Теперь, когда нам известны все сопротивления, составим схему в Multisim
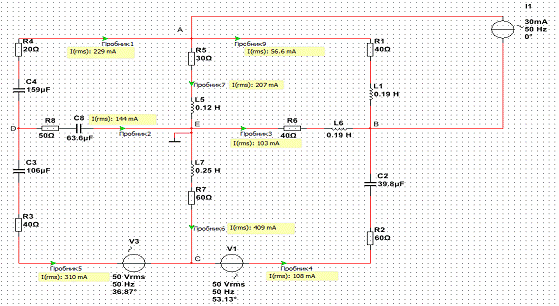
Задание 2. Составить уравнения методом контурных токов
Задаем в каждом независимом контуре схемы свой контурный ток: I11, I22,
I33, I44 и выбираем произвольно условно-положительное направление каждого из
них (по часовой стрелке или против)
I11 (Z1 + Z6 + Z5)
+ I22 Z6 + I33 * 0 - I44 Z5
- J9 ( Z5 + Z6 ) = 0;11 Z6
+ I22 (Z6 + Z2 + Z7) - I33
Z7 + I44 * 0 - J9 Z6 = E2;11
*0 - I22Z7 + I33 (Z7 + Z8
+ Z3) + I44 Z8 = - E3;
I11 Z5 + I22 *0 + I33
Z8 + I44 (Z5 + Z8 + Z4)
+ J9 Z5 = 0;
Задание 3. Во всех ветвях рассчитать токи МКТ. Уравнения
токов представить в алгебраической и полярной (показательной) форме
Из системы выпишем матрицу сопротивлений и напряжений для расчета матрицы
токов с помощью MATLAB и сразу подставим в нее числовые значения:
Z = 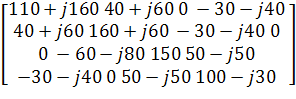 =
= 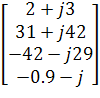
Полученная система уравнений рассчитывается по методу Крамера:
= ∆11/ ∆; I22 = ∆22/ ∆; I33 = ∆33/ ∆
, I44= = ∆44/ ∆
где ∆- определитель системы уравнений
∆ = 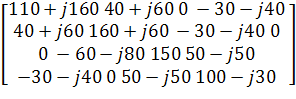
∆11 = 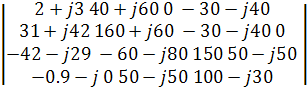
∆22 = 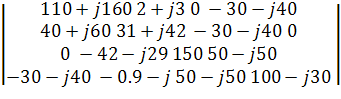
∆33 = 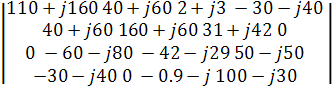
∆44 = 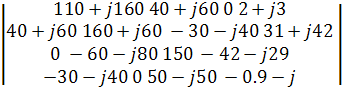
Теперь найдем токи по вышеуказанным формулам:
I11 = 0.0105 - 0.0471i= 0.0891 + 0.0604i= - 0.3067 - 0.0285i=
0.2149 - 0.0845i
Учтем, что1 = I11
I2 = I223 = -I334 = I44
I5 = I4 - I1 + J96
= I1 + I2 - J9
Тогда1
= 0.0105 - 0.0471i2 = 0.0891 + 0.0604i3 = 0.3067 +
0.0285i4 = 0.2149 - 0.0845i
I5 = 0.2044 - 0.0375i
I6 = 0.0996 + 0.0133i
I7 = 0.3958 + 0.0889i
I8 = 0.0918 + 0.1130i
Теперь представим значения токов в показательной форме. Для этого нужно
найти модуль комплексного числа по формуле
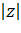 =
=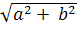
и показатель числа, используя алгоритм:
) Если a>0 (1-ая и 4-ая координатные четверти, или правая
полуплоскость), то аргумент нужно находить по формуле
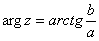 .
.
) Если a<0, b>0 (2-ая координатная четверть), то аргумент нужно
находить по формуле
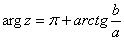 .
.
) Если a<0,b<0 (3-я координатная четверть), то аргумент нужно
находить по формуле
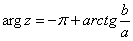 .
.
Отсюда:
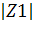 = 0.0482 arg(Z1) =77.4325= 0.0482*
= 0.0482 arg(Z1) =77.4325= 0.0482*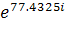
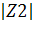 = 0.1076 arg(Z2) = 34.1329= 0.1076*
= 0.1076 arg(Z2) = 34.1329= 0.1076*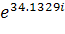
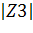 = 0.3080 arg(Z3) = 5.3084= 0.3080*
= 0.3080 arg(Z3) = 5.3084= 0.3080*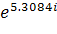
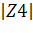 = 0.2309 arg(Z4) = -21.4650= 0.2309*
= 0.2309 arg(Z4) = -21.4650= 0.2309*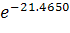
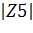 = 0.2078 arg(Z5) = -10.3960= 0.2078*
= 0.2078 arg(Z5) = -10.3960= 0.2078*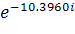
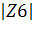 = 0.1004 arg(Z6) = 7.6059= 0.1004*
= 0.1004 arg(Z6) = 7.6059= 0.1004*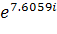
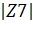 = 0.4056 arg(Z7)= 12.6590= 0.4056*
= 0.4056 arg(Z7)= 12.6590= 0.4056*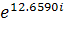
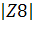 = 0.1455 arg(Z8 )= 50.9099= 0.1455*
= 0.1455 arg(Z8 )= 50.9099= 0.1455*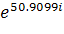
Топологический метод
Составим матрицу B по принципу:
Каждая строка соответствует одному контурному току, и если его
направление совпадает с током в ветви, то пишем 1, если противоположно то -1,
если ток в ветви не относится к данному контурному то 0.
B = 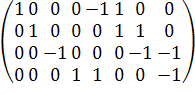
Составим диагональную матрицу из Zn (n=1..8):
Z = 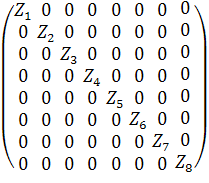
Составим матрицу E, поставив значение En в строки, с их порядковым
номером:
E = 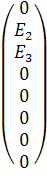
И матрицу J:
J = 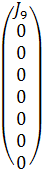
Теперь составим матричное уравнение:
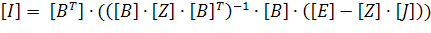
Решив его при помощи Matlab получим:
I1 = 0.0105 - 0.0471i2 = 0.0891 +
0.0604i3 = 0.3067 + 0.0285i4 = 0.2149 - 0.0845i5
= 0.2044 - 0.0375i6 = 0.0996 + 0.0133i7 = 0.3958 + 0.0889i
I8 = 0.0918 + 0.1130i
В показательной форме значения токов имеют вид:
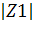 = 0.0482 arg(Z1) =-77.4325= 0.0482*
= 0.0482 arg(Z1) =-77.4325= 0.0482*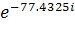
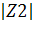 = 0.1076 arg(Z2) = 34.1329= 0.1076*
= 0.1076 arg(Z2) = 34.1329= 0.1076*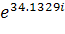
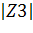 = 0.3080 arg(Z3) = 5.3084= 0.3080*
= 0.3080 arg(Z3) = 5.3084= 0.3080*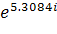
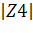 = 0.2309 arg(Z4) = -21.4650= 0.2309*
= 0.2309 arg(Z4) = -21.4650= 0.2309*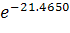
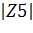 = 0.2078 arg(Z5) = -10.3960= 0.2078*
= 0.2078 arg(Z5) = -10.3960= 0.2078*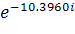
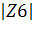 = 0.1004 arg(Z6) = 7.6059= 0.1004*
= 0.1004 arg(Z6) = 7.6059= 0.1004*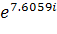
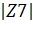 = 0.4056 arg(Z7)= 12.6590= 0.4056*
= 0.4056 arg(Z7)= 12.6590= 0.4056*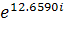
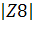 = 0.1455 arg(Z8 )= 50.90998 = 0.1455*
= 0.1455 arg(Z8 )= 50.90998 = 0.1455*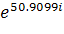
Задание 4. Составить уравнения методом узловых потенциалов.
Расчет матриц выполнить по методу Крамера. Рассчитать токи и напряжения во всех
ветвях. Сравнить полученные токи с токами, вычисленными по МКТ. Потенциалы и
напряжения представить в полярной форме
Заземлим узел E. Тогда ϕe = 0;
Вычислим проводимости в каждой ветви, как обратную величину к
сопротивлению:
Y1 = 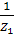 , Y2 =
, Y2 = 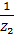 , Y3 =
, Y3 = 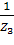 , Y4 =
, Y4 = 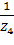 , Y5 =
, Y5 = 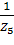 , Y6 =
, Y6 = 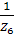 , Y7 =
, Y7 = 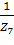 , Y8 =
, Y8 = 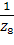 .
.
Теперь составим систему уравнений для каждого из узлов (кроме Е):
А: (Y1+Y4+Y5)∙φa - Y1∙φb - 0∙φc - Y4∙φd = J9
B: -Y1∙φa + (Y1 + Y2 + Y6)∙φb - Y2 ∙φc - 0∙φd = - J9 + E2Y2
С: 0∙φa - Y2∙φb + (Y2 + Y3 + Y7)∙φc - Y3∙φd = - E3∙Y3
- E2∙Y2
D: - Y4∙φa - 0∙φb - Y3∙φc + (Y3 + Y4 + Y8 )∙φd = E3∙Y3
Из данной системы уравнений получим матричное уравнение:
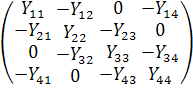 ∙
∙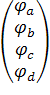 =
= 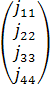
Где
Y11 = Y1+Y4+Y5, Y12 = Y1, Y14 = Y4;
Y21 = Y1, Y22 = Y1+Y2+Y6, Y23 = Y2;
Y32 =Y2, Y33 =Y2+Y3+Y7, Y34 = Y3;
Y41 = Y4, Y43 = Y3,
Y44 = Y3+Y4+Y8.
j11 = J9
j22 = - J9 + E2*Y2,33
= - E3∙Y3 - E2∙Y2 ,44
= E3∙Y3.
Расчёт напряжений проведем по формулам:
Uba = φb - φa,
Ubc = φb - φc,
Udc = φd - φc,
Uda = φd - φa,
Ueb = φe - φb,
Uec = φe - φc,
Ued = φe - φd.
Расчёт токов по формулам:
I1 = 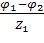 ,
,
I2 = 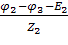 ,3 =
,3 = 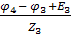 ,4 =
,4 = 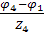 ,5 =
,5 = 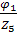 ,
,
I6 = 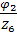 ,7 =
,7 = 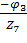 ,8 =
,8 = 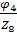 .
.
φa = 7.6316 + 7.0543iВ
φb = 3.1861 + 6.5077iВ
φc = -30.8600 -26.3300iВ
φd = 10.2397 + 1.0644iВ
φe = 01 = 0.0105 - 0.0471i2
= 0.0891 + 0.0604i3 = 0.3067 + 0.0285i4 = 0.2149 -
0.0845i5 = 0.2044 - 0.0375i6 = 0.0996 + 0.0133i7
= 0.3958 + 0.0889i8 = 0.0918 + 0.1130iba = 4.4455 +
0.5466ibc = 34.0461 +32.8377idc = 41.0997 +27.3944ida
= 2.6081 - 5.9899iea = 7.6316 + 7.0543ieb = 3.1861 + 6.5077i
Uec = -30.8600 -26.3300iUed = 10.2397 + 1.0644i
Теперь представим полученные значения в показательной форме:
φa = 10.393 *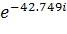 B
B
φb = 7.246 *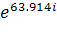 B
B
φc = 40.566 *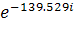 B
B
φd = 10.295 *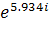 B
B
φe = 01 = 0.0482*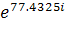 2 = 0.1076*
2 = 0.1076*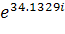 3 = 0.3080*
3 = 0.3080*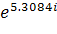 4 = 0.2309*
4 = 0.2309*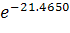 5 = 0.2078*
5 = 0.2078*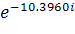 6 = 0.1004*
6 = 0.1004*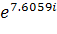
I7 = 0.4056*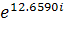
I8 = 0.1455*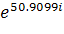
Топологический метод:
Составим матрицу А, где каждая строка будет соответствовать узлу по
принципу: если ток втекает в узел то пишем -1, если вытекает то 1 и 0 если не
имеет отношения к узлу.
A = 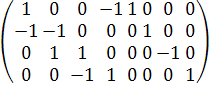
Составим диагональную матрицу из Yn (n=1..8):
Y = 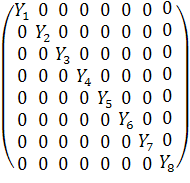
Составим матрицу E, поставив значение En в строки, с их порядковым
номером:
E = 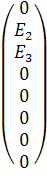
И матрицу J:
J = 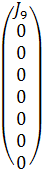
Теперь составим матричное уравнение и решим его в MATLAB:
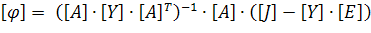
φa = 7.6316 + 7.0543iВ
φb = 3.1861 + 6.5077iВ
φc = -30.8600 -26.3300iВ
φd = 10.2397 + 1.0644iВ
φe = 0
Значения потенциалов совпали.
Задание 5. Определить режимы работы источников. Составить
уравнение баланса мощности. Определить расхождение баланса мощностей источников
и потребителей в процентах
Проверим выполнения баланса мощностей в цепи . Он устанавливает равенство
(баланс) алгебраической суммы мощностей, развиваемых источниками энергии, сумме
мощностей, расходуемых приемниками энергии.
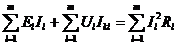 ,
,
где
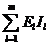 - алгебраическая сумма мощностей источников ЭДС,
причем мощность положительна, если направление
- алгебраическая сумма мощностей источников ЭДС,
причем мощность положительна, если направление 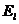 и
и  совпадают, и отрицательна - если не совпадают;
совпадают, и отрицательна - если не совпадают;
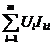 -
алгебраическая сумма мощностей источников тока
-
алгебраическая сумма мощностей источников тока 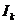 .
.
Мощность
положительна ,если ток источника тока подтекает к точке с большим потенциалом,
и отрицательна, если это условие не выполняется;
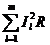 -сумма
мощностей, потребляемых всеми сопротивлениями, где все слагаемые положительны.
-сумма
мощностей, потребляемых всеми сопротивлениями, где все слагаемые положительны.
Исходя
из вышеуказанных правил составим уравнение:
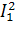 ∙Z1
+
∙Z1
+ 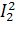 ∙Z2 +
∙Z2 + 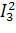 ∙Z3
+
∙Z3
+ 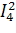 ∙Z4 +
∙Z4 + 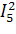 ∙Z5
+
∙Z5
+ 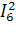 ∙Z6 +
∙Z6 + 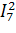 ∙Z7
+
∙Z7
+ 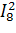 ∙Z8 + J9∙U9 = E2∙I2 + E3∙I3
∙Z8 + J9∙U9 = E2∙I2 + E3∙I3
11.3913 +16.3033i = 11.6700 +15.7170i
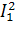 ∙Z1
+
∙Z1
+ 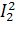 ∙Z2 +
∙Z2 + 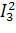 ∙Z3
+
∙Z3
+ 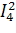 ∙Z4 +
∙Z4 + 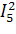 ∙Z5
+
∙Z5
+ 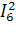 ∙Z6 +
∙Z6 + 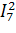 ∙Z7
+
∙Z7
+ 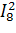 ∙Z8 + J9∙U9 = 11.3913 +16.3033i
∙Z8 + J9∙U9 = 11.3913 +16.3033i
E2∙I2 + E3∙I3 = 11.6700 +15.7170i
.3913 +16.3033i ≈ 11.6700 +15.7170i
Таким образом баланс мощностей выполняется.
Задание 6. Определить число необходимых уравнений,
составленных по законам Кирхгофа. Составить уравнения по законам Кирхгофа для
расчета токов и рассчитать их
Электрическая схема содержит 9 ветвей и 5 узлов. Составляем уравнения по
первому закону Кирхгофа. Число их на единицу меньше числа узлов y=Nуз-1(для
схемы с пятью узлами нужно составить четыре таких уравнения которые являются
линейно-независимыми):
a) -I1 + I4 - I5 + J9
= 0,) I1 + I2 - I6 - J9 = 0,) -I2 - I3 + I7 = 0,
d) I3 - I4 - I8 = 0,
Если к одному из узлов присоединен источник тока, то ток этого источника
тоже должен быть учтен.
Выбираем произвольно направление обхода каждого контура и составляем
уравнения по второму закону Кирхгофа.
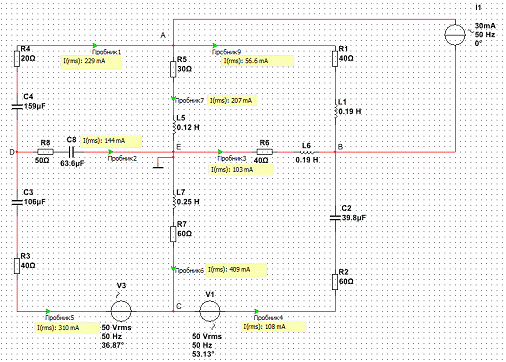
Контуры, для которых составляются уравнения, нужно выбирать так, чтобы
каждый из них включал в себя хотя бы одну новую ветвь. Только при этом условии
уравнения будут независимы друг от друга, а контуры - независимыми. Число
уравнений, составленных по второму закону Кирхгофа, вычисляется по формуле:
=Nв - Nуз + 1 - Nт = 9-5+1-1=4,
где Nв-число ветвей, уз- число узлов,т- число источников тока.
I1*Z1 - I5*Z5 + I6*Z6 =0,
I2*Z2 + I6*Z6 + I7*Z7
= E2,3*Z3 + I7*Z7 + I8*Z8
= E3,4*Z4 + I5*Z5 - I8*Z8
= 0.
В этих уравнениях все ЭДС и токи, совпадающие с направлением обхода
контура, записываются со знаком плюс; ЭДС и токи, направленные навстречу обходу
- со знаком минус.
Общее число уравнений, составленных по первому и второму законам
Кирхгофа, равно числу неизвестных токов, т.е. числу ветвей за исключением
ветвей с источниками тока.
Уравнения Кирхгофа представим в матричной форме:
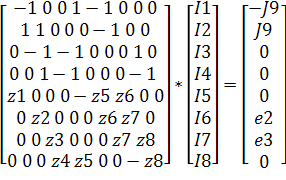
Вычислим значения токов в MATLAB:
I1 = 0.0105 - 0.0471i2 = 0.0891 +
0.0604i3 = 0.3067 + 0.0285i4 = 0.2149 - 0.0845i5
= 0.2044 - 0.0375i6 = 0.0996 + 0.0133i7 = 0.3958 + 0.0889i
I8 = 0.0918 + 0.1130i
Значения токов совпали с ранее найденными.
Задание 7. Рассчитать ток в одной ветви связи МЭГ
Разорвем цепь №2:
Запишем проводимости как величину, обратную сопротивлению для всех
контуров:
Y2 = 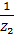 , Y3 =
, Y3 = 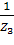 , Y4 =
, Y4 = 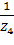 , Y5 =
, Y5 = 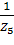 , Y6 =
, Y6 = 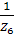 , Y7 =
, Y7 = 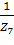 , Y8 =
, Y8 = 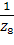 .
.
Система уравнений для узлов a, b, c, d:
a) (Y1+Y4+Y5)∙φa - Y1∙φb - 0∙φc - Y4∙φd = J9,
b) 0∙φa + (Y1 + Y6)∙φb - 0 ∙φc - 0∙φd = - J9,
c) 0∙φa - 0∙φb + (Y3 + Y7)∙φc - Y3∙φd = - E3∙Y3,
d) - Y4∙φa - 0∙φb - Y3∙φc + (Y3 + Y4 + Y8 )∙φd = E3∙Y3.
Из составленных уравнений получим матричное уравнение:
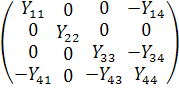 ∙
∙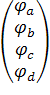 =
= 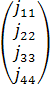 ,
,
где Y11 = Y1+Y4+Y5, Y14 = Y4;
Y22 = Y1+Y6
Y33 = Y3+Y7, Y34
= Y3;41 = Y4, Y43 = Y3,
Y44 = Y3+Y4+Y8.11 = J9,
j22 = - J9, j33 = - E3∙Y3,
j44 = E3∙Y3.
Отсюда, воспользовавшись MATLAB получим:
φa = 7.6316 + 7.0543iВ
φb = 3.1861 + 6.5077iВ
φc = -30.8600 -26.3300iВ
φd = 10.2397 + 1.0644iВ
φe = 0
Найдем ток короткого замыкания.
Направление токов I11, I22, I33, I44:
Система уравнений для токов I11, I22, I33, I44:
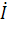 11*( Z5+Z6) +
11*( Z5+Z6) + 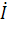 22*Z6 +
22*Z6 + 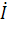 33* 0 - I44*Z5 - J9*(Z5+Z6)
= 0,11*Z6 + I22*(Z2+Z6+Z7)
+ I33*Z7 + I44* 0 - J9*Z6
= 0,11* 0 + I22*Z7 + I33*(Z3+Z7+Z8)
- I44*Z8 = E3,
33* 0 - I44*Z5 - J9*(Z5+Z6)
= 0,11*Z6 + I22*(Z2+Z6+Z7)
+ I33*Z7 + I44* 0 - J9*Z6
= 0,11* 0 + I22*Z7 + I33*(Z3+Z7+Z8)
- I44*Z8 = E3,
I11*Z5 + I22* 0 - I33*Z8
+ I44*( Z4+Z5+ Z8)
+ J9*Z5 = 0.
Матричное уравнение:
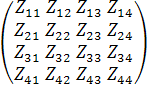 ∙
∙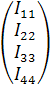 =
= 
где Z11 = Z5+Z6, Z12 = Z6, Z13 = 0, Z14 = -Z5;
Z21 = Z6, Z22 = Z2+Z6+Z7, Z23 = Z7, Z24 = 0;
Z31 = 0, Z32 = Z7, Z33 = Z3+Z7+Z8, Z34 = -Z8;
Z41 = -Z5, Z42 = 0, Z43 = -Z8, Z44 = Z4+Z5+Z8.
E11
= J9*(Z5+Z6), E22 = J9*Z6, E33 = E3, E44 = - J9*Z5.
Сопротивление нагрузки
Zнагр = 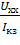 =
= 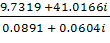 = 288.64+264.67i
= 288.64+264.67i
Ток вычислим по формуле
I2 = 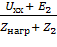
I2 = 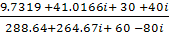 = = 0.0891 + 0.0604i
= = 0.0891 + 0.0604i
Задание 8. Рассчитать и построить топографические диаграммы
Топографическая диаграмма токов:
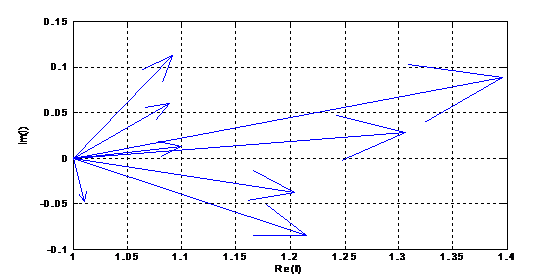
Топографическая диаграмма потенциалов и напряжений:
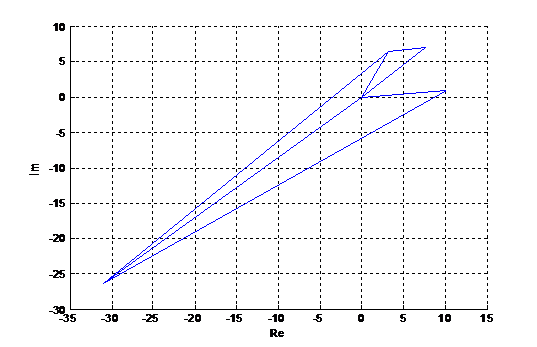
ток
короткий замыкание мощность
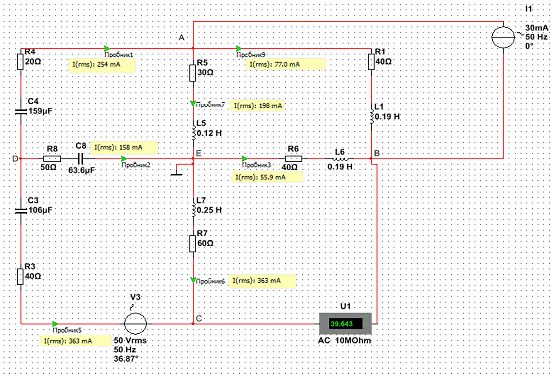
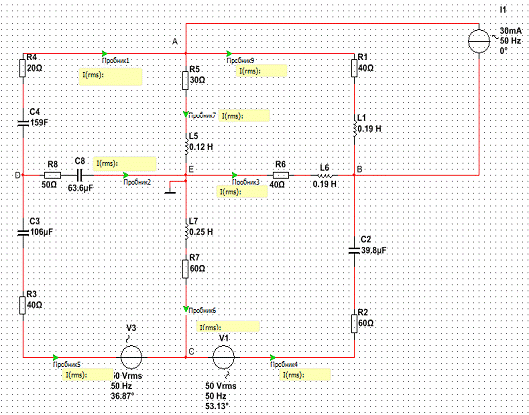
Задание 9. Собрать схему в среде Multisim