Математическая статистика
Содержание
Тема № 1. Теория статистики
Формы статистического наблюдения
Виды статистического наблюдения
Способы статистического наблюдения
Виды группировок
Группировочный признак. Интервал группировки, частота
Тема № 2. Статистическое наблюдение
Виды динамических рядов
Аналитические показатели динамики
Структура ряда динамики
Анализ сезонных колебаний
Анализ взаимосвязанных рядов динамики
Тема № 3. Статистические величины
Абсолютные величины
Относительные величины
Тема № 4. Выборочный метод
Понятия генеральной совокупности и выборки
Представление выборки в виде статистического ряда, графическое
отображение статистического ряда: полигон частот, гистограмма
Эмпирическая функция распределения
Тема № 5. Точечное оценивание
Несмещенность и состоятельность оценок
Асимптотический подход к сравнению оценок
Тема № 6. Интервальное оценивание
Доверительный интервал и вероятность
Тема № 7. Проверка статистических гипотез
Уровень значимости и мощность
Построение оптимальных критериев
Критерии согласия
Критерии, основанные на доверительных интервалах
Тема № 8. Оценивание статистической зависимости
Ковариация и коэффициент корреляции
Тема
№ 1. Теория статистики
Формы
статистического наблюдения
К основным организационным формам статистического наблюдения
относят: статистическая отчетность; специально организованное наблюдение.
Важнейшей формой статистического наблюдения является
отчетность.
Отчетность - это форма статистического наблюдения, при
которой в соответствующие статистические органы поступают в определенные сроки сведения
от предприятий и организация, которые осуществляют экономическую деятельность.
Сведения должны подаваться в установленном законом порядке отчетных документов.
Отчетные документы должны быть заполнены на основании данных
первичного учета и подписаны лицами, ответственными за предоставленные
сведения. Органами государственной статистики утверждаются формы статистической
отчетности.
В коммерческой деятельности отчетность подразделяется на:
) общегосударственную - обязательна для всех организаций и
представляется в сводном виде в органы государственной статистики;
) внутриведомственную - эта отчетность действует в пределах
ведомств и министерств.
Существуют следующие формы отчетности:
) типовой называют отчетность, которая содержит показатели,
одинаковые для всех предприятий, учреждений различных организационных форм, а
также для иных видов деятельности;
) если предприятие имеет свои определенные особенности, то в
эту организацию вводится специализированная отчетность;
) отчетность, предоставляемая каждым предприятием в
одинаковые промежутки времени, называется периодической;
) отчетность, которая поступает в органы статистики по мере
необходимости, называется единовременной отчетностью. Каждая организация вправе
выбирать, по какому способу ей предоставить отчетные данные.
В настоящее время существует большое множество способов
поступления статистических данных в органы статистики, например почтовая и
срочная предоставляется по телеграфу, телетайпу факсу и другими способами.
Специально организованное статистическое наблюдение - это сбор сведений
посредством переписей, единовременных обследований и учета. Примером специально
организованного статистического наблюдения может служить инвентаризация на
предприятии.
Все формы статистической отчетности утверждаются Росстатом. В
правовой статистике наблюдение проводится главным образом в форме
государственной статистической отчетности, которая поступает в отделы
статистики соответствующих органов МВД России, Прокуратуры РФ, Верховного суда
РФ, Высшего Арбитражного Суда РФ и Минюста России.
Генеральная прокуратура Российской Федерации совместно с
заинтересованными федеральными министерствами и ведомствами разрабатывает
систему и методику единого учета и статистической отчетности о состоянии
преступности, раскрываемости преступлений, следственной работе и прокурорском
надзоре, а также устанавливает единый порядок формирования и представления
отчетности в органах прокуратуры. В этих целях используются формы
статистической отчетности.
Данные статистической отчетности могут служить эффективным
средством управления социальными процессами лишь при соблюдении следующих общих
требований к отчетности:
отчетные данные должны быть достоверными, полными, точными и
своевременными;
данные отчетности должны быть сопоставимы, то есть, единообразны
по своим качественным признакам и отрезкам времени.
Следующая форма статистического наблюдения - специально
организованное статистическое наблюдение. Данная форма наблюдения применяется
при необходимости получения показателей, не охваченные официальной
статистической отчетностью. Наиболее простым примером данного наблюдения
является перепись. Перепись - это специально организованное наблюдение,
повторяющееся, как правило, через равные промежутки времени, с целью получения
данных о численности, составе и состоянии объекта наблюдения по ряду признаков.
Из всех переписей наиболее известны переписи населения.
В правовой статистике данная форма наблюдения используется
редко. Например, при изучении эффективности мер борьбы с преступностью может
возникнуть необходимость изучить участие сотрудников правоохранительных органов
в правовой пропаганде, работу по повышению их квалификации. В этих целях
соответствующими подразделениями органами внутренних проводятся специально
организованные плановые и внеплановые проверки (обследования).
Регистровая форма наблюдения - это форма непрерывного
статистического наблюдения за долговременными процессами, имеющими
фиксированное начало, стадию развития и фиксированный конец. В практике
статистики различают регистры населения и регистры предприятий. В правовой
статистике данная форма наблюдения не применяется.
В настоящее время получило распространение специально
организованное систематическое наблюдение за состоянием явлений и процессов,
объектов совокупности, то есть мониторинг. Мониторинг используется для
характеристики и слежения за социальными индикаторами, позволяющими
исследовать, например, качество жизни, ее уровень и т.д. Так, в целях принятия
мер по противодействию легализации (отмыванию) доходов, полученных преступным
путем, и финансированию терроризма и координирующим деятельность в этой сфере
иных федеральных органов исполнительной власти Правительством РФ была
образована Федеральная служба по финансовому мониторингу. Одной из функций
данной службы является осуществление сбора, обработки и анализа информации об
операциях (сделках) с денежными средствами или иным имуществом, подлежащих
контролю в соответствии с законодательством Российской Федерации.
Виды
статистического наблюдения
Статистическое наблюдение по времени регистрации фактов
подразделяется на:
текущее наблюдение - наблюдение, которое проводится, когда
необходимо зарегистрировать все единицы совокупности, случаи, факты и т.п. по
мере их возникновения и с целью изучения динамики какого-либо явления;
периодическое наблюдение - наблюдение, которое проводится
через определенные промежутки или периоды времени. Например, перепись
населения.
единовременное наблюдение - наблюдение, которое производится
по мере возникновения потребности в сборе данных, в исследовании конкретного
явления или процесса, не охватываемого показателями текущей статистики.
По полноте охвата единиц исследуемой совокупности
статистическое наблюдение бывает следующих видов:
сплошное наблюдение - это полный учет всех единиц
совокупности. Основные недостатки данного вида наблюдения: не обеспечение
полного охвата всех без исключения единиц совокупности и большие расходы на его
проведение;
несплошное наблюдение - это наблюдение, при котором
регистрации подлежит только часть единиц изучаемой совокупности. В свою
очередь, несплошное наблюдение можно подразделить на способы основного массива,
выборочный и монографический. Несплошное наблюдение по способу основного
массива основывается на регистрации и изучении самых существенных, наиболее
крупных единиц совокупности. Например, при изучении криминальной ситуации в
области для статистического наблюдения отбираются районы, занимающие
преобладающее значение по основным показателям (территории, совершенным
преступлениям и т.п.). Монографический способ несплошного наблюдения
применяется для глубоко изучения единичных, но типичных в криминологическом
отношении объектов. Оно проводится в основном с целью выявления имеющихся или
намечающихся тенденций в развитии какого-либо явления. Выборочный способ несплошного
наблюдения заключается в исследовании доступной наблюдению либо специально
отобранной части (выборки) совокупности, в основном из-за того, что не всегда
можно изучить всю совокупность в целом.
Способы
статистического наблюдения
Непосредственное получение статистической информации
проводятся разнообразными способами.
Непосредственное наблюдение - это метод сбора информации об
изучаемом объекте путем непосредственного восприятия и регистрации фактов,
касающихся изучаемого объекта и значимых с точки зрения целей исследования. К
таким фактам можно отнести взвешивание, замер, подсчет и т.п. В процессе
применения данного наблюдения появляется возможность существенно расширить
программу наблюдения за счет новых ранее не предполагавшихся с точки зрения
обстоятельств. Объектами такого наблюдения могут быть:
результаты действия (бездействия) правонарушителей, а также
лиц, осуществляющих профилактику правонарушений;
высказывания, реакции, суждения правонарушителей или лиц из
контрольной группы;
поведение правонарушителей в условиях конкретной ситуации;
По положению наблюдателя, его участию в исследуемой ситуации
наблюдение бывает полным, включенным и наблюдением-участием.
Полное наблюдение - это наблюдение, где исследователь изучает
значимые явления пассивно, как бы со стороны.
Включенное наблюдение предполагает изучение криминогенных
явлений и процессов изнутри путем непосредственного восприятия исследователем
изучаемой ситуации, группы, событий повседневной жизни. Исследователь как бы
смешивается с группой, становится одним из ее членов. Основным недостатком
данного наблюдения является то, что для внедрения в какую-либо группу перед
исследователем может встать нравственно-этический вопрос об участии в
аморальных или, например, противоправных действиях, что недопустимо.
При наблюдении - участии наблюдатель позитивно участвует в
изучаемых им процессах и явлениях, то есть непосредственно являющиеся активными
членами изучаемой группы, событий повседневной жизни. Например, сотрудники
правоохранительных органов, изучающие криминальные явления, активно участвующие
в противодействии им путем проведения следственной, прокурорской работы.
В зависимости от источника статистической информации
различают два способа наблюдения:
документальный способ основан на использовании в качестве
источника статистической информации различного рода документов, в основном
носящие учетный характер. На документах базируется отчетность.
Способ опроса, где источником информации являются сами
опрашиваемые лица. Данный способ основан на непосредственном или опосредованном
взаимодействии между исследователем и опрашиваемым лицом.
математическая статистика ряд динамика
В зависимости от того, с какой точность надо провести
наблюдение, возможность практического применения того или иного способа,
материальных возможностей можно выделить следующие способы опроса:
очный опрос - это способ сбора информации, основанный на
непосредственном взаимодействии между исследователем и опрашиваемым лицом.
Например, данный способ опроса можно применить к лицам ближайшего окружения
преступника. На достоверность информации полученной в ходе данного сбора
информации влияет ряд обстоятельств: момент, время и место опроса,
подготовленность интервьюера, процедура оповещения респондента о предстоящем
вопросе.
интервью - это способ сбора информации, основанный на
посредственном взаимодействии между исследователем и опрашиваемым лицом.
Различают свободное и направленное (программируемое) интервью.
анкетный опрос - одни из эффективных и широко применяемых в
правовых исследованиях методов получения сведений о мнениях и настроениях лиц,
уровнях понимания ими проблем правосознания и т.п. Основными преимуществами
данного опроса по отношению к очному опросу является, то что он дает
возможность в короткий срок и при сравнительно небольших материальных затратах
охватить представительскую группу изучаемых лиц, получить сведения "из
первых рук"; быстро провести повторные опросы через определенный
промежуток времени в целях выявления происшедших изменений и т.п.
С точки зрения цели получения данных могут использоваться
следующие способы собирания данных.
Экспедиционный (устный) способ основан на проведении опроса в
виде заполнения формуляров (анкет, переписные листы и т.п.) специально
подготовленными регистраторами, которые одновременно контролируют правильность
получаемых ответов.
Корреспондентский способ заключается в предоставлении
исследователю информации добровольными корреспондентами на специально
разработанном бланке.
Явочный способ предусматривает предоставление данных в
органы, ведущие наблюдение в явочном порядке, например, при регистрации браков,
разводов, налоговых деклараций и т.п.
Не менее важное место в организации проведения
статистического наблюдения занимает подготовка кадров, их инструктаж по
вопросам заполнения статистических документов, соблюдения сроков и
ответственности за качество работы.
Размножение документации самого наблюдения, рекомендации по
заполнению статистических отчетов, их рассылка на места также относятся к
организационным вопросам.
Виды
группировок
При проведении группировки приходится
решать ряд задач:
) выделение группировочного признака;
) определение числа групп и величины
интервалов;
) при наличии нескольких группировочных
признаков описание того, как они комбинируются между собой;
) установление показателей, которыми
должны характеризоваться группы, т.е. сказуемого группировки.
Статистические группировки и классификации
преследуют цели выделения качественно однородных совокупностей, изучения
структуры совокупности, исследования существующих зависимостей. Каждой из этих
целей соответствует особый вид группировки: типологическая, структурная,
аналитическая (факторная).
Типологическая группировка решает
задачу выявления и характеристики социально-экономических типов (частных
подсовокупностей).
Структурная дает возможность описать
составные части совокупности или строение типов, а также проанализировать
структурные сдвиги.
Аналитическая (факторная) группировка
позволяет оценивать связи между взаимодействующими признаками.
В зависимости от числа положенных в их основание
признаков различают простые и многомерные группировки.
Группировка, выполненная по одному
признаку, называется простой.
Многомерная группировка производится
по двум и более признакам. Частным случаем многомерной группировки является комбинационная
группировка, базирующаяся на двух и более признаках, взятых во взаимосвязи,
в комбинации.
Структурная группировка применяется для
характеристики структуры совокупности и структуры сдвигов.
Структурный называется группировка, в
которой происходит разделение выделенных с помощью технологической группировки
типов явлений, однородных совокупностей на группы, характеризующие их структуру
по какого либо варьирующему признаку. Например, группировка населения по
размеру среднедушевого дохода. Анализ структурных группировок взятых за ряд
периодов или моментов времени, показывает изменения структуры изучаемых
явлений, то есть структурные сдвиги. В изменении структуры общественных явлений
отражаются важнейшие закономерности их развития.
Показатель численности групп представлен
либо частотой (количеством единиц в каждой группе), либо частотностью (удельным
весом каждой группы).
Среди простых группировок особо выделяют
ряды распределения.
Ряд распределения - это группировка, в
которой для характеристики групп (упорядоченно расположенных по значению
признака) применяется один показатель - численность группы. Другими словами,
это ряд чисел, показывающий, как распределяются единицы некоторой совокупности
по изучаемому признаку.
Ряды, построенные по атрибутивному
признаку, называются атрибутивными рядами распределения.
Ряды распределения, построенные по
количественному признаку, называются вариационными рядами.
Примером атрибутивных рядов могут служить
распределения населения по полу, занятости, национальности, профессии и т.д.
Примером вариационного ряда распределения
могут служит распределения населения по возрасту, рабочих - по стажу работы,
заработной плате и т.д.
Вариационные ряды распределения состоят их
двух элементов вариантов и частот.
Вариантами называются числовые значения
колличественного признака в ряду распределения, они могут быть положительными и
отрицательными, абсолютными и относительными.
Частоты - это численности
отдельных вариантов или каждой группы вариационного ряда. Сумма всех частот
называется объемом совокупности и определяет число элементов всей совокупности.
Вариационные ряды в зависимости от
характера вариации подразделяются на дискретные и интервальные.
Группировочный
признак. Интервал группировки, частота
Основными вопросами метода группировок являются выбор
группировочного признака и определение числа групп или интервала группировок.
Группировочный признак - признак, принимаемый за основу
образования групп в процессе статистической группировки. Группировочный признак
иначе называется основанием группировки. В зависимости от задач исследования в
качестве группировочного признака может быть взят один или несколько признаков.
Например, при группировке предприятий по их размерам в качестве группировочного
признака могут быть взяты объем выпущенной продукции, стоимость основных
производственных фондов, число работающих и др., каждый в отдельности или 2-3 в
сочетании. Выбор группировочного признака в значительной степени определяет
результаты группировки и выводы, делаемые на их основе.
Социально-экономические явления отличаются большим
многообразием форм своего развития, и поэтому при группировке встает вопрос о
выборе определяющих признаков, которые наиболее полно и точно характеризуют
изучаемый объект, позволяют выбрать его типичные черты и свойства. Например,
промышленное предприятие характеризуется различными признаками, каждый из
которых имеет определенное значение. Тем не менее, основным, существенным
признаком величины предприятия является объем произведенной продукции.
Правильный выбор группировочных признаков возможен лишь на
основе анализа сущности явления, базирующегося на учете особенностей развития
изучаемого явления в конкретных условиях места и времени. Учет конкретных
условий приводит к тому, что один и тот же тип явления может быть выявлен в
одних условиях по одному признаку, а в других - по другому.
После выбора группировочного признака устанавливается
количество групп (n) и величина интервала (i), которые между собой
взаимосвязаны. Одним из основных требований, возникающих при решении данного
вопроса, является выбор такого числа групп и величины интервала, которые
позволяют более равномерно распределить единицы совокупности по группам и
достичь при этом их представительности, качественной однородности.
Выбор числа групп зависит от целей исследования, значения
изучаемого признака, объема статистической информации и т.д. Количество групп
во многом зависит от группировочного признака. Нередко атрибутивные
группировочные признаки предопределяют число групп (группировка работников по
образованию, по квалификации). Аналогично расчленяется совокупность по
дискретному признаку, изменяющемуся в незначительном диапазоне (например, семей
- по числу их членов).
Интервалы групп устанавливаются только при значительной
колеблемости дискретного признака или при непрерывно изменяющемся
количественном признаке. Разность между верхней и нижней границами интервала
составляет его величину. Правильное установление величины интервала имеет
первостепенное значение для образования качественно однородных групп, нельзя объединять
в одну группу явления, которые относятся к разным частным совокупностям. При
группировке рабочих по проценту выполнения норм времени не следует включать в
одну и ту же группу рабочих, выполняющих и не выполняющих нормы времени.
Например, нецелесообразно образовывать группу 95-110%, надо образовать две
группы 95-100% и 101-110%.
В зависимости от степени колеблемости группировочного
признака, характера распределения статистической совокупности устанавливаются
равные или неравные интервалы. Величина равных интервалов определяется как
разность между максимальным и минимальным значениями признака в совокупности,
деленная на заранее заданное число образуемых групп. Не существует строгих
научных приемов, позволяющих определить число групп для любых взаимосвязей
показателей. Число групп тесно связано с объемом совокупности, иногда для
определения для определения интервала группировок может быть использована
формула Стерджесса (обычно при незначительной вариации признаков):
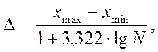
где 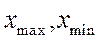 - максимальное и минимальное значение признака
ряда распределения;- число единиц совокупности.
- максимальное и минимальное значение признака
ряда распределения;- число единиц совокупности.
Например, при 200 единицах совокупности число групп
определяется следующим образом:
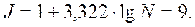
Если колеблемость признака осуществляется неравномерно и в
больших пределах, используются неравные интервалы, прогрессивно возрастающие
или убывающие. Обычно неравные интервалы увеличиваются при переходе к большим
значениям признака. Например, выделяются следующие группы промышленных
предприятий по численности рабочих: до 100, 101-200, 201-500, 501-1000,
1001-3000, 3001-10000, 10001 и более.
Интервалы могут быть закрытыми и открытыми. Закрытыми
называются интервалы группировок, у которых обозначены обе границы интервалов,
открытыми - интервалы, у которых указана только одна граница - верхняя у
первого, нижняя - у последнего интервала группировок. Необходимость в открытых
интервалах обусловлена большой колеблемостью изучаемого признака, разбросом его
количественных значений, требующих образования множества групп, если отделять
их обеими границами. При обработке статистических данных интервалы необходимо
закрывать. Величина первого интервала принимается равной величине второго, а
последнего - величине предыдущего.
При отнесении единиц совокупности к той или иной группе
важное значение имеет точное установление границ, которые в большинстве случаев
обозначаются значением признака "от" - "до". Например
группы предприятий по числу работающих обозначаются следующим образом: 101-200,
201-500501-1000 и т.д. Этот прием позволяет четко обозначить границы и
правильно распределить единицы совокупности по группам. Однако на практике
нередко (при непрерывно изменяющемся признаке) одно и то же число служит
верхней и нижней границами двух смежных групп. Например, группы рабочих по
заработной плате обозначаются: до 150 тыс. руб., 150-180, 180-210, 210-240,
свыше 240 тыс. руб. При таком построении интервала отнесение единиц
совокупности к группам решается двумя способами: по принципу
"включительно" рабочие, имеющие заработную плату 150 тыс. руб., будут
отнесены к первой группе; по принципу "исключительно" этот рабочий
включается во вторую группу. Применение данных принципов зависит от формы написания
интервалов, особенно первой и последней групп. В данном примере рабочих,
заработная плата которого 240 тыс. руб., включается в предпоследнюю группу,
т.к. границы предпоследней группы обозначены 210-240, а последней - свыше 240
тыс. руб. Соответственно работник с заработной платой 150 тыс. руб. относится к
первой группе. Если бы последний интервал обозначался "240 и более",
то по принципу "исключительно" рабочий с заработной платой 240 тыс.
руб. должен быть отнесен к последней группе. На практике применяются оба
принципа, но предпочтение отдается принципу "исключительно".
Тема № 2.
Статистическое наблюдение
Виды
динамических рядов
Ряд в статистике - это цифровые данные, показывающие,
изменение явления во времени или в пространстве и дающие возможность
производить статистическое сравнение явлений как в процессе их развития во
времени, так и по различным формам и видам процессов. Благодаря этому можно
обнаружить взаимную зависимость явлений.
Процесс развития движения социальных явлений во времени в статистике
принято называть динамикой. Для отображения динамики строят ряды динамики
(хронологические, временные), которые представляют собой ряды изменяющихся во
времени значений статистического показателя (например, число осуждённых за 10
лет), расположенных в хронологическом порядке. Их составными элементами
являются цифровые значения данного показателя и периоды или моменты времени, к
которым они относятся.
Важнейшая характеристика рядов динамики - их размер (объём,
величина) того или иного явления, достигнутых в определённых период или к
определённому моменту. Соответственно, величина членов ряда динамики - его
уровень.
Различают начальный, средний и конечный уровни динамического
ряда. Начальный уровень показывает величину первого, конечный - величину последнего
члена ряда.
Средний уровень представляет собой среднюю хронологическую
вариационного рада и исчисляется в зависимости от того, является ли
динамический ряд интервальным или моментным.
Ещё одна важная характеристика динамического ряда - время,
прошедшее от начального до конечного наблюдения, или число таких наблюдений.
Существуют различные виды рядов динамики, их можно
классифицировать по следующим признакам.
) В зависимости от способа выражения уровней ряды динамики
подразделяются на ряды абсолютных и производных показателей (относительных и
средних величин).
) В зависимости от того, как выражают уровни ряда состояние
явления на определённые моменты времени (на начало месяца, квартала, года и
т.п.) или его величину за определённые интервалы времени (например, за сутки,
месяц, год и т.п.), различают соответственно моментные и интервальные ряды
динамики. Моментные ряды в аналитической работе правоохранительных органов
используются сравнительно редко.
В теории статистики выделяют рады динамики и по ряду других
классификационных признаков: в зависимости от расстояния между уровнями - с
равностоящими уровнями и неравностоящими уровнями во времени; в зависимости от
наличия основной тенденции изучаемого процесса - стационарные и не
стационарные.
Ряды динамики обладают значительным научно-познавательным
потенциалом и вместе с тем являются одним из наиболее простых и показательных
приёмов отображения изменений правонарушений вообще и преступности во времени в
частности.
Аналитические
показатели динамики
Рядами динамики называются ряды расположенных в
хронологическом порядке показателей, характеризующих изменение какой-либо
величины во времени. Ряды динамики включают два основных элемента: показатели
времени - t и соответствующие им показатели величины - Y.
Ряды динамики делятся на моментные и интервальные. Моментные
ряды динамики отображают состояние изучаемой величины на определенные момент
времени. Интервальные ряды отображают состояние изучаемой величины за отдельные
интервалы времени.
Приведу пример. Допустим, 1 января хлеб стоит 13 рублей, 1
февраля - 14 рублей, 1 марта - 15 рублей, это моментный ряд. Если за январь мы
купили 10 буханок хлеба, за февраль - 12 буханок, за март - 14 буханок, это
интервальный ряд. Заметим, что интервальный ряд обладает свойством суммарности,
т.е. показатели можно складывать, и получится что-то осмысленное, например,
потребление хлеба за три месяца.
Имея ряд показателей, можно просчитать всевозможные
аналитические производные показатели. Производные показатели могут
рассчитываться двумя основными способами - цепным и базисным.
При цепном методе каждый последующий показатель
сопоставляется с предыдущим, при базисном - с одним и тем же показателем,
принятым за базу сравнения. Обычно это первый показатель ряда.
Рассмотрим некоторые аналитические производные показатели:
Аналитические производные показатели
. Абсолютный прирост. Разность значений двух показателей ряда
динамики. Базисный абсолютный прирост - разность текущего значения и значения
принятого за постоянную базу сравнения
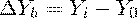
Цепной абсолютный прирост - разность текущего и предыдущего
значений
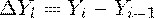
. Темп роста
Отношение двух уровней ряда (может выражаться в процентах).
Базисный темп роста - отношение текущего значения и значения
принятого за постоянную базу сравнения
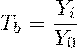
Цепной темп роста - отношение текущего и предыдущего значений
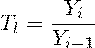
. Темп прироста
Отношение абсолютного прироста  к сравниваемому
показателю.
к сравниваемому
показателю.
Базисный темп прироста - отношение абсолютного базисного
прироста и значения принятого за постоянную базу сравнения
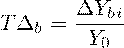
Цепной темп прироста - отношение абсолютного цепного прироста
и предыдущего значения показателя
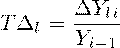
. Ускорение
Абсолютное ускорение - разница между абсолютным приростом за
данный период и абсолютным приростом за предыдущий период равной длительности.
Измеряется только цепным способом
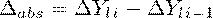
Относительное ускорение - отношение цепного темпа прироста за
данный период и цепного темпа прироста за предыдущий период
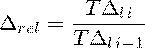
. Темп наращивания
Отношение цепных абсолютных приростов к уровню, принятому за
постоянную базу сравнения
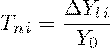
. Абсолютное значение одного процента прироста Отношение
абсолютного прироста к темпу прироста, выраженное в процентах. После раскрытия
формула упрощается до. Для получения обобщающих характеристик динамики
изучаемого ряда рассчитываются средние показатели динамики. Средние показатели
динамики
. Средний уровень
Характеризует типичную величину показателей
В интервальном динамическом ряду рассчитывается как простое
арифметическое среднее
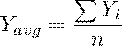
В моментном динамическом ряду с равными промежутками времени
между отсчетами как хронологическое среднее
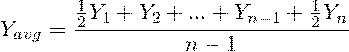
. Средний абсолютный прирост
Обобщающий показатель скорости абсолютного изменения значений
динамического ряда
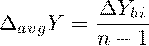
. Средний темп роста
Обобщающий характеристика темпов роста ряда динамики
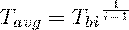 (корень степени i - 1)
(корень степени i - 1)
. Средний темп прироста
Отношение тоже что и между темпом роста и темпом прироста
Структура
ряда динамики
Динамика - процесс развития, движения
социально-экономических явлений во времени.
Ряды динамики - последовательность упорядоченных во
времени числовых показателей, характеризующих уровень развития изучаемого
явления.
Основные элементы рядов динамики:
1) показатель времени - t (определенные даты времени
или отдельные периоды);
2) уровни развития изучаемого явления - у.
Уровень рядов динамики - уровень, отражающий
количественную оценку развития во времени изучаемого явления.
Способы выражения уровней рядов динамики:
1) абсолютные величины;
) относительные величины;
) средние величины.
Классификация рядов динамики в зависимости от
характера изучаемого явления:
1) моментные ряды;
) интервальные ряды.
Моментные ряды динамики - ряды, отображающие
состояние изучаемых явлений на определенные даты (моменты) времени.
Суммирование уровней моментного ряда динамики не имеет смысла, так как одни и
те же единицы совокупности обычно входят в состав нескольких уровней.
Интервальные ряды динамики - ряды, отображающие итоги
развития изучаемых явлений за отдельные периоды (интервалы) времени. В
интервальном ряду динамики уровни за примыкающие друг к другу периоды времени
можно суммировать, получая итоги (уровни) за более продолжительные периоды.
Полный ряд динамики - ряд, в котором
одноименные моменты времени или периоды времени строго следуют один за другим в
календарном порядке.
Неполный ряд динамики - это ряд, в котором уровни
зафиксированы в неравностоящие моменты.
Основные случаи несопоставимости рядов динамики:
1) территориальные изменения объекта исследования, к которому
относится изучаемый показатель;
) разновеликие интервалы времени, к которым относится
показатель;
) изменение даты учета;
) изменение методологии учета или расчета показателя;
) изменение цен;
) изменение единиц измерения.
На сопоставимость уровней ряда динамики непосредственно
влияет методология учета или расчета показателей.
Периодизации динамики - процесс выделения
однородных этапов развития.
Характеристика рядов динамики в зависимости от
расстояния между уровнями:
1) с равностоящими уровнями;
) с неравностоящими уровнями во времени.
Равностоящие ряды динамики - ряды динамики одинаковых
периодов, или следующих через равные промежутки времени показателей.
Неравностоящие ряды динамики - ряды с неровными
периодами или неравномерными промежутками между датами.
Основное условие правильного построения ряда
динамики - сопоставимость всех входящих в него уровней.
Смыкание рядов динамики - объединение в одни ряд
(более длинный) двух или нескольких рядов динамики, уровни которых исчислены по
разной методологии или разным территориальным границам.
Условия смыкания рядов; необходимо, чтобы по одному из
периодов (переходному) имелись данные, исчисленные по разной методологии (или в
разных границах).
Анализ
сезонных колебаний
Уровень сезонности оценивается с помощью:
индексов сезонности;
гармонического анализа.
Индексы сезонности показывают, во сколько раз фактический
уровень ряда в момент или интервал времени t больше среднего уровня либо
уровня, вычисляемого по уравнению тенденции f (t). При анализе сезонности
уровни временного ряда показывают развитие явления по месяцам (кварталам)
одного или нескольких лет. Для каждого месяца (квартала) получают обобщенный индекс
сезонности как среднюю арифметическую из одноименных индексов каждого года.
Индексы сезонности - это, по либо уровень существу, относительные величины
координации, когда за базу сравнения принят либо средний уровень ряда, либо
уровень тенденции. Способы определения индексов сезонности зависят от наличия
или отсутствия основной тенденции.
Если тренда нет или он незначителен, то для каждого месяца
(квартала) индекс рассчитывается по формуле 32:
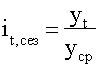 (32)
(32)
где 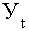 - уровень показателя за месяц (квартал) t;
- уровень показателя за месяц (квартал) t;
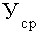 - общий уровень показателя.
- общий уровень показателя.
Как отмечалось выше, для обеспечения устойчивости показателей
можно взять больший промежуток времени. В этом случае расчет производится по
формулам 33:
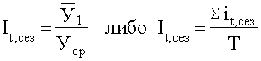 (33)
(33)
где 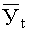 - средний уровень показателя по одноименным
месяцам за ряд лет;
- средний уровень показателя по одноименным
месяцам за ряд лет;
Т - число лет.
При наличии тренда индекс сезонности определяется на основе
методов, исключающих влияние тенденции. Порядок расчета следующий:
для каждого уровня определяют выравненные значения по тренду
f (t);
рассчитывают отношения
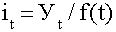 ;
;
при необходимости находят среднее из этих отношений для одноименных
месяцев (кварталов) по формуле 34:
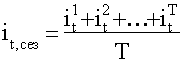 , (Т - число лет). (34)
, (Т - число лет). (34)
Другим методом изучения уровня сезонности является
гармонический анализ. Его выполняют, представляя временной ряд как совокупность
гармонических колебательных процессов.
Для каждой точки этого ряда справедливо выражение, записанное
в виде формулы 35:
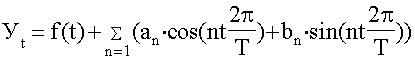 (35)
(35)
при t = 1, 2, 3,., Т.
Здесь 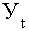 - фактический уровень ряда в момент (интервал)
времени t;(t) - выравненный уровень ряда в тот же момент (интервал) t
- фактический уровень ряда в момент (интервал)
времени t;(t) - выравненный уровень ряда в тот же момент (интервал) t
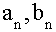 - параметры колебательного процесса (гармоники)
с номером n, в совокупности оценивающие размах (амплитуду) отклонения от общей
тенденции и сдвиг колебаний относительно начальной точки.
- параметры колебательного процесса (гармоники)
с номером n, в совокупности оценивающие размах (амплитуду) отклонения от общей
тенденции и сдвиг колебаний относительно начальной точки.
Общее число колебательных процессов, которые можно выделить
из ряда, состоящего из Т уровней, равно Т/2. Обычно ограничиваются меньшим
числом наиболее важных гармоник. Параметры гармоники с номером n определяются
по формулам 36 - 38:
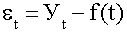 ; (36)
; (36)
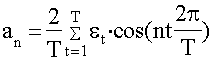 (37)
(37)
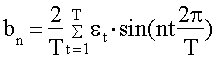 при n=1,2,., (T/2 - 1);
при n=1,2,., (T/2 - 1);
) 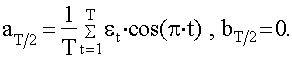 (38)
(38)
Анализ
взаимосвязанных рядов динамики
В простейших случаях для характеристики взаимосвязи двух или
более рядов их приводят к общему основанию, для чего берут в качестве базисных
уровни за один и тот же период и исчисляют коэффициенты опережения по темпам
роста или прироста.
Коэффициенты опережения по темпам роста - это отношение
темпов роста (цепных или базисных) одного ряда к соответствующим по времени
темпам роста (также цепным или базисным) другого ряда. Аналогично находятся и
коэффициенты опережения по темпам прироста.
Анализ взаимосвязанных рядов представляет наибольшую
сложность при изучении временных последовательностей. Однако нередко совпадение
общих тенденций развития может быть вызвано не взаимной связью, а прочими
неучитываемыми факторами. Поэтому в сопоставляемых рядах предварительно следует
избавиться от влияния существующих в них тенденций, а после этого провести
анализ взаимосвязи по отклонениям от тренда. Исследование включает проверку
рядов динамики (отклонений) на автокорреляцию и установление связи между
признаками.
Тема № 3.
Статистические величины
Абсолютные и относительные величины, их виды. Средние
величины, их виды, формы, области применения. Показатели структуры
вариационного ряда. Показатели вариации. Дисперсионный анализ. Выборочное
наблюдение, доверительные интервалы.
Абсолютные
величины
Результаты статистических наблюдений представляют собой абсолютные
величины, отражающие уровень развития какого-либо явления или процесса
(например, величина экспорта/импорта i-го товара в j-ю страну).
Абсолютные величины обозначаются X, а их общее количество в
статистической совокупности N.
Абсолютные величины всегда имеют свою единицу измерения
(размерность), присущую изучаемому явлению. Широко распространены следующие виды
единиц измерения:
1) натуральные, подразделяющиеся на
простые (например, штуки, тонны, метры) и сложные (составные), представляющие
собой комбинацию двух разноименных величин (например, киловатт-час);
2) условно-натуральные (например, общая масса
энергоносителей - дрова, торф, каменный уголь, нефтепродукты, природный газ -
измеряется в т. у. т. - тонны условного топлива, поскольку каждый его
вид имеет разную теплотворную способность, а за стандарт принято 29,3 МДж/кГ;
общее количество школьных тетрадей измеряется в у. ш. т. - условные
школьные тетради размером 12 листов; продукция консервного производства
измеряется в у. к. б. - условные консервные банки емкостью 0,33 литра;
продукция моющих средств приводится к условной жирности 40%.);
3) стоимостные, позволяющие соизмерить
в денежной форме товары, которые нельзя соизмерить в натуральной форме (доллары
США, рубли и т.д.).
Количество единиц с одинаковым значением признака обозначается f
и называется частота. Очевидно, что суммируя число всех единиц с
одинаковыми значениями признака, получаем N, то есть 1):
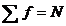 . (1)
. (1)
Анализируя абсолютные величины, например, статистические данные о
торговле, необходимо сопоставлять эти данные во времени и пространстве,
исследовать закономерности их изменения и развития, изучать структуру
совокупностей. С помощью абсолютных величин эти задачи не выполнимы, в этом
случае необходимо использовать относительные величины.
Относительные
величины
Относительная величина - это результат деления
(сравнения) двух абсолютных величин. В числителе дроби стоит величина, которую
сравнивают, а в знаменателе - величина, с которой сравнивают (база сравнения).
Например, если сопоставить величины экспорта США и России, которые в 2005 году
составили 904,383 и 243,569 млрд. долл. соответственно, то относительная
величина покажет, что величина экспорта США в 3,71 раза (904,383/243,569)
больше экспорта России, при этом базой сравнения является величина экспорта
России. Полученная относительная величина выражена в виде коэффициента,
который показывает, во сколько раз сравниваемая абсолютная величина больше
базисной. В данном примере база сравнения принята за единицу. В случае если
основание принимается за 100, относительная величина выражается в процентах
(%), если за 1000 - в промилле (‰). Выбор той или иной
формы относительной величины зависит от ее абсолютного значения:
– если сравниваемая величина больше базы сравнения в 2
раза и более, то выбирают форму коэффициента (как в вышеприведенном примере);
– если относительная величина близка к единице, то, как
правило, ее выражают в процентах (например, сравнив величины экспорта России в
2006 и 2005 годах, которые составили 304,5 и 243,6 млрд. долл. соответственно,
можно сказать, что экспорт в 2006 году составляет 125% от 2005 года
[304,5/243,6*100%]);
– если относительная величина значительно меньше
единицы (близка к нулю), ее выражают в промилле (например, в 2004 году Россия
экспортировала в страны-СНГ всего 4142 тыс. т нефтепродуктов, в том числе в
Грузию 10,7 тыс. т, что составляет 0,0026 [10,7/4142], или 2,6 ‰ от
всего экспорта нефтепродуктов в страны СНГ).
Различают относительные величины динамики, структуры,
координации, сравнения и интенсивности, для краткости именуемые в дальнейшем индексами.
Индекс динамики характеризует изменение какого-либо явления во времени. Он
представляет собой отношение значений одной и той же абсолютной величины в
разные периоды времени. Данный индекс определяется по формуле (2):
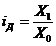 , (2)
, (2)
где цифры означают: 1 - отчетный или анализируемый период, 0 -
прошлый или базисный период.
Критериальным значением индекса динамики служит единица (или
100%), то есть если 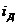 >1, то имеет место рост (увеличение)
явления во времени; если
>1, то имеет место рост (увеличение)
явления во времени; если 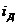 =1 - стабильность; если
=1 - стабильность; если 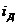 <1 - наблюдается спад (уменьшение)
явления. Еще одно название индекса динамики - индекс изменения, вычитая
из которого единицу (100%), получают темп изменения (динамики) с
критериальным значением 0, который определяется по формуле 3):
<1 - наблюдается спад (уменьшение)
явления. Еще одно название индекса динамики - индекс изменения, вычитая
из которого единицу (100%), получают темп изменения (динамики) с
критериальным значением 0, который определяется по формуле 3):
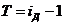 . (3)
. (3)
Если T>0, то имеет место рост явления; Т=0 -
стабильность, Т<0 - спад.
В рассмотренном выше примере про экспорт России в 2006 и 2005 году
был рассчитан именно индекс динамики по формуле (2): iД =
304,5/243,6*100% = 125%, что больше критериального значения 100%, что
свидетельствует об увеличении экспорта. Используя формулу 3) получим темп
изменения: Т = 125% - 100% = 25%, который показывает, что экспорт
увеличился на 25%.
Разновидностями индекса динамики являются индексы планового
задания и выполнения плана, рассчитываемые для планирования различных величин и
контроля их выполнения.
Индекс планового задания - это отношение планового значения признака к базисному. Он
определяется по формуле (4):
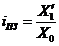 , (4)
, (4)
где X’1 - планируемое значение; X0
- базисное значение признака.
Например, таможенное управление перечислило в федеральный бюджет в
2006 году 160 млрд. руб., а на следующий год запланировали перечислить 200
млрд. руб., значит по формуле (4): iпз = 200/160 = 1,25, то
есть плановое задание для таможенного управления на 2007 год составляет 125% от
предыдущего года.
Для определения процента выполнения плана необходимо рассчитать индекс
выполнения плана, то есть отношение наблюдаемого значения признака к
плановому (оптимальному, максимально возможному) значению по формуле 5):
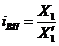 . (5)
. (5)
Например, на январь-ноябрь 2006 года таможенные органы
запланировали перечислить в федеральный бюджет 1,955 трлн. руб., но фактически
перечислили 2,59 трлн. руб., значит по формуле 5): iВП =
2,59/1,955 = 1,325, или 132,5%, то есть плановое задание выполнили на 132,5%.
Индекс структуры (доля) - это отношение какой-либо части объекта (совокупности) ко всему
объекту. Он определяется по формуле (6):
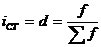 (6)
(6)
В рассмотренном выше примере про экспорт нефтепродуктов в страны
СНГ, была рассчитана доля этого экспорта в Грузию по формуле (6): d=10,7/4142
= 0,0026, или 2,6‰.
Индекс координации - это отношение какой-либо части объекта к другой его части,
принятой за основу (базу сравнения). Он определяется по формуле 7):
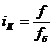 . (7)
. (7)
Например, импорт России в 2006 году составил 163,9 млрд. долл.,
тогда, сравнив его с экспортом (база сравнения), рассчитаем индекс координации
по формуле 7): iК = 163,9/304,5 = 0,538, который показывает
соотношение между двумя составными частями внешнеторгового оборота, то есть
величина импорта России в 2006 году составляет 53,8% от величины экспорта.
Меняя базу сравнения на импорт, по той же формуле получим: iК =
304,5/163,9 = 1,858, то есть экспорт России в 2006 году в 1,858 раза больше
импорта, или экспорт составляет 185,8% от импорта.
Индекс сравнения - это сравнение (соотношение) разных объектов по одинаковым
признакам. Он определяется по формуле (8):
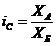 , (8)
, (8)
где А, Б - сравниваемые объекты.
В рассмотренном выше примере, в котором сопоставлялись величины
экспорта США и России, был рассчитан именно индекс сравнения по формуле (8): iс
= 904,383/243,569 = 3,71. Меняя базу сравнения (то есть экспорт
России - объект А, а экспорт США - объект Б), по той же формуле получим: iс
= 243,569/904,383 = 0,27, то есть экспорт России составляет 27% от
экспорта США.
Индекс интенсивности - это соотношение разных признаков одного объекта между собой. Он
определяется по формуле 9):
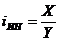 . (9)
. (9)
где X - один признак объекта; Y - другой признак
этого же объекта
Например, показатели выработки продукции в
единицу рабочего времени, затрат на единицу продукции, цены единицы продукции и
т.д.
Тема № 4.
Выборочный метод
Понятия
генеральной совокупности и выборки
Выборка или выборочная
совокупность - множество случаев (испытуемых, объектов, событий, образцов),
с помощью определённой процедуры выбранных из генеральной совокупности для
использования в исследовании.
Характеристики выборки:
· Качественная
характеристика выборки - что именно мы выбираем и какие способы построения
выборки мы для этого используем.
· Количественная
характеристика выборки - сколько случаев выбираем, другими словами объём
выборки.
Необходимость выборки
· Объект исследования очень
обширный. Например, потребители продукции глобальной компании - огромное
количество территориально разбросанных рынков.
· Существует необходимость
в сборе первичной информации.
Генеральная совокупность, генеральная выборка (от лат.
<#"662752.files/image042.gif">
где µn (x) - число членов вариационного ряда,
меньших x, которая является оценкой функции распределения F (x) случайных
величин x1, x2, x3,., xn.
Промежуток xнабл = [x (1) - x (n)]
= [xmin_набл - xmax_набл] между крайними членами вариационного
ряда называется интервалом варьирования, его длина Wn = x
(n) - x (1) = xmax_набл - xmin_набл
называется размахом выборки.
Крайние члены вариационного ряда
min_набл = x (1) = min{xk} для k=1.
n иmax_набл = x (n) = max{xk} для k=1. n
называются экстремальными значениями.
Величина x (k) называется k-й порядковой
статистикой.
Использование вариационного ряда для определения выборочной
медианы основано на определении его центрального члена:набл = x
(m), где m= (n+1) /2 при нечетном n,набл = (x (m) +x
(m+1)) /2, где m=n/2 при четном n.
По функции распределения F (x) исходных случайных величин x1,
x2, x3,., xn вычисляются распределения любого
члена вариационного ряда и совместные распределения его членов.
Представление
выборки в виде статистического ряда, графическое отображение статистического
ряда: полигон частот, гистограмма
Первоначально выборку представляют в виде вариационного ряда 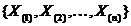 , упорядочивая выборочные значения в
порядке возрастания:
, упорядочивая выборочные значения в
порядке возрастания: 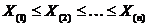 . Величину
. Величину 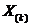 ,
, 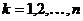 называют при этом
называют при этом 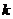 -ой порядковой статистикой. Далее
результаты эксперимента записывают в виде статистического ряда.
-ой порядковой статистикой. Далее
результаты эксперимента записывают в виде статистического ряда.
Если 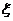 - дискретная случайная величина, число
возможных значений которой невелико, и соответственно с этим выборка содержит
много повторяющихся значений, то поступают следующим образом.
- дискретная случайная величина, число
возможных значений которой невелико, и соответственно с этим выборка содержит
много повторяющихся значений, то поступают следующим образом.
Выписывают все неповторяющиеся значения в вариационном ряде 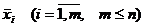 . Подсчитывают частоты
. Подсчитывают частоты 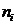 - количество повторов каждого из значений
- количество повторов каждого из значений
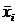 в выборке и определяют относительные
частоты
в выборке и определяют относительные
частоты 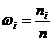 . Очевидно:
. Очевидно:  . Совокупность пар чисел
. Совокупность пар чисел 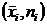 называют статистическим рядом абсолютных частот, а
совокупность пар чисел
называют статистическим рядом абсолютных частот, а
совокупность пар чисел 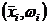 называют статистическим рядом
относительных частот. Статистические ряды отображают в виде таблицы.
называют статистическим рядом
относительных частот. Статистические ряды отображают в виде таблицы.
Очевидно, что статистический ряд относительных частот
приближенно оценивает ряд распределения дискретной случайной величины.
Пример 1. Дана выборка 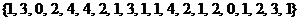 . Записать статистический ряд.
. Записать статистический ряд.
Решение: Объем выборки 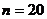 . Записываем вариационный ряд:
. Записываем вариационный ряд: 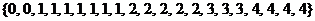 . Подсчитываем частоты и представляем выборочные данные в
виде статистического ряда:
. Подсчитываем частоты и представляем выборочные данные в
виде статистического ряда:
|
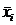 01234 01234
|
|
|
|
|
|
|
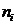 26534 26534
|
|
|
|
|
|
|
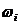 0,10,30,250,150,2 0,10,30,250,150,2
|
|
|
|
|
|
Если же величина 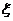 - непрерывная, или число возможных значений
- непрерывная, или число возможных значений 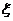 велико, то в этом случае делают
группировку данных. Для этого интервал, в котором содержатся все элементы
выборки, делится на
велико, то в этом случае делают
группировку данных. Для этого интервал, в котором содержатся все элементы
выборки, делится на 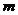 равных (иногда неравных)
последовательных, непересекающихся интервалов
равных (иногда неравных)
последовательных, непересекающихся интервалов 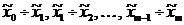 , и подсчитывают частоты
, и подсчитывают частоты 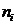 - число элементов выборки, попавших в
- число элементов выборки, попавших в 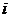 -ый интервал. При этом элемент, совпавший
с границей интервала, относят к верхнему интервалу. Число интервалов
группирования определяют, например, по формуле Стерджесса:
-ый интервал. При этом элемент, совпавший
с границей интервала, относят к верхнему интервалу. Число интервалов
группирования определяют, например, по формуле Стерджесса: 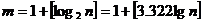 . При разбивке на интервалы следует
следить за тем, чтобы частоты
. При разбивке на интервалы следует
следить за тем, чтобы частоты 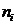 для каждого из интервалов были одного порядка. В противном случае
следует объединять соседние интервалы, добиваясь относительно равномерного
распределения частот по интервалам. Далее подсчитываются относительные частоты
для каждого из интервалов были одного порядка. В противном случае
следует объединять соседние интервалы, добиваясь относительно равномерного
распределения частот по интервалам. Далее подсчитываются относительные частоты 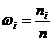 для каждого из интервалов и плотности
частот
для каждого из интервалов и плотности
частот 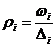 , где
, где 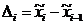 - длины соответствующих интервалов группирования. В результате
получаем следующий статистический ряд:
- длины соответствующих интервалов группирования. В результате
получаем следующий статистический ряд:
Пример 2. Дана выборка объемом 20 из некоторой генеральной
совокупности: {0,70; - 0,28; 1,24; 2,28; 2, 20; 2,73; - 1,18; 0,77; 2,10; -
0,09; 0,31; - 0,69; - 0,85; 0,02; 0,23; - 1,12; 0,43; 0,60; 1,13; 0,63}.
Представить выборку в виде группированного статистического ряда.
Решение. Записываем вариационный ряд: {-1,18; - 1,12; - 0,85; -
0,69; - 0,28; - 0,09; 0,02; 0,23; 0,31; 0,43; 0,60; 0,63; 0,70; 0,77; 1,13;
1,24; 2,10; 2, 20; 2,28; 2,73}. Определяем число интервалов группирования по
формуле Стерджесса: 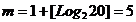 . Выберем в качестве нижней границы
. Выберем в качестве нижней границы 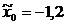 , в качестве верхней
, в качестве верхней 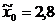 . Тогда длина каждого интервала (при
условии равенстве длин интервалов):
. Тогда длина каждого интервала (при
условии равенстве длин интервалов): 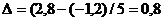 . Разбиваем на интервалы и формируем статистический ряд:
. Разбиваем на интервалы и формируем статистический ряд:
|
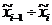 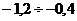 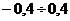 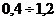 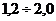 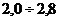
|
|
|
|
|
|
|
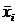 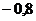    
|
|
|
|
|
|
|
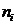 45614 45614
|
|
|
|
|
|
|
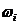 0,20,250,30,050,2 0,20,250,30,050,2
|
|
|
|
|
|
|
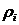 0,250,31250,3750,06250,25 0,250,31250,3750,06250,25
|
|
|
|
|
|
Графическая
иллюстрация статистических рядов
В качестве графической иллюстрации статистических рядов
используются:
Полигон частот - ломанная, отрезки которой соединяют точки 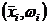 , либо
, либо 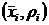 (рис 1). Для дискретной случайной величины полигон частот
является оценкой многоугольника распределения, для непрерывной случайной
величины полигон частот есть оценка кривой плотности распределения.
(рис 1). Для дискретной случайной величины полигон частот
является оценкой многоугольника распределения, для непрерывной случайной
величины полигон частот есть оценка кривой плотности распределения.

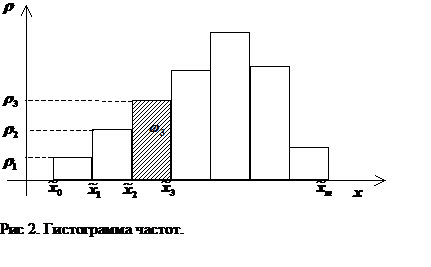
Гистограмма частот - ступенчатая фигура, состоящая из 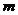 прямоугольников, опирающихся на частичные
интервалы. Высота
прямоугольников, опирающихся на частичные
интервалы. Высота 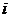 -го прямоугольника полагается равной
плотности частоты
-го прямоугольника полагается равной
плотности частоты 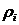 . Соответственно площадь каждого
прямоугольника равна
. Соответственно площадь каждого
прямоугольника равна 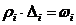 - относительной частоте. Гистограмма частот
также является статистическим аналогом кривой плотности распределения (рис 2).
- относительной частоте. Гистограмма частот
также является статистическим аналогом кривой плотности распределения (рис 2).
Эмпирическая
функция распределения
Эмпирической функцией распределения, полученной по выборке 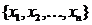 , называется функция, при каждом
, называется функция, при каждом 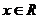 равная
равная
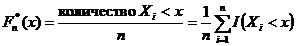 , (1.1)
, (1.1)
где 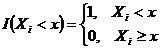 .
.
Очевидно, что 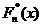 ступенчатая функция (рис 3), имеющая разрыва в точках,
соответствующих, наблюдаемым выборочным значениям. Величина скачка в точке
ступенчатая функция (рис 3), имеющая разрыва в точках,
соответствующих, наблюдаемым выборочным значениям. Величина скачка в точке 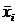 равна относительной частоте
равна относительной частоте 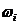 значения
значения 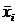 . Эмпирическая функция распределения является оценкой функции
распределения.
. Эмпирическая функция распределения является оценкой функции
распределения.

Числовые
характеристики выборки
В качестве числовых характеристик выборки используются:
Выборочное среднее: 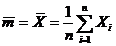 . (1.2)
. (1.2)
Выборочная дисперсия 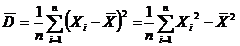 . (1.3)
. (1.3)
Несмещенная выборочная дисперсия 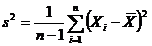 . (1.4)
. (1.4)
Выборочные начальные и центральные моменты 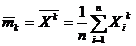 ,
, 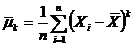 . (1.5)
. (1.5)
По статистическому ряду значения этих величин могут быть
найдены по формулам:
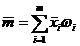 ,
,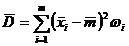 ,
,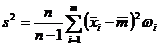 ,
,
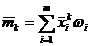 ,
,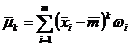 . (1.6)
. (1.6)
(для группированных данных формулы (1.6) дают приближенные
значения выборочных характеристик.). Выборочные характеристики очевидно есть
числовые характеристики дискретной случайной величины, ряд распределения
которой совпадает со статистическим рядом. Выборочные характеристики являются
приближенными значениями соответствующих числовых характеристик случайной
величины 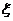 . Выборочные характеристики являются
случайными величинами, т.к. являются функциями случайной выборки.
. Выборочные характеристики являются
случайными величинами, т.к. являются функциями случайной выборки.
Тема № 5.
Точечное оценивание
Статистические оценки - это статистики,
которые используются для оценивания неизвестных параметров распределений
случайной величины.
Например, если 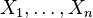 - это независимые
случайные величины, с заданным нормальным распределением
- это независимые
случайные величины, с заданным нормальным распределением 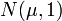 , то
, то 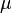 будет средним
арифметическим результатов наблюдений.
будет средним
арифметическим результатов наблюдений.
Задача статистической оценки
формулируется так:
Пусть 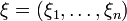 - выборка из генеральной
совокупности с распределением
- выборка из генеральной
совокупности с распределением 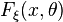 . Распределение
. Распределение 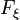 имеет известную
функциональную форму, но зависит от неизвестного параметра
имеет известную
функциональную форму, но зависит от неизвестного параметра 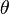 . Этот параметр может
быть любой точкой заданного параметрического множества
. Этот параметр может
быть любой точкой заданного параметрического множества 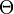 . Используя
статистическую информацию, содержащуюся в выборке
. Используя
статистическую информацию, содержащуюся в выборке 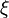 , сделать выводы о
настоящем значении параметра
, сделать выводы о
настоящем значении параметра 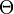 .
.
Несмещенность
и состоятельность оценок
Рассмотрим оценку θn числового параметра θ, определенную при n
= 1, 2, … Оценка θn называется состоятельной,
если она сходится по вероятности к значению оцениваемого параметра θ при безграничном возрастании объема выборки. Выразим сказанное
более подробно. Статистика θn является состоятельной
оценкой параметра θ тогда и только тогда,
когда для любого положительного числа ε справедливо предельное
соотношение
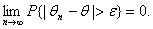
Пример 3. Из закона больших чисел
следует, что θn = 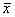 является состоятельной
оценкой θ = М (Х) (в приведенной выше теореме Чебышёва
предполагалось существование дисперсии D (X); однако, как доказал А.Я.
Хинчин [6], достаточно выполнения более слабого условия - существования
математического ожидания М (Х)).
является состоятельной
оценкой θ = М (Х) (в приведенной выше теореме Чебышёва
предполагалось существование дисперсии D (X); однако, как доказал А.Я.
Хинчин [6], достаточно выполнения более слабого условия - существования
математического ожидания М (Х)).
Пример 4. Все указанные выше оценки
параметров нормального распределения являются состоятельными.
Вообще, все (за редчайшими исключениями)
оценки параметров, используемые в вероятностно-статистических методах принятия
решений, являются состоятельными.
Пример 5. Так, согласно теореме
В.И. Гливенко, эмпирическая функция распределения Fn (x) является
состоятельной оценкой функции распределения результатов наблюдений F (x).
При разработке новых методов оценивания следует
в первую очередь проверять состоятельность предлагаемых методов.
Второе важное свойство оценок - несмещенность.
Несмещенная оценка θn - это оценка параметра θ, математическое ожидание которой равно значению оцениваемого
параметра: М (θn) = θ.
Пример 6. Из приведенных выше
результатов следует, что 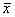 и
и 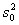 являются несмещенными
оценками параметров m и σ2 нормального
распределения. Поскольку М (
являются несмещенными
оценками параметров m и σ2 нормального
распределения. Поскольку М (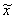 ) = М (m**) = m, то выборочная
медиана
) = М (m**) = m, то выборочная
медиана 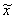 и полусумма крайних
членов вариационного ряда m** - также несмещенные оценки математического
ожидания m нормального распределения. Однако
и полусумма крайних
членов вариационного ряда m** - также несмещенные оценки математического
ожидания m нормального распределения. Однако
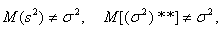
поэтому оценки s2 и (σ2) ** не являются состоятельными оценками дисперсии σ2 нормального распределения.
Оценки, для которых соотношение М (θn) = θ неверно, называются
смещенными. При этом разность между математическим ожиданием оценки θn и оцениваемым параметром θ, т.е. М (θn) - θ, называется смещением
оценки.
Пример 7. Для оценки s2,
как следует из сказанного выше, смещение равно
М (s2) -
σ2 = - σ2/n.
Смещение оценки s2
стремится к 0 при n → ∞.
Оценка, для которой смещение стремится к
0, когда объем выборки стремится к бесконечности, называется асимптотически
несмещенной. В примере 7 показано, что оценка s2 является
асимптотически несмещенной.
Практически все оценки параметров,
используемые в вероятностно-статистических методах принятия решений, являются
либо несмещенными, либо асимптотически несмещенными. Для несмещенных оценок
показателем точности оценки служит дисперсия - чем дисперсия меньше, тем оценка
лучше. Для смещенных оценок показателем точности служит математическое ожидание
квадрата оценки М (θn - θ) 2. Как следует из основных свойств математического
ожидания и дисперсии,
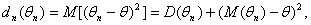 (3)
(3)
т.е. математическое ожидание квадрата
ошибки складывается из дисперсии оценки и квадрата ее смещения. Для
подавляющего большинства оценок параметров, используемых в
вероятностно-статистических методах принятия решений, дисперсия имеет порядок
1/n, а смещение - не более чем 1/n, где n - объем выборки.
Для таких оценок при больших n второе слагаемое в правой части (3)
пренебрежимо мало по сравнению с первым, и для них справедливо приближенное
равенство
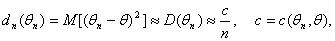 (4)
(4)
где с - число, определяемое методом
вычисления оценок θn и истинным значением
оцениваемого параметра θ.
Метод максимального правдоподобия - еще один разумный
способ построения оценки неизвестного параметра. Состоит он в том, что в
качестве "наиболее правдоподобного" значения параметра берут значение
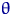 , максимизирующее
вероятность получить при
, максимизирующее
вероятность получить при 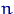 опытах данную выборку
опытах данную выборку 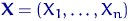 . Это значение параметра
. Это значение параметра 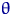 зависит от выборки и
является искомой оценкой.
зависит от выборки и
является искомой оценкой.
Решим сначала, что такое "вероятность получить данную
выборку", т.е. что именно нужно максимизировать. Вспомним, что для
абсолютно непрерывных распределений 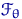 их плотность
их плотность 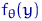 - "почти" (с
точностью до
- "почти" (с
точностью до  ) вероятность попадания в точку
) вероятность попадания в точку 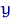 . А для дискретных
распределений
. А для дискретных
распределений 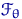 вероятность попасть в точку
вероятность попасть в точку 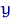 равна
равна 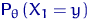 . И то, и другое мы будем
называть плотностью распределения
. И то, и другое мы будем
называть плотностью распределения 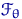 . Итак,
. Итак,
Определение 5.
Функцию
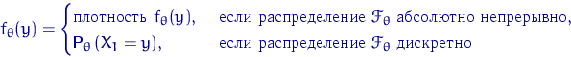
мы будем называть плотностью распределения 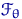 .
.
Для тех, кто знаком с понятием интеграла по мере, нет ничего
странного в том, что мы ввели понятие плотности для дискретного распределения.
Это - не плотность относительно меры Лебега, но плотность относительно
считающей меры.
Если для дискретного распределения величины 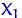 со значениями
со значениями 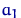 ,
, 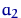 ,
, 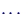 ввести считающую меру
ввести считающую меру  на борелевской
на борелевской 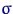 -алгебре как
-алгебре как
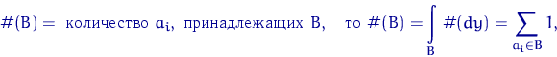
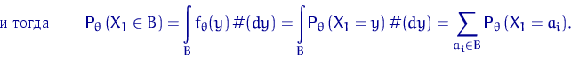
Если же 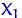 имеет абсолютно непрерывное распределение, то
имеет абсолютно непрерывное распределение, то 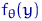 есть привычная плотность
относительно меры Лебега
есть привычная плотность
относительно меры Лебега 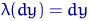 :
:

Определение 6.
Функция (случайная величина при фиксированном 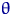 )
)
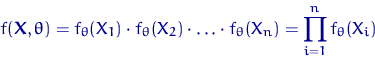
называется функцией правдоподобия. Функция (тоже случайная)
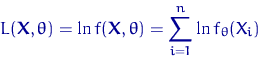
называется логарифмической функцией правдоподобия.
В дискретном случае функция правдоподобия 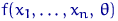 есть вероятность выборке
есть вероятность выборке
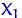 ,
,  ,
,  в данной серии
экспериментов равняться
в данной серии
экспериментов равняться 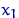 ,
,  ,
,  . Эта вероятность меняется в зависимости от
. Эта вероятность меняется в зависимости от 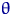 :
:
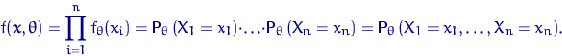
Определение 7.
Оценкой максимального правдоподобия  неизвестного параметра
неизвестного параметра 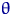 называют значение
называют значение 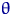 , при котором функция
, при котором функция 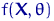 достигает максимума (как
функция от
достигает максимума (как
функция от 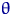 при фиксированных
при фиксированных 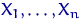 ):
):
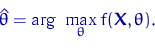
Замечание 7.
Поскольку функция 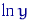 монотонна, то точки
максимума
монотонна, то точки
максимума 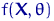 и
и 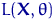 совпадают. Поэтому
оценкой максимального правдоподобия (ОМП) можно называть точку максимума (по
совпадают. Поэтому
оценкой максимального правдоподобия (ОМП) можно называть точку максимума (по 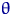 ) функции
) функции 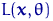 :
:
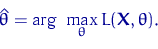
Напомним, что точки экстремума функции - это либо точки, в
которых производная обращается в нуль, либо точки разрыва функции/производной,
либо крайние точки области определения функции.
Пример 7.
Пусть 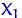 ,
,  ,
,  - выборка объема
- выборка объема 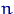 из распределения
Пуассона
из распределения
Пуассона  , где
, где  . Найдем ОМП
. Найдем ОМП  неизвестного параметра
неизвестного параметра 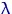 .
.
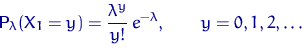
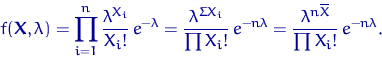
Поскольку эта функция при всех  непрерывно
дифференцируема по
непрерывно
дифференцируема по 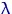 , можно искать точки экстремума, приравняв к нулю
частную производную по
, можно искать точки экстремума, приравняв к нулю
частную производную по 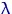 . Но удобнее это делать для логарифмической
функции правдоподобия:
. Но удобнее это делать для логарифмической
функции правдоподобия:
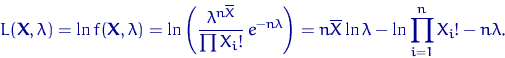
Тогда 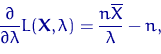
и точка экстремума  - решение уравнения:
- решение уравнения: 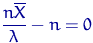 , то есть
, то есть 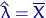 .
.
Сравнение оценок.
Используя метод моментов и метод максимального правдоподобия,
мы получили для каждого параметра уже достаточно много различных оценок. Каким
же образом их сравнивать? Что должно быть показателем "хорошести"
оценки?
Понятно, что чем дальше оценка отклоняется от параметра, тем
она хуже. Но величина 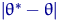 для сравнения непригодна: во-первых, параметр
для сравнения непригодна: во-первых, параметр 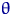 неизвестен, во-вторых,
неизвестен, во-вторых, 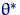 - случайная величина,
так что эти величины обычно сравнить нельзя. Как, например, сравнивать
- случайная величина,
так что эти величины обычно сравнить нельзя. Как, например, сравнивать 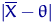 и
и 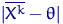 ? Или, на одном
элементарном исходе,
? Или, на одном
элементарном исходе, 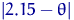 и
и 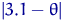 ?
?
Поэтому имеет смысл сравнивать не отклонения как таковые, а
средние значения этих отклонений, то есть 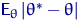 .
.
Но математическое ожидание модуля с. в. считать обычно затруднительно,
поэтому более удобной характеристикой для сравнения оценок считается 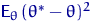 . Она удобна еще и тем,
что очень чутко реагирует на маловероятные, но большие по абсолютному значению
отклонения
. Она удобна еще и тем,
что очень чутко реагирует на маловероятные, но большие по абсолютному значению
отклонения 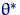 от
от 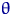 (возводит их в квадрат).
(возводит их в квадрат).
Заметим еще, что 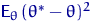 есть функция от
есть функция от 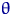 , так что сравнивать эти
"среднеквадратические" отклонения нужно как функции от
, так что сравнивать эти
"среднеквадратические" отклонения нужно как функции от 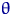 - поточечно. Такой
подход к сравнению оценок называется среднеквадратическим.
- поточечно. Такой
подход к сравнению оценок называется среднеквадратическим.
Разумеется, в зависимости от потребностей исследователя можно
пользоваться и другими характеристиками, например, 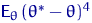 или
или 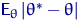 .
.
Существует и так называемый асимптотический подход к
сравнению оценок, при котором для сравнения оценок используется некая
характеристика "разброса" оценки относительно параметра при больших 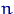 .
.
Пусть 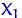 ,
,  ,
,  - выборка объема
- выборка объема 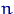 из параметрического
семейства распределений
из параметрического
семейства распределений 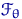 , где
, где  .
.
Определение 8.
Говорят, что оценка 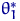 лучше оценки
лучше оценки 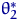 в смысле
среднеквадратического подхода, если для любого
в смысле
среднеквадратического подхода, если для любого 

и хотя бы при одном 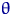 это неравенство строгое.
это неравенство строгое.
Существует ли среди всех оценок наилучшая в смысле
среднеквадратического подхода? Скептик сразу ответит "нет". Покажем,
что он прав. Предположим, что мы имеем дело с невырожденной задачей: ни для
какой статистики 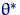 невозможно тождество:
невозможно тождество: 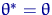 при любых
при любых  .
.
Теорема 4.
В классе всех возможных оценок наилучшей в смысле
среднеквадратического подхода оценки не существует.
Доказательство теоремы
<#"662752.files/image186.gif"> - наилучшая, то есть для любой другой
оценки 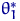 , при любом
, при любом  выполнено
выполнено

Пусть 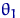 - произвольная точка
- произвольная точка  . Рассмотрим статистику
. Рассмотрим статистику  . Тогда
. Тогда 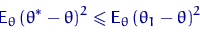 при любом
при любом  . В частности, при
. В частности, при 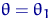 получим
получим 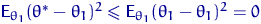 . Поэтому
. Поэтому 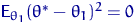 . Но, поскольку
. Но, поскольку 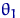 произвольно, то при
любом
произвольно, то при
любом  выполняется
выполняется 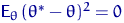 . А это возможно только
если
. А это возможно только
если 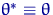 (оценка в точности
отгадывает неизвестный параметр), т.е. для вырожденной с точки зрения
математической статистики задачи. Вырожденными являются, например, следующие
задачи: для выборки из
(оценка в точности
отгадывает неизвестный параметр), т.е. для вырожденной с точки зрения
математической статистики задачи. Вырожденными являются, например, следующие
задачи: для выборки из 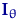 ,
, 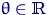 , выполнено тождество
, выполнено тождество 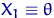 ; для выборки из
; для выборки из 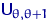 ,
, 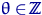 , выполнено тождество
, выполнено тождество 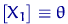 .
.
Асимптотический
подход к сравнению оценок
Возьмем две случайные величины: 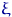 из нормального
распределения
из нормального
распределения 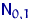 и
и 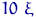 из нормального
распределения
из нормального
распределения 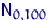 . Если для
. Если для 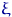 , например,
, например, 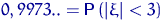 , то для
, то для 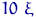 уже
уже 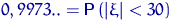 . Разброс значений
величины
. Разброс значений
величины 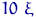 гораздо больший, и дисперсия
(показатель рассеяния) соответственно больше. Что показывает коэффициент
асимптотической нормальности? Возьмем две АНО с коэффициентами 1 и 100:
гораздо больший, и дисперсия
(показатель рассеяния) соответственно больше. Что показывает коэффициент
асимптотической нормальности? Возьмем две АНО с коэффициентами 1 и 100:
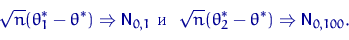
При больших 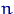 разброс значений величины
разброс значений величины 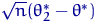 около нуля гораздо
больше, чем у величины
около нуля гораздо
больше, чем у величины 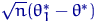 , поскольку больше предельная дисперсия (она же
коэффициент асимптотической нормальности).
, поскольку больше предельная дисперсия (она же
коэффициент асимптотической нормальности).
Но чем меньше отклонение оценки от параметра, тем лучше.
Отсюда - естественный способ сравнения асимптотически нормальных оценок:
Определение 12.
Пусть 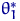 - АНО с коэффициентом
- АНО с коэффициентом 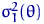 ,
, 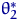 - АНО с коэффициентом
- АНО с коэффициентом 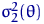 . Говорят, что
. Говорят, что 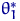 лучше, чем
лучше, чем 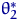 в смысле
асимптотического подхода, если для любого
в смысле
асимптотического подхода, если для любого 
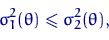
и хотя бы при одном 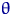 это неравенство строгое.
это неравенство строгое.
Пример 13
<#"662752.files/image227.gif">. Для 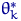 коэффициент асимптотической нормальности
имеет вид
коэффициент асимптотической нормальности
имеет вид 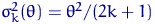 . Коэффициент тем меньше, чем больше
. Коэффициент тем меньше, чем больше 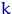 , то есть каждая следующая оценка в этой
последовательности лучше предыдущей.
, то есть каждая следующая оценка в этой
последовательности лучше предыдущей.
Оценка 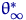 , являющаяся "последней", могла
бы быть лучше всех оценок в этой последовательности в смысле асимптотического
подхода, если бы являлась асимптотически нормальной.
, являющаяся "последней", могла
бы быть лучше всех оценок в этой последовательности в смысле асимптотического
подхода, если бы являлась асимптотически нормальной.
Неравенство Рао - Крамера
Пусть 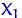 ,
,  ,
,  - выборка объема
- выборка объема 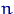 из параметрического семейства распределений
из параметрического семейства распределений
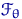 ,
,  , и семейство
, и семейство 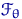 удовлетворяет условию регулярности (R)
<#"662752.files/image232.gif"> существует, положительна и непрерывна
по
удовлетворяет условию регулярности (R)
<#"662752.files/image232.gif"> существует, положительна и непрерывна
по 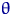 во всех точках
во всех точках  .
.
Справедливо следующее утверждение.
Неравенство Рао - Крамера.
Пусть семейство распределений 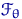 удовлетворяет условиям (R)
<#"662752.files/image233.gif">, дисперсия которой
удовлетворяет условиям (R)
<#"662752.files/image233.gif">, дисперсия которой 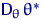 ограничена на любом компакте в области
ограничена на любом компакте в области  , справедливо неравенство
, справедливо неравенство
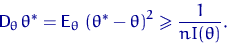
Тема № 6.
Интервальное оценивание
Доверительный
интервал и вероятность
Оценка параметра распределения является приближенной величиной,
поэтому чтобы использовать ее необходимо знать погрешность оценки, то есть
границы 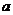 и
и 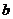 интервала, в котором находится истинное значение оцениваемого
параметра. Поскольку эти границы могут быть определены только на основании
случайных результатов опыта, то они также являются случайными величинами.
Следовательно, необходимо не только указать интервал
интервала, в котором находится истинное значение оцениваемого
параметра. Поскольку эти границы могут быть определены только на основании
случайных результатов опыта, то они также являются случайными величинами.
Следовательно, необходимо не только указать интервал 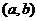 , но и указать надежность этого интервала,
то есть вероятность того, что истинное значение параметра будет лежать в данном
интервале. Следует заметить, что чем больше уверенность, что параметр
принадлежит интервалу, то тем больше интервал. Так что искать интервал,
которому принадлежит
, но и указать надежность этого интервала,
то есть вероятность того, что истинное значение параметра будет лежать в данном
интервале. Следует заметить, что чем больше уверенность, что параметр
принадлежит интервалу, то тем больше интервал. Так что искать интервал,
которому принадлежит 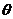 с вероятностью 1 бессмысленно - это вся
область возможных значений параметра.
с вероятностью 1 бессмысленно - это вся
область возможных значений параметра.
Определение. Интервал
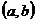 , содержащий неизвестный параметр
, содержащий неизвестный параметр 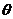 с заданной вероятностью
с заданной вероятностью 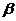 , называют доверительным интервалом
соответствующим доверительной вероятности
, называют доверительным интервалом
соответствующим доверительной вероятности 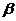 . То есть, если
. То есть, если 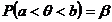 , то
, то 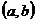 - доверительный интервал, а
- доверительный интервал, а 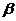 - доверительная вероятность.
- доверительная вероятность.
Замечание 1. Так как случайными являются границы интервала, а не
параметр 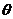 , то обычно говорят "интервал
, то обычно говорят "интервал 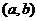 накрывает параметр
накрывает параметр 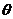 ", а не "
", а не "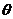 содержится в интервале
содержится в интервале 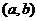 ".
".
Замечание 2. Для дискретных распределений точное равенство 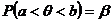 возможно не для всех значений
возможно не для всех значений 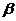 , в этом случае под доверительным
интервалом, соответствующим вероятности
, в этом случае под доверительным
интервалом, соответствующим вероятности 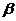 понимается интервал
понимается интервал 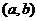 , удовлетворяющий условию
, удовлетворяющий условию 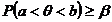 .
.
Определение. Интервал
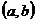 называется асимптотическим доверительным
интервалом для параметра
называется асимптотическим доверительным
интервалом для параметра 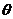 соответствующим доверительной
вероятности
соответствующим доверительной
вероятности 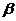 , если
, если 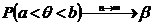 .
.
Число 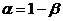 называют уровнем значимости,
оно определяет вероятность того, что доверительный интервал не накроет
оцениваемый параметр. Уровень значимости
называют уровнем значимости,
оно определяет вероятность того, что доверительный интервал не накроет
оцениваемый параметр. Уровень значимости  отделяет события практически невозможные от возможных. Выбор
конкретного значения
отделяет события практически невозможные от возможных. Выбор
конкретного значения 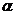 (или
(или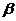 ) зависит от объема выборки и характера решаемой задачи. Обычно
) зависит от объема выборки и характера решаемой задачи. Обычно 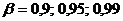 .
.
Общий принцип построения доверительных интервалов таков:
Находим статистику 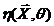 , зависящую от неизвестного параметра
, зависящую от неизвестного параметра 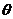 , закон распределения которой известен (и
не зависит от
, закон распределения которой известен (и
не зависит от 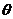 ). Причем необходимо, чтобы статистика
). Причем необходимо, чтобы статистика 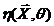 была обратима относительно
была обратима относительно 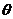 .
.
Находим квантили 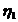 и
и 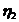 распределения статистики
распределения статистики 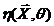 , такие что
, такие что 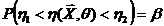 . Заметим, что существует бесконечное множество пар чисел
. Заметим, что существует бесконечное множество пар чисел 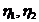 , для которых
, для которых 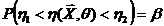 . Обычно в качестве
. Обычно в качестве 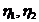 выбирают квантили распределения
статистики
выбирают квантили распределения
статистики 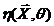 уровней
уровней 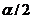 и
и 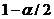 соответственно. Напомним, что квантилем
порядка
соответственно. Напомним, что квантилем
порядка 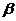 случайной величины
случайной величины 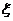 называется значение
называется значение 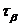 , для которого
, для которого 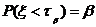 . (см. рис.)
. (см. рис.)
Разрешив неравенство 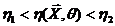 относительно
относительно 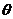 , находим границы доверительного интервала.
, находим границы доверительного интервала.
Аналогично находится и асимптотический доверительный интервал, с
той лишь разницей, что на первом этапе находим статистику 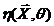 закон распределения которой при
закон распределения которой при 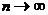 стремится к известному закону, не
зависящему от параметра
стремится к известному закону, не
зависящему от параметра 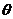 .
.
Доверительный интервал для математического ожидания нормальной
величины при известном среднеквадратическом отклонении 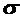 .
.
Пусть 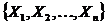 выборка, полученная из нормальной
генеральной совокупности
выборка, полученная из нормальной
генеральной совокупности 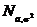 с известным среднеквадратичным
отклонением
с известным среднеквадратичным
отклонением 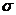 . Требуется построить доверительный
интервал для параметра
. Требуется построить доверительный
интервал для параметра 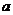 , соответствующий доверительной
вероятности
, соответствующий доверительной
вероятности 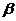 .
.
Так как каждая из величин 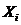 распределена по закону
распределена по закону 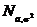 , то выборочное среднее
, то выборочное среднее 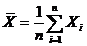 распределено также нормально с параметрами
распределено также нормально с параметрами
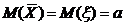 ,
, 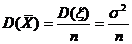 .
.
Тогда 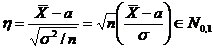 .
.
Найдем 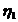 и
и 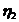 , для которых
, для которых 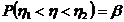 . Так как распределение
. Так как распределение 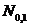 симметрично, то разумно взять
симметрично, то разумно взять 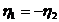 , где
, где 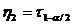 - квантиль распределения
- квантиль распределения 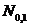 порядка
порядка 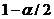 (рис). Тогда:
(рис). Тогда:
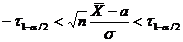 ,
,
или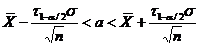 (3.1)
(3.1)
или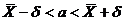 , где
, где 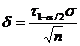
Замечание 1. Если для нахождения квантилей используется функция Лапласа 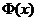 , то следует использовать соотношение:
, то следует использовать соотношение: 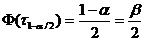 .
.
Пример. Найти доверительный интервал для математического ожидания
нормальной случайной величины 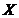 с надежностью
с надежностью 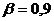 , если
, если 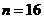 ,
, 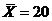 ,
, 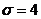 .
.
Решение. Имеем 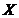 - нормальная случайная величина с
известным
- нормальная случайная величина с
известным 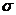 . Требуется построить доверительный
интервал для математического ожидания этой величины, то есть для параметра
. Требуется построить доверительный
интервал для математического ожидания этой величины, то есть для параметра 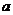 . По таблицам функции Лапласа находим
. По таблицам функции Лапласа находим 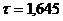 , для которого
, для которого 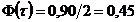 . Следовательно,
. Следовательно, 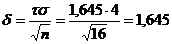 . Таким образом, с вероятностью
. Таким образом, с вероятностью 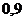 :
:
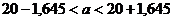 или
или 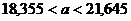 .
.
Замечание 2. Если значение 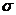 неизвестно, то с помощью статистики
неизвестно, то с помощью статистики 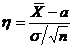 невозможно построить точный доверительный
интервал для параметра
невозможно построить точный доверительный
интервал для параметра 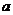 нормальной случайной величины. Однако,
при больших
нормальной случайной величины. Однако,
при больших 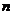 величину
величину 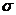 можно заменить состоятельной оценкой)
можно заменить состоятельной оценкой) 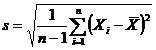 (или
(или 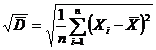 ), построив статистику
), построив статистику 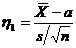 . Так как
. Так как 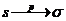 , то
, то 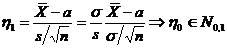 , то есть статистику
, то есть статистику 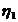 можно использовать для построения АДИ для параметра
можно использовать для построения АДИ для параметра 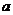 . Тогда, если
. Тогда, если 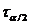 ,
, 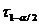 - квантили распределения
- квантили распределения 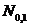 то:
то: 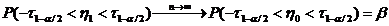 и искомый интервал имеет вид:
и искомый интервал имеет вид: 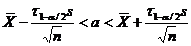 .
.
Кроме того, поскольку, в соответствии с центральной предельной
теоремой, величина 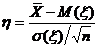 распределена асимптотически нормально для
любой случайной величины
распределена асимптотически нормально для
любой случайной величины 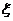 , имеющей конечные математическое ожидание
и дисперсию, при больших
, имеющей конечные математическое ожидание
и дисперсию, при больших 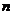 эту величину можно использовать для
построения асимптотических доверительных интервалов для математического
ожидания при любом законе распределения величины
эту величину можно использовать для
построения асимптотических доверительных интервалов для математического
ожидания при любом законе распределения величины 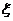 . Если же неизвестна величина
. Если же неизвестна величина 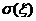 , то при больших
, то при больших 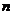 ее можно заменить состоятельными оценками
ее можно заменить состоятельными оценками 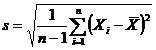 или
или 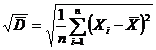 .
.
Замечание 3. Функция 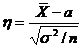 не годится для построения доверительного
интервала для
не годится для построения доверительного
интервала для 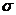 нормальной случайной величины при
известном параметре
нормальной случайной величины при
известном параметре 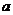 , а тем более при неизвестном а.
Действительно, разрешая неравенство относительно
, а тем более при неизвестном а.
Действительно, разрешая неравенство относительно 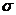 , мы получим
, мы получим 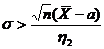 (при условии
(при условии 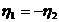 ) - бесконечный доверительный интервал.
) - бесконечный доверительный интервал.
Асимптотический
доверительный интервал для параметра l распределения Пуассона
Пусть 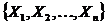 выборка, полученная из генеральной
совокупности случайной величины
выборка, полученная из генеральной
совокупности случайной величины 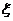 , распределенной по закону Пуассона
, распределенной по закону Пуассона 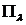 с неизвестным параметром
с неизвестным параметром 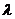 . Требуется построить доверительный интервал для параметра
. Требуется построить доверительный интервал для параметра 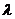 , соответствующий доверительной
вероятности
, соответствующий доверительной
вероятности 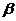 .
.
Рассмотрим статистику 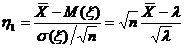 . В соответствии с ЦПТ, при
. В соответствии с ЦПТ, при 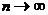
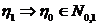 . Пусть
. Пусть 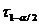 квантиль распределения
квантиль распределения 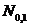 уровня
уровня 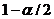 (
(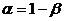 ), тогда:
), тогда:
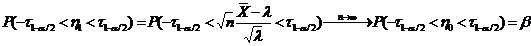 .
.
Однако, разрешить неравенство относительно 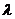 не просто из-за корня в знаменателе.
Попробуем заменить в знаменателе
не просто из-за корня в знаменателе.
Попробуем заменить в знаменателе 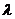 на состоятельную оценку этого параметра
на состоятельную оценку этого параметра 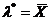 , построив статистику
, построив статистику 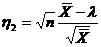 . Не изменится ли при этом характер
сходимости? Вспомним свойство сходимости по распределению: если
. Не изменится ли при этом характер
сходимости? Вспомним свойство сходимости по распределению: если 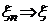 а
а 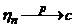 , то
, то 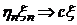 . Тогда:
. Тогда:
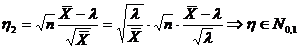 , т.к.
, т.к. 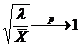 .
.
Следовательно 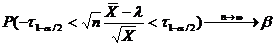 ,
,
или 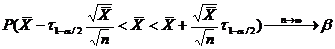 .
.
Таким образом, искомый асимптотический доверительный интервал
уровня 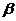 имеет вид:
имеет вид:
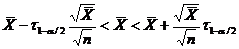 . (3.3)
. (3.3)
Асимптотический
доверительный интервал для параметра a показательного
распределения
Пусть 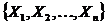 выборка, полученная из генеральной
совокупности случайной величины
выборка, полученная из генеральной
совокупности случайной величины 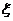 , распределенной по показательному закону
, распределенной по показательному закону 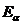 с неизвестным параметром
с неизвестным параметром 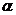 . Требуется построить доверительный
интервал для параметра
. Требуется построить доверительный
интервал для параметра 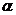 , соответствующий доверительной
вероятности
, соответствующий доверительной
вероятности 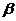 .
.
Рассмотрим статистику 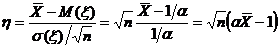 . В соответствии с ЦПТ, при
. В соответствии с ЦПТ, при 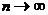
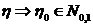 . Пусть
. Пусть 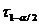 квантиль распределения
квантиль распределения 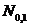 уровня
уровня 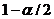 (
(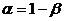 ), тогда:
), тогда:
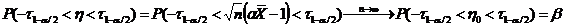 ,
,
или 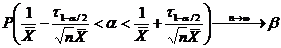 .
.
Таким образом, искомый асимптотический доверительный интервал
уровня 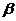 имеет вид:
имеет вид:
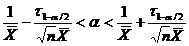 . (3.3)
. (3.3)
Распределения,
связанные с нормальным
Поставим задачу: построить точные ДИ для параметров
нормального распределения.
1. Для параметра 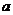 при известном
при известном 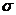 - уже построен - (3.1).
- уже построен - (3.1).
. Для параметра 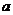 при неизвестном
при неизвестном 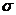 .
.
. Для параметра 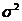 при известном
при известном 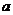 .
.
. Для параметра 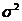 при неизвестном
при неизвестном 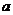 .
.
Для построения подходящих статистик, рассмотрим ряд
распределений, связанных с нормальным.
Гамма
распределение и его свойства.
Определение. Случайная
величина 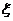 имеет гамма распределение
имеет гамма распределение 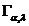 , где
, где 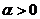 ,
, 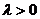 , если ее плотность распределения имеет
вид:
, если ее плотность распределения имеет
вид:
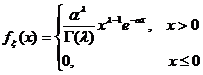 (3.4)
(3.4)
Здесь  - гамма функция.
- гамма функция.
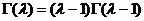 ,
, 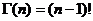 ,
, 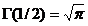 .
.
Найдем характеристическую функцию случайной величины 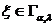 :
:
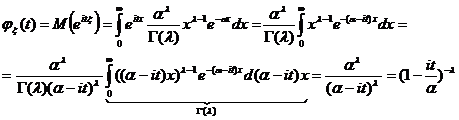
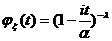 (3.5)
(3.5)
Используя, характеристическую функцию легко найти математическое
ожидание и дисперсию гамма-распределения:
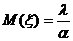 ,
, 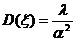 .
.
Свойство 1. 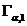 есть показательное распределение с параметром
есть показательное распределение с параметром 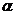 .
.
Действительно, если 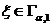 , то
, то 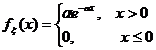 - есть плотность распределения случайной
величины, распределенной по показательному закону с параметром
- есть плотность распределения случайной
величины, распределенной по показательному закону с параметром 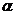 .
.
Свойство 2. Если 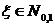 , то
, то 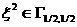 .
.
Доказательство. Найдем функцию распределения 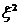 :
:
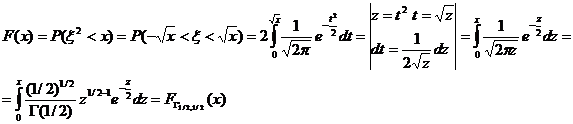
Свойство 3. Если 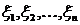 независимы и
независимы и 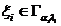 , то
, то 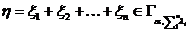 .
.
Доказательство. По свойству характеристической функции
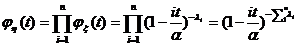 - что есть характеристическая функция случайной величины,
распределенной по
- что есть характеристическая функция случайной величины,
распределенной по 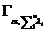 .
.
Свойство 4. Если 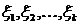 независимы и имеют стандартное нормальное
распределение, то
независимы и имеют стандартное нормальное
распределение, то 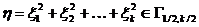 .
.
Доказательство. Вытекает из свойств 2 и 3.
Распределение
"хи-квадрат"
Определение. Распределение
суммы квадратов 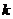 независимых стандартных нормальных
случайных величин называют распределением "хи-квадрат" с
независимых стандартных нормальных
случайных величин называют распределением "хи-квадрат" с 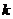 степенями свободы и обозначают
степенями свободы и обозначают 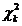 . (Саму случайную величину также часто
обозначают
. (Саму случайную величину также часто
обозначают 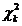 ).
).
Согласно этому определению и свойству 4 предыдущего раздела, 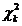 - есть гамма распределение
- есть гамма распределение 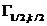 . Следовательно, плотность распределения
. Следовательно, плотность распределения 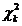 :
:
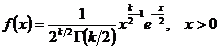 , (3.6)
, (3.6)
а основные числовые характеристики 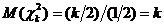 ,
, 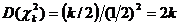 , мода распределения, при
, мода распределения, при 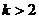 , равна
, равна 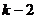 .
.
Графики плотности вероятностей для различных степеней свободы 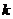 приведены на рис
приведены на рис
Если случайные величины 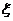 и
и 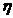 независимы и
независимы и 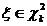 ,
, 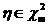 , то, очевидно, их сумма
, то, очевидно, их сумма 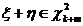 .
.
Распределение
Стьюдента
Определение. Пусть
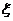 - случайная величина распределенная по
закону
- случайная величина распределенная по
закону 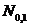 , а
, а 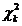 - независимая от нее случайная величина распределенная по закону
хи-квадрат с
- независимая от нее случайная величина распределенная по закону
хи-квадрат с 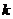 степенями свободы. Тогда распределение
величины
степенями свободы. Тогда распределение
величины
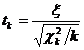 (3.7)
(3.7)
называется распределением Стьюдента с 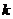 степенями свободы и обозначают
степенями свободы и обозначают 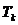 . Плотность распределения Стьюдента:
. Плотность распределения Стьюдента:
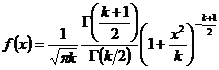 ,
, 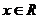 (3.8)
(3.8)
Числовые характеристики: 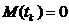 ,
, 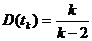 .
.
Распределение Стьюдента симметрично относительно 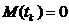 .
.
Так как при 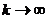 , согласно закону больших чисел,
, согласно закону больших чисел,
 , то при
, то при 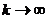
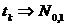 .
.
Преобразования
нормальных выборок. Лемма Фишера
Теорема 1 (об ортогональном преобразовании нормального вектора). Пусть 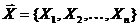 - случайный вектор, координаты которого независимы и имеют
стандартное нормальное распределение, а
- случайный вектор, координаты которого независимы и имеют
стандартное нормальное распределение, а 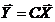 , где
, где 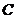 - ортогональная матрица порядка
- ортогональная матрица порядка 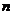 (т.е.
(т.е. 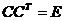 ),. Тогда координаты
),. Тогда координаты 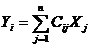 вектора
вектора  независимы и имеют стандартное нормальное
распределение.
независимы и имеют стандартное нормальное
распределение.
Доказательство. Запишем плотность распределения вектора  . Так как величины
. Так как величины 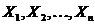 независимы и имеют стандартное нормальное
распределение, то:
независимы и имеют стандартное нормальное
распределение, то:
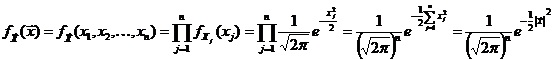 ,
,
где 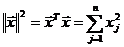 .
.
Чтобы записать плотность распределения вектора 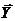 , воспользуемся формулой для плотности при
линейном преобразовании вектора: если
, воспользуемся формулой для плотности при
линейном преобразовании вектора: если 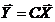 , то
, то  . Тогда, с учетом того, что
. Тогда, с учетом того, что 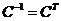 и
и 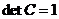 получим:
получим:
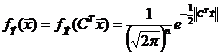 .
.
Но, умножение вектора на ортогональную матрицу не меняет нормы
вектора, действительно:
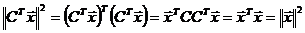 .
.
Следовательно, 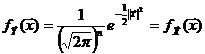 , т.е. величины
, т.е. величины 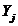 также как и величины
также как и величины 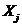 , независимы и имеют стандартное нормальное распределение.
, независимы и имеют стандартное нормальное распределение.
Теорема 2 (лемма Фишера). Пусть 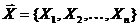 - выборка из
- выборка из 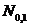 и
и 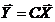 , где
, где 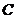 - ортогональная матрица порядка
- ортогональная матрица порядка 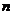 . Тогда для любого
. Тогда для любого 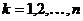 статистика
статистика 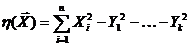 распределена по закону
распределена по закону 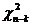 , и не зависит от
, и не зависит от 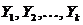 .
.
Доказательство. Так как 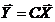 , то
, то 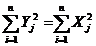 (см. доказательство предыдущей теоремы). Тогда
(см. доказательство предыдущей теоремы). Тогда
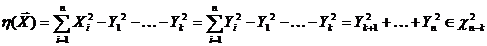 .
.
Основные
следствия леммы Фишера
Пусть 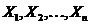 независимы и имеют нормальное
распределение
независимы и имеют нормальное
распределение
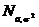 ,
, 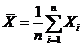 ,
, 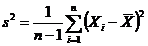 ,
, 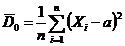 . Тогда:
. Тогда:
. 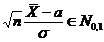 ; (3.9)
; (3.9)
. 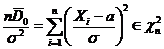 ; (3.10)
; (3.10)
. 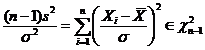 ; (3.11)
; (3.11)
. 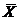 и
и 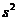 независимы;
независимы;
. 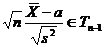 . (3.12)
. (3.12)
Доказательство.
1. Доказано ранее.
2. Так как величины 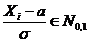 , то величина
, то величина 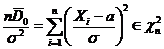 .
.
. Рассмотрим статистику 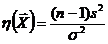 .
.
Введем стандартные нормальные величины 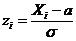 и выразим
и выразим 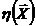 через
через 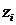 :
:
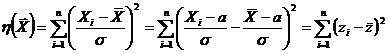 , где
, где 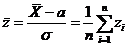 .
.
То есть можно изначально считать, что величины 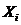 имеют стандартное нормальное
распределение. Попробуем применить к
имеют стандартное нормальное
распределение. Попробуем применить к 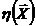 лемму Фишера, для этого представим
лемму Фишера, для этого представим 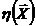 в виде:
в виде:
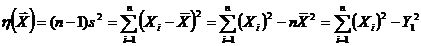 , где
, где 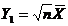 .
.
Покажем, что найдется ортогональная матрица 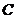 такая, что вектор
такая, что вектор 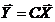 , будет иметь координату
, будет иметь координату 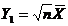 . Возьмем в качестве первой строки матрицы
. Возьмем в качестве первой строки матрицы
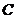 строку,
строку, 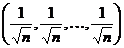 .
.
Тогда 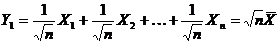 . Так как норма этой строки (длина
вектора) равна 1, то эту строку всегда можно дополнить до ортогональной матрицы
(строки и столбы ортогональной матрицы - есть ортонормированные вектора).
. Так как норма этой строки (длина
вектора) равна 1, то эту строку всегда можно дополнить до ортогональной матрицы
(строки и столбы ортогональной матрицы - есть ортонормированные вектора).
Тогда в соответствии с леммой Фишера, статистика 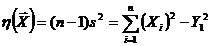 имеет распределение хи-квадрат с
имеет распределение хи-квадрат с 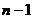 степенью свободы.
степенью свободы.
. В соответствии с леммой Фишера, статистика 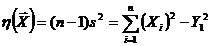 и величина
и величина 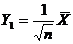 независимы, то есть
независимы, то есть 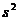 и
и 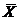 независимы.
независимы.
. Преобразуем 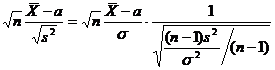 . Величина
. Величина 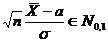 , а
, а
величина 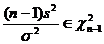 , и по следствию 4 эти величины
независимы. Следовательно,
, и по следствию 4 эти величины
независимы. Следовательно, 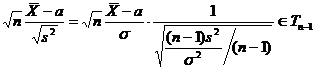 .
.
Точные
доверительные интервалы для параметров нормального распределения
1. Для параметра 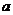 при известном
при известном 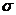 .
.
С вероятностью 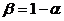 :
: 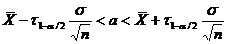 , где
, где 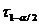 - квантиль стандартного нормального распределения уровня
- квантиль стандартного нормального распределения уровня 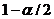 .
.
. Для параметра 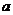 при неизвестном
при неизвестном 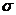 .
.
Из следствия 5 леммы Фишера, учитывая симметрию распределения
Стьюдента, с вероятностью 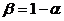 получим:
получим:
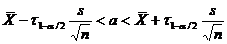
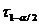 , (3.13)
, (3.13)
где 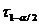 - квантиль распределения Стьюдента уровня
- квантиль распределения Стьюдента уровня
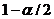 . Заметим, что квантиль
. Заметим, что квантиль 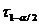 распределения Стьюдента называется
коэффициентом Стьюдента
распределения Стьюдента называется
коэффициентом Стьюдента 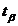 уровня
уровня 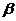 .
.
. Для параметра 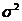 при неизвестном
при неизвестном 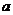 .
.
Из следствия 2 леммы Фишера, с вероятностью 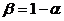 получим:
получим:
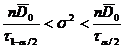 , (3.14)
, (3.14)
где 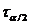 ,
, 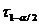 - квантили распределения хи-квадрат с
- квантили распределения хи-квадрат с 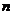 степенями свободы уровней
степенями свободы уровней 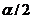 и
и 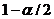 соответственно.
соответственно.
. Для параметра 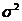 при неизвестном
при неизвестном 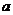 .
.
Из следствия 3 леммы Фишера, с вероятностью 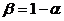 получим:
получим:
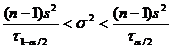 , (3.15)
, (3.15)
где 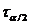 ,
, 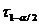 - квантили распределения хи-квадрат с
- квантили распределения хи-квадрат с 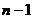 степенью свободы уровней
степенью свободы уровней 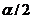 и
и 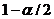 соответственно.
соответственно.
Пример 1.
Найти доверительный интервал для дисперсии нормальной величины с надежностью 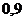 , если
, если  .
.
Решение. По
таблицам распределения 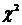 для
для 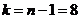 степеней свободы находим квантили распределения уровней
степеней свободы находим квантили распределения уровней 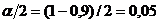 и
и 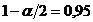 :
: 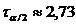 ,
, 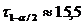 . Следовательно, доверительный интервал:
. Следовательно, доверительный интервал:
 .
.
Пример 2. Найти доверительный интервал для математического ожидания
нормальной случайной величины с надежностью 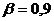 , если
, если 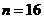 ,
, 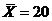 ,
, 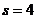 .
.
Решение. По
таблицам распределения Стьюдента для 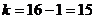 степеней свободы находим коэффициент Стьюдента уровня
степеней свободы находим коэффициент Стьюдента уровня 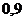 :
: 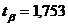 . Таким образом, с вероятностью
. Таким образом, с вероятностью 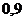 :
:
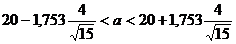 или
или 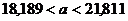 .
.
Тема № 7.
Проверка статистических гипотез
В математической статистике считается, что данные, получаемые
в результате наблюдений, подчинены некоторому неизвестному вероятностному
распределению, и задача состоит в том, чтобы извлечь из данных правдоподобную
информацию об этом неизвестном распределении. В настоящей главе мы обсудим еще
один подход к этой общей задаче, состоящий в проверке гипотез. Статистической
гипотезой называют предположение о распределении вероятностей, которое
необходимо проверить по имеющимся данным.
Статистический критерий - строгое математическое правило, по
которому принимается или отвергается та или иная статистическая гипотеза с
известным уровнем значимости. Построение критерия представляет собой выбор
подходящей функции от результатов наблюдений (ряда эмпирически полученных
значений признака), которая служит для выявления меры расхождения между
эмпирическими значениями и гипотетическими.
Непараметрические критерии
Группа статистических критериев, которые не включают в расчёт
параметры вероятностного распределения и основаны на оперировании частотами или
рангами.критерий Розенбаумакритерий Манна-Уитни
Критерий Уилкоксона
Критерий Пирсона
Критерий Колмогорова-Смирнова
Параметрические критерии
Группа статистических критериев, которые включают в расчет
параметры вероятностного распределения признака (средние и дисперсии).критерий
Стьюдента
Критерий Фишера
Критерий отношения правдоподобия
Критерий Романовского
Определения
Пусть в (статистическом) эксперименте доступна наблюдению
случайная величина X, распределение которой неизвестно полностью или частично.
Тогда любое утверждение, касающееся называется статистической гипотезой.
Гипотезы различают по виду предположений, содержащихся в них:
Статистическая гипотеза, однозначно определяющая
распределение, то есть, где какой-то конкретный закон, называется простой.
Статистическая гипотеза, утверждающая принадлежность
распределения к некоторому семейству распределений, то есть вида, где -
семейство распределений, называется сложной.
На практике обычно требуется проверить какую-то конкретную и
как правило простую гипотезу H0. Такую гипотезу принято называть нулевой. При
этом параллельно рассматривается противоречащая ей гипотеза H1, называемая
конкурирующей или альтернативной.
Выдвинутая гипотеза нуждается в проверке, которая
осуществляется статистическими методами, поэтому гипотезу называют
статистической. Для проверки гипотезы используют критерии, позволяющие принять
или опровергнуть гипотезу.
В большинстве случаев статистические критерии основаны на
случайной выборке фиксированного объема из распределения. В последовательном
анализе выборка формируется в ходе самого эксперимента и потому её объем
является случайной величиной
Уровень
значимости и мощность
При проверке статистической гипотезы
возможны ошибки. Есть два рода ошибок. Ошибка первого рода заключается в том,
что отвергают нулевую гипотезу, в то время как в действительности эта гипотеза
верна. Ошибка второго рода состоит в том, что принимают нулевую гипотезу, в то
время как в действительности эта гипотеза неверна.
Вероятность ошибки первого рода называется
уровнем значимости и обозначается α. Таким образом, α = P{U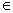 Ψ | H0}, т.е. уровень значимости α - это вероятность события {U
Ψ | H0}, т.е. уровень значимости α - это вероятность события {U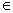 Ψ}, вычисленная в предположении, что верна нулевая гипотеза Н0.
Ψ}, вычисленная в предположении, что верна нулевая гипотеза Н0.
Уровень значимости однозначно определен,
если Н0 - простая гипотеза. Если же Н0 -
сложная гипотеза, то уровень значимости, вообще говоря, зависит от функции
распределения результатов наблюдений, удовлетворяющей Н0.
Статистику критерия U обычно строят так, чтобы вероятность события {U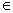 Ψ} не зависела от того, какое именно распределение (из
удовлетворяющих нулевой гипотезе Н0) имеют результаты
наблюдений. Для статистик критерия U общего вида под уровнем значимости
понимают максимально возможную ошибку первого рода. Максимум (точнее, супремум)
берется по всем возможным распределениям, удовлетворяющим нулевой гипотезе Н0,
т.е. α = sup P{U
Ψ} не зависела от того, какое именно распределение (из
удовлетворяющих нулевой гипотезе Н0) имеют результаты
наблюдений. Для статистик критерия U общего вида под уровнем значимости
понимают максимально возможную ошибку первого рода. Максимум (точнее, супремум)
берется по всем возможным распределениям, удовлетворяющим нулевой гипотезе Н0,
т.е. α = sup P{U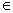 Ψ | H0}.
Ψ | H0}.
Если критическая область имеет вид,
указанный в формуле (9), то
{U > C | H0} =
α. (10)
Если С задано, то из последнего
соотношения определяют α. Часто поступают по
иному - задавая α (обычно α = 0,05, иногда α = 0,01 или α = 0,1, другие значения α используются гораздо
реже), определяют С из уравнения (10), обозначая его Сα, и используют критическую область Ψ = {U > Cα} с заданным уровнем
значимости α.
Вероятность ошибки второго рода есть P{U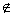 Ψ | H1}. Обычно используют не эту вероятность, а
ее дополнение до 1, т.е. P{U
Ψ | H1}. Обычно используют не эту вероятность, а
ее дополнение до 1, т.е. P{U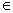 Ψ | H1} = 1 - P{U
Ψ | H1} = 1 - P{U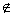 Ψ | H1}. Эта величина носит название мощности
критерия. Итак, мощность критерия - это вероятность того, что нулевая гипотеза
будет отвергнута, когда альтернативная гипотеза верна.
Ψ | H1}. Эта величина носит название мощности
критерия. Итак, мощность критерия - это вероятность того, что нулевая гипотеза
будет отвергнута, когда альтернативная гипотеза верна.
Понятия уровня значимости и мощности
критерия объединяются в понятии функции мощности критерия - функции,
определяющей вероятность того, что нулевая гипотеза будет отвергнута. Функция
мощности зависит от критической области Ψ и действительного
распределения результатов наблюдений. В параметрической задаче проверки гипотез
распределение результатов наблюдений задается параметром θ. В этом случае функция мощности обозначается М (Ψ,θ) и зависит от критической области Ψ и действительного значения исследуемого параметра θ. Если
Н0: θ = θ0,Н1: θ = θ1,то
М (Ψ,θ0) = α,
М (Ψ,θ1) = 1 - β,
где α - вероятность ошибки
первого рода, β - вероятность ошибки второго рода. В
статистическом приемочном контроле α - риск изготовителя, β - риск потребителя. При статистическом регулировании технологического
процесса α - риск излишней наладки, β - риск незамеченной разладки.
Функция мощности М (Ψ,θ) в случае одномерного параметра θ обычно достигает минимума, равного α, при θ = θ0, монотонно возрастает
при удалении от θ0 и приближается к 1 при |
θ - θ0 | → ∞.
В ряде вероятностно-статистических методов
принятия решений используется оперативная характеристикаL (Ψ,θ) - вероятность принятия нулевой гипотезы в зависимости от
критической области Ψ и действительного
значения исследуемого параметра θ. Ясно, что
(Ψ,θ) = 1 - М (Ψ,θ).
Построение
оптимальных критериев
Следующее замечательное утверждение, по недоразумению
называемое леммой, заявляет, что оптимальные во всех трех смыслах (минимаксные,
байесовские, наиболее мощные) критерии могут быть построены в самом общем
случае простым выбором различных констант в одном и том же критерии - критерии
отношения правдоподобия.
Пусть 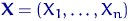 - выборка (набор независимых, одинаково
распределенных величин), и имеются две гипотезы о распределении
- выборка (набор независимых, одинаково
распределенных величин), и имеются две гипотезы о распределении 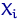 :
:
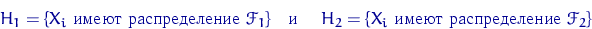
Пусть 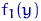 - плотность распределения
- плотность распределения 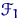 ,
, 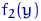 - плотность
распределения
- плотность
распределения 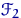 , а
, а
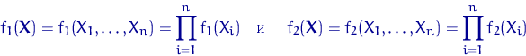
соответствующие функции правдоподобия
<#"662752.files/image453.gif"> и 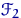 либо оба дискретны, либо
оба абсолютно непрерывны.
либо оба дискретны, либо
оба абсолютно непрерывны.
Замечание 17.
Если одно из распределений дискретно, а другое абсолютно
непрерывно, то всегда существует критерий с нулевыми вероятностями ошибок.
Смешанные распределения мы рассматривать не будем. Математики вместо этого
могут предполагать, что оба распределения абсолютно непрерывны относительно
одной и той же 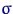 -конечной меры и имеют относительно нее плотности
-конечной меры и имеют относительно нее плотности
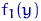 и
и 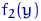 .
.
Мы будем выбирать гипотезу в зависимости от отношения функций
правдоподобия. Напомним, что функция правдоподобия есть плотность распределения
выборки.
Обратимся к примеру 30
<#"662752.files/image150.gif"> лежит правее точки пересечения плотностей 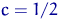 . То есть там, где вторая плотность
больше, принимать вторую гипотезу, там, где первая - первую.
. То есть там, где вторая плотность
больше, принимать вторую гипотезу, там, где первая - первую.
Такой критерий сравнивает отношение 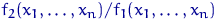 с единицей, относя к критической области ту часть
с единицей, относя к критической области ту часть 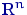 , где это отношение больше единицы.
Заметим, что при этом мы получим ровно один, не обязательно оптимальный,
критерий с некоторым фиксированным размером и мощностью.
, где это отношение больше единицы.
Заметим, что при этом мы получим ровно один, не обязательно оптимальный,
критерий с некоторым фиксированным размером и мощностью.
Если же нужно получить критерий c заранее заданным размером 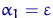 , либо иметь возможность варьировать и
размер, и мощность критерия, то следует рассмотреть класс похожих критериев,
введя свободный параметр:
, либо иметь возможность варьировать и
размер, и мощность критерия, то следует рассмотреть класс похожих критериев,
введя свободный параметр:
там, где вторая плотность в 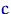 раз превосходит первую, выбирать вторую гипотезу, иначе - первую,
раз превосходит первую, выбирать вторую гипотезу, иначе - первую,
т.е. сравнивать отношение плотностей 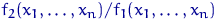 не с единицей, а с некоторой постоянной
не с единицей, а с некоторой постоянной 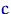 .
.
Назовем отношением правдоподобия частное
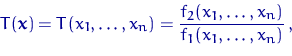 (18)
(18)
рассматривая его лишь при таких значениях 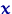 , когда хотя бы одна из плотностей отлична
от нуля. Имеется в виду, что
, когда хотя бы одна из плотностей отлична
от нуля. Имеется в виду, что 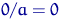 ,
,  .
.
Конструкция критерия, который мы живописали выше, сильно
усложнится в случае, когда распределение случайной величины 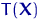 не является непрерывным, т.е. существует
такое число
не является непрерывным, т.е. существует
такое число 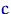 , что вероятность
, что вероятность 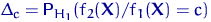 отлична от нуля. Это означает, что на
некотором "большом" множестве значений выборки обе гипотезы
"равноправны": отношение правдоподобия постоянно. Относя это
множество целиком к критическому множеству или целиком исключая из него, мы
меняем вероятность ошибки первого рода (размер) критерия на положительную
величину
отлична от нуля. Это означает, что на
некотором "большом" множестве значений выборки обе гипотезы
"равноправны": отношение правдоподобия постоянно. Относя это
множество целиком к критическому множеству или целиком исключая из него, мы
меняем вероятность ошибки первого рода (размер) критерия на положительную
величину 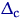 :
:
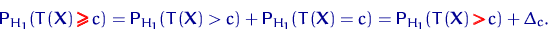
И если вдруг мы захотим приравнять вероятность ошибки первого рода
к заранее выбранному числу 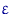 , может случиться так, что критерий с критическим множеством
, может случиться так, что критерий с критическим множеством 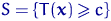 имеет размер больший, чем
имеет размер больший, чем 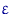 , а критерий с критическим множеством
, а критерий с критическим множеством 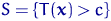 - размер меньший, чем
- размер меньший, чем 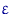 .
.
Поэтому для математиков, не читающих [1] <#"662752.files/image466.gif"> имеет при верной первой гипотезе непрерывную функцию
распределения, т.е. 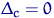 для любого
для любого 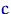 .
.
Критерии
согласия
Критериями согласия называют критерии, предназначенные для
проверки простой гипотезы 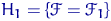 при сложной альтернативе
при сложной альтернативе 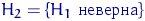 . Мы рассмотрим более
широкий класс основных гипотез, включающий и сложные гипотезы, а критериями
согласия будем называть любые критерии, устроенные по одному и тому же
принципу. А именно, пусть задана некоторая функция отклонения эмпирического
распределения от теоретического, распределение которой существенно разнится в
зависимости от того, верна или нет основная гипотеза. Критерии согласия
принимают или отвергают основную гипотезу исходя из величины этой функции
отклонения.
. Мы рассмотрим более
широкий класс основных гипотез, включающий и сложные гипотезы, а критериями
согласия будем называть любые критерии, устроенные по одному и тому же
принципу. А именно, пусть задана некоторая функция отклонения эмпирического
распределения от теоретического, распределение которой существенно разнится в
зависимости от того, верна или нет основная гипотеза. Критерии согласия
принимают или отвергают основную гипотезу исходя из величины этой функции
отклонения.
Итак, имеется выборка 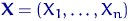 из распределения
из распределения  . Мы сформулируем ряд
понятий для случая простой основной гипотезы, а в дальнейшем будем их
корректировать по мере изменения задачи. Проверяется простая основная гипотеза
. Мы сформулируем ряд
понятий для случая простой основной гипотезы, а в дальнейшем будем их
корректировать по мере изменения задачи. Проверяется простая основная гипотеза 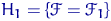 при сложной альтернативе
при сложной альтернативе
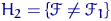 .
.
K1.
Пусть возможно задать функцию 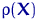 , обладающую свойствами:
, обладающую свойствами:
а)
если гипотеза 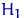 верна, то
верна, то 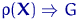 , где
, где 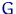 - непрерывное
распределение;
- непрерывное
распределение;
б)
если гипотеза 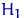 неверна, то
неверна, то 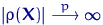 при
при  .
.
K2.
Пусть такая функция 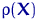 задана. Для случайной
величины
задана. Для случайной
величины  из распределения
из распределения 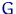 определим постоянную
определим постоянную 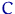 из равенства
из равенства 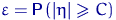 .
.
Построим критерий:
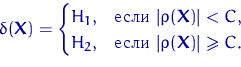 (22)
(22)
Мы построили критерий согласия. Он "работает" по
принципу: если для данной выборки функция отклонения велика (по абсолютному
значению), то это свидетельствует в пользу альтернативы, и наоборот. Убедимся в
том, что этот критерий имеет (асимптотический) размер 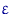 и является
состоятельным.
и является
состоятельным.
Определение 29.
Говорят, что критерий 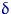 для проверки простой
гипотезы
для проверки простой
гипотезы 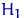 является критерием
асимптотического размера
является критерием
асимптотического размера 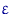 , если его размер приближается к
, если его размер приближается к 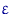 с ростом
с ростом 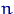 :
:
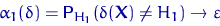 при
при  .
.
Поскольку альтернатива 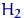 всегда является сложной, то, как мы уже отмечали в замечании 16
<#"662752.files/image488.gif"> есть функция
всегда является сложной, то, как мы уже отмечали в замечании 16
<#"662752.files/image488.gif"> есть функция 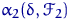 от конкретного распределения
от конкретного распределения 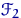 из списка возможных альтернатив
из списка возможных альтернатив 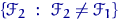 . Или, при ином виде основной гипотезы, из числа распределений,
отвечающих альтернативе
. Или, при ином виде основной гипотезы, из числа распределений,
отвечающих альтернативе 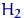 .
.
Определение 30.
Критерий 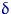 для проверки гипотезы
для проверки гипотезы 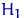 против сложной
альтернативы
против сложной
альтернативы 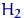 называется состоятельным, если для любого
распределения
называется состоятельным, если для любого
распределения 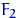 , отвечающего альтернативе
, отвечающего альтернативе 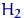 , вероятность ошибки
второго рода стремится к нулю с ростом объема выборки:
, вероятность ошибки
второго рода стремится к нулю с ростом объема выборки:
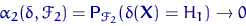 при
при  .
.
Свойство 10.
Для критерия 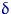 , заданного в (22
<#"662752.files/image483.gif">:
, заданного в (22
<#"662752.files/image483.gif">:
. 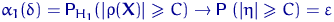 ;
;
. 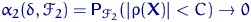 для любого распределения
для любого распределения 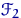 , отвечающего
, отвечающего 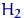 .
.
Иначе говоря, построенный критерий имеет асимптотический размер 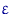 и состоятелен.
и состоятелен.
Критерий Колмогорова
Имеется выборка 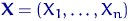 из распределения
из распределения 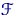 . Проверяется простая гипотеза
. Проверяется простая гипотеза 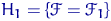 против сложной альтернативы
против сложной альтернативы 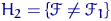 . В том случае, когда распределение
. В том случае, когда распределение 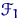 имеет непрерывную функцию распределения
имеет непрерывную функцию распределения 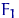 , можно пользоваться критерием
Колмогорова. Пусть
, можно пользоваться критерием
Колмогорова. Пусть
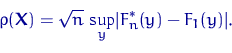
Покажем, что 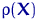 удовлетворяет условиям K1 (a, б)
<#"662752.files/image479.gif"> верна, то
удовлетворяет условиям K1 (a, б)
<#"662752.files/image479.gif"> верна, то 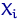 имеют распределение
имеют распределение 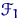 . По теореме Колмогорова <#"662752.files/image499.gif">, где
. По теореме Колмогорова <#"662752.files/image499.gif">, где  имеет распределение с функцией распределения Колмогорова.
имеет распределение с функцией распределения Колмогорова.
б) Если гипотеза 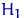 неверна, то
неверна, то 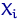 имеют какое-то распределение
имеют какое-то распределение 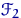 , отличное от
, отличное от 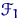 . По теореме Гливенко - Кантелли
<#"662752.files/image500.gif"> для любого
. По теореме Гливенко - Кантелли
<#"662752.files/image500.gif"> для любого 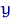 при
при  . Поскольку
. Поскольку 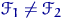 , найдется
, найдется 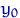 такое, что
такое, что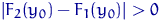 . Но
. Но
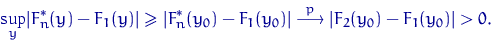
Умножая на 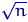 , получим при
, получим при  , что
, что
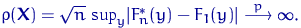
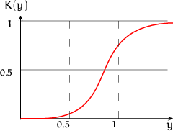
Пусть случайная величина  имеет распределение с
функцией распределения Колмогорова
имеет распределение с
функцией распределения Колмогорова
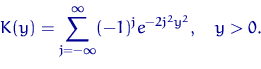
Это распределение табулировано, так что по заданному 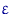 легко найти
легко найти  такое, что
такое, что 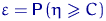 .
.
Критерий Колмогорова выглядит так:
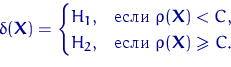
Критерии,
основанные на доверительных интервалах
Имеется выборка 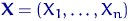 из семейства распределений
из семейства распределений
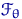 . Проверяется простая
гипотеза
. Проверяется простая
гипотеза 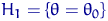 против сложной
альтернативы
против сложной
альтернативы 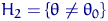 .
.
Пусть имеется точный (асимптотически точный) доверительный
интервал 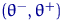 для параметра
для параметра 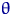 уровня доверия
уровня доверия  . Взяв произвольное
. Взяв произвольное 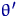 , для выборки из
распределения
, для выборки из
распределения 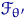 имеем
имеем
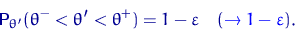
Тогда критерий
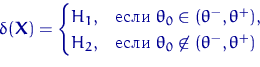
имеет точный (асимптотический) размер 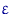 . Действительно,
. Действительно,
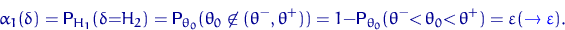
Если доверительный интервал строится с помощью 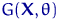 , то эта же функция годится и в качестве
"функции отклонения"
, то эта же функция годится и в качестве
"функции отклонения" 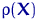 для построения критерия согласия.
для построения критерия согласия.
Пример 33.
Посмотрим на критерий (28)
<#"662752.files/image479.gif"> принимается, только если 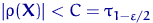 , что равносильно неравенству
, что равносильно неравенству
Сравните то, что получилось, с точным доверительным интервалом (13)
<#"662752.files/image523.gif"> нормального распределения с известной
дисперсией.
Тема № 8.
Оценивание статистической зависимости
Оценка ковариации и коэффициента корреляции. Доверительный
интервал для коэффициента корреляции. Регрессионная модель и уравнение регрессии.
Оценки метода максимального правдоподобия и метода наименьших квадратов (МНК)
параметров уравнения регрессии. Множественная линейная регрессия, оценка
параметров уравнения по МНК. Числовые характеристики оценок параметров
уравнения множественной линейной регрессии. Оценка дисперсии предсказания для
модели множественной линейной регрессии. Доверительные интервалы для параметров
линейной модели в случае нормального распределения остатков. Значимость
регрессионной модели, коэффициент детерминации, критерий Фишера-Снедекора.
Значимость коэффициентов регрессионной модели, критерий Стьюдента.
Доверительный интервал для значений, определяемых уравнением уравнения
регрессии.
Ковариация и
коэффициент корреляции
При формировании портфеля степень взаимосвязи между
доходностями двух ценных бумаг можно определить с помощью таких показателей как
ковариация и коэффициент корреляции.
Ковариация говорит о степени зависимости двух случайных
величин. Она может принимать положительные, отрицательные значения и равняться
нулю. Если ковариация положительна, это говорит о том, что при изменении
значения одной переменной другая имеет тенденцию изменяться в том же
направлении. Так, при положительной ковариации доходностей двух бумаг с ростом
доходности первой бумаги доходность второй также будет расти. При падении
доходности первой бумаги доходность второй также будет снижаться.
При отрицательной ковариации переменные имеют тенденцию
изменяться в противоположных направлениях. В таком случае рост доходности
первой бумаги будет сопровождаться падением доходности второй бумаги, и
наоборот. Чем больше значение ковариации, тем сильнее зависимость между
переменными. Если ковариация равна нулю, никакой зависимости между переменными
не наблюдается.