Задачи о точках с рациональными координатами

Задачи о точках с рациональными координатами

Задачи о точках с рациональными координатами

Автор Фильчев Э.Г.

Россия

В результате анализа дерева ПТ возникли ряд интересных задач о пифагоровых треугольниках с целочисленными значениями сторон. Решение этих задач может найти практическое использование в геодезии, в атомных и молекулярных структурах, и в астрономических расчетах.

Y

                М(x, y )

                           Z                      y

0                                 X                           x

Рис. 1 Точка в прямоугольной системе координат

Считаем, что координаты точки М имеют целочисленные значения.

Задача 1

“ Имеем массив ПТ с x и y. Известно, что в этом массиве имеются такие ПТ, у которых при одинаковых значениях x имеют место разные пары значений y и z. Требуется определить метод нахождения ПТ с одинаковыми значениями x “

Значения X могут быть четными или нечетными. Для четных значений имеем

 = 2m² + 2mn= 2m(m + n ), тогда y = n² + 2mn = n (n + 2m ) ( 1 )

Для нечетных значений имеем

 = n² + 2mn = n (n + 2m ), тогда y = 2m² + 2mn = 2m(m + n ) ( 2 )

При z = n² + 2mn + 2m² = ( n + m )² + m² ( 3 )

. Пусть ( J ) x = 2m² + 2mn, следовательно ( → ) x = 2m(m + n ), y = n (n + 2m ).

Рассмотрим ПТ( 4, 3, 5 ). Здесь x = 4 = 2∙ 1∙( 1 + 1 ) → m = 1, n = 1. Других вариантов, представления  в виде двух целых сомножителей, нет. Вывод: Других ПТ с x = 4 нет.

. На втором уровне дерева ПТ находятся три ПТ, а именно ПТ₁( 120, 119, 129 ),

ПТ₂( 12,5, 13 ), ПТ₃( 15, 8, 17 ). Рассмотрим каждый из этих ПТ. Здесь x > y.

.1. J имеем ПТ₁( 120, 119, 169 ). Здесь x = 120 = 2∙ 60 → = 60, Число 60 имеет следующие варианты в виде двух целочисленных сомножителей 60 = 1∙60 = 2∙ 30 = 3∙20 = 4∙15 = 5∙12 = 6∙10. Итого имеем 6 ПТ с x = 120. Определим эти ПТ.

.1.1. J x = 2∙ 1∙ 60. По формуле ( 1 ) x = 2m(m + n ) → m = 1, (m + n ) = 60 → n = 59. Определим элементы ПТ.

 = 2m² + 2mn = 2 + 2∙1∙59 = 120, y = n² + 2mn = 3481 + 118 = 3599,

z = n² + 2mn + 2m² = 3599 + 2 = 3601→ ПТ₁( 120, 3599, 3601 ).

.1.2. Аналогично получим ПТ₂( 120, 896, 904), ПТ₃( 120, 391, 409), ПТ₄( 120, 209, 241 ),

ПТ₅ ( 120, 119, 169 ), ПТ₆( 120, 64, 136 ). Здесь имеют место как основные, так и не основные ПТ. Так, например, ПТ₂( 120, 896, 904) и ПТ₆( 120, 64, 136 ) - это не основные ПТ. Итого, при x = 120 получили 4 ПТ

ПТ₁( 120, 3599, 3601 ), ПТ₃( 120, 391, 409), ПТ₄( 120, 209, 241 ), ПТ₅ ( 120, 119, 169 ).

. J x имеет нечетные значения → x = n² + 2 mn = n ( n + 2m ). Рассмотрим ПТ( 15, 8, 17 ).

Здесь имеем x = 1∙ 15 = 3∙5

.1 J x = 1∙ 15 → n = 1, m = 7. Определим y = 2m² + 2mn = 98 + 14 = 112 → z = 113.

.2 J x = 3∙ 5 → n = 3, m = 1. Определим y = 2m² + 2mn = 2 + 6 = 8 → z = 17

Таким образом при x = 15 имеем ПТ₁( 15, 8, 17) и ПТ₂( 15, 112, 113).

Задача решена!

Выводы 1. Число ПТ с четным целочисленным значением x равно числу вариантов  в виде двух сомножителей.

. Число ПТ с не четным целочисленным значением x равно числу вариантов представления x в виде двух сомножителей.

. В числе полученных ПТ могут иметь место не основные ПТ.

Пример 1. Как элемент основного ПТ, задано x = 93240. Необходимо определить все ПТ с этим значением x.

Решение. 1. Определяем сомножители числа 93240. 93240 faktor → 2³∙3²∙5∙7∙37

. Заданное число x - четное. Поэтому определяем  = 2²∙3²∙5∙7∙37

. Определяем все возможные пары сомножителей числа

→ 46620 = 1∙ 46620 = 2∙23310 = 3∙ 15540 = 4∙11655 = 5∙ 9324 = 6∙7770 = 7∙ 6660 = 9∙5180

= 10∙4662 = 12∙3885 = 14∙3330 = 15∙ 3108 = 18∙ 2590 = 20∙ 2331 = 21∙2220

= 28∙1665 = 30∙ 1554 = 35∙1332 = 36∙1285 = 37∙1260 = 42∙ 1110 = 45∙1036

= 60∙ 777 = 63∙ 740 = 70∙ 666 = 74∙ 630 = 84∙ 555 = 90∙ 518 = 105∙ 444 = 111∙ 420

= 126∙ 370 = 140∙ 333 = 148∙ 315 = 180∙ 259 = 185∙ 252 = 210∙ 222

В результате получили 36 вариантов представления числа  = 46620 в виде двух сомножителей, что соответствует утверждению “ В прямоугольной системе координат имеется 36 пифагоровых треугольников с целочисленными сторонами, при условии, что один из катетов равен числу 93240 “ .

. Определим эти ПТ. Пусть x = 2m² + 2mn = 93240 →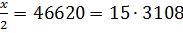

→ m = 15, ( m + n ) = 3108 → n = 3108 - 15 = 3093. Теперь, имея значения m и n , по формулам Системы mn параметров, вычислим значения всех элементов ПТ.

x = 2m² + 2mn = 93240, y = n² + 2mn = 3093² + 2∙15∙3093 = 9659439, z = y + 2mn

→ z = 9659439 + 2∙15² = 9659889. Получили ПТ(93240, 9659439, 9659889 ).

Аналогично определяются остальные 35 ПТ. Все 36 ПТ представлены в таблице 1.

пифагоров треугольник сомножитель задача

Таблица 1

Из данных этой таблицы следует, что если в значениях m и n имеется общий множитель, то ПТ является не основным. Так, например, ПТ ( 93240, 6707776, 6708424 ) - это не основной ПТ. Если разделить каждый из элементов на 8, то получим основной ПТ(11655, 838472, 838553).

Определим в таблице 1 не основные ПТ.

Строка 2 . Здесь имеем m =2, n = 23308, x = 93240, y = 543356096, z = 543356104 .

Запишем числа (x, y, z ) в виде произведения сомножителей → x = 93240 faktor = 2³∙3²∙5∙7∙37,

y = 543356096 faktor = 2⁶∙ 31∙47∙5827, z = 543356104 faktor = 2³∙3∙29881. В этих числах общим множителем имеем 2³ = 8. Сократим на 8 каждый из элементов, тогда получим основной ПТ,

ПТ ( 11655, 67919512, 67919513 ). Из данных таблицы 1 следует, что при x = 93240 имеется 17 основных ПТ и 19 не основных ПТ. Значения m, записанные в виде кортежа, для основных ПТ имеют вид ( 1, 4, 5, 7, 9, 20, 28, 35, 37, 45, 60, 63, 111,140, 148, 180,185 ).

Задача 1 “Задано значение четное значение x, как элемент основного пифагорова треугольника (ПТ), необходимо определить все ПТ с данным значением x “.

Данная задача в методическом представлении может иметь два варианта:

указать методику определения всех ПТ

при заданном четном числе x, определить все ПТ при разделении полученных данных на основные и не основные ПТ.

Задача 2

“Задано значение нечетное значение x, как элемент основного пифагорова треугольника (ПТ), необходимо определить все ПТ с данным значением x “.

В задаче 2 x = n² + 2mn = n∙( n +2m ). Здесь x надо записать в виде двух сомножителей. При этом за n надо принять меньший множитель. Тогда больший множитель будет равен ( n +2m ).

→ m =  .

Далее методика, определения ПТ, как в примере 1.

В заключении можно сделать два утверждения

Утверждение 1 “ Для четных значений x, как элемента исходного ПТ, в соответствии с Системой mn параметров, x = 2m(m + n ). При этом общее число ПТ, как основных, так и не основных равно числу вариантов представления исходного числа x в виде двух сомножителей “.

Утверждение 2 “ Для нечетных значений x, как элемента исходного ПТ, в соответствии с Системой mn параметров, x = n (n + 2m). При этом общее число ПТ , как основных, так и не основных равно числу вариантов представления исходного числа x в виде двух сомножителей “.

Предложенная задача может найти применение в геодезии, в атомных и молекулярных структурах, и в астрономических расчетах.