Составление топографической основы

Содержание

Введение

1. Подготовка геодезических данных для проектирования

2. Перевычисление координат вершин полигонов разных систем в единую

3. Составление топографической основы для проектирования

4. Определение площадей

4.1 Аналитический способ определения площадей

4.2 Графический способ определения площадей

4.3 Механический способ определения площадей

5. Спрямление ломаных границ участков

5.1 Графический способ

5.2 Аналитический способ

5.3 Механический способ

6. Проектирование участков

6.1 Аналитический способ

6.1.1 Проектирование недостающей площади методом треугольников

6.1.2 Проектирование недостающей площади четырёхугольником

6.1.3 Проектирование недостающей площади трапецией

6.2 Графический способ

6.3 Механический способ

7. Перенесение проекта в натуру

Заключение

Список литературы

Введение

Рациональное и эффективное использование земли является актуальной задачей современности. Поэтому в землеустройстве особое место занимает научно-обоснованный и точный учет земель.

Для организации Использования земли необходимо иметь точные количественные и качественные сведения о земле, которые можно получить путем инженерных измерений, расчётов и графических построений, связанных с подготовкой к составлению проектов землеустройства, сельскохозяйственной мелиорации, объектов сельскохозяйственного и несельскохозяйственного назначения, составлением планово-картографического материала.

Повышающийся уровень организации сельскохозяйственного производства требует графического отображения каждого земельного участка, а полное использование планово-картографических материалов дает возможность специалистам сельскохозяйственного производства все свои усилия направить на рациональное и эффективное использование каждого земельного участка на территории землепользования.

В целях организации рационального использования земельных ресурсов на территории землепользований ведутся геодезические работы.

Наиболее часто встречающиеся геодезические работы, которые выполняются специалистами-землеустроителями при разработке проектов землеустройства, рассмотренных в данном курсовом проекте.

1. Подготовка геодезических данных для проектирования

При вычислительной обработке результатов во время проведения геодезических работ при землеустройстве возникает необходимость решать прямую и обратную геодезические задачи.

Решение обратной геодезической задачи заключается в том, что по известным координатам начала и конца линии (например, координатам точек А и В линии АВ) находятся дирекционный угол линии αАВ и проложение (длина) этой линии SAB. Задача решается в форме таблицы 1.

Приращение координат ∆ линии АВ - это разность координат конечной В и начальной точки А данной линии, определяемая по формуле:

∆ХАВ=ХВ-ХА

∆YАВ=YВ-YА

Дирекционный угол tgα - это угол, отсчитываемый от северного направления осевого меридиана по ходу часовой стрелки до ориентируемой линии, определяемый по формуле:

Tgα=∆Y/∆Х

Румб - это угол, отсчитываемый от ближайшего направления меридиана (северного или южного) до ориентируемой линии.

Длина линии SAB определяется по формуле:

SAB=∆ХАВ/cosαАВ=∆YАВ/sinαАВ

топографическая основа геодезический землеустройство

Таблица 1

Решение обратной геодезической задачи.

№ точки	Координаты		Приращения		Дирекционный угол		Длина линии S, м
	Х	Y	∆Х	∆Y	arctgα	α
Полигон I
А	321,96	117,32	+54,64	-24,16	23.85°	156,15°	59,75
В	267,32	141,48	+24.97	-44,44	60,67°	119,33°	50,98
1	242,35	185,92	-118,63	+24,17	11,52°	348,48°	121,05
2	360,98	161,75	-82,74	+33,52	22,05°	337,95°	89,28
3	443,72	128,23	+63.23	+15,59	13,85°	193,85°	65,12
4	380,49	112,64	+58,53	-4,68	4,57°	175,43°	58,73
Контроль			∑=0	∑=0
Полигон II
3	1019,35	230,33	-61,98	-19,97	17,86°	197.86°	65,12
4	957,37	210,36	+2,77	-39,65	86,00°	274,00°	39,73
5	960,14	170,71	+114,14	-20,94	10,40°	349,6°	116,02
6	1074,28	149,77	+9,98	+92,13	83,82°	83.82°	92,69
7	1084,26	241,90	-64,91	-11,57	10,11°	190.11°	65,92
Контроль			∑=0	∑=0
Полигон III
А	1033,59	111,05	-55,82	+21,27	20,86°	159,14°	59,74
В	977,77	132,32	-27,37	-29,54	47,18°	227.18°	40,27
8	950,40	102,78	+19,64	-31,75	58,26°	301,74°	37,33
9	970,04	71,03	+49,8	-10,66	12,08°	347,92°	50,94
10	1019,84	60,37	+41,51	-11,73	2,39°	357,61°	41,52
11	1061,35	58,64	+33,03	+11,1	18,58°	18,58°	34,85
12	1094,38	69,74	-2,08	+30,7	87,00°	93,00°	39,75
4	1092,30	109,44	-58,71	+1,61	1,57°	178,43°	58,75
Контроль			∑=0	∑=0

Определим приращение координат линий для 3 наших полигонов.

I полигон:

Приращение координат линии А4:

Δx = 380,49 - 321,96 = 58,53

Δy = 112,64 - 117,32 = - 4,68

Приращение координат линии 43:

Δx = 443,72 - 380,49 = 63,23

Δy= 128,23 - 112,64 = 15,59

Приращение координат линии 32:

Δx = 360,98 - 443,72 = - 82,74

Δy= 161,75 - 128,23 = 33,52

Приращение координат линии 21:

Δx = 242,35 - 360,98 = - 118,63

Δy= 185,92 - 161,75 = 24,17

Приращение координат линии 1В:

Δx = 267,32 - 242,35 = 24,97

Δy= 141,48 - 185,92 = - 44,44

Приращение координат линии ВА:

Δx = 321,96 - 267,32 = 54,64

Δy= 117,32 - 141,48 = - 24,16

II Полигон:

Приращение координат линии 34:

Δx = 957,37 - 1019,35 = - 61,98

Δy= 210,36 - 230,33 = - 19,97

Приращение координат линии 45:

Δx = 960,14 - 957,37 = 2,77, Δy= 170,71 - 210,36 = - 39,65

Приращение координат линии 56:

Δx = 1074,28 - 960,14 = 114,14

Δy= 149,77 - 170,71 = - 20,94

Приращение координат линии 67:

Δx = 1084,26 - 1074,28 = 9,98

Δy= 241,90 - 149,77 = 92,13

Приращение координат линии 73:

Δx = 1019,35 - 1084,26 = - 64,91

Δy= 230,33 - 241,90 = - 11,57

III Полигон:

Приращение координат линии АВ:

Δx = 977,77 - 1033,59 = - 55,82

Δy= 132,32 - 111,05 = 21,27

Приращение координат линии В8:

Δx = 950,40 - 977,77 = - 27,37

Δy= 102,78 - 132,32 = - 29,54

Приращение координат линии 89:

Δx = 970,04 - 950,40 = 19,64

Δy= 71,03 - 102,78 = - 31,75

Приращение координат линии 910:

Δx = 1019,84 - 970,04 = 49,8

Δy= 60,37 - 71,03 = - 10,66

Приращение координат линии 1011:

Δx = 1061,35 - 1019,84 = 41,51

Δy= 58,64 - 60,37 = - 1,73

Приращение координат линии 1112:

Δx = 1094,38 - 1061,35 = 33,03

Δy= 69,74 - 58,64 = +11,1

Приращение координат линии 124:

Δx = 1092,30 - 1094,38 = - 2,08

Δy= 109,44 - 69,74 = 30,7

Приращение координат линии 4А:

Δx = 1033,59 - 1092,30 = - 58,71

Δy= 111,05 - 109,44 = 1,61

Таблица 2.

Определение дирекционных углов и румбов по знаками приращений

I четверть от 0 до 90°		II четверть от 90° до 180°		III четверть от 180° до 270°		IV четверть от 270° до 360°
СВ		ЮВ		ЮЗ		СЗ
Δx	Δy	Δx	Δy	Δx	Δy	Δx	Δy
+	+	-	+	-	-	+	-
r = α		r = 180 - α		r = α - 180		R = 360 - α
α = r		α = 180 - r		α = 180 + r		Α = 360 - r

Рассчитаем дирекционные углы для 3-х полигонов.

I полигон:

r_A-4 = tg (-4,68/+58,53) = 4,57^°; α_А-4 = 180 - r = 175,43^°

r_4-3 = tg (+15,59/+63.23) = 13,85^°; α_4-3 = 180 - r = 166.15^°

r3-2 = tg (+33,52/- 82,74) = 22,05^°; α3-2 = 360 - r = 337.95^°

r2-1 = tg (+24,17/- 118,63) = 11,52^°; α_2-1 = 360 - r = 348.48^°-B= tg (-44,44/ (+24,97)) = 60,67^°; α1-B = 180 - r = 119.33^°

rB-_А = tg (-24,16/ (+54,64)) = 23.85^°; Αb-_А = 180 - r = 156,15^°

 

II полигон:

r_3-4 = tg ( (-19.97) / (-61,98)) = 17,86^°; α_3-4 = 180 + r = 197.86^°

r_4-5 = tg ( (-39,65) / 2,77) = 86,00^°; α_4-5 = 360 - r = 274.00^°

r_5-6 = tg ( (-20,94) / 114,14) = 10,40^°; α_5-6 = 360 - r = 349,6^°

r_6-7 = tg (92,13/ 9,98) = 83,82^°; α_6-7 = r = 83.82^°

r_7-3 = tg ( (-11,57) / (-64,91)) = 10,11^°; α_7-3 = 180 + r = 190.11^°

 

III полигон:

r_А-В = tg (21,27/ (-55,82)) = 20,86^°; α_А-В = 180 - r = 159,14^°

r_В-8 = tg ( (-29,54) / (-27,37)) = 47,18^°; α_В-8 = 180 + r = 227.18^°

r_8-9 = tg ( (-31,75) / 19,64) = 58,26^°; α_8-9 = 360 - r = 301,74^°

r_9-10 = tg ( (-10,66) / 49,80) = 12,08^°; α_9-10 = 360 - r = 347.92^°

r_10-11 = tg (1,73/ 41,51) = 2,39^°; α_10-11 = 360 - r = 357,61^°

r_11-12 = tg (11,1/33,03) = 18,58^°; α_11-12 = r = 18,58^°

r₁₂₄ = tg (30,7/ (-2,08)) = 87,00^°; α₁₂₄ = 180 - r = 93,00^°

r_4А = tg (1,61/ (-58,71)) = 1,57^°; α_4А = 180 - r = 178,43^°

 

Определим длины линий у 1, 2 и 3 полигона.

S = Δx / cos α = Δy / sin α

Полигон I:

S_А-4 = 58.53/cos 175,43^° = 58,72 S_А-4 = (-4,68) / sin 175,43^° = 58.74_А-4 = (58,72 + 58,74) / 2 = 58,73 м_4-3= 63.23/cos 166.15^° = 65.12 S43 = 15.59/sin 166.15^° = 65.13_4-3 = (65.12 + 65.13) / 2 = 65.13 м_3-2 = (-82.74) / cos 337.95^° = 89.27 S₃₂ = 33.52/sin 337.95^° = 89.29_3-2 = (89.27 + 89.29) / 2 = 89.28 м_2-1 = (-118.63) / cos 348.48^° = 121.07 S₂₁ = 24.17/sin 348.48^° = 121.03_2-1 = (121.07 + 121.03) / 2 = 121.05 м_1-B = 24.97/cos 119.33^° = 50.98 S_1B = (-44.44) / sin 119.33^° = 50.97_{! - B} = (50.98 + 50.97) / 2 = 50.98 м_B-А = 54.64/cos 156.15^° = 59.74 S_BА = (-24,16) / sin 156.15^° = 59.75-_А = (59.74 + 59.75) / 2 = 59.75 м

Полигон II:

S_3-4 = (-61,98) / cos 197,86^° = 65,12 S₃₄ = (-19,97) / sin 197,86^° = 65,11_3-4 = (65,12 + 65,11) / 2 = 65,12 м_4-5 = 2,77/cos 94,00^° = 39,71 S₄₅ = (-39,65) / sin 94,00^° = 39,75_4-5 = (39,71 + 39,75) / 2 = 39,73 м_5-6 = 114,14/cos 169,6^° = 116,05 S₅₆ = (-20,94) / sin 169,6^° = 116,00_5-6 = (116,05 + 116,00) / 2 = 116,03 м_6-7 = 9,98/cos 83,82^° = 92,71 S₆₇ = 92,13/sin 83,82^° = 92,66_6-7 = (92,71 + 92,66) / 2 = 92,69 м_7-3 = (-64,91) / cos 190,11^° = 65,93 S₇₃ = (-11,57) / sin 190,11^° = 65,91_7-3= (65,93 + 65,91) / 2 = 65,92 м

Полигон III:

S_А-В = (-55,82) / cos 159,14^° = 59,74 S_АВ = 21,27/sin 159,14^° = 59,73

S_А-В= (59,74 + 59,73) / 2 = 59,73 м

S_В-8 = (-27,37) / cos 227,18^° = 40,27 S_В8 = (-29,54) / sin 227,18^° = 40,27

S_В-8= (40,27 + 40,27) / 2 = 40,27 м_8-9 = 19,64/ cos 121.74^° = 37,33 S₈₉ = (-31,75) / sin 121.74^° = 37,33_8-9= (37,33 + 37,33) / 2 = 37,33 м_9-10 = 49,8/ cos 167.92^° = 50,93 S₉₁₀ = (-10,66) / sin 167.92^° = 50,94_9-10= (50,93 + 50,94) / 2 = 50,94 м_10-11= 41,51/ cos 357,61^°= 41,54 S₁₀₁₁ = - 1.73/ sin 357,61°= 41,48_10-11= (41,54 + 41,48) / 2 = 41,52 м_11-12= 33,03/ cos 18,58^°= 34,85 S₁₁₁₂ = 11,1/ sin 18,58°= 34,84_11-12= (34,85 + 34,84) / 2 = 34,85 м_12-4 = (-2.08) / cos 93,00^°= 39,74 S₁₂₄ = 30,7/ sin 93,00°= 39,75_12-4 = (39,74 + 39,75) / 2 = 39,75 м_4-А= (-58,71) / cos 178,43^°= 58,73 S_4А = 1,61/ sin 178,43^°= 58,76_4-А= (58,73 + 58,79) / 2 = 58,75 м

Решение прямой геодезической задачи состоит в том, что по координатам одного конца линии, дирекционному углу этой линии и ее горизонтальному проложению (длине) вычислить координаты другого конца линии.

2. Перевычисление координат вершин полигонов разных систем в единую

В практике землеустроительных и геодезических работ для сельского хозяйства и других потребителей часто приходится составлять планы нескольких землепользований, отдельных участков обособленных съемок.

Для этого используют планы крупномасштабных съемок отдельных сельскохозяйственных предприятий.

При преобразовании координат из обособленных систем в единую используют различные способы.

)        Сплошное перевычисление координат всех точек.

При сплошном перевычислении координат точек используют первичные материалы полевых измерений углов, длин линий и заново выполняют вычисления, при этом увязку углов, а затем приращений проводят совместно для всей группы ходов и полигонов. Этим методом проводят вычисления, когда теодолитные ходы опираются на несколько твердых точек.

Твердыми точками являются вершин углов поворотов дорог, канав, строений, угодий.

)        Перевычисление координат угловых точек методом полигонов.

Перевычисление частных систем координат в одну можно упростить, если вычисления вести только для узловых точек. По координатам частных систем полигонов вычисляют дирекционные углы и длины замыкающих звеньев линий в первом, втором и т.д. полигонах. Для каждой смежной замыкающей линии получают два значения, из которых берут среднее, если их разность, отнесенная к длине, не превышает 1: 500. По дирекционным углам этих линий вычисляют горизонтальные углы между замыкающими линиями во всех полигонах, после чего система полигонов упроститься. Принимая вычисленные горизонтальные углы и линии за первичные материалы, полигоны обрабатывают, т.е. увязывают углы, приращения координат и вычисляют обычным путем координаты узловых точек.

В каждом из полученных полигонов будет угловая невязка, которая не должна превышать величины, вычисленной по формуле:

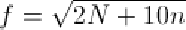
где N - число углов, полученных только по дирекционным углам замыкающих линий;- число углов в полигоне, полученных с участием дирекционных углов граничных линий.

Относительная невязка в приращениях координат не должна превышать 1: 1 000

Число полигонов можно уменьшить и свести до одного. После увязки углов и приращений координат вычисляют координаты узловых точек в одной системе координат. Полученные координаты точек после их нанесения на бумагу создают опору сборного плана. Пользуясь планами отдельных землепользований, все точки граничных ходов, а также все контурные точки и другие подробности можно перенести на сборный план графическим или механическим путем.

)        Построение узловых точек графическим способом

Работа по созданию опоры сборного плана будет значительно упрощена, если узловые точки наносить методом линейных засечек. Сначала, точки первого полигона по координатам наносят на сборный план, а для графического нанесения узловых точек необходимо знать длины линий между ними, которые можно получить путем вычисления по координатам частных систем или графически по планам с помощью штангенциркуля и масштабной линейки. При графическом определении длин линий надо учитывать деформацию планов, по которым определяется линия.

При нанесении узловой точки методом линейной засечки нельзя допускать пересечения линий под очень острым или тупым углом, так как от этого снижается точность положения точки на сборном плане. Когда на плане получены узловые точки, можно полигоны заполнять подробностями. В результате этого будет получен сборный план.

) Перевычисление координат с помощью введения поправок в приращения координат путем введения в приращения поправок, вычисляемых по формулам:

δ_x = (-δ_α) / ρ ∙ ∆y, δ_y = (+δ_α) /ρ ∙ ∆x

где δ_{α -} разность дирекционных углов, вычисляемая по формуле

δ_α = α_{1 -} α_2,здесь α_{1 -} дирекционный угол общей стороны смежных полигонов, вычисленный по координатам вершин 1 полигона;

α_{2 -} дирекционный угол той же стороны, вычисленный по координатам 2 полигона;

ρ - сумма длин полигона, координаты которого подвергаются перевычислению.

δ_r = │r-_{34 -} r_3-4│= 13,85 - 17,86 = 4,01

δ_x = (-4,01) / 379,48 ∙ (-19,97) = 0,21

δ_x = (-4,01) / 379,48 ∙ (-39,65) = 0,42

δ_x = (-4,01) / 379,48 ∙ (-20.94) = 0,22

δ_x = (-4,01) / 379,48 ∙ 92,13 = - 0,97

δ_x = (-4,01) / 379,48 ∙ (-11,57) = 0,12

δ_y =4,01/379,48 ∙ (-61,98) = - 0,66

δ_y =4,01/379,48 ∙ 2,77 = 0,03

δ_y =4,01/379,48 ∙ 114,14 = 1,21

δ_y =4,01/379,48 ∙ 9,98 = 0,11

δ_y =4,01/379,48 ∙ (-64,91) = - 0,69

Поправки в приращения вычислять с округлением до 0,1 м. Контроль: суммы в столбцах 3, 4, 5, 6, 7, 8 должны быть равны нулю.

Таблица 3.

Ведомость перевычисления координат вершин полигона 1 (δ_α = 5.99^°)

№ точки	Длина линии	Приращения (старые)		Поправки		Приращения перевычисленные		Координаты в системе 1 полигона
		∆x	∆y	δx	δy	∆x	∆y	X	y
1	2	3	4	5	6	7	8	9	10
3	65,12	-61.98	-19.97	+0.21	-0.66	-61.77	-20.63	443,72	128,23
4	39,73	+2.77	-39.65	+0,42	+0,03	+3.19	-39.62	381,95	107,61
5	116,03	+114.14	-20.94	+0.22	+1,21	+114.36	-19.73	385,14	67,99
6	92,69	+9.98	+92.13	-0,97	+0.11	+9,01	+92.24	499,5	48,25
7	65,92	-64,91	-11.57	+0.12	-0,69	-64.79	-12.26	508,51	140,49
	p=379,48
Контроль		∑=0	∑=0	∑=0	∑=0	∑=0	∑=0

). Перевычисление координат путём введения поправок δ_α в старые дирекционные углы. По новым дирекционным углам вычисляют новые приращения и увязывают их между координатами точек.

δ_r = │r_{АВ -} r_АВ│ = │23,85^° - 20,86^°│ = 2,99^°

 

Приращение координат вычисляют по формулам:

∆x_AB = S_AB ∙ cos α_AB

∆y_AB = S_AB ∙ sin α_AB

∆x_А-В = 59,73 ∙ cos 162,13^° = - 56,85 ∆y_А-В = 59,74 ∙ sin 162,13^° = 18,33

∆x_В-8 = 40,27 ∙ cos 230,17^° = - 25,79 ∆y_В-8 = 40,27 ∙ sin 230,17^° = - 30,92

∆x_8-9 = 37,33 ∙ cos 304,73^° = 21,27 ∆y_8-9 = 37,33 ∙ sin 304,73^° = - 30,68

∆x_9-10 = 50,94 ∙ cos 350,91^° = 50,30 ∆y_9-10 = 50,94 ∙ sin 350,91^° = - 8,04

∆x_10-11 = 41,52 ∙ cos 360,6^° = 41,52 ∆y_10-11 = 41,52 ∙ sin 360,6^° = 0,43

∆x_11-12 = 34,85 ∙ cos 21,57^° = 32,41 ∆y_11-12 = 34,85 ∙ sin 21,57^° = 12,81

∆x_12-4 = 39,75 ∙ cos 95,99^° = - 4,14 ∆y_12-4 = 39,75 ∙ sin 95,99^° = 39,53

∆x_4-А = 58,75 ∙ cos 181,42^° = - 58,72 ∆y_4-А = 58,75 ∙ sin 181,42^° = - 1,46

Координата последующей точки равна координате предыдущей точки плюс приращение на линию между этими точками.

x_B = x_A + ∆x_AB

y_B = y_A + ∆y_AB

x_А = 321,96 - 56,85 = 265,11 y_А = 117,32 + 18,33 = 135,65₈ = 265,11 - 25,79 = 239,32 y₈= 135,65 - 30,92 = 104,73₉ = 239,32 + 21,27= 260,59 y9 = 104,73 - 30,68 = 74,05₁₀ = 260,59 + 50,30 = 310,89 y₁₀ = 74,05 - 8,04 = 66,01₁₁ = 310,89 + 41,52 = 352,41 y₁₁ = 66,01 + 0,43 = 66,44

x₁₂ = 352,41 + 32,41 = 384,82 y₁₂ = 66,44 + 12,81 = 79,25₄ = 384,82 - 4,14 = 380,68 y₄ = 79,25 + 39,53 = 118,78

x_А = 380,68 - 58,72 = 321,96 y_A= 118,78 - 1,46 = 117,32

Таблица 4.

Ведомость перевычисления координат вершин полигона 3 (δ_α = 2,99^°)

№ точки	Длина линии	Дирекционные углы		Приращения		Координаты в системе 1 полигона
		старые	новые	∆x	∆y	X	Y
1	2	3	4	5	6	7	8
А	59,73	159,14°	162,13°	-56,85	+18,33	321,96	117,32
В	40,27	227,18°	230,17°	-25,79	-30,92	265,11	135,65
8	37,33	301,74°	304,73°	+21,27	-30,68	239,32	104,73
9	50,94	347,92°	350,91°	+50,30	-8,04	260,59	74,05
10	41,521	357,61°	360,60°	+41,52	+0,43	310,89	66,01
11	34,85	18,58°	21,57°	+32,41	+12,81	352,41	66,44
12	39,75	93,00°	95,99°	-4,14	+39,53	384,82	79,25
4	58,75	178,43°	181,42°	-58,72	-1,46	380,68	118,78
				∑=0	∑=0

3. Составление топографической основы для проектирования

Составление топографической основы для проектирования включает следующие виды работ.

. Подготовка основы для составления - состоит в нанесении на нее рамки листа, координатной сетки и опорных пунктов.

. Перенос изображения на основу с исходных картографических материалов - выполняется картографом, графически по клеткам с применением пропорционального циркуля или масштабного треугольника.

. Генерализация изображения - процесс отбора показываемых на карте предметов и явлений, обобщения их контуров, а также качественных и количественных характеристик с целью изображения наиболее существенных свойств и характеристик местности.

. Закрепление генерализованного изображения - выполняется тушью в соответствующих условных знаков.

4. Определение площадей

В зависимости от хозяйственного назначения земельных участков, их местоположения, площади, наличия и качества картографических материалов применяются следующие способы определения площадей: аналитический, графический, и механический.

4.1 Аналитический способ определения площадей

Аналитический способ - наиболее точный способ в определении площади по результатам измерений линий и углов на местности или по их функциям (координатам) по специальным формулам.

Наиболее распространенным алгоритмом вычисления площадей земельных участков аналитическим способом является алгоритм вычисления площадей по координатам вершин. Площади земельных участков аналитическим способом вычисляются по формулам:

          n

Р = ∑ y_{i (}x_{i-1 -} x_i+1)

        1

         n

Р = ∑ x_{i (}y_{i+1 -} y_i-1)

        1

Если внимательно посмотреть на разности в формулах (3) и (4), то можно получить контроль правильности вычисления площадей (только для замкнутого полигона):

 n                      n

∑ y_{i (}x_{i-1 -} x_i+1) = ∑ x_{i (}y_{i+1 -} y_i-1) = 0

1                       1

При определении площадей по результатам измерения линий и углов участки разбивают на геометрические фигуры (треугольники, прямоугольники и трапеции).

1). Площадь треугольника по двум сторонам и углу между ними:

P=S1*S2* sinß

) Площадь четырёхугольника:

по четырём сторонам S1 S2 S3 S4 и двум противоположным углам ß2 ß4

2P= S1*S2*sinß2 + S3*S4 *sinß4

по трём сторонам S1 S2 S3 и двум углам ß2 ß3 заключенными между ними

2Р= (S1*S2 sinß2 + S2*S3 sinß3 + S1*S3 sin (ß2+ß3-180)

I Полигон:

) 2P₁ = S4-A*S3-4*sinß4 + S3-4*S2-3*sinß3 + S4-A*S2-3*sin (ß4+ß3 - 180)

P₁= 58.73*65.12*sin 161.58 + 65.12*89.28*sin 35.9 + 58.73*89.28*sin (161.58+35.9-180)

P1= 6192.56 м²

2) 2P₂= S1-2*SB-1*sin ß1 + SB-1 - SA-B*sin ßB + S12*SA-B*sin (ß1+ß2 - 180)

P₂=121.05*50.98*sin41.15+50.98*59.75*sin143.18+121.05*59.75*sin (49.15+143.18-180)

P₂= 8037.996 м²

2P_1п= 2P₁+2P₂

P_1п= 14230.556 м²

P_1п= 7115.278 м²

Р_1п= 0.71 га

II Полигон:

1) 2Р1= S6-7*S7-3*sin ß7

P1= 92.69*65.92*sin73.71

P1= 5864.829 м²

2) 2P₂= S3-4*S4-5*sin ß4 + S4-5*S5-6*sin ß5 + S3-4*S5-6*sin (ß4+ß5-180)

P₂=65.12*39.73*sin103.86+39.73*116.028sin104.4+65.12*116.02*sin (103.86+104.4-180)

P₂= 10553.744 м²

2Р_2п= 2Р₁+2Р₂

Р_2п= 16418.573 м²

Р_2п= 8209.287 м²

Р_2п= 0.82 га

Таблица 5. Ведомость вычисления площадей по координатам

Номер вершины	Координаты		Результаты вычислений
	X, м	Y, м	xi-1-xi+1	yi (xi-1-xi+1)	yi+1-yi-1	xi (yi+1-yi-1)
I полигон
А	321,96	117,32	-113,17	-13277,1044	-28,84	-9285,3264
В	267,32	141,48	-79,61	-11263,2228	-68,6	-18338,152
1	242,35	185,92	+93,66	+17413,2672	-20,27	-4912,4345
2	360,98	161,75	+201,37	+32571,5975	+54,69	+20824,9362
3	443,72	128,23	+19,51	+2501,7673	+49,11	+21791,0892
4	380,49	112,64	-121,76	-13715,0464	+10,91	+4151,1459
			∑=0	2P=14231,2584 P=0,71 га	∑=0	2P=14231,2584 P=0,71 га
II полигон
3	1019,35	230,33	+126,89	+29226,5737	-31,54	-32150,299
4	957,37	210,36	+59,21	+12455,4156	-59,62	-57078,3994
5	960,14	170,41	-116,91	-19957,7061	-60,59	-58174,8226	1074,28	149,77	-124,12	-18589,4524	+71, 19	+76477,9932
7	1084,26	241,90	+54,93	+13287,567	+80,56	+87347,9856
			∑=0	2P=16422,3978 P=0,82 га	∑=0	2P=16422,3978 P=0,82 га
III полигон
А	1033,59	111,05	+114,53	+12718,5565	+22,88	+23648,5392
В	977,77	132,32	+83, 19	+11007,7008	-8,27	-8086,1579
8	950,40	102,78	+7,73	+794,4894	-61,29	-58250,016
9	970,04	71,03	-69,44	-4932,3232	-42,41	-41139,3964
10	1019,84	60,37	-91,31	-5512,3847	-12,39	-12635,8176
11	1061,35	58,64	-74,54	-4371,0256	+9,37	+9944,8495
12	1094,38	69,74	-30,95	-2158,453	+50,8	+55594,504
4	1092,30	109,44	+60,79	+6652,8576	+41,31	+45122,913
			∑=0	2P=14199,4178 P=0,71 га	∑=0	2P=14199,4178 P=0,71 га

4.2 Графический способ определения площадей

В этом способе площади земельных участков вычисляются:

·        по результатам измерения углов и линий на планах или картах

·        с помощью палетки (квадратной или параллельной).

1). Площадь участка разбивают на ряд простейших геометрических фигур (треугольник, прямоугольник, трапеция) и вычисляют искомую площадь как сумму площадей элементарных геометрических фигур. Максимальная точность определения площадей получается при делении общей площади на треугольники. Запишем формулу вычисления площади треугольника:

 

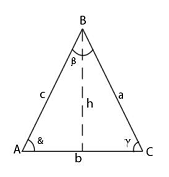
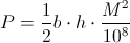
Для контроля и повышения точности вычислений площадь каждого треугольника определяется дважды: по двум различным основаниям и высотам, затем берется среднее значение, если расхождение между двумя определениями допустимое. Допустимое расхождение определяется по формуле:

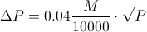
где М - знаменатель численного масштаба плана или карты.

Таблица 6.

Ведомость определения площадей графическим способом

№ треугольника	№ измерения	Результаты измерений		Результаты вычислений
		Основания, b, м	высоты, h, м	удвоенной площади 2P, га	Среднего значения площади 2Р, га	Допуска Δ Pдоп., га
II полигон
I	1 2	93 66	63 89	0,5859 0,5874	0,58665	0,0031
II	1 2	116 97,5	69 81	0,8004 0,7898	0,7951	0,0036
III	1 2	83 40	31 64	0,2573 0,2560	0,2567	0,002
					∑2P=1,63845 га P=0,82 га
I полигон
I	1 2	89 65	38.5 53	0,34265 0,3445	0,343575	0.0023
II	1 2	59 53	47 52	0,2773 0,2756	0,27645	0.0021
III	1 2	59 59	56 56	0,3304 0,3304	0,3304	0.0023
IV	1 2	121 95	38 48,5	0,4598 0,4608	0,4603	0,0027
					∑2P=1,410725 га P=0,71
III полигон
I	1 2	60 34,8	22 38	0,1320 0,1322	0,1321	0.0015
II	1 2	61 58,7	51 53	0,3111 0,3111	0,3111	0,0022
III	1 2	41,5 53	52 41	0,2158 0,2173	0,2166	0.0019
IV	1 2	59,7 83	52,5 38	0,3134 0,3154	0,3144	0.0022
V	1 2	62 50,9	50 61	0,3100 0,3105	0,3103	0,0022
VI	1 2	40 37,3	36 39	0,1440 0,1455	0,1448	0,0015
					∑2P=1,4293 га P=0,71

 

2). Палетка представляет собой сетку квадратов, нанесенную с высокой точностью на целлулоиде, прозрачном пластике или же на кальке. Размеры сторон квадратов составляют 1 - 5 мм.

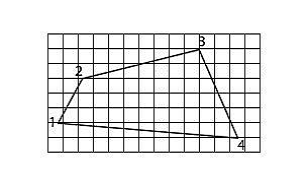
Площадь участка с учетом масштаба можно вычислить по формуле:

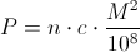
где М - знаменатель масштаба плана или карты;

n - число клеток, занимаемых участком;

c - площадь одной клетки в сантиметрах квадратных.

Площадь неполных клеток определяется на глаз.

Линейная (или параллельная) палетка представляет собой ряд параллельных

линий, проведенных на прозрачной основе через 1-2 мм. При использовании

линейной палетки измеряемый контур располагается таким образом, чтобы

крайние точки участка располагались на линиях палетки.

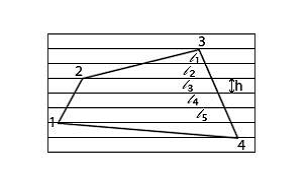
Общая площадь участка определяется как сумма площадей трапеций с одинаковой высотой:

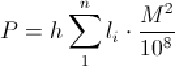
Точность однократного определения площадей квадратной или линейной палеткой вычисляют по формуле:

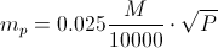
где М - знаменатель масштаба плана или карты.

4.3 Механический способ определения площадей

Для определения площадей механическим способом применяют специальный прибор - планиметр. Основными частями полярного планиметра являются: обводной рычаг, полюсный рычаг и отсчетное устройство. При определении площади планиметром угол между обводным и полюсным рычагом должен быть не менее 30 и не более 150. При измерении небольших участков полюс располагается вне измеряемого контура. При измерении площадей больших участков - внутри фигуры. Обводной индекс совмещается с начальной точкой контура и по отсчетному устройству снимается отсчет m₁.

Далее производится обвода индекс совмещается с начальной точкой и по отсчетному устройству берется отсчет m₂.

Площадь фигуры определяется по формуле:

 

P = c (m₂ - m₁),

где c - цена деления планиметра.

Цена деления планиметра определяется заранее путем измерения известной площади, обычно за такую площадь принимают квадрат координатной сетки на карте (или плане). Цена деления определяется по формуле:

 

С = P_{известная} / (m₂ - m₁₎

Для повышения точности и исключения грубых ошибок измерений определение цены деления и площадей выполняют дважды с установкой полюса справа и слева от измеряемого участка. Расхождение разности отсчетов не должно превышать трех делений планиметра. Площади участков менее 2 кв. см. измерять планиметром не рекомендуется. Точность определения площадей планиметром можно вычислить по формуле (для площадей 200 см² на плане или карте):

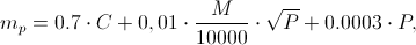
где С - цена деления планиметра; M - знаменатель масштаба карты или

5. Спрямление ломаных границ участков

Новые границы землепользований проектируют в тех случаях, когда образуются землепользования вновь, а также при прирезках и отрезках к существующим землепользованиям участков земли. Спрямляют границы при значительной изломанности их, так как ломаные границы затрудняют правильное использование прилегающих участков земли, в частности ограничивают возможность применения сложной машинной техники.

При спрямлении: ломаной границы новую границу устанавливают так, чтобы она была по возможности прямолинейна, где это допустимо по условиям местности, проходила в заданном направлении, а площади участков, отрезаемых и прирезаемых ею, были бы равновелики.

Задача: произвести спрямление границ землепользования в районе точек 8-С-1-2 с условием сохранения площадей землепользования, т. е площадь отрезаемого участка должна быть равной площади прирезаемого участка. По эскизному решению граница должна проходить от т.8 до линии 1-2.

Рассмотрим варианты решения этой задачи различными способами.

5.1 Графический способ

Наиболее простой способ решения этой задачи - графический. Для этого из т. С проводят на плане линию, параллельную линии 8-, и в пересечении её с линией 1-2 получают т.М. Линия 8-М будет новой границей, потому что треугольники 8С1 и 8М1 равновелики как имеющие общее основание и одинаковые высоты.

5.2 Аналитический способ

Находим площадь треугольника 534:

2Р_∆534 = S4-3*S5-4*sinß4

Р_∆534 = 39.73*65.12*sin103.86

Р_∆534 = 2511.888 м²

Р_∆534 = 1255,944 м²

Р_∆534 = 0.13 га_∆5-3-M = S_5-3*S_3-M-sinß_33-M = 2P/ (S_5-3*sin ß₃)

∆X_5-3 = X₃ - X₅ = 1019.35 - 960.14 = 59.21

∆y 5-3 = y₃ - y₅ = 230.33 - 170.71 = 59.62= 45.2º

α_5-3 = r = 45.2º

S_5-3 = 59.21/cos 45.2 = 84.03 м_5-3 = 59.62/sin 45.2 = 84.02 м_5-3 = 84.03 м_3-M = 2P/ (S_5-3*sinß3)

S_3-M = 32.4 м

ß₃ = α_5-3 + 180 - α_3-2 = 45.2 + 180 - 157.05 = 67.25º

∆X_3-M = S_3-M*cosα_{3-M (3-2)} = 32.4 * cos 157.95= - 30.03

∆Y_3-M = S_3-M*sinα_{3-M (3-2)} = 32.4 * sin 157.95 = 12.16_M= X₃+∆_3-M = 443.72 - 30.03 = 413.69 м_M= Y₃+∆_3-M = 128.23 + 12.16 = 140.39 м

Эту задачу можно решить несколько иначе:

Вычислим координаты точки пересечения М по формуле

∆X_3-M= ( (Y_M-Y₃) - (X_M-X₃) *tgα_4-M) / (tgα_{3-2 -} tgα_4-M) = ( (107.6 - 128.23) - (381.95 - 443.72)) / (tg157.95 - tg 45.2) = - 29.44 м

∆Y_3-M= ∆X_{3-M -} tgα_3-2 = 11.92 м

Х_М = 443.72 - 29.44 = 414.3 М

Y_M = 128.23 + 11.92 = 140.2 М

5.3 Механический способ

Другой вариант решения задачи состоит в том что графическим или механическим способом определяют площадь треугольника 5-4-3, затем измеряют расстояние от т.5 до линии 3-2 которое будет высотой h треугольника

а1 = 84

а2 = 41

h1 = 30

h2 = 62

P = 0.2520

P = 0.2542

P = 0.2531

P_Доп = 0.04*1000/10000*√0,2531 = 0.002

S_3-M = 2531/77 = 32.9 м, h₃ = 77 м

6. Проектирование участков

Проектирование участков - процесс обратный вычислению (определению) площадей, если площадь вычисляют по линейным и угловым величинам, измеренным на местности или плане, то при проектировании участка вычисляют его линейные и угловые величины по заданной площади.

Участки проектируют: графическим, механическим, аналитическим способами.

графическое проектирование производят в два этапа: вначале вычисляют площадь предварительно спроектированного участка, а затем проектируют недостающую часть или избыточную площадь либо треугольником, когда проектная линия проходит через определенную точку, либо трапецией, когда проектная линия проходит параллельно заданному направлению.

При проектировании трапециями по заданной площади и сумме оснований, определенным по плану графически, вычисляют высоту трапеции, а затем боковые стороны. Графическое проектирование участков в форме многоугольников заключается в разбивке фигуры на элементарные треугольники и трапеции, в предварительном вычислении их площадей и увязке их к общей площади, после чего проектирование участков сводят к проектированию треугольниками и трапециями недостающих и избыточных площадей.

Допустимые неувязки между суммой площадей запроектированных участков и общей площадью массива при графическом проектировании не должны превышать значений найденных по формуле (7):

ƒ_доп=+0,05∙М/10000∙S (7)

механический способ (планиметром) производят путем последовательного приближения до тех пор, пока расхождения между полученным результатом и заданной площадью будут не больше 2-3 делений планиметра. Во избежание значительного числа приближений проектирование планиметром комбинируют с графическим способом: планиметром определяют только начальную (приблизительную) и окончательную площади, а все отрезки и прирезки проектируют графически.

При большой контурности планов проектирование ведут набором контуров; при этом площади частей контуров, рассекаемых проектной границей, вычисляют и увязывают в пределах площади контура.

Допустимые невязки между суммой площадей запроектированных участков и общей площадью массива не должны превышать значений найденных по формуле (8):

ƒ_доп=+0,01∙М/10000∙S (8)

аналитический способ предусматривает использование известных формул геометрии, тригонометрии и аналитической геометрии. Аналитическое проектирование сводится к определению элементов (сторон, высот) простейших геометрических фигур - трапеций, треугольников, реже четырехугольников.

6.1 Аналитический способ

Проектирование аналитическим способом заключается в вычислении проектных отрезков по заданной площади и по результатам измерений углов и линий на местности или по их функциям - координатам точек.

При проектировании площадей могут быть заданы два условия:

) проектная линия проходит через данную точку, тогда заданную площадь проектируют треугольником или четырехугольником;

) проектная линия проходит параллельно заданному направлению (по заданному дирекционному углу), тогда заданную площадь проектируют трапецией.

Проектирование площади в один прием можно выполнить только тогда, когда участок имеет форму треугольника, четырехугольника или трапеции. Во всех остальных случаях аналитическим способом вычисляют площадь предварительно намеченного участка, после этого проектируют недостающую или избыточную площадь до заданной - треугольником, квадратом или трапецией.

6.1.1 Проектирование недостающей площади методом треугольников

Рассмотрим проектирование недостающей площади на примере II полигона

Р_пр = 0.45 га

Р_∆3-4-5 = S_3-4*S_4-5*sinß₄ = 65.12*39.73*sin103.86 = 2511.888 м²

Р_∆3-4-5 = 1255.94 м² = 0.13 га

Р_прип = Р_пр - Р_∆3-4-5 = 0.45 га - 0.13 га = 0.32 га

2Р_∆3-5-М = S_3-5*S_5-M*sinß_{15-M =} 2Pт_∆3-5-М / (S_3-5*sinß₁)

∆_3-5 = X₅ - X₃ = 960.14 - 1019.35 = - 59.21 м

∆_3-5 = Y₅ - Y₃ = 170.71 - 230.33 = - 59.62 м

r = 45.2º

α_3-5 = 180 + r = 225.2º

S_3-5 = 84.03 м

S_3-5 = 84.03 м_3-5 = 84.02 м

ß₁ = α_3-5 + 180 - α_{5-М (5-6)} = 225.2 + 180 - 349.6 = 55.6º

S_5-M = (2*0.32*10000) / (84.03*sin55.6) = 92.31 м

Находим координаты точки М:

∆X_5-M = S_5-M*cosα_{5-M (5-6)} = 90.79 м

∆Y_5-M = S_5-M*sinα_{5-M (5-6)} = - 16.66 м_M = X₅+∆X_5-M = 960.14+97.9 = 1050.93 м_M = Y₅+∆Y_5-M = 170.71 - 16,66 = 154,05 м

Р_∆3-5-М = X₃ (Y₅-Y_M) +X₅ (Y_M-Y₃) +X_M (Y₃-Y₅) = 1019.35 (170.71-154.05) +960.14 (154.05-230.33) +1050.93 (230.33-170.71) = 6399.3384 м²

Р_∆3-5-М = 3199.6692 м² = 0.32 га

6.1.2 Проектирование недостающей площади четырёхугольником

В полигоне I выделим участок под пашню площадью 0.65 га. Проектная линия должна проходить через точку 4.

Р_пр = 0.65 га

Р_А-В-1-2 = S_A-B*S_B-1*sinß_B+S_B-1*S_1-2*sinß₁+S_A-B*S_1-2*sin (ß_B+ß₁ - 180) = 59.75*50.98*sin143.18+50.98*121.05*sin49.15+121.05*59.75*sin (143.18+49.15-180) = 8037.996 м² = 0.4 га

Р_{при резке} = Р_пр - Р_А-В-1-2 = 0.65 - 0.4 = 0.25 га

2Р_4-А-2-М = S_4-A * S_A-2 * sinß₂ + S_A-2 * S_2-M * sinß₃ + S_4-A *S_2-M*sin (ß₂+ß₃ - 180)_2-M = (2P - S_4-A * S_A-2 * sinß₂) / (S_A-2 * sinß₃ + S_4-A * sin (ß₂+ß₃-180)

P_M-A-2-4 = S_M-2 * S_2-A * sinß₃ + S_2-A * S_A-4 * sinß₂ + S_M-2 * S_A-4 *sin (ß₂+ß₃ - 180)_M-2 = (2P - S_2-A * S_A-4 * sinß₂) / (S_2-A *sinß₃ + S_A-4 *sin (ß₂+ß₃ - 180)

∆X_2-A = X_A - X₂ = 321.96 - 360.98 = - 39.02 м

∆Y_2-A = Y_A - Y₂ = 117.32 - 161.75 = - 44.43 м

r = 48.71º

α_2-A = 180 + 48.71 = 228.71_2-A = 59.13_2-A = 59.13_2-A = 59.13

ß₂ = α_2-A + 180 - α_A-4 = 228.71 + 180 - 355.43 = 53.28º

∆X_A-4 = 58.53

∆Y_A-4 = 4.68

r = 4.57º

α_A-4 = 355.43

ß₃ = α_3-2 + 180 - α_2-A = 157.95+180-228.71 = 109.24º

S_М-2 = (5000-59.13*58.72*sin53.28) / (59.13*sin109.24+58.72*sin (109.24+58.28-180) = 30.18 м

∆Х_М-2 = S_M-2*cosα_{2-M (2-3)} = 30.18 * cos 337.95 = 27.97 м

∆Y_M-2 = S_M-2*sinα_{2-M (2-3)} = 30.18 * sin 337.95 = - 11.33 м

Х_М = Х₂+∆Х_М-2 = 388.95 м

Y_M= Y₂ +∆Y_M-2 = 150.42 м

Р_М-2-А-4 = 388.95* (161.75-112.64+360.98) * (117.32-150.32) +321.96* (112.64-161.75) +380.49* (150.42-117.32) = 3935.6599 м²

Р_М-2-А-4 = 1967.82995 м²= 0.2 га

6.1.3 Проектирование недостающей площади трапецией

В полигоне III выделим участок площадью 0.21 га

Проектная линия должна быть параллельной линии 4-12

Р_пр = 0.21 га

Р_∆11-12-4 = S_11-12*S_12-4*sinß₁₂ = 94.85*39.75*sin105.58 = 1334.387021 м²

Р_∆11-12-4 = 667, 194 м² = 0,067 га

∆Х_11-4 = Х_{4 -} X₁₁ = 30.95

∆Y_11-4 = Y₄ - Y₁₁ = 50.8= 58.65º

α_11-4 = r = 58.65º

S_11-4 = 59.49_11-4 = 59.49_11-4 = 59.48

α_12-4 = 93º

φ = α_11-4 + 180 - α_11-M = 58.65+180-178.43 = 60.22

∆Х_11-12 = Х₁₂ - X₄ = 2.08

∆Y_11-12 = Y₁₂ - Y₄ = - 30.7

r = 87º

α_11-12 = 360 - r - 87 = 273º

α_M-11 = 273º

σ = 178.43+180-273=85.43 º

ω = α_M-11+180-α_11-4=273+180-58.65

Находим длины

S_4-M=S_11-4/sin σ - sin ω

S_M-11= S_11-4/sin σ*sin φ = 59.49/sin85.43*sin60.22 = 51.80 м_4-M=33.67 м

P_∆4-M-11 = S_4-M * S_M-11 * sin σ = 33.67*51.80*sin85.43 = 1738.561023 м²

Р = 0,087 га

Р_пр = 0,21 га

Р₁ = Р_∆11-12-4 + Р_4-М-11 = 0,067 га + 0,087 га = 0,15 га

Р_{при резке} = Р_{пр -} Р₁ = 0,21 - 0,15 = 0,06 га

2Р = (S_11-M - S_O-K) / (ctgα+ctgß)

2P* (ctgα+ctgß) = S_11-M² - S_O-K²

S_O-K = √ (S_11-M ² - 2Р * (ctgα+ctgß))

S_O-K = √ (51.80^{2 -} 1200 (ctg84,61+ctg94,57))

α = α_10-11 + 180 - α_{11-М (12-4)} = 84,61_O-K = √ (2683.24 - 17.3047416) = 51.63 м= 2Р_2/ (S_11-M+S_O-K) = 1200/103.18 = 11.63 м

MK = 11.67 м

11-O = h / sinα = 11.63/sin86.41 = 11.68 м

Находим координаты точки M

∆Х_4-М = ( (Y₁₁ - Y₄) - (X₁₁ - X₄) * tgα_12-4) / (tgα_{4-A -} tgα_12-4)

∆Х_4-М = ( (58.64 - 109.44) - (1061.35 - 1092.30) *tg93) / (tg178.43 - tg93)

∆Х_4-М = - 33.661 м

∆Y_4-М = ∆Х * tg_4-A

∆Y_4-M = 0.923_M = X₄ + ∆Х_4-M = 1092.30 - 33.661 = 1058.64 м_M = Y₄ + ∆Y_4-M = 109.44 + 0.923 = 110.36 м

6.2 Графический способ

Участки часто проектируют графическим способом путем вычисления площади предварительно спроектированного участка и последующего проектирования недостающей или избыточной площади к заданной. Предварительно спроектированную площадь в зависимости от наличия или отсутствия геодезических данных по границам определяют планиметром или аналитическим способом. Недостающую или избыточную площадь проектируют треугольником или трапецией.

Проектирование треугольником выполняют, когда проектная линия должна проходить через определенную точку. Тогда по заданной площади и известной высоте (основанию) определяют неизвестное основание (высоту).

Следует отметить, что с какой относительной погрешностью измерена высота, с такой же относительной погрешностью будет вычислено и основание a (и наоборот).

Проектирование трапецией производят, если проектная линия должна проходить параллельно заданному направлению. По заданной площади и длине средней линии или по сумме оснований (что предпочтительнее, точнее), сразу получаем длины оснований и, тогда, спроектировав участок на глаз, определяют по плану сумму длин его оснований, вычисляют высоту h¢ и по ней более точно снова определяют сумму оснований, затем h². Вычисления прекращаются, когда поля, усадебные участки, имеющие длинные параллельные стороны, при графическом способе проектируют, как правило, трапециями.

В частном случае, когда гон или квартал имеет форму треугольника, ширину участков получают пропорционально их площадям. Если же они имеют форму трапеции, каждый участок проектируют самостоятельно. Заданную площадь каждого участка делят на свою среднюю линию или на полу сумму оснований трапеции.

Разница в результатах будет меньше на плане более крупного масштаба.

Графическое проектирование участков в многоугольных фигурах начинают с предварительного вычисления площадей трапеций, на которые разбивают фигуры.

6.3 Механический способ

Графический и аналитический способы удобны лишь в случае, когда гоны (линии) и участки имеют небольшое число поворотов и проектирование не требует больших затрат времени на производство вычислений. При большой изломанности контуров землепользований применение планиметра делает процесс проектирования более простым (но менее точным), вследствие чего механический способ проектирования участков при помощи планиметра наиболее распространен, а для многих районов нашей страны является единственно возможным.

Проектирование участков не выполняют только планиметром, так как этот прибор не дает возможности по заданной площади и одному линейному измерению определить другое линейное измерение. Поэтому возникает необходимость проектировать участки последовательными приближениями до тех пор, пока величина недостающей или излишней площади до заданной не будет превышать допустимой погрешности вычисления площади.

Во избежание большого числа приближений при проектировании механический способ комбинируют с графическим, т.е. планиметром определяют площадь участка, спроектированного на глаз, а недостающую или избыточную площадь проектируют графически треугольником или трапецией. Тогда погрешность проектирования участка будет складываться из погрешности определения предварительно спроектированной площади планиметром и погрешности проектирования недостающей или избыточной площади графическим способом.

Так как точность определения площади планиметром меньше, чем графическим способом, и погрешности проектирования недостающих или избыточных участков вносят малую долю в общую погрешность, то погрешности проектирования площадей механическим способом в сочетании с графическим можно считать примерно равными погрешностям определения площадей планиметром и рассчитывать по соответствующим формулам. Площадь определяют при помощи отъюстированного планиметра двукратным обводом.

7. Перенесение проекта в натуру

Проект землеустройства в натуру переносят способом промеров - мерным прибором (оптические и электрооптические дальномеры, длинномер, лента, рулетка), угломерным способом - теодолитом и мерным прибором, графическим способом - мензулой.

Геодезической опорой для перенесения проекта в натуру служат пункты всех видов геодезических сетей (триангуляции, полигонометрии, теодолитных ходов), а при отсутствии их - твердые контурные точки: вершины углов поворотов дорог, канав, строений, угодий и др.

Если проектирование производилось аналитическим способом, то перенесение проекта в натуру производится способом промеров или угломерным способом и геодезической опорой служат пункты геодезических сетей.

Если проектирование производилось графическим и механическим способами, то проект в натуру переносят любым из способов и в качестве геодезической опоры используются как пункты геодезических сетей, так и твердые контурные точки.

Наиболее точным является способ промеров и угломерный способ, если опорой для перенесения проекта служат пункты геодезических сетей, так как твердые контурные точки всегда обладают большими ошибками положения, а графический способ перенесения проекта по точности соответствует ошибкам положения контурных точек. Поэтому перед перенесением проекта часто прокладывают теодолитные ходы, служащие геодезической опорой при перенесении проекта в натуру.

Перенесению проекта в натуру предшествует подготовительная работа, завершающаяся составлением разбивочного (рабочего) чертежа, на который наносят все используемые пункты геодезической опоры или твердые контурные точки, границы спроектированных участков и проектные точки, надписывают все промеры линий (длины проектных отрезков) и углы, которые строят в натуре при перенесении проекта.

Если проектирование участков производилось аналитическим способом, то указанные промеры и величины углов получаются вычислением в процессе проектирования, и они записываются на проектном плане и на разбивочном чертеже.

Если проектирование производилось графическим и механическим способами, то на проектный план и разбивочный чертеж также записывают все промеры, получающиеся вычислением в процессе проектирования. Если же эти промеры в процессе проектирования не вычислялись, то их определяют графически по плану, с учетом деформации бумаги, и увязывают в длине ранее измеренной линии.

Для перенесения проекта в натуру мензулой на разбивочный чертеж наносят только пункты геодезической опоры, твердые контурные точки, границы спроектированных участков и проектные точки, так как промеры, необходимые для перенесения проекта, определяют графически по плану и записывают их на разбивочном чертеже в процессе перенесения проекта.

Разбивочным чертежом предусматривается порядок перенесения проекта, последовательность, направление промеров между точками, служащими опорой при перенесении проекта, поэтому на проектном плане промеры записываются против сторон участков, а на разбивочном чертеже - против проектных точек нарастающим итогом от начальной до конечной опорной точки, на которые опирается проектная линия.

Если проектирование участков производилось графическим и механическим способами, а перенесение проекта производится угломерным способом, то проектные стороны хода и углы хода вычисляют по графическим координатам проектных точек и аналитическим координатам начальной и конечной точек проектного хода (решая обратные геодезические задачи), на которые он опирается. В этом случае ошибки графического определения координат проектных точек, а, следовательно, ошибки вычисления сторон и углов хода не оказывают влияния на его линейную невязку при перенесении проекта в натуру.

Полевой процесс перенесения проекта в натуру состоит в откладывании (отмеривании) на местности проектных промеров (отрезков) от опорных точек и построении проектных углов, записанных на разбивочном чертеже или определяемых по плану при перенесении проекта в натуру мензулой.

Если проектирование производилось аналитическим способом или в натуру переносится проектный ход, то при откладывании промеров в них вводят со знаком плюс поправки за наклон местности, превышающий 1,5°. Поправки вычисляют по формуле:

∆d=1,5ʋ2∙S/10000=i2∙S/2=h2/2S,

где ʋ - угол наклона местности (град.), измеряемый эклиметром или теодолитом;- длина промера, в который вводится поправка;- уклон местности;- превышение между концами промера, определяемое по горизонталям плана.

Исправленные за наклон промеры полезно вычислять заранее при составлении разбивочного чертежа, записав их на нем в скобках.

Расхождение результата измерения линии между пунктами геодезической сети при перенесении проекта в натуру с ее известным значением не должно быть более допускаемого между двумя измерениями для данного мерного прибора.

Если проектирование производилось аналитическим способом, то в положения проектных точек на линии вводятся поправки за полученное расхождение пропорционально расстояниям от начала линии до проектной точки, в положении которой вводится поправка.

Если проектная линия опирается на твердые контурные точки, то расхождение результата измерения при перенесении проекта в натуру с измеренным по плану не должно быть более 1 мм на плане. Если это расхождение превышает 0,2 мм на плане, то в положения проектных точек вводятся поправки за полученное расхождение пропорционально расстояниям от начала линии до проектной точки, в положение которой вводится поправка

Линейная невязка в проектном теодолитном ходе, построенном между пунктами геодезической сети, допускается не более 1/1000 от длины хода. Ход на местности увязывают способом параллельных линий. Для этого помимо линейной невязки при помощи буссоли измеряют азимут невязки (с точностью до градуса) и поэтому азимуту вводят поправки в положения точек хода пропорционально расстояниям от начала хода до точки, в положение которой вводится поправка.

Все получаемые расхождения в измерениях проектных линий и линейные невязки в проектных ходах записываются на разбивочном чертеже.

Для перенесения проекта в натуру подготавливают геодезические данные - направления и расстояния от имеющихся на плане опорных пунктов до проектных точек. При этом опорными пунктами служат поворотные точки теодолитных ходов, проложенных по границам землепользования, населенных пунктов, контурам ситуации и дорогам, а также вершины углов ситуационных контуров, четко выраженных на планах.

Данные для перенесения проекта выписывают на рабочий чертеж перенесения проекта, который составляют на копии плана организации территории, при этом промеры по прямым линиям подписывают возле проектных точек нарастающим итогом от начала прямой (опорной точки) в направлении движения ленты,

В зависимости от условий местности и наличия опорных точек перенесение проекта в натуру можно производить следующими способами: методом промеров с помощью мерной ленты; теодолитом и мерной лентой; при помощи мензулы.

При перенесении проекта в натуру с помощью мерной ленты линии между опорными точками провешивают по ним, производят необходимые измерения, при этом проектные линии между опорными точками измеряют от начала до конца. Если проектная линия является ломаной, то в натуру ее переносят путем восстановления перпендикуляров от магистральной линии между опорными точками, прокладываемой вблизи проектной.

Величины перпендикуляров от магистральной линии до изломов проектной и расстояния между основаниями перпендикуляров определяют по плану графически. Перпендикуляры до 20 м восстанавливают на глаз, а более 20 м - с помощью эккера. Перпендикуляры длиннее 100 м при масштабе плана 1: 10000 и 200 м при масштабе плана 1: 25000 не допускаются. Длины перпендикуляров определяют мерной лентой и рулеткой.

Перенесение проекта в натуру при помощи теодолита и мерной ленты применяют на закрытой занесенной местности со сложным рельефом, а также когда проектные границы представляют собой ломаные линии и при их построении требуется измерять углы.

Перенесение проекта в натуру мензулой и кипрегелем-дальномером производят по планам мензульной съемки. Если ход имеет невязку, не превышающую 1/300 его периметра, то ее увязывают методом параллельных линий.

Если проект внутрихозяйственного землеустройства составлен на основе материалов аэрофотосъемки, то в качестве опорных точек для перенесения проекта в натуру используют углы поворота границ контуров ситуации, а именно: пересечения дорог, каналов, лесополос, пересечения контуров, имеющих разный растительный покров, а также предметы местности, четко отображенные на фотопланах.

Во всех случаях перенесения проекта в натуру расхождения между значениями длины линии, измеренной в натуре, и данными проектного плана не должны превышать:

: 1000, если линию измеряли ранее при проложении теодолитных ходов или вычисляли по аналитическим координатам;

,5 мм на плане, если линию определяли графически по плану между точками теодолитных ходов;

,7 мм на плане, если линию определяли графически по плану между контурными точками.

При перенесении в натуру проектных линий, проходящих через препятствия (стога сена, скирды, соломы, дома и пр.), эти препятствия обходят, используя различные геометрические построения.

Углы проектных участков закрепляют в натуре граничными знаками установленного образца. Их закапывают в створе между точками линий, на которые опираются границы полей, или в створе суходольных границ контуров ситуации. Границы проектных участков, опирающиеся на обе стороны дорог общего пользования или внутрихозяйственной магистральной дороги, закрепляют столбами, которые устанавливают каждый на своей стороне дороги.

Границы полей севооборотов и других проектных участков пропахивают в одну борозду. Дороги и скотопрогоны пропахивают с обеих сторон.

Границы проектных участков, совмещенных с границами контуров ситуации (овраги, речки, лесополосы, леса и пр.), не пропахивают. В этом случае столбы устанавливают только на концах проектных линий, на пересечении их с границами этих контуров.

В условиях сложного рельефа перед пропашкой границы проектных линий провешивают из середины.

Заключение

В данном курсовом проекте были освоены способы определения площадей, проектирования участков и подготовки данных для перенесения проектов в натуру на основе индивидуальных данных.

Площадь угодий определяли аналитическим, графическим и механическим способами.

Также проводили спрямление границ, так как границы были значительно изломаны, а это затрудняет правильное использование прилегающих участков земли.

Список литературы

1. Геодезические работа при землеустройстве / А.В. Маслов, А.Г. Юнусов, Г.И. Горохов. М.: Недра. 1990.

. Геодезические работы при землеустройстве: методические указания / А.В. Лянденбурская, В.В. Лянденбурский. - Пенза: РИО ПГСХА, 2010. - 53 с.

. Геодезия/ А.В. Маслов, А.В. Гордеев, Ю.Г. Батраков. М.: Недра, 1993.

. Неумывакин Ю.К., Смирнов А.С., Практикум по геодезии. М.: Недра, 1995.