|
ЭДС, В
|
Сопротивление, Ом
|
|
Е1
|
Е2
|
Е3
|
R1
|
R2
|
R3
|
R4
|
R5
|
R6
|
|
14
|
25
|
28
|
5
|
2
|
8
|
2
|
2
|
6
|
2. Расчет схемы
Расчет схемы по законам Кирхгофа
Обозначим ток в ветвях I1, I2…,I6 выбирая индексы тока соответственно номерам приемников, стоящих в
этих ветвях.
Данный метод подразумевает
составление системы уравнений, позволяющих определить значения тока в ветвях
непосредственно по первому и второму законам Кирхгофа.
Количество неизвестных токов
определяет порядок сложности цепи N и равно количеству ветвей. В рассматриваемом примере: в=N=6.
Следовательно, необходимо составить
систему из шести уравнений.
По первому закону Кирхгофа
составляется количество уравнений на одно меньше, чем узлов. Для данной схемы у=4.
Следовательно, по первому закону Кирхгофа составляем:
NI = y-1;
NI=4-1=3.
Выбираем три узла - 1,2,3, для
которых записываем уравнения, соответственно, по первому закону Кирхгофа:
() 1: I3 +I6 -I4 = 0 (1)
() 2: - I6 + I1 + I5 = 0 (2)
() 3: I4 - I2 - I5 = 0 (3)
По второму закону Кирхгофа
составляется NII = N - NI уравнений.
Следовательно, для данной схемы NII = 3.
Выбираем три независимых контура I-III (рис. 3) так, чтобы
каждый последующий контур содержал хотя бы одну новую ветвь.
Принимаем направления обхода
контуров I-III - по часовой стрелке.
Cоставляем уравнения по второму закону Кирхгофа:
I4R4
+I5R5 + I6R6 = 0 (4)5R5
+ I2R2 + I1R1 = E1 - E2
(5)3R3 + I2R2 + I4R4
= - E2 + E3 (6)
Полная система уравнений примет вид:
I3 + I6
- I4 = 06 + I1 + I5 = 04 -
I2 - I5 = 0 (7)
I4R4
+ I5R5 + I6R6 = 05R5
+ I2R2 + I1R1 = E1 - E23R3
+ I2R2 + I4R4 = - E2 + E3
Решение системы уравнений (7) с
помощью математического редактора Mathcad, дает искомые значения тока в ветвях цепи. Знак «минус» указывает
на то, что выбранное на схеме направление тока не совпадает с его реальным
направлением. Результаты сведены в табл. 2.
Баланс мощности
Для проверки правильности
выполненных расчетов составляем баланс мощности. В любой замкнутой
электрической цепи сумма значений мощности, отдаваемой источниками, равна сумме
значений мощности, потребляемой приемниками:
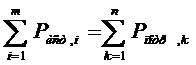 (8)
(8)
Для рассматриваемой схемы,
содержащей три источника (m=3)
Pист
= I1E1 - I2E2 +I3E3;
(9)
Pист = (-1,434) · 14 - (-0,879) ·25 +(0.555)·28 =17,44 (Вт).
Для потребителей:
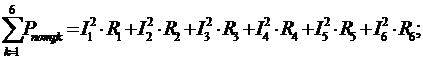 (10)
(10)
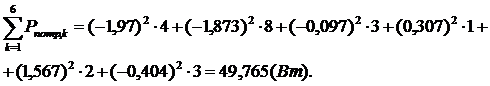

∑Pпотр,к=(-1,434)2
∙5 + (-0,879)2 ∙2 + (0,555)2 ∙8 +
(0,157)2 ∙ 2 +(1,036)2 ∙2 +
(-0,398)2 ∙6
= 17,44 (Вт)
Баланс мощности для
рассчитываемой схемы:
17,44 Вт = 17,44 Вт
Баланс мощности
выполняется, следовательно, расчет токов по законам Кирхгофа выполнен верно.
Вычислим относительную погрешность
измерения:
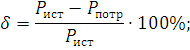
цепь ток сложный кирхгофа
В инженерных расчетах отличие правой
части баланса от левой допускается не более чем на 3%:
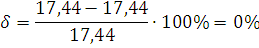
Расчет схемы методом контурных токов
Для данной схемы NII = 3. Выбираем те
же контуры, которые рассматривались в предыдущем методе, обозначаем направления
контурных токов J1, J2, J3 (рис. 4) и
составляем расчетные уравнения:
I: J1(R4 + R5 + R6) - J2R5 - J3R4 = 0 (11)
II: J2(R1 + R2 + R5) - J1R5 + J3R2 = E2 - E1 (12)
III: J3(R3
+ R2 + R4) +J1R3 + J2R2
= E2 - E3 (13)
Запишем систему в упорядоченном
виде:
J1(R4 + R5 + R6) - J2R5 - J3R4 =0
J1R5 + J2(R1 + R2 + R5) +J3R2 = E2 - E1 (14)
J1R4
+ J2R2 + J3(R3+ R2 + R4)
= E2 - E3
В матричной форме:
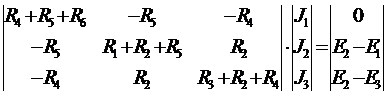 (15)
(15)
Полученная матрица
должна быть симметричной. Так можно проверить правильность составления системы.
Решение системы уравнений (15) с
помощью математического редактора Mathcad дает искомые значения контурных токов:
J1 = -0,257 (A); J2 = -1,281 (A); J3 = -0,063 (A).
Реальные токи в ветвях цепи находим
с учетом направлений протекающих по ветвям токов:
I1 = - J2
= -1,281 (A) (16)2 = J3 +J2 = -1,287 (A)
(17)
I3 = - J3
= -0,063 (A) (18)
I4 = J1 +
J2 = -1,538 (A) (19)5 = J1-J2 =1,023
(A) (20)
I6 = J1
= -0,257 (A) (21)
Результаты расчета, полученные
методом контурных токов (см. табл. 2), совпадают с результатами расчета по
законам Кирхгофа.
Таблица 2. Результат аналитического
расчета и моделирования схемы
|
Метод получения результата
|
Сила тока Ii, A
|
|
I1
|
I2
|
I3
|
I4
|
I5
|
I6
|
|
Расчет по законам Кирхгофа
|
3,038
|
0,356
|
-3,394
|
1,196
|
-0,84
|
-2,198
|
|
Расчет методом контурных токов
|
3,038
|
0,356
|
-3,394
|
1,196
|
-0,84
|
-2,198
|
|
Моделирование
|
3,037
|
0,356
|
-3,393
|
1,196
|
-0,839
|
-2,197
|
Вывод: Составленный по результатам
расчета баланс мощности выполняется и данные моделирования приблизительно равны
данным аналитического расчета, следовательно расчет сложной электрической цепи
выполнен верно.